Abstract
Correspondence analysis has frequently been used for codon usage studies but this method is often misused. Because amino acid composition exerts constraints on codon usage, it is common to use tables containing relative codon frequencies (or ratios of frequencies) instead of simple codon counts to get rid of these amino acid biases. The problem is that some important properties of correspondence analysis, such as rows weighting, are lost in the process. Moreover, the use of relative measures sometimes introduces other biases and often diminishes the quantity of information to analyse, occasionally resulting in interpretation errors. For instance, in the case of an organism such as Borrelia burgdorferi, the use of relative measures led to the conclusion that there was no translational selection, while analyses based on codon counts show that there is a possibility of a selective effect at that level. In this paper, we expose these problems and we propose alternative strategies to correspondence analysis for studying codon usage biases when amino acid composition effects must be removed.
INTRODUCTION
Since the precursor work of Grantham et al. (1) on preferential codon usage among different organisms, correspondence analysis (CA) has often been used to analyse codon usage. Multivariate statistical methods like CA are particularly well adapted to the multi-dimensional nature of the data. CA was (and still is) very popular for analysing codon usage biases in microbial genomes: it has been applied to study species like Escherichia coli (2,3), Bacillus subtilis (4–8), Borrelia burgdorferi (9,10), Chlamydia trachomatis (11), Mycoplasma genitalium (12), Helicobacter pylori (13) and Pseudomonas aeruginosa (14). The result most frequently observed when studying codon preferences in unicellular organisms is that translational selection is the main driving force and that highly expressed genes tend to preferentially use codons corresponding to the most abundant tRNAs in the cell (15–18). For bacteria like B.burgdorferi and C.trachomatis, it seems that replicational and/or strand-specific mutational biases are the main sources of variation in codon composition (9–11), while hydropathy of the encoded proteins is one of the major factors shaping codon usage in Mycobacterium species (19).
CA has also been used in other bioinformatics studies over the past 15 years. For example, it has been used for predicting coding regions in prokaryotes and eukaryotes (20), for studying the evolution of repeated sequences in primates (21) and in rodents (22), for analysing trends in amino acid composition in E.coli (23) and for detecting sequencing errors like frameshifts (24).
CA is designed for use with data tables containing counts (25), but in most of the papers dealing with codon usage the tables used contain relative measures. The reason invoked for using these measures instead of counts is to avoid biases linked to amino acid composition that may mask the effects that are directly linked to codon preferences. For example, integral membrane proteins that are highly enriched in hydrophobic amino acids will have a codon composition biased toward their corresponding codons. We show that the use of such kinds of modified data tables strongly affects the results produced by CA. We give different examples taken from the genomes of B.subtilis, E.coli, B.burgdorferi and M.genitalium. As the desire to remove amino acid effects is justified in some cases, we propose alternative strategies for the use of CA to study codon usage in microbial genomes.
MATERIALS AND METHODS
Correspondence analysis
Strictly speaking, the data that should be used with CA are contingency tables (25). In such tables, rows and columns play equivalent roles and can be exchanged. By extension of its properties, CA can be applied to tables containing counts (i.e. absolute frequencies). A limitation is that the profiles (rows and columns sums) of these tables must have a meaning. This rule is guided by the fact that CA weights rows and columns using these profiles, as described below. Let X = [xij] be our original data table with n rows and p columns. In the case of codon composition data, the rows will correspond to the genes and the columns to the 61 sense codons (in the case of an organism using the standard genetic code). We denote the row and column sums of X as xi. and x.j, respectively, x.. corresponding to the grand total. The relative contribution or weight of row i to the total variation in the data set is then denoted ri and is calculated as:
ri = xi./x.. 1 ≤ i ≤ n1
while the relative contribution of column j is denoted as cj and is calculated as:
cj = x.j/x.. 1 ≤ j ≤ p2
Similarly, the contribution of each individual element of X to the total variation in the data set is denoted as fij and is calculated as:
fij = xij/x..3
The above calculations produce two vectors R = [ri] and C = [cj] of length n and p, respectively, and one matrix F = [fij] of dimension n × p. We use these vectors and this matrix to determine the values of yij, which are calculated as:
yij = [fij/(ricj)] – 14
These values define the matrix Y = [yij], which is the one used for CA computation. When n > p (which is the case when computing CA on codon usage), the principle of the method is the diagonalisation of a p × p matrix A containing χ2 distances and defined as:
A = Dp1/2YtDnYDp1/25
where Dp is a p × p matrix with the elements of vector C along the diagonal and 0 elsewhere. Similarly, Dn is an n × n matrix with the elements of R on the diagonal and 0 elsewhere. Diagonalisation of A produce p eigenvalues (at least one of which will be 0) and eigenvectors. These eigenvectors are ranked according to their eigenvalues and the eigenvalue for an eigenvector indicates its importance in the analysis.
The results of a CA are viewed graphically, usually by plotting the coordinates of all genes along the first eigenvectors. Genes that are strongly associated as measured by their χ2 distances will lie in a similar direction from the origin.
Relative frequencies
In a few studies, the authors used relative frequencies to compute CA (3,7). These frequencies are defined as the ratio between the number of a given codon in a gene over the number of all the synonymous codons corresponding to the amino acid encoded. Let zij be the relative frequency of codon j in gene i. It can be computed as:
where the notation j′/Cl(j′) = k means that the sum is only for the columns of the table belonging to class k, this class gathering all the synonymous codons corresponding to the amino acid encoded by codon j. In the table Z = [zij] containing relative frequencies, the number of columns will be limited to 59 instead of 61, because there is only one codon (AUG and UGG, respectively) for methionine and tryptophan in organisms using the standard genetic code. The relative frequencies of these codons is equal to 1 for the genes containing at least one of them and is not defined for the genes containing no codon of that type. The cases of indetermination that exist when a given amino acid is not present in a gene are solved by giving a value equal to 1 over the number of synonymous codons for that amino acid, this for all the synonymous codons considered. Also, note that the row sum is the same for all rows and is equal to the number of classes of synonymous codons: zi. = 18, ∀i.
Relative synonymous codon usage
In almost all published papers using CA for codon usage studies, the data table contains relative synonymous codon usage (RSCU) values. This codon usage measure corresponds to the ratio between the observed number of a codon over its expected value under the hypothesis of a random distribution of all the synonymous codons encoding a given amino acid (26). With the same formalism as before, let wij be the RSCU value for codon j in gene i. It can be computed as:
where sk is the number of synonymous codons for class k. As with relative frequencies (and for the same reasons), a table containing RSCU values will be limited to 59 columns instead of 61. In the corresponding data table W = [wij], the row sum is the same for all rows and is equal to the number of synonymous codons: wi. = 59, ∀i.
Codon adaptation index
The codon adaptation index (CAI) is a univariate measure of synonymous codon usage (27). For a given gene, the value ai of this index is calculated as:
where ωj is the relative adaptiveness of codon j. This value is defined as the ratio between the frequency of codon j over the frequency of the major synonymous codon for the same amino acid, as estimated from examining a set of reference genes. Usually, this set is made up of highly expressed genes and, thus, the CAI is an estimator of gene expressivity through codon usage. For the purpose of this study, we used the original reference table established for E.coli with 27 putatively highly expressed genes (27).
Sequences
Sequences of the protein genes from the complete genomes studied in this paper have been extracted from the EMGLib database (28). To compute the CA on codon composition, we used only genes longer than 150 nt to minimise the influence of stochastic variations that may occur in small genes. To identify the axes discriminating highly expressed genes, we used ribosomal protein genes plus a set of 24 additional genes for which a high expression level has been determined experimentally in E.coli (29) and for which the CAI value was ≥0.55 (Table 1). For the species other than E.coli, we used as markers the orthologs identified by BLAST searches (E value ≤ 10–10) and sequence annotations scanning. This solution was preferred to the use of ribosomal protein genes alone, as this class of sequences may have a biased amino acid composition (30). The number of orthologs identified was equal to 15 in B.subtilis, 14 in M.tuberculosis, 11 in B.burgdorferi and 8 in M.genitalium.
Table 1. List of the 25 genes coding for proteins other than ribosomal proteins that have been used as indicators for high expression in the CAs computed in this study.
| Name | Product | CAI | Bs | Mt | Bb | Mg |
|---|---|---|---|---|---|---|
| acpP | Acyl carrier protein | 0.676 | + | – | + | – |
| ahpC | Alkyl hydroperoxide reductase | 0.804 | + | + | – | – |
| cspA | Cold shock-like protein CspA | 0.811 | + | + | – | – |
| cspC | Cold shock-like protein CspC | 0.695 | + | – | – | – |
| cspE | Cold shock-like protein CspE | 0.586 | – | – | – | – |
| eno | Enolase | 0.844 | + | + | + | + |
| fusA | Elongation factor G | 0.753 | + | + | + | + |
| gapA | Glyceraldehyde 3-phosphate dehydrogenase A | 0.840 | + | + | + | + |
| gpmA | Phosphoglycerate mutase 1 | 0.590 | – | + | + | – |
| hns | DNA-binding protein H-ns | 0.596 | – | – | – | – |
| hupA | DNA-binding protein Hu-α | 0.669 | + | + | – | – |
| icdA | Isocitrate dehydrogenase [NADP] | 0.579 | + | + | – | – |
| ilvC | Ketol-acid reductoisomerase | 0.598 | – | + | – | – |
| lpp | Major outer membrane lipoprotein | 0.856 | – | – | – | – |
| metK | S-adenosylmethionine synthetase | 0.626 | + | + | + | + |
| mopA | 60 kDa chaperonin | 0.797 | + | + | + | + |
| ompA | Outer membrane protein A | 0.791 | – | – | – | – |
| ompC | Outer membrane protein C | 0.824 | – | – | – | – |
| ompF | Outer membrane protein F | 0.667 | – | – | – | – |
| ppa | Inorganic pyrophosphatase | 0.664 | – | + | – | + |
| ptsH | Phosphocarrier protein Hpr | 0.642 | + | – | + | – |
| tig | Trigger factor | 0.739 | + | + | + | + |
| tufA | Elongation factor Tu | 0.822 | + | + | + | + |
| yjgF | Protein YjgF | 0.590 | + | – | – | – |
Name, name of the gene in E.coli; Product, protein encoded by the gene; CAI, CAI value in E.coli; Bs, Mt, Mg, Bb, presence (+) or absence (–) of an ortholog in B.subtilis, M.tuberculosis, M.genitalium and B.burgdorferi.
Computer programs
All computations presented in this paper have been realised using the CA module from the multivariate statistics package ADE-4 (31). This package runs on microcomputers under the MacOS (7.1 or higher) and Windows (95 or higher) operating systems. It may be downloaded from the Pôle Bioinformatique Lyonnais (PBIL) World Wide Web server at http://pbil.univ-lyon1.fr/ADE-4. A new version will soon be available under the form of a package for the R statistical computing environment.
RESULTS
Bacillus subtilis
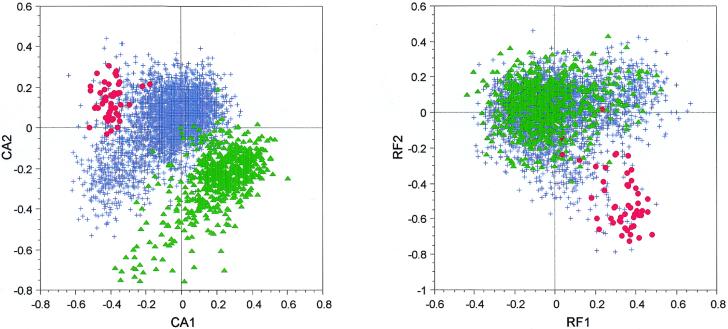
If we compute a CA on the codon composition of B.subtilis genes, using codon counts (CA/counts), we can see that the first axis separates genes coding for ribosomal proteins from the others (Fig. 1). This is a well-established result that has been shown many times: gene expressivity is the main force shaping codon usage in a lot of bacterial species, including B.subtilis (4,5,7). But the second axis separates another group of genes from the main group. If we compute the gravy score (a measure of hydrophobicity) (32) of all the proteins encoded by the genes used in our analysis, we see that the proteins separated from the others on the second axis have very high scores and, so, are hydrophobic. This is an example of amino acid bias, which is superimposed on a codon usage bias. If we use relative codon frequencies to compute the CA (CA/RF), as Moszer et al. did (7), this amino acid composition effect is removed from the analysis (Fig. 1).
Figure 1.
Factor maps obtained by crossing the first and second axes of two correspondence analyses computed on 4052 B.subtilis genes. CA1 × CA2 is the plot of the analysis computed on codon counts, while RF1 × RF2 is the plot of the analysis computed on relative frequencies. Red dots, highly expressed genes; green triangles, genes encoding proteins having a gravy score >0.3 (i.e. highly hydrophobic proteins); blue crosses, all other genes.
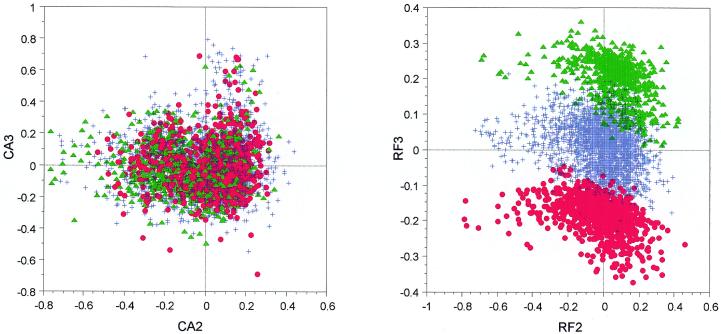
On the other hand, the plot obtained by crossing the second and third axes shows three distinct groups on the CA/RF when there is nothing comparable with the CA/counts (Fig. 2). This, we show, is a purely artifactual effect induced by the use of relative frequencies and linked to a single amino acid. Cysteine is the second rarest amino acid in B.subtilis, after tryptophan, and is encoded by two synonymous codons: UGC and UGU. A large number of B.subtilis proteins do not contain any cysteine (27%) or only one (21%) residue. For these genes, UGC/UGU codon counts are, respectively, equal to 0/0 and 1/0 or 0/1 and they are transformed by the relative frequencies method as 0.5/0.5, 1/0 and 0/1. After CA computation, genes are artificially separated into three classes: genes containing both UGC and UGU codons or none (the central class in Fig. 2), genes containing only UGC, and genes containing only UGU. Unexpectedly, the attempt to remove amino acid biases has introduced another bias associated with cysteine abundance.
Figure 2.
Factor maps obtained by crossing the second and third axes of two correspondence analyses computed on 4052 B.subtilis genes. CA2 × CA3 is the plot of the analysis computed on codon counts, while RF2 × RF3 is the plot of the analysis computed on relative frequencies. Red dots, genes where the relative frequencies of UGC/UGU codons are equal to 1/0; green triangles, genes where the relative frequencies of UGC/UGU codons are equal to 0/1; blue crosses, all other genes.
Mycobacterium tuberculosis H37Rv
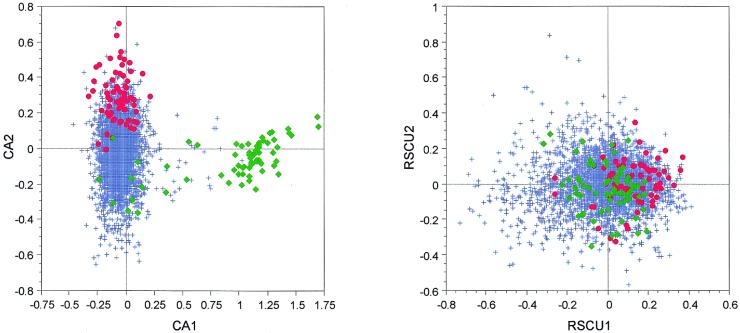
On the factor map obtained by crossing the first two axes of a CA/counts for all M.tuberculosis H37Rv genes we can see that the first axis clearly separates a small group of genes, while the second separates highly expressed genes (Fig. 3). If we take a look at the annotations of the genes having the highest positive scores on the first axis, we can see that almost all of them encode proteins belonging to the PE-PGRS family of M.tuberculosis. The proteins from this family are known to be highly enriched in glycine and alanine, these two amino acids sometimes representing up to 60% of protein content. If we now take a look at the CA computed with RSCU values (CA/RSCU), the highly expressed genes are weakly separated from the others on the first axis of the analysis while proteins belonging to the PE-PGRS family are spread all over the plot (Fig. 3). In this case, the use of RSCU values allows us to get rid of this trivial amino acid effect and the translational selection effect appears on the first axis of the CA, which may be considered as an advantage. On the other hand, the separation of the highly expressed genes from the others is weaker in the analysis computed on RSCU.
Figure 3.
Factor maps obtained by crossing the first and second axes of two correspondence analyses computed on 3912 M.tuberculosis (strain H37Rv) genes. CA1 × CA2 is the plot of the analysis computed on codon counts, while RSCU1 × RSCU2 is the plot of the analysis computed on RSCU values. Red dots, highly expressed genes; green diamonds, genes encoding proteins belonging to the PE-PGRS family; blue crosses, all other genes.
Escherichia coli K12
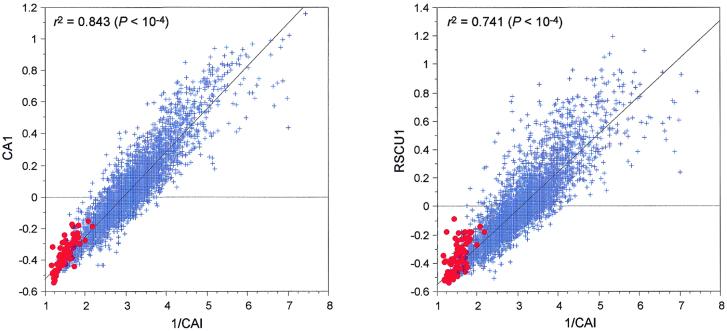
It has been well known for a long time that the main force shaping codon composition in E.coli is gene expressivity (33). These results have been confirmed by many studies using multivariate statistics approaches, including CA (2,3,34). The first axis of a CA computed on E.coli codon composition is thus highly correlated with the inverse of CAI values, either when using codon counts or RSCU values (Fig. 4). But if we compare the correlation coefficients obtained in these two analyses, we can see that the value is higher for the CA/counts, indeed, in this case r2 = 0.843 (P < 10–4), while r2 = 0.741 (P < 10–4) for the CA/RSCU. If we get rid of the amino acid effect, we remove information from the original data table and the correlation with gene expressivity measured by CAI is significantly lowered. This is understandable if we take into account the fact that amino acid composition is also biased relative to gene expressivity in E.coli (23).
Figure 4.
Regression plots between the factor scores on the first axes of two correspondence analyses computed on 4254 E.coli (strain K12) genes and the inverse of their respective CAI values. 1/CAI × CA1 is the plot of the analysis computed on codon counts, while 1/CAI × RSCU1 is the plot of the analysis computed on RSCU values. Red dots, highly expressed genes; blue crosses, all other genes.
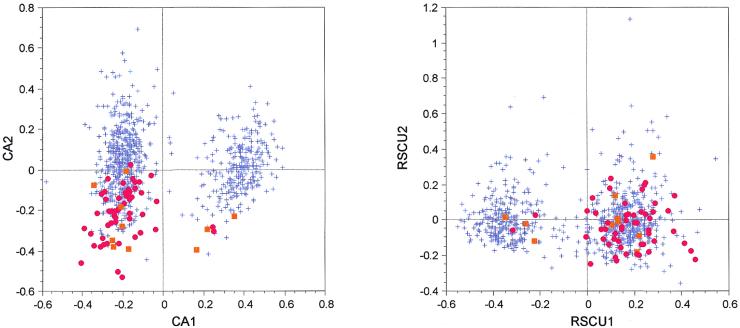
Borrelia burgdorferi
The main trend in codon usage in B.burgdorferi is linked to strand asymmetries that have been caused by selective pressures at the replicational and transcriptional levels (9). To study that effect, the author used a CA/RSCU. The plots for CA/counts and CA/RSCU for B.burgdorferi genes are shown in Figure 5. On the first axis both analyses split the genes into two groups: those located on the leading strand and those located on the lagging strand. But, in the case of CA/RSCU, there is almost no difference between highly expressed genes and the other genes. This result led two independent groups to conclude that there was no translational selection in this organism (9,10), but this affirmation seems unlikely as a separation is visible on the second axis of the CA/counts, with the highly expressed genes (coding for ribosomal and for other proteins) having highly negative scores on this axis. A t-test comparing the distribution of scores for highly expressed genes versus the other genes on the second axis is highly significant (t = 12.049, P < 10–4) in the case of CA/counts, while it is not significant in the case of CA/RSCU (t = 1.640, P = 0.101).
Figure 5.
Factor maps obtained by crossing the first and second axes of two correspondence analyses computed on 821 B.burgdorferi genes. CA1 × CA2 is the plot of the analysis computed on codon counts, while RSCU1 × RSCU2 is the plot of the analysis computed on RSCU values. Red dots, ribosomal protein genes; orange squares, other highly expressed genes (see Table 1); blue crosses, all other genes.
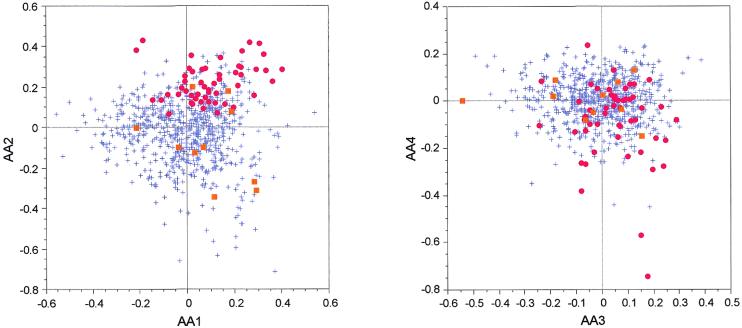
To be sure that the grouping of our set of highly expressed genes on the second axis of CA/counts is not due to a bias in protein composition, we computed a CA on the amino acid counts (CA/AA) of the proteins encoded by B.burgdorferi genes. On the two factor maps obtained by crossing the first four axes of this analysis, the ribosomal proteins cluster together while the other proteins encoded by highly expressed genes are spread all over the cloud (Fig. 6). Moreover, there is no correlation between any of the first four axes of CA/AA and the second axis of our CA/counts.
Figure 6.
Factor maps obtained by crossing the first four axes of a correspondence analysis computed on 821 B.burgdorferi proteins. AA1 × AA2 is the plot crossing the first and second axes, while AA3 × AA4 is the plot crossing the third and fourth axes. Red dots, ribosomal protein genes; orange squares, other highly expressed genes (see Table 1); blue crosses, all other genes.
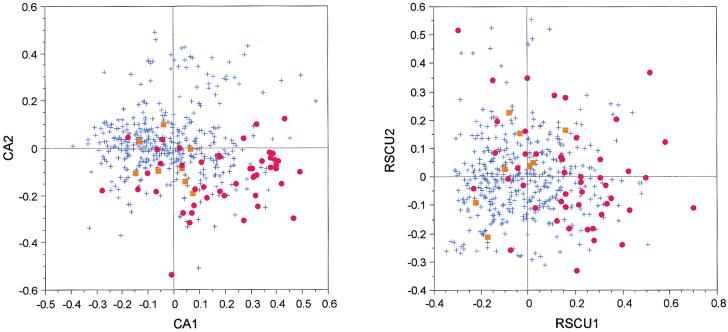
Mycoplasma genitalium
On the factor map obtained by crossing the first two axes of the CA/counts in M.genitalium, a visual inspection shows that the highly expressed genes are separated from the others by both axes (Fig. 7). But, on the CA/RSCU, this trend is almost invisible. The tests comparing the distributions of the score between highly expressed genes and the other genes are highly significant for the first (t = 7.403, P < 10–4) and second (t = 6.385, P < 10–4) axes of the CA/counts. For the CA/RSCU, the test for the distributions is also highly significant (t = 6.318, P < 10–4) on the first axis, but it is not significant (t = 0.883, P = 0.378) on the second axis. In both analyses the first axis is linked to the GC content of the genes, highly expressed genes having a tendency to use GC-ending synonymous codons more frequently, this for almost all amino acids (Table 2). Indeed, except for glutamine, aspartic acid, cysteine and phenylalanine, the ratio of GC-ending synonymous codons is always higher in highly expressed genes. Note that no effect linked to compositional strand asymmetry was detected in the two CAs. Lastly, to estimate if the grouping of highly expressed genes could be linked with protein composition bias, we computed a CA/AA and found that the second axis of the CA/counts is significantly correlated with the first axis of CA/AA (r2 = 0.851, P < 10–4).
Figure 7.
Factor maps obtained by crossing the first and second axes of two correspondence analyses computed on 466 M.genitalium genes. CA1 × CA2 is the plot of the analysis computed on codon counts, while RSCU1 × RSCU2 is the plot of the analysis computed on RSCU values. Red dots, ribosomal protein genes; orange squares, other highly expressed genes (see Table 1); blue crosses, all other genes.
Table 2. Percentage of GC-ending synonymous codons for each amino acid in M.genitalium genes.
| Amino acid | High | Others |
|---|---|---|
| Arg | 30.5 | 28.0 |
| Leu | 23.0 | 22.2 |
| Ser | 24.1 | 17.8 |
| Thr | 30.0 | 22.1 |
| Pro | 21.9 | 15.1 |
| Ala | 15.4 | 12.3 |
| Gly | 27.9 | 25.5 |
| Val | 22.5 | 17.1 |
| Lys | 30.8 | 25.7 |
| Asn | 48.3 | 38.6 |
| Glna | 17.1 | 18.8 |
| His | 52.4 | 34.8 |
| Glu | 24.5 | 19.7 |
| Aspa | 13.9 | 13.9 |
| Tyr | 33.3 | 25.8 |
| Cysa | 20.0 | 20.0 |
| Phea | 12.5 | 13.5 |
| Trp | 50.0 | 35.2 |
| Ile | 29.2 | 21.8 |
High, highly expressed genes; Others, all other genes.
aThe GC-ending codons are less abundant in highly expressed genes than in the other genes.
Even if the second axis of CA/counts is related to amino acid composition, it seems that there is a trend grouping highly expressed genes on the basis of their GC content. Indeed, the distribution of the scores on the first axis of CA/RSCU (which completely removes the amino acid effect) is also significantly different for this group of genes. Taking into account the fact that M.genitalium has an AT-rich genome, this enrichment in GC for the highly expressed genes may be linked to a selective effect. It seems difficult then to completely reject the possibility of a translation selection effect, as was proposed in a previously published paper (12).
DISCUSSION
The preceding results demonstrate that the advantages provided in some cases by the use of relative frequencies or RSCU values are often counter-balanced by their negative effects. Indeed, even if relative measures allow us to avoid some amino acid biases (e.g. as in B.subtilis and M.tuberculosis), they frequently blur the information, so that an effect such as translational selection may disappear from the analysis. In some cases they even introduce other biases linked to amino acid composition.
Another problem is the fact that data tables containing relative frequencies or RSCU values are not really suited for CA, even if it is technically possible to use them. Other multivariate statistical methods exist that can be applied to codon usage data, and we shall now discuss these possibilities. The simplest alternative option would be to perform a principal component analysis (PCA) on relative frequencies or on RSCU values. This method has already been applied to different codon usage measures (18,19,34), but still not to RSCU values. Another alternative option suited to tables containing relative frequencies (but not RSCU values) is fuzzy correspondence analysis (FCA) (35). This method was especially designed for fuzzy categorical data. With FCA, variables are represented by modalities, the sum of all modalities for a given variable being equal to 1. This is exactly the case of tables with relative frequencies of synonymous codons (equation 6).
However, even if we use methods that are much more suited to relative frequencies or RSCU values, this will not remove the fact that the transformation performed on the original data (i.e. the absolute frequencies) decreases the amount of information and introduces new biases. For instance, a PCA or a FCA computed on B.subtilis relative codon frequencies still gives the UGC/UGU bias linked to the rarity of cysteine in the proteins of this organism. A solution would be to remove these codons from the analyses when studying organisms in which cysteine is not abundant, but this problem may arise for other rare amino acids encoded by two codons (e.g. tryptophan in Mycoplasma species).
To conclude, we suggest that a good solution to these problems would be, as in all the analyses presented here, to compute in parallel CA on counts and on relative frequencies and then to compare the results. This approach has already been successfully used in studies devoted to codon usage in H.pylori (13) and on transposable elements (36). On the other hand, the variety of multivariate statistical methods available is much greater than the few that are systematically used for biological sequence studies. Depending on the aims of the study, methods more adapted than CA may be used. For instance, among the methods implemented in the ADE-4 package (31) are: non-centred/decentred PCA or CA, fuzzy PCA or CA, internal CA, non-symmetric CA, between and within class PCA, CA or multiple correspondence analysis (MCA), discriminant analysis on PCA, CA or MCA, tens of variants of two table coupling methods such as co-inertia analysis-based methods, canonical correlation analysis, canonical CA and redundancy analysis, plus at least 10 k-table analysis methods, without taking into account the various centring and standardisation options.
Acknowledgments
ACKNOWLEDGEMENTS
Thanks are due to Manolo Gouy for his helpful comments and careful reading of the manuscript. This work was supported by grants from the CNRS and MENRT.
REFERENCES
- 1.Grantham R., Gautier,C. and Gouy,M. (1980) Codon frequencies in 119 individual genes confirm consistent choices of degenerate base according to genome type. Nucleic Acids Res., 8, 1892–1912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Holm L. (1986) Codon usage and gene expression. Nucleic Acids Res., 14, 3075–3087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Médigue C., Rouxel,T., Vigier,P., Hénaut,A. and Danchin,A. (1991) Evidence for horizontal gene transfer in Escherichia coli speciation. J. Mol. Biol., 222, 851–856. [DOI] [PubMed] [Google Scholar]
- 4.Shields D.C. and Sharp,P.M. (1987) Synonymous codon usage in Bacillus subtilis reflects both translational selection and mutation biases. Nucleic Acids Res., 15, 8023–8040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sharp P.M., Higgins,D.G., Shields,D.C., Devine,K.M. and Hoch,J.A. (1990) Bacillus subtilis gene sequences. In Zukowski,M.M., Ganesan,A.T. and Hoch,J.A. (eds), Genetics and Biotechnology of Bacilli. Academic Press, San Diego, CA, pp. 89–98.
- 6.Perrière G., Gouy,M. and Gojobori,T. (1994) NRSub: a non-redundant data base for the Bacillus subtilis genome. Nucleic Acids Res., 22, 5525–5529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moszer I., Glaser,P. and Danchin,A. (1995) SubtiList: a relational database for the Bacillus subtilis genome. Microbiology, 141, 261–268. [DOI] [PubMed] [Google Scholar]
- 8.Moszer I., Rocha,E.P.C. and Danchin,A. (1999) Codon usage and lateral gene transfer in Bacillus subtilis. Curr. Opin. Microbiol., 2, 524–528. [DOI] [PubMed] [Google Scholar]
- 9.McInerney J.O. (1998) Replicational and transcriptional selection on codon usage in Borrelia burgdorferi. Proc. Natl Acad. Sci. USA, 95, 10698–10703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lafay B., Lloyd,A.T., McLean,M.J., Devine,K.M., Sharp,P.M. and Wolfe,K.H. (1999) Proteome composition and codon usage in spirochaetes: species-specific and DNA strand-specific mutational biases. Nucleic Acids Res., 27, 1642–1649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Romero H., Zavala,A. and Musto,H. (2000) Codon usage in Chlamydia trachomatis is the result of strand-specific mutational biases and a complex pattern of selective forces. Nucleic Acids Res., 28, 1084–2090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.McInerney J.O. (1997) Prokaryotic genome evolution as assessed by multivariate analysis of codon usage patterns. Microbial Comp. Genomics, 2, 1–10. [Google Scholar]
- 13.Lafay B., Atherton,J.C. and Sharp,P.M. (2000) Absence of translationally selected synonymous codon usage bias in Helicobacter pylori. Microbiology, 146, 851–860. [DOI] [PubMed] [Google Scholar]
- 14.Gupta S.K. and Ghosh,T.C. (2001) Gene expressivity is the main factor in dictating the codon usage variation among the genes in Pseudomonas aeruginosa. Gene, 273, 63–70. [DOI] [PubMed] [Google Scholar]
- 15.Ikemura T. (1981) Correlation between the abundance of Escherichia coli transfer RNAs and the occurrence of the respective codons in its protein genes. J. Mol. Biol., 146, 1–21. [DOI] [PubMed] [Google Scholar]
- 16.Ikemura T. (1982) Correlation between the abundance of yeast transfer RNAs and the occurrence of the respective codons in protein genes. Differences in synonymous codon choice patterns of yeast and Escherichia coli with reference to the abundance of isoaccepting transfer RNAs. J. Mol. Biol., 158, 573–587. [DOI] [PubMed] [Google Scholar]
- 17.Bennetzen J.L. and Hall,B.D. (1982) Codon selection in yeast. J. Biol. Chem., 257, 3026–3031. [PubMed] [Google Scholar]
- 18.Kanaya S., Yamada,Y., Kudo,Y. and Ikemura,T. (1999) Studies of codon usage and tRNA genes of 18 unicellular organisms and quantification of Bacillus subtilis tRNAs: gene expression level and species-specific diversity of codon usage based on multivariate analysis. Gene, 238, 143–155. [DOI] [PubMed] [Google Scholar]
- 19.de Miranda A.B., Alvarez-Valin,F., Jabbari,K., Degrave,W.M. and Bernardi,G. (2000) Gene expression, amino acid conservation and hydrophobicity are the main factors shaping codon preferences in Mycobacterium tuberculosis and Mycobacterium leprae. J. Mol. Evol., 50, 45–55. [DOI] [PubMed] [Google Scholar]
- 20.Fichant G. and Gautier,C. (1987) Statistical methods for predicting protein coding regions in nucleic acids sequences. Comput. Appl. Biosci., 3, 287–295. [DOI] [PubMed] [Google Scholar]
- 21.Quentin Y. (1988) The Alu family developed through successive waves of fixation closely connected with primate lineage history. J. Mol. Evol., 27, 194–202. [DOI] [PubMed] [Google Scholar]
- 22.Quentin Y. (1989) Successive waves of fixation of B1 variants in rodent lineage history. J. Mol. Evol., 28, 299–305. [DOI] [PubMed] [Google Scholar]
- 23.Lobry J.R. and Gautier,C. (1994) Hydrophobicity, expressivity and aromaticity are the major trends of amino acid usage in 999 Escherichia coli chromosome-encoded genes. Nucleic Acids Res., 22, 3174–3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fichant G.A. and Quentin,Y. (1995) A frameshift error detection algorithm for DNA sequencing projects. Nucleic Acids Res., 23, 2900–2908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hill M.O. (1974) Correspondence analysis: a neglected multivariate method. Appl. Stat., 23, 340–354. [Google Scholar]
- 26.Sharp P.M., Tuohy,T.M.F. and Mosurski,K.R. (1986) Codon usage in yeast: cluster analysis clearly differentiates highly and lowly expressed genes. Nucleic Acids Res., 14, 5125–5143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sharp P.M. and Li,W.H. (1987) The codon adaptation index—a measure of directional synonymous codon usage bias and its potential applications. Nucleic Acids Res., 15, 1281–1295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Perrière G., Labedan,B. and Bessières,P. (2000) EMGLib: the Enhanced Microbial Genomes Library (update 2000). Nucleic Acids Res., 28, 68–71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wei Y., Lee,J.M., Richmond,C., Blattner,F.R., Rafalski,J.A. and LaRossa,R.A. (2001) High-density microarray-mediated gene expression profiling of Escherichia coli. J. Bacteriol., 183, 545–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lin K., Kuang,Y., Joseph,J.S. and Kolatkar,P.R. (2002) Conserved codon composition of ribosomal protein coding genes in Escherichia coli, Mycobacterium tuberculosis and Saccharomyces cerevisiae: lessons from supervised machine learning in functional genomics. Nucleic Acids Res., 30, 2599–2607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Thioulouse J., Chessel,D., Dolédec,S. and Olivier,J.M. (1997) ADE-4: a multivariate analysis and graphical display software. Stat. Comput., 7, 75–83. [Google Scholar]
- 32.Kyte J. and Doolittle,R.F. (1982) A simple method for displaying the hydropathic character of a protein. J. Mol. Biol., 157, 105–132. [DOI] [PubMed] [Google Scholar]
- 33.Gouy M. and Gautier,C. (1982) Codon usage in bacteria: correlation with gene expressivity. Nucleic Acids Res., 10, 7055–7073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kanaya S., Kudo,Y., Nakamura,Y. and Ikemura,T. (1996) Detection of genes in Escherichia coli sequences determined by genome projects and prediction of protein production levels, based on multivariate diversity in codon usage. Comput. Appl. Biosci., 12, 213–225. [DOI] [PubMed] [Google Scholar]
- 35.Chevenet F., Doledec,S. and Chessel,D. (1994) A fuzzy coding approach for the analysis of long-term ecological data. Freshwater Biol., 31, 295–309. [Google Scholar]
- 36.Lerat E., Biémont,C. and Capy,P. (2000) Codon usage and the origin of P elements. Mol. Biol. Evol., 17, 467–468. [DOI] [PubMed] [Google Scholar]