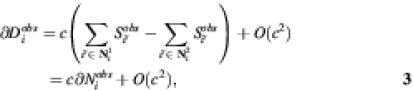Improving DNA array data quality by minimising ‘neighbourhood’ effects

Abstract

Gene expression studies using cDNA arrays require robust and sensitive detection methods. Being extremely sensitive, radioactive detection suffers from the influence of signals positioned in each other’s vicinity, the ‘neighbourhood’ effect. This limits the gene density of arrays and the quality of the results obtained. We have investigated the quantitative influence of different parameters on the ‘neighbourhood’ effect. By using a model experimental system, we could show that the effect is linear and depends only on the intensity of the hybridisation signal. We identified a common factor that can describe the influence of the neighbour spots based on their intensities. This factor is <1%, but it has to be taken into account if a high dynamic range of gene expression is to be detected. We could also derive the factor, although with less precision, from comparison of duplicate spots on arrays of 4565 different clones and replication of the hybridisation experiments. The calculated coefficient applied to our actual experimental results not only revealed previously undetected tissue or cell-specific expression differences, but also increased the dynamic range of detection. It thus provides a relatively simple way of improving DNA array data quality with few experimental modifications.

INTRODUCTION

Array-based gene expression analysis has become a widely used technique in biomedical research (1,2). It involves immobilisation of a set of gene sequences on a solid support, the DNA array, followed by hybridisation with labelled DNA copies of mRNA populations isolated from different cells and tissues. High-density immobilisation and low amounts of starting RNA material are highly desirable in optimal application of the technique. It facilitates analysis of large numbers of genes in parallel with samples derived from, for example, precious biopsies.

Since radioactivity still provides the highest sensitivity and the largest dynamic range of detection, the radioactive labelling of RNA samples is the method of choice for such an application (3–5). Unfortunately, radioactive detection suffers from what is known as overshining, or the neighbourhood effect, manifested as overlapping signals from neighbouring spots. This is caused by the non-confocal method of radioactive detection: the distance between the radioactive source, the array in this case, and the image plates used for detection is finite (6). In addition, there are some other decisive factors that should be taken into account, such as the spacing between the DNA spots on the array, the properties of the solid support, the physical characteristics of the particular isotope used for labelling, the image plates, etc. Increased array densities lead to substantial influences between neighbours. A bright spot affects a weak spot corresponding to a low expressed gene and/or an ‘empty’ spot used to estimate the local background (7,8), causing overestimation of background signals and making it difficult to measure relative differences between genes expressed at low levels. Since individual intensities of hybridisation cannot be estimated a priori, experimental design to separate spots of higher and lower expressed genes cannot be a solution to compensate for the overshining effect. The effect is usually neglected, either because low-density array spotting is used, or because the errors of experimental fluctuations are higher than the errors introduced by correcting for the overshining (8).

In this study, we constructed arrays containing 4565 different cDNAs spotted in duplicates. Most of the cDNAs resulted from subtraction libraries and were partially characterised by sequencing and the oligonucleotide fingerprinting method (9). These arrays were used for screening different tissues and cell culture samples (see Materials and Methods for details). We observed that the neighbourhood effect could not be neglected.

Here we suggest an approach to compensate for the effect by introducing a correction factor. We found that the shape of the detectable signals is very reproducible and does not depend on the signal intensity. We were able to estimate the neighbourhood effect and derive a simple computational approach to correct it. Because the distance between spots was very reproducible, we postulated that the effect has a common factor that can simply be deducted from the measured signals. We show that the factor is reproducible over different arrays and hybridisations. Adding ∼0.4% of the neighbour signals, this factor should be taken into account if gene expression quantification over three to four orders of magnitude is to be achieved.

Using replicate arrays for each hybridisation we were also able to estimate experimental errors for every gene and assign a confidence level to the expression data. Therefore, radioactive labelling of the RNA samples, hybridisation of arrays in three to four replicas and introduction of the overshining correction coefficient can be a very realistic and cost-effective approach to derive statistically reliable gene expression data.

MATERIALS AND METHODS

All reagents were purchased from Merck (Darmstadt, Germany) and standard buffers were prepared according to Sambrook and Russell (10).

Target preparation

Targets were prepared by PCR amplification directly from bacterial glycerol stocks. Large-scale PCR was carried out according to the manufacturer’s protocol (Qiagen, Germany). Briefly, the PCR mixture contained 1× PCR buffer, 1× Solution Q, 150 µM of each dNTP, 2.5 mM MgCl₂ and 0.05 U/µl Taq polymerase. Cycling conditions were as follows: initial denaturation at 95°C for 5 min followed by 30 cycles of 94°C for 10 s and 65°C for 5 min. We found that Solution Q is an important additive to facilitate amplification directly from bacteria and that the two-step PCR protocol was sufficient to yield products representing >98% of the library clones. After amplification, PCR products were directly re-pipetted into 384-well polystyrene microtitre plates (Genetix, UK) and subsequently used for array spotting without any purification (11).

Amplification of the control 23S ribosomal gene was performed starting from 1 ng of Escherichia coli genomic DNA according to the large-scale protocol above with the following primers: 5′-GGTTAAGCGA CTAAGCGTAC ACGGTGGATG CCCTGGCAGT-3′ and 5′-TTTCCCACTT AACCATGACT TTGGGACCTT AGCTGGCGGT-3′, producing a PCR fragment of 1029 bp. After amplification all aliquots were pooled. The concentration of the amplified product was estimated by PicoGreen measurements. Briefly, PCR products were diluted 1/4 and 1/20 in TE buffer. Twenty microlitres of these dilutions were mixed with 80 µl of a 1:400 dilution of PicoGreen (PicoGreen® dsDNA Quantitation Kit; Molecular Probes, The Netherlands) and measured in a plate reader at 480 nm excitation and 520 nm emission wavelengths. A standard curve was prepared as above from a dilution series of λDNA/HindIII (New England Biolabs, Germany) molecular weight standards.

cDNA clones and RNA detection samples

The clones used for array production were derived from different sources. Most of them represent EST fragments derived from subtraction experiments similar to those described previously (12). A collection of different tumour biopsy samples have been used to derive a set of cancer specific genes. The clones were further characterised by hybridisation with a set of oligonucleotides to eliminate redundancy, and some of the clones were partially sequenced (unpublished data). To evaluate expression of the selected ESTs among different tissues, the clones were hybridised in an arrayed form with a set of different RNA samples derived from different tissues and cell lines. In the current studies we describe hybridisation with stomach and skeletal muscle mRNA samples purchased from Clontech (Heidelberg, Germany).

Array preparation

Arrays were spotted using a robotic system from KAYBEE (UK) on a nylon membrane Biodyne B (Pall, UK). A similar spotting procedure has been described earlier (7). The spotting head contained 384 solid flat-bottom pins of 250 µm in diameter constructed in a format complementary to the polystyrene 384-well plates. In order to increase the amount of DNA in a spot and to equalise variances during the transfer, the PCR content of each well was spotted 20 times. The size of each spot, estimated by spotting ink and fluorescently labelled DNA, was ∼350 µm and the distance between each spot was 833 µm. Each robot run takes 6–20 h for 36 to 160 arrays depending on the array configuration.

Probe labelling and hybridisation

Four aliquots of the RNA sample each containing between 250 ng and 1.5 µg of total RNA were prepared. Each aliquot was handled as independently as possible. They were mixed with 0.6 µg of random hexamers (dN)₆ heated at 70°C for 3 min and chilled on ice. The volume was adjusted to 20 µl with buffer according the SuperScript II manufacturer’s protocol (Life Technologies, UK). The labelling reaction contained a final concentration of 1 mM each dATP, dGTP, dTTP, 50 µCi ³³P-dCTP (corresponding to ∼0.5 µM) and 100 U SuperScript II. After 1 h incubation at 42°C, probes were purified on mini Quick Spin DNA columns (Roche, Germany) followed by denaturation in 0.5 M NaOH at 65°C for 20 min, neutralisation with 1 M Na-phosphate buffer at pH 7.5 and pooling of all four aliquots. The typical incorporation rate was ∼70% and we estimate that the amount of synthesised cDNA is ∼30 ng.

We used three arrays with duplicate features for each hybridisation. These arrays contained the same clones but had differences in batch preparation, e.g. different robot runs or different PCR aliquots. Arrays were initially prehybridised for at least 2 h and then hybridised for 20 h at 50°C in a buffer containing 50% formamide, 6× SSC, 7% SDS and 50 mM Na-phosphate, pH 7.5. The typical hybridisation volume was 50 ml. After hybridisation, arrays were washed twice for 15 min in Washing buffer I (2× SSC, 0.5% SDS) and then twice for 15 min in Washing buffer II (0.1× SSC, 0.5% SDS). Before wrapping with SaranWrap, excess liquid was removed by placing membranes on Whatman paper for a few seconds.

Scanning and image processing

Arrays were exposed for 100 h to Fuji BAS-IP MS 2025 plates and scanned at 25 µm resolution on a Fuji BAS-5000 phosphorimager (Raytest, Germany) (13,14). The acquired images were then analysed with a publicly available image analysis package VisualGrid™ (free download from http://www.gpc-biotech.com/site_usa/com_main.html; GPC Biotech, Germany). The diameter of the circular area used to quantify the spots, the node mask, was 27 pixels, which corresponds to 675 µm. The VisualGrid™ generates a text-file format output that was further used for data processing and analysis.

Data processing

Data processing included the following steps: subtraction of local background, correction for the neighbourhood effect (when required) and normalisation. Calculation of the background was based on the empty dots present in each block. The local background of a block was taken as a mean value of the empty dots located in the block and in the neighbouring blocks. The number of neighbouring blocks differs from three to eight depending on the location of the block.

Correction for the neighbourhood effect was performed only for a restricted set of experiments after quantification of the neighbourhood factor. A certain fraction of the sum of the signals of the horizontally and vertically neighbouring spots was subtracted. The fraction (4.2 × 10^–3) is defined by the neighbourhood coefficient that was determined by means of linear regression analysis (see Appendix for more details).

Normalisation was important to compensate for differences caused by different labelling efficiencies of RNA samples. We identified a set ‘housekeeping’ cDNA clones consisting of 384 clones whose expression signals showed only a small variation between various tissue types (data not shown). The mean signal intensity of this set of clones was set to ‘one’ for all experiments. In addition, the normalised signals from the six replicas (three replica arrays times two duplicates) were used to calculate the mean and standard error for every clone. These data were stored in a gene expression database that is based on Oracle and J2EE (raw and processed data are available on request).

Data analysis

The expression data of two different probes were analysed by means of a two-tailed t-test for independent samples. A significance level of 95% was used. A clone is defined as being significantly deregulated if its t-value is smaller than the 2.5-percentile, or larger than the 97.5-percentiles of the corresponding Student’s distribution.

Similarly, a clone is defined as being significantly expressed if in a particular probe its mean signal is larger than 1.96 times its standard error.

RESULTS

By setting up a large-scale expression profiling system with 4565 cDNA clones spotted in duplicates on a palm-sized (8 × 12 cm) array, we attempted to estimate the different factors influencing the quality of data, similar to the analyses of Schuchhardt et al. (8) and to improve the quality of the results. The focus of our current investigation was the ‘neighbourhood’ effect.

Influence of different neighbours on duplicate spots

Twelve 384-well plates containing PCR products were spotted in duplicate on each array and hybridised with a complex RNA sample. The spotting and hybridisation patterns for one of the 384 blocks (12 plates following a 5 × 5 pattern) are shown in Figure 1A. Initially, we designed the spotting pattern to simplify automated grid finding (I.Scholl and M.Kietzmann, personal communication): each of the duplicate pairs differs in angle and distance between duplicate spots. For example, one pair of dots corresponding to plate 1 (coordinates aII and aIV on Fig. 1A) is on a horizontal line and one spot apart from each other.

Figure 1.

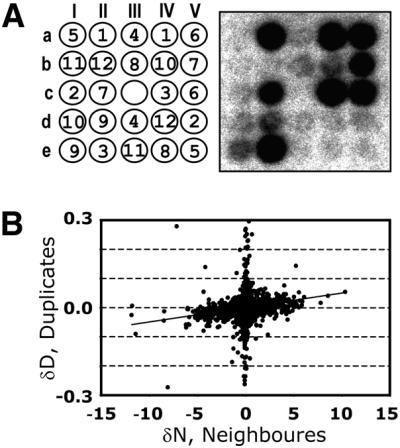
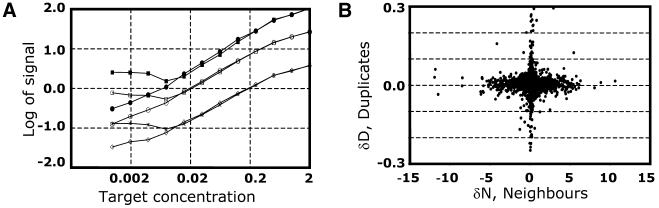
Demonstration of the neighbourhood effect. Twelve 384-well microtitre plates were spotted in duplicate in a 5 × 5 pattern. (A) A spotting pattern and a log-transformed hybridisation image for one of the 384 blocks of the array. The numbers in circles correspond to the plate numbers. The empty spot (c-III) was used to evaluate local background. (B) Differences in intensities between a duplicate were plotted against intensity differences of the duplicate neighbours. The errors could not be shown due to the individual nature of the experiment. A positive bias of the linear regression line reflects the neighbourhood effect.

In order to evaluate the neighbourhood effect we tried to estimate the influence of different neighbour signals on duplicate signals. We plotted the differences in signal intensity between the duplicates (δD) versus the difference between the sum of the nearest neighbour signal intensities (δN) corresponding to these duplicates (Fig. 1B). Calculation of the differences in signal intensities meant we could avoid any errors caused, for example, by local background.

If the neighbourhood effect were negligible, δD and δN values would not correlate. In contrast, as shown in Figure 1B, the distribution shows a positive correlation. It is worth noting that absolute values of δD are obviously smaller than δN. Since most of the spots on the array showed low signals, being neighbours for some of the duplicates they also resulted in negligible differences and appeared to comprise the vertical line around zero. In fact, they represented the majority of all data points.

Below, we show that we were able to make a precise estimate of the neighbourhood coefficient corresponding to the angle to the horizontal axis. Before we addressed this question, we had to make sure that the effect is linear. In other words, that the shapes of the spots for low and highly expressed genes were the same.

Spot profiles

We investigated the spot profiles using the following model system. As a target we chose a PCR fragment of 23S rRNA from E.coli. Three different arrays were spotted: with 20, 2 or 0.2 ng/µl final concentration of the PCR products as defined in the solutions used for spotting.

Each array consisted of 96 equal spots positioned at 9000 µm from each other. Therefore, any interference between spots can be neglected.

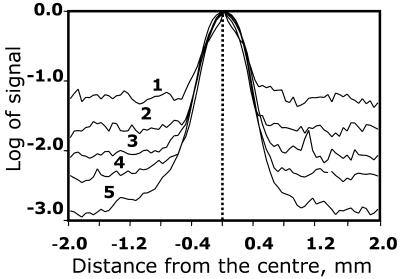
To generate a probe for hybridisation we labelled 5 µg of total E.coli RNA by reverse transcription. We estimate that the amount of synthesised cDNA was ∼30 ng (see Materials and Methods). The labelled probe was used for hybridisation either directly, mixed with hybridisation buffer, or in two different 10-fold dilutions (3 and 0.3 ng). Such a dilution series should simulate differential expression of three genes over two orders of magnitude. After hybridisation and washing, arrays were exposed for the same duration. The time of exposure to the image plates was chosen to avoid saturation of the strongest signals corresponding to the highest target (20 ng) and the highest probe (30 ng) amounts at the scanned resolution of 25 µm. This resolution provided more than 600 pixels per spot with the 27 × 27 node mask used (see Materials and Methods). The profiles were averaged over all 96 spots. Figure 2 shows the profiles corresponding to the different conditions. The profiles were normalised to make the maximum of intensity identical. As shown in Figure 2, all profiles are identical for the different conditions within an area of 400 µm from the centre of the spot. This value is higher than the estimated diameter of the DNA spot (equal to 350 µm). The tails of the distributions are determined by noise. The absolute level of noise is similar for all profiles, but appears to be different due to the normalisation of all the different maxima in Figure 2.

Figure 2.

Comparison of spot profiles for different probe and target concentrations. For each target amount, we prepared an array with 96 blocks containing only one spot per block with 9 mm between blocks. Each curve is an average over the 96 blocks. The maximum values of all curves were normalised to 1. The first curve (1) corresponds to 20 ng/µl spotting concentrations of target and 0.3 ng of probe per 50 ml hybridisation volume; (2) 0.2 ng/µl target, 30 ng/50 ml probe; (3) 20 ng/µl target, 3 ng/50 ml probe; (4) 2 ng/µl target, 30 ng/50 ml probe; (5) 20 ng/µl target, 30 ng/ 50 ml probe. Estimated size of a spot is 350 µm and the distance between spots is 833 µm.

Estimations of the neighbourhood coefficient

Similar to the evaluation of spot pixel distributions, we designed a model system to simulate different signal intensities spanning more than three orders of dynamic range. We produced an array so that each block contained 12 of 2-fold dilution of the PCR in duplicate. The spotting pattern was chosen to maximise the neighbourhood differences. For example, the most concentrated solution was spotted as a nearest neighbour to the most diluted solution.

The arrays were then hybridised at three different probe concentrations (similar to the previous experiment). We then plotted the differences in duplicates δD versus the difference of their neighbours δN (Fig. 3B, as in Fig. 1B) and used weighted regression to fit the linear model (see Appendix) to these data. The best-fit line corresponds to the coefficient of (4.2 ± 0.4) × 10^–3. In other words, the overshining effect can be interpreted as a linear additive of ∼0.4% of each signal and the results were independent of the probe concentration (data not shown).

Figure 3.

Calculation of the neighbourhood correction factor. (A) A spotting pattern (similar to Fig. 1) and an image of one of the 96 blocks of the array representing the 12 sequential 2-fold dilution series of target DNA. The image is in a log-transformed form to ensure visualisation of all the spots on the array. (B) A plot of differences between a duplicate (y-axis) versus differences between nearest neighbours of the duplicate (x-axis). All data points were collected from 96 blocks of the array, and the absolute errors derived from the repetitions are shown. The best-fit line is a calculation of the linear regression factor k = (4.2 ± 0.4) × 10^–3 corresponding to the neighbourhood correction factor.

In addition to the model experiments, we also estimated a neighbourhood coefficient from the actual experiments (Fig. 1). We again used weighted regression to fit the linear model to the data shown in Figure 1B. We obtained a neighbourhood coefficient of (3.8 ± 0.6) × 10^–3 that is slightly lower than the neighbourhood coefficient obtained with the model experiment. The same approach was used to individually estimate the neighbourhood coefficient for each replica. As can be seen in Table 1, all neighbourhood coefficients are identical within their errors. Thus, the value of the neighbourhood coefficient is reproducible with different arrays and hybridisation parameters. It should be noted that the estimate using the model experiment is slightly more precise, i.e. the error is smaller. This is due to the fact that the experiment was designed such that the difference of the neighbouring signals is maximal for low intensity spots.

Table 1. Estimation of the neighbourhood coefficient.

Data set	Neighbourhood
Figure 3	(4.2 ± 0.4) × 10–3
Figure 1, all replicates	(3.8 ± 0.6) × 10–3
Figure 1, replicate 1	(4.7 ± 0.5) × 10–3
Figure 1, replicate 2	(3.7 ± 0.8) × 10–3
Figure 1, replicate 3	(4.3 ± 0.5) × 10–3

The coefficient was determined by means of linear regression analysis as described in the Appendix. The estimation was performed for different sets of data: the first set refers to the model experiment (Fig. 3); the second set refers to the three replicates used in the actual experiment (Fig. 1). The subsequent sets refer to one replicate each.

Influence of the neighbourhood correction on data analysis

We further investigated the influence of the neighbourhood effect as well as its correction on the experimental system. At first we used the data from the model experiment and investigated the dependence of the hybridisation signal on spotted target amount (Fig. 4A). The strength of the signals showed almost linear dependence on the spotted target amount (the coefficient is ∼0.8–0.9 in log–log scale) and reached a plateau at high target amounts. Applying the correction factor to the data set we could increase the linearity by at least another order of magnitude.

Figure 4.

Recalculation of data with the correction factor for overshining. (A) The data were obtained from the dilution series outlined in Figure 3. Hybridisation signals were plotted against different target spotted concentrations with and without neighbourhood correction. This dependence was investigated at three different probe concentrations: 30 ng per 50 ml of hybridisation buffer (filled circles and squares of the upper curves, with and without correction, respectively), 3 ng/50 ml (open circles and squares, with and without correction, respectively) and 0.3 ng/50 ml (open diamonds and stars, with and without correction, respectively). The plots represent 96 independent data points with the average signal normalised to 1. (B) The data used for Figure 1B were recalculated with the correction factor k = (4.2 ± 0.4) × 10^–3 obtained from the graph (Fig. 3B). The data were plotted as in Figure 1B. This time the linear regression coincides with the x-axis indicating that dependence of the duplicate signals on the neighbours has been eliminated.

We further recalculated the data set used to illustrate the overshining effect in Figure 1 with the correction factors obtained from the dilution series (Fig. 3). The data were again plotted as differences in duplicates versus the difference in signal intensities between the sums of their neighbour spots (Fig. 4B). In this plot there is no influence of the neighbours on duplicates as shown by the fact that all data points are along the x-axis.

In addition, we applied the correction strategy in a classical experiment of pair-wise comparison of stomach (N1) and skeletal muscle (N2) RNA samples. Three replicas of the arrays containing 4565 clones in duplicate (384-block array with 5 × 5 pattern) were hybridised with the RNA samples. Among the 4565 clones we could identify only 1296 that were significantly expressed in both tissues simultaneously. These results were not surprising since most of the cDNA clones derived from subtraction experiments and did not contain stomach or skeletal muscle specific genes.

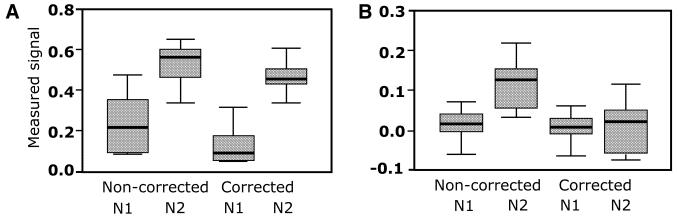
Figure 5 shows two examples of the misleading interpretation of experimental results without taking neighbourhood correction into account. In Figure 5A, the gene in question is apparently not significantly differentially regulated between stomach and skeletal muscle, if one also takes errors into account. In contrast, after applying correction calculations the gene in question is clearly down-regulated in stomach compared to skeletal muscle. The reverse situation is shown in Figure 5B. The gene appears to be differentially regulated, whereas after introduction of correction factors, it is obvious that the gene is expressed at the same level in both tissues.

Figure 5.

Influence of the neighbourhood correction on pair-wise comparison of two genes. Box-plot shows the signals, normalised and corrected for background, of clones labelled 3F15 (A) and 4I12 (B) hybridised by probes derived from two different samples (N1 and N2), with and without neighbourhood correction. A total of six measurements for each sample are represented in this plot. The thick line is the median value. The middle of the box is the mean value. The height of the box is two standard deviations. The error bars show the minimum and maximum values.

After applying the analysis and neighbourhood correction we could identify with confidence 639 differentially expressed genes from the 1292 expressed in common. Of these, 28 genes could not be identified before correction, while 39 genes that were identified before correction were shown to be potentially false positive.

DISCUSSION

Standard cDNA arrays are usually produced to include duplicate spots of every represented gene. Although the use of duplicates reduces the space on the array, comparison of signals between duplicates is a valuable measure of the data quality. For example, similarities between duplicates are used by the image analysis system to position the grid, while setting up a threshold for the duplicate differences helps to eliminate signals caused by non-specific background (7,8).

Performing complex hybridisations with arrays containing 4565 different cDNAs spotted in duplicate, we observed that differences between duplicates are not random: the differences between duplicates and differences between their nearest neighbours on the spotting pattern show a correlation (Fig. 1). Nevertheless, this experiment was not sufficient to prove the linearity of the neighbourhood effect because of the large number of data points in the low signal region. Genes expressed at low levels comprise the majority of all expressed genes (3). They usually show no, or close to background signals. Therefore, we designed an additional model system of different target and probe dilutions to mimic the different hybridisation signals strengths observed in our actual experiments.

We used the fact, illustrated in Figure 4A, that hybridisation with an immobilised target follows second-order kinetics (15,16). Although the target amount (nanogram range) is usually much higher than the amount of the probe (picogram range), such hybridisation reactions do not follow pseudo-first-order kinetics but rather depend on both probe concentration and the amount of immobilised target. The strength of the signals shows almost linear dependence on the spotted target concentration (in log–log scale the coefficient is ∼0.8–0.9). If the probe concentration is constant, low target amounts show low signals and the same is true for different probe concentrations and a constant amount of target DNA. Simply by varying the concentration of the probe or spotted concentration of the target we can achieve a different dynamic range of the hybridisation signal. In our case, we used a dilution range of >4000-fold of the target and 100-fold of the probe during the model experiments.

Using arrays with well separated individual spots we showed that the shape and the profiles of the spots are identical and independent of both the amount of DNA spotted onto the nylon membrane and the probe concentrations (Fig. 2). Due to this fact, the neighbourhood effect could be approximated as a common factor, which does not depend on the strength of the signal. This factor can be calculated from a model experiment and be applied for analysis of any other experiments, as long as characteristics of the array (distance between the spots, etc.) are the same.

The factor, (4.2 ± 0.4) × 10^–3 of the nearest neighbours signal, was estimated by creating an array with each block containing different dilutions of the target spanning more than three orders of magnitude. Alternatively, a correction factor can also be directly estimated from actual experiments, although in our case it proved slightly less precise than for the model experiment. By this means, we obtained a neighbourhood coefficient of (3.8 ± 0.6) × 10^–3 that agrees well with the estimation from our model experiment, and was reproducible over several arrays. This approach certainly has the advantage that no additional model experiment is necessary and that parameters (e.g. distance between spots, type of membrane, scanning parameters, etc.) can be changed without making it necessary to repeat the model experiment.

We only considered the influence of the horizontal and vertical nearest neighbours for our calculation. Outside of the spot, the signal decreases exponentially with the distance (see Fig. 2). This means that if the coefficient for the horizontally and vertically direct neighbours is c_direct = c, the coefficient for the diagonal neighbours is c_diagonal = (c_direct)^√2. For c = 4.2 × 10^–3 (see below), c_direct is 4 × 10^–4, thus, the influence of spots located on the diagonal to the duplicate is a negligible influence and can be ignored.

It is obvious that overshining mainly affects the low or non-significant signals and background spots. It was demonstrated by calculating the effect for a set of low expressed signals from the target dilution experiments (Fig. 4A). At low concentrations of the target, signals are reaching saturation. By applying correction factors we were able to ‘expand’ the linear dependence of the signal to low target amounts. Moreover, these graphs show that correction was not necessary for signals (target amount) spanning the two highest orders of the detection range. It points out again that the overshining effect is ∼1% of the neighbour values and that the correction has to be taken into consideration only if a large dynamic range of signals needs to be analysed.

The fact that the signals follow the second-order rate, especially at the low concentration range, only after correction, is an indirect proof of our method. By applying this to the hybridisation with a tissue- or cell line-derived complex RNA sample (Fig. 5) we could show that the methods may identify potential false-positive and false-negative signals otherwise non-detectable without the neighbourhood correction.

At the same time, we would like to acknowledge that correction for the neighbourhood effect represents a technical improvement to the current analysis of hybridisation signals, and not an alternative evaluation method. Affecting low intensity hybridisation signals, it may change the number and identity of significantly deregulated genes, but independent confirmation or validation techniques should subsequently be applied (17). However, such confirmatory analyses in our case are associated with certain technological challenges since the genes affected by the neighbourhood effect are obviously expressed at very low levels. In order to compare gene representation in two different complex RNA samples we would have to rely on normalisation, which in the case of northern blots as well as RT–PCR refers to very abundant gene products, e.g.18S or 28S rRNAs, β-actin, etc. Optimum direct validation of our method would be the information derived from a digital northern (18), oligonucleotide fingerprinting (9) or designing a specific biological assay. Application of any of these methods falls outside the scope of the present work.

In conclusion, accounting for the neighbourhood effect improves the data quality of radioactive-based DNA array detection. It can be evaluated using either a model system sharing the same array properties or using data from the actual experiments to be analysed, if arrays contain duplicate spots in an optimised pattern. By replicating hybridisation experiments together with correcting for the neighbourhood effect we could achieve a higher dynamic range of detection as well as improve the detection of differences between RNA samples that would otherwise be masked by the effect.

APPENDIX

Determination of the neighbourhood coefficient

The correction is based on the linear model:

where S_i^obs is the observed signal for spot i (arbitrary units), B_i is the local background, s_i is some clone-dependent constant, X_i is the expression of the target contained in spot i, c is the neighbourhood coefficient, and N_i is the set of direct neighbours of spot i.

As has been shown, the shape of the spots for genes expressed at low and high level were the same. Therefore, the neighbourhood coefficient c is independent of the signals of the spot itself and the neighbouring signals. From equation 1 it follows that:

Since c is small in terms of order, c² can be neglected. This then yields:

where ∂D_i^obs is the observed difference of the duplicates, and ∂N_i^obs is the observed difference of the neighbouring spots. This means that the neighbouring coefficient c can be derived as the constant between ∂D_i^obs and ∂N_i^obs. We use weighted linear regression to obtain an estimate for c. Their weights were set proportional to the inverse of the squared standard error of the signals X_i.

Based on the linear model (equations 1 and 2) we correct the signals according to:

where S_i^corr is the corrected signal for spot i.