Determination of base and backbone contributions to the thermodynamics of premelting and melting transitions in B DNA

Abstract

In previous papers of this series the temperature-dependent Raman spectra of poly(dA)·poly(dT) and poly(dA–dT)·poly(dA–dT) were used to characterize structurally the melting and premelting transitions in DNAs containing consecutive A·T and alternating A·T/T·A base pairs. Here, we describe procedures for obtaining thermodynamic parameters from the Raman data. The method exploits base-specific and backbone-specific Raman markers to determine separate thermodynamic contributions of A, T and deoxyribosyl-phosphate moieties to premelting and melting transitions. Key findings include the following: (i) Both poly(dA)·poly(dT) and poly(dA–dT)· poly(dA–dT) exhibit robust premelting transitions, due predominantly to backbone conformational changes. (ii) The significant van’t Hoff premelting enthalpies of poly(dA)·poly(dT) [ΔH_vH^pm = 18.0 ± 1.6 kcal·mol^–1 (kilocalories per mole cooperative unit)] and poly(dA–dT)·poly(dA–dT) (ΔH_vH^pm = 13.4 ± 2.5 kcal·mol^–1) differ by an amount (∼4.6 kcal·mol^–1) estimated as the contribution from three-centered inter-base hydrogen bonding in (dA)_n·(dT)_n tracts. (iii) The overall stacking free energy of poly(dA)· poly(dT) [–6.88 kcal·mol_bp^–1 (kilocalories per mole base pair)] is greater than that of poly(dA–dT)· poly(dA–dT) (–6.31 kcal·mol_bp^–1). (iv) The difference between stacking free energies of A and T is significant in poly(dA)·poly(dT) (ΔΔG_st = 0.8 ± 0.3 kcal· mol_bp^–1), but marginal in poly(dA–dT)·poly(dA–dT) (ΔΔG_st = 0.3 ± 0.3 kcal·mol_bp^–1). (v) In poly(dA)· poly(dT), the van’t Hoff parameters for melting of A (ΔH_vH^A = 407 ± 23 kcal·mol^–1, ΔS_vH^A = 1166 ± 67 cal·°K^–1·mol^–1, ΔG_vH(25°C)^A = 60.0 ± 3.2 kcal·mol^–1) are clearly distinguished from those of T (ΔH_vH^T = 185 ± 38 kcal·mol^–1, ΔS_vH^T = 516 ± 109 cal·°K^–1·mol^–1, ΔG_vH(25°C)^T = 27.1 ± 5.5 kcal·mol^–1). (vi) Similar relative differences are observed in poly(dA–dT)· poly(dA–dT) (ΔH_vH^A = 333 ± 54 kcal·mol^–1, ΔS_vH^A = 961 ± 157 cal·°K^–1·mol^–1, ΔG_vH(25°C)^A = 45.0 ± 7.6 kcal· mol^–1; ΔH_vH^T = 213 ± 30 kcal·mol^–1, ΔS_vH^T = 617 ± 86 cal·°K^–1·mol^–1, ΔG_vH(25°C)^T = 29.3 ± 4.9 kcal·mol^–1). The methodology employed here distinguishes thermodynamic contributions of base stacking, base pairing and backbone conformational ordering in the molecular mechanism of double-helical B DNA formation.

INTRODUCTION

An important objective in nucleic acid research is to understand the forces that contribute to the stability of DNA at physiological conditions. Calorimetric, hydrodynamic, mechano-optical and spectroscopic methods have been extensively employed for this purpose (1–9). A common aim of these studies is to assess the dependence of thermodynamic melting parameters, such as changes in free energy (ΔG), enthalpy (ΔH) and entropy (ΔS) on specific structural or environmental factors, including nearest neighbor interactions of the bases, backbone conformation, phosphate electrostatic environment, degree of helix hydration, superhelical density, protein binding, small molecule ligation, and the like (10–13). Calorimetric (ΔH_cal) and van’t Hoff (ΔH_vH) enthalpies of DNA melting and derived thermodynamic parameters have been extensively reported (14–16). Current data tabulations rely primarily on the results of differential scanning calorimetry (DSC) and ultraviolet (UV) absorption or circular dichroism (CD) measurements (12,17,18).

Recently, temperature-dependent Raman spectra have also been used to calculate thermodynamic parameters of DNA melting (19). The Raman results were found to compare favorably with those obtained from calorimetric and optical spectroscopic determinations. An advantage of the Raman method is that it offers a diversity of spectral bands for thermodynamic analysis. Typically, the Raman spectrum of DNA comprises several dozen well resolved bands, each originating from a specific and highly localized normal mode of vibration of a base, sugar or phosphate moiety (20). The temperature dependency of a given band directly reflects changes in the local conformation or interactions of the vibrating group to which it corresponds. In principle, Raman melting profiles of double-stranded (ds) DNA can provide thermodynamic parameters governing changes in (i) Watson– Crick base pairing, (ii) base stacking, (iii) phosphate– counterion interactions and (iv) phosphodiester conformation. Whereas changes in (i), (ii) and (iii) with increasing temperature are thermodynamically unfavorable to double helix formation, changes in (iv) are favorable, owing to the positive entropy change with increasing torsional freedom of phosphodiester linkages. Raman spectroscopy has the potential to resolve each of these factors and the related thermodynamic constants (19,21,22). DNA structural perturbations that precede the onset of strand separation, or premelting (10), can also be probed by the Raman approach (21,22).

The use of Raman spectroscopy to investigate thermally induced structure transformations of nucleic acids was initiated in several laboratories in the early 1970s (23–28). Since that time, dramatic improvements in the versatility and sensitivity of Raman instrumentation have greatly enhanced the potential of the method (19,21,22). In recent years, studies of thermally induced structural changes of DNA have combined the data of Raman spectroscopy with other approaches, including DSC (19), sequence analysis (29), ultraviolet-resonance Raman (UVRR) spectroscopy (30), CD and Fourier-transform infrared (FTIR) spectroscopies (31) and superheating of solutions at high pressure (32).

In this paper, we describe methods for thermodynamic analysis of temperature-dependent Raman spectra of double-helical B DNA. The methodology, which has the capability to delineate enthalpic and entropic contributions to DNA melting and premelting transitions, is applied here to the sequence isomers, poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT). High-resolution Raman spectral data are available for both of these DNA structures (21,22), and the premelting and melting phases of their denaturation processes are of considerable interest (30,33–36). The thermodynamic parameters calculated from the Raman data are compared with results obtained from previous DSC and optical (UV and CD) spectroscopic analyses.

The present procedures are based only upon the assumption that thermally induced changes in Raman band intensities (or wavenumber values) reflect structural modifications in the DNA subgroups to which the spectral bands are assigned. With reliable assignments this approach can be adapted to other DNA structures as well as to complexes of DNA with proteins and other ligands.

MATERIALS AND METHODS

Sample preparations

Poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) were purchased as sodium salts from Amersham Pharmacia Biotech (Alameda, CA) and used without further purification. Weighed samples were dissolved to 30–40 mg/ml in H₂O containing 100 mM NaCl at pH 7.0 ± 0.1. Aliquots (∼6 µl) of the polydeoxynucleotide solutions were degassed, sealed in glass capillaries (Kimax No. 34502) and maintained at a constant specified temperature during data collection protocols (37).

Raman spectroscopy

Raman spectra were excited with the 514.5-nm line of an argon laser (Innova 70; Coherent Inc., Santa Clara, CA) using ∼200 mW of radiant power at the sample. Spectra were collected in the 90° scattering geometry using a single monochromator spectrograph (Spex 500M; ISA, Edison, NJ) of high spectral resolution (±3 cm^–1) and signal throughput. The instrumentation utilizes a holographic bandpass filter to eliminate interfering laser emissions, a notch filter to reject Rayleigh scattering and a liquid-nitrogen cooled charge-coupled device detector. Typically 7–12 accumulations of 10 s each were averaged to generate the spectral data from which thermodynamic constants were calculated. In terms of overall signal-to-noise ratio, the Raman spectra of poly(dA–dT)· poly(dA–dT) and poly(dA)·poly(dT) were improved by ∼10² over previously published data (34,38). Further details of the spectrometer and data collection protocols have been described (19,21,22,39).

Raman spectra were collected at intervals of 5°C in the range 5–95°C on samples maintained to within ±0.5°C of the temperature indicated, which reflects the solution temperature near the focus of the laser beam as measured by a calibrated thermocouple insert. Raman intensities were normalized using the peak height of the band at 1092 cm^–1, which is assigned to the PO₂^– symmetric stretching mode of the polydeoxynucleotide phosphate group. The peak height of the 1092 cm^–1 band is a reliable intensity standard for both native and synthetic DNAs of the B conformation throughout the temperature range 10–90°C (19,39). The invariance of the 1092 cm^–1 band intensity was verified independently in the present study using the 980 cm^–1 band of SO₄^2– (Na₂SO₄, added as an intensity standard). Digital subtractions of spectra for measurement of intensity differences of DNA were carried out as in previous work (13,19).

Thermodynamic parameters

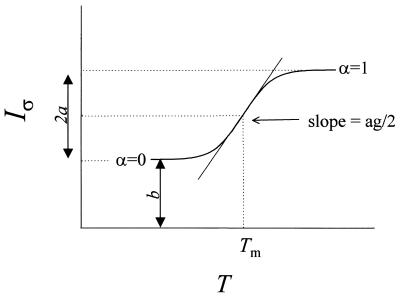
Using the formalism of Breslauer and co-workers (12,14,18) and others (6,8,40), we assume a reversible transition between ds and single-stranded (ss) DNA. At temperature T the fractions of molecules present as ssDNA and dsDNA are α(T) and 1 – α(T), respectively. For a transition profile that is symmetrical with respect to the median melting temperature (T_m), α(T) = x/2a, where x is the absolute value of the difference between the ordinate at T and at a temperature corresponding to the duplex (α = 0), and 2a is the maximum change in ordinate between the two temperatures, as shown in Figure 1. Equilibrium melting properties are extracted from the thermal profile of a Raman band fitted to a plot of α(T) versus T (14). The van’t Hoff transition enthalpy is derived from the equilibrium constant K(T) for dsDNA dissociation as follows:

Figure 1.

Idealized melting profile for a Raman band of dsDNA that is intrinsically hypochromic with respect to double-strand formation. The abscissa is the temperature (T) and the ordinate is the normalized intensity (I_σ) of the Raman band at wavenumber σ. The low temperature limit (left asymptote) corresponds to the duplex structure and the high temperature limit (right asymptote) corresponds to the random-coil single strand. Labels refer to the parameters of the empirical fitting function of equation 6, the definition of α(T), and the slope at the mid-point (arrow) of the transition (see text). The melting temperature T_m is defined as the temperature at which α(T) = 1/2 and I_σ = a + b.

ΔH_vH = RT²{[d ln K(T)]/dT}_T=Tm = –R{d[ln K(T)]/d(1/T)}_T=Tm1

In terms of α(T), T_m and the reaction stoichiometry (n = 2), ΔH_vH is given by:

ΔH_vH = (2n + 2)RT²_m(∂α/∂T)_T=Tm = 6RT_m²(∂α/∂T)_T=Tm2

The standard-state free energy change (ΔG°) is given by:

ΔG° = –RT ln K(T) = –RT ln {[α(T)X_T]/[1 – α(T)]ⁿ}3

where X_T = (n/C_T)^n–1 for non-self-complementary strands and X_T = (1/nC_T^n–1) for self-complementary strands, and C_T is the total strand concentration (14). The van’t Hoff entropy (ΔS_vH) is given by:

ΔS_vH = ΔH_vH/T_m 4

Also, the size of the cooperative unit for the two-state transition, 〈n_melt〉, can be inferred by comparing ΔH_vH with the calorimetric enthalpy, ΔH_cal (19):

〈n_melt〉 = ΔH_vH/ΔH_cal5

Data analysis

Curve fitting of Raman melting profiles and calculation of the van’t Hoff enthalpy and entropy of melting. Figure 1 illustrates non-linear curve fitting of an idealized temperature-dependent Raman band exhibiting hypochromic behavior. Such a two-state melting profile can be fitted satisfactorily by a simple sigmoidal function f(T), given by:

f(T) = {(2a + b)exp[g(T – T_m)] + b}/{exp[g(T – T_m)] + 1}6

where T_m is the melting transition temperature, and a and b are positive constants defining the lower and upper limits of the ordinate (Raman spectral band intensity). The steepness of the transition is represented by the factor g, which is positive for a hypochromic band and negative for a hyperchromic band. In accordance with the definition of α(T), equation 6 can be rearranged to yield:

α(T) = [f(T) – b]/2a and (∂α/∂T)_T=Tm = g/4 for a hypochromic band7

and

α(T) = [2a + b – f(T)]/2a and (∂α/∂T)_T=Tm = –g/4 for a hyperchromic band8

With equations 7 and 8, the thermodynamic parameters obtained from a particular Raman band are:

ΔH_vH = (3/2)RT_m²|g|9

ΔS_vH = (3/2)RT_m|g|10

Curve fitting and derivation of thermodynamic parameters were performed using the SigmaPlot 6.0 software package (SPSS Inc., Chicago, IL).

Calculation of the base stacking free energy. The base stacking free energy (ΔG_st) of dsDNA is defined as the lowering in free energy that results from stacking of Watson–Crick base pairs. A typical Raman melting curve exhibits variable slope with a maximum at the mid point (T_m) of the transition (Fig. 1). At T_m, the normalized Raman intensity is b + a and the slope is ag/2. ΔG_st can be calculated from the slope of the Raman melting curve at T = T_m (41):

T_m(∂α/∂T)_T=Tm = 0.13τ^2/3     (for self-complementary strands)11a

or

T_m(∂α/∂T)_T=Tm = 0.13(τ/2)^2/3     (for non-self-complementary strands)11b

where

τ = exp[–(ΔG_st/RT_m)]12

In terms of the experimental parameter g of the Raman melting curve (equation 7 or 8), we obtain from equation 12:

ΔG_st = [–(3RT_m/2)] ln [(|g|T_m)/0.52]     (for self-complementary strands)13a

or

ΔG_st = [–(3RT_m/2)] ln {[(|g|T_m)/0.52](1/0.63)}     (for non-self-complementary strands)13b

The slope of the melting transition also provides information on the average length (〈h〉) of non-melted segments of dsDNA at T_m (41):

〈h〉 = (t_m/0.302)[(∂α/∂T)_T=Tm] = (|g|t_m)/1.20814

where t_m is the melting temperature in °C units. Finally, the melting cooperativity coefficient (σ) can be calculated from 〈h〉 through the relationship (19):

σ = (1/〈h〉)²15

RESULTS

Derivation of thermodynamic constants from Raman spectra

Detailed Raman band assignments and structural interpretations for the temperature-dependent Raman spectra of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) have been given previously (21,22). At physiological temperature, both sequence isomers adopt a conformation of the B-DNA type, and both exhibit well-defined premelting and melting transitions. For poly(dA–dT)·poly(dA–dT), the temperature domains of premelting (10 < t < 66°C) and melting (66 < t < 75°C) are ∼5–6°C lower than those of poly(dA)·poly(dT) (10 < t < 70°C and 70 < t < 80°C, respectively). At temperatures above 80°C, no further structural changes are evident from the Raman spectra. Although both poly(dA– dT)·poly(dA–dT) and poly(dA)·poly(dT) exhibit Raman markers of the B-DNA conformation, their Raman spectra are not identical at any temperature prior to the onset of melting. A distinctive Raman signature persists for each duplex throughout the premelting phase; conversely, the melting signatures of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are very similar.

The Raman bands of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) that exhibit measurable temperature dependency are listed in the first columns of Tables 1 and 2, respectively. The bands are grouped from top to bottom within the table in accordance with their assignment to adenine only, thymine only, or the sugar–phosphate backbone. Other columns of the tables list parameters relating to equations 6–8 and 11–15. Thermodynamic melting parameters obtained from equations 1–5 and 9–10 are given for both duplexes in Table 3. Similar analyses applied to the pre melting phases of poly(dA–dT)·poly(dA–dT) and poly(dA)· poly(dT) yield the data of Table 4. In the foregoing analyses, we have focussed on the use of Raman bands that represent highly localized vibrations and exhibit minimal spectral overlap. Nevertheless, the intrinsic cooperativity of DNA melting imposes some degree of coupling between structural transitions monitored by Raman markers of A and T. Accordingly, the thermodynamic parameters derived from Raman markers of each base represent primarily, but not exclusively, the specific contribution of that base. More detailed discussions of these tabulations are given below.

Table 1. Temperature dependency and derived thermodynamic constants for selected Raman bands of poly(dA–dT)·poly(dA–dT)^a.

Band (cm–1)	Assignmentb	tm [Δtm] (°C)	g (°C–1)	ΔGstc (kcal·molbp–1)	〈h〉 (bp)	σ × 104 (bp–2)
728	A	71.4 ± 0.2 [10]	0.77 ± 0.08	–6.40	45	4.8
1209	A	73.1 ± 2.4 [16]	0.97 ± 1.09	–6.67	58	2.9
1262	A	73.2 ± 1.1 [9]	–0.04 ± 0.01	d	d	d
1301	A	71.6 ± 0.3 [12]	0.64 ± 0.06	–6.02	31	10.4
1513	A	71.5 ± 0.4 [16]	–0.03 ± 0.01	d	d	d
1579	A	71.4 ± 1.1 [5]	1.07 ± 0.09	–6.74	63	2.5
1016	T	75.2 ± 1.0 [<2]	0.66 ± 0.08	–6.33	41	5.8
1144	T	69.9 ± 1.1 [14]	–0.29 ± 0.08	d	d	d
1182	T	72.4 ± 0.2 [16]	0.62 ± 0.04	–6.20	37	7.3
1236	T	71.6 ± 0.1 [15]	0.48 ± 0.02	–5.92	28	12.4
1375	T	72.2 ± 1.0 [12]	0.63 ± 0.24	–6.21	38	7.0
1673	T	70.9 ± 1.0 [5]	0.82 ± 0.19	d	d	d
792	dp	71.6 ± 0.7 [∼16]e	–0.32 ± 0.06	–	–	–
842	dp	71.2 ± 0.9 [∼17]e	–0.05 ± 0.01	–	–	–
924	dr	71.8 ± 2.9 [∼10]e	–0.43 ± 0.04	–	–	–

^aWavenumber values and assignments for poly(dA–dT)·poly(dA–dT) are from Movileanu et al. (21). Melting temperature (t_m), melting range (Δt_m) and steepness factor (g) are defined in the text.

^bA, T, dr or dp indicates a band due to adenine, thymine, deoxyribose or deoxyribose-phosphate, respectively.

^cAverage stacking free energies obtained from the tabulated data for adenine, thymine and all bases are ΔG_st^A = –6.46 ± 0.33, ΔG_st^T = –6.17 ± 0.17 and ΔG_st^A,T = –6.31 ± 0.29 kcal·mol_bp^–1, respectively. Only Raman bands that are assignable exclusively to either A or T and that do not vary significantly in band center or band width with temperature are included. Here and in subsequent tables, averages and standard deviations for subsets were obtained by weighing equally the entries contributing to each subset. The overall average and deviation were computed by weighing equally all entries of all subsets.

^dData do not permit a reliable determination. See text.

^eEstimated value for the melting domain only; for the combined premelting and melting domains, ΔT > 20°C. See text.

Table 2. Temperature dependency and derived thermodynamic constants for selected Raman bands of poly(dA)·poly(dT)^a.

Band (cm–1)	Assignmentb	tm [Δtm] (°C)	g (°C–1)	ΔGstc (kcal·molbp–1)	〈h〉 (bp)	σ × 104 (bp–2)
728	A	76.8 ± 0.5 [16]	–1.05 ± 0.06	–7.32	66	2.3
1209	A	76.1 ± 0.5 [7]	–1.15 ± 0.07	–7.40	72	1.9
1262	A	75.4 ± 0.8 [12]	–0.35 ± 0.06	d	d	d
1301	A	76.2 ± 0.4 [13]	0.66 ± 0.08	–6.83	42	5.6
1513	A	75.2 ± 0.5 [14]	–0.44 ± 0.05	d	d	d
1579	A	76.8 ± 0.9 [5]	1.16 ± 0.12	–7.43	74	1.8
1016	T	76.1 ± 0.5 [<4]	0.35 ± 0.06	–6.17	22	20.3
1144	T	76.1 ± 0.8 [14]	–0.56 ± 0.07	d	d	d
1182	T	76.1 ± 0.6 [9]	0.58 ± 0.08	–6.68	36.4	7.5
1236	T	76.3 ± 0.5 [9]	0.56 ± 0.06	–6.65	35	8.0
1375	T	76.4 ± 0.9 [12]	0.54 ± 0.06	–6.62	34	8.5
1673	T	76.6 ± 0.9 [6]	1.10 ± 0.12	d	d	d
792	dp	76.9 ± 0.6 [∼6]e	–0.87 ± 0.06	–	–	–
842	dp	75.3 ± 0.7 [∼9]e	–0.56 ± 0.05	–	–	–
924	dr	76.9 ± 1.1 [∼9]e	–0.62 ± 0.06	–	–	–

^aWavenumber values and assignments for poly(dA)·poly(dT) are from Movileanu et al. (22). Melting temperature (t_m), melting range (Δt_m) and steepness factor (g) are defined in the text.

^bA, T, dr or dp indicates a band due to adenine, thymine, deoxyribose or deoxyribose-phosphate, respectively.

^cAverage stacking free energies obtained from the tabulated data for adenine, thymine and all bases are ΔG_st^A = –7.25 ± 0.28, ΔG_st^T = –6.53 ± 0.24 and ΔG_st^A,T = –6.88 ± 0.45 kcal·mol_bp^–1, respectively. Only Raman bands that are assignable exclusively to either A or T and that do not vary significantly in band center or band width with temperature are included.

^dData do not permit a reliable determination. See text.

^eEstimated value for the melting domain only; for the combined premelting and melting domains, ΔT > 20°C. See text.

Table 3. Thermodynamic parameters for melting transitions of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT)^a.

Band (cm–1)	Assignment	Poly(dA–dT)·poly(dA–dT)				Poly(dA)·poly(dT)
		ΔHvH (kcal·mol–1)	ΔSvH (cal·°K–1·mol–1)	ΔGvH(25°C) (kcal·mol–1)	〈nmelt〉 (bp)	ΔHvH (kcal·mol–1)	ΔSvH (cal·°K–1·mol–1)	ΔGvH(25°C) (kcal·mol–1)	〈nmelt〉 (bp)
728	A	272	790	36.5	32	381	1090	56.5	43
1209	A	345	997	47.7	41	418	1197	61.0	47
1579	A	378	1097	50.9	45	424	1212	62.6	48
Average	A	333 ± 54	961 ± 157	45.0 ± 7.6	39 ± 7	407 ± 23	1166 ± 67	60.0 ± 3.2	46 ± 3
1016	T	241	691	35.0	29	128	366	18.9	14
1182	T	219	635	29.7	26	210	602	30.5	24
1236	T	170	493	23.0	20	203	581	29.8	23
1375	T	223	649	29.5	27	197	564	29.0	22
Average	T	213 ± 30	617 ± 86	29.3 ± 4.9	26 ± 4	185 ± 38	516 ± 109	27.1 ± 5.5	21 ± 5

^aVan’t Hoff melting (ΔH_vH, ΔS_vH, ΔG_vH(25°C)) and melt-size (〈n_melt〉) parameters for poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are given in the left and right halves of the table, respectively, and are based upon analysis of bands assigned to A and T as indicated in the second column. The combined analysis of all bands of poly(dA–dT)·poly(dA–dT) yields ΔH_vH^A,T = 272 ± 71 kcal·mol^–1, ΔS_vH^A,T = 789 ± 206 cal·°K^–1·mol^–1, ΔG_vH(25°C)^A,T = 37.1 ± 9.7 kcal·mol^–1, 〈n_melt〉 = 32 ± 8 bp; combined analysis for poly(dA)·poly(dT) gives ΔH_vH^A,T = 296 ± 117 kcal·mol^–1, ΔS_vH^A,T = 847 ± 335 cal·°K^–1·mol^–1, ΔG_vH(25°C)^A,T = 43.5 ± 17.0 kcal·mol_bp^–1, 〈n_melt〉 = 33 ± 13 bp. Calculations of 〈n_melt〉 by equation 5 are based upon the published calorimetric enthalpies, ΔH_cal = 8.4 kcal·mol_bp^–1 for poly(dA–dT)·poly(dA–dT) and ΔH_cal = 8.9 kcal·mol_bp^–1 for poly(dA)·poly(dT) (43,44).

Table 4. Van’t Hoff premelting enthalpies and entropies of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT)^a.

Band (cm–1)	Assignmentb	Poly(dA–dT)·poly(dA–dT)			Poly(dA)·poly(dT)
		Tpm (°C)	ΔHvHpm (kcal·mol–1)	ΔSvHpm (cal·°K–1·mol–1)	Tpm (°C)	ΔHvHpm (kcal·mol–1)	ΔSvHpm (cal·°K–1·mol–1)
792	dp	30	14.7 ± 1.9	48.0 ± 5.7	41	18.0 ± 1.9	57.3 ± 6.1
842	dp	30	15.0 ± 1.2	49.5 ± 4.0	38	19.7 ± 1.1	63.3 ± 3.5
924	dr	37	10.5 ± 0.8	33.9 ± 2.6	39	16.4 ± 1.3	52.6 ± 4.2
Average		32 ± 4	13.4 ± 2.5	43.8 ± 8.6	39 ± 1	18.0 ± 1.6	57.7 ± 5.4

^aVan’t Hoff premelting parameters (T_pm, ΔH_vH^pm, ΔS_vH^pm) for poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are given in the left and right halves of the table, respectively, and are based upon analysis of bands assigned to the DNA backbone as indicated in the second column.

^bdp or dr indicates a band assigned to the deoxyribose-phosphate or deoxyribose moiety, respectively.

Melting and premelting transitions

To characterize the melting transitions of poly(dA–dT)· poly(dA–dT) and poly(dA)·poly(dT), we obtained temperature profiles (melting curves) for all Raman bands of the deoxyadenosine (dA) and thymidine (dT) residues that exhibited behavior consistent with a two-state transition (Fig. 1 and equation 6). Several such bands were identified by Movileanu et al. (21). Non-linear curve fitting was applied to each band to determine the midpoint of the transition (t_m) and the corresponding steepness factor (g) (Tables 1 and 2). Another Raman indicator of melting cooperativity is the temperature range (Δt_m) over which 90% of the total change in Raman band intensity occurs, in accordance with equation 6 and Figure 1. The calculated Δt_m values for each band of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are included in Tables 1 and 2, respectively. The data indicate for poly(dA–dT)·poly(dA–dT) an average melting temperature 〈t_m〉 = 71.9 ± 1.2°C, and for poly(dA)·poly(dT) 〈t_m〉 = 76.2 ± 0.6°C.

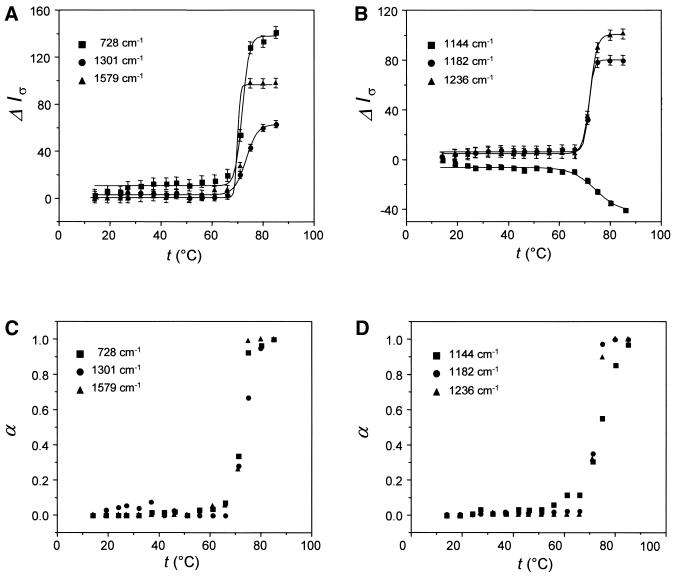
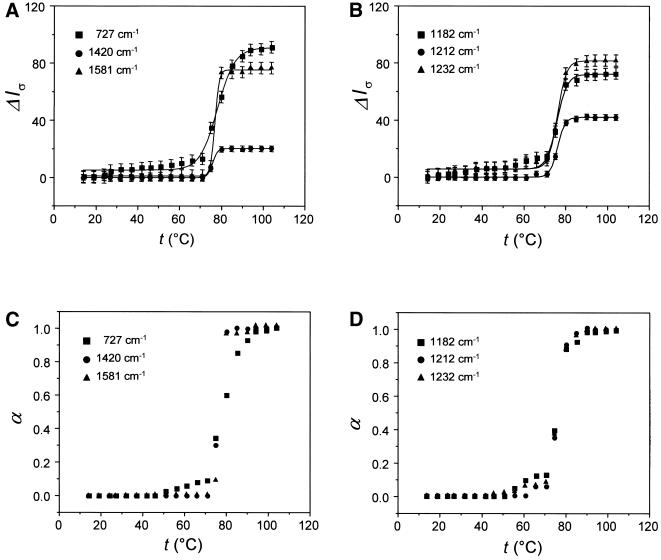
Temperature profiles for representative Raman bands of the dA and dT residues of poly(dA–dT)·poly(dA–dT) are shown in Figure 2. Corresponding data for poly(dA)·poly(dT) are shown in Figure 3. Each band has been assigned to a vibration localized largely within the base residue and each exhibits Raman intensity that is sensitive to base unstacking with increasing temperature (21,24). Interestingly, the band of dT near 1144 cm^–1 is hyperchromic; all others are hypochromic with respect to base stacking.

Figure 2.

Melting profiles for selected Raman bands of dA (A) and dT residues (B) of poly(dA–dT)·poly(dA–dT). The ordinate ΔI_σ represents the Raman intensity difference for the band at the indicated wavenumber value. The intensity scale is arbitrary, but the relative intensity changes for the respective bands are accurately represented. Thus, in (A), the hypochromicity of the 1579 cm^–1 band is approximately twice that of the 1301 cm^–1 band and approximately two-thirds that of the 728 cm^–1 band (21). Normalized melting profiles plotted as α(T) versus temperature are shown in (C) and (D).

Figure 3.

Melting profiles for selected Raman bands of dA (A) and dT residues (B) of poly(dA)·poly(dT). Conditions are as given in the legend of Figure 2. Normalized melting profiles plotted as α(T) versus temperature are shown in (C) and (D).

Despite large intensity changes in the melting domain, all Raman bands depicted in Figures 2 and 3 show little or no intensity change in the premelting domain. Conversely, certain other Raman bands exhibit temperature dependence that departs substantially from the idealized two-state transition behavior of Figure 1 (21; data not shown). Such bands generally occur within the spectral interval 600–900 cm^–1 and have been assigned to vibrational modes localized mainly in the deoxyribose-phosphate moiety (21). Several are included in the bottom sections of Tables 1 and 2. The temperature-dependent behavior of these bands is considered typical of non-cooperative structural change.

Base stacking (melting) free energy

The base stacking free energy (ΔG_st) is strongly correlated with the melting temperature (t_m) and steepness factor (g) of the melting transition (equation 13) (42,43). Although ΔG_st may be calculated from the melting profile of any Raman band assigned to a base vibration, those exhibiting a relatively narrow melting interval (Δt_m < 20°C) and precisely determined steepness factor (large g) are expected to provide the more accurate determinations.

Values of ΔG_st determined from various Raman bands of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are listed in Tables 1 and 2. Reliable values for the adenine stacking free energy (ΔG_st^A) are obtained from dA markers at 728, 1209 and 1579 cm^–1. Excellent results are also obtained from the band at 1301 cm^–1, which is due predominantly to dA residues. Similarly, the thymine stacking free energy (ΔG_st^T) is reliably obtained from thymine markers at 1016, 1182, 1236 and 1375 cm^–1. The average adenine and thymine stacking free energies in poly(dA–dT)·poly(dA–dT) (Table 1) are ΔG_st^A = –6.46 ± 0.33 and ΔG_st^T = –6.17 ± 0.17 kcal·mol_bp^–1 (kilocalories per mole base pair). For both base types combined, ΔG_st^A,T = –6.31 ± 0.29 kcal·mol_bp^–1. The apparent difference between adenine and thymine stacking free energies in poly(dA–dT)· poly(dA–dT) (ΔΔG_st ∼ 0.3 kcal·mol_bp^–1) may be significant.

The average adenine and thymine stacking free energies in poly(dA)·poly(dT) (Table 2) are ΔG_st^A = –7.25 ± 0.28 kcal·mol_bp^–1 and ΔG_st^T = –6.53 ± 0.24 kcal·mol_bp^–1. For both base types, ΔG_st^A,T = –6.88 ± 0.45 kcal·mol_bp^–1. We find that ΔG_st values of poly(dA)·poly(dT) are consistently larger than their counterparts in poly(dA–dT)·poly(dA–dT), even though the differences observed between the two duplexes are rather close to the limits of experimental uncertainty (Tables 1 and 2). Greater stacking energy in poly(dA)·poly(dT) is con sistent with its higher melting temperature compared with poly(dA–dT)·poly(dA–dT).

Raman markers near 1144 (dT), 1262 (dA), 1513 (dA) and 1673 cm^–1 (dT), although affected by base stacking (21,22), are not well suited for ΔG_st determinations either because of inherent band broadness, low intensity, significant shift of the band center with temperature, overlap with one or more other temperature-dependent Raman bands, low cooperativity (small steepness factor) or a combination of these characteristics.

The van’t Hoff melting enthalpy, entropy and free energy

The van’t Hoff enthalpy (ΔH_vH) of melting, which is defined by equation 1, can be determined from the temperature dependency of the Raman band melting parameter α given in equation 2. Table 3 lists values of ΔH_vH determined for poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) from Raman bands of the bases that exhibit the appropriate properties noted in the preceding section. The enthalpy of melting of poly(dA)·poly(dT) clearly exceeds that of poly(dA–dT)·poly(dA–dT). Interestingly, in both duplexes Raman bands of dA yield a significantly higher van’t Hoff enthalpy than bands of dT.

The van’t Hoff entropy (ΔS_vH) of the melting transition is given by equation 4. Table 3 lists the values obtained from several Raman bands. The results indicate similar overall melting entropies for the two duplexes, although the dA residues consistently exhibit a higher van’t Hoff melting entropy than dT residues.

The van’t Hoff free energy change for the melting transition at 25°C (16), which is obtained from the relation ΔG_vH(25°C) = ΔH_vH – 298.15ΔS_vH, is also listed for each band in Table 3. In accord with the ΔH_vH and ΔS_vH results, the computed ΔG_vH(25°C) value for dA greatly exceeds that for dT in each duplex. Thus, in the case of poly(dA–dT)·poly(dA–dT) we find ΔG_vH(25°C)^A = 45.0 ± 7.6 kcal·mol^–1 (kilocalories per mole cooperative unit) and ΔG_vH(25°C)^T = 29.3 ± 4.9 kcal· mol^–1, and for poly(dA)·poly(dT) we obtain ΔG_vH(25°C)^A = 60.0 ± 3.2 kcal·mol^–1 and ΔG_vH(25°C)^T = 27.1 ± 5.5 kcal· mol^–1.

The number of base pairs in the cooperative melting unit, 〈n_melt〉, can be obtained from the van’t Hoff (ΔH_vH) and calorimetric (ΔH_cal) transition enthalpies using equation 5 (19) and previously reported calorimetric data (43,44). Results are included in Table 3. For both duplexes, the overall cooperative melting unit falls within a relatively narrow range, roughly 20 < 〈n_melt〉 < 45 bp. The apparent cooperative melting unit for dA residues is significantly larger than that for dT residues. The presently measured range for 〈n_melt〉 compares favorably with the range indicated for 〈h〉, the average helix length at t_m (Tables 1 and 2). The Raman-based length parameters 〈n_melt〉 and 〈h〉 are also in accord with values determined by calorimetric methods (43).

The parameter 〈h〉 provides the basis (equation 15) for calculation of the cooperativity parameter σ, listed in Tables 1 and 2. Thus, for the dA and dT Raman markers noted above, a modest range of values is observed for the cooperativity parameter, consistent with previous determinations (45,46).

The van’t Hoff premelting enthalpy

Table 4 shows that the median premelting temperature (T_pm) of poly(dA–dT)·poly(dA–dT) is 32 ± 4°C, while that of poly(dA)·poly(dT) is 39 ± 1°C. Averaging of the van’t Hoff premelting enthalpy data for poly(dA–dT)·poly(dA–dT) gives ΔH_vH^pm = 13.4 ± 2.5 kcal·mol^–1, and for poly(dA)·poly(dT) ΔH_vH^pm = 18.0 ± 1.6 kcal·mol^–1. These results suggest that in each duplex the van’t Hoff premelting enthalpy is ∼20 times smaller than the van’t Hoff melting enthalpy.

DISCUSSION

Previous spectroscopic and calorimetric studies of dsDNA have established a range of premelting temperatures within which the double helix is conformationally altered but not dissociated into single strands (10,21,27,28). These earlier studies show that DNA premelting is not sequence specific, although the phenomenon has been most extensively investigated for DNA molecules containing (dA)_n·(dT)_n tracts (22,30,35,36,47,48). A comparison of previous and present results on DNA containing (dA)_n·(dT)_n tracts is given in Table 5.

Table 5. Premelting parameters for DNA containing (dA)·(dT) tracts determined by different spectroscopic methods.

Method	Sample	Tpm (°C)	ΔHvHpm (kcal·mol–1)	Reference
UV	Poly(dA)·poly(dT)	30	20	Herrera and Chaires (53)
CD	Poly(dA)·poly(dT)	39	20 ± 5	Chan et al. (35)
Raman	Poly(dA)·poly(dT)	39 ± 1	18.0 ± 1.6	This work
CD	(dA)5·(dT)5a	32 ± 2	16	Chan et al. (36)a
CD	d(CGCAAATTTGCG)	30	15	Mukerji and Williams (48)

^aDetermined for phased (dA)₅·(dT)₅ tracts in 45-bp DNA.

In oligonucleotide X-ray crystal structures, the (dA)_n·(dT)_n tract exhibits highly propeller-twisted base pairs, which are compatible with three-centered hydrogen bonds involving an N6H₂ donor in the adenine strand with two C4O acceptors in the opposing thymine strand (49–51). The X-ray structure suggests a simple mechanism to account for premelting in DNA containing (dA)_n·(dT)_n tracts; namely, the conversion of the three-centered A·T hydrogen bonds to conventional Watson–Crick hydrogen bonds. While such a mechanism is consistent with the premelting evidenced in Raman spectra of poly(dA)·poly(dT) (22), it does not account for the similar observation on poly(dA–dT)·poly(dA–dT) (21). Three- centered hydrogen bonds are not observed in oligonucleotide crystal structures containing the alternating d(AT)_n tract (52). We conclude that the premelting transitions monitored by temperature-dependent Raman band profiles do not simply reflect the elimination of three-centered hydrogen bonding between A and T in (dA)_n·(dT)_n tracts.

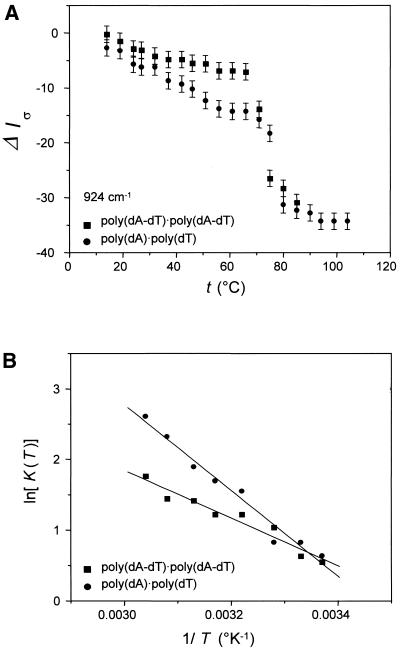
Figure 4A compares temperature-dependent Raman intensity profiles of the 924 cm^–1 bands of poly(dA–dT)· poly(dA–dT) and poly(dA)·poly(dT). The 924 cm^–1 marker, which is assigned to the deoxyribosyl moiety, is very sensitive to premelting in each duplex. For both poly(dA–dT)· poly(dA–dT) and poly(dA)·poly(dT) the band suffers significant intensity change throughout the premelting range (10 < t < 60°C), typical of a non-cooperative structural transition. The van’t Hoff premelting enthalpy ΔH_vH^pm and premelting entropy ΔS_vH^pm associated with the change in deoxyribosyl backbone conformation in each DNA is obtained from the corresponding slope of Figure 4B. Comparable results for other temperature-dependent backbone markers of the two DNAs are listed in Table 4. Although the average premelting parameters for poly(dA–dT)·poly(dA–dT) (ΔH_vH^pm = 13.4 ± 2.5 kcal·mol_bp^–1, ΔS_vH^pm of 43.8 ± 8.6 cal·°K^–1·mol^–1) are measurably lower than those for poly(dA)·poly(dT) (ΔH_vH^pm = 18.0 ± 1.6 kcal·mol_bp^–1, ΔS_vH^pm = 57.7 ± 5.4 cal·°K^–1·mol^–1), it is clear that robust premelting transitions occur in both DNAs.

Figure 4.

(A) Premelting (t < 65°C) and melting (t > 65°C) profiles of the deoxyribosyl Raman marker at 924 cm^–1 in poly(dA–dT)·poly(dA–dT) (squares) and poly(dA)·poly(dT) (circles). (B) Semi-logarithmic van’t Hoff plots [ln K(T) versus 1/T] for the premelting data of (A).

The premelting phenomena of poly(dA–dT)·poly(dA–dT) and poly(dA)·poly(dT) are similar with respect to temperature interval, non-cooperativity, Raman band sensitivity and enthalpic and entropic costs. This suggests a similar molecular mechanism for premelting. We propose that the premelting detected by Raman spectroscopy represents a change in the state of hydration of the double helix and that this change in hydration state is accompanied by a conformational adjustment to the deoxyribosyl-phosphate backbone. We note that a similar conclusion was reached by Herrera and Chaires (53), who attributed premelting to the disruption and release of an ordered ‘spine of hydration’ in the relatively narrow minor groove of poly(dA)·poly(dT). The alternating d(AT)_n sequence of poly(dA–dT)·poly(dA–dT), which can also adopt a conformation characterized by a narrow minor groove and an ordered spine of hydration (51,52), may therefore undergo a structurally and thermodynamically similar premelting transition. This is in complete accord with the similar backbone conformations of poly(dA)·poly(dT) and poly(dA– dT)·poly(dA–dT) at low temperature (22) and with the remarkably close agreement between ΔH_vH^pm determinations by different methods for DNAs containing (dA)_n·(dT)_n tracts (Table 5).

Although the present results support qualitatively similar premelting mechanisms for poly(dA)·poly(dT) and poly(dA– dT)·poly(dA–dT), the two transitions are not identical, as evidenced by the higher enthalpic cost of poly(dA)· poly(dT) premelting (ΔΔH ∼ 4.6 kcal·mol^–1, Table 4). Recently, UVRR and CD spectroscopy have been exploited to probe differences in inter-base hydrogen bonding in oligonucleotides containing (dA)_n·(dT)_n and d(AT)_n tracts (30,48). The UVRR data suggest that three-centered inter-base hydrogen bonding specific to the (dA)_n·(dT)_n tract may contribute ∼20% of the total van’t Hoff premelting enthalpy (measured by CD as ∼15–20 kcal·mol^–1, Table 5), i.e. ∼3–4 kcal·mol^–1. The previous UVRR and present off-resonance Raman analyses of van’t Hoff premelting differences are thus in excellent agreement. We emphasize, however, that because the premelting-sensitive Raman markers of both poly(dA–dT)·poly(dA–dT) and poly(dA)· poly(dT) include bands assigned to vibrational modes of the deoxyribose ring and deoxyribosyl-phosphate linkages the conformational change accompanying premelting cannot be considered localized to inter-base hydrogen-bonding sites. As first suggested in molecular modeling computations (54) and later supported by biochemical experiments (53), hydration and conformation are intimately linked in DNA. Disruption of the ordered spine of hydration affects both backbone helical geometry and inter-base interactions, leading to changes in local (propeller twist) and global (groove dimension) aspects of DNA structure.

Raman-based determinations of premelting (t_pm) and melting (t_m) temperatures, stacking free energy (ΔG_st) and van’t Hoff melting parameters (ΔH_vH^pm, ΔH_vH, ΔS_vH, ΔG_vH(25°C), 〈n_melt〉) provide independent confirmation that poly(dA)·poly(dT) forms a thermodynamically more stable secondary structure than poly(dA–dT)·poly(dA–dT). Stacking free energies and melting temperatures are in excellent accord with the scant data available on related structures (42,44,55–58). Derived values for the parameters 〈h〉 > 25 bp and σ ∼ 10^–3–10^–4 bp^–2 are indicative of highly cooperative melting in both polynucleotide duplexes, also consistent with previously reported findings for other double-helical B DNAs (19,46,59,60).

CONCLUSIONS

We have described procedures for the determination of thermodynamic parameters governing base stacking (ΔG_st), van’t Hoff premelting (ΔH_vH^pm, ΔS_vH^pm) and van’t Hoff melting (ΔH_vH, ΔS_vH, ΔG_vH(25°C), 〈n_melt〉) transitions in DNA of defined base sequences using the data of temperature-dependent Raman spectra. Applications to poly(dA)·poly(dT) and poly(dA–dT)·poly(dA–dT) illustrate the capability to differentiate thermodynamic contributions of A, T and deoxyribosyl-phosphate interactions to the structural transformations of these DNA duplexes. The results affirm and quantify melting and premelting phenomena in DNAs containing (dA)_n·(dT)_n and d(AT)_n tracts. The findings also suggest that A and T melting events may be less coupled in the homopurine and homopyrimidine tracts of poly(dA)·poly(dT) than in the alternating A/T tracts of poly(dA–dT)· poly(dA–dT).

Importantly, these studies reveal robust premelting phenomena for both (dA)_n·(dT)_n (ΔH_vH^pm = 18.0 ± 1.6 kcal· mol^–1) and d(AT)_n (ΔH_vH^pm = 13.4 ± 2.5 kcal·mol^–1) sequences. The observed difference (ΔΔH_vH^pm = 4.6 kcal· mol^–1) is proposed as the enthalpic contribution from three-centered inter-base hydrogen bonding in (dA)_n·(dT)_n tracts. This estimate is in good agreement with a recent independent determination employing UVRR spectroscopy (48).

The present analysis confirms that poly(dA)·poly(dT) is significantly more thermostable (t_m = 76.2 ± 0.6°C) than poly(dA–dT)·poly(dA–dT) (t_m = 71.9 ± 1.2°C). Within experimental uncertainty all Raman bands of a given DNA, irrespective of assignment, yield the same melting temperature (Tables 1 and 2). The enhanced thermostability of poly(dA)·poly(dT) vis-à-vis poly(dA–dT)·poly(dA–dT) is reflected in more robust base stacking interactions (ΔΔG_st ∼ 0.5 kcal·mol_bp^–1) and appreciably greater van’t Hoff melting parameters (e.g. ΔΔG_vH(25°C)^A,T ∼ 6 kcal·mol_bp^–1). We also find that in poly(dA)·poly(dT) the stacking free energy of A exceeds that of T by an amount (ΔΔG_st ∼ 0.8 kcal·mol_bp^–1) comparable to the stacking free energy difference between the two duplexes. This suggests that efficient stacking of adenines along the poly(dA) strand is sufficient to account for the higher van’t Hoff melting enthalpy of poly(dA)·poly(dT).

It should be noted that in the present treatment the thermodynamic parameters for the melting transitions have been computed for the temperature range pursuant to premelting. The combination of premelting (10–40°C) and melting (40–85°C) further underscores the greater overall stability of poly(dA)·poly(dT) vis-à-vis poly(dA–dT)· poly(dA–dT). Thus, the sum of van’t Hoff premelting and melting enthalpies for poly(dA)·poly(dT) is 335 kcal·mol^–1 versus 285 kcal·mol^–1 for poly(dA–dT)·poly(dA–dT).

We have shown that temperature-dependent Raman spectra of poly(dA)·poly(dT) and poly(dA–dT)·poly(dA–dT) have the capability to distinguish contributions of A and T bases and of backbone moieties to the thermodynamic stability of B DNA. The results delineate three molecular mechanisms contributing to DNA stability: base stacking, which is highly cooperative and extensively perturbs vibrational states of base and sugar–phosphate moieties; base pairing, which perturbs vibrational states of localized base sites and is also coupled to base stacking; and backbone conformational ordering, which is highly uncooperative and dominates the premelting interval. We anticipate that the methods used here should be applicable to other DNA sequences and to specific DNA–ligand complexes.