Multistage carcinogenesis and the incidence of colorectal cancer

Abstract

We use general multistage models to fit the age-specific incidence of colorectal cancers in the Surveillance, Epidemiology, and End Results registry, which covers ≈10% of the U.S. population, while simultaneously adjusting for birth cohort and calendar year effects. The incidence of colorectal cancers in the Surveillance, Epidemiology, and End Results registry is most consistent with a model positing two rare events followed by a high-frequency event in the conversion of a normal stem cell into an initiated cell that expands clonally to give rise to an adenomatous polyp. Only one more rare event appears to be necessary for malignant transformation. The two rare events involved in initiation are interpreted to represent the homozygous loss of adenomatous polyposis coli gene function. The subsequent transition of a preinitiated stem cell into an initiated cell capable of clonal expansion via symmetric division is predicted to occur with a frequency too high for a mutational event but may reflect a positional effect in colonic crypts. Our results suggest it is not necessary to invoke genomic instability to explain colorectal cancer incidence rates in human populations. Temporal trends in the incidence of colon cancer appear to be dominated by calendar year effects. The model also predicts that interventions, such as administration of nonsteroidal anti-inflammatory drugs, designed to decrease the growth rate of adenomatous polyps, are very efficient at lowering colon cancer risk substantially, even when begun later in life. By contrast, interventions that decrease the rate of mutations at the adenomatous polyposis coli locus are much less effective in reducing the risk of colon cancer.

The first attempts to formulate a quantitative description of carcinogenesis reflecting essential biological processes on the pathway from a normal cell to a cancer cell go back almost half a century (1). Perhaps the best known model is due to Armitage and Doll (2), who noticed that the age-specific incidence of many carcinomas appeared to increase approximately with power of age, which could be related to the number of rate-limiting steps involved in the formation of a malignant tumor. However, it was also realized that a two-stage model with clonal expansion of intermediate cell populations could generate similar age-specific incidence curves (3). These considerations, combined with the idea of recessive oncogenesis first formulated by Knudson (4), led to the two-stage clonal expansion (TSCE) model, which explicitly incorporates clonal expansion as a stochastic process during carcinogenesis (5–7).

Recent studies of the genetic profiles of various tumors suggest the involvement of several genes during tumorigenesis. A case in point is colorectal cancer, perhaps the best studied cancer in terms of the putative sequence of genetic events in its pathogenesis (8–12). Over the past 10 years, an impressive number of studies have been carried out identifying several molecular pathways involved in the development of colorectal cancer (see ref. 13). To the extent that disruptions of these pathways are associated with early- or late-stage mutations in colon cancer, these studies motivate the use of models with sequential steps for describing the pathogenesis of this cancer. Of particular interest are events leading to clonally expanding cell populations on the pathway to malignancy.

Among the earliest premalignant lesions observed in colorectal cancer are the so-called aberrant crypt foci (ACF). Dysplastic ACF, also referred to as adenomatous crypts or microadenoma, frequently show loss of heterozygosity on 5q, the locus of the adenomatous polyposis coli (APC) gene (14–17). ACF are believed to be precursors to the adenomatous polyps, which in turn are widely believed to be precursor lesions for colon carcinoma. The transition from adenoma to high-grade dysplasia (HGD) appears to involve the TP53 gene, considered a guardian of the genome (12). Once HGD occurs, it has been suggested that “genetic chaos” ensues, setting the stage for malignant transformation (18).

Important insights into age effects and temporal trends in cancer incidence can be obtained from carefully collected data in good population-based registries. The Surveillance, Epidemiology, and End Results (SEER) registry covers ≈10% of the U.S. population and has more than 20 years of incidence data. Our main goal in this paper is to analyze the incidence of colorectal cancers in the SEER database by using extensions of the TSCE model to obtain insights into the number and nature of the steps involved in colon carcinogenesis. The relevant mathematical construct for predicting incidence is the hazard function, which measures the rate of occurrence of cancer in previously tumor-free individuals. The characteristic shape of this function can be shown to depend (although in a complicated way) on the number of rate-limiting events, their rates, and the rate of clonal expansion.

We assume that all individuals in the population are at risk for colon cancer, although variations in susceptibility are known to exist (19). The idea has been suggested that a fraction of the population is “immune” to developing colon cancer (20–22). However, this hypothesis appears inconsistent with the prevailing paradigm that colon cancer is the result of specific somatic mutations.

The analysis of population data is complicated by the fact that the observed incidence of colorectal cancer also reflects temporal trends associated with diet and other lifestyle factors, as well as with progress in cancer screening and detection. To isolate the age effect of cancer, the model-derived hazard function is adjusted for both birth cohort and calendar year. A comprehensive model of the pathogenesis of colon cancer provides a framework for the evaluation of screening, intervention, and prevention strategies.

Materials and Methods

The SEER Data.

Incidence data for cancers of the colon and rectum were obtained from the SEER registry for the years 1973–1996. See the SEER Cancer Statistics Review (23) for details concerning this database. For our analyses, we use the reported incidence of colorectal cancers by gender, race, age, and calendar year in the nine SEER geographic areas, which together represent an estimated 9.5% of the U.S. population. The individual records were screened for ICD9 code 153 (colon excluding rectum), 154.0 and 154.1 (rectum and rectosigmoid), and 230.3 (carcinoma in situ of the colon).

The population bases were obtained from the SEER population files (based on data from the U.S. Census Bureau) by sex and race and were crosstabulated by calendar year (1973–1996) and 5-yr age groups (ages 0–85+). Model fits were restricted to the two largest population subgroups [whites (including white Hispanics) and African Americans], each by gender. For all years combined, a total of about 126,000 white male cases and about the same number of white female cases were available for the analyses. For African Americans, ≈10,000 male and ≈11,000 female cases were available.

Mathematical Model.

We describe a mathematical framework for the sequence of genetic events that define the main pathway in colorectal cancer. A characteristic of this pathway is the recessive loss or mutation of the APC gene before clonally expanding adenomatous polyps occur in the colon. Therefore, it is natural to consider extensions of the TSCE model that allow for additional rate-limiting events before the stage of clonal expansion, reflecting the recessiveness of inactivation of a tumor suppressor or caretaker gene such as the APC gene and possibly the involvement of protooncogenes such as the RAS gene.

The TSCE model posits that a malignant cell arises after two rare events in a susceptible stem cell. After the first event, assumed to occur with rate μ₀ per cell per year, the initiated stem cell expands clonally, giving rise to an intermediate (initiated) lesion. Initiated stem cells divide symmetrically with rate α and die or differentiate with rate β. With rate μ₁, however, an initiated cell may divide asymmetrically, giving rise to a malignant daughter cell, the progenitor of a carcinoma. Although malignant tumor progression can also be modeled as a stochastic process (see ref. 24), we treat the time between the occurrence of the first malignant cell and clinical detection of a carcinoma as a constant. Because the results of our analyses are not very sensitive to the choice of this lag time, we set it to zero. The growth of the intermediate lesion is described mathematically by a stochastic birth–death process. The assumption here is that cell birth and cell death (or differentiation) are independent random processes with exponential waiting times, which is clearly an oversimplification. Further details can be found in refs. 6, 7, and 25.

A logical extension of the TSCE model, consistent with the ideas mentioned in the introduction, is a model in which colonic stem cells may undergo a series of preinitiation steps, accumulating mutations that disrupt homeostasis and set the stage for clonal expansion. We define “promotion” as the clonal expansion of initiated cells, the result of which is amplification of the pool of initiated cells increasing the probability that an initiated cell will become malignantly transformed. According to this model, preinitiated stem cells do not give rise to clonally expanding populations until they have accumulated a critical number of events in their genome. Colonic stem cells, assumed to reside near the bottom of the crypts of the colon (26), appear to divide continually in asymmetric fashion feeding cells into the proliferative zone of the crypts (27). Cells in this zone are in transition and will either differentiate further (into Goblet or Paneth cells) or migrate further up toward the intestinal lumen. However, if as a result of genomic alterations, normal (asymmetric) division is perturbed, leading occasionally to a division in which both daughters retain the clonogenic characteristics of a stem cell, altered stem cells may accumulate. Within the framework of the models presented in Fig. 1, the basic process that leads to such perturbations is assumed to be a stem cell division that gives rise to a daughter cell with a specific genomic defect and a daughter that retains the genetic makeup of the original stem cell. Mathematically, this process is described by an asymmetric cell division process. Phenotypically, however, this division may appear symmetric. Clonal expansion leading eventually to an adenomatous polyp occurs only after the stem cell has become initiated. The majority of divisions of initiated stem cells are asymmetric, but a few are symmetric, setting the stage for clonal expansion if not compensated for by apoptosis. A consequence of this model is that an adenomatous polyp will contain both initiated stem cells and differentiated cells.

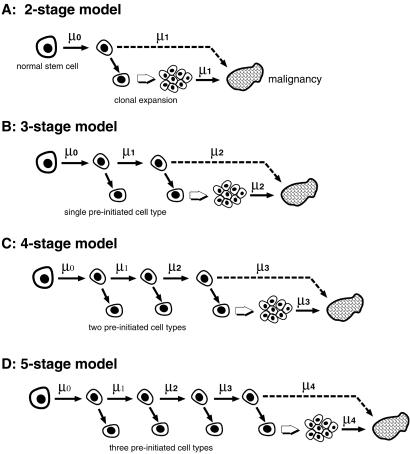
Fig 1.

Schematic representation of the TSCE model (A) for colon cancer together with its three- (B), four- (C), and five-stage (D) extensions. Shown is the stepwise progression of a normal stem cell to an initiated cell. With the exception of the TSCE model, this involves preinitiation stages. Once initiated, stem cells may divide symmetrically with cell division rate α, die or differentiate with rate β, or undergo an asymmetric division with rate μ_{k − 1} that results in a malignant cell.

Here we derive and use extensions of the TSCE model that incorporate one, two, and three preinitiation stages. Mathematical expressions for the respective hazard functions are published as supporting information on the PNAS web site, www.pnas.org. The hazard function represents the (instantaneous) rate at which new cancers arise in a previously cancer free population, thus it is the proper estimator for cancer incidence. However, the hazard functions reveal an identifiability problem, i.e., not all biological model parameters can be estimated from incidence data alone (25). Details are published as supporting information on the PNAS web site.

We assume the number of normal stem cells in the human colon to be ≈10⁸, which is approximately the number of crypts in the colon (28). Thus, we assume that there is a single stem cell per crypt, although a small number of stem cells per crypt would not alter our conclusions substantially. There is recent experimental evidence, using epigenetic markers, that each crypt is maintained by a small niche of “quasi-immortal” stem cells whose number may range from four to perhaps several hundred cells (29).

Statistical Analysis.

In addition to the prominent role of age, cancer incidence is also known to depend on epoch of birth and year of diagnosis (i.e., birth cohort and calendar year). Log-linear models, the so-called age-cohort-period models, have traditionally been used for the analyses of cancer registry data. For a review, see ref. 30. Here, the age effect is derived from multistage models, and birth cohort and calendar year effects are incorporated into the analyses, which are published as supporting information on the PNAS web site. In brief, we model the age-specific incidence (age a) occurring in calendar year j as

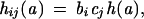where h(a) is the hazard function derived from a multistage model; c_j, a coefficient that adjusts for calendar year j; and the coefficient b_i adjusts for birth cohort i (i = j − a, stratified in 5-yr groups starting in 1885). The coefficients are normalized arbitrarily by setting c₁₉₉₀ = b_1885−1889 = 1.

Results

We fit the models shown in Fig. 1 to the incidence of colorectal cancer among whites and African Americans in the SEER registry (1973–1996). Separate analyses were carried out for males and females. Of interest are the estimates of the biological parameters and the predictions for birth cohort and calendar year related effects in each population. We found that the four-stage model, i.e., a model postulating two preinitiation stages, had the highest likelihood. Parameter estimates for the fit using the four-stage model are shown in Table 1. As mentioned above, not all of the biological parameters can be identified from incidence data alone. Aside from the parameters representing the rate of APC mutations (μ₀ = μ₁), we provide estimates of the initiation index μ₂/α, the product of the malignant transformation rate and the cell division rate of initiated cells, i.e., αμ₃, and the net cell proliferation rate α − β. The fits of the other models are published as supporting information on the PNAS web site (Table 3).

Table 1.

Maximum likelihood estimates of the four-stage model parameters from analyses of colorectal cancer incidence in SEER

	APC mutation rate, per year	Initiation index	Malignant transformation rate ×α, per year2	Adenoma growth rate, per year
White males	1.4⋅10−6	9.0	5.2⋅10−7	0.15
African American males	1.2⋅10−6	4.3	1.8⋅10−6	0.15
White females	1.3⋅10−6	0.7	1.2⋅10−5	0.13
African American females	1.1⋅10−6	2.9	5.2⋅10−6	0.13

With one exception (African American females) the four-stage model gave the best fits. Corresponding parameter estimates for the two-, three-, and five-stage models are published as supporting information on the PNAS web site.

Perhaps the most interesting feature of the parameter estimates of the four-stage model is that a single high-frequency event follows two rare events to create an initiated cell. An interpretation of this sequence in terms of biological processes is given in Discussion.

We found that the estimated rate of clonal expansion of initiated cells, α − β, was quite stable and independent of the number of stages assumed for the model (published as supporting information on the PNAS web site). We note here that α measures the rate of symmetric divisions of initiated stem cells, which form only a fraction of the total cell divisions as noted above.

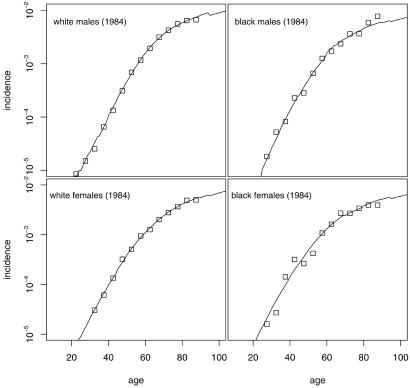
Fig. 2 shows the observed and model-generated age-specific incidence curves (adjusted for birth cohort effects) by race and gender in 1984. Fig. 2 shows that the pattern of colorectal cancer incidence is comparable in white and African American populations.

Fig 2.

Observed (squares) and predicted (lines) incidence of colorectal cancer by race and gender in the SEER registry (1984). Predicted incidence is for the four-stage model using the parameter estimates in Table 1.

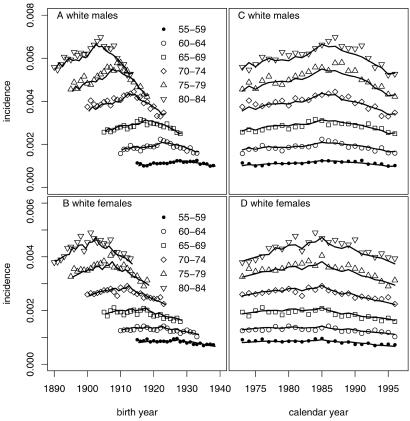
Our analyses indicate that temporal trends in colorectal cancer incidence were modest over the period of the study and were driven largely by calendar year effects. The importance of calendar year effects is obvious from Fig. 3, which shows the observed and predicted incidence among white males and females as a function of birth year (Fig. 3 A and B) and calendar year (Fig. 3 C and D) for several age groups. Predicted curves were generated by the four-stage model, which yielded the best fit (highest likelihood). Patterns were similar for African Americans but, due to the smaller population base, somewhat noisier. Note that, for a given age group, incidence increased with calendar year until about 1985 and then decreased modestly (Fig. 3 C and D). Fig. 3 A and B, showing incidence by birth cohort in various age groups, also exhibit shifting peaks near calendar year 1985. The increase in incidence by calendar year may be related to improved screening for colon cancer, whereas the drop after 1985 could be due to the gradual wearing off of the resulting “harvesting” effect (31).

Fig 3.

Observed and predicted (using the four-stage model) incidence of colorectal cancer in SEER (1973–1996) by gender for the white population. Shown as a function of birth year (A and B) and as a function of calendar year (C and D) for the age groups 55–59 through 80–84. Similar results are obtained for the African American population.

Estimates of the calendar year coefficients c_j (j = 1973, 1974, … , 1996), and of the birth year coefficients b_i [i = (1885–1889), (1890–1894), … ], are published as supporting information on the PNAS web site (Figs. 6 and 7) for the four-stage model.

Discussion

The extensions of the two-stage clonal expansion model considered here to study the age-specific incidence are motivated by the laboratory evidence, suggesting that multiple steps are involved in colon carcinogenesis. Incidence data in the SEER registry appear to be consistent with three rare events for the genesis of colon cancer, in general agreement with previous analyses of colon cancer incidence in Birmingham (28) and colon cancer mortality in the U.S. (21, 22). We note that the estimates of the rare event rates in the four- and five-stage models are consistent with measured locus-specific mutation rates. This finding suggests that it is not necessary to invoke genomic instability to explain age-specific incidence rates in human populations, although it does not preclude genomic instability from occurring late in the process or subsequent to malignant conversion (e.g., see refs. 32 and 33). Tomlinson and Bodmer (34) reached similar conclusions. However, both four- and five-stage models predict that, in addition to the rare events, a high-frequency event is required for the conversion of a preinitiated cell into an initiated stem cell. We suggest an interpretation of this high-frequency event below.

Conceptually, it is useful to consider separately the steps leading from normal epithelium to adenoma, and from adenoma to carcinoma.

(i) From Normal Epithelium to Adenoma.

There is substantial evidence (see, e.g., ref. 35) that the vast majority of adenomatous polyps have mutations in both copies of the APC gene. Our model of choice (the four-stage model) posits two rare events followed by a frequent event in the conversion of a normal stem cell into an initiated cell that serves as a precursor to an adenomatous polyp. We identify the two required rare events with mutations at the two APC loci. What of the third, frequent, event? Clearly, it is too frequent an event to be a mutation in the traditional sense. It could be an epigenetic event, related to methylation, but there is another, perhaps more intriguing, possibility.

We believe that the hallmark of a normal stem cell is its ability to generate the cells of colonic crypts by asymmetric division with amplification (27, 36). The asymmetric division of a stem cell preserves the stem cell and gives rise to a daughter that is committed to differentiation and death. We posit that an initiated stem cell is one in which the ability to divide asymmetrically has been partially lost so that an initiated stem cell occasionally divides symmetrically into two initiated daughters. Such divisions will give rise to clonal expansion of initiated cells and, ultimately, to a polyp. Note that in this view, polyps will contain a mixture of initiated stem cells and differentiated cells produced by asymmetric cell division.

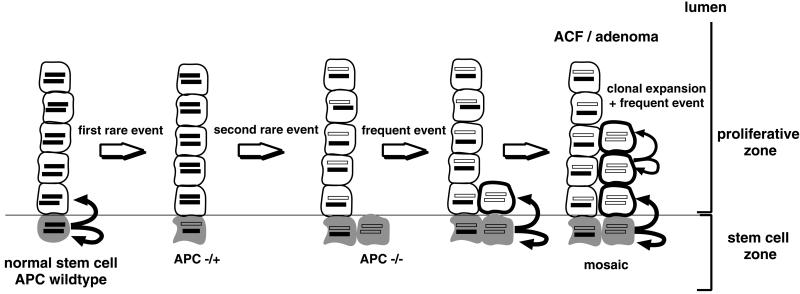
We suggest that the third, frequent, event following mutations at the two APC loci could be a positional event. Explicitly (see Fig. 4), after the two mutations occur in a stem cell, regular (asymmetric) divisions continue to generate progeny that move from the stem cell zone into the proliferative zone of the crypt where they are freed from the constraints placed on them by the microenvironment at the bottom of the crypt. In the proliferative zone, these cells are free to expand clonally via an occasional symmetric cell division. Thus, according to this hypothesis, the microenvironment plays an important role in maintaining normal cell behavior. Disruption of the normal interaction between a cell and its microenvironment may play a role in carcinogenesis (37). The rate of clonal expansion is not large. Our estimates of effective expansion rate in the four-stage model is ≈0.15 per year, which implies a doubling time of about 5 years. This estimate of the net expansion rate of initiated stem cells is somewhat lower than that of Herrero-Jimenez et al. (21) and somewhat higher than our estimate in the Birmingham data (28). If an initiated stem cell undergoes both symmetric cell divisions and apoptosis, then clones of initiated stem cells could become extinct with high probability. The (asymptotic) probability of extinction is given by the ratio β/α, of the rates of apoptosis and cell division. Using a division rate of 9 per year (21) for symmetric cell division, we see that β/α = 1 − (α − β)/α ≈ 1 − 0.15/9 ≈ 0.98. Thus, initiated stem cells become extinct with high probability. However, the mutated progenitor at the bottom of the crypt is considered immortal in our model and continues to undergo asymmetric divisions that replenish the pool of initiated cells. Although this process contributes to the clonal expansion of an adenoma, it is modeled as a separate birth process, similar in mechanism to the preceding rare events.

Fig 4.

The formation of an adenoma in the four-stage model, schematically. The basic steps involved (left to right) in a section of the colonic crypt: normal stem cell division maintaining the crypt. Step 1: rare mutation in a stem cell inactivates one allele of the APC gene. Unless the normal (APC–wild-type) stem is inactivated or dies, the crypt may become mosaic, i.e., may consist of a mixture of APC–wild-type and APC+/− cells. Step 2: second rare event leads to biallelic inactivation of the APC gene in a stem cell. Step 3: frequent asymmetric divisions of the defective stem cell populate proliferative zone with APC−/− progeny that may undergo clonal expansion.

Shih et al. (38) provide evidence for a “top-down” morphogenesis in the development of colorectal tumors. Genetic and immunohistological analyses of dysplastic crypts in small adenomas revealed a separation of the crypt epithelia into two zones: morphologically normal appearing cells near the bottom of the crypts and dysplastic cells that harbor APC inactivating mutations and contain cytoplasmic β catenin, near the colonic lumen. A likely explanation for these observations (favored by Shih et al.) is that the precursors of the dysplastic cells actually reside in the intercryptal zones at the surface of the mucosa rather than at the base of the crypts. Dysplastic offspring then spread laterally and downward, pushing the normal epithelium in adjacent crypts toward the bottom of the mucosal layer. However, the observations are also consistent with the more conventional view (as admitted by Shih et al.) that neoplastic cells may originate in the stem cell zone at the base of the crypt then “migrate up the crypt and thereafter become part of the superficial mucosae … .” Because our mathematical model contains no a priori structural information, our findings can be interpreted in much the same way in both morphological models of colonic epithelium.

ACF have been described in the earliest stages of the formation of adenomatous polyps and are seen in both normal individuals and in individuals afflicted with familial adenomatous polyposis (FAP). Individuals with FAP have inherited the first step (first APC mutation) on the pathway to malignancy and therefore require only one rare event (the second APC mutation) for the creation of an initiated stem cell. Therefore, one would expect ACF and adenomatous polyps to be much more common among FAP subjects than in the normal population. In fact, our estimates of the mutation rates in colon cancer allow us to generate estimates of the number of ACF in normal individuals and subjects with FAP as a function of age. A comparison of these expected numbers, generated by using our preferred four-stage model, with some observations in the literature is shown in Table 2. Our predictions are in the right range. The median number of ACF in normal individuals over the age of 70 was estimated by Takayama et al. (15) by using magnifying endoscopy to be 3 with an interquartile range of 0–5. We estimate an expected number of 0.6. Roncucci et al. (39) attempted to determine the number of ACF from resected colon segments from subjects with FAP. They saw considerable heterogeneity but reported a mean number of 20 ACF per cm². If we assume that the colon is ≈130 cm long and ≈10 cm in circumference, this density translates into ≈26,000 ACF per colon among FAP subjects, a value that is associated with very large uncertainty. Using the four-stage model, we predict an expected number of ≈3,700 ACF.

Table 2.

Predicted and observed number of ACF (mean and interquartile range) in normal subjects and in subjects with FAP

	Normal subjects (age 80) Mean (interquartile range)	FAP subjects (age 27) Mean (interquartile range)	Ratio FAP/normal
Predicted	0.6 (0–1)	3,740 (3,700–3,780)	6,330
Observed	3 (0–5)	26,000 (–)	8,670
Refs.	Takayama et al. (15)	Roncucci et al. (39)

^*Based on an estimated density of 20 ± 19 ACF per cm². See text for more details.

In a recent paper, Pinsky (40) describes a model for adenomatous polyps based on the idea that polyps arise from single stem cells that have sustained biallelic loss of APC function. Thus, Pinsky's model corresponds to our view of polyp development in the three-stage model but differs from our preferred model in that he does not consider a high-frequency (positional) event before symmetric division and polyp formation. His estimate of the net rate of cell proliferation in polyps is ≈0.30 per year, compared with our (much lower) estimate of ≈0.15 per year. However, Pinsky's estimated rate is based on the sizes of the observed adenomas, which contain differentiated cells in addition to mutated stem cells, whereas our estimate applies strictly to symmetric cell divisions, which give rise only to undifferentiated initiated cells.

(ii) From Adenoma to Carcinoma.

Our preferred model suggests that only one rare event is necessary for the conversion of an initiated stem cell into a malignant cell. This rare event could be identified with mutation of one copy of the TP53 gene, assuming that a single copy of the gene could bring about homozygous loss of function by dominant negative action (8). Interestingly, a recent study by Wang et al. (41) of the prevalence of somatic alterations in the colorectal cancer cell genome also points toward rare somatic mutations in colorectal tumors with rates similar to mutation rates in normal tissue. On the other hand, even small adenomas are found to harbor numerous allelic losses and gains consistent with widespread chromosomal changes (42). Indeed, loss of heterozygosity on 17p, the locus of the TP53 gene, is frequently observed in colon cancer. It may therefore be the combination of a common chromosomal loss caused by genomic instability and a rare mutation of TP53 (or of a gene in the same pathway) that is responsible for malignant conversion.

Unfortunately, we are not able to estimate the rate of the malignant transformation event directly. However, we are able to estimate the product of the rate of malignant transformation and α, the rate of symmetric cell division of initiated cells (see Table 1). If we accept, as before, the estimate of α provided in ref. 21 of nine per year, we obtain estimates of the rate of transformation in the range of 6 × 10⁻⁸ per cell year for white males to 1 × 10⁻⁶ per cell year for white females. However, if we assume a total (symmetric and asymmetric) division rate of 20–50 cell divisions per year in the polyp, which is about the cell turnover of stem cells in human colon (27), the transformation frequencies would be in the range between 1 × 10⁻⁹ and 1 × 10⁻⁷ per cell division, suggesting that malignant conversion could be accomplished by a single rare event.

(iii) Implications for Chemoprevention.

Nonsteroidal anti-inflammatory drugs (NSAIDs) inhibit cyclooxyenase activity and are known to reduce the risk of colorectal cancer (43). Although the precise mechanisms by which NSAIDs prevent colon cancer are not yet known, experimental evidence suggests that NSAIDs induce apoptosis in proliferating cells inhibiting or reversing the growth of colorectal tumors (44, 45).

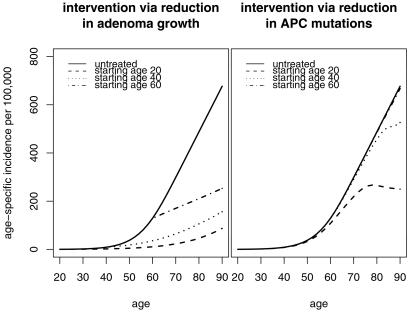
Using the four-stage model with the estimated parameter values for white males (given in Table 1), we explore the potential health benefits of nonsteroidal anti-inflammatory drugs under the assumption that their continued use reduces the net rate of cell proliferation in polyps. Fig. 5 shows the predicted age-specific incidence after the growth rate of polyps is reduced by 50% starting at ages 20, 40, and 60 (Left). For comparison (Right), we also show the effect of a hypothetical intervention that reduces the rate of APC mutations (first and second step in the model) by 50%. This example shows that drugs that decrease the rate of clonal expansion in adenomatous polyps may be very effective in reducing the colon cancer risk even when the intervention is begun later in life. In contrast, interventions that seek to lower the rate of APC mutations are likely to be less effective.

Fig 5.

Expected age-specific incidence of colorectal cancer assuming that an intervention occurs at ages 20, 40, or 60, or not at all. (Left) Hypothetical intervention that reduces the net cell proliferation rate of cells in polyps by 50%. (Right) Hypothetical intervention that reduces the rate of APC mutations by 50%.

Abbreviations

• APC, adenomatous polyposis coli

• FAP, familial adenomatous polyposis

• SEER, Surveillance, Epidemiology, and End Results

• TSCE, two-stage clonal expansion

• ACF, aberrant crypt foci