Abstract
In mixtures of cetyltrimethylammonium bromide (CTAB) and sodium perfluorooctanoate (FC7) in aqueous solution, novel bilayer cylinders with hemispherical end caps and open, flat discs coexist with spherical unilamellar vesicles, apparently at equilibrium. Such equilibrium among bilayer cylinders, spheres, and discs is only possible for systems with a spontaneous curvature, Ro, and a positive Gaussian curvature modulus, κ̄. We have measured the size distributions of the spherical vesicles, cylinders, and discs by using cryo-electron microscopy; a simple analysis of this length distribution allows us to independently determine that the mean curvature modulus, κ ≈ 5 ± 1 kBT and κ̄ ≈ 2 ± 1 kBT. This is one of the few situations in which Ro, κ, and κ̄ can be determined from the same experiment. From a similar analysis of the disk size distribution, we find that the edges of the discs are likely stabilized by excess CTAB. The fraction of discs, spherical vesicles, and cylinders depends on the CTAB/FC7 mole ratio: increasing CTAB favors discs, while decreasing CTAB favors cylinders. This control over aggregate shape with surfactant concentration may be useful for the design of templates for polymerization, mesoporous silicates, etc.
Keywords: cryogenic transmission electron microscopy, surfactants, vesicles
The starting point for the description of bilayer organization in solution is the harmonic approximation to the bending free energy (1):
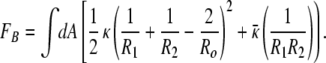 |
R1 and R2 are the principle radii of curvature of the structures, Ro is the spontaneous radius of curvature, κ and κ̄ are the mean and Gaussian curvature elastic constants, respectively, and A is the area of the bilayer membrane. The harmonic approximation is appropriate when the membrane thickness (1–3) [here ≈3 nm (4)] and the Debye length for ionic surfactants (2, 5, 6) [also ≈1–3 nm (4)] are small compared with R1 and R2 (≈20–30 nm, see Fig. 1). The differences of the bending free energy, FB, of different aggregate geometries can often be of the order of kBT, leading to the possibility of multiple structures in equilibrium.
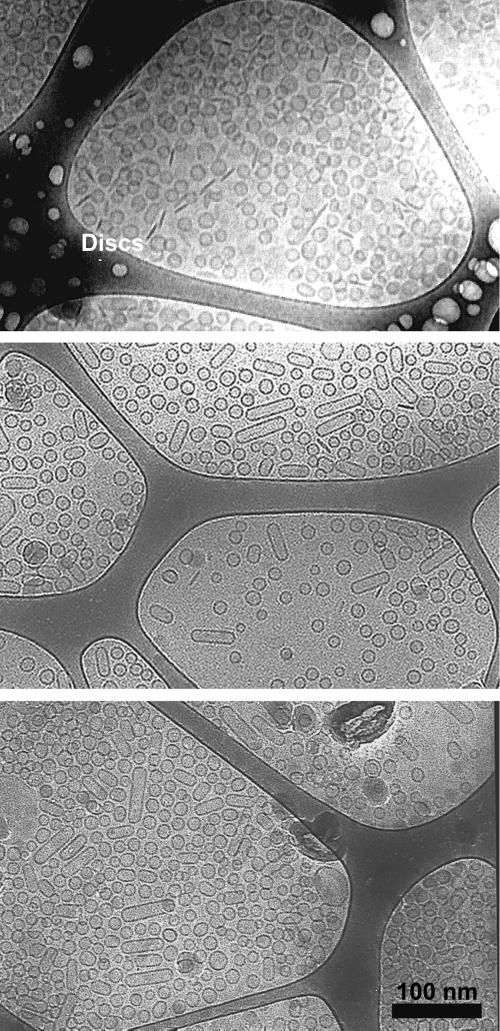
Fig 1.
Cryo-TEM images of 2 wt % total surfactant CTAB/FC7 mixtures at different CTAB/FC7 ratios. Discs (discs appear as narrow dark lines in the images), cylinders, and spheres are present in each image. The size distribution of discs, spheres, and cylinders did not change with the CTAB/FC7 ratio, only the relative numbers of each structure. (Top) At CTAB/FC7 ratios of 25:75, unilamellar spherical vesicles coexist with open discs and there are very few cylinders. The spherical vesicles were monodisperse with a mean radius of 25 ± 2.9 nm, and the discs were also quite monodisperse with a mean radius of 35 ± 4 nm. (Middle) At a CTAB/FC7 ratio of 20:80, the mean size of the spherical vesicles were essentially unchanged with a mean radius of 23 ± 2.7 nm, but a significant population of cylindrical vesicles with hemispherical end caps was observed, along with fewer discs. The cylinders had a mean radius of 24 ± 2 nm and a length of 136 ± 36 nm. The mean size of the discs was also unchanged with changes in composition; the mean disk radius was 33 ± 6 nm. (Bottom) At a CTAB/FC7 ratio of 15:85, the fraction of cylindrical vesicles increased and the fraction of discs decreased. The overall size distribution of the vesicles and cylinders does not change with composition over the range studied.
The two elastic constants, κ and κ̄, play very different roles in determining bilayer organization. The magnitude of κ reflects the energy needed to bend the bilayer away from its spontaneous radius of curvature, Ro. For κ ∼ kBT, thermal fluctuations give rise to significant curvature fluctuations, which lead to a net repulsive interaction between bilayers at short distances. This steric repulsion can stabilize unilamellar vesicles over multilamellar liposomes (3, 4, 7, 8). Larger values of κ (≫kBT), combined with a spontaneous curvature that picks out a particular vesicle radius, lead to unilamellar vesicles as the curvature variations inherent to multilamellar structures are energetically prohibited (3, 4, 9). A spontaneous bilayer curvature (1/Ro ≠ 0) is only possible when nonideal surfactant mixing causes the interior and exterior monolayers of the vesicle bilayer to have different compositions or environments (3, 10, 11).
κ̄ influences only the topology (and hence the number) of the structures formed (3, 4, 12). The Gauss–Bonnet theorem states that the integral of the Gaussian curvature over a given structure only depends on the genus of the structure (3, 13, 14). Hence, the magnitude of κ̄ has little effect at equilibrium as long as curvature fluctuations take place at constant topology or constant vesicle number. However, transformations between discs and closed spheres or between multiple spheres and cylinders are influenced by κ̄.
Although Eq. 1 has become the accepted description of bilayer organization, there are relatively few measurements of κ and almost no measurements of κ̄ for sub-μm surfactant bilayer vesicles (see refs. 12 and 15 for review). There are no general methods for determining these elastic constants; moreover, many of the methods in the literature probe κ and κ̄ at length scales much larger than those relevant to sub-μm vesicles (15–19). κ̄ is especially difficult to measure as it influences topological transformations between structures such as the number and genus of objects [such as the distribution of material between vesicles (3, 12), the size and distribution of various defect structures (18, 19), or the transition between lamellar and L3 phases (13, 14)] and does not influence the more readily measured fluctuations of the structure (12, 13, 15). A key requirement to the understanding and possible control of surfactant structural organization is developing both experimental and theoretical tools to relate Ro, κ, and κ̄ to surfactant molecular structure and solution conditions (9, 12, 15, 20). Here we show that the coexistence of cylindrical and spherical vesicles with nearly monodisperse radii allow us to extract values of Ro, κ, and κ̄ from the size distributions measured by cryo-transmission electron microscopy (cryo-TEM).
Samples were prepared by first mixing stock solutions of either cetyltrimethylammonium bromide (CTAB, Aldrich) or sodium perfluorooctanoate (FC7, PCR Research Chemicals, Gainesville, FL) with water to the desired surfactant weight fractions. The stock solutions were then combined in the appropriate amounts, and we allowed several weeks for equilibration. The vesicular structures only form on the FC7-rich side at concentrations between ≈1 wt % and 4 wt % total surfactant and for mixing ratios greater than ≈70 wt % FC7. Although it is possible to prepare metastable vesicles by shearing lamellar phases (21, 22), there is no indication of either a bulk lamellar phase at the concentrations of interest here, nor that shear has influenced the formation or size distribution of the structures shown. Small angle neutron scattering (minimal to zero shear) and cryo-TEM imaging (significant shear to prepare thin film samples) show identical characteristic structure dimensions (4). Various zero shear sample preparation methods including dialysis, isothermal counterdiffusion of two micellar dispersions, and in situ surfactant synthesis have shown that catanionic vesicles including the mixtures of interest here form independently of the method of sample preparation (23). Similar catanionic vesicles recover their size distribution after sonication or heat treatment, confirming that the size distribution is an equilibrium feature of the dispersions (23).
To prepare samples for cryo-TEM, a thin (<1 μm) layer of the surfactant-water mixture was spread on a lacey carbon grid (Ted Pella, Inc., Redding, CA) in a temperature-controlled chamber (24) saturated with the solution of interest. The grid was plunged into a mixture of liquid ethane and liquid propane cooled by liquid nitrogen (25). The frozen samples are transferred to a GATAN (Pleasanton, CA) cold stage and imaged directly at 100 kV by using a JEOL 100CXII. Bright-field, phase-contrast TEM micrographs were recorded by using standard low-dose procedures on either film or with a GATAN charge-coupled device camera. Hundreds of individual aggregates were measured to determine the size distributions reported here as mean and standard deviations. Samples for electron microscopy were made over the course of several weeks to ensure that neither the structures nor the size distributions were changing with time.
Fig. 1 shows the variety of structures observed after months of equilibration in mixtures of CTAB and FC7 at 2 total wt % surfactant in water at CTAB/FC7 ratios of 25:75 (Fig. 1 Top), 20:80 (Fig. 1 Middle), and 15:85 (Fig. 1 Bottom) (4, 25). Monodisperse spherical unilamellar vesicles coexist with cylindrical vesicles with hemispherical end caps (having a diameter equal to the spherical vesicle diameter) and open discs at all concentration ratios. The composition and extent of the “vesicle” phase was reproducible regardless of the sample history or mixing path, and the vesicle size distributions were stable for months (4, 26–28). The apparent equilibrium between open discs and closed bilayer vesicles and cylinders is consistent with recent time-resolved neutron and x-ray scattering experiments by Gradzielski and coworkers (29), who showed that after mixing anionic and cationic surfactant solutions, the micelles break up to form bilayer discs, and these discs slowly grow and close over the course of minutes to hours to form closed structures. These vesicles likely open and close with some frequency as dye or glucose within the vesicles is not retained (26). The surfactant monomer concentration is quite high in comparison to more typical double chain lipids that form bilayers, suggesting that any osmotic pressure or composition gradients within or between vesicles can be quickly relaxed (4, 27, 28).
At CTAB/FC7 ratios of 25:75 (Fig. 1 Top), unilamellar spherical vesicles coexist with open discs and there are very few cylinders. The spherical vesicles were monodisperse with a mean radius of 25 ± 2.9 nm, and the discs were also quite monodisperse with a mean radius of 35 ± 4 nm. At a CTAB/FC7 ratio of 20:80 (Fig. 1 Middle), the mean size of the spherical vesicles was essentially unchanged with a mean radius of 23 ± 2.7 nm, but a significant population of cylindrical vesicles with hemispherical end caps were observed, along with fewer discs. The cylinders had a mean radius of 24 ± 2 nm and a length of 134 ± 36 nm. The mean size of the discs also did not change with composition; the mean disk radius of the CTAB/FC7 ratio of 20:80 was 33 ± 6 nm. At a CTAB/FC7 ratio of 15:85, the fraction of cylindrical vesicles increased, and the fraction of discs decreased (Fig. 1 Bottom). The size distribution of discs, spheres, and cylinders did not change with the CTAB/FC7 ratio, only the relative numbers of each structure. The invariance of size distribution of the spherical vesicles suggests that the spontaneous curvature, Ro, and the sum of the bending constants, κ + κ̄/2, does not change significantly with the CTAB/FC7 ratio (4, 30).
For cylindrical and spherical vesicles to coexist at equilibrium, the curvature energy of a single spherical vesicle of total bilayer area, A, must be approximately equal to a cylindrical vesicle with hemispherical end caps, also of total area A [this assumes that the area per molecule is the same in all surfactant structures in equilibrium (3, 20, 31)]. To simplify the calculations, the cylindrical vesicle is idealized as a right circular cylinder of radius Ro and length L, capped by two hemispheres, also of radius Ro. The Gaussian curvature term (second term in Eq. 1) is constant (4πκ̄) as the integral of this curvature is invariant for closed objects of the same genus (Gauss–Bonnet theorem) (32). For the sphere, R1 = R2 = R and the curvature energy is
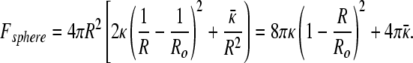 |
For the cylinder of radius Ro and length L we have R1 = Ro and R2 = ∞. Hence, the curvature energy, Fcyl is:
 |
The curvature energy of the two structures will be equal when:
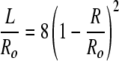 |
subject to the constraint that the sphere and cylinder have the same bilayer area (or number of surfactant molecules):
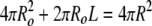 |
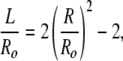 |
which gives a quadratic equation for the crossover at which Fcyl = Fsphere:
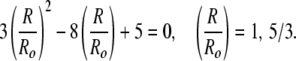 |
The root R = Ro is for the sphere of radius Ro, or a cylinder with L = 0. The second root R = 5 Ro/3 corresponds to a cylinder of length L = 32 Ro/9, or 3.56 Ro. The total length, l, of the cylindrical vesicle is 5.56 Ro. Hence, we expect a crossover between spheres and cylinders whenever a cylindrical vesicle is longer than about 5.6 times its radius.¶ From our images, Ro = 23 nm (4),∥ and the cylinder length is 134 ± 36 nm. This gives l/Ro = 134/23 = 5.8 ± 1.6, (L/Ro = 3.8) which is consistent with the prediction of 5.56 Ro. This crossover is only a consequence of the geometry of the aggregates and is independent of the values of κ and κ̄.
What is surprising is that there are so many cylinders. The crossover from sphere to cylinder does not occur until R/Ro = 5/3. For the CTAB/FC7 vesicles, this corresponds to spherical vesicles of radius 38 nm; this is about 6 SDs larger than the mean vesicle size. Hence, there are very few such large vesicles in this distribution as they are quite unfavorable with respect to the minimum energy sphere of radius Ro (4). Although cylinders are more stable than such large vesicles (for R/Ro > 5/3), cylinders should be exceedingly rare if they only form due to an instability of individual large vesicles. As cylinders are common in the images, it is more likely that a cylinder can have a curvature energy equal to a number of spherical vesicles of radius Ro with the same area (number of molecules) as the cylinder. This leads to a relationship between the Gaussian and mean curvature elastic constants of the bilayer as shown below.
The measured size distribution of the cylinders in Fig. 1 is centered around a bilayer area (number of molecules) approximately the same as three vesicles of radius Ro. The three spheres have a small bending energy (effectively zero as R → Ro), but a net Gaussian curvature energy that is three times the Gaussian curvature of one cylinder. For cylinders of L = 3.8 Ro:
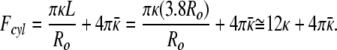 |
In comparing the three spheres with the single cylinder, there is likely a small contribution from the increased entropy of the three spheres compared with the single cylinder, but the entropy difference should be less than 2 kB:**
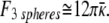 |
For spheres and cylinders to coexist, the free energies of spheres and cylinder (per unit area of bilayer) must be roughly equal:
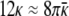 |
Eq. 9 shows that κ̄ > 0 because κ ≥ 0 (1). Theory suggests that vesicles are stable if κ̄ is sufficiently negative, but only if the spontaneous bilayer curvature is zero (12, 13), which is not the case here. Assuming that the bilayers in both cylinders and spheres have the same bending constants and spontaneous curvature at a given surfactant composition, we can use the parameter values measured from the vesicle size distribution (4) to provide a second relationship between the bending constants:
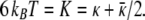 |
Solving Eqs. 9 and 10 simultaneously gives κ ≈ 5 ± 1 kBT, κ̄ ≈ 2 ±1 kBT. This is one of the few situations in which all of the relevant parameters in the Helfrich free energy can be measured from a single set of experiments.
In all of the samples, there is also a small population of open bilayer discs, which is consistent with the SANS results of Schmölzer et al. (29). The size distribution of the discs does not change appreciably with concentration; only the relative number of discs changes with concentration. The discs have a mean radius centered around Rd ≅ 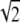 Ro, which have the same area (number of molecules) as spherical vesicles of radius of 0.7–0.8 Ro. Spherical vesicles of this size are only 1.5–2 SDs from the mean, so there are a reasonable number of such vesicles at equilibrium (3). The disk has zero curvature (R1 = R2 = ∞), which leads to a bending energy due to the spontaneous curvature, but zero Gaussian curvature:
Ro, which have the same area (number of molecules) as spherical vesicles of radius of 0.7–0.8 Ro. Spherical vesicles of this size are only 1.5–2 SDs from the mean, so there are a reasonable number of such vesicles at equilibrium (3). The disk has zero curvature (R1 = R2 = ∞), which leads to a bending energy due to the spontaneous curvature, but zero Gaussian curvature:
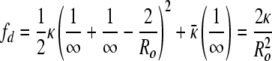 |
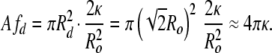 |
The equivalent area sphere has a curvature energy of
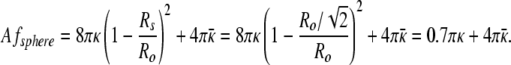 |
The disk also has an energy associated with the edge, which should have a very different environment than the bulk of the disk. As the discs are at higher densities in the solutions with higher CTAB fractions, it is likely that the CTAB is stabilizing this edge. CTAB likes high curvature environments such as rod-like micelles (26). If λ = energy/length of this edge, the disk (Eq. 11) and the equivalent sphere (Eq. 12) curvature energies are known from the parameters determined earlier, Eq. 13 determines this edge energy:
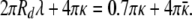 |
Using the values κ ≈ 5 kBT, κ̄ ≈ 2 kBT determined above, λ ≈ −0.1 kBT/nm, suggesting a preference of the CTAB for the edge of the disk. This also suggests why smaller discs are not observed. The ratio of disk edge to disk area goes like 2/Rd, which would require a larger fraction of excess CTAB for smaller discs. Larger discs, of course, are unstable relative to spherical vesicles.
For the variety of aggregates seen in Fig. 1 to coexist at equilibrium, the variation of curvature energies between the various aggregates must be of order kBT. Moreover, from these size and shape distributions, it is possible to determine all of the important parameters in the Helfrich model of curvature free energy. It is likely that in many surfactant mixtures, including the CTAB/FC7 system, spherical vesicles are not the only form of bilayer organization to occur at equilibrium. Unilamellar, bilamellar, and multilamellar vesicles may coexist, depending on the surfactant or counterion chemistry or concentration (4, 8, 26, 27, 33–36); vesicles may coexist with micelles (33, 34, 37); discs may coexist with lamellar phases or vesicles (2, 38), or unusual shapes like icosahedra (9) or cylinders may form. If a degree of control over the bilayer organization can be gained through a better understanding of the molecular origins of κ, κ̄, and Ro, it may be possible to control and optimize bilayer organization into novel structures useful as templates for polymerization, mesoporous silicates, or other applications (39).
Acknowledgments
We thank J. Israelachvili and M. Gradzielski for helpful discussions. J.A.Z., E.W.K., and B.C. gratefully acknowledge support from National Science Foundation Grant CTS-9814399, the National Science Foundation Materials Science and Engineering Research Centers Program, and National Institutes of Health Grant GM47334. H.-T.J. and S.Y.L. acknowledge support from Brain Korea 21, CUPS, and the BSAN (Biological Self-Assembling Nanomaterial Center) project.
Abbreviations
TEM, transmission electron microscopy
CTAB, cetyltrimethylammonium bromide
FC7, sodium perfluorooctanoate
This paper was submitted directly (Track II) to the PNAS office.
Helfrich predicted a general sphere to ellipsoidal instability for R/Ro= 6 in ref. 1.
The radius of the minimum curvature energy vesicle, r0, determined from the mean of the size distribution of the spherical vesicles, is related to the spontaneous curvature, R0, in Eq. 1 by R0 = 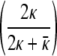 r0. This can be derived by minimizing the energy density (terms in square brackets in Eq. 2) with respect to R. For our measured values of r0 = 23 nm, κ = 5 kBT, and κ̄ = 2 kBT, this gives a spontaneous curvature, R0 = 19–20 nm. R0 is smaller than the mean vesicle size because κ̄ is positive. A positive κ̄ means that the Gaussian curvature energy increases proportionally to the number of vesicles. Hence, the minimum energy vesicle (or cylinder) has a radius larger than the spontaneous curvature to minimize the total curvature energy. However, using the mean vesicle or cylinder diameter or the corrected value of the spontaneous curvature does not have an effect on the values we calculate for κ and κ̄ within experimental error.
r0. This can be derived by minimizing the energy density (terms in square brackets in Eq. 2) with respect to R. For our measured values of r0 = 23 nm, κ = 5 kBT, and κ̄ = 2 kBT, this gives a spontaneous curvature, R0 = 19–20 nm. R0 is smaller than the mean vesicle size because κ̄ is positive. A positive κ̄ means that the Gaussian curvature energy increases proportionally to the number of vesicles. Hence, the minimum energy vesicle (or cylinder) has a radius larger than the spontaneous curvature to minimize the total curvature energy. However, using the mean vesicle or cylinder diameter or the corrected value of the spontaneous curvature does not have an effect on the values we calculate for κ and κ̄ within experimental error.
The ideal gas entropy difference of three spheres relative to one sphere is 2 kB; however, this overestimates the entropy difference here, because there are additional orientational modes for a cylinder that contribute to the entropy. However, the entropy contribution is negligible in comparison to the errors in the experimental measurements.
References
- 1.Helfrich W. (1973) Z. Naturforsch. 28 693-703. [DOI] [PubMed] [Google Scholar]
- 2.Dubois M. & Zemb, T. (2000) Curr. Opin. Colloid Interface Sci. 5 27-37. [Google Scholar]
- 3.Safran S. A., (1994) Statistical Thermodynamics of Surfaces, Interfaces, and Membranes (Addison–Wesley, Reading, MA).
- 4.Jung H. T., Coldren, B., Zasadzinski, J. A., Iampietro, D. & Kaler, E. W. (2001) Proc. Natl. Acad. Sci. USA 98 1353-1357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fogden A. & Ninham, B. W. (1999) Adv. Colloid Interface Sci. 83 85-110. [Google Scholar]
- 6.Fogden A., Carlsson, I. & Daicic, J. (1998) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 57 5694-5706. [DOI] [PubMed] [Google Scholar]
- 7.Helfrich W. (1978) Z. Naturforsch. 33 305-315. [Google Scholar]
- 8.Herve P., Roux, D., Bellocq, A. M., Nallet, F. & Gulik-Krzywicki, T. (1993) J. Phys. II (France) 3 1255-1270. [Google Scholar]
- 9.Dubois M., Deme, B., Gulik-Krzywicki, T., Dedieu, J. C., Vautrin, C., Desert, S., Perez, E. & Zemb, T. (2001) Nature 411 672-675. [DOI] [PubMed] [Google Scholar]
- 10.Safran S. A., Pincus, P. & Andelman, D. (1990) Science 248 354-355. [DOI] [PubMed] [Google Scholar]
- 11.Safran S. A., Pincus, P. A., Andelman, D. & MacKintosh, F. C. (1991) Phys. Rev. A At. Mol. Opt. Phys. 43 1071-1078. [DOI] [PubMed] [Google Scholar]
- 12.Safran S. A. (1999) Adv. Phys. 48 395-448. [Google Scholar]
- 13.Freyssingeas E., Nallet, F. & Roux, D. (1996) Langmuir 12 6028-6035. [Google Scholar]
- 14.Porte G., Appell, J., Bassereau, P. & Marignan, J. (1989) J. Phys. (France) 50 1335-1347. [Google Scholar]
- 15.Gradzielski M. (1998) Curr. Opin. Colloid Interface Sci. 3 478-484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Schneider M. B., Jenkins, J. T. & Webb, W. W. (1984) J. Phys. (France) 45 1457-1472. [Google Scholar]
- 17.Rawicz W., Olbrich, K. C., McIntosh, T., Needham, D. & Evans, E. (2000) Biophys. J. 79 328-339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bouglet G., Ligoure, C., Bellocq, A. M., Dufourc, E. & Mosser, G. (1998) Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 57 834-842. [Google Scholar]
- 19.Boltenhagen P., Lavrentovich, O. & Kleman, M. (1991) J. Phys. II 1 1233-1252. [Google Scholar]
- 20.Israelachvili J. N., (1992) Intermolecular and Surface Forces (Academic, London).
- 21.Hao J. C., Hoffmann, H. & Horbaschek, K. (2000) J. Phys. Chem. B 104 10144-10153. [Google Scholar]
- 22.Horbaschek K., Hoffmann, H. & Hao, J. (2000) J. Phys. Chem. B 104 2781-2784. [Google Scholar]
- 23.McKelvey, C. A., Hentze, H.-P., Edlund, H., Kaler, E. W. & Zasadzinski, J. A. (2002) Langmuir, in press.
- 24.Bellare J. R., Davis, H. T., Scriven, L. E. & Talmon, Y. (1988) J. Electron Microsc. Technol. 10 87-111. [DOI] [PubMed] [Google Scholar]
- 25.Chiruvolu S., Naranjo, E. & Zasadzinski, J. A. (1994) in ACS Symposium Series, eds. Herb, C. A. & Prud'homme, R. K. (Am. Chem. Soc., Washington, DC), Vol. 578, pp. 86–104. [Google Scholar]
- 26.Brasher L. L., Herrington, K. L. & Kaler, E. W. (1995) Langmuir 11 4267-4277. [Google Scholar]
- 27.Kaler E. W., Murthy, A. K., Rodriguez, B. E. & Zasadzinski, J. A. N. (1989) Science 245 1371-1374. [DOI] [PubMed] [Google Scholar]
- 28.Iampietro D. & Kaler, E. W. (1999) Langmuir 15 8590-8601. [Google Scholar]
- 29.Schmölzer, S., Gräbner, D., Gradzielski, M. & Narayanan, T. (2002) Phys. Rev. Lett. 88, http://link.aps.org/abstract/PRL/v88/e258301. [DOI] [PubMed]
- 30.Denkov N. D., Yoshimura, H., Kouyama, T., Walz, J. & Nagayama, K. (1998) Biophys. J. 74 1409-1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Israelachvili J. N., Mitchell, D. J. & Ninham, B. W. (1976) J. Chem. Soc. Faraday Trans. II 72 1526-1568. [Google Scholar]
- 32.Hilbert D. & Cohn-Vossen, S., (1983) Geometry and the Imagination (Chelsea, New York).
- 33.Miller D. D., Bellare, J. R., Evans, D. F., Talmon, Y. & Ninham, B. W. (1987) J. Phys. Chem. 91 674-685. [Google Scholar]
- 34.Miller D. D., Evans, D. F., Warr, G. G., Bellare, J. R. & Ninham, B. W. (1987) J. Colloid Interface Sci. 116 598-601. [Google Scholar]
- 35.Kaler E. W., Herrington, K. L., Murthy, A. K. & Zasadzinski, J. A. (1992) J. Phys. Chem. 96 6698-6707. [Google Scholar]
- 36.Regev O. & Guillemet, F. (1999) Langmuir 15 4357-4364. [Google Scholar]
- 37.Brady J. E., Evans, D. F., Kachar, B. & Ninham, B. W. (1984) J. Am. Chem. Soc. 106 4280-4282. [Google Scholar]
- 38.Zemb T., Dubois, M., Deme, B. & Gulik-Krzywicki, T. (1999) Science 283 816-820. [DOI] [PubMed] [Google Scholar]
- 39.Zasadzinski J. A., Evans, C. A., Kisak, E. & Boyer, C. (2001) Curr. Opin. Colloid Interface Sci. 6 85-90. [Google Scholar]