A computational method for resequencing long DNA targets by universal oligonucleotide arrays

Abstract

Universal arrays contain all possible oligonucleotides of a certain length, typically 6–10 bases. They can determine in a single experiment all substrings of that length that occur along a target sequence. That information, also called the spectrum of the sequence, is not sufficient to uniquely reconstruct a sequence longer than a few hundred bases. We have devised a polynomial algorithm that reconstructs the sequence, given the spectrum and an additional reference sequence, homologous to the target sequence. Such a reference is available, for example, in the identification of single-nucleotide polymorphisms. The algorithm can handle errors in the spectrum as well as substitutions, insertions, and deletions in the target sequence. We present extensive simulation results, which show that the algorithm correctly reconstructs target sequences of >2,000 nucleotides from error-prone 8-mer spectra when realistic levels of single-nucleotide polymorphisms are present.

Sequencing by Hybridization

Sequencing by hybridization (SBH) was invented in the late 1980s as an alternative to gel-based sequencing (1–3). This method makes use of a universal DNA microarray, which harbors all oligonucleotides of length k (called k-words, or simply words when k is clear). These oligonucleotides are hybridized to an unknown DNA fragment, whose sequence we would like to determine. Under ideal conditions, this target molecule would hybridize to all words whose Watson–Crick complements occur somewhere along its sequence. Thus, in principle, one could determine in a single microarray reaction the set of all k-long substrings of the target and try to infer the sequence from those data. The technique was validated in arrays of 7 and 8 mers (4, 5), and up to 10 mers are possible with current array technology.

The fundamental computational problem in SBH is the reconstruction of a sequence from its spectrum, the set of all words occurring along the sequence. Pevzner (6) reduced that problem (assuming the number of occurrences of each word is known) to the polynomial task of finding an Eulerian path in a graph.

The main weakness of SBH is ambiguous solutions: When several sequences have the same spectrum, there is no way to determine the true sequence. Theoretical analysis and simulations (4, 7) have shown that even when the spectrum is errorless and contains the multiplicity of each word, the average length of a uniquely reconstructible sequence using an 8-mer array is <200 bases, far below a single read length on a commercial gel-lane machine.

Although an effective and competitive sequencing solution using SBH has yet to be demonstrated, this strategy continues to attract attention. In principle, SBH holds promise to considerably economize on the task of sequencing, one of the major efforts in modern biotechnology. Alternative array designs (8–10) as well as interactive protocols (11) were suggested.

Similar Sequences Are Ubiquitous

Similarity among DNA sequences is a fundamental phenomenon in biology, caused by evolution: different contemporary sequences have evolved by mutations from a single ancestral molecule. Such related (homologous) sequences exhibit similarity to their common ancestor, and thus to each other. Homology is routinely encountered in genome analysis: individuals of the same species have almost identical genomes, repeat elements are highly similar, and paralogous members of a gene family, as well as orthologous genes in related species, exhibit varying degrees of similarity.

Because sequence data accumulate in an accelerated rate, an increasing number of sequencing targets have a homolog whose sequence is already known. This availability of homologues motivates the development of new sequencing strategies that utilize homology information. Genotyping single-nucleotide polymorphisms at previously identified locations has been successfully accomplished by hybridization to custom-made microarrays (12–14). A recent review on genetic testing noted the desirability and lack of an effective and generic microarray solution for resequencing (15). To the best of our knowledge, this study is the first proposal to use standard universal arrays and homology information for resequencing.

Our Contribution

We describe here a method for resequencing, by combining information on a reference sequence with experimental spectrum data obtainable from a universal array. We call the technique spectrum alignment, because the algorithm attempts to find the best “alignment” of the reference sequence with the spectrum. The algorithm is polynomial, and it handles substitutions, insertions, and deletions between the reference and the target sequences. No prior knowledge of the sought mutations is needed, although such information can be exploited, if available. The method accommodates noise in the spectrum, which is common in hybridization results. It does not require knowledge of the multiplicities of the words in the spectrum. Our method can also handle profiles and hidden Markov models as homology information (see ref. 16), instead of a particular reference sequence. Simulations show that this method allows an order of magnitude increase of reconstructed target length compared to regular SBH.‡

Preliminaries

Scoring by Hybridization Data.

Let Σ = {A, C, G, T} be our alphabet. We denote sequences by a string of symbols from Σ between angle brackets (〈〉). A k-spectrum of a sequence 𝒯 = 〈t₁t₂ ⋯ t_L〉 is the set of all k-long substrings (words) of 𝒯. For each word x→ = 〈x₁x₂ ⋯ x_k〉 ∈ Σ^k, we define 𝒯(x→) to be 1 if x→ is a substring of 𝒯, and 0 otherwise. We denote K = 4^k.

A hybridization experiment measures, for each word x→ ∈ Σ^k, the intensity of its hybridization signal. Due to the stochastic nature of hybridizations, most signal levels cannot be binarized satisfactorily. We therefore use a probabilistic representation. The relevant information in a hybridization signal can be transformed to probabilities P₀(x→) and P₁(x→), where the probability of this observed intensity is P₁(x→), assuming x→ is a substring of 𝒯, and P₀(x→) otherwise. Such probabilities can in fact be experimentally obtained (18). We therefore define a probabilistic spectrum Ψ to be a pair (P₀, P₁) of functions P_i : Σ^k ↦ [0, 1]. If the experiment were perfect, i.e., if the probabilities were all zero or one [with P₀(x→) + P₁(x→) ≡ 1], then the hybridization data would directly imply a unique k-spectrum. In practice, though, both P₀(x→), P₁(x→) are positive, and any deterministic binarization of the hybridization signal will contain errors. Our algorithms will therefore use the probabilistic data.

The de Bruijn graph of order k is a directed graph G(V, E) whose vertices are labeled by all the (k − 1) mers V = Σ^k−1, and its arcs are labeled by k mers, E = Σ^k. The arc labeled 〈x₁x₂ ⋯ x_k〉 leads from the vertex 〈x₁x₂ ⋯ x_k−1〉 to the vertex 〈x₂ ⋯ x_k〉. There is a 1:1 correspondence between candidate L-long target sequences and (L − k + 1)-long paths in G, whose arc labels comprise the target spectrum. In case the spectrum dataset is perfect and the multiplicities are known, omitting all zero probability arcs from G one gets Pevzner's formulation, i.e., every solution sequence is an Eulerian path (6). To handle noisy spectra, we devise a scoring scheme for paths and search for the highest-scoring path in G. Hereafter, we interchangeably refer to arcs and their labels and also to sequences and their corresponding paths. Observe that because words may reoccur, paths are not necessarily simple.

We assume that hybridization results of different oligonucleotides are mutually independent. Define w(x→) =log(P₁(x→)/P₀(x→)) and consider the experimental likelihood L^e(𝒯^) = Prob(Ψ|𝒯^) of a candidate target sequence 𝒯̂. We can thus write:

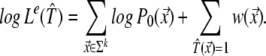The first term is a constant, independent of 𝒯̂, and is omitted hereafter.

Let p = e₀, … , e_L−k be the path in G corresponding to 𝒯̂. Then

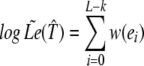is an approximate likelihood score. Although it deviates from the true likelihood whenever an arc is revisited along p, it approximates the true score and is easier to compute.

Scoring by Homology Information.

We now show how to use homology information to obtain a prior distribution on the space of candidate target sequences. Assume the unknown target sequence 𝒯 = 〈t₁ ⋯ t_l〉 has a known homologous reference ℋ = 〈h₁ ⋯ h_l〉 that differs from it by some substitutions without indels. Due to the prevalence of single-nucleotide polymorphisms in intraspecies variation (19), this situation is common when the target 𝒯 is taken from an individual while ℋ is the wild-type genomic sequence. We assume a set of 4 × 4 position-specific substitution matrices ℳ⁽¹⁾, … , ℳ^(l) are known, where for position j along the sequence:

The setting just presented implies a distribution on the space of possible target sequences. This prior distribution for ungapped homology, D^u, can be written for each candidate target sequence 𝒯̂ as:

We denote ℒ^(j)[x, y] ≡logℳ^(j)[x, y].

Spectrum Alignment

In this section, we show how to combine our two sources of information on the target sequence, i.e., the result Ψ of the hybridization experiment, and the reference sequence ℋ. We formulate a Bayesian score, which is a composition of the scores discussed above, and present a fast dynamic programming algorithm to compute this score.

Ungapped Score.

The probability of a candidate solution sequence 𝒯̂, given the information we have, is:

Given 𝒯̂, the hybridization signal is independent of ℋ:

Thus, omitting the constant Prob(ℋ)/Prob(ℋ, Ψ), we can write:

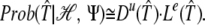We shall use the approximated likelihood, 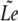(𝒯̂), and after taking logarithms, we obtain the following ungapped score of a candidate target:

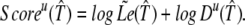Dynamic Programming Algorithm.

We can compute the highest-scoring target sequence by dynamic programming. For each vertex y→ = 〈y₁ ⋯ y_k−1〉 ∈ Σ^k−1 and integer j = k − 1, k, k + 1, … , l, we compute S^u[y→, j], the maximum score of a j-long sequence ending with y→ = 〈y₁ ⋯ y_k−1〉 aligned to 〈h₁ ⋯ h_j〉, according to the following recursion:

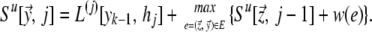As in the Smith–Waterman algorithm (20), a sequence 𝒯* attaining the optimal score can be reconstructed by standard means from the matrix S^u. The time complexity is O(lK). Note that although the complexity is exponential in k (K = 4^k), it is linear in l for a given array and not too large for practical values of k.

A crucial issue for the practicality of this algorithm is memory requirement. A naive implementation uses O(lK) space, which is prohibitive for typical data parameters. By following the paradigm of Hirschberg (21), we provide an algorithm implementing Eq. 7 in O(K) space, at the price of increasing the time complexity by an O(log l) factor. Exact details appear in ref. 17.

Handling Gaps.

Suppose substitutions, as well as indels, with respect to the reference sequence may occur along the target. This kind of homology with gaps can be probabilistically modeled by HMMs as demonstrated by their use for profiling protein families (22). We use a similar formulation to describe homology between nucleotide sequences. The reference, along with the statistical assumptions, actually creates a profile.

Consider an HMM profile with a state-set Q, comprised of a chain of l_Q states that describe matches/mismatches to positions in the reference sequence, and additional states describing indels. Let L be some bound on the length of the target sequence. Define a three-dimensional array S, where for each q ∈ Q, y→ = 〈y₁ ⋯ y_k−1〉 ∈ V, r = k, … , L, S[q, y→, r] is the maximum score of an r-long sequence ending with 〈y₁ ⋯ y_k−1〉, whose alignment to the profile ends in q. S can be computed by dynamic programming. For efficiency, one can compute only S entries whose q, r coordinates are along the R-wide diagonal strip.

The time complexity is O(R(l_Q + L)⋅K⋅log L), and the space complexity is O(R(l_Q + L)⋅K) (17).

Exact Scoring Algorithm.

The algorithms presented above optimize the approximated score. This approximation is quite good when only few words reoccur along the target sequence. However, when this is not the case, that score considerably deviates from the true likelihood. For small values of k, the best solution according to the approximated score often places high-scoring words in wrong positions in addition to their correct positions. The score sums the contributions of all words along the sequence, and repeated words contribute repeatedly. This is why words with high contribution tend to reappear. The correct likelihood score adds the weight of each different word along the sequence only once. The misplaced duplicated words usually appear concatenated to each other to form a duplicated region, compensating the overall score of this region for poor contribution by the homology component of its score. Consequently, in such erroneously duplicated regions, the algorithm admits many differences between the reference sequence and the suggested solution.

To overcome this problem, we first identify regions in the putative solution that contain either substitutions or repeated words. For each such region, we apply the dynamic programming algorithm using the respective fragment of the reference sequence and a modified probabilistic spectrum. In that spectrum, the arc weight w(x→) is redefined as 0 for every x→ that occurs outside the reference fragment. Iterated application of this procedure usually eliminates artifact repeats and gives a score that is very close to the correct likelihood.

Computational Results

Simulation Setup.

The algorithm was extensively tested in simulations. Each simulation scenario specified the sequence length, mutation probabilities, probe length, and hybridization error rates. As a reference, we used prefixes of real coding sequences, arbitrarily taken from GenBank's collection of human transcripts. Sequences with long repeats were discarded. For testing the reconstruction of long targets, we pooled (concatenated) several transcripts. For each simulation scenario, we collected statistics from 100 sequences.

Each simulation run was performed as follows:

• (i)  Introduce mutations in the reference sequence R and obtain the target sequence T.

• (ii)  Form the probabilistic spectrum of T.

• (iii)  Reconstruct the target from the reference R and the spectrum using the dynamic programming algorithm.

• (iv)  Compare the reconstructed sequence to T.

For simplicity, substitutions by different nucleotides were equiprobable, and mutation rates remained fixed along the sequence. In some of the simulation scenarios, we restricted mutations to substitutions only. We simulated hybridization signals using two parameters for the hybridization error: the rates for FNs and FPs. If x→ occurred in T, then the signal was positive with probability 1 − FN and negative with probability FN. If x→ did not occur in T, then the signal was positive with probability FP and negative with probability 1 − FP. For positive signals, (P₀(x→), P₁(x→)) were set to (FP, 1 − FN) and for negative signals, to (1 − FP, FN).

All probabilistic parameters were position/word independent.

We quantified performance by two figures of merit:

• (i)  Perfect reconstruction rate. The fraction of runs for which T was perfectly reconstructed.

• (ii)  Average sequencing error. The fraction of base-calling errors in the reconstruction.

Our basic simulation scenario assumed hybridization to an 8-mer array, with FP = FN = 0.05. Mutations were substitutions only, with the single-nucleotide polymorphism (SNP) rate being 1:200 bp. This rate is in fact higher than the SNP rate observed in human DNA (19). To examine the effects of different parameters, we performed several series of simulations. In each such series, we changed one or more parameter values while keeping the rest at their basic scenario values.

The algorithm was implemented in C++. Running times on a Pentium 3 600-MHz machine with a Linux operating system, ranged from roughly 7 min for a 500-bp-long sequence to 2.5 h for 6 kb. Only the main memory was used, with the application consuming at most 40 Mb.

Results.

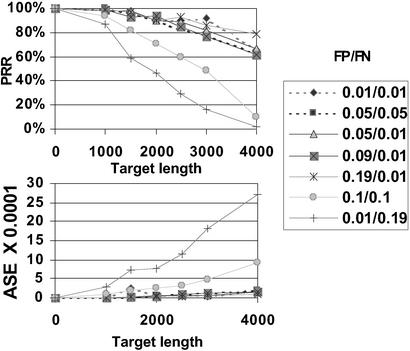
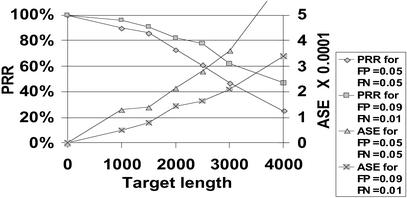
With 8-mer arrays, assuming realistic levels of hybridization error, one can resequence 2–2.5 kb with perfect reconstruction rate of ≈90% and base-call error rate below 1:10,000 (Fig. 1). These results are quite robust to changes in hybridization error rate. High FN rate has a stronger effect than high FP rate. Because most of the FP signals correspond to arcs of the de Bruijn graph that are far from high-scoring paths, they do not damage performance as much as FNs do.

Fig 1.

Performance for different false positive (FP)/false negative (FN) rates and for targets of different lengths.

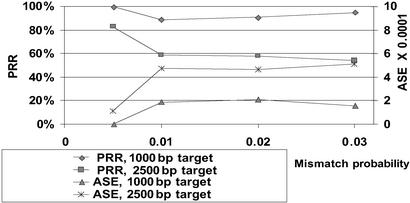
Higher mutation rates still comfortably allow sequencing 1 kb, although performance for 2.5 kb severely deteriorates (Fig. 2). This length enables, for example, sequencing a chimpanzee gene using the known human homolog as a reference. The nonmonotonicity of the plots is not a statistical error but rather an artifact of our simplified simulation setup (23). It is not expected to occur on real data where FP and FN are position dependent.

Fig 2.

Impact of mutation rate on performance for different target lengths.

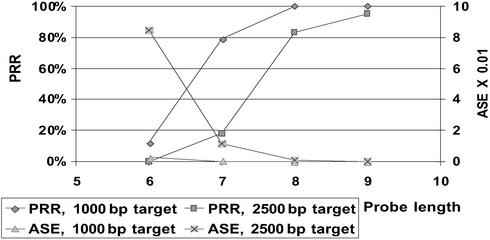
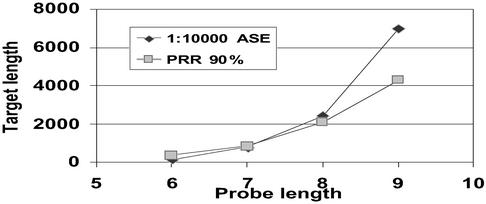
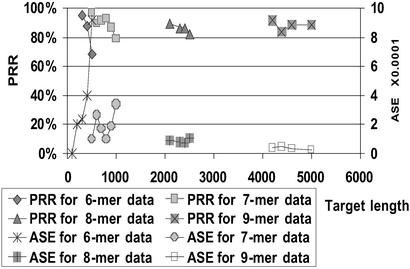
When comparing arrays with probes of increasing lengths (Figs. 3–5), the expected improvement in performance is evident. Incrementing the probe length by one (i.e., quadrupling the array size) increases the length of reconstructible target 2- to 3-fold.

Fig 3.

Impact of probe length on performance for different target lengths.

Fig 5.

Impact of probe length on the maximum length of a target reconstructible at high fidelity.

Fig. 6 demonstrates performance in the presence of insertions and deletions as well as substitutions. Even in this case, we are able to achieve good performance with an 8-mer array for targets of 2 kb, which is three to four times the read length in current sequencing machines.

Fig 6.

Impact of indels: The plots show the effect of target length on performance for different FP/FN rates in the presence of mismatches and indels. Deletion and insertion probabilities were set to 1:600 and 1:2,000, respectively.

Discussion

We have developed a computational method that combines hybridization data from a universal array and homology information to reconstruct a target sequence. The method is general enough to allow for insertions and deletions, hybridization errors, and a profile or a hidden Markov model instead of a single reference sequence. Because the spectrum data needed originate from standard arrays that can easily be mass produced, the cost of generating the hybridization data can potentially be reduced to a small fraction in comparison to current special-purpose arrays.

Performance of our method on simulated data is encouraging. In realistic noise levels, 8-mer arrays enable reconstruction of 2- to 2.5-kb targets, longer than most human genes. [In fact, the target can also be a collection of DNA segments of that total length (17)]. A notable simplification of our model is the independence assumption regarding probe hybridizations. This assumption can be relaxed at the expense of increased computational complexity.

Our approach is not limited to array oligonucleotide hybridization data: It can be applied by using any other technology that gives the word contents of the sequence, e.g., beads, primer extension, etc. Further research is needed to validate this approach on real data from any such technology.

Our method may have important implications for high-throughput genotyping: universal arrays can be manufactured rapidly and economically on a large scale, and this method enables their use for resequencing genomic information. This ability to determine the sequence of any gene of choice, or a selection of exons from different genes involved in a particular disease or pathway, has wide applications. Potential uses include resequencing somatic variants for cancer-predictive medicine, accurate allele typing of the human leukocyte antigen, and identification of pathogens and pathogen strains. Methods similar to ours can also be used for correction of sequencing errors during genome assembly. We believe this work may have great impact on these applications.

Fig 4.

The combined impact of target and probe lengths on performance.

Abbreviations

• SBH, sequencing by hybridization

• FN, false negative

• FP, false positive