Abstract
In ancient genes whose products have known 3-dimensional structures, an excess of phase zero introns (those that lie between the codons) appear in the boundaries of modules, compact regions of the polypeptide chain. These excesses are highly significant and could support the hypothesis that ancient genes were assembled by exon shuffling involving compact modules. (Phase one and two introns, and many phase zero introns, appear to arise later.) However, as more genes, with larger numbers of homologs and intron positions, were examined, the effects became smaller, dropping from a 40% excess to an 8% excess as the number of intron positions increased from 570 to 3,328, even though the statistical significance remained strong. An interpretation of this behavior is that novel inserted positions appearing in homologs washed out the signal from a finite number of ancient positions. Here we show that this is likely to be the case. Analyses of intron positions restricted to those in genes for which relatively few intron positions from homologs are known, or to those in genes with a small number of known homologous gene structures, show a significant correlation of phase zero intron positions with the module structure, which weakens as the density of attributed intron positions or the number of homologs increases. These effects do not appear for phase one and phase two introns. This finding matches the expectation of the mixed model of intron origin, in which a fraction of phase zero introns are left from the assembly of the first genes, while other introns have been added in the course of evolution.
The debate over the origin of the first introns has consisted largely of a dispute between two camps: introns early (1–13), holding that the first introns were extremely ancient structures dating to before the divergence between the three domains of life, and introns late (14–18), holding that introns have arisen more recently, during early eukaryotic evolution. On the former model, introns participated in the creation of the first genes through recombination within introns to yield novel gene products, a process referred to as exon shuffling; on the latter, the first introns were inserted into previously intact coding regions.
Perhaps the most hotly debated issue in the introns-early/introns-late debate is the correlation of intron positions with protein structure. Study of this correlation has a long history. Blake (1) first suggested that if introns were in fact ancient features and had facilitated the formation of early genes by assembling complex proteins from small pieces, these pieces should be self-contained units, and one would thus expect a correspondence between intron positions and the boundaries of elements of protein structure. Go (4) then tested this notion by dividing hemoglobin into four compact “modules” and demonstrating that the two known intron positions lay at the boundaries of modules, one between the first and second modules and the other between the third and fourth. This left the second-third module boundary, and she predicted that an intron would be found at this boundary. This prediction was fulfilled by the finding of a new intron in plant leghaemoglobin, yielding a structure in which intron positions exactly delineated module structures (19).
To detect truly ancient shuffling, analysis of a gene found throughout nature was necessary (5). Gilbert and collaborators (6) demonstrated that the 10 triose-phosphate isomerase (TPI) introns known at the time lay in positions corresponding to 10 of the 11 boundaries separating the 12 TPI modules and further predicted that a new intron would be found at the remaining boundary, a prediction fulfilled by the genetic structure of TPI in the mosquito Culex (20). This one-to-one correspondence between introns and module boundaries seemed a striking confirmation of a prediction of introns-early (but see ref. 17).
Larger scale correlation studies of 570 intron positions from eukaryotic copies of 32 ancient genes by de Souza and coworkers (9) supported the gene–protein structural correspondence, finding a nearly 40% excess over the random expectation for introns lying in module boundary regions. When this study was expanded to a larger set of 988 intron positions from 44 ancient genes (10), the authors were able to identify a subset of intron positions, those in phase zero (meaning between codons, as contrasted with phase one and phase two, meaning falling after the first and second bases of codons, respectively), as primarily responsible for the correlation. There was a 35% excess over the random expectation for phase zero introns lying in module boundary regions, with P values around 0.001. Fedorov et al. (13) recently reported a similar calculation, yielding a nearly 10% excess for a set of 3,328 phase zero introns in 276 ancient proteins, with P values around 10−6.
These results have been questioned on two grounds. First, many studies over the past few years have described intron patterns not easily explained by an introns-early model, chief among these the discovery of narrowly phylogenetically distributed intron positions, showing that at least some, and probably very many, introns are the results of recent processes (15, 17). Second, the gradual reduction of the predictive power of the model, from a one-to-one correspondence, to a 40% excess, to a 30% excess, and finally to a 10% excess, has led some authors to wonder whether the original correlation was specious (18). These are important objections that must be answered. We here attempt to take up this task.
If many introns are the results of recent insertion, as seems likely, a demonstration that all introns correlate equally strongly with module boundaries would, in fact, be strong evidence against the current formulation of the introns-early theory: if recently inserted introns were to correlate with module boundaries because of some insertional bias, the correlation of other introns would be irrelevant to the debate about their ancient character. Alternatively, a demonstration that the correspondence to module boundaries is limited to subsets of intron positions that are candidates for ancient positions by independent criteria reinforces the notion that this correlation is real evidence of ancient introns.
We have previously reported several tests using similar reasoning. Roy et al. (11) showed that those phase zero intron positions that appear to be ancient by phylogenetic criteria (having introns at identical or near-identical positions in organisms from two or more eukaryotic kingdoms) are significantly more strongly correlated with module boundaries than are other phase zero introns. Fedorov et al. (13) showed that there is no correlation between phase zero introns and module boundaries in genes found only in the eukaryotes and therefore not thought to be assembled through ancient intron shuffling. Roy et al. (12) used similar reasoning to show that there is a smaller excess of introns in phase zero and a smaller fraction of symmetric exons (thought to be additional signatures of ancient introns) in those Caenorhabditis elegans genes that appear to have been laterally transferred from non-intron-bearing bacteria or archaea (and thus thought to harbor only inserted introns).
Here we undertake a fourth such test. In Fedorov et al.'s (13) recent analysis of 276 ancient proteins, they adhered to the convention of de Souza et al. (9) in studying intron positions from all known copies of a given gene. The inclusion of intron positions from the sequences of hundreds of homologs in some cases led to overall intron densities of up to one intron per codon (see below). Clearly, these reconstructed ancient gene structures are not reconcilable with the Exon Theory of Genes, which postulates that the original exons would have been on the order of 15–30 codons long. The vast majority of introns in these families are thus expected to be the products of insertion and therefore, if correlation with module boundaries is an indication of ancient character, should not correlate with module boundaries.
One can attack the problem in two ways. One could reason as follows: the inclusion of many homologs of a gene increases the evolutionary distance over which the gene has had the opportunity to acquire introns. As one examines more and more homologous genes, at some point all ancient positions will have been found, but the identification of random additions of introns should continue, increasing the noise. Thus, the correlation with module boundaries should decrease as intron positions from more and more homologous genes are included. Alternatively, one might look directly at the intron density of the reconstructed gene structures. In cases in which the number of intron positions greatly exceeds the number postulated by the Exon Theory of Genes, there should be a strong reduction of the correlation with module boundaries.
We show here that both predictions are fulfilled: phase zero introns in those ancient genes with low to moderate collective attributed intron density or with a comparatively small number of intron-containing homologs for which gene structures are known show a stronger correlation with module boundaries than do introns in more intron-dense or homolog-rich families. Thus, those reconstructed intron–exon structures that appear most “ancient” have introns which exhibit a characteristic expected of ancient introns: correlation with module boundaries.
Methods
Module Boundaries.
Modules were defined by using the Go-plot method, as calculated by our program Intermodule (9, 10, 13). This program identifies maximal linear regions of polypeptide for which the difference between no pair of residues in a region exceeds a given distance. Module boundaries are then defined as the overlaps between these regions (see ref. 9 for a thorough explanation).
Tests of Significance.
To test the significance of an elevated correspondence with module boundaries of a given subset of intron positions, we asked for the chance of randomly drawing a subset of positions of the same size as the real subset that has at least as great a correspondence with module boundaries. This was accomplished by using a Monte Carlo calculation. For each real subset to be tested, 10,000 random subsets were generated. P values are then given by dividing the number of random subsets with at least as great a module boundary correspondence as the real subset by 10,000.
Results
Fedorov et al. (13) compiled sets of all intron positions found in the members of “ancient” gene families. They first identified ancient genes by searching GenBank for prokaryotic homologs of those eukaryotic proteins for which a crystal structure is found in PDB. Hits were identified as ancient conserved regions (ACRs). They next found all eukaryotic intron-containing homologs for each gene. The positions of the introns from all of these genes were mapped onto the coding sequence for the representative protein structure through multiple alignments [see Fedorov et al. (13) for a more detailed discussion]. This process yielded 276 different ACRs, containing a total of 6,612 distinct intron positions.
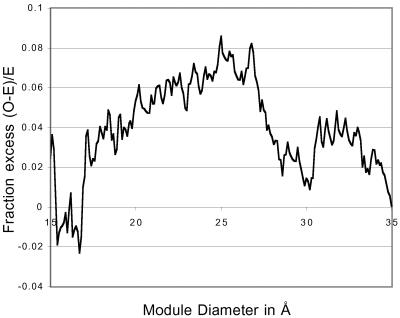
Fedorov et al. (13) showed that phase zero intron positions in the ACRs correlate with module boundaries and that phase one and two positions do not. Fig. 1 shows the correlation between phase zero intron positions and module boundaries for distances between 15 and 35 Å (extracted from ref. 13).
Fig 1.
Correlation of phase zero intron positions with module boundaries for 276 ACRs. Fraction excess is the observed number of intron positions in module boundaries minus the expected number divided by the expected number [(O − E)/E]. This figure is extracted from figure 3 of Fedorov et al. (13).
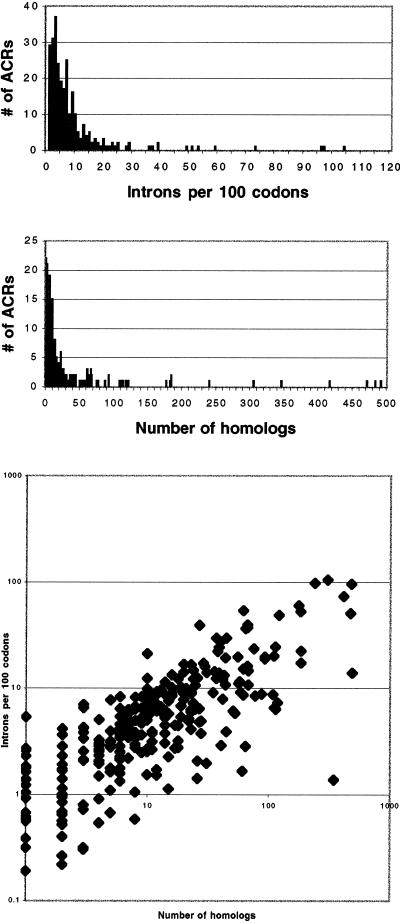
We first examined the ACR's to try to better understand the correlation between phase zero intron positions and module boundaries. The intron positions are not evenly distributed among the 276 ACRs. As one can see from Fig. 2, there are huge variations among ACRs in both overall intron densities and numbers of intron-containing homologs of known gene structure. Intron densities range from less than 1 intron per 100 codons to one intron per codon; the number of known homolog structures per ACR ranges from one to nearly 500. Fig. 2 further shows, as one would expect, that those gene families with a larger number of intron-containing members in the database have a higher overall intron density, increasing roughly linearly.
Fig 2.
Overall intron density and number of homologs. (Top) The distribution of 276 ACRs with respect to intron density. (Middle) The distribution of the same ACRs with respect to the number of intron-containing homologs in GenBank. (Bottom) The relationship between the two.
A short note is in order here. As Fig. 2 demonstrates, there is a correlation between the density of introns and the number of homologs, as one expects. From this point forward, we will perform similar calculations that examine the relationships of correspondence with module boundaries to each of these two metrics. Thus, the two apparent effects that we present, though different in important ways, are in essence just two ways at getting at the same phenomenon: the drowning out of the ancient signal by the noise of insertion.
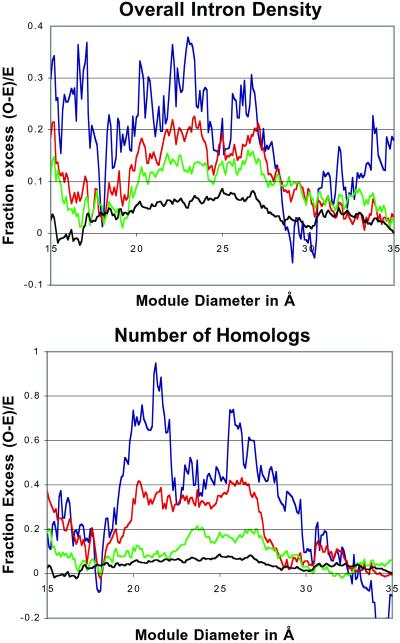
To explore the behavior of intron-sparse (or homolog-poor) genes, we defined several nested subsets: for “intron-sparse” genes we grouped genes of d or fewer introns/100 residues for d = 2, 4, 6, and 8. We also defined nested subsets of “homolog-poor” genes: genes with h or fewer intron-containing homologs for h = 1, 5, 10, and 20. We calculated the excess of introns in module boundaries over expectation over a wide range of module sizes for each of these subsets of introns. Fig. 3 shows that all of the curves are noticeably elevated in comparison to that of the phase zero intron set as a whole. The excess of intron positions in module boundaries is highest for the sparsest (or fewest homologs) and falls off as the density (or number of homologs) increases. The values of d involved correspond to the expectations of the Exon Theory of Genes, which postulates that original exons were 15–30 codons long, corresponding to d values between 3 and 7.
Fig 3.
Relationship of phase zero intron–module boundary correlation to overall intron density and number of homologs. (Upper) The correlation for all phase zero positions in ACRs (black) and for the subsets of ACRs with d or fewer intron positions per 100 codons for d = 2 (blue), d = 6 (red), and d = 8 (green). The plot for d = 4, which follows the trend, has been omitted for clarity. (Lower) The correlation for all phase zero positions in ACRs (black) and for the subsets of ACRs with h or fewer intron-containing homologs for which gene structures are known for h = 1 (blue), h = 5 (red), and h = 10 (green).
Are these deviations of the various intron-sparse (homolog-poor) curves from the curve for the entire set significant? To study this, we calculated the average excess of the entire set over the region where the excess in module boundaries is >5%. This corresponds to module sizes from 21 to 27 Å. We calculated the analogous value for each of the intron sparse sets, and then asked for the probability of drawing a subset of the given size from the entire phase zero set that would have an excess of introns in module boundaries greater than or equal to the real subset. This was done by a Monte Carlo calculation in which we generated 10,000 subsets. The P values are then simply given by the number of subsets with a value equal to or higher than that of the real subset divided by 10,000.
Table 1 gives these values for each of our intron-sparse (homolog-poor) subsets. The excesses are significant for all four values of d and for three of the four values of h. As one would expect, the significance first increases as the number of introns involved becomes larger, then falls as the noise becomes larger. However, the significance holds for a large range. These significant differences confirm our prediction that reconstructed gene structures in the range postulated by the Exon Theory of Genes show even stronger correlation with module boundaries.
Table 1.
Tests for significance for phase zero positions
| Data set | No. of positions | Excess in module boundaries, % | P |
|---|---|---|---|
| Overall intron density | |||
| d = 2 | 94 | 24.9 | 0.05 |
| d = 4 | 350 | 19.5 | 0.011 |
| d = 6 | 611 | 17.4 | 0.0044 |
| d = 8 | 991 | 13.0 | 0.016 |
| All phase zero | 3,328 | 6.7 | |
| No. of homologs | |||
| h = 1 | 38 | 53.8 | 0.0058 |
| h = 5 | 206 | 34.8 | 0.0001 |
| h = 10 | 610 | 14.7 | 0.0023 |
| h = 20 | 1,132 | 8.4 | 0.26 |
| All phase zero | 3,328 | 6.7 |
P values are based on 10,000 random samples of the given size. P values in italics are significant at the P = 0.05 level.
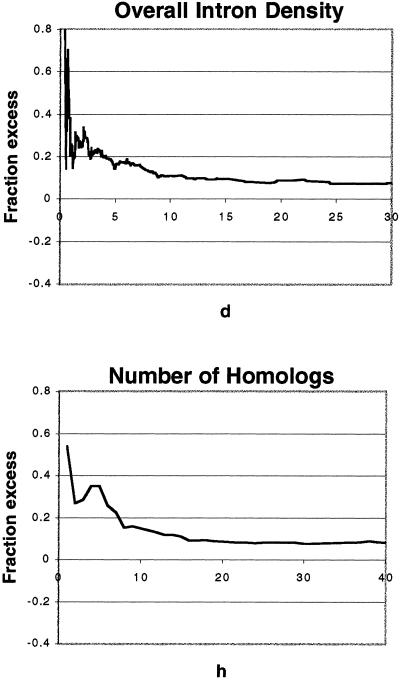
However, because these values of d and h were arbitrary, we wanted to be certain that the observed variations were not caused by serendipitous choice of cutoffs. We therefore did the analogous calculation for all possible intron-sparse and homolog-sparse subsets; that is, we did the calculation for two series of subsets, one for which we added one gene at a time in increasing order of overall intron density (increasing d by very small increments) and the other for which we incremented h by one at a time. Fig. 4 shows that the observed average excess of introns in module boundaries falls generally with both measures.
Fig 4.
Relationship of phase zero intron–module boundary correlation to overall intron density and number of homologs. (Upper) The fraction excess in module boundaries as a function of d. (Lower) The fraction excess in module boundaries for ACRs as a function of h.
We next calculated P values for each subset based on 10,000 subsets of each appropriate size. Virtually all subsets from d = 2.0 to 11.4 introns per 100 residues are significantly more strongly correlated with module boundaries than is the full phase zero set (of 164 subsets in this region, 78 gave P values <0.01, 78 gave P values <0.05, and 8 gave P values between 0.05 and 0.08). This finding corresponds to subsets of sizes from 95 to 1,480 intron positions out of a total of 3,474 phase zero positions, or subsets from 3% of the phase zero intron positions to nearly half. Similarly, subsets from h = 1 to 12 intron-containing homologs are significantly more strongly correlated with module boundaries than is the full phase zero set. This finding corresponds to subsets of sizes from 38 to 758 intron positions, or from 1% to nearly a quarter of the full set. The effect is thus seen over a large range for both measures.
If the observed deviation in ACRs is in fact caused by the ancient character of phase zero introns and if the phase one and phase two sets are more completely recent in origin, as previous analyses have suggested, then one would not expect to see such a deviation in these sets of introns. Table 2 shows that there is no appearance of trends or statistical significance for phase one and two subsets of increasing intron density or number of homologs. However, there is an isolated point, phase 2, d = 4, which shows a significant excess. On closer examination, phase two subsets from d = 3.1 to 4.2 introns per 100 residues, corresponding to subsets of size from 124 to 175 positions, are significantly better correlated with module boundaries than is the whole set of 1,544 positions. However, this is a narrow range, comprising only from 8% to 11% of the whole set, and because there is no corresponding effect in the number of homologs calculation, we consider this to be due to random fluctuation.
Table 2.
Tests for significance for phase one and phase two positions
| Data set | No. of positions | Excess in module boundaries, % | P |
|---|---|---|---|
| Overall intron density | |||
| Phase 1 | |||
| d = 2 | 94 | 8.1 | 0.18 |
| d = 4 | 350 | −6.2 | 0.53 |
| d = 6 | 611 | −6.8 | 0.59 |
| d = 8 | 991 | −9.0 | 0.82 |
| All phase 1 | 1,740 | −5.5 | |
| Phase 2 | |||
| d = 2 | 38 | 10.8 | 0.30 |
| d = 4 | 206 | 18.1 | 0.025 |
| d = 6 | 610 | 9.3 | 0.11 |
| d = 8 | 1,132 | 7.8 | 0.10 |
| All phase 2 | 1,544 | 2.1 | |
| No. of homologs | |||
| Phase 1 | |||
| h = 1 | 94 | 0.3 | 0.4 |
| h = 5 | 350 | −9.1 | 0.64 |
| h = 10 | 611 | −11.3 | 0.86 |
| h = 20 | 991 | −6.9 | 0.65 |
| All phase 1 | 1,740 | −5.5 | |
| Phase 2 | |||
| h = 1 | 38 | 31.7 | 0.17 |
| h = 5 | 206 | 0.9 | 0.54 |
| h = 10 | 610 | 1.0 | 0.58 |
| h = 20 | 1,132 | 2.1 | 0.50 |
| All phase 2 | 1,544 | 2.1 |
P values are based on 10,000 random samples of a given size. P values in italics are significant at the P = 0.05 level.
Discussion
We show here that intron positions in those ancient gene families whose known collective intron density resembles that hypothesized by the Exon Theory of Genes have a stronger correspondence to module boundaries than does the phase zero set as a whole. We also show that overall correspondence of phase zero introns to module boundaries in ACRs decreases with the number of intron-containing homologs. These results suggest that the correlation between intron positions and module boundaries in ancient genes is in fact caused by the presence of ancient introns rather than to some vague and elusive protein-structure-correlated insertion bias.
This is an important result for the introns-early/introns-late debate. Reduction of the correlation of introns with module boundaries with increasing data has been a general trend since the correlation was first observed 20 years ago. As one expects that statistical power will increase with increasing data, this has been a troubling result indeed. Some have seen this diminishing effect as evidence that the correlation is not real. These results suggest another alternative. Because of the finite number of hypothesized ancient introns, each of which is expected to be more widely distributed through the gene tree, the number of known ancient positions is expected to plateau with the sequencing of more and more homologs. On the other hand, the number of more recently inserted positions will increase without limit as the gene structures of more and more homologs are known. Thus, a washing out of the signal that has dominated the history of this debate would be expected in a mixed origin scenario.
In fact, the size of the correlation with module boundaries decreases either with the overall intron density of a reconstructed gene structure or with the absolute number of intron-containing homologs mapped. Furthermore, the P values are very significant over a large range of densities (or number of homologs). This is exactly the pattern one expects if there were a limited number of ancient positions and a potentially unlimited number of recently acquired positions. That this effect is not seen for phase one or phase two ACR introns further supports the notion that the observed effect in phase zero intron positions is caused by the ancient character of a subset of these positions.
These results embody the fulfillment of yet another subtle prediction of a mixed model of intron origin. The difference seen here is predicted by neither a strictly introns-early model of intron evolution (on which all introns should correlate equally well) nor a strictly introns-late model (on which there should be no difference in intron correlation due to differences in intron density or other such differences). Thus, in predicting the trend seen here, a mixed-origin model is superior to more absolutist models.
This result complements our recent work in demonstrating the ability of the mixed-model to distinguish between different subsets of introns. We have now shown that widely phylogenetically distributed intron positions correlate more strongly with module boundaries (11) and have a stronger phase zero bias than do other introns (12), that introns in nonancient genes do not correlate with module boundaries (13) and that introns in genes that may be products of horizontal gene transfer have a weaker phase zero bias than do vertically inherited genes (12). These are all fulfilled predictions that refine the conception of ancient introns and suggest that a signal of ancient introns persists in modern-day genomes, even in the face of convincing evidence for a large number of recent intron insertions.
Acknowledgments
We thank S. J. de Souza and M. Long for valuable comments and critiques of the manuscript.
Abbreviations
ACR, ancient conserved region
References
- 1.Gilbert W. (1978) Nature 271 501. [DOI] [PubMed] [Google Scholar]
- 2.Blake C. C. F. (1978) Nature 273 267. [Google Scholar]
- 3.Doolittle W. F. (1978) Nature 272 581-582. [Google Scholar]
- 4.Go M. (1981) Nature 291 90-92. [DOI] [PubMed] [Google Scholar]
- 5.Blake C. C. F. (1983) Nature 306 535-537. [DOI] [PubMed] [Google Scholar]
- 6.Gilbert W., Marchionni, M. & McKnight, G. (1986) Cell 46 151-153. [DOI] [PubMed] [Google Scholar]
- 7.Gilbert, W. (1987) Cold Spring Harbor Symp. Quant. Biol. 901–905. [DOI] [PubMed]
- 8.Long M., Rosenberg, C. & Gilbert, W. (1995) Proc. Natl. Acad. Sci. USA 92 12495-12499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.de Souza S. J., Long, M., Shoenbach, L., Roy, S. W. & Gilbert, W. (1996) Proc. Natl. Acad. Sci. USA 93 14632-14636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.de Souza S. J., Long, M., Klein, R. J., Roy, S., Lin, S. & Gilbert, W. (1998) Proc. Natl. Acad. Sci. USA 95 5094-5099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Roy S. W., Nosaka, M., de Souza, S. J. & Gilbert, W. (1999) Gene 238 85-91. [DOI] [PubMed] [Google Scholar]
- 12.Roy S. W., Lewis, B. P., Fedorov, A. & Gilbert, W. (2001) Trends Genet. 17 496-498. [DOI] [PubMed] [Google Scholar]
- 13.Fedorov A., Cao, X., Saxonov, S., de Souza, S. J., Roy, S. W. & Gilbert, W. (2001) Proc. Natl. Acad. Sci. USA 98 13177-13182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cavalier-Smith T. (1985) Nature 315 283-284. [DOI] [PubMed] [Google Scholar]
- 15.Dibb N. J. & Newman, A. J. (1989) EMBO J. 8 2015-2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Stoltzfus A., Spencer, D. F., Zuker, M., Logsdon, J. M. & Doolittle, W. F. (1994) Science 265 202-207. [DOI] [PubMed] [Google Scholar]
- 17.Logsdon J. M., Tyshenko, M. G., Dixon, C., Jafari, J. D., Walker, V. K. & Palmer, J. D. (1995) Proc. Natl. Acad. Sci. USA 92 8507-8511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Logsdon J. M. (1998) Curr. Opin. Genet. Dev. 8 637-648. [DOI] [PubMed] [Google Scholar]
- 19.Jensen E. O., Paludan, K., Hyldignielsen, J. J., Jorgensen, P. & Marcker, K. A. (1981) Nature 291 677-679. [Google Scholar]
- 20.Tittiger C., Whyard, S. & Walker, V. K. (1993) Nature 361 470-472. [DOI] [PubMed] [Google Scholar]