Statistical learning of new visual feature combinations by infants

Abstract

The ability of humans to recognize a nearly unlimited number of unique visual objects must be based on a robust and efficient learning mechanism that extracts complex visual features from the environment. To determine whether statistically optimal representations of scenes are formed during early development, we used a habituation paradigm with 9-month-old infants and found that, by mere observation of multielement scenes, they become sensitive to the underlying statistical structure of those scenes. After exposure to a large number of scenes, infants paid more attention not only to element pairs that cooccurred more often as embedded elements in the scenes than other pairs, but also to pairs that had higher predictability (conditional probability) between the elements of the pair. These findings suggest that, similar to lower-level visual representations, infants learn higher-order visual features based on the statistical coherence of elements within the scenes, thereby allowing them to develop an efficient representation for further associative learning.

Present theories of high-level vision posit that object recognition is based on internal representations of complex features stored in extrastriate cortical areas (1–4), and that these features are constrained by mechanisms at the level of retinal ganglion cells (5) and striate cortex simple cells (6) which are tuned optimally to explore statistical regularities in the visual input. However, it is not clear what process governs the selection and learning of complex features, specific views (7), or object-parts (8) that serve as the canonical building blocks for representing the higher-order structure of objects. It has been proposed that any effective associative learning of higher-order visual features requires access to the predictability of one element's appearance in the presence of another element, i.e., the conditional probabilities between image elements (9, 10). In the absence of such information, the observer will be unable to differentiate the actual underlying structure of scenes from meaningless coincidences. However, there has not been a demonstration that human infants could rely on conditional probabilities of image elements in developing complex visual representations of their environment.

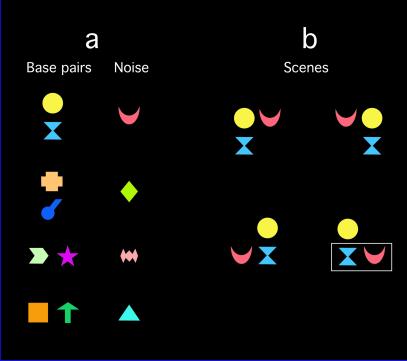
We tested 9-month-old infants in three experiments by using a habituation paradigm to determine whether they naturally extract statistics from unknown scenes that would allow them to develop new higher-order representations efficiently. In each experiment, infants first were familiarized to a series of scenes, each composed of 3 elements of a pool of 12 colored geometric shapes (Fig. 1). Eight of the elements were grouped into two horizontal and two vertical pairs (base pairs), so that the elements within pairs always appeared together in a fixed spatial relationship. Four elements were “noise” elements, in that they appeared without a fixed spatial relationship to any other element. Each scene consisted of one base pair and one noise element placed within an invisible 2 by 2 grid. Each noise element was assigned to one particular base pair, so that the noise element and the related base pair always appeared together, but in one of four different spatial relationships within the available locations of the grid. Thus, there were a total of 16 possible scenes repeated many times in random order during the habituation phase. Each scene was presented for 2 sec in a looming format to maximize the infants' interest (11). The scenes were composed of arbitrary shapes in a regular layout rather than multipart nonsense objects or sets of Gabor stimuli to avoid any interference between preexisiting mechanisms sensitive to low-level attributes (e.g., orientation) or Gestalt principles (e.g., proximity or shape-similarity) and our goal of measuring the statistical relationships between elements (12). Because the infant could easily discriminate between the elements in the scenes, which appeared many times, only the higher-order structure of element cooccurrences could serve as relevant information for representing the scenes.

Fig 1.

Stimulus elements and scenes used in the experiments. (a) The twelve shapes were grouped into four base pairs and four noise elements, with each noise element appearing with only one base pair. (b) The four possible scenes created by one base pair and its noise element. In Experiment 1, all four scenes were presented during habituation; in Experiments 2 and 3, again, all four scenes were presented for low-frequency base pairs, but only two scenes (shown in the right column) were presented for high-frequency base pairs, which appeared twice as often as individual scenes with low-frequency base pairs. Because this doubling of appearance frequency was equally split between the two scenes containing the high-frequency base pair, the non-base pair (marked by the white rectangle in the lower right scene) appeared the same number of times as a low-frequency base pair.

Once each infant was habituated, as indexed by a predetermined criterion of decline in looking time to the display, the test phase began. For the test, two base pairs and two non-base pairs were selected randomly for each infant. The non-base pairs consisted of one element of a base pair and the corresponding noise element that appeared with that pair. The base and non-base test pairs were presented in a standard posthabituation test phase to assess looking times to these two types of test pairs. A significant difference in looking time signaled that the infant could discriminate the base pair from the non-base pair.

Materials and Methods

Synthetic scenes were generated off-line by the Canvas drawing program and integrated into a presentation program written in MacroMedia DIRECTOR. Each infant was tested individually while seated on the parent's lap 85 cm from the display in a separated section of a dark room. Stimuli were presented on a 32" TV screen connected to an Apple G3 computer. An observer inside the room but invisible to the infant monitored the infant's looking behavior with the use of a video system. The observer initiated the presentation sequences and coded the infant's looking behavior by using the keyboard of the computer but was unaware of the stimuli being presented on the screen.

During the habituation phase, the infant's gaze was first directed to a pulsing checkerboard pattern (the attention-getter), accompanied by sound effects, located in the middle of the screen. When the infant looked at the attention-getter, the habituation sequence was initiated, with the precomposed scenes appearing in random order in the center of the screen. Each scene grew in size (loomed) from a minimum of 3.14° (element size = 1.35°) to a maximum of 9.41° (element size = 4.05°) over the course of 1.5 sec, and then paused at this size for 0.5 sec. This scene then disappeared and the next scene appeared at its smallest size and went through the same looming pattern. During the habituation phase, multiple randomized blocks of the 16 possible scenes were concatenated into a master list. A habituation trial consisted of the looming presentation of scenes from this master list, with a maximum trial duration of 60 sec or until the infant's fixation was directed away from the display for 2 consecutive sec. Looks away from the display that were less than 2 sec resulted in a pause of the looming stimulus until the infant looked back to the display, whereupon it started the looming cycle where it had left off before the look-away. When the maximum duration, 60 sec, or the more-than-2-sec look-away criterion occurred, the duration of looking to the display on that trial was stored, and the attention-getter automatically reappeared to align the infant's gaze for the onset of the next habituation trial. A test trial was very similar to a habituation trial except that each test trial consisted of a single display repeated over and over, rather than the random sequence of displays presented during each habituation trial.

Each infant met a preset criterion of habituation before proceeding to the test phase. Habituation trials proceeded until the infant's cumulative looking time on four consecutive trials, measured online by the program during the experiment, declined to a value less than 50% of their cumulative looking time on the first four habituation trials. If this criterion was not satisfied in 12 trials, the habituation was considered unsuccessful, and the infant's data were excluded from the analysis. Infants received 6–12 habituation trials (mean, 7.89 trials; SE, 0.38), depending on the speed of their habituation. The average exposure to the habituation sequence combined across all trials was 159.6 sec (SE, 14.1 sec); thus, each infant viewed ≈80 scenes (i.e., each unique scene roughly five times) before the test phase (see Figs. 5–7, which are published as supporting information on the PNAS web site, www.pnas.org). There were 24 infants tested successfully in each experiment. Because of the effectiveness of the looming stimuli in maintaining the infants' interest, only nine infants failed to meet the criterion of habituation across the three experiments combined.

Immediately after each infant met the habituation criterion, two types of test displays were presented on successive test trials. In Experiments 1 and 2, one type consisted of a base pair and the other consisted of a non-base pair, whereas in Experiment 3 one type consisted of a single low-frequency element and the other consisted of a single high-frequency element. With each infant, two different examples of each of these two types of test trials were repeated three times in random order, yielding a total of 12 test trials per infant. The selection of the actual base pairs and non-base pairs as well as the presentation order of the pairs presented to each infant were randomized by the computer and fully balanced across infants. Elements within all pairs were either vertically or horizontally arranged, and the orientation of base and non-base pairs were balanced across trials within the test for each infant. Each test trial began with the same attention-getter used during habituation, followed by a test pair (or element) that loomed repetitively in the same manner as in habituation. Each test trial continued until the infant looked away from the screen for 2 consecutive sec or until 60 sec of looking had occurred. Mean cumulative looking time across each of the two types of test trials provided the dependent measure used to assess posthabituation performance.

Results and Discussion

In Experiment 1, all scenes were shown an equal number of times; thus, the infants saw each individual element equally often. However, the cooccurrence of two elements in a particular spatial relationship was not balanced: elements within base pairs appeared four times as often in their given spatial arrangement as any base pair element and its corresponding noise element in their arrangement. An analogy can be drawn between our habituation sequence and a “toy-world” where snapshots of four rigid objects (the four base pairs) were shown repeatedly, surrounded by some clutter (the noise element). Alternatively, one could think of the toy-world scenes as a set of four multipart flexible objects with one larger part (the base pair) and one smaller part (the noise element) in different arrangements.

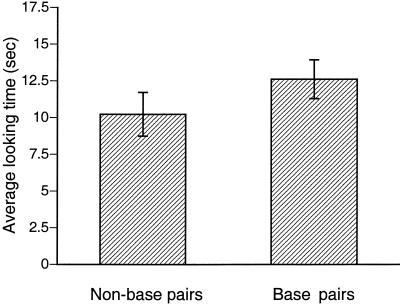
Infants showed a very strong looking preference for base pairs in the posthabituation test phase of Experiment 1 (Fig. 2). Only 3 of 24 infants looked longer at the non-base pairs, and the comparison of mean looking times for the base pairs and non-base pairs across infants was highly significant [t(23) = 5.313, P < 0.0001]. This familiarity preference is in agreement with earlier reports finding either a familiarity or a novelty effect in various visual experiments using the habituation paradigm depending on the complexity of the task, with a tendency to find a familiarity effect as task complexity increases (13, 14).

Fig 2.

Results of Experiment 1. There was a very strong looking preference for base pairs over non-base pairs, suggesting that infants noticed the higher cooccurrence of elements within the base pairs.

Because there were an equal number of exposures to the individual elements in Experiment 1, these results cannot be explained by familiarity for particular elements because of more frequent appearance during habituation. A follow-up experiment, identical to Experiment 1 with 24 new infants, in which the specific assignment of the tested base pairs and the base pairs used for creating the non-base pairs was reversed, revealed the same posthabituation preference for base pairs over non-base pairs [t(23) = 2.964, P < 0.007]. Thus, these results also cannot be explained by accidental preferences for individual elements or particular spatial arrangements of elements within pairs. Rather, the infants reliably encoded the higher coherence of the elements within the base pairs because of either their higher cooccurrence frequency or their higher predictability (conditional probability) of elements over the non-base pairs, and this encoding led them to preferentially fixate these base pairs during the test.

It is crucial to note that element cooccurrence and element predictability do not necessary coincide. Effective associative learning of new complex visual features requires the detection of “suspicious coincidences” from the array of subelements in the scene, and this learning can be accomplished only if the observer has access to the predictability between the subelements (9, 10). Element cooccurrence is less reliable than element predictability because an element may be very frequent in the environment, thereby cooccurring with many other elements. In contrast, an element may be quite infrequent, but it may cooccur with only one other element. In the former case, element cooccurrence is high but not predictive of which of many possible other elements is likely to cooccur with it. In the latter case, although element cooccurrence is low, it is highly predictive of the particular other element with which it will cooccur. Therefore, one needs to demonstrate that humans are capable of extracting predictability between elements and events independently of their cooccurrence to support the claim that the visual system performs associative learning in an efficient manner. In our Experiment 1, high cooccurrence frequency and high predictability of elements were coupled, because the base pairs with 1.0 predictability between elements were also the element-pairs that appeared more frequently (embedded in the scene) than the non-base pairs. To assess whether predictability or higher cooccurrence frequency determined which element-pairs infants preferred after habituation, we ran two more experiments where these two statistics were decoupled.

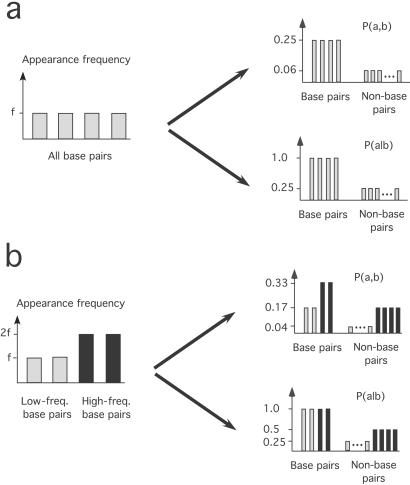
In Experiment 2, the basic arrangement of base pairs and noise elements was the same as in Experiment 1, with two key changes. First, two of the four base pairs were assigned into a low-frequency group, and the other two were assigned into a high-frequency group, with scenes containing the high-frequency base pairs shown twice as often during habituation as those with the low-frequency base pairs. Second, of the four possible scenes for a given high-frequency base pair, only two were used during habituation (see Fig. 1b). As a result of these manipulations, pairs comprising one of the high-frequency base pair elements and the corresponding noise element (referred to as a frequency-balanced non-base pair) appeared in their particular spatial configuration exactly as often as the two elements within the low-frequency base pairs. Thus, the cooccurrence frequency of the two elements in the low-frequency base pairs compared with that in the frequency-balanced non-base pairs were identical. However, the element predictability in these two test pairs differed, because whenever they were present, the elements of the low-frequency base pairs always appeared in a particular spatial configuration, whereas the elements in the frequency-balanced non-base pairs alternated evenly between two possible spatial configurations (Fig. 3).

Fig 3.

Relation between the appearance frequency of the base pairs and the cooccurrence and predictability of their elements. (a) In Experiment 1, all base pairs were presented an equal number of times to create the scenes (Left). Therefore, the cooccurrence of the elements of each base pair [measured by the joint probability P(a,b), Upper Right] was uniformly higher than that of the non-base pairs. In addition, this relation was identical whether measured by the cooccurrence of elements or by the predictability between the elements quantified by the conditional probability P(a,b) (Lower Right). (b) In Experiments 2 and 3, there were base pairs used with low (gray) and high (black) frequency to generate the scenes (Left). Consequently, there were differences in cooccurrence frequency and predictability within both the base pairs and the non-base pairs of the low- and high-frequency types. With appropriate selection of relative frequencies, the cooccurrence of elements within the low-frequency base pairs (Upper Right, gray bars) was equated with that of the high-frequency non-base pairs (Upper Right, black bars), whereas the predictability of elements within those two types remained significantly different (Lower Right), thereby decoupling cooccurrence frequency and predictability.

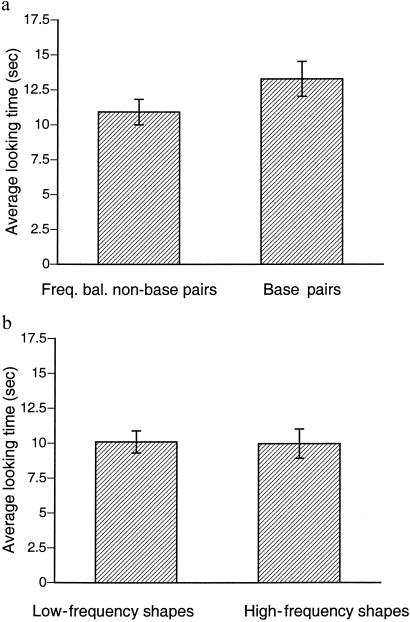
The results of Experiment 2 showed that infants looked significantly longer to the low-frequency base pairs than to the frequency-balanced non-base pairs [t(23) = 2.764, P < 0.012], even though (in contrast to Experiment 1) the cooccurrence frequency of these two test-pairs was equated (Fig. 4a). Only 6 of the 24 infants looked longer to the frequency-balanced non-base pairs than to the base pairs. However, before concluding that the predictability of element pairs ruled the infant's behavior, one needs to exclude an alternative explanation that stems from the fact that the individual elements in the low-frequency base pairs appeared only half as often during habituation as the elements in the frequency-balanced non-base pairs. Thus, the results of Experiment 2 could be accounted for by a preference for the lower frequency of the elements in the tested base pairs rather than to the higher predictability of the base pairs themselves. For this alternative to be viable, infants must have switched from a familiarity preference in Experiment 1 to a novelty preference in Experiment 2. This alternative explanation was tested in Experiment 3.

Fig 4.

(a) Results of Experiment 2. Infants had a strong looking preference for the base pairs with higher predictability between elements than for the frequency-balanced non-base pairs with lower predictability, even though the appearance frequency of elements in the frequency-balanced non-base pairs was higher by a factor of 2 for elements in the base pairs, and the cooccurrence frequency of the low-frequency base pairs and the frequency-balanced non-base pairs was equated. (b) Results of Experiment 3. Infants showed no discrimination of single elements despite their varying in appearance frequency by a factor of 2. The absence of a posthabituation preference for individual elements in this control experiment rules out element frequency as an explanation of the preference for low-frequency base pairs in Experiment 2.

Experiment 3 was an exact replica of Experiment 2 with one exception: we tested posthabituation preferences to single elements rather than to pairs of elements. In the test session, we compared low-frequency base pair elements to high-frequency elements that either were high-frequency noise elements or came from within high-frequency base pairs. If the results of Experiment 2 were caused by a novelty preference for the low-frequency elements, then infants should show sensitivity to the difference in appearance frequency of the individual elements in Experiment 3. In contrast, the results showed almost identical looking times for high- and low-frequency element types (10.1 sec vs. 9.97 sec for low- and high-frequency elements, respectively), with no significant preference [t(23) = 0.241, P > 0.81] despite the 2-fold difference in element frequency (Fig. 4b). There was no significant difference whether the low-frequency base pair was tested against high-frequency base pair elements [t(23) = 0.693, P > 0.49] or high-frequency noise elements [t(23) = 0.212, P > 0.83]. Thus, the results of Experiment 2, which were obtained with exactly the same set of habituation displays that were presented in Experiment 3, cannot be attributed to a posthabituation novelty preference for the low-frequency elements. Rather, the results of Experiment 2 must be due to a familiarity preference for the higher predictability of elements within the base pairs over the frequency-balanced non-base pairs.

These results suggest several conclusions concerning the mechanism by which visual features are extracted by infants from initially unfamiliar, complex scenes. First, 9-month-old infants are sensitive not only to the cooccurrence frequency of elements in their visual world, but also to the predictability between elements as manifested by the conditional probability relations between those elements. This learning mechanism provides a powerful and necessary tool to extract significant features from their visual environment (9, 10) and also suggests a unified strategy for developing internal representations that is applied at both low, middle, and higher levels of the visual system (15, 16). At a low level, a number of studies have shown that cells in the lateral geniculate nucleus and the primary visual cortex achieve statistically optimal tuning to the structure of the noisy visual input by evolutionary and individual adaptation, which can be characterized by the conditional probabilities of luminance among neighboring patches in the visual scene (5, 10). At a mid-level, it has been argued that the perception of visual surfaces is best described as a result of learning based on ecological optics, where predictable events are learned over frequent events based on the conditional probabilities of viewing specific images, given a particular surface (17). At a higher level, several models have proposed that new complex features (conjunctions of subfeatures) are based on the conditional probabilities of cooccurrences (18, 19). Our results give experimental support to these theories.

Our second conclusion is that infants preferentially attend to the previously extracted features when they are subsequently presented “out of context” in different displays. This familiarity preference for extracted features might be a mechanism for learning even more complex features in a hierarchical fashion during development. The third conclusion is that infants are apparently unable to keep track of the statistics of the individual elements that are embedded within the coherent base pairs. This inability (or greater difficulty) stands in sharp contrast to that of adults, who automatically and in parallel extract both the conditional probabilities of pairs and the higher frequency of individual elements within these pairs (20) and also in contrast to earlier infant results with non-embedded test items (13). Thus, the ability to analyze visual information at multiple statistical scales in parallel might mature with age.

We believe the “statistical” account of our results may also shed new light on the longstanding controversy between the “view-based” (21, 22) and the “structural description” (8, 23) accounts of the representation of visual objects in the brain. The strategy of encoding information in multielement scenes according to their internal statistical structure can be taken as support for either of these accounts. Specifically, because visual input of different objects provides the observer with different statistical structures, including cases with large differences between the cooccurrence frequency and the predictability of the spatial arrangement between subelements of the object, this input may lead to quite different visual representations. For example, when an object is seen relatively few times, when it does not have many articulated parts, or when its appearance does not change drastically across exemplars (e.g., changes in size or illumination, but not orientation or internal configuration), a “view-based” representation might be an adequate description of how the developing internal code is formed. However, when an object consists of multiple, highly segmentable or flexible parts, and it is encountered many times in different arrangements such that the cooccurrence and predictability between its parts are not highly correlated, a representation based on a structural description might be closer to what naturally develops. Thus, the two types of representations might coexist in the brain, and their development might be determined by the inherent statistics of the visual input combined with the purpose for which the representation is used. This account of the development of high-level object representations is supported by recent findings that view-based and structural description representations are stored at different cortical sites in the brain (24).

Finally, although the present results emphasize the statistical nature of human visual feature extraction, there are undoubtedly many innate, low-level, and special-purpose mechanisms that influence the type of features that the developing visual system incorporates in object representations (25). Clarifying the interplay between what we have shown in this report, that humans at an early age are able to extract the statistical structure of visual input that is critical for learning higher-level visual features, and these numerous constraints implemented by the evolution of basic visual analyzers is necessary for gaining a deeper understanding of the development of the visual system.