Testing neoclassical competitive market theory in the field

Abstract

This study presents results from a pilot field experiment that tests predictions of competitive market theory. A major advantage of this particular field experimental design is that my laboratory is the marketplace: subjects are engaged in buying, selling, and trading activities whether I run an exchange experiment or am a passive observer. In this sense, I am gathering data in a natural environment while still maintaining the necessary control to execute a clean comparison between treatments. The main results of the study fall into two categories. First, the competitive model predicts reasonably well in some market treatments: the expected price and quantity levels are approximated in many market rounds. Second, the data suggest that market composition is important: buyer and seller experience levels impact not only the distribution of rents but also the overall level of rents captured. An unexpected result in this regard is that average market efficiency is lowest in markets that match experienced buyers and experienced sellers and highest when experienced buyers engage in bargaining with inexperienced sellers. Together, these results suggest that both market experience and market composition play an important role in the equilibrium discovery process.

Over half a century ago, Chamberlain (1) executed what is believed to be the first experiment to test neoclassical competitive market theory. In his data, which were gathered from Harvard students participating in decentralized one-shot markets, volume was typically higher and prices typically lower than predicted by competitive models of equilibrium. Vernon Smith, a participant in one of Chamberlain's market sessions and a pioneer of experimental economics, has since considerably refined the analysis in several fundamental ways. In an early experimental study using student subjects at Purdue University, Smith (2) varied two key aspects of the Chamberlain design: (i) centrally occurring open outcry of bids and offers (versus decentralized negotiation); and (ii) multiple market rounds (versus one-shot markets). The results were staggering: Smith's market sessions produced quantity and price levels that were very near competitive levels. Smith (3) later recalled that he “did not seriously expect competitive price theory to be supported,” but that the double auction would give the theory its best shot. It is fair to say that this general result remains one of the most robust findings in experimental economics. For thoughtful reviews, see Holt (4) and Roth (5).

This study takes a fresh look at neoclassical price theory by experimentally examining decentralized outcomes, in the spirit of Chamberlain, in a naturally occurring marketplace: the sports card market. A major advantage of this particular field experimental design is that my laboratory is the marketplace: subjects are engaged in buying, selling, and trading activities whether I run an exchange experiment or am a passive observer.† In this sense, I am gathering data in a natural environment while still maintaining the necessary control to execute a clean comparison between treatments.

The experimental design consists of four market treatments. Each market treatment mirrors Chamberlain's construct, in that I give each buyer (seller) a reservation price for each unit they demand (supply) and allow agents to engage in bilateral haggling and bargaining until they make a contract or the trading period terminates. One major difference between my experimental design and Chamberlain's design is that I allow for learning, because subjects interact in multiple market periods. A more fundamental difference, of course, is that I am observing the behavior of agents who have endogenously chosen certain roles within the market [such as being a buyer (nondealer) or seller (dealer), intense or casual market participant, etc.]. A further important characteristic of my field experiment is that I organize the four market treatments in a manner that allows me to explore the role of buyer and seller experience on market outcomes: treatment one includes randomly chosen buyers and randomly chosen sellers; a second treatment matches super-experienced buyers with relatively inexperienced sellers; a third treatment matches inexperienced buyers with super-experienced sellers; and a fourth treatment matches super-experienced buyers with super-experienced sellers.

The main results of the study fall into two categories. First, the competitive model predicts reasonably well in some market treatments, as the expected price and quantity levels are approximated in many market rounds. Second, the data suggest that market composition is important: buyer and seller experience levels impact not only the distribution of rents but also the overall level of rents captured. An unexpected result in this regard is that average market efficiency is lowest in markets that match experienced buyers and experienced sellers and highest when experienced buyers engage in bargaining with inexperienced sellers. Together, these results suggest that both market experience and market composition play an important role in the equilibrium discovery process.

I. Experimental Design

My test of neoclassical competitive market theory departs from previous studies by examining individual behavior in a well-functioning marketplace: on the floor of a sports card show. With the rise in popularity of sports cards and memorabilia in the past two decades, markets have naturally arisen that organize buyers and sellers. Temporal assignment of the physical marketplace is typically done by a professional association or local sports card dealer who rents a large space, such as a gymnasium or hotel conference center, and allocates 6-foot tables to dealers for a nominal fee. When the market opens, consumers mill around the marketplace, haggling and bargaining with dealers, who have their merchandise prominently displayed on their 6-foot tables. The duration of a typical sports card show is a weekend, and a lucrative show may provide any given dealer hundreds of exchange opportunities (buying, selling, and trading of goods).

In this sense, the current experimental design matches real-world settings that economic theory attempts to explain: traders endogenously select into the market, and they are likely to have previous experience buying, selling, and trading. This experimental strategy may lead to different results than an experiment with exogenously induced roles (e.g., subjects are randomly placed in the buyer or seller role), but it is my belief that a rigorous examination of behavior in an actual environment, which our theory intends to explain, is an important step in testing the validity of economic models.

Each participant's experience typically followed four steps: (i) consideration of the invitation to participate in an experiment; (ii) learning the market rules; (iii) actual market participation; and (iv) conclusion of the experiment and exit interview. In i, before the market opened, a monitor approached dealers at the sports card show and inquired about their interest in participating in an experiment that would take ≈60 minutes during the show. The monitor also asked particular questions about the dealer's level of market experience. Because most dealers are accompanied by at least one other employee, it was not difficult to obtain agreements after it was explained that the participants could earn money during the experiment. To gather the nondealer subject pool, a monitor approached potential subjects entering the sports card show and inquired about their level of market experience and interest in participating in an experiment that would last ≈60 minutes.

In these treatments, the level of market experience is an important variable. To examine whether market experience influences market outcomes, I organize the four market treatments in a manner that allows me to explore the role of buyer and seller experience on market outcomes. In the first treatment, I randomly match buyers and sellers. In the second treatment, I match super-experienced buyers with relatively inexperienced sellers, whereas in the third treatment, I flip-flop experience levels by matching inexperienced buyers with super-experienced sellers. The fourth and final treatment matches super-experienced buyers with super-experienced sellers.

In defining experience levels, I consider both the number of years the subject has participated in the market and the intensity of market activity within those years. In particular, using List's (7) data as a benchmark, super-experienced nondealers are those consumers that trade 12 or more times per month and have been in the market for at least 16 years (12 and 16 are one standard deviation above the average trading rate and average number of years of market experience). Using similar selection criteria, super-experienced sellers are those dealers who trade more than 25 times in a typical month and have been in the market for at least 17 years. Relatively inexperienced subjects are those that are at least one standard deviation below the average trading rate and average number of years of market experience (one trade and 1 year of market experience for nondealers, and three trades and 3 years of market experience for dealers).

Once 12 dealers (sellers) and 12 nondealers (buyers) who fit the treatment criterion agreed to participate, in step ii, monitors thoroughly explained the experimental rules. The experimental instructions were taken from Davis and Holt (ref. 8; pp. 47–55) and adjusted accordingly. Before proceeding, I should highlight a few key aspects of the experimental design. First, all individuals were informed that they would receive a $10 participation fee on completion of the experiment. Second, consumers (nondealers) were informed that the experiment consisted of five rounds, and that they would be buyers in the experiment. In each of five rounds, each buyer would be given a “buyer's card,” which contained a number, known only to that buyer, representing the maximum price that he or she would be willing to pay for one unit of the commodity. Dealers were informed that they would be sellers in the market. In each of five rounds, each seller would be given a “seller's card,” which contained a number, known only to that seller, representing the minimum price for which he or she would be willing to sell one unit. Importantly, both buyers and sellers were informed that this information was strictly private and that reservation values would change each round. They were further informed that the market included 12 buyers and 12 sellers with potentially different values. I was careful to explain to buyers (in the presence of sellers) that sellers potentially have different reservations values. And, to avoid spillover effects, only one treatment was run per sports card show.

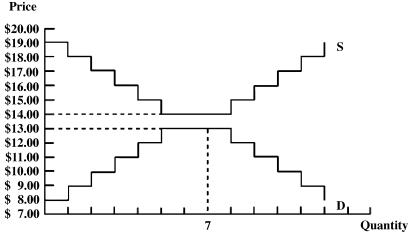
Third, the monitor explained how earnings were determined: for buyers, the difference between the contract price and the maximum reservation price determined earnings. Likewise, sellers' earnings were determined by the difference between the actual contract price and the minimum reservation price. Several examples illustrated the irrationality associated with buying (selling) the commodity above (below) the induced value. Fig. 1 and Table 1 present buyer- and seller-induced values in each treatment and are taken from Davis and Holt (ref. 8; pp. 14–15). It is important to note from Table 1 that (unbeknownst to buyers and sellers) within each treatment, each buyer (seller) received at least two maximum (minimum) reservation prices that would place them “in the market” if competitive predictions prevail. In Fig. 1, each step represents a distinct induced value that was given to buyers (demand curve) and sellers (supply curve). The efficient perfectly competitive outcome yields $37 in rents per round, which occurs where competitive price theory predicts a tendency for the static price/quantity equilibrium of price = $13–14 and quantity = seven to be reached, which is the extreme point of the intersection of the buyer and supplier rent areas in Fig. 1.

Fig 1.

Supply and demand structure. S and D represent seller- and buyer-induced values in each treatment. Equilibrium occurs at their intersection.

Table 1.

Buyer and seller reservation values (in dollars) by market period

	Period
	1	2	3	4	5
Buyer
1	19	14	17	13	14
2	18	9	10	17	11
3	17	10	11	16	13
4	16	11	12	15	9
5	13	12	16	14	18
6	14	13	14	19	15
7	15	16	14	12	19
8	12	14	15	11	16
9	11	15	13	10	17
10	10	17	18	9	14
11	9	18	19	14	10
12	14	19	9	18	12
Seller
1	13	18	9	12	13
2	9	17	13	11	14
3	10	16	13	9	15
4	11	15	8	10	16
5	12	14	10	13	17
6	8	13	11	13	18
7	13	13	12	14	8
8	14	12	14	15	9
9	15	11	15	16	10
10	16	10	16	17	11
11	17	9	17	18	12
12	18	8	18	8	13

Fourth, the homogeneous commodities used in the experiment were 12 1982 Ben Oglivie Topps baseball cards, on which I had artfully drawn a moustache, making the cards valueless outside of the experiment. Thus, the assignment given to buyers was clear: enter the marketplace and purchase the Oglivie “moustache” card for as little as possible. Likewise, the task confronting sellers was also clear and an everyday occurrence: sell the Oglivie “moustache” card for as much as possible. The cards and dealer participants were clearly marked to ensure no buyers had trouble finding the commodity of interest. Fifth, buyers and sellers engaged in two 5-minute practice periods to gain experience with the market.

In step iii, subjects participated in the market. Each market treatment consisted of five market periods that lasted 10 minutes each. After each period, a monitor privately gathered with the 12 buyers and gave them a new buyer's card, whereas a different monitor privately gave the 12 sellers a new seller's card. It should be noted that, throughout the market process, careful attention was paid to prohibiting discussions between sellers (or buyers) that could induce collusive outcomes. Much like the early researchers in this area, I wanted to give neoclassical theory its best chance to succeed. And, by allowing interaction over several market periods, buyers had the ability to explore relationships with multiple sellers, or to develop a “long-term relationship” with one seller. This design feature highlights the fact that, for example, some dealers may have attempted to send signals in the experiment that they were “good” dealers to invoke positive reciprocity in future exchanges (but, note buyers were aware that sellers had different reservation values). Rather than view this as a loss in control, I find it an interesting design parameter, because some of my dealer (nondealer) subjects were local dealers (nondealers) who constantly interacted in the local market, whereas others were regional dealers (nondealers) who infrequently attended the local shows (e.g., Las Vegas dealers who rarely attended shows in Tucson, AZ). I suppress further discussion of this issue here but note that it is fertile ground for future research. Step iv concluded the experiment; after subjects completed a survey, they were privately paid their earnings.

I follow this simple procedure in each of the four treatments. In summary, in each treatment, the monitor gives each buyer and seller a reservation price for one unit and allows agents to engage in bilateral haggling and bargaining until they make a contract or the trading period terminates. After each contract is completed, a monitor (i) posts the exchange price on a public board and (ii) monitors inform all buyers and sellers in the market in case they are removed from the public board. Given that each of the four treatments had five market periods, my experiment includes data from 20 unique market periods. And, because buyers and sellers competed in only one treatment, my experiment included 48 buyers and 48 sellers.

II. Experimental Results

Table 2 contains summary statistics for the experimental data. Entries in Table 2 are at the period level and include average price and its standard deviation, quantity traded, total buyer and seller per period profits, and a measure of efficiency [total profits divided by available profits ($37)]. Table 2 can be read as follows: in period 1 of the “random” treatment, eight cards were purchased at an average trading price of $14.06 (SD = 2.2). Total buyer and seller profit was $12.50 and $20.50, and traders captured 89% of the available rents for the period.

Table 2.

Experimental results

Treatment	Market period
	1	2	3	4	5
Random
Average price	14.06	13.56	13.29	13.64	13.32
SD	2.2	1.9	2.1	0.8	1.1
Quantity	8	9	7	7	7
Profits
Buyers	12.50	16.00	15.00	17.50	18.75
Sellers	20.50	16.00	17.00	18.50	17.25
Efficiency, %	89	86	86	97	97
Experienced buyers/inexperienced sellers
Average price	12.21	13.22	12.96	12.75	13.13
SD	1.7	1.8	0.9	1.4	1.4
Quantity	7	8	7	6	8
Profits
Buyers	21.50	20.25	21.30	22.50	21.00
Sellers	9.50	15.75	14.70	12.50	14.00
Efficiency, %	84	97	97	95	95
Experienced buyers and sellers
Average price	13.12	14.29	13.53	13.86	12.86
SD	1.5	2.1	2.0	1.9	1.4
Quantity	8	7	7	9	7
Profits
Buyers	18.05	13.00	15.25	13.25	21.00
Sellers	13.95	13.00	14.75	15.75	14.00
Efficiency, %	86	70	81	78	95
Inexperienced buyers/experienced sellers
Average price	15.21	14.04	14.33	14.49	13.99
SD	1.2	2.3	1.0	2.6	0.8
Quantity	6	7	6	7	7
Profits
Buyers	7.75	10.75	13.00	7.60	14.10
Sellers	27.25	19.25	22.00	14.40	21.90
Efficiency, %	95	81	95	59	97

Numbers represent average period price, SD of period price, quantity traded in period, and total buyer and seller profits in period. For example, in the “random” treatment (market period 1), the average trading price was $14.06 with a SD of $2.20. Eight cards were purchased, and total buyer (seller) profit was $12 ($20.50).

Results from the market where subjects are randomly drawn (row 1 in Table 2) suggest that competitive price theory does an adequate job of organizing the data. For example, four of five market periods had average trading prices within the predicted $13–14 competitive range, and 16 of 38 executed trades were within the competitive market range. In addition, three of these four market periods had the theoretically correct quantity level of seven units traded, and efficiency levels were very high, reaching 97% in the latter periods.

Data from the other treatments do not paint as compelling a picture, but they are remarkably consistent, because average market price for any period is never more than 9% from the predicted price, and market quantity is always between six and nine units. Yet market efficiency is quite variable, as low as 59% in period 4 of the inexperienced buyers/experienced sellers' market and reaching as high as 97% in various other treatments. Overall, I do not observe the persistent pattern of results found in Chamberlain (volume consistently too high and price consistently too low). I suspect that the level of market experience among my subjects is the reason Chamberlain's anomaly is not observed herein: it was clear that, in this setting, market participants' bargaining behavior made the decentralized setting resemble Smith's double auctions, because consumers were unrelenting in their pursuit of profits, rapidly moving from dealer to dealer in search of the lowest price.

Yet, as persistent as consumers appeared, market experience did play a major role in market outcomes and rent distribution. One can glean this from examination of the average trading price across treatments. In the market with experienced buyers and inexperienced sellers, prices tended toward the lower range of competitive predictions ($12.21–13.22). Alternatively, when the seller pool had market experience advantages, prices tended toward the upper range of the competitive prediction ($13.99–15.21). This difference in average realized prices also mapped into heterogeneous buyer and seller average profits across these two treatments: when buyers (sellers) had an experience advantage, their average profit was $8.88 ($8.73), and sellers' (buyers') average profit was $5.53 ($4.43). Using a small sample t test, I find that these differences in rents are significant at the P < 0.01 level for both buyers and sellers (e.g., $8.88 and $8.73 are both statistically different from $5.53 and $4.43).

Although the individual level of market experience is found to influence the allocation of rents, an interesting query revolves around market outcomes when inexperienced and experienced agents on the same side of the market commingle. Because I allow this sort of intermixing only in the random treatment, I examine data from the experienced agents in this treatment. Even though sample sizes are small (four experienced buyers and three experienced sellers were in this treatment), the trend is sharp. The four experienced buyers had average profits of $6.25, and the three experienced sellers had average profits of $8.88. For buyers, these average profit levels are 30% below received profits when only experienced buyers populate the market. Despite the sample size, a small sample t test shows that this difference is statistically significant at the P < 0.05 level using a one-sided alternative. Thus, it appears market composition matters: experienced buyers earn more rents when they commingle with other experienced buyers than when they commingle with inexperienced buyers. This result suggests that there may well be a “curse of competitors' knowledge”: inexperienced buying agents serve to provide a readily available pool of buyers at higher prices, pushing up the level of buyer competition as well as the overall reservation price of sellers. This finding does not carry over to the seller side of the market, however, because experienced sellers earn similar rents across these two market composition types.

In terms of overall market rents, I find an unexpected result: considering all five market periods, average market efficiency is lowest in markets that match experienced buyers and experienced sellers (82%) and highest when experienced buyers engage in bargaining with inexperienced sellers (93%). [In a related vein, see the results in Smith and Williams (9), who examine competitive price behavior in a centralized double-auction with rent asymmetries.] Using a matched-pairs t test across periods, I find that at the P < 0.05 level rents obtained in markets that match experienced buyers and experienced sellers are significantly lower than rents obtained in markets where subjects are, (i) randomly drawn and (ii) populated by experienced buyers and inexperienced sellers. Previous research suggests that structural and institutional features of the market are important; the data herein suggest that the composition of the market may also influence outcomes: market experience not only affects rent allocation but also impacts overall rents. There are other examples in which an asymmetric advantage improves overall rents. For example, in ultimatum games, first mover advantages have been found to lead to offers that appear higher than necessary to induce acceptance, but the paucity of rejections also means that efficiency is higher.

III. Concluding Remarks

In this study, I depart from a traditional experimental investigation of neoclassical competitive theory by using the tools of experimental economics in an actual marketplace. Examining behavior in four field treatments yields two unique insights. First, outcomes are considerably closer to competitive expectations than Chamberlain observed. Second, market composition affects not only the distribution of rents but also the overall market rents obtained.

I view this study as only a beginning in a systematic effort to test neoclassical price theory in an actual marketplace. Merely by varying demand and supply parameters, or the ability for temporal interaction in the above treatments, one could gain considerable insights about the market adjustment process. In this regard, an appropriate field experimental design would permit a test to distinguish between the Walrasian hypothesis and the “excess rent” hypothesis (10). In addition, studying collusion in such a marketplace could provide considerable insights. Finally, whether subject-specific demographic characteristics affect market outcomes (rent allocation, actual contracts completed) is touched on herein but remains largely unresolved and can be more closely examined in this market setting, because heterogeneous subjects populate the marketplace. I defer a more extensive discussion of these results until another occasion.