Growing and navigating the small world Web by local content

Abstract

Can we model the scale-free distribution of Web hypertext degree under realistic assumptions about the behavior of page authors? Can a Web crawler efficiently locate an unknown relevant page? These questions are receiving much attention due to their potential impact for understanding the structure of the Web and for building better search engines. Here I investigate the connection between the linkage and content topology of Web pages. The relationship between a text-induced distance metric and a link-based neighborhood probability distribution displays a phase transition between a region where linkage is not determined by content and one where linkage decays according to a power law. This relationship is used to propose a Web growth model that is shown to accurately predict the distribution of Web page degree, based on textual content and assuming only local knowledge of degree for existing pages. A qualitatively similar phase transition is found between linkage and semantic distance, with an exponential decay tail. Both relationships suggest that efficient paths can be discovered by decentralized Web navigation algorithms based on textual and/or categorical cues.

The link structure of the Web is attracting considerable attention. Several studies have shown that the degree sequence of Web pages has a power-law distribution, Pr(k) ∼ k^−γ where k is the degree of a page (number of inlinks or outlinks) and γ is a constant exponent (1–5). Two aspects of this scale-free link topology of the Web that may have important applications, for example, in the design of the next generation of Web search tools, are (i) growth models to explain the emergence of popular Web sites and (ii) navigation models to build effective crawlers.

The first goal of this article is to develop a generative model that predicts Web degree distributions based on realistic assumptions about what motivates authors to pick the sites to which they link their pages. I do not assume global knowledge of degree or other link information and I aim to tie the attachment process to a plausible content-based metric, modeling the author's intent to link a new page to existing sites that are both popular and related semantically. In the next section I report on a surprising relationship between the probability that two pages belong to a common link neighborhood and a content-based distance measure. A phase transition is observed between a region where linkage is not determined by content and one where linkage decays according to a power law with increasing content-based distance. Such a finding motivates a generative model based on this relationship and on the observed distribution of the content-based distance measure among pairs of Web pages. The model is described in the third section, where it is shown to accurately predict the distribution of degree in a large Web sample. There have been some other, more theoretical efforts recently to unify Web content and link generation based on latent semantic and link eigenvalue analysis (6, 7). My finding and model are motivated entirely by more empirical observations and actual data.

The second goal of this article is to tie the theoretical existence of optimal navigation algorithms for small world networks and the actual viability of efficient content-driven Web crawlers. Given the Web's small world and power-law topology (1, 2, 4, 5), its diameter scales as Θ(logN/loglogN) (8); therefore, if two pages belong to a connected component of the Web, some short path exists between them. Can a crawler navigate such a short path? In the fourth section I show that although purely link-based algorithms can be efficient in terms of path length (9, 10), the number of pages that must actually be crawled to determine the path is unreasonably large. I then draw a connection between the link-content analysis and a theoretical result regarding the existence of efficient decentralized algorithms to navigate small world networks in which links are generated based on a geographic topology (11, 12). An analogous connection is drawn by discovering an exponential relationship between link neighborhood probability and semantic distance between pages. My measurements reveal that the Web's linkage topology is consistent with network models where links are generated based on a topical hierarchy, for which the existence of efficient navigation algorithms is also known (13, 36). These findings suggest that realistic Web crawling algorithms based on textual and/or categorical cues can efficiently discover relevant pages and are consistent with data from state-of-the-art crawling algorithms.

Power-Law Relationship Between Web Content and Linkage

To gain insight into the Web's scale-free growth and mechanisms for efficient navigation, I want to study the connection between the two topologies induced over the Web by links and textual content. I start by introducing a distance measure based on the lexical similarity between the textual content of pages. Let us define such a lexical distance

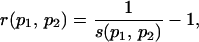where (p₁, p₂) is a pair of Web pages and

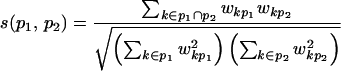is the cosine similarity function traditionally used in information retrieval (w_kp is some weight function for term k in page p, e.g., term frequency). The r distance measure is a natural local cue readily available in the Web, with the target content specified by a query, topic, or bookmark page of interest to the user. This measure also does not suffer from the dimensionality bias that makes L-norms inappropriate in the sparse word vector space.

To investigate the relationship between the lexical topology induced by r and the link topology, it would be desirable to measure the probability that two pages at a certain lexical distance from each other have a direct link between them. Unfortunately, such a probability is extremely difficult to measure directly because the low ratio between the average degree of Web pages and the size of the Web makes the likelihood that two random pages link to each other negligibly small. Therefore let us instead focus on a neighborhood relation in link space, which approximates link probability but is easier to measure and is also used to identify Web communities (4, 14). I measured the frequency of neighbor pairs of pages as a function of the lexical distance:

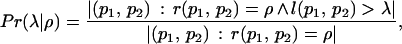where the neighborhood between two pages is expressed by the function

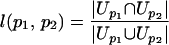and U_p is the URL set representing p's neighborhood (inlinks, outlinks, and p itself). Note that l is akin to the well known cocitation and bibliographic coupling measures used in directed graphs for outlinks and inlinks, respectively. The neighborhood threshold λ models the ratio of local versus long-range links, where we think of local links as those characteristic of clustered nodes and long-range links as those characteristic of random connections. In small world networks such as the Web, local and random structures coexist in the form of node clusters (communities) connected by high-degree nodes (hubs).

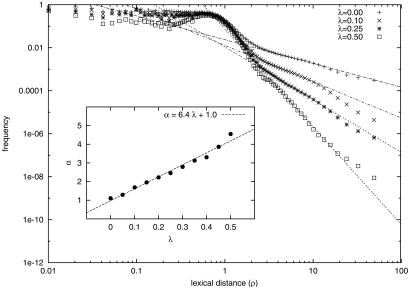
Fig. 1 plots Pr(λ|ρ) versus ρ for various values of λ.‡ We observe an interesting phase transition between two distinct regions around a critical distance ρ* that does not depend on λ (ρ* ≈ 1). For ρ < ρ* the probability that two pages are neighbors does not seem to be correlated with their lexical distance; for ρ > ρ* the probability decreases according to a power law

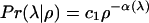so that that the majority of clustered pages are lexically similar, but there is a long tail of pages that are clustered despite a very large lexical distance. These could be clusters around very popular hub pages or communities where textual content fails to capture the semantic relationship between pages. A fit of the tails to the power-law model reveals that the clustering exponent α grows roughly linearly with the linkage threshold λ for λ ≤ 0.5 (see Fig. 1 Inset):

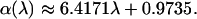For ρ > ρ* the relationship between Pr(λ|ρ), ρ, and λ is qualitatively consistent with the intuitive correlation between the lexical and linkage topologies of the Web; pages that are semantically related tend to be both lexically similar and clustered, therefore pages that are more similar in content have a higher likelihood to be neighbors. However, for sufficiently small lexical distances (ρ < ρ*) there is no additional information about link clustering to be gained from content.

Fig 1.

Cluster probability Pr(λ|ρ) as a function of lexical distance ρ, for various values of the linkage threshold λ. A nonlinear least-squares fit of the tail of each distribution to the power law model Pr(λ|ρ) ∼ ρ^−α is also shown. (Inset) Plot of the relationship between the linkage threshold λ and the clustering exponent α of the power-law tail. The frequency data are based on ≈4 × 10⁹ pairs of Web pages sampled from the Open Directory Project (http://dmoz.org).

Web Growth

Background.

Several models have been proposed to interpret the power-law distribution of Web page degree, for example, based on stochastic growth rates of Web sites (3). Here I focus on generative models, which attempt to explain the Web topology based on the behavior of individual authors linking new pages to existing ones. Most generative models are based on preferential attachment, whereby one node at a time is added to the network with m new edges to existing nodes selected according to some probability distribution, typically a function of some characteristic of the existing nodes. The best known preferential attachment model is the Barabási-Albert (BA) model, where a node i receives a new edge with probability proportional to its current degree, Pr(i) ∝ k(i) (2, 15). The BA model generates network topologies with power-law degree distributions, but is based on the unrealistic assumption that Web authors have complete global knowledge of the Web degree. According to the BA model, links are generated according to popularity alone, and consequently the oldest nodes are those with highest degree.

To give newer nodes a chance to compete for links, some extensions of the BA model use Pr(i) ∝ η(i)k(i), where η(i) is the fitness of page i. These models still yield power-law degree distributions, but after enough time the winning pages are those with highest fitness (16, 17). Another class of variations that allow new pages to compete for links is based on linking to a node based on its degree with probability ψ or to a uniformly chosen node with probability 1 − ψ (18–20). Such a mixture model generates networks that can fit not only the power-law degree distribution of the entire Web, but also the unimodal degree distribution of subsets of Web pages such as university, company, or newspaper homepages (20). Unfortunately, all of these models still rely on global knowledge of degree. Furthermore, they fail to capture the cognitive processes that lead authors to pick pages to link. Neither the global fitness measure nor the uniform distribution match the heterogeneous nature of the Web and of the authors' interests.

The “copying” model (21, 22) implements a rich-get-richer process equivalent to the BA model, but without requiring explicit global knowledge of node degrees. For each new node, an existing prototype node i is first chosen at random. Then each link j from the new node is either attached to a uniformly chosen node with probability ϕ, or to the target of i's jth link with probability 1 − ϕ. Higher-degree nodes are automatically favored by the copying mechanism, producing the same power-law degree distributions as the BA model. The prototype node could correspond to a related page known to the author, thus modeling some sort of local selection process.

A generative model that uses local information even more explicitly was recently proposed for trees (23). Nodes are given random coordinates in the unit square. Then new nodes are attached to existing ones based on a linear combination of linkage and geographic bias. In this model a new node j is deterministically linked to the node arg min_i(φr_ij + g_i), where r_ij is the Euclidean distance and g_i is a “centrality” measure of i in the tree. It is shown that for critical values of φ (φ̃ ≤ φ = o(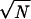), where φ̃ is a constant and N is the number of nodes), this model yields a power-law degree distribution. The Euclidean distance here is independent of link topology and thus could be used to model the factors that lead authors to link their pages to other pages based on, say, content rather than popularity alone. However, the linear combination model still requires global knowledge of the tree structure, and the uniform distribution of nodes in the unit square as a geographic model does not capture a realistic content topology.

Content-Based Generative Model.

The phase transition in Fig. 1 suggests a straightforward way to interpret the growth of the Web's link structure based on the content similarity between pages. I want to model an author's desire to link new pages to sites that are both similar (hence probably related) and popular (hence probably important). Let us assume in keeping with current models that page importance or popularity is correlated with degree. However, I do not assume that an author has global knowledge of degree; instead, an author has only local knowledge of degree, i.e., knowledge of importance only for pages with similar content. This is quite realistic as such pages are probably known to the author or else can be discovered simply by using a search engine.

I propose a generative model based on the above assumptions. At each step t one new page p_t is added, and m new links are created from p_t to m existing pages {p_i, i < t}, each selected with probability:

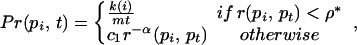where k(i) is the indegree of p_i,§ ρ* is a lexical distance threshold, and c₁ and α are constants. This growth process is driven by local link decisions based on content. It is consistent with the phase transition of Fig. 1: lexical independence for close pages and an inverse power-law dependence for distant pages (where I model the link probability after the neighborhood probability expressed by Eq. 5).

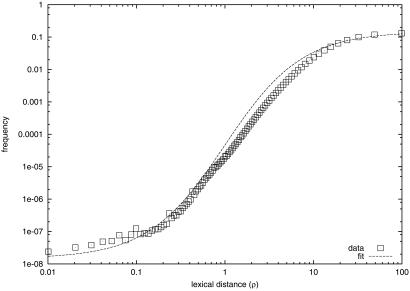
To test this model one needs a prior distribution for the values of r across Web pages. The frequency

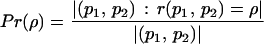measured from a large number of pairs of Web pages is shown in Fig. 2. I used a nonlinear fit of this frequency data to the exponential model

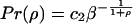as a PDF to generate realistically distributed random r(p_i, p_j) values for any pair (p_i, p_j), i < j. I then simulated the generative model of Eq. 7 to build a network with N nodes. The parameters of the simulation are shown in Table 1.

Fig 2.

Probability distribution of lexical distance, Pr(ρ). The frequency data are based on ≈4 × 10⁹ pairs of Web pages sampled from the Open Directory Project (http://dmoz.org). A nonlinear least-squares fit of the distribution to the exponential model Pr(ρ) ∼ β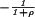 is also shown.

Table 1.

Parameter values for generative model simulation

Parameter	Value	Source (Open Directory data)
ρ*	3	Fig. 1
c1	0.01282	Fig. 1, Eq. 5, λ = 0.1
α	1.68894	Fig. 1, Eq. 5, λ = 0.1
c2	0.14723	Fig. 2, Eq. 9, ∫ Pr(ρ)dρ = 1
β	107	Fig. 2, Eq. 9
N	109,648	Fig. 3
m	15	Fig. 3

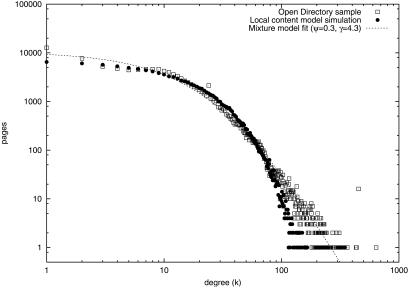
Fig. 3 shows the degree distribution obtained by the simulation of the local content-based generative model and compares it with the distribution measured from a sample of Web pages. Given the relatively small N and the fact that the sampled pages tend to be quite specific, the degree distribution of the data diverges significantly from the “pure” power laws reported for massive Web crawls (5). The general mixture model (20) matches the data very well for a preferential attachment coefficient ψ ≈ 0.3. The novel result here is that the degree distribution generated by the local content-based model also yields a very accurate fit of the data. The tails of all three distributions are consistent with a single power law with exponent γ ≈ 4.3, as shown in Table 2.

Fig 3.

Degree sequence distributions N Pr(k) generated by a simulation of the local content-based generative model and by a sample of N = 109,648 Web pages from the Open Directory Project (http://dmoz.org). A nonlinear least-squares fit of the Open Directory Project data to the mixture model 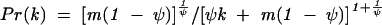(adapted from ref. 20 for directed links) is also shown, yielding ψ ≈ 0.3(γ = 1 + 1/ψ ≈ 4.3).

Table 2.

Asymptotic power law exponents from least-squares fit of degree distribution tails, with standard errors

Distribution	γ̄	σγ̄
Open Directory sample	4.28	0.14
Mixture model (20)	4.31	0.22
Local content model	4.26	0.07

Web Navigation

Background.

The relationships between Web link topology and notions of semantic similarity stemming from page content or topic classification have important applications for the design of more effective search tools (24, 25). Topic-driven crawlers (26–30) are increasingly seen as a way to address the scalability limitations of current universal search engines, by distributing the crawling process across users, queries, or even client computers. The context available to such crawlers can guide the navigation of links with the goal of efficiently locating highly relevant target pages. Given the need to find unknown target pages, we are interested only in decentralized crawling algorithms, which can use only information available locally about a page and its neighborhood. Starting from some source Web page we aim to visit a target page by visiting ℓ ≪ N pages, where N is the size of the Web, several billion pages.

Since the Web is a small world network (1, 2, 4, 5) we know that its diameter [at least for the largest connected component (5, 31)] scales logarithmically with N, or more precisely a short path of length

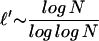is likely to exist (8) between some source (e.g., a bookmarked page or a hit returned by a search engine) and some unknown relevant target page. Can a crawler navigate such a short path?

If the only local information available is about the hypertext link degree of each node and its neighbors, then simple greedy algorithms that always pick the neighbor with highest degree lead to paths whose length ℓ′ scales logarithmically (ℓ′ ∼ log N) (10) or sublinearly (ℓ′ ∼ N^ɛ, ɛ ≈ 0.7 < 1) (9). However, a real Web crawler would have to visit all of the neighbors of a page to determine their degree. Due to the power-law degree distribution, moving to high-degree nodes leads to covering most of the nodes in a short number of steps. For example, simulations suggest that the number of steps to cover N/2 nodes scales as N^0.24 < ℓ′ (9). Therefore a small ℓ′ implies a large ℓ (ℓ ∼ N), making the degree-seeking strategy too costly for actual Web navigation.

Kleinberg (11–13) and Watts et al. (36) characterized certain classes of networks whose link topology depends on external geographic or hierarchical structures, showing that in these special cases navigation algorithms are guaranteed to exist with polylogarithmic bounds ℓ = O(log^ɛN), ɛ ≥ 1. I now outline these models and show that they can be applied to the Web.

Content-Based Crawling Algorithms.

If the link topology of a network follows a D-dimensional lattice, with local links to lattice neighbors plus some long-range connections, and information about the geographic location of nodes is available, Kleinberg (11, 12) proved that a greedy algorithm, which always picks the neighbor geographically closest to the target, yields a bound ℓ = O(log²N). In this geographic model the optimal path length is achieved if, and only if, long-range links are chosen with probability Pr(r) ∼ r^−α, where r is the lattice (L₁) distance between the two nodes, and α is a critical constant clustering exponent dependent on the dimensionality of the lattice (α = D).

While Kleinberg's geographic model is inspired by social small world networks where location knowledge exists, the lattice model cannot be applied directly to the Web where such a notion of L₁ norm-based geography is unrealistic. However, Kleinberg's result would be applicable to the Web if one could use a realistic topological distance measure for r. In fact, the result of the second section, namely the power law in Eq. 5 obtained from the tail of the conditional probability distribution in Fig. 1, makes the distance induced by the lexical similarity between the textual content of pages an obvious candidate for r. In the lattice model, local links are equiprobable whereas long-range links are governed by the power-law distribution. Analogously, in the Web lexical similarity defines the geographic topology of the pages and the critical distance ρ* marks the border between local links (whose probability is independent of r) and long-range links. Therefore my finding suggests that Kleinberg's analysis based on geographic networks can be applied to the Web to infer the existence of efficient crawling algorithms. There is one caveat. Kleinberg's result requires a critical clustering exponent α = D, but what is the meaning of D in the Web? One could imagine defining an analogous “Web dimensionality” based, say, on the communities induced by the Web's link structure (14). Fortunately, it is not necessary to quantify such a dimensionality to extend Kleinberg's analysis to the Web; it is sufficient to assume that the dimensionality can be defined by a “critical neighborhood threshold” λ*. Then Eq. 6 can be used to obtain a corresponding critical clustering exponent α* = α(λ*). Since the power-law relationship of Eq. 5 holds over a wide range of λ values (compare Fig. 1), it is reasonable to conjecture the existence of a decentralized Web navigation algorithm that can be proven to be optimally efficient under the linkage topology induced by λ* and the geographic topology induced by r.

A qualitatively similar result (the existence of polylogarithmic navigation algorithms, ℓ = O(log^ɛN) was given by Kleinberg for the case where information about a semantic hierarchy is available, where nodes are classified into the leaves of a topical tree and links are drawn from a critical probability distribution based on the semantic distance between nodes induced by the tree (13). The link probability distribution must have an exponential tail Pr(h) ∼ ξ^−h where ξ is a constant and h is the semantic distance between two nodes, expressed by the height of the lowest common ancestor in the tree. The hierarchical model is more plausible than the geographic model for the Web because directories such as Yahoo and the Open Directory Project can play the role of semantic hierarchy trees. An almost identical hierarchical model was proposed by Watts et al. (36) with an even stronger (constant) bound on navigation time.

I have previously studied the relationship between link topology and semantic similarity by analyzing the probability of finding links to a set of pages on a certain topic as one crawls away from that set. This probability remains remarkably constant in exhaustive breadth-first crawls of depth up to three links starting from pages classified by Yahoo (34). This finding has been confirmed and extended by recent experiments based on crawls from the Open Directory Project, showing that the linkage probability is significantly higher between pages on the same topic than between pages on different topics (25). To investigate whether the hierarchical model analysis can be applied to the Web, let us define a semantic distance between topics:

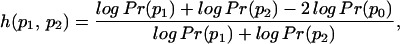where p₀ is the lowest common ancestor of p₁ and p₂, and Pr(p) represents the fraction of pages classified at node p. This is a straightforward extension of the information-theoretic semantic similarity measure (32), and it generalizes the hierarchical models to account for the fact that pages are classified by actual Web directories into internal nodes as well as leaves.

The relationship between semantic distance h and link topology can be analyzed in the same way as was done for lexical distance r in the second section, by measuring the frequency of neighbor pairs of pages as a function of the semantic distance:

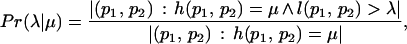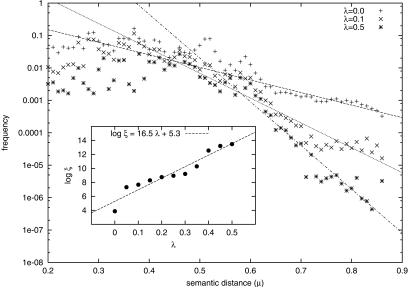
where h was computed by using the Open Directory Project tree.¶ Fig. 4 plots the tail of Pr(λ|μ) versus μ for various values of λ. We observe a good fit between the data and the exponential model

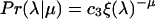for μ > μ* ≈ 0.5. The fit also reveals that the base ξ(λ) is roughly exponential in λ (see Fig. 4 Inset). As for the geographic model, this finding suggests that the analyses based on hierarchical networks can be applied to the Web to conclude that efficient crawling algorithms exist. In fact, the crawler proposed in ref. 27 attempts to prioritize links based on h estimates obtained from a classifier and thus is an implementation of the optimal greedy algorithm described in ref. 13.

Fig 4.

Tail of cluster probability Pr(λ|μ) as a function of semantic distance μ, for various values of the linkage threshold λ. A nonlinear least-squares fit of each tail to the exponential model Pr(λ|μ) ∼ ξ^−μ is also shown. (Inset) Plot of the relationship between the linkage threshold λ and the base ξ of the exponential tail. The data are based on the same Open Directory Project sample used for Fig. 1.

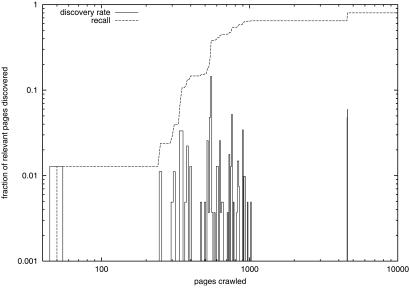
The greedy algorithm proposed by Kleinberg (12) would locate a target page by visiting ℓ ≤ c₄ log² N pages with a constant c₄ ≈ 128. For N ≈ 10¹⁰, ℓ ≤ 10⁴ pages. This finding is consistent with our experimental data, as illustrated by the discovery time distribution in Fig. 5; the majority of relevant pages are located based on local content before 10⁴ pages have been crawled.∥

Fig 5.

Distribution of discovery times for unknown relevant pages obtained by a crawler using a content-driven (and slightly less greedy) version of the algorithm described in ref. 12. The crawler is given a short topic query and a limited store for unvisited URLs and starts at least three links away from any relevant pages.

Conclusion

In this article I addressed two questions of considerable interest for potential Web applications: whether one can effectively model the emergence of the scale-free topology of the Web from realistic assumptions about authors' local knowledge and behavior and whether one can design crawling algorithm to efficiently locate unknown pages of interest to a user or search engine.

I found that the answer to both of these questions is yes, and in doing so I uncovered two interesting relationships between the Web's link topology and distance metrics based on lexical and semantic similarity. The two relationships (compare Figs. 1 and 4) are qualitatively very similar: in both cases a critical distance (μ* or ρ*) marks a phase transition between a relatively flat section at small distances and a decay at large distances. The decay has a long (power law) tail in the case of lexical distance and a short (exponential) tail for semantic distance. These are probably two manifestations of the same behavior. Authors tend to link their pages to semantically related clusters, identified via page content. The link probability decreases rapidly with increasing semantic/lexical distance. But among the most closely related pages, the choice of which pages to link is largely driven by other factors such as authority or popularity.

This analysis led to a generative model for the Web graph based on local content cues, which accurately matches the distribution of degree in a representative sample of Web pages. This generative model yielded accurate predictions of degree sequence based on page content data. My model may help us gain a better understanding of the evolving structure of the Web and its cognitive and social underpinnings and may lead to more effective authoring guidelines as well as to improved ranking, classification, and clustering algorithms.

Finally, the link/lexical power law relationship and the related link/semantic exponential relationship led to analogies between the Web and special classes of geographic and hierarchical graphs for which the existence of optimally efficient (polylogarithmic) navigation algorithms was proven. These results strongly suggest that short paths can be discovered by decentralized Web crawlers based on textual and/or categorical cues. These data-supported results yielded efficient bounds on the number of pages visited by Web crawlers to reach unknown targets. The field of focused crawlers is gaining much empirical attention owing to its potential to cope with the scalability limitations of current search engine technology. The present findings are consistent with, and give some theoretical grounding to, data from a growing body of work on crawling algorithm design; they may have a large impact toward the construction of effective decentralized search tools.

Abbreviations

• BA, Barabási-Albert