The Cretaceous superchron geodynamo: Observations near the tangent cylinder

Abstract

If relationships exist between the frequency of geomagnetic reversals and the morphology, secular variation, and intensity of Earth's magnetic field, they should be best expressed during superchrons, intervals tens of millions of years long lacking reversals. Here we report paleomagnetic and paleointensity data from lavas of the Cretaceous Normal Polarity Superchron that formed at high latitudes near the tangent cylinder that surrounds the solid inner core. The time-averaged field recorded by these lavas is remarkably strong and stable. When combined with global results available from lower latitudes, these data define a time-averaged field that is overwhelmingly dominated by the axial dipole (octupole components are insignificant). These observations suggest that the basic features of the geomagnetic field are intrinsically related. Superchrons may reflect times when the nature of core–mantle boundary heat flux allows the geodynamo to operate at peak efficiency.

Superchrons provide an opportunity to view the geomagnetic field in its extreme, when reversals are rare or absent altogether (1). They represent robust features that are useful for the affirmation of theoretical and numerical models of the geodynamo (2). However, to gain a complete picture of the geodynamo we must move beyond polarity to characterize the morphology, secular variation, and intensity of the field. Few studies have done this. Often, geological and associated experimental alteration prohibits the simultaneous definition of paleofield directions and intensities. As a result, only piecemeal data from disparate sources are available. This has contributed, perhaps not unexpectedly, to some sharply contrasting viewpoints about the nature of the field during a superchron.

Recently, we developed a method for the measurement of paleointensity that uses single plagioclase crystals separated from basaltic lava flows (3, 4). These crystals, which contain sub-μm-sized titanomagnetite and magnetite inclusions, are less susceptible to alteration during the laboratory heatings required by paleointensity analysis. The method provides a means to obtain high-resolution paleointensity data from sequences of basalt flows, which can in turn be studied to characterize secular variation.

When applied to lavas of the Rajmahal Traps, which erupted between 113 and 116 millions of years ago (Ma) during the Cretaceous Normal Polarity (K-N) Superchron, this approach yielded a paleomagnetic dipole moment of 12.5 × 10²² Am². This intensity value is 2–3 times greater than that thought to characterize times when the field was reversing frequently (5). Furthermore, the time-averaged field data showed less dispersion in pole space than that seen from lavas formed during the last 5 million years (6). These data suggest the field may be strongest and most stable when the frequency of reversals is at a minimum (7, 8).

This conclusion conflicts with that of other studies (based on paleointensity data considered separately from directions) that claim reversal frequency and intensity are decoupled (9, 10). Adding to these differing opinions is a recent suggestion that the past time-averaged field may have had significant nondipole components. The geomagnetic field at a radius r, colatitude θ, and longitude φ can be described by the gradient of the scalar potential (Φ):

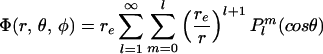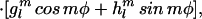where P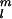 are partially normalized Schmidt functions, r_e is the radius of the Earth, and the Gauss coefficients g 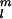and h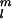 describe the size of spatially varying fields. Van der Voo and Torsvik (11) call for an axial octupole (g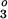) during Permian to early Tertiary times equal to ≈10% of the axial dipole field (g).

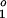A continental flood basalt province in the high Canadian Arctic (12) formed during the K-N Superchron affords an opportunity to address these contrasting ideas. As shown below, the high Canadian Arctic was near the tangent cylinder, that imaginary cylinder about the rotational axis that is tangent to the solid inner core, during the Cretaceous. This region is of special significance with respect to numerical models of the geodynamo (13).

Cretaceous Lavas of the High Canadian Arctic

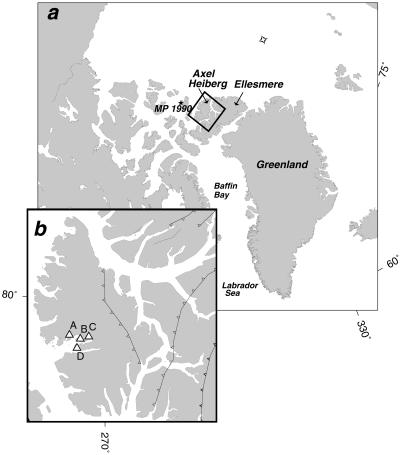
Volcanic rocks of the Strand Fiord Formation on Axel Heiberg and Ellesmere islands (Fig. 1) are ≈95 million years old [based on ⁴⁰Ar/³⁹Ar radiometric age data (12)] and therefore erupted well within the K-N Superchron. The lavas are extremely well exposed in geologic structures related to the pivotal motion of Greenland in Late Cretaceous to Eocene times that culminated in the Eurekan orogeny (14). We studied four stratigraphic sections through the Strand Fiord basalts (sections A–D, Fig. 1b). In three of the sections, shallow marine shales and minor siltstone of the Bastion Ridge Formation (14–65 m thick) interfinger with the lowermost flows, separating them from the lavas higher in the sequence. At one section (Expedition Fiord), the Bastion Ridge Formation is not present or poorly exposed, but an unusually large volume of intrusive rock occurs in the underlying Christopher Formation. Through the stratigraphies of each of these sections, and by analogy with continental flood basalt provinces elsewhere, the duration of volcanism was likely >1 million years long.

Fig 1.

(a) Overview of the Arctic region with position of the magnetic pole (MP) in 1990. (b) Axel Heiberg Island site locations: A, Agate Fiord; B, Dragon Creek; C, Expedition Fiord; D, Blacknose Ridge. Fault traces (14) are also shown.

All samples were collected as field-drilled cores and oriented with a Pomeroy sun compass (ASC Scientific, Carlsbad, CA), a necessity given the nature of the steep gorge exposures, proximity of the magnetic pole (Fig. 1), and the high diurnal variation of the field at the sampling sites (14). Bedding is well defined by sediments overlying and interbedded with the lavas. Dip was recorded by using a Brunton compass (ASC Scientific). Strike was measured by using a sun compass (a D-Pro-CC dial fixed to an aluminum plate). Strike data were validated with air photos and geological maps. The sections range in thickness from 150 to >400 m, and the flows are generally >10 m thick (up to 50 m). Therefore only 7–14 flows are available in each section. However, the sections form an array that is not separated by thrust faults (Fig. 1), allowing us to exclude an uncertainty in prior work (15) and combine results from the sections to obtain a mean direction and pole.

All paleomagnetic direction and paleointensity measurements (see below) were done at the University of Rochester by using a DC SQUID magnetometer (2G Enterprises, Pacific Grove, CA) with a 4-cm access and a high-resolution sensing coil configuration. Thermal demagnetization of whole rocks (25°C increments to 650°C) showed similar behavior to that described in previous studies (15). Results from the 37 lava flows reported here are of normal polarity and are based solely on principal component analysis of the thermal demagnetization data.

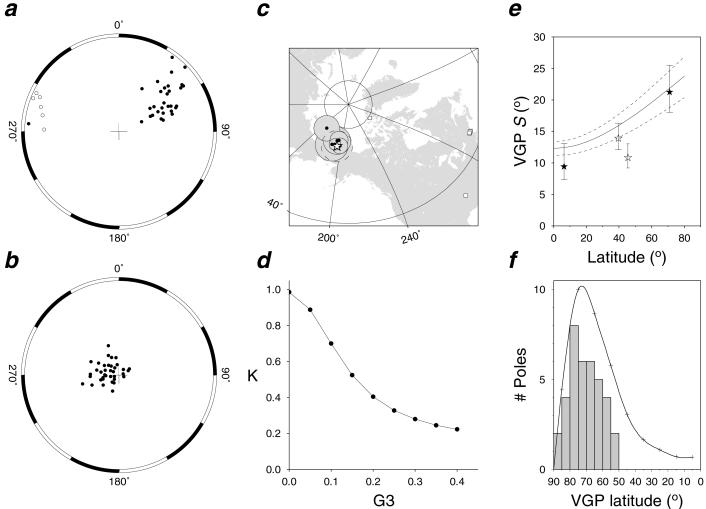
Characteristic remanent magnetization directions from the lavas converge after unfolding (k₂/k₁ = 14), indicating a positive fold test (16, 17) significant at the 95% confidence level (Fig. 2 a and b). We cannot reject the null hypothesis that the unfolded declinations and inclinations are Fisherian distributed (at the 95% confidence level; M_u = 0.646; M_e = 0.537) (18). These data indicate a mean direction of 80.1°, 284.8° (n = 37, k = 44, α₉₅ = 3.5°) (Table 1, which is published as supporting information on the PNAS web site, www.pnas.org). The expected direction, based on an updated mid-Cretaceous reference pole (19), is 80.8°, 297.3° (using 79.4° N, 267.8° E, as a reference site). This result indicates the site has been fixed in latitude relative to cratonal North America since the Cretaceous (Fig. 2c). In pole space, the data suggest a 12° counterclockwise rotation of the study area, but the value is uncertain [±19°, 95% confidence interval (20)] because of the difficulties inherent in the determination of vertical axis rotations when inclinations are very steep. Nevertheless, we note the similarity of the mean value and that predicted if the principal driving force was the opening of the Labrador Sea (14, 21), as well as with rotations found in other paleomagnetic studies of igneous (15, 22, 23) and sedimentary (14) rocks from Axel Heiberg and Ellesmere islands.

Fig 2.

Paleomagnetic characteristic remanent magnetization directions from thermal demagnetization before (a) and after (b) unfolding. (c) Paleomagnetic pole (star) calculated from this direction data shown versus mid-Cretaceous poles of the North American craton (19). (d) Normalized estimate of precision parameter (K) for mid-Cretaceous North American poles (A–F of ref. 19) and the high Canadian Arctic (this work, assuming a 12° vertical axis rotation). Values shown assume various contributions of an octupole relative to the dipole field (G3). (e) Angular dispersion (S) of time-averaged VGPs and select data sets from the K-N Superchron (solid stars, Northern Hemisphere; open stars, Southern Hemisphere) shown with 95% confidence intervals (28). Also shown is fit of secular variation model (27) G to 0–5 Ma data (6) (solid curve) and 95% confidence interval (dashed curves). (f) Comparison of VGPs from the Cretaceous Canadian Arctic (normalized to 90° mean latitude) and Neogene lavas of Iceland (30, 31).

Field Morphology During the Cretaceous Superchron

Other North American sites with mid-Cretaceous data useful for constraining apparent polar wander are from paleolatitudes between ≈37° and 45° N. We consider only data from igneous rocks with thorough demagnetization data and radiometric age control [poles A–F reviewed by Tarduno and Smirnov (19)]. Because our Canadian Arctic site remained contiguous with North America in terms of latitude, we have >3,700 km of stable latitudinal distance to test models for the zonal geometry of the time-averaged field during the K-N Superchron (Fig. 2c). We examine a potential octupole (G3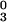 = g/g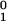) contribution to the field by assuming a 12° rotation of our Arctic field area and by considering that both the inclination we have observed and those recorded by sites further south record a dipole field with progressively higher amounts of octupole contributions. Poles calculated by using these assumptions should be best grouped at the true G3 value of the time-averaged field. This test differs from that of Van der Voo and Torsvik (11) in that data are from a single craton (we avoid errors associated with plate reconstructions and require no assumptions about site distributions).

The observed inclinations (I_o) with G3 terms are related to the expected colatitude (θ_e) of the sample sites by

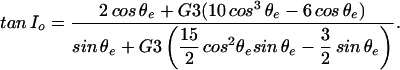After solving for θ_e by an iterative method and summarizing the results in pole space, we find the data are in best agreement when no octupole contribution is included (Fig. 2d); this is also the case for quadrupole contributions. This conclusion holds for rotations >5° [including a larger rotation value reported from the study of Permian volcanic rocks (23)]. For rotation values <5°, a G3 value of 0.05 cannot be excluded with this approach. But because four independent studies (14, 15, 22, 23) have indicated rotations >5°, we conclude that G3 contributions were insignificant in the time-averaged K-N Superchron field.

Paleosecular Variation

Some lavas in flood basalt sequences are thought to have flowed over distances comparable to that separating each of our sections from its nearest neighbor. Differences in the stratigraphy between the sections sampled, however, provide a geologic basis for treating the flows as independent records of the field. Accordingly, we proceed below, assigning equal weight to each flow.

To quantify secular variation as recorded at our Arctic site, we calculated the angular dispersion of the lava mean poles, S:

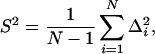where N is the number of virtual geomagnetic poles (VGPs) and Δ_i is the angle between the ith VGP and the mean VGP. We compare our value (S = 21.3°, corrected for within-site dispersion) with results from 0–5 Ma lavas (6). Here we select only the best-constrained data, excluding latitude-band means with 95% confidence regions exceeding 2°. We further average values from the Northern and Southern hemispheres because it is as yet unclear whether the hemisphere asymmetry observed reflects the field or differential data quality.

We also compare our value with data from other studies of lavas formed during the K-N Superchron (Fig. 2e). We apply the following selection criteria: (i) radiometric ages, stratigraphic evidence, and magnetic polarity must be compatible with formation during the K-N Superchron; (ii) results must be based on thermal and alternating field demagnetization with principal component analyses used to fit directions; (iii) more than five flows must be available with multiple samples (n > 2) for each flow; (iv) the results should be free of evidence for remagnetization; and (v) the tectonic setting should be sufficiently simple such that local faulting is not a potential source of intersite scatter. Furthermore, we have excluded VGPs with latitudes <55° (6).

Paleomagnetic results meeting these requirements have been reported from only the Rajmahal Traps (5, 24), the flood basalts of Madagascar (25), and the Mount Carmel basalts of Israel (26). We examine the select 0–5 Ma and Cretaceous data by using a secular variation model where the field is composed of independent dipole (antisymmetric) and quadrupole (symmetric) families (model G) (27). Although the model is probably correct only as an approximation (6), it is nonetheless appealing because it relates secular variation to results from dynamo theory. After an analysis of the present-day field (27), the quadrupole family is independent of latitude whereas the dipole family is linear with respect to latitude.

The S values for the K-N Superchron data considered here at low and mid latitudes are less than those of the 0–5 Ma data (Fig. 2e), suggesting that the contributions of the quadrupole family to the field were smaller during the K-N Superchron (27). S at high latitudes during K-N Superchron may have also been less, but such a conclusion is limited by the uncertainty in our Arctic value and that in the available 0–5 Ma data.

But a consideration of VGP dispersion values provides only a partial picture of the stability of the field. Our new paleolatitude value for the Strand Fiord lavas (71° N, 95% confidence range of 77.5° to 65.0° N) is near the Cretaceous tangent cylinder (≈77°). The dynamics inside and outside the tangent cylinder differ in most numerical simulations of the geodynamo and are thought to be separated by a complex transitional zone in the core (13). In statistical models, the frequency of low-latitude virtual geomagnetic poles is greatest for high-latitude sites (29). And ≈10% of reliable virtual geomagnetic poles from Neogene Icelandic basalts show latitudes <40° (30, 31). Interestingly, similar low-latitude VGPs are absent in our Arctic data (Fig. 2f).

Paleointensity

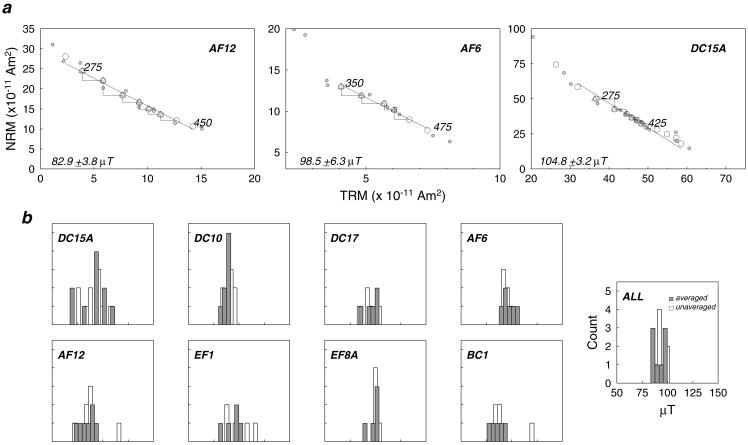
Several lava flows from our sections contained plagioclase feldspars similar to those in modern (3) and Cretaceous (4) rocks that have been used in paleointensity studies (Fig. 3a). To investigate the potential of these plagioclase crystals for paleointensity study, a series of rock magnetic experiments were performed. Magnetic hysteresis data, collected by using an alternating gradient force magnetometer, indicate pseudosingle to single domain behavior of the crystals (Fig. 3 c–e). The crystals show much less change after heating than whole rock basalt samples, indicating that they are more reliable paleointensity recorders.

Fig 3.

(a) Typical plagioclase crystal used for rock magnetic and paleointensity experiments. (b) Transmission electron microscope image [using a JEOL JEM 2000 Ex, 200 keV (1 eV = 1.602 × 10⁻¹⁹ J)] of a magnetic separate from a plagioclase crystal. (c and d) Magnetic hysteresis data measured on a Princeton Measurements (Princeton, NJ) alternating gradient force magnetometer for a whole rock basalt sample and plagioclase feldspar. (e) Magnetic hysteresis data for whole rock basalts and plagioclase feldspar summarized on a Day plot (33). M_r/M_s, saturation remanence/saturation magnetization ratio; H_cr/H_c, coercivity of remanence/coercivity ratio; SD, single domain; PSD, pseudosingle domain; MD, multidomain. (f) Warming curve of a magnetization (solid line) acquired by a plagioclase crystal at 20 K in a 2.5 T field measured by using a Quantum Design (San Diego) Magnetic Property System (MPMS-XL) at the Institute for Rock Magnetism (University of Minnesota, Minneapolis). Dotted line is the inverse of the derivative.

Magnetic hysteresis data were also collected by varying the orientation of a crystal by 45° increments on alternating gradient force magnetometer probe heads oriented parallel and perpendicular to the applied dc field. In no case was a significant anisotropy of hysteresis parameters observed as would be expected if elongate grains were aligned in the crystals. Low temperature data (Fig. 3f) show a blurred remanence transition that is shifted to temperatures slightly lower than those that characterize the cubic to monoclinic Verwey transition in magnetite. These results are consistent with the presence of a titanomagnetite remanence carrier in the crystals (32) similar to that in the whole rocks. Transmission electron microscopy of magnetic separates from crystals indicate equant to slightly elongated particles 100–400 nm in size (Fig. 3b), consistent with our magnetic hysteresis results. These grains are distinctly smaller than the magnetite rods tens of microns long formed by exsolution in plagioclase of plutonic rocks (34).

Seven lava flows and a narrow sill (from Expedition Fiord) contained optically clear plagioclase feldspars 0.5–2.0 mm long that were suitable for paleointensity measurements. The lavas are spread throughout the stratigraphic sequence (three units below the Bastion Ridge Formation and four units above) and therefore should represent a subsample that averages secular variation. To test this assumption, we calculate a mean direction from the sites excluding directions from the sill whose tectonic orientation was uncertain. This subset yields a direction (I = 85.5°, 328.5°, k = 38, α₉₅ = 8.6°) that is indistinguishable from the larger data set at the 95% confidence level; the directional dispersions of the subset and complete lava flow data are also similar.

The experimental methods for paleointensity determinations and criteria used to evaluate the data follow those described by Cottrell and Tarduno (3, 4). In this study, crystals were set inside 3-mm-diameter quartz tubes to lower the intensity of our blank. An applied field of 60 μT was used in an ASC thermal demagnetization oven (ASC Scientific) for the modified Thellier–Thellier experiment (3, 4, 35). Temperature steps of 50°C were used for the first 250°C (an unblocking temperature range dominated by viscous overprints in our samples), followed by demagnetization and partial thermoremanent magnetization (TRM) acquisition at 25°C increments until >90% of the natural remanent magnetization (NRM) was lost or the magnetizations were no longer stable (Fig. 4).

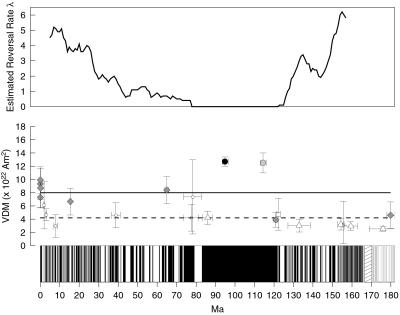
Fig 4.

(a) Typical plots of NRM versus TRM. Partial TRM checks are shown by triangles. Large open circles are three-point sliding-window average of raw data (small circles). Labeled points are temperatures (°C) representing the range used to determine paleointensity. (b) Summary of paleointensity data meeting reliability criteria from Arctic lavas. AF, Agate Fiord; EF, Expedition Fiord; DC, Dragon Creek; BC, Blacknose Ridge. Averaged data shaded; unaveraged data, unshaded.

Changes in NRM and TRM intensities during the Thellier–Thellier experiments using plagioclase crystals are typically very small (sometimes <5 × 10⁻¹² Am²). Background measurements on the superconducting rock magnetometer range from 4 to 8 × 10⁻¹³ Am². Typical quartz sample holders have magnetizations of ≈1–2 × 10⁻¹² Am². To reduce the influence of measurement noise a three-point sliding average of NRM and TRM intensities was used over the optimal temperature range identified in the orthogonal vector plots. These averaged data were used in assessing the quality of the data through reliability checks and in the calculation of final paleointensities. Fifty-one of the 110 crystals measured met the selection criteria (3, 4). This success rate (46%) is higher than that seen in a study of plagioclase from the Rajmahal Traps (success rate of 38%) (4) and may be related to our use of quartz tubes as sample holders. Averaged data meeting reliability criteria described above are available from multiple samples of the eight time-independent units (Fig. 5; Tables 2–4, which are published as supporting information on the PNAS web site). Together these data yield a mean intensity of 93.8 ± 5.2 μT (1σ error). This value is not significantly different from that obtained by fitting the unaveraged data (93.9 ± 4.3 μT). The principal effect of averaging is to reduce within-flow scatter.

Fig 5.

Geomagnetic reversal time scale (base), select Thellier–Thellier results, and estimated reversal rate (based on a 10-million-year sliding window). Select Thellier–Thellier studies with 1σ errors. Filled symbols are paleomagnetic dipole moments; open symbols are virtual dipole moments. Data sources are those selected by Tarduno et al. (5) with the addition of a new basaltic data set from China (36). Only studies based on more than nine Thellier–Thellier determinations are shown. Small symbols, <25 samples; large symbols, >25 samples. Data types: triangles, baked contacts; squares, SBG; diamonds, basalt whole rocks; circles, basalt plagioclase (from ref. 5 and this work). Dashed horizontal line, a proposed mean Cretaceous-Cenozoic value based on SBG (38). Solid horizontal line, modern field intensity.

The mean intensity from the Arctic lavas is ≈21% higher than that reported from the Rajmahal Traps, which formed at mid-latitudes (≈45° S) (5). This difference is in accord with that predicted by the geocentric axial dipole hypothesis. The Arctic field intensities indicate a virtual dipole moment of 12.7 ± 0.7 × 10²² Am² (12.7 ± 0.6 × 10²² Am² unaveraged values), which can be considered a paleomagnetic dipole moment because directions from the cooling units, combined with geological evidence, indicate time has been averaged. Thellier–Thellier results with coincident directional data demonstrating that a paleomagnetic dipole moment has been recorded are rare (5), but the value from the Arctic lavas is clearly much higher than available data from times of frequent reversals (Fig. 5).

Discussion and Conclusions

The time window within the K-N Superchron represented by the Arctic lavas examined here is likely 3 orders of magnitude longer than the electromagnetic time constant of the solid inner core. During this interval, fluctuations in the fluid outer core were apparently of insufficient size or duration to reverse the field throughout the inner core (37). The Cretaceous Arctic region was at high latitudes near the tangent cylinder and should be especially sensitive to the extremes in secular variation (13, 29–31). The lack of large departures of poles from the mean in the Arctic dataset also suggests that fluctuations were not great enough to give rise to geomagnetic excursions. Instead, it seems that most of the geodynamo energy was devoted to the generation of a stable axial dipole field.

This conclusion is consistent with other characteristics of the directions from the Arctic lavas. Comparisons of these data with those from lower-latitude sites indicate that octupole contributions to the time-averaged field were negligible and that there was an overall lower contribution of the quadrupole (symmetric) family. The presence of a stable, efficient dynamo during the K-N Superchron is also supported by our analyses of intensity. The field intensity values we report are not outside the range of virtual dipole moments reported from 0–5 Ma basalt and basaltic glass (38, 39). However, the mean value is 2–3 times greater, with much less variation. For example, some estimates of the field strength over the last 5 million years suggest a SD of 30% to >40% of the mean (38, 39), several times greater than results reported here.

Paleointensity results from the Arctic lavas and Rajmahal Traps based on plagioclase feldspar probably cover no more than 10% of the duration of the K-N Superchron. Intensity values from a few individual flows (25) elsewhere provide clues that these high values might be more broadly characteristic of the K-N Superchron, but this view conflicts with the idea that the field value was weak based on some analyses of submarine basaltic glass (SBG) (10). The SBG data from the K-N Superchron are not time-averaged, and the total number of analyses is small. Moreover, some of the virtual dipole moments are exceptionally low (10) (e.g., 2.6 × 10²² Am²), similar to those reported for the Laschamp (40) and other geomagnetic field excursions (41), and during field reversals (42). Results from calibrated relative sedimentary records suggest a critical field value of ≈4 × 10²² Am² below which excursional directions are seen (43). Hence, if the field was as weak as suggested by some of the SBG data for thousands to millions of years during the K-N Superchron, excursions should be common. We did not observe that in the Arctic data reported here, and they are not commonly seen in sedimentary data (44). Although we do not exclude significant temporal variations of field behavior during the K-N Superchron (particularly near its edges), we nevertheless conclude that the strong, stable field we have defined is consistent with available time-averaged intensity and directional data.

In summary, we find that the pole dispersion and paleointensity data from an opportune high-latitude site are best explained by an exceptionally strong and stable field during the K-N Superchron, dominated by the axial dipole. The differences in the time scales between core processes and the length of superchrons suggest a mantle control on the frequency of reversals. Numerical simulations that vary the pattern of heat flux across the core-mantle boundary result in a stable geodynamo with a highest dipole moment (2) qualitatively similar to our observations. Our analyses further suggest that geomagnetic reversals, field morphology, secular variation, and intensity, which are sometimes considered to be isolated phenomena, may instead be related on time scales of thousands (45) to hundreds of millions of years (7, 8).

Abbreviations

• K-N, Cretaceous Normal Polarity

• Ma, millions of years ago

• VGP, virtual geomagnetic pole

• NRM, natural remanent magnetization

• TRM, thermoremanent magnetization

• SBG, submarine basaltic glass