Abstract
Senescence is a nearly universal feature of multicellular organisms, and understanding why it occurs is a long-standing problem in biology. The two leading theories posit that aging is due to (i) pleiotropic genes with beneficial early-life effects but deleterious late-life effects (“antagonistic pleiotropy”) or (ii) mutations with purely deleterious late-life effects (“mutation accumulation”). Previous attempts to distinguish these theories have been inconclusive because of a lack of unambiguous, contrasting predictions. We conducted experiments with Drosophila based on recent population-genetic models that yield contrasting predictions. Genetic variation and inbreeding effects increased dramatically with age, as predicted by the mutation theory. This increase occurs because genes with deleterious effects with a late age of onset are unopposed by natural selection. Our findings provide the strongest support yet for the mutation theory.
Senescence is the decline in organismal fitness and performance with age, and it is a nearly universal feature of multicellular organisms (1–5). Two evolutionary models predict that senescence will evolve because, with few exceptions, the force of natural selection declines with adult age (6). Both theories require the existence of genes with age-specific effects, but the kind of age-specific gene action that is required differs (6). According to the antagonistic pleiotropy (AP) theory, pleiotropic alleles that increase survival or reproduction early in life but decrease survival or reproduction late in life can accumulate in populations, because the selective advantage of the early benefits outweighs the late-life disadvantage. Under the mutation accumulation (MA) theory, alleles with purely detrimental effects can also accumulate if those effects are confined to late life when selection against them is weak. Thus under both theories, populations harbor alleles that are deleterious in old but not in young individuals.
Ramifications of the two theories are quite different. Under AP, senescence is due to a “tradeoff” between early- and late-life fitness, and any genetic or evolutionary change in senescence will be accompanied by changes in early-life fitness components. In contrast, the MA theory suggests that senescence is caused, at least in part, by alleles that are neutral early in life, and thus genetic or evolutionary changes in senescence need not be accompanied by any change in early-life fitness. In principle, senescence could be slowed or delayed by artificially selecting on late-life fitness or by genetic manipulation of late-acting deleterious alleles, and there would be no cost incurred at earlier ages.
These two theories have been subjected to several experimental tests, but previous attempts to distinguish between them have been inconclusive because of a lack of clear and contrasting predictions (4, 7–9). Of the two, AP has received the strongest support, with studies consistently showing negative genetic correlations between early- and late-life fitness, which is a prediction only of the AP theory (reviewed in refs. 9 and 10). Thus far, the evidence in support of MA is more ambiguous. Most tests have concentrated on measuring age-specific additive genetic variation in fitness traits, because an age-related increase was predicted under MA (11). Some studies have reported such an increase (12, 13), whereas others show an early increase followed by a late-life decline in variance (7, 14, 15). These studies leave the issue unresolved, because they differed in both experimental and statistical methodology (8) and subsequent theoretical work showed that increases in additive variance with age could result under the AP as well as the MA theories (7).
Recently, new quantitative genetic models have provided several predictions that can be used to distinguish the two processes (7). For example, if MA contributes to senescence, fitness components such as reproductive success and survival will exhibit age-related increases in dominance (VD) and homozygous genetic variance (VH) in addition to additive variance (VA). Inbreeding depression (ID) will also increase with age. The increase occurs because the genetic variances and inbreeding load are proportional to the equilibrium frequencies of deleterious alleles, and these frequencies will increase with age under MA. In contrast, AP will not lead to age-related increases in VD, VH, or ID, although it can contribute to increases in VA under some conditions (7).
We tested these predictions by measuring age-specific reproductive success for 100 different genotypes of Drosophila melanogaster, produced from all possible crosses among 10 isogenic lines derived from a single, randomly breeding population. We chose to measure reproductive success rather than survival because of the complications involved in estimating variance components for survival data (8, 16). The age-specific reproductive output of 6,000 flies contributed to these measures, and 66,183 offspring of these flies were counted to get age-specific measures of genetic variance and ID.
Methods
We first created 25 different isogenic lines from wild-type flies from the Ives (IV) laboratory population of D. melanogaster. This population is inversion-free and laboratory-adapted (13, 17, 18), which minimizes biases in genetic variance estimates due to novel-environment effects (19). Each line was genetically identical for both the second and third chromosome, which accounts for ≈80% of the Drosophila genome. We first placed the second and third chromosome balancer T (2, 3) A1-W (20) on an IV genetic background to create a balancer stock in which the X and Y chromosomes were derived from the IV population. These and all subsequent crosses were conducted so as to avoid hybrid dysgenesis (e.g., ref. 13). Crossing females from the balancer stock to a single wild-type male from the IV population and then backcrossing a single F1 male to balancer females produced F2 flies that were identically heterozygous for a single wild-type second and third chromosome balanced over the T (2, 3) A1-W reciprocal translocation. X-chromosome variation was present in these lines, but all X chromosomes were derived from the IV population. This within-line variation due to X-linked genes would have contributed to the residual and not the genetic variation among lines. We randomly chose 10 lines from the original 25, the only criterion being that the wild-type chromosomes were homozygous-viable. The 10 isogenic lines were crossed in all possible combinations, with each line used as both sire and dam (a complete diallel design with reciprocal crosses) to yield 100 different genotypes (10 homozygous genotypes resulting from crossing a line to itself, and 90 heterozygous genotypes resulting from crossing two different lines). Six replicate crosses were made per genotype, organized into three blocks that each contained two replicates of each cross. Different sets of parents were used in each replicate, and thus none of the six replicates shared any individual parents.
Virgin males and females were collected from each isogenic line. Three to six days after collection, we placed equal numbers of males and females (20–40) into laying bottles in each of the 100 different combinations of the diallel design. Laying bottles contained molasses-agar laying medium and yeast paste. During a single 12-h period, we collected first-instar larvae from each bottle and transferred them to rearing vials at a density of 20 larvae per vial. Adult virgin males and females representing the 100 experimental genotypes then were collected from each rearing vial during a single 12-h period. For each replicate of each genotype, five male and five female flies from each line were placed together in a vial to assay the age-specific reproductive success of the genotype. Flies were transferred to fresh vials without anesthesia every 7 days until all flies in a vial had died. At each transfer dead flies were removed and counted. Each laying vial was retained for 10 days after the experimental flies were removed. This period maximizes the number of first-generation offspring produced while eliminating the possibility of counting any second-generation offspring. All offspring from each vial were counted, and the age-specific reproductive success of each set of experimental flies was recorded.
We calculated age-specific additive and dominance variance from the noninbred crosses using the method of Cockerham and Weir (21, 22). This method estimates genetic variance components from the general and specific combining abilities of the parental lines plus reciprocal-general and reciprocal-specific combining abilities from the reciprocal effects of parental lines. The full diallel design uses each parental line as both sire and dam and therefore includes reciprocal crosses for each unique combination of second and third chromosomes. We first tested for reciprocal effects in parental lines and in crosses within lines by constructing general linear models including and excluding these effects and comparing likelihood ratios. Because the reciprocal effects all were nonsignificant (reciprocal effects within parental line: χ2 = 1.50, P = 0.22; reciprocal effects within cross: χ2 = 0.01, P > 0.92), we reduced the model to one containing only general and specific combining abilities, from which estimates of additive, dominance, and residual variance were computed (23, 24). Only noninbred lines were used in this analysis to avoid bias from ID in the homozygous lines.
After square-root transformation, data from the first four age classes (days 7, 14, 21, and 28) of the heterozygous crosses conformed well to the assumptions of the variance component analyses. Older age classes (>28 days) deviated substantially from assumptions of normality and homoscedasticity, because few replicates were still producing offspring at those ages, yielding large numbers of zero values. We therefore report variance components only for the first four age classes. No replicates were lost during this time period, thus avoiding the problem of some previous analyses in which late-age variance components could be biased because only a subset of the replicates were represented at late ages (14, 15). Predictions of the population-genetic models of MA and AP (7) refer to scaled variance components such that the transformed data from each age and block were standardized to a mean value of 1.0 before analysis.
To test the significance of the genetic effects and the change of variance components with age, we fit a general linear model that included the effects of block, age, parental line (line), crosses between parental lines (cross), and all interactions of these effects. Block and age were treated as fixed effects. Line, cross, and all interactions involving line or cross were treated as random effects. The line effect provides a test for significance of the general combining ability of lines and therefore a test of the hypothesis that VA > 0. The cross effect provides a test for the significance of special combining ability and tests the hypothesis that VD > 0. The line-by-age interaction allowed us to test the hypothesis that VA changes significantly with age, and the cross-by-age interaction provides the analogous test for VD. To conduct these tests, we used SAS Proc Mixed with restricted maximum-likelihood estimation of random effects and likelihood ratio tests of significance (25).
ID was calculated as (wo − wi)/wo, where wo was the mean age-specific reproductive success of noninbred lines, and wi was the mean of inbred lines (26). We calculated ID for the first six age classes (7–42 days). We did not calculate ID after 42 days, because some lines would have had to be dropped from the analysis because all the flies had died, and these ages therefore would have yielded biased estimates of ID. To avoid pseudoreplication in testing for significant ID, we calculated the mean for all inbred and outbred lines in a block and then conducted paired t tests on the block means of square-root-transformed data. A significant difference between inbred and outbred means was taken as evidence that the ID was significantly greater than zero; tests were one-tailed based on the expectation that inbred means would be less than noninbred means. The reported values and standard errors of ID were calculated from block means of untransformed data. To determine whether inbreeding load increased significantly with age, we conducted a two-way ANOVA on the block mean estimates of reproductive success for inbred and noninbred individuals. The effects of age, inbreeding status (inbred or noninbred), and interaction were included in the model; all were treated as fixed effects. All significance tests were performed on transformed, standardized data.
We calculated the genetic variance among homozygous lines (VH) as the among-line variance component in a general linear model using restricted maximum-likelihood procedures; standard errors were calculated as described for ID. One isogenic line had a mean inbred fitness of <50% of the outbred mean. ID and VH were calculated both with and without this line, because recessive alleles with sublethal effects might have genetic properties unrepresentative of mildly detrimental alleles (27).
We also calculated genotypic correlations between age classes using restricted maximum likelihood by fitting two parameters (genetic and nongenetic) and constraining other components to be zero in the quantitative genetic program QUERCUS (28). The significance of correlations was tested by likelihood ratio tests, and the reported standard errors were the large-sample standard errors calculated by QUERCUS.
Results
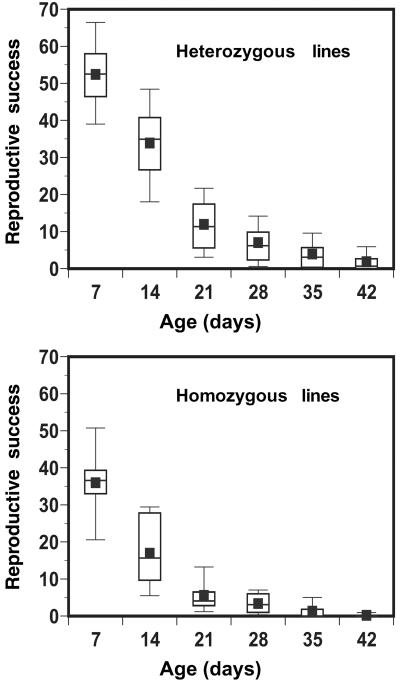
Mean reproductive success decreased with age for both homozygous and heterozygous genotypes, indicating substantial senescence (Fig. 1). ID was significantly greater than zero at each age, and the magnitude of ID increased 3-fold between 7 and 42 days of adult age (Table 1). A two-way ANOVA of the block means of reproductive success for inbred and noninbred individuals showed that the effects of age, inbreeding status, and interaction were all highly significant (Table 2). We evaluated the linear trend of ID with age by treating age as a continuous covariate in an analysis of covariance with inbreeding status as the main effect. The inbreeding-by-age interaction was significant [F(1,32) = 41.7, P < 0.0001]. To determine whether the trend was solely due to the dramatic increase in ID in the last two age classes, we repeated this analysis with the last age class excluded and with the last two age classes excluded. The interaction term was significant in both cases [F(1,26) = 19.1, P = 0.0002 and F(1,20) = 13.9, P = 0.013, respectively].
Fig 1.
Box plots of age-specific reproductive success. The horizontal axis is age, and the vertical axis is reproductive success (number of offspring). (a) Heterozygous lines. (b) Homozygous lines. The boxes show 25th, 50th, and 75th percentiles of distribution, whiskers show 10th and 90th percentiles, and the square symbols indicate the mean.
Table 1.
Age-specific reproductive success of noninbred (wo) and inbred (wi) flies, and the ID [ID = (wo − wi)/wo]
| Age, days | wo (SE) | wi (SE) | ID (SE) | t | P |
|---|---|---|---|---|---|
| All lines included | |||||
| 7 | 54.44 (4.13) | 35.98 (2.20) | 0.34 (0.05) | 8.52 | 0.007 |
| 14 | 36.22 (1.32) | 16.95 (2.23) | 0.53 (0.08) | 5.45 | 0.016 |
| 21 | 12.64 (2.61) | 5.60 (2.56) | 0.56 (0.11) | 10.15 | 0.005 |
| 28 | 7.48 (0.88) | 3.37 (1.17) | 0.55 (0.12) | 8.07 | 0.008 |
| 35 | 4.28 (0.71) | 1.33 (0.62) | 0.69 (0.13) | 7.78 | 0.008 |
| 42 | 2.06 (0.24) | 0.20 (0.13) | 0.90 (0.05) | 26.91 | <0.001 |
| One low-fitness line excluded | |||||
| 7 | 55.82 (3.97) | 38.53 (2.26) | 0.28 (0.06) | 3.93 | 0.030 |
| 14 | 35.48 (1.38) | 18.09 (1.87) | 0.49 (0.07) | 6.53 | 0.011 |
| 21 | 12.31 (2.56) | 6.13 (2.75) | 0.50 (0.12) | 10.08 | 0.005 |
| 28 | 7.47 (0.94) | 3.67 (1.24) | 0.51 (0.13) | 8.28 | 0.007 |
| 35 | 4.42 (0.80) | 1.48 (0.69) | 0.67 (0.13) | 7.47 | 0.009 |
| 42 | 2.16 (0.29) | 0.22 (0.15) | 0.90 (0.05) | 23.42 | <0.001 |
t tests have two degrees of freedom.
Table 2.
Effects of inbreeding status and age on reproductive success when all lines were included
| Source | Degrees of freedom | Mean squares | F ratio | P > F |
|---|---|---|---|---|
| Age | 5 | 0.056 | 4.18 | 0.007 |
| Inbreeding | 1 | 2.730 | 202.87 | <0.0001 |
| Inbreed × age | 5 | 0.091 | 6.75 | 0.0005 |
| Residual | 24 | 0.013 |
With line 8 excluded: age, P = 0.025; inbreeding, P < 0.0001; inbreeding × age, P = 0.0002.
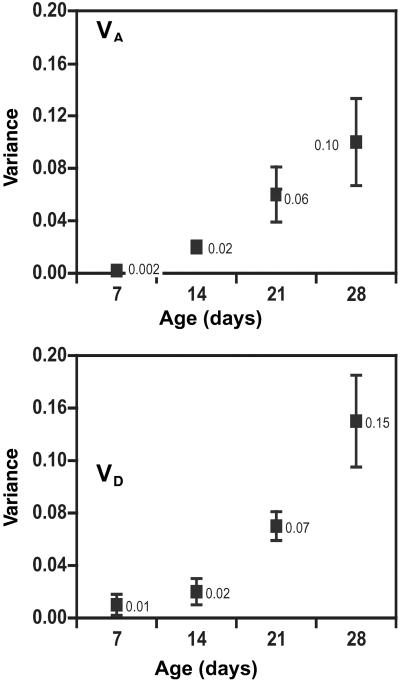
Similar to the ID, the additive and dominance genetic variation increased dramatically between 7 and 28 days of age (Fig. 2). The analysis shown in Table 3 indicates that effects of line and cross were highly significant, as were the line-by-age and cross-by-age interactions, indicating that both the general and specific combining abilities change significantly with age. Because the fitness measure was the total age-specific reproductive success of 10 individuals of a specific genotype, there is a possibility that some of the change in genetic variance with age might have been caused by density- or frequency-dependent fitness changes among genotypes. We therefore repeated the above analysis on a data set that included only those observations in which six or more individuals remained alive after the 21-day census. The analysis therefore was restricted to observations in which only small or moderate changes in density occurred over the time period under investigation (45 vials were excluded). The line-by-age and cross-by-age effects were still significant (line × age: χ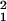 = 40.3, P < 0.0001; cross × age: χ
= 40.3, P < 0.0001; cross × age: χ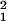 = 5.1, P = 0.02), and the proportion of total variance accounted for by each of these effects remained essentially unchanged (line × age: 0.122 before vs. 0.150 after exclusion; cross × age: 0.080 before vs. 0.082 after exclusion), indicating that the increase in genetic variance with age was unlikely to be caused by density-dependent fitness effects. Unfortunately, we could not evaluate the potential for sex ratio-dependent fitness effects in this experiment, because we did not census males and females separately. It should also be noted that variance due to epistasis and linkage disequilibrium can contribute to the variance estimates reported here (23, 29–31). However, these effects would have to increase systematically with age to account for our results, a pattern that to our knowledge has not been reported.
= 5.1, P = 0.02), and the proportion of total variance accounted for by each of these effects remained essentially unchanged (line × age: 0.122 before vs. 0.150 after exclusion; cross × age: 0.080 before vs. 0.082 after exclusion), indicating that the increase in genetic variance with age was unlikely to be caused by density-dependent fitness effects. Unfortunately, we could not evaluate the potential for sex ratio-dependent fitness effects in this experiment, because we did not census males and females separately. It should also be noted that variance due to epistasis and linkage disequilibrium can contribute to the variance estimates reported here (23, 29–31). However, these effects would have to increase systematically with age to account for our results, a pattern that to our knowledge has not been reported.
Fig 2.
Age-specific estimates of additive (VA), dominance (VD), and homozygous variance (VH) with standard error bars. Standard errors were calculated from block means. Numbers next to the symbols are the mean variance estimates.
Table 3.
Effects of line, cross, and age on reproductive success estimated by restricted maximum-likelihood analysis of standardized, transformed data
| Effect | Variance component | −2LL | χ2 | P |
|---|---|---|---|---|
| Line (GCA) | 0.009 | 651.1 | 55.72 | <0.00001 |
| Cross (SCA) | 0.012 | 595.4 | 25.03 | <0.00001 |
| Line × block | 0.005 | 570.4 | 13.87 | 0.0001 |
| Cross × block | 0.043 | 556.5 | 17.24 | 0.00003 |
| Line × age | 0.028 | 539.3 | 61.08 | <0.00001 |
| Cross × age | 0.015 | 478.2 | 7.32 | 0.0068 |
| Line × age × block | 0.003 | 470.9 | 1.33 | 0.2488 |
| Cross × age × block | 0.000 | 469.5 | <0.05 | >0.823 |
| Residual | 0.072 | 469.5 | ||
| Total | 0.187 |
Residual log-likelihood (× −2) of the model. −2LL is distributed as χ2 with one degree of freedom.
The MA theory also predicts that the variance among homozygous lines (VH) will increase with age, whereas the AP theory does not predict an increase. We found that with all lines included, VH increased dramatically between 7 and 21 days of adult life but then declined to zero (Table 4). With the low-fitness line 8 excluded, VH behaved similarly. By 28 days, two-thirds (40/60) of the homozygous replicates had zero reproductive success. The analysis at 28 days therefore had little power to detect significant variation among lines (1-β = 0.27 for α = 0.05). With only ages 7–21 days included, the age-by-line interaction was marginally nonsignificant (χ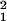 = 3.22, P = 0.07). However, the linear trend with age was highly significant (χ
= 3.22, P = 0.07). However, the linear trend with age was highly significant (χ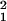 = 18.2, P < 0.0001).
= 18.2, P < 0.0001).
Table 4.
Homozygous variance (VH) estimates
| Age, days | Variance component | F | P |
|---|---|---|---|
| All lines included | |||
| 7 | 0.015 | 2.34 | 0.059 |
| 14 | 0.028 | 2.16 | 0.078 |
| 21 | 0.086 | 2.82 | 0.029 |
| 28 | −0.007 | 0.94 | 0.51 |
| One low-fitness line excluded | |||
| 7 | 0.0005 | 0.01 | 0.806 |
| 14 | 0.022 | 2.89 | 0.034 |
| 21 | 0.074 | 2.01 | 0.111 |
| 28 | −0.019 | 2.75 | 0.04 |
The AP and MA theories also make contrasting predictions with respect to genetic correlations (rG) between age classes (13, 32). The antagonistic interactions between early- and late-age effects that characterize the AP theory should lead to negative genetic correlations (rG < 0) between early and late fitness traits. MA predicts that rG < 1, because genetic effects at different ages will be at least partially independent. Under MA, correlations between adjacent age classes can be high (rG ≫ 0) if deleterious alleles have effects that span several age classes (32). Our estimates of genetic correlations were positive and generally moderate in value; they also had large standard errors, which is typical of genetic correlations even in large experiments (Table 5). One correlation was large and significantly positive (that between 21 and 28 days of age), but the others were not significantly different from zero by likelihood ratio tests. These estimates suggest that genetic correlations among early and late ages were not negative and probably fell in the range predicted by MA, although the large standard errors make this conclusion tentative. All estimates of phenotypic correlations were also positive, with four of six being significantly greater than zero.
Table 5.
Genetic (above diagonal) and environmental correlations (below diagonal) between reproductive success at different ages
| Age, days | 7 days | 14 days | 21 days | 28 days |
|---|---|---|---|---|
| 7 | 0.534 (0.47) | 0.263 (0.08) | 0.247 (0.06) | |
| 14 | 0.170 (0.41) | 0.540 (0.13) | 0.346 (0.11) | |
| 21 | 0.590 (0.46) | 0.618 (0.43) | 0.558 (0.02) | |
| 28 | 0.369 (0.43) | 0.439 (0.41) | 0.869 (0.19) |
P < 0.05,
P < 0.01,
P < 0.10, before correction; bold indicates P < 0.05 after sequential Bonferroni correction for multiple tests.
Discussion
We found strong support for all the predictions of the MA theory of the evolution of senescence. In a previous test of these predictions, ID and additive variance were found to increase with age for two measures of male fitness, but neither trait exhibited significant dominance variance (7). The previous study evaluated the results of a partial diallel breeding design that included more parental lines, but fewer crosses among the lines, than the full diallel used here. Thus the present study had better power for detecting dominance variance. The power to detect VD is critical to tests of senescence theories, because an age-related increase in VD appears to be a unique prediction of the MA theory, whereas VA can increase under either model. ID also can increase in the absence of MA if old individuals are more susceptible to the deleterious effects of inbreeding. We therefore believe this study presents the strongest support yet for the MA model of senescence.
Although providing good power to detect changes in VD, a potential drawback of the complete diallel design we used is that relatively fewer chromosomes can be sampled from the base population than if a partial diallel design were used. However, the goal here was not to make broad inferences about the standing genetic variation in the base population, as has been done elsewhere (13, 33), but to test specific predictions that genetic variation and inbreeding load should increase with age. This prediction was upheld for the sample of genotypes tested. Also, there is no a priori reason to suspect that the genotypes we used were unrepresentative. In fact, our estimates of ID and genetic variance in young flies (7 days) were very similar to those reported for other early-life Drosophila fitness components. On a standardized scale [the mild detrimental load, Dm (34), adjusted for the portion of the genome made homozygous], our measure of the inbreeding load was 0.46 compared with 0.39 for an estimate for male mating success (33) and 0.35 for estimates of egg-adult viability (34). Our estimates for additive and dominance variance [again on a standardized scale of coefficients of genetic variation (35)] were 4.5 and 11.8 respectively, compared with mean values of 7.2 and 12.4 for several other early-life fitness components (36).
There have been two other reports of age-specific measures of variance components that were used to test the MA model, but neither provided conclusive evidence in support of or against the model. Promislow et al. (14) and Tatar et al. (15) measured mortality rates and female fecundity in 25 heterozygous genotypes produced from a partial diallel cross among 10 second-chromosome isogenic lines. Neither study reported ID estimates, because within-line crosses were not made, and neither study found significant VD at any age. The relatively small number of heterozygous genotypes used (25 vs. 100 in our experiment) could account for the failure to detect significant VD. The experiments should have had reasonable power to detect changes in VA. The VA estimates for female fecundity behaved somewhat erratically early in life but did increase late in life. Overall, the pattern was consistent with a linear age-specific increase over the span of ages reported (3–31 days) (15).
Mortality data demonstrated increasing VA during the first 3 (female) or 5 (male) weeks of life, but VA decreased in both sexes at later ages (14). Our analysis of VA did not extend beyond 4 weeks of age because of cessation of reproduction of many replicates beyond that age; thus, if a decrease in VA occurs beyond this age, we would not have observed it. However, there were sources of bias in the Promislow et al. (14) study that might have contributed to the apparent decrease at late ages. Uncontrolled genetic variation from the balancer stock was present in the isogenic lines used in that study, and there was apparently no control for hybrid dysgenesis. Both factors would contribute additional within-genotype heterogeneity that was not present in our study. Uncontrolled variation within genotypes is a concern, because it can lead to dramatic underestimates of genetic variance at late ages (37, 38). Thus, although it is not possible to eliminate all sources of within-genotype variation (39), our experiment contained fewer sources of such variation. In addition, the earlier study included different subsets of observations at different ages, because some observations had no live flies during late-age classes and thus were excluded, whereas other replicates were excluded at early ages because they had zero mortality.
Alternately, the contrasting results could reflect real differences in the genetic variation that influences age-specific mortality and reproductive success. A recent treatment of the MA model indicates that deleterious mutations with effects spanning age classes can lead to plateaus in VA at late ages (32). If mutations affecting different life-history traits vary in their degree of age specificity, different patterns of genetic variance with age will arise. Currently there is little data relevant to this question, although one study has indicated high, positive mutational correlations between reproduction and longevity (40).
Although our results support the MA theory, they do not necessarily contradict the AP theory. AP has received considerable support from artificial-selection experiments (9), which probably are the best way to detect negative genetic correlations between early- and late-life fitness components. The AP and MA processes are not mutually exclusive, and both could contribute to senescence. One indication that both processes are operating in our population is that the age-related increase in additive variance is nearly as large as the increase in dominance variance. If MA alone causes senescence, the dominance variance should increase much faster than the additive variance (7). In our study, the two components increased at nearly the same rate until day 21 (Fig. 2), although the dominance variance increased faster after that age. AP could have caused some of the increase in the additive component. Also, AP can lead to senescence even if pleiotropic genes contribute very little genetic variation, because selection can cause near fixation of alleles with beneficial early and deleterious late effects and near elimination of alleles with the reverse pattern of action (41, 42). Indeed, many of the recently discovered “aging” genes in Drosophila and other model organisms may fall into this category (43–48). Many of these genes seem to have antagonistic pleiotropic effects, but thus far there is no evidence that polymorphism in these genes is associated with fitness variation within natural populations.
The AP model is consistent with the existence of a few genes with individually large effects on late-life fitness, whereas the MA process should lead to the maintenance of many deleterious alleles at intermediate frequencies within populations, and these alleles can have individually small effects on late-life performance and health. Current methods of identifying aging genes (such as mutation studies and quantitative trait locus-mapping experiments) are most effective in finding alleles of large effect, and even well designed studies will probably miss genes with small effects. Novel approaches are needed to find such genes, and a promising technique is illustrated by a recent mRNA microarray study that indicated that aging is accompanied by changing expression levels in thousands of genes (49). Combining this technique with assays of within-population genetic variation could be a fruitful approach to identifying the genes of small effect predicted under the MA model.
Acknowledgments
We thank C. Caceres, B. Charlesworth, K. Dixon, P. Hedrick, J. Leips, R. Olendorf, K. Paige, G. Robinson, M. Kidwell, and two anonymous reviewers for insightful comments on previous versions of the manuscript. B. Ruedi, K. Combs, and K. Hill helped with the experiments. Funding for this research was provided by National Science Foundation Grant DEB 9734008, National Institutes of Health Grant R03 HS35793, and the School of Integrative Biology at the University of Illinois.
Abbreviations
AP, antagonistic pleiotropy
MA, mutation accumulation
ID, inbreeding depression
IV, Ives
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Lithgow G. J. & Kirkwood, T. B. L. (1996) Science 273, 80. [DOI] [PubMed] [Google Scholar]
- 2.Finch C. E., (1990) Longevity, Senescence, and the Genome (Univ. of Chicago Press, Chicago).
- 3.Rose M. R., (1991) The Evolutionary Biology of Aging (Oxford Univ. Press, Oxford, U.K.).
- 4.Partridge L. & Barton, N. H. (1993) Nature 362, 305-311. [DOI] [PubMed] [Google Scholar]
- 5.Kirkwood T. B. L. & Austad, S. N. (2000) Nature 408, 233-238. [DOI] [PubMed] [Google Scholar]
- 6.Charlesworth B., (1994) Evolution in Age-Structured Populations (Cambridge Univ. Press, Cambridge, U.K.).
- 7.Charlesworth B. & Hughes, K. A. (1996) Proc. Natl. Acad. Sci. USA 93, 6140-6145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Shaw F. H., Promislow, D. E. L., Tatar, M., Hughes, K. A. & Geyer, C. J. (1999) Genetics 152, 553-566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Partridge L. & Gems, D. (2002) Nat. Rev. Genet. 3, 165-175. [DOI] [PubMed] [Google Scholar]
- 10.Partridge L. (2001) Exp. Gerontol. 36, 641-650. [DOI] [PubMed] [Google Scholar]
- 11.Rose M. R. & Charlesworth, B. (1981) Genetics 97, 173-186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hughes K. A. & Charlesworth, B. (1994) Nature 367, 64-66. [DOI] [PubMed] [Google Scholar]
- 13.Hughes K. A. (1995) Evolution (Lawrence, Kans.) 49, 521-537. [DOI] [PubMed] [Google Scholar]
- 14.Promislow D. E. L., Tatar, M., Khazaeli, A. A. & Curtsinger, J. W. (1996) Genetics 143, 839-848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tatar M., Promislow, D. E. L., Khazaeli, A. A. & Curtsinger, J. W. (1996) Genetics 143, 849-858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Promislow D. E. L., Tatar, M., Pletcher, S. & Carey, J. R. (1999) J. Evol. Biol. 12, 314-328. [Google Scholar]
- 17.Rose M. R. & Charlesworth, B. (1980) Nature 287, 141-142. [DOI] [PubMed] [Google Scholar]
- 18.Charlesworth B. & Charlesworth, D. (1985) Heredity 54, 71-84. [Google Scholar]
- 19.Service P. M. & Rose, M. R. (1985) Evolution (Lawrence, Kans.) 39, 943-945. [DOI] [PubMed] [Google Scholar]
- 20.Lindsley D. L. & Zimm, G. G., (1992) The Genome of Drosophila melanogaster (Academic, San Diego).
- 21.Cockerham C. C. & Weir, B. S. (1977) Biometrics 33, 187-203. [PubMed] [Google Scholar]
- 22.Lynch M. & Walsh, B., (1998) Genetics and Analysis of Quantiative Traits (Sinauer, Sunderland, MA).
- 23.Griffing B. (1956) Aust. J. Biol. Sci. 9, 463-493. [Google Scholar]
- 24.Becker W. A., (1984) Manual of Quantitative Genetics (Academic Enterprises, Pullman, WA).
- 25.SAS Institute, (2000) SAS/STAT User's Guide (SAS Institute, Cary, NC), Version 8.
- 26.Charlesworth D. & Charlesworth, B. (1987) Annu. Rev. Ecol. Syst. 18, 237-268. [Google Scholar]
- 27.Mukai T., Cardellino, R. A., Watanabe, T. K. & Crow, J. F. (1974) Genetics 78, 1195-1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shaw R. G. (1987) Evolution (Lawrence, Kans.) 41, 812-826. [DOI] [PubMed] [Google Scholar]
- 29.Kempthorne O., (1957) An Introduction to Genetic Statistics (Wiley, New York).
- 30.Tachida H. & Cockerham, C. C. (1988) Genet. Res. 51, 47-53. [DOI] [PubMed] [Google Scholar]
- 31.Charlesworth B. & Barton, N. H. (1996) Genet. Res. 67, 27-41. [DOI] [PubMed] [Google Scholar]
- 32.Charlesworth B. (2001) J. Theor. Biol. 210, 47-65. [DOI] [PubMed] [Google Scholar]
- 33.Hughes K. A. (1995) Genet. Res. 65, 41-52. [DOI] [PubMed] [Google Scholar]
- 34.Simmons M. J. & Crow, J. F. (1977) Annu. Rev. Genet. 11, 49-78. [DOI] [PubMed] [Google Scholar]
- 35.Houle D. (1992) Genetics 130, 195-204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Charlesworth B. & Hughes, K. A. (2000) in Evolutionary Genetics from Molecules to Morphology, eds. Singh, R. S. & Krimbas, C. B. (Cambridge Univ. Press, Cambridge, U.K.), pp. 369–391.
- 37.Pletcher S. D. & Curtsinger, J. W. (2000) Genet. Res. 75, 321-329. [DOI] [PubMed] [Google Scholar]
- 38.Service P. M. (2000) Am. Nat. 156, 1-13. [DOI] [PubMed] [Google Scholar]
- 39.Khazaeli A. A., Pletcher, S. D. & Curtsinger, J. W. (1998) Mech. Ageing Dev. 105, 301-317. [DOI] [PubMed] [Google Scholar]
- 40.Houle D., Hughes, K. A., Hoffmaster, D. K., Ihara, J., Asimacopolous, S., Canada, D. & Charlesworth, B. (1994) Genetics 138, 773-785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Curtsinger J. W., Service, P. M. & Prout, T. (1994) Am. Nat. 144, 210-228. [Google Scholar]
- 42.Hedrick P. W. (1999) Heredity 82, 126-133. [Google Scholar]
- 43.Kenyon C., Chang, J., Gensch, E., Rudner, A. & Tabtiang, R. (1993) Nature 366, 461-464. [DOI] [PubMed] [Google Scholar]
- 44.Lin Y. J., Seroude, L. & Benzer, S. (1998) Science 283, 943-946. [DOI] [PubMed] [Google Scholar]
- 45.Guarente L. & Kenyon, C. (2000) Nature 408, 255-262. [DOI] [PubMed] [Google Scholar]
- 46.Rogina B., Reenan, R. A., Nilsen, S. P. & Helfand, S. L. (2000) Science 290, 2137-2140. [DOI] [PubMed] [Google Scholar]
- 47.Clancy D. J., Gems, D., Harshman, L. G., Oldham, S., Stocker, H., Hafen, E., Leevers, S. J. & Partridge, L. (2001) Science 292, 104-107. [DOI] [PubMed] [Google Scholar]
- 48.Tatar M., Kopelman, A., Epstein, D., Tu, M. P., Yin, C. M. & Garofalo, R. S. (2001) Science 292, 107-110. [DOI] [PubMed] [Google Scholar]
- 49.Pletcher S. D., Macdonald, S. J., Marguerie, R., Certa, U., Stearns, S. C., Goldstein, D. B. & Partridge, L. (2002) Curr. Biol. 12, 712-723. [DOI] [PubMed] [Google Scholar]