Response properties of an integrate-and-fire model that receives subthreshold inputs

Abstract

A computational technique is described for calculation of the interspike interval and poststimulus time (PST) histograms for the responses of an integrate-and-fire (I&F) model to arbitrary inputs. The effects of the model parameters on the response statistics were studied systematically. Specifically, the probability distribution of the membrane potential was calculated as a function of time, and the mean interspike interval and PST histogram were calculated for arbitrary inputs. For stationary inputs, the regularity of the output was studied in detail for various model parameters. For non-stationary inputs, the effects of the model parameters on the output synchronization index were explored. The results show that enhanced synchronization in response to low-frequency stimuli required a large number (n > 25) of weak inputs. Irregular responses and a linear input-output rate relationship required strong (but subthreshold) inputs with a small time constant. A model cell with mixed-amplitude synaptic inputs can respond to stationary inputs irregularly and have enhanced synchronization to non-stationary inputs that are phase-locked to low-frequency inputs. Both of these response properties have been reported for some cells in the ventral cochlear nucleus in the auditory brainstem.

1. Introduction

One fundamental question in the study of nervous-system function is how a single neuron responds to and processes the information received from other neurons. In the auditory system, approximately 30,000 primary auditory-nerve (AN) fibers with different characteristic frequencies (CF) connect the auditory sensory organ, the cochlea or inner ear, to the cochlear nucleus (CN) in the brainstem. The CN receives all of the information in the acoustic signal represented by the temporally structured spike discharges in the population of AN fibers and is the first stage of information processing in the central auditory system. The CN contains a variety of cells that differ in their responses to a relatively homogeneous input and therefore presents a unique opportunity for quantitatively studying input-output transformations by neurons and the relationships between a neuron’s function and its underlying mechanisms.

In this study, computational techniques for the study of neural models were developed. These methods are generally applicable to problems at many levels of the nervous system involving responses of neurons to convergent inputs. Here we applied the methods to an ongoing set of problems associated with understanding the nature of the convergence of AN fibers onto bushy cells in the CN.

While the importance of spike timing in the millisecond range in cortical areas remains a topic of intense debate (e.g., König et al., 1996), the significance of temporal coding for auditory perception, and especially for sound localization, has been widely accepted (e.g., Joris et al., 1998). It is thus of great interest to understand temporal coding and processing along the auditory pathway and its underlying mechanisms. Considerable progress has been made over the decades. Temporal information is first encoded in the discharge pattern of AN fibers, which are phase-locked to the temporal features of the acoustic waveform up to 4–5 kHz (Kiang et al., 1965; Johnson, 1980). In the ventral division of the cochlear nucleus (VCN), the bushy cells appear to be specialized to preserve and even enhance the temporal information encoded in AN fibers (Joris et al., 1994a,b). Temporal information is further transmitted to the superior olivary complex, where cells are sensitive to interaural timing differences from their binaural inputs (see review by Yin, 2002).

The capability of bushy cells to preserve or even enhance timing information relies on their synaptic configuration and membrane properties. Bushy cells receive large somatic AN terminals, called the end bulbs of Held (see review by Cant, 1992), that differ in number and size: spherical bushy cells (SBC) have fewer and larger end bulbs, while globular bushy cells (GBC) have more and smaller end bulbs. The somatic inputs bypass the dendritic low-pass filtering and thus have a very short time constant in their synaptic current. Bushy cells also have short membrane time constants (Oertel 1983, 1985) caused by the activation of a low-threshold potassium conductance at the resting potential. Recent experimental (Manis and Marx, 1991; Rothman and Manis, 2003c) and modeling (Rothman et al., 1993, 2003a,b) studies have satisfactorily explained how the membrane properties of the bushy cell contribute to its precise preservation of temporal information.

Analysis of neural responses is very useful for estimating the parameters of synaptic inputs (the number and size of the inputs) to bushy cells because these parameters are believed to be crucial to bushy cell input-output functions. SBCs usually have prepotential waveforms (Bourk, 1976; reviewed by Rhode and Greenberg, 1992) and have discharge patterns similar to those of AN fibers. They are thus referred to as primarylike (PL), suggesting that SBCs may receive suprathreshold inputs. Modeling studies by Rothman et al. (1993) suggest that bushy cells with primarylike-with-notch (PLn) responses to high-frequency tones at CF must also receive suprathreshold inputs to maintain their irregularity. PLn responses are associated with GBSs. Evidence that bushy cells receive subthreshold inputs also is available. Some bushy cells demonstrate onset with low sustained rate (On-L) discharge patterns that can be successfully modeled using many weak subthreshold inputs (Rothman et al., 1993; Kipke and Levy, 1997; Kalluri and Delgutte, 2003a,b). Consistent with models receiving subthreshold inputs, enhanced phase-locking has been observed (Joris et al., 1994a,b) in low-CF bushy cells in the AVCN responding to CF tones and in high-CF PLn response types responding to low-frequency tones.

The reports that high-CF bushy cells respond irregularly to CF tones and have enhanced synchronization in response to low-frequency tones (Joris et al., 1994a) suggest that the same synaptic configuration (number and size of the AN inputs) must be capable of both input-output relationships. In the studies from Rothman and his colleagues (Rothman et al., 1993; Rothman and Young, 1996; Rothman and Manis, 2003a), a compartmental model was used to explore the model responses with different synaptic configurations. Their results support the hypothesis that subthreshold inputs are capable of producing enhanced-sync responses to low-frequency tones, and suprathreshold inputs are more suitable to describe the PL and PLn responses of bushy cells. The results also suggested that the different arrangements of synaptic inputs may affect the input-output rate relationships of bushy cells. However, the relative importance of such arrangements was not reported in their study because their model also included complex (nonlinear) effects of neural dynamics.

Because of its simplicity and mathematical tractability, statistical analysis of neural activity based on integrate-and-fire (I&F) model estimations of neuronal physiological and anatomical parameters has a long history in theoretical neuroscience (Tuckwell, 1988). The I&F model was also the first neural model to capture the essential properties of neural behavior: synaptic integration and threshold for responding. A generalization of this simple phenomenological model (known as the Spike Response Model, see Gerstner and Kistler, 2002) can emulate more physiologically realistic Hodgkin-Huxley type (channel) models (Kistler et al., 1997) and has been widely used in the study of neural coding, synaptic plasticity, and pattern formation. I&F models have been used to study the regularity properties of spontaneous activity in auditory neurons (Molnar and Pfeiffer, 1968), the phase-locking properties of bushy cells (Joris et al., 1994a), and the discharge pattern of Onset neurons in the CN (Kalluri and Delgutte, 2003a,b). Stochastic processes have been employed in modeling the responses of single neurons using the I&F model. For example, Stein (1965) proposed a discontinuous Markov process as a neural model that incorporated the exponential decay of the membrane potential. Computational methods have provided quantitative statistical descriptions of the model response (Molnar and Pfeiffer, 1968; Colburn and Moss, 1981). However, previous methods for analyzing the I&F model have been limited to conditions with stationary inputs; and new techniques are needed to explore model responses to non-stationary (phase-locked) inputs.

Kempter et al. (1998) investigated the coincidence-detection properties of an I&F model in response to periodic spike inputs. Their analysis concerns the dependence of the model response rate on neural parameters such as the number of synapses, the threshold, and the time course of the postsynaptic responses. They also explored the effects of these parameters on the neuron’s ability to convert a temporal code into a rate code. An extended study (Burkitt and Clark, 2001) has also evaluated the interspike interval (ISI) histogram and the period histogram for neural responses to ongoing periodic inputs. Both studies assume that there is a large number of small inputs to the model and that the membrane potential is approximated by a Gaussian random variable, and they limit their analyses to a model without refractoriness. In a series of studies, Gerstner, Plesser, and coworkers presented an analytical framework to study the I&F neuron model with non-stationary (periodical) input (Plesser and Geisel, 1999; Plesser and Gerstner 2000; Herrmann & Gerstner, 2000, 2001). Their approach requires an explicit description of either the diffusion noise (stochastic description of the membrane potential) or the escape noise (stochastic description of firing probability). Their work provides insights to the I&F model with a large number of inputs.

In the present study, we explored how the neural response statistics change with different synapse configurations using an I&F model. The model cell received a varying number of convergent AN inputs, which were superimposed and modeled as a non-stationary Poisson point process. A computational method based on Stein’s model is proposed to calculate accurately the ISI histogram and post-stimulus time histogram (PST) of the I&F model in response to an arbitrary stimulus waveform. The method presented here applies to the I&F model without any limitations on the model parameters and is especially efficient when there is small number of inputs with fast membrane decay time constants. The model parameters were systematically investigated using responses to both stationary and non-stationary inputs. Various response properties of the model cell were explored, including the rate response of the model cell, regularity in response to stationary inputs, and phase-locking in response to non-stationary input. The general conclusions about the effect of model parameters on the neural response statistics apply to all cells that receive convergent inputs, though the statistics we investigated here are of particular interest for the study of bushy cells in the VCN, which are known to receive a relatively small number of large inputs from AN fibers (Manis and Marx, 1991; Cant, 1992) and which have fast membrane dynamics (Oertel, 1983).

2. Method

2.1 The I&F Model:

The model used in the present study is a simple I&F neuron with the following properties:

1. Each input spike (except those that arrived during the model’s dead time) at time t_k from channel i generated an excitatory postsynaptic potential (EPSP) given by

$$V_{i,t_k}(t)=A_i{e}^{-(t-t_k)/{\tau }_i}.$$ (1)

The amplitude (A_i) and time constant (τ_i) of the EPSP (V_i,tk) represent the basic configuration of the synapse integration and were explored systematically, along with different input stimuli.

1. The membrane potential V(t) (0 at rest) was the linear sum of all incoming EPSPs.

2. The model cell fired when the membrane potential V(t) exceeded the threshold. The threshold was always set to 1 so the EPSP amplitude represented the synapse strength relative to threshold.

3. The membrane potential V(t) was reset to zero after firing, with a dead time of 0.7 ms. (Spikes that arrived during the deadtime did not generate EPSPs.)

How the membrane potential V(t) changed with time after firing was very important to the neural response statistics. When the neuron was not discharging (assuming the dead-time period ended at t = 0, that is, the previous spike time was at t = −0.7 ms) and the model input was a Poisson stationary process with arrival rate R, the mean and variance of the model’s membrane potential values were given by (Stein, 1965):

$${\mu }_{\nu }=RA\tau (1-e^{-t/\tau }),$$ (2)

and

$${\sigma }_{\nu }^2=R{A}^2(\tau /2)(1-e^{-2t/\tau }).$$ (3)

2.2 Stimulus description and superposition of AN inputs

The discharge pattern of the AN fiber can be described as a nonhomogeneous Poisson process modified to include refractory effects (Johnson and Swami, 1983). Since the EPSPs are integrated linearly by the I&F model, inputs from multiple AN fibers that produce EPSPs with identical amplitudes and time constants can be superimposed. (This simplification is considered further in the Discussion). The equivalent input can then be described by a nonhomogeneous Poisson process (Cox, 1962) as the number of input fibers increases. Figure 1 illustrates the change of the interspike interval (ISI) distribution of the superimposed input with different numbers of input AN fibers. Each model AN fiber’s discharge times were produced by a renewal process that simulated a stationary input (100 sp/sec) modified by refractoriness (Carney, 1993). The ISI curves (calculated based on 100,000 simulated spikes) are plotted on normalized axes so that they are comparable with each other. (The solid line represents the ISI for a Poisson process.) The simulation shows that the superimposed input could be approximated by a Poisson process (i.e., the effect of input refractoriness on ISI could be ignored) when there were more than five independent AN-fiber inputs.

Figure 1.

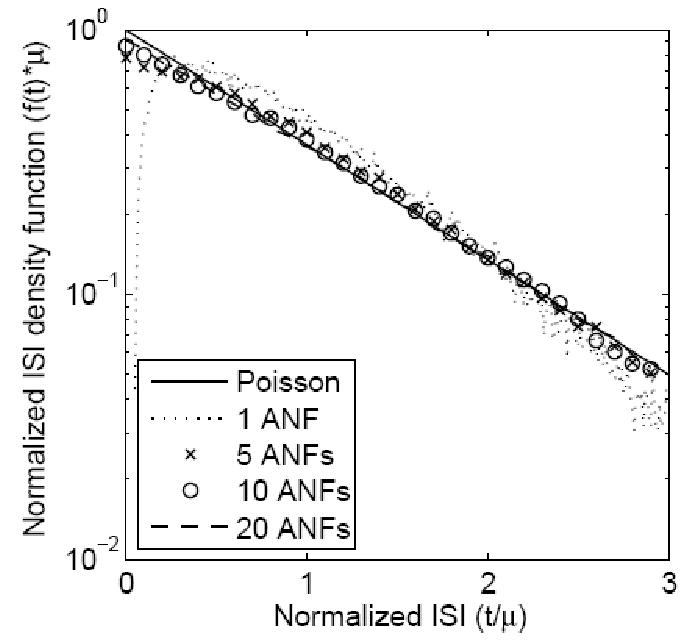
ISI (interspike interval) distribution of a superposition model with different numbers of independent AN inputs. Each input model AN fiber had a stationary Poisson response of 100 sp/sec modified by refractoriness (Carney, 1993). The input spikes were interleaved, and the ISI was calculated based on 100,000 simulated discharges. Both axes were normalized (either multiplied or divided by the mean interval-spike time μ) to make the ISI distributions comparable. The ISI distribution goes to zero at the absolute refractory period for a single AN input (dotted line). As the number of independent inputs increased (to values larger than 5), the combined input spikes could be approximated by a simple Poisson process (solid line).

For the model cell that received stationary input from multiple AN fibers, we treated the total input spike train as a Poisson process with rate R. When the input was periodic, the total input spike train was described as a nonhomogeneous Poisson process with an instantaneous rate of firing s_AN(t) given by (see Colburn, 1973; Colburn et al., 2003):

$$S_{AN}(t)=R\frac{e^{\varphi \mathrm{\hspace{0.17em} }\text{sin}(2\pi ft)}}{f{\int }_0^{1/f}{e}^{\varphi \mathrm{\hspace{0.17em} }\text{sin}(2\pi ft)}dt},$$ (4)

where the exponential function in the numerator represents the periodic signal, with φ and f determining the strength of phase-locking and frequency of the input. The parameter R is the mean firing rate of the non-stationary Poisson process. The exponential function is normalized by the denominator, which is the modified Bessel function I₀[g] described in Colburn et al. (2003).

2.3 Analytical calculations of the ISI and PST for the I&F model with stationary and non-stationary inputs

Stein (1965) proposed a discontinuous Markov process model to describe the statistics of the membrane potential for the I&F model mentioned above. Molnar and Pfeiffer (1968) used this model to numerically calculate the ISI of the output for the case with stationary input. The following analysis and computational results extend this method to include both the ISI and PST histograms of the model output.

Given that the previous output spike time is at t=0 and that the potential V(t') is always less than 1 for t’ in the interval [0,t), we define F_c[V_x,t’] as the conditional cumulative probability that the membrane potential V(t’) is less than the potential V_x at time t’, for all t’ in the interval [0,t). Thus, F_c[V_x,t’] = Prob (V(t’) ≤ V_x), and F_c[V_x=1,t’] = 1. For a stationary Poisson input with rate R, the probability of an input spike occurring in a short time interval from t to t+Δ can be represented as RΔ, and the membrane potential V(t+Δ) at time t+Δ could exceed 1 because of the incoming spikes (all the incoming EPSPs are assumed to be added at the end of the interval, t+Δ). Therefore, we can only express the unconditional cumulative probability function F[V_x, t+Δ] [defined as Prob(V(t+Δ) ≤ V_x) at time t+Δ] in terms of the conditional cumulative probability F_c[V_x, t] at time t based on the transition of the Markov process model (Stein, 1965) as:

$$F[V_x,t+\mathrm{\Delta }]=(1-R\mathrm{\Delta })F_c[V_x{e}^{\mathrm{\Delta }/\tau },t]+R\mathrm{\Delta }{F}_c[V_x{e}^{\mathrm{\Delta }/\tau }-A,t],$$ (5)

where A and τ are the amplitude and time constant of the input EPSP.

For a threshold voltage equal to 1, the probability that the model cell will have an output spike in the time interval from t to t+Δ is approximated by 1-F[V_x=1,t+Δ]. The conditional cumulative probability F_c[V_x,t’] at time t’ in the interval (t,t+Δ) can be approximated by the unconditional cumulative probability, F[V_x,t’] (approximated by F[V_x,t+Δ]) divided by the cumulative probability that the voltage remains below threshold, F[1,t’] (which is approximated by F[1, t+Δ]):

$$\begin{array}{l}{F}_c[{\text{V}}_{\text{x}},{\text{t}}^{\prime }]=F[{\text{V}}_{\text{x}},\text{t}+\mathrm{\Delta }]/F[1,t+\mathrm{\Delta }]\mathrm{\hspace{0.17em} }{\text{for all V}}_{\text{x}}>1,\text{ and}\\ F_c[{\text{V}}_{\text{x}},{\text{t}}^{\prime }]=1\mathrm{\hspace{0.17em} }{\text{for all V}}_{\text{x}}\ge 1.\end{array}$$ (6)

This allows the computation of F_c[V_x,t) for all t and all V_x, by computing a new value in each Δ interval. If there is a spike, V_x is reset to zero and the process is restarted. Thus, the output of the I&F model can be described as a renewal process (Cox, 1962) with a hazard function ρ(t), which is defined as the rate of a renewal (spike) event that occurs at time t and is determined by:

$$\rho (t)=(1-F[1,t])/\mathrm{\Delta }.$$ (7)

The ISI of the model output with stationary input can be specified by:

$${\text{f}}_{\text{ISI}}(\text{t})=S(\text{t})\rho (\text{t}),$$ (8)

where S(t) is the survival function of the renewal process, or the probability that there is no renewal (spike) event between 0 and t. S(t) can be written in terms of the hazard function as:

$$S(t)=e^{-{\int }_0^t\rho (x)dx}.$$ (9)

The above analysis can be easily extended to the situation where the input is a nonhomogeneous Poisson process described by R(t) with a previous output spike time at t_0. In this case, the phase-dependent first-passage time density to threshold is represented as f_ISI(t-t₀ | t₀), which can be easily derived from Eqs. 5–9 by resetting the membrane potential at time t₀. The survival and hazard functions can also be written as S(t-t₀ | t₀) and ρ(t-t₀ | t₀). In this form, for which the arguments of S(·), ρ(·), and f_ISI(·) are intervals, (t-t₀), the functions are phase (t₀) dependent. The calculation accuracy of the phase-dependent f_ISI(·) from the above equations is not affected by the frequency of the input oscillation or the mean ISI of the output spikes with respect to the length of the integration window. The unconditional firing probability P(t) (which is an estimate of the PST histogram) of the model output to the input R(t) can described as (Cox, 1962):

$$P(t)={\int }_{-\infty }^{t}P(x)f_{ISI}(t-x|x)dx,$$ (10)

where x represents the spike time before time t.

The calculation of P(t) from the above equation is not possible computationally because the duration over which the integral is computed is not limited.

We now assume that the cumulative conditional probability of the membrane potential F_c[V_x,t | t₀] (where t₀ is the previous spike time) is determined by the input spikes during the preceding time period (t-T, t), where T >> τ. This is a reasonable assumption since the potential contributed by spikes before t-T decays with a time constant τ and can be neglected compared to the potential contributed by recent spikes if T >> τ. For all previous spike times for which t₀<t-T, the cumulative probabilities of the membrane potential, F_c[V_x,t | t₀] and F[V_x,t | t₀], can be approximated as F_c[V_x,t | t-T] and F[V_x,t | t-T], and the hazard function ρ(t-t₀ | t₀) derived from Eq. 7 can be approximated by ρ(T | t-T). Since ρ(T | t-T) is independent of the previous spike time t₀, the unconditional firing probability P(t) can be calculated numerically (see appendix in Herrmann and Gerstner, 2001). Here P(t) can be rewritten as:

$$\begin{array}{l}P(t)={\int }_{-\infty }^{t}P(x)f_{ISI}(t-x|x)dx\\ ={\int }_{-\infty }^{t}P(x)S(t-x|x)\rho (t-x|x)dx\\ \approx {\int }_{-\infty }^{t-T}P(x)S(t-x|x)\rho (T|t-T)dx+{\int }_{t-T}^{t}P(x)S(t-x|x)\rho (t-x|x)dx\\ =\rho (T|t-T){\int }_{-\infty }^{t-T}P(x)S(t-x|x)dx+{\int }_{t-T}^{t}P(x)S(t-x|x)\rho (t-x|x)dx\end{array}$$ (11)

The integral on the second line was separated into two integrals on the third line, and for all spike times previous to x < t-T, ρ(t-x | x) was approximated by ρ(T | t-T), which was the hazard function at time t given a previous spike at t-T. The second integral in the final line of the above equation has a limited duration, and thus the numerical calculation based on Eqs. 7–10 is possible. The first integral in the final line of the above equation can be further simplified as:

$$\begin{array}{l}{P}_{residue}(t+\mathrm{\Delta })\triangleq {\int }_{-\infty }^{t+\mathrm{\Delta }-T}P(x)S(t+\mathrm{\Delta }-x|x)dx\\ \approx {\int }_{-\infty }^{t-T}P(x)S(t+\mathrm{\Delta }-x|x)dx+P(t-T)S(T|t-T)\mathrm{\Delta }\\ \approx {\int }_{-\infty }^{t-T}P(x)[S(t-x|x)+\mathrm{\Delta }\cdot dS(t-x|x)]dx+P(t-T)S(T|t-T)\mathrm{\Delta },\\ ={\int }_{-\infty }^{t-T}P(x)S(t-x|x)[1+\mathrm{\Delta }\cdot \frac{dS(t-x|x)}{S(t-x|x)}]dx+P[t-T]S(T|t-T)\mathrm{\Delta }\\ =(1-\rho (T|t-T)\mathrm{\Delta })P_{residue}(t)+P(t-T)S(T|t-T)\mathrm{\Delta }\end{array}$$ (12)

where the last step of the derivation is based on the relationship between the survival function S(t) and the hazard function ρ(t) (Cox, 1962):

$$\frac{dS(t)}{S}=\rho -(t).$$ (13)

The final line in Eq. 12 can be described by a differential equation and calculated numerically

$$d{P}_{residue}=-P_{residue}\rho (T|t-T)+P(t-T)S(T|t-T)dt.$$ (14)

Using the above relationships, P(t) can be calculated given R(t), and the mean ISI for a non-stationary input from time t₁ to t₂ can be represented by

$${\overline{f}}_{ISI}(t)=\frac{{\int }_{t1}^{t2}P(x)f_{ISI}(t|x)dx}{{\int }_{t1}^{t2}P(x)dx}$$ (15)

and calculated numerically. (This is not shown in detail because we are not interested here in the ISI for the non-stationary input.)

For a model receiving input EPSPs with two different amplitudes but the same time constant, the Markov process of the I&F model (Eq. 5) can be described as:

$$\begin{array}{l}F[V_x,t+\mathrm{\Delta }]=P_{00}{F}_c[V_x{e}^{\mathrm{\Delta }/\tau },t]+P_{10}{F}_c[V_x{e}^{\mathrm{\Delta }/\tau }-A_1,t]\\ +P_{01}{F}_c[V_x{e}^{\mathrm{\Delta }/\tau }-A_2,t]+P_{11}{F}_c[V_x{e}^{\mathrm{\Delta }/\tau }-A_1-A_2,t],\end{array}$$ (16)

where P₀₀, P₁₀, P₀₁, P₁₁ represent the joint probability of input spikes from two channels with different EPSP amplitudes (A₁ and A₂) in the interval from t to t+Δ. The derivation above can then be extended to calculate the PST and ISI histograms of the model response to arbitrary inputs with mixed-amplitude EPSPs. The same technique can be applied to allow multiple spikes to arrive in a time window Δ (such that a large Δ can be used to approximate the Poisson process), making this computation more efficient.

3. Results

3.1 Predictions for a model that receives stationary inputs

The steady-state response of an AN fiber to a CF tone at a high frequency is generally assumed to be a stationary point process (Siebert, 1965; Kiang et al., 1965). The response of a neuron receiving stationary inputs can be modeled successfully as a stationary renewal process fully characterized by the ISI interval of the mean, μ, and standard deviation, σ, of the process (Cox, 1962). The mean rate of the model output is defined as:

$$\text{Rate}=1/\text{mean interval}=1/\mu ,$$ (17)

and the quantitative measure of the response regularity is described by the coefficient of variation (CV):

$$CV=\alpha /\mu .$$ (18)

This regularity measure of the cell response is important since it may represent different underlying processing mechanisms, and it has been used as one of the criteria to classify different response types in the CN (Young et al., 1988; Blackburn and Sachs, 1989). A cell with a CV value close to 1 is considered irregular, and its response can be treated as a process essentially similar to the Poisson process (σ=μ). It is more realistic to model a cell with a dead-time-modified (τ_d) Poisson process, and the measure of CV for such a process is affected by the response firing rate R_out (1/R_out = μ = σ +τ_d, and CV = σ/μ = 1−R_outτ_d) (Rothman et al., 1993). To reflect the more fundamental nature of the underlying process, the modified coefficient of variation (CV ’) of the cell responses (Rothman et al., 1993) is used as a measure of the cell regularity:

$$C{V}^{\prime }=\sigma /(\mu -{\tau }_{\text{d}}).$$ (19)

The mean rate and CV ’ measurements of the I&F model responses to stationary inputs with various model parameters are shown in Figs. 2 and 3. The input to the I&F model was a stationary Poisson process, and the calculations were based on the equations described in Section 2.

Figure 2.

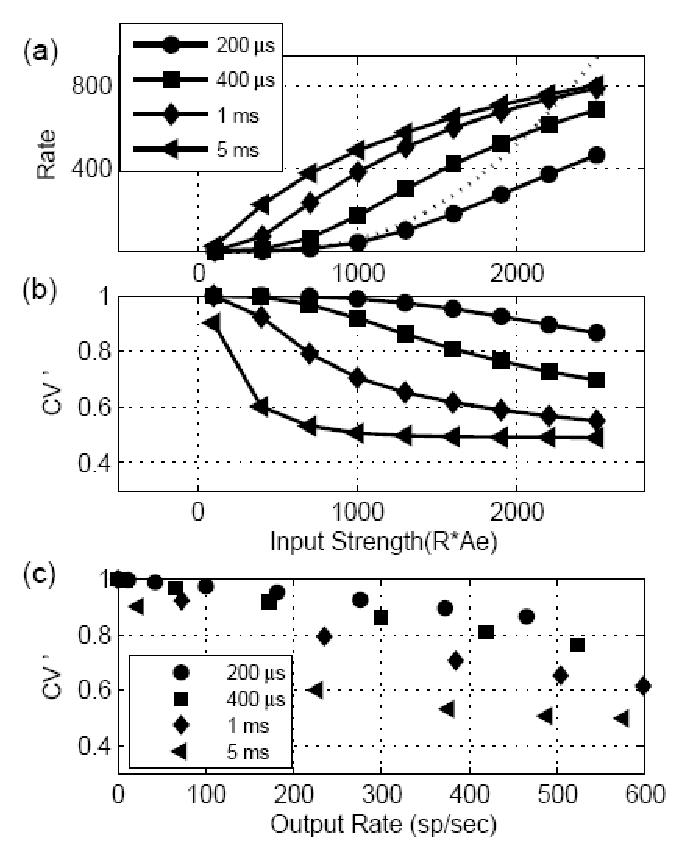
Responses for models with different EPSP time constants to stationary inputs. The EPSP amplitude was fixed at 1/3 for all models, and model threshold was equal to 1. The abscissa in (a) and (b) is input strength, which is defined as input rate multiplied by the EPSP amplitude. (a) Model response rate as a function of input strength. For high input strength, the output rate was limited by the dead time of the I&F model. For small input strength, the input-output rate function was determined by the EPSP time constant. The model rate responses initially changed linearly with input strength for large EPSP time constants and increased nonlinearly for small EPSP time constants. For reference, the function described in Eq. 20 is plotted (dotted curve) with k = 4, and w = 200 μs. (b) Regularity measure (CV ’) of model response as a function of input strength. The CV ’ generally dropped as the input strength increased, but remained high (> 0.65) for model cells with short time constants (up to 400 μs). (c) Regularity measure replotted as a function of model response rate. The increase in irregularity of the model response was caused by the EPSP time constant and not by the drop in the model response rate.

Figure 3.

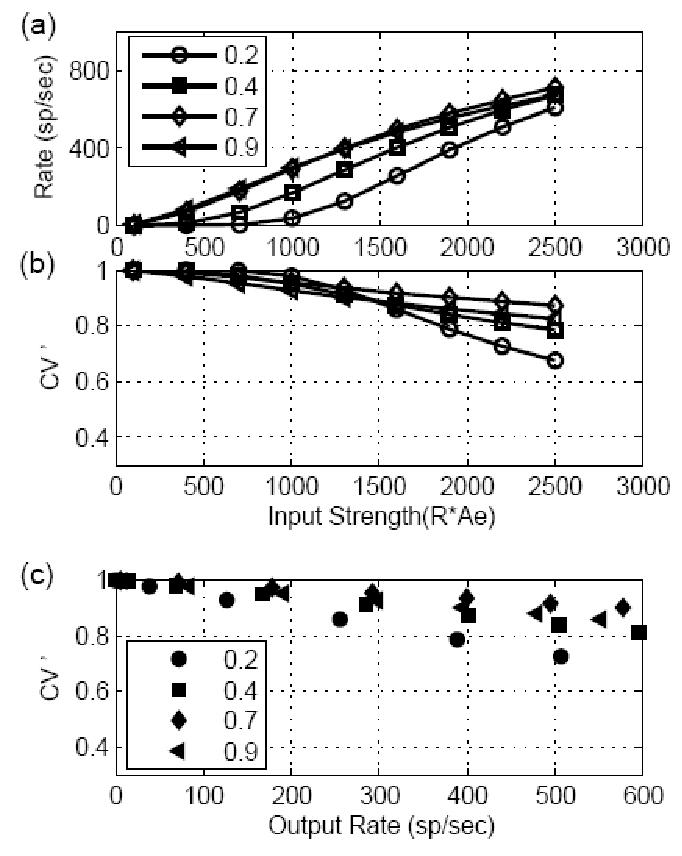
Responses of models receiving stationary inputs with different EPSP amplitudes and a fixed time constant (400 μs). Data are plotted in the same manner as in Fig. 2. (a) The input-output rate function was more linear for models with large EPSP amplitude and more nonlinear for models with small EPSP amplitude. (b) Regularity measure CV ’ of model responses. The change of model EPSP amplitude did not affect the CV ’ of the model responses; the CV ’ remained high, presumably because of the short EPSP time constant used in the computation. (c) CV ’ replotted as a function of model response rate. When model cells had same output rate, there was no clear monotonic relationship between CV ’ and the model EPSP amplitude.

Figure 2 illustrates the effect of the time constant (τ) of the EPSP (with a fixed amplitude of 1/3; threshold is equal to 1) on the model cell responses. The response rate of the model cell was plotted as a function of input strength (input discharge rate R multiplied by the EPSP amplitude) in Fig. 2(a). With a large time constant, the model output was more affected by the integration (energy) of the input EPSPs, and the model response rate changed more linearly with the input strength. When the time constant was short, the model cell’s response was dominated by the coincidence-detection mechanism, and the probability of discharge in an effective time window w was approximated by (Stein, 1965):

$$P_f=\frac{R^k{w}^{k-1}{e}^{-Rw}}{(k-1)!},$$ (20)

where k equals the number of input spikes that are required to arrive within the time window w (proportional to τ) to generate an output spike. The model response rate increased rapidly (and nonlinearly) as the input rate R increased.

The regularity measure (CV ’) of the model response is plotted in Fig. 2b as a function of input strength. The CV ’ of the model response decreased as the input rate increased for all time constants. However, model cells with short time constants (up to 400 μs) were still classified as irregular (CV ’ of the model response was higher than 0.65). When the time constant of the model cell was long, the model cell discharged more regularly (with small CV ’). This is because the probability of discharge of the model cell was greatly affected by the integration time constant of the membrane potential after the deadtime, because the mean and variance of the model potential increased slowly after the deadtime (see Eqs. 2 and 3). Figure 2c shows the regularity measure of the model cell response as a function of the model response rate. For a fixed output response rate, model cells with large time constants were more regular than cells with short time constants, showing that the decrease of the irregularity in Fig. 2b with increasing EPSP time constant for a fixed input rate was not caused by the increased response rate.

Model responses for input EPSPs with different amplitude are shown in Fig. 3. The time constant of the model EPSP was fixed at 400 μs, and the amplitude was always below the threshold of 1 (otherwise the model response process would have been the same as the input process, modified only by refractoriness). The model response rate as a function of input strength is plotted in Fig. 3a. Since the input strength is defined as EPSP amplitude multiplied by the input rate, the input rate for each model cell (with different amplitude EPSPs) differed at each abscissa value, but the total energy of the input was the same. The response rate of the model output increased as the input strength increased; however, model cells with small inputs required greater input strength to generate the same response rate. Weak inputs required a larger number (k) of input spikes in an effective time window w and the rate tended to change nonlinearly as the input strength increased, as expected from Eq. 20. The CV ’ of the model response (Fig. 3b) dropped as input strength increased but remained high for all model cells, regardless of EPSP amplitude. When the regularity measure is plotted as a function of the output response rate in Fig. 3c, it is clear that relationship between CV ’ and the strength of the synapse input (amplitude of the EPSP) is not simple. The CV ’ changed non-monotonically with increased amplitude of the model EPSPs. This result shows that the regularity of model cells that received subthreshold inputs was determined primarily by the time constant of the input EPSPs.

3.2 Predictions for the model that receives synchronized input

The most prominent feature of AN fiber responses to low-frequency tones is that the discharges phase-lock to the stimulus frequency up to about 4–5 kHz (Johnson, 1980). Enhanced phase-locking has been reported in VCN bushy cells (Joris et al., 1994a, b) and can be modeled as a consequence of converging subthreshold AN inputs (Joris et al., 1994a; Rothman et al., 2003a). The combined input from convergent AN discharges to the I&F model was represented by a single non-stationary (periodic) Poisson process, as described in association with Eq. 4. The PST of the model response to such an input is also periodic and can be calculated numerically based on the methods described in Section 2. The degree of phase-locking of the model response was quantified by the synchronization index (SI), which is defined as SI = B/A, where B is the fundamental frequency (stimulus frequency) component and A is the DC component of the Fourier series of the response PST histogram (Johnson, 1980).

The responses for I&F models with different time constants are plotted as a function of input synchronization index (SI) in Fig. 4. The model EPSP amplitude was fixed at 1/3 (threshold was equal to 1), and the combined input had a constant rate of 2400 spikes/sec. The input stimulus had a frequency of 500 Hz, and its SI was varied systematically. The model rate responses are illustrated in the top panel of Fig. 4. The model response with a short time constant changed dramatically when the input SI increased (i.e., when the input spikes were more synchronized). For a large time constant, the model response rate primary depended on the total energy of the input and did not change dramatically as the input SI changed. The SI measure of the output response is plotted in the bottom panel of Fig. 4; the dotted line is the result for which the output SI equals the input SI. The model responses with short time constants had more enhanced synchronization than did model responses with large time constants, and the SI measure was not affected by the model time constant when the inputs were highly synchronized.

Figure 4.

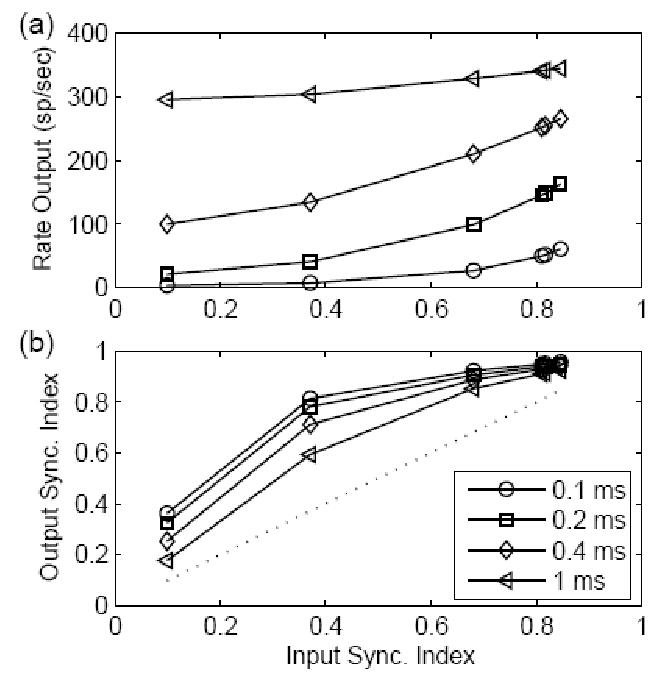
Responses for models with different EPSP time constants (see legend) and a fixed amplitude EPSP (1/3) to non-stationary inputs. The input waveform had a frequency of 500 Hz and a fixed average rate of 2400 spikes/sec (Eq. 4). The results were plotted as a function of input synchronization index (SI). (a) Rate responses for different models. For a small time constant (see legend), the model response rate increased dramatically when the input SI increased (a timing code was converted to a rate code in this situation). For a large time constant, the model response rate did not change much as the input SI changed. (b) The SI measure of the model output; the dotted line represents output SI equal to input SI. The model responses with short time constants had more enhanced synchronization than did model responses with large time constants, and the SI measure is nearly independent of model time constants when the inputs were highly synchronized.

Figure 5 is similar to Fig. 4 except that the stimulus frequency was 2000 Hz. With a high input frequency, the response rate of the model was similar to the result in Fig. 3, but the output SI measure was affected by the model time constant for both highly and weakly synchronized inputs. The response of the model with a large time constant (left triangle) had degraded synchronization as compared to the input SI measure (dotted line). The reduction of synchronization due to the large time constant was most effective at high frequencies. This may explain, in part, the physiological observation that the SI of CN cells in response to tones at CF is enhanced with respect to AN fibers at low frequencies but is lower than that of AN fibers t mid frequencies (Blackburn and Sachs, 1992; Joris et al., 1994a).

Figure 5.

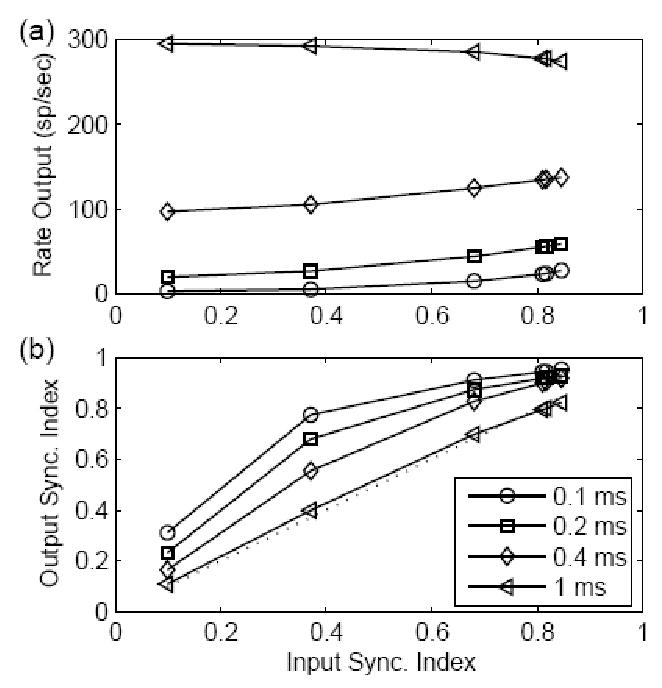
Similar plot to Fig. 4 except that the stimulus frequency was 2000 Hz. The output SI measure was greatly affected by the model time constant for both highly and weakly synchronized inputs.

The responses of a model with different EPSP amplitudes (with a fixed time constant of 400 μs) are plotted as a function of input SI in Fig. 6. The stimulus frequency was 500 Hz, and the input strength (EPSP amplitude multiplied by the mean input rate) was fixed at 800. With strong inputs (a large model EPSP amplitude), the model response rate (top panel) changed slowly as the input SI measure changed, and the synchronization enhancement (re: input SI, bottom panel) was also lowest for the model with the largest EPSP amplitude (model threshold was equal to 1). When the input had a high SI measure (usually true for low-frequency inputs), the amplitude of the inputs had a larger effect on the output SI measure than did the model time constant (see Figs. 4 and 6).

Figure 6.

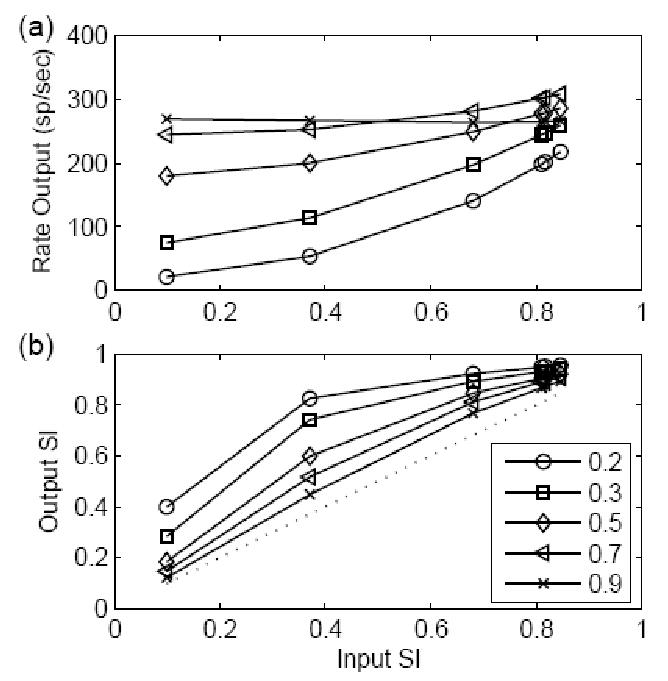
Responses of models with different EPSP amplitudes and a fixed EPSP time constant of 400 μs to non-stationary inputs. The results are plotted in the same way as Fig. 4. The stimulus had a frequency of 500 Hz with fixed input strength of 800. Since the input strength was defined as the EPSP amplitude multiplied by the input rate, the input rate doubled when the model amplitude was decreased by half. In this way, the energy of the model inputs was kept constant for different input SIs. (a) Model rate responses. (b) The SI measure of the model responses. The EPSP amplitude had a larger effect on the degradation of the output SI when the input SI was high as compared to the effects of time constant illustrated in Fig. 4.

The synchronization of actual AN inputs to CN cells changes systematically as a function of the stimulus frequency (Johnson, 1980). Model cell responses to inputs with realistic synchronization at each stimulus frequency are illustrated in Fig. 7. The input spike rate was fixed at 2400 spikes/sec, and each input spike generated a model EPSP with an amplitude of 1/3 and a time constant of 400 μs. The SI measure for each input frequency was plotted in the bottom panel (circles) of the figure and fitted to AN fiber data (Johnson 1980; Rothman and Manis, 2003a). Model response rate (top panel) changed non-monotonically as the input frequency increased. At low frequencies, the dead time (absolute refractoriness) of the model prevented multiple discharges in each cycle, and the rate increased as stimulus frequency increased, since the model cell fired once in each stimulus cycle. The model response rate dropped with increasing stimulus frequency, because the inputs were less synchronized. The SI measure of the model output (diamonds in the bottom panel of Fig. 7) was higher than the input SI across all stimulus frequencies. If we assume that a time jitter of 70 μs (Kopp-Scheinpflug et al., 2002, p. 11006) was added to each output spike (we assumed the time jitter¹ had a normal distribution with standard deviation 70 μs; the calculation was based on the convolution of the output PST and this normal distribution), the SI measure of the model output was more comparable to the observation that some CN cell types have enhanced synchronization in response to low frequencies and reduced synchronization, as compared to their AN inputs, in response to higher frequencies (e.g., see Joris et al., 1994a).

Figure 7.

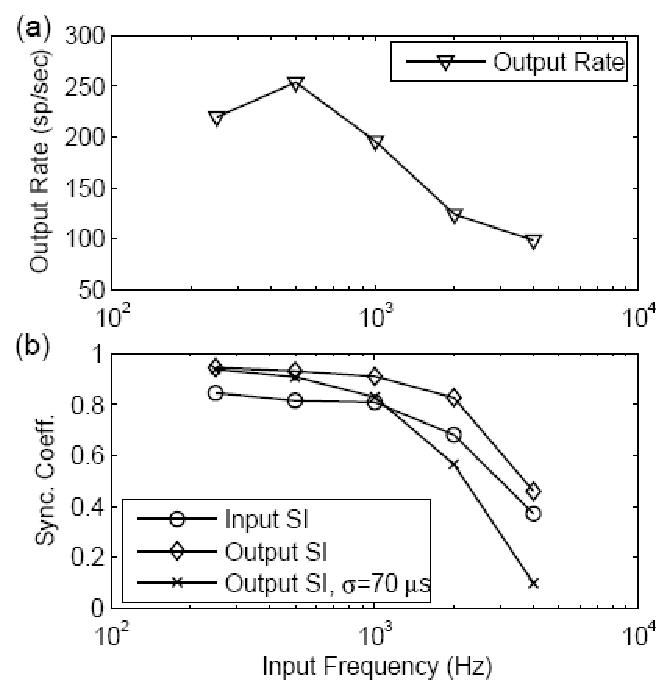
Responses as a function of stimulus frequency for a model with EPSP amplitude of 1/3 and a time constant of 400 μs. The input spike rate was fixed at 2400 spikes/sec, and the input SI varied with frequency systematically to fit the AN fiber data (Johnson 1980; Rothman and Manis, 2003a, plotted as circles in the bottom panel). (a) Model response rate changed non-monotonically as input frequency increased. (b) SI of the model output with and without time jitter added (crosses and diamonds, respectively). The time jitter had a normal distribution with a standard deviation of 70 μs; the calculation was based on the convolution of the output PST and this normal distribution.

3.3 Effects of mixed-amplitude inputs on model responses

As illustrated in the above results, the model cell response to stationary inputs required a short time constant to maintain appropriate irregularity and required strong inputs for a linear input-output rate function (e.g., to explain high-CF PL responses to CF tones). However, the model cell response to non-stationary inputs required a large number of weak inputs to create enhanced synchronization, and required a large time constant to be more responsive to both synchronized and nonsynchronized inputs without showing a reduction of the enhancement of the synchronization at low frequencies (when the input SI measure was high; see Fig. 4). We hypothesized that cells with mixed-amplitude inputs would respond to high-frequency stimuli (i.e. stationary inputs) irregularly and also show enhanced phase-locking to low-frequency stimuli (i.e., non-stationary inputs). This combination of responses is required to explain the behavior of high-frequency PL and PLn cells in the VCN.

The responses of models with mixed-amplitude EPSP parameters to stationary inputs across different input strengths are plotted in Fig. 8. The time constant of the models was fixed at 400 μs, and the other parameters for each model (plotted in different symbols) are described in the figure legend. For the model with mixed-amplitude inputs, the amplitudes of the weak and strong inputs were fixed at 1/6 and 7/10, respectively (threshold was equal to 1), and the rate for both strong and weak inputs changed with the input strength. The responses of models for both mixed-amplitude inputs and single-amplitude inputs had high values of regularity (bottom panel of the plot), consistent with the finding that the CV depends primarily on the time constant of the model (see Fig. 2). For the models with similar output rates, the model with mixed-amplitude inputs tended to respond more linearly to the change of the input strength (top panel). Increasing the EPSP amplitude for the model with the same inputs made the model respond more linearly, but this manipulation reduced the enhancement of phase-locking in response to low-frequency stimuli.

Figure 8.

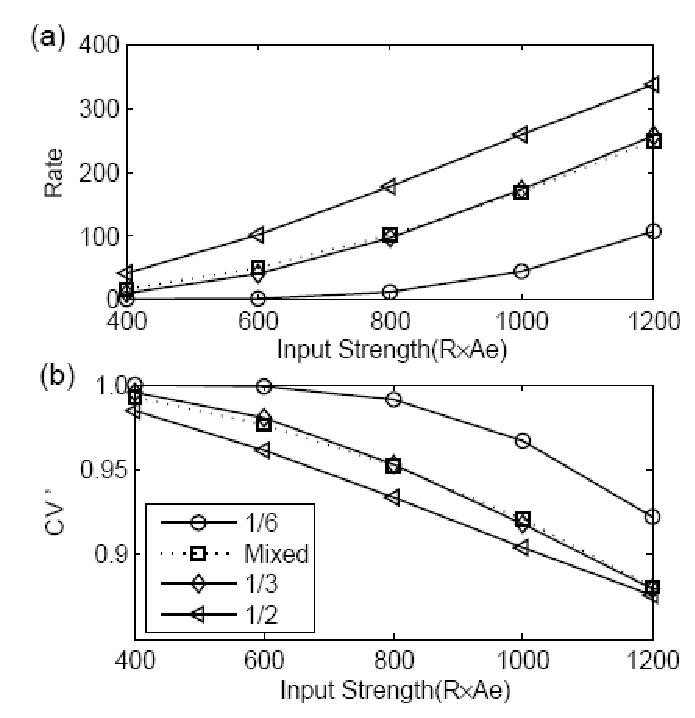
The responses for models with different synaptic configurations to stationary inputs. All model EPSPs had a fixed time constant of 400 μs. The results for models with same-amplitude inputs were plotted with a solid line and different symbols (see legend for EPSP amplitude). The model with mixed-amplitude inputs (dotted line with squares) had EPSPs with amplitudes of 1/6 and 7/10, and the ratio of weak input rate to strong input rate was fixed at 28.8:1 (results were plotted against the weak input strength for this model). (a) Model response rate. Compared to the same-amplitude input model with similar responses, the model with mixed-amplitude inputs had a higher response rate with small inputs and a lower response rate with large inputs. (b) CV ’ measure of the model responses. All model responses had CV ’ measures that would be classified as irregular cells, presumably because of the short EPSP time constant used.

Figure 9 shows the effects of model parameters on responses to synchronized inputs. The models with same-amplitude inputs had a constant input strength of 1200. For models with mixed-amplitude inputs, the input strength was 1200 for weak inputs with an amplitude of 1/6, and the strength was 1600 for weak inputs with an amplitude of 1/12. The rate of strong inputs for the mixed-amplitude model was fixed at 250 spikes/second; the strong input amplitude was 7/10. Other parameters for the model and stimulus are described in the legend. The rate responses (top panel) for all models changed non-monotonically as a function of stimulus frequency. For the mixed-amplitude model, the response rate (plotted with asterisks and downward triangles) to the low-frequency inputs depended on the synchronized weak inputs; as stimulus frequency increased, the inputs were less synchronized and the model response was more dependent on the strong inputs. The SI measure of the model responses with mixed-amplitude inputs dropped more quickly with increasing stimulus frequency than did that of the models with same-amplitude inputs. At low frequencies, the SI measure of the model response stayed high because the output was dominated by the discharges generated by the weak inputs. At high frequencies, the model response was determined by the strong input, and thus the synchronization of the input was not enhanced. In general, the cell with mixed-amplitude inputs had a more linear input-output rate function in response to high-frequency tones than did model cells with same-amplitude inputs, and the SI degraded more rapidly as stimulus frequency increased². Both properties are desirable to explain the physiological responses of the globular bushy cells in the CN.

Figure 9.

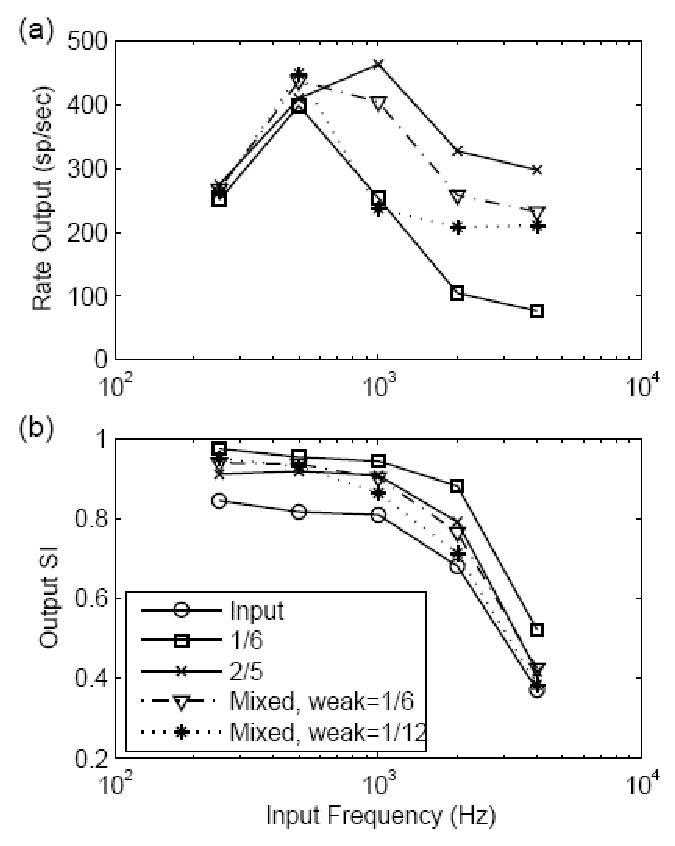
Responses for models with different synaptic configurations to non-stationary inputs. The results are plotted in the same way as in Fig. 7. The solid lines (see legend for model EPSP amplitude) represent the results for same-amplitude input models. The results for mixed-amplitude input models are plotted with a dotted line (stars) and a dot-dashed line (downward triangles). All model EPSP time constants were fixed at 400 μs. The input strength was fixed at 1200 for the same-amplitude input models and was 1200 and 1600 for the mixed-amplitude input models with weak amplitudes of 1/6 and 1/12, respectively. The strong inputs for both mixed-amplitude input models had a rate of 250 spikes/sec and each input EPSP had an amplitude of 7/10. (a) Model rate responses. (b) SI measure of the model responses. The SI measure of the stimulus input (fitted to AN fiber data) was plotted with circles. The SI measure for mixed-amplitude input models stays high in response to low frequencies and drops more quickly than that of the same-amplitude input model as the input frequency increased.

4. Discussion

4.1 Calculation of the PSTs and ISIs of I&F models with non-stationary inputs

Statistical analysis of neural activity, together with stochastic neuron models, have proven to be very useful tools for estimating neuronal physiological and anatomical parameters and elucidating the different functions of various neurons (Tuckwell, 1988). In addition to the discrete Markov process discussed here, other stochastic neuron models have been proposed, including the Ornstein-Uhlenbeck Process (OUP) approximating diffusions, and partial differential equations modeling the spatial extent of neurons (especially for dendrites) (Tuckwell 1989, Chapter 5). However, little progress has been made to provide a satisfactory analytical solution for the first passage time problem for these models, and researchers have generally either analyzed their models with limited ranges of parameters (e.g., Kempter et al., 1998) or resorted to Monte Carlo simulations. The numerical method proposed in this study provides a way to calculate the statistics of the neuron model with more accuracy and efficiency than using Monte Carlo simulations, without the compromise of using only stationary inputs or limiting the model’s parameter space. Because Eqs. 11–14 depend only on the assumptions that the neuron can be modeled as a renewal process and that only recent input discharges determine the response, the method can be generalized in different ways as long as the conditional first passage time can be calculated numerically:

1. Relative refractoriness can be incorporated by changing the firing threshold as a function of time (assuming the previous discharge time occurs at time zero);

2. Inhibitory effects may be incorporated based on Eq. 16, in which the amplitude of inhibitory EPSPs is negative and arriving inhibitory discharges decrease the model potential;

3. The assumption that the membrane potential decays exponentially simplifies our analysis by allowing the EPSPs of incoming spikes to be combined, without having to keep track of the history of input spike times. It is possible to extend the model in more biologically realistic situations, where integrative properties of neurons are altered by synaptic conductances. For example, potentials contributed by recently incoming discharges could be implemented using voltage-dependent EPSPs, where potentials contributed by earlier discharges could be included in the exponential decay tail. Such an extension would be particularly useful in situations with small numbers of inputs, in which other analyses are limited (Burkitt 2001; Richardson, 2004);

4. Noise that is intrinsic to the neuron can be introduced as a diffusion of the potential distribution at each step of the calculation.

4.2 Regularity of the model cell response to stationary inputs; Effects of time constant, synapse amplitude, and refractoriness

Regularity analysis of the model responses suggested that a small value for the EPSP time constant was important to prevent the cell from regular firing, and this prediction agrees with findings in physiological studies (Blackburn and Sachs, 1989; Young et al., 1988). The EPSP inputs to a bushy cell have a very short time constant since the somatic synapse bypasses any dendritic filtering and the low-threshold potassium channels reduce the effective membrane time constant (Rothman and Manis, 2003a). All three response types associated with bushy cells (PL, PLn, and On-L) demonstrate irregular discharge patterns (Rothman et al., 1993), regardless of possible differences in their input synapse strengths. In contrast, the chopper response type, which usually has a regular response pattern, is believed to be related to stellate cells in VCN which have large dendritic trees contacted by AN fibers (Young et al., 1988) and long duration EPSPs (Oertel, 1983). Regularity is also affected by the relative refractoriness of the cell responses (which is not corrected for in the calculation of CV ’), especially when the mean ISI interval is comparable to the duration of refractoriness. Our simulations for model AN responses showed that the CV ’ of a Poisson process modified by relative refractoriness decreased dramatically as model response rate increased (not shown). This result is consistent with the simulations reported by Rothman et al. (Fig. 9A in Rothman et al., 1993) using a channel-based (Hodgkin-Huxley-like) model. Their model responses had the lowest regularity measure when the input EPSP was just above the absolute threshold, where the refractoriness effect was strongest. Response regularity was higher for models with just subthreshold inputs, since the combination of two required inputs was much higher than the absolute threshold. Rothman et al. (1993) argued that a secure input, which generates an EPSP much higher than threshold, is necessary to maintain response irregularity for PLn cells, because the strong input decreases the relative refractory period. They also argued that the regular response of the model onset cell, which may not be physiological realistic, could be improved with inclusion of inhibition. Yet it is possible, as illustrated in their later study (Rothman and Young, 1996), that an inhibitory mechanism can also be used to increase the irregularity of the PLn model cell responses without the requirement of a strong suprathreshold input. Other mechanisms may also reduce the effect of refractoriness (Rothman and Manis, 2003a) and thus increase the irregularity of the model cell responses.

4.3 Effect of EPSP amplitude on the input-output rate function

The input-output rate function of the model response was strongly affected by the amplitude of the model EPSPs. The input rate and amplitude had different effects on the statistics of the model potential distribution. While increasing both the input rate and EPSP amplitude increased the expected value (mean) of the membrane potential, the variance of the potential was proportional to the square of the EPSP amplitude but had a linear relationship with the input rate. With the same input strength (EPSP amplitude multiplied by the input rate), the potential of the model with larger EPSP amplitudes had larger variance, and the model cell response depended more on the fluctuations of the potential. The input-output rate function of the model cell tended to be exponential when the relative potential variance was small and to be linear when there were large potential fluctuations (Tuckwell and Richter, 1978).

This prediction has important implications for the synapse conditions of bushy cells. The input discharge rate to bushy cells changes dramatically during tone bursts, as a result of onset adaptation in high-spontaneous-rate AN fibers. The fact that bushy cells with PL or PLn response types have response rates during tone bursts that are similar to those of the input AN fibers suggests that they receive at least one large input. Further, the On-L response type bushy cells that have a nonlinear input-output rate function may receive many small inputs. These predictions agree with the morphological correlates of the different cell types in the CN (see review by Cant, 1992). The PL responses are usually observed in SBCs, which have one or a few large synapses known as endbulbs of Held. The PLn and On-L response type units are more closely related to the GBC, which receives smaller modified endbulbs (as compared to the larger endbulb of Held) that are varied in number and size.

The model of linear summation of mixed-amplitude EPSPs may also be interpreted as an approximation of a model with nonlinear summation. The arrival of a large EPSP at the cell changes the membrane properties and thus would influence the contributions from subsequent inputs. Of course, it would be interesting to determine in future work whether a nonlinear model with more realistic voltage-dependent mechanisms shows the properties predicted by a mixed-input model with linear summation.

4.4 Enhanced phase locking and its relation to EPSP amplitude and time constant

Increasing the EPSP amplitude increased the potential fluctuation and degraded-phase locking of the model response. With a large number of small inputs, the membrane potential usually followed the expected value of the potential with a small variance, and the model potential could be treated as deterministic. The model cell fired very precisely around the time that the expected value of the potential crossed the threshold. This conclusion may also apply to the channel-based model, in which all the EPSPs are linearly summed. Of course, the small variance in the potential may be disturbed by other nonlinear properties, such as refractoriness. Realistically, for large inputs that generate EPSPs just above threshold, the timing of the action potentials was affected by the amplitude of the EPSPs (Rothman et al., 1993), and this relationship degraded the phase-locking of the model cell to the synchronized inputs (especially to the mid-frequency inputs; see Rothman et al., 1993). Small inputs, in fact, helped increase the precise timing of action potentials, since action potentials generated early in the periodic cycle, when there was a low rate of small inputs, had a large delay, and action potentials generated later had a small delay. This was illustrated in our study of mixed-amplitude inputs when the strong input amplitude was near, but still below, threshold.

Enhanced phase-locking was not greatly affected by the EPSP time constant as long as the EPSP time constant was short (e.g., by about a factor of 4) as compared to the cycle of the stimulus frequency. Of course, the time constant is still much smaller than observed in other neurons that are not specialized for temporal coding. The short time constant of the membrane conductance has other effects on the precise timing of the neuron’s response, such as refractoriness.

It is interesting to consider the effect of spatiotemporal summation resulting from adjacent auditory-nerve fiber inputs. Instead of expressing the spatial spread of inputs explicitly (Huhlmann et al., 2002), the spatial spread of inputs can be modeled as a decrease of synchronization in the combined input (see Figs. 4 and 5). The EPSP time constant was more important for enhancement of phase-locking when the inputs were effectively spatially separated (i.e. for small synchronization index in Figs. 4 and 5).

4.5 Implications of mixed-amplitude inputs for the bushy cell model

Results from this study show that model cells that receive mixed-amplitude inputs demonstrated response properties that have been observed in some cells in the CN. The neurons encode or enhance the temporal information at low frequencies and also carry rate information at high frequencies. These properties made the model neurons more efficient in processing information in different conditions. The inputs to high-CF cells in the CN in response to complex sounds usually have temporal (envelope) fluctuations due to narrowband peripheral filtering. A cell that receives mixed-amplitude inputs can benefit from both spectral and temporal cues. The different number and size of the endbulbs may contribute to the different synapse configurations for bushy cells, and the dendrites that branch profusely within several hundred microns of the cell body (Rhode and Greenberg, 1992) could also provide weak inputs to enhance timing information in response to complex sounds.

4.6 Potential effects of inhibition on model responses

Inhibitory inputs to bushy cells have been shown to exist in physiological studies (; Wu and Oertel, 1986). The function of inhibitory inputs on model response statistics can be interpreted in several ways. First, inhibitory inputs will have different effects on the mean and variance of the model potential if the inhibitory postsynaptic potential (IPSP) is integrated linearly in the I&F model. The mean of the potential will decrease as the inhibitory input rate increases, while the variance of the membrane potential will be equal to the sum of the potential variances contributed by excitatory and inhibitory inputs. The model cell responses will depend primarily on the variance of the potential distribution (that is, the fluctuation of the voltage) when the inhibitory and excitory inputs are balanced. This situation is similar to what occurs when the amplitude of individual EPSPs increases; thus, including inhibition may make the cell’s response rate vary more linearly with the input rate. Second, inhibition will have different effects on the peaks and valleys of a non-stationary input. IPSPs usually have a larger time constant; therefore, the integral of the IPSPs in response to non-stationary inputs will not fluctuate as much as the integral of the EPSPs. As a result, the model cell will tend to respond more at the peak of the synchronized inputs, and the inhibition will contribute to enhanced phase-locking. Finally, inhibition in bushy cells will have several nonlinear effects on the membrane properties. Inhibition will effectively make the membrane time constant faster by adding membrane conductance, and it will also decrease the effective amplitude of EPSPs, thus reducing the amplitude of a secure synapse to an amplitude that is just above or even below the threshold.

In summary, while the membrane properties of a neuron define the cell’s capacity to process the information carried in the input spikes, the synaptic configuration of the cell’s inputs determines how the information is actually processed in response to various stimuli. For example, a cell that has synapses that generate mixed-amplitude EPSPs has a linear input-output rate function when the inputs are stationary and enhanced synchronization of its output to the stimulus when the inputs are non-stationary. In this manner, the nervous system may achieve numerous signal-processing functions that are advantageous for specific stimuli.

NOTES

1. The time jitter applied here may be caused by the dynamics of spike generation, refractoriness, or degraded timing due to the strong inputs. (The effective coincidence window for strong inputs is larger than that for weak inputs.)

2. Previously, we assumed a constant time jitter to degrade the SI at high frequency. If the SI in response to high frequencies is already degraded, a smaller time jitter is required, which thus maintains the timing information at low frequencies.

3. Caspary et al.'s (1994) study showed that inhibition has the same receptive field as excitation and that the role of inhibition is generally not lateral inhibition, which is often described as a mechanism for sharpening the receptive field. This on-frequency inhibition can be interpreted as a modulation filter that extracts the envelope fluctuation in the inputs (Nelson and Carney, 2004). As discussed here, inhibition could also contribute to the enhanced timing of the cell responses in CN.