Effect of Errors in the System Matrix on MAP Image Reconstruction

Abstract

Statistically based iterative image reconstruction methods have been developed for emission tomography. One important component in iterative image reconstruction is the system matrix, which defines the mapping from the image space to the data space. Several groups have demonstrated that an accurate system matrix can improve image quality in both SPECT and PET. While iterative methods are amenable to arbitrary and complicated system models, the true system response is never known exactly. In practice, one also has to sacrifice the accuracy of the system model because of limited computing and imaging resources. This paper analyzes the effect of errors in the system matrix on iterative image reconstruction methods that are based on the maximum a posteriori principle. We derived an analytical expression for calculating artifacts in a reconstructed image that are caused by errors in the system matrix using the first-order Taylor series approximation. The theoretical expression is used to determine the required minimum accuracy of the system matrix in emission tomography. Computer simulations show that the theoretical results work reasonably well in low-noise situations.

1. Introduction

Statistically based iterative image reconstruction methods have been developed for emission tomography to improve image quality [Fessler, 1994, Mumcuoglu et al, 1994, Fessler and Hero, 1995, Bouman and Sauer, 1996]. Compared to analytic approaches, which generally require an idealized system model and do not account for nonuniform noise in the data, iterative methods are amendable to an arbitrary, complicated, and realistic system model that defines the mapping from source to detectors. Furthermore, iterative methods allow for proper modeling of the statistical properties of the acquired data and result in better tradeoffs of resolution verses noise. In the past decade, tremendous effort has been devoted to developing accurate system models for image reconstruction, e.g., [Bai et al, 2002, Bai et al, 2000, Beekman et al, 1997, Formiconi et al, 1989, Frey and Tsui, 1990, Gilland et al, 1994, Jaszczak et al, 1984, King et al, 1995, King et al, 1996a, Laurette et al, 2000, Meikle et al, 1994, Metz et al, 1980, Qi et al, 1998, Tsui et al, 1994a, Tsui et al, 1998, Welch and Gullberg, 1998, Wells et al, 1997]. In positron emission tomography (PET) the line integral model had been considered to be reasonably accurate. Even so, resolution is affected by the combined effects of positron range, noncolinearity of the photon pair, variations in detector-pair sensitivity along the line of response (LOR), and the spatially variant response of the detector caused by intercrystal penetration and scatter. The resolution in filtered backprojection degrades significantly as the target is moved from the center of the scanner to radially off-center locations. By modeling these effects in an iterative reconstruction framework, one can obtain high-resolution images [Veklerov et al, 1988, Mumcuoglu et al, 1996]. In single photon emission computed tomography (SPECT), line-integrals are a far less accurate model. The collimators produce pronounced depth dependence in resolution that is not included in the line integral model. The single photon detection process results in attenuation that can differ between each voxel and each detector element. Iterative methods can explicitly model these effects in the system matrix. It is been shown, for example, that correct modeling of collimator response can reduce partial volume effect and reduce bias in kinetic parameter estimation [Kadrmas et al, 1999], and that accurate attenuation and scatter correction improves the quantitation in cardiac scans [King et al, 1996b, Tsui et al, 1994b] and the signal to noise ratio of cold lesions [Beekman et al, 1997, Hutton et al, 1996, Hutton, 1997]. Clinical studies also show improved sensitivity and specificity in the diagnosis and evaluation of coronary artery disease [Ficaro et al, 1996, Ficaro and Corbett, 2004].

One approach in implementing iterative algorithms is to precompute and store the system matrix. If the system matrix needs to be computed only once as is often the case in PET, computation time is not an issue. The system matrix can be computed using analytic calculations [Huesman et al, 2000] or Monte Carlo simulations [Floyd and Jaszczak, 1985, Veklerov et al, 1988], or it can be measured directly [Formiconi et al, 1989]. However, one challenge is the huge size of system matrices for fully 3D imaging systems. Even storing only the non-zero elements can be a daunting task. Researchers have exploited sparse matrix structures and used various approximations to make this approach practical [Johnson et al, 1995, Floyd and Jaszczak, 1985, Qi et al, 1998].

To avoid the precomputation and storage of a huge projection matrix, on-the-fly calculations are used. The simplest one uses a ray-tracing technique that is essentially the same as the line integral model. A more sophisticated approach is to trace multiple rays for each LOR in order to model the geometric response [Huesman et al, 2000, Laurette et al, 2000]. To include other physical effects in the forward model, Monte Carlo simulations can be used to perform forward and back projection [Kudrolli et al, 2002, Beekman et al, 2002]. Monte Carlo software packages with very accurate physical models of PET and SPECT systems are available. However, computation time is still high if every detail in the photon detection process is modeled, and one must trade off between computation time and model accuracy.

Regardless of the approach, errors are inevitable in the system matrix. When data noise and modeling error both follow a white Gaussian distribution, a well-known solution to this problem is the total least squares (TLS) method [Golub and Van Loan, 1996], which minimizes the combined error in both the system matrix and data measurements. It has been studied for image restoration [Mesarovic et al, 1995a, Mesarovic et al, 1995b, Mesarovic et al, 2000] and image reconstruction [Zhu et al, 1997, Brankov et al, 1999, Zhu et al, 1998, Zhu et al, 1999]. However, due to the high computational cost of TLS methods, most of the work has focused on spatially invariant linear inverse problems, although methods have also been proposed for nonconvolutional linear inverse problems [Zhu et al, 1997, Zhu et al, 1999]. When noise is not white Gaussian, such as in emission tomography, TLS methods are not directly applicable. Because of these limitations of TLS methods, the majority of the image reconstruction methods still assume that the system matrix is exact. Thus, it is important to understand the effect of modeling errors on these reconstruction methods.

In this paper, we study the error propagation from the system matrix into reconstructed images in MAP reconstruction. Unlike the existing work that often focuses on a specific type of modeling error, such as geometric response, attenuation, or scatter, we derive a general theoretical formula that is not limited to a single type of modeling error. We use the result to determine the minimum required accuracy for the system matrix, such that the effect of the modeling error is small compared to the intrinsic noise in the data. An earlier work on quantitative analysis of effects of the modeling errors can be found in [Tekalp and Sezan, 1990], but it is limited to linear space-invariant image restoration with stationary noise. Here we focus on nonconvolutional imaging systems and nonstationary noise models. We analyze iterative reconstruction at convergence using the fixed-point condition [Fessler, 1996]. Thus, the result is independent of the particular optimization algorithm, as long as the algorithm is iterated to effective convergence.

2. Theory

2.1. Approximations

For a given imaging system with measured data y ∈ ℝ^M×1, the maximum a posteriori (MAP) reconstruction $\widehat{\mathit{x}}\in {ℝ}^{N\times 1}$ is found by maximizing the log-posterior density function:

$$\widehat{\mathit{x}}=\underset{\mathit{x}\ge 0}{\text{arg max}}[L(\mathit{y};\mathit{x})-\beta U(\mathit{x})],$$ (1)

where L(y; x) is the log-likelihood function, U(x) is energy function of a Gibbs prior, which can be written as

$$p(\mathit{x})=\frac{1}{Z}{e}^{-\beta U(\mathit{x})},$$ (2)

where β is the hyperparameter that controls the resolution of the reconstructed image, and Z is a normalization constant.

We focus our attention on the reconstruction problems in which the expectation of the data, $\overline{\mathit{y}}$, can be related to the unknown image x by the following equation

$${\overline{y}}_i=f({[\mathit{Px}]}_i)+r_i.$$ (3)

where f(·) is a one-to-one function, P ∈ ℝ^M×N is the system matrix that defines the mapping from the image space to the data space, [Px]_i denotes the ith element of Px, and r_i accounts for the mean of background events in the ith measurement.

For example, in emission tomography the (i, j)th element of P contains the probability of detecting an event emitted from the jth image element at the ith sinogram bin, f(z) = z, and the log-likelihood function is

$$L(\mathit{y};\mathit{x})=\sum _i(y_i\mathrm{\hspace{0.17em} }\text{log\hspace{0.17em}}{\overline{y}}_i-{\overline{y}}_i-\text{log\hspace{0.28em}}{y}_i!).$$ (4)

Equation (3) assumes a discrete-to-discrete (DD) imaging model [Barrett and Myers, 2003], where the unknown image is represented by a linear combination of a set of basis functions (image elements) with x containing the corresponding coefficients. The most commonly used basis functions in image reconstruction are pixels in two dimensions and voxels in three dimensions, although other basis functions, such as blobs [Matej and Lewitt, 1996], and natural pixels [Buonocore et al, 1981], have also been proposed. The analysis here is not restricted to any particular form of basis function. The DD model in (3) is not even required to have zero image error (see Ch. 7.4.3 in [Barrett and Myers, 2003] for a discussion on image errors), because we focus on analyzing how changes in the system matrix P affect the estimate of the finite dimension coefficient x. The representation error of a continuous object by the basis functions is beyond the scope of this paper.

To simplify the notation in the following derivation, we first assume that the log-likelihood function L(y; x) can be decomposed as follows

$$L(\mathit{y};\mathit{x})=\sum _i{h}_i({[\mathit{Px}]}_i).$$ (5)

Such decomposition is always possible when measured data contain independent noise, but independence is not a necessary requirement. For the Poisson log-likelihood function in (4), we have

$$h_i(z)=y_i\mathrm{\hspace{0.17em} }\text{log}[f(z)+r_i]-f(z)-r_i-log{y}_i!$$

We shall show later that the above requirement in (5) can be relaxed.

The necessary condition for $\widehat{x}$ to be the solution of (1) is the Kuhn-Tucker condition [Luenberger, 1984]:

$$\begin{array}{l}\sum _i{P}_{ij}{\dot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)-\beta \frac{\partial }{\partial x_j}U(\widehat{\mathit{x}})\{\begin{array}{c}=0,{\widehat{x}}_j>0\\ \le 0,{\widehat{x}}_j=0\end{array}\\ j=1,\dots ,N,\end{array}$$ (6)

where ${\dot{h}}_i(z)\equiv d{h}_i(z)/dz$.

For a given data vector y, equation (6) implicitly defines the relationship between the system matrix P and the corresponding MAP reconstruction $\widehat{\mathit{x}}$. Let us denote the “true” system matrix^‡ by $\overline{\mathit{P}}=\mathit{P}-\mathrm{\Delta }\mathit{P}$. The reconstructed image with the “true” system matrix, ${\widehat{\mathit{x}}}^{*}$, satisfies

$$\begin{array}{l}\sum _i{\overline{P}}_{ij}{\dot{h}}_i({[\overline{\mathit{P}}{\widehat{\mathit{x}}}^{*}]}_i)-\beta \frac{\partial }{\partial x_j}U({\widehat{\mathit{x}}}^{*})\{\begin{array}{c}=0,{\widehat{x}}_j^{*}>0\\ \le 0,{\widehat{x}}_j^{*}=0.\end{array}\\ j=1,\dots ,N,\end{array}$$ (7)

Considering $\widehat{\mathit{x}}$ as a function of P, when ΔP is small, we can use the first-order Taylor series approximation to calculate the error propagation, i.e.,

$$\mathrm{\Delta }{x}_j\equiv {\widehat{x}}_j-{\widehat{x}}_j^{*}\approx \sum _{m,n}\frac{\partial {\widehat{x}}_j(\mathit{P})}{\partial P_{mn}}\mathrm{\Delta }{P}_{mn},$$ (8)

where $\partial {\widehat{x}}_j(\mathit{P})/\partial P_{mn}$ denotes the partial derivative of ${\widehat{x}}_j$ with respect to P_mn evaluated at P. Here the Taylor series is expanded at the noisy system matrix P. However, the expansion can also be taken at the “true” system matrix $\overline{\mathit{P}}$, because the first-order Taylor series approximation essentially assumes that the first derivatives are constant.

To proceed, we assume that the zero regions in $\widehat{\mathit{x}}$ and ${\widehat{\mathit{x}}}^{*}$ are the same, so $\partial {\widehat{x}}_j(\mathit{P})/\partial P_{mn}=0\mathrm{\hspace{0.17em} }\text{for\hspace{0.28em}}j:{\widehat{\mathit{x}}}_j=0$. Thus, we can exclude zero regions from the following analysis by removing the columns in P that correspond to the zero image elements and reducing the number of unknowns in x. Without loss of generality, we shall assume that ${\widehat{x}}_j>0$ for all j = 1, …, N in the rest of the derivation.

To find the expression of $\partial {\widehat{x}}_j(\mathit{P})/\partial P_{mn}$ for the nonzero image elements, we differentiate equation in (6) with respect to P_mn by applying the chain rule [Fessler, 1996] and get

$$\begin{array}{l}0=\sum _i\frac{\partial P_{ij}}{\partial P_{mn}}{\dot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)+\sum _i{P}_{ij}{\ddot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)\left[\frac{\partial {[\mathit{P}\widehat{\mathit{x}}]}_i}{\partial P_{mn}}+\sum _k\frac{\partial {[\mathit{P}\widehat{\mathit{x}}]}_i}{\partial {\widehat{x}}_k}\frac{\partial {\widehat{x}}_k(\mathit{P})}{\partial P_{mn}}\right]-\beta \sum _k\frac{{\partial }^{2}U(\widehat{\mathit{x}})}{\partial x_j\partial x_k}\frac{\partial {\widehat{\mathit{x}}}_k(\mathit{P})}{\partial P_{mn}}\\ =\sum _i{\delta }_{jn}{\delta }_{im}{\dot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)+\sum _i{P}_{ij}{\ddot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)\left[{\delta }_{im}{\widehat{x}}_n+\sum _k{P}_{ik}\frac{\partial {\widehat{x}}_k(\mathit{P})}{\partial P_{mn}}\right]-\beta \sum _k\frac{{\partial }^{2}U(\widehat{\mathit{x}})}{\partial x_j\partial x_k}\frac{\partial {\widehat{x}}_k(\mathit{P})}{\partial P_{mn}}\\ ={\delta }_{jn}{\dot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)+P_{mj}{\ddot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)x_n+\sum _k\left\{\sum _i{P}_{ij}{\ddot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)P_{ik}-\beta \frac{{\partial }^{2}U(\widehat{\mathit{x}})}{\partial x_j\partial x_k}\right\}\frac{\partial {\widehat{x}}_k(\mathit{P})}{\partial P_{mn}},\\ j=1,2,\dots ,N;m=1,2,\dots ,M;n=1,2,\dots ,N\end{array}$$ (9)

where δ_mn is the Kronecker delta function defined as

$${\delta }_{mn}=\{\begin{array}{c}1,\mathrm{\hspace{0.17em} }m=n\\ 0,\mathrm{\hspace{0.17em} }m\ne n\end{array}$$

and ${\ddot{h}}_i(z)\equiv d^{2}h(z)/d{z}^2$.

Solving the linear equations in (9) yields

$$\frac{\partial {\widehat{x}}_j(\mathit{P})}{\partial P_{mn}}=\sum _k{[{\mathit{H}}^{-1}]}_{jk}\left[{\delta }_{kn}{\dot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)+P_{mk}{\ddot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m){\widehat{x}}_n\right],$$ (10)

where the (j, k) element of H is

$$H_{jk}=-\sum _i\left\{P_{ij}{\ddot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)P_{ik}-\beta \frac{{\partial }^{2}U(\widehat{\mathit{x}})}{\partial x_j\partial x_k}\right\}.$$

and [H⁻¹]_jk denotes the (j, k)th element of H⁻¹. Here we assume that the symmetric matrix H is positive definite.

Substituting (10) into (8), we get

$$\begin{array}{l}\mathrm{\Delta }{x}_j\approx \sum _{m,n}\sum _k{[{\mathit{H}}^{-1}]}_{jk}\left[{\delta }_{kn}{\dot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)+P_{mk}{\ddot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m){\widehat{x}}_n\right]\mathrm{\Delta }{P}_{mn}\\ =\sum _k{[{\mathit{H}}^{-1}]}_{jk}\left\{\sum _m\mathrm{\Delta }{P}_{mk}{\dot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)+\sum _m{P}_{mk}{\ddot{h}}_m({[\mathit{P}\widehat{\mathit{x}}]}_m)\sum _n\mathrm{\Delta }{P}_{mn}{\widehat{x}}_n\right\}.\end{array}$$ (11)

The above equation can be written in a matrix form

$$\mathrm{\Delta }\widehat{x}\approx {\mathit{H}}^{-1}\left\{(\mathrm{\Delta }\mathit{P}{)}^{\prime }\left[{\dot{h}}_i({[\mathit{P}\widehat{\mathit{x}}]}_i)\right]+{\mathit{P}}^{\prime }\text{diag}\left[{\ddot{h}}_i({[\mathit{P}\widehat{x}]}_i)\right](\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}\right\},$$ (12)

where diag[y_i] denotes a diagonal matrix with (i, i)th element being y_i, [c_i] denotes a column vector with the ith element being c_i, and ‘′’ denotes the matrix transpose.

As we have mentioned above, the decomposition in (5) is not essential to the derivation. The fundamental requirement is that the log-likelihood function can be written as

$$L(\mathit{y};\mathit{x})=\mathrm{\Phi }(\mathit{y},\mathit{q}),$$ (13)

where q = Px. Following the same procedure, we can show that the error propagation formula for the likelihood function in (13) is

$$\mathrm{\Delta }\widehat{\mathit{x}}\approx {\left[-{\mathit{P}}^{\prime }{\nabla }^{02}\mathrm{\Phi }(\mathit{y},\mathit{P}\widehat{\mathit{x}})\mathit{P}+\beta {\nabla }^{2}U(\widehat{\mathit{x}})\right]}^{-1}\left\{(\mathrm{\Delta }\mathit{P}{)}^{\prime }{\nabla }^{01}\mathrm{\Phi }(\mathit{y},\mathit{P}\widehat{\mathit{x}})+{\mathit{P}}^{\prime }{\nabla }^{02}\mathrm{\Phi }(\mathit{y},\mathit{P}\widehat{\mathit{x}})(\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}\right\},$$ (14)

where the (j, k)th element of ∇⁰²Φ(y, q) is $\frac{{\partial }^2}{\partial q_j\partial q_k}\mathrm{\Phi }(\mathit{y},\mathit{q})$, the jth element of ∇⁰¹Φ(y, q) is $\frac{\partial }{\partial {\mathit{q}}_j}\mathrm{\Phi }(\mathit{y},\mathit{q})$, and ${\nabla }^{2}U(\widehat{\mathit{x}})$ is a symmetric matrix with the (j, m)th element being $\frac{{\partial }^2}{\partial x_j\partial x_m}U(\widehat{\mathit{x}})$.

Equations (12) and (14) are the main results of this paper. They can be applied to a range of likelihood functions and image priors so long as the first-order Taylor series approximation (8) and equation (13) hold. In the following we shall show the applications of these results to emission tomography and transmission tomography problems.

2.2. Emission Tomography

Emission data are often modeled as independent Poisson random variables with the expectation $\overline{\mathit{y}}$ related to the unknown image x through an affine transform

$$\overline{\mathit{y}}=\mathit{Px}+\mathit{r},$$

where r accounts for the mean of the background events, such as randoms and scatters. For the Poisson likelihood function, we have

$$h_i(z)=y_i\mathrm{\hspace{0.17em} }\text{log}(z+r_i)-z-r_i-\text{log\hspace{0.28em}}{y}_i!$$ (15)

$${\dot{h}}_i(z)=\frac{y_i}{z+r_i}-1$$ (16)

$${\ddot{h}}_i(z)=-\frac{y_i}{{(z+r_i)}^2}$$ (17)

Substituting (16) and (17) into (12), we get the following expression for error propagation in emission tomography

$$\mathrm{\Delta }\widehat{\mathit{x}}\approx {\left[\mathit{F}+\beta {\nabla }^{2}U(\widehat{\mathit{x}})\right]}^{-1}\left[(\mathrm{\Delta }\mathit{P}{)}^{\prime }\left(\frac{\mathit{y}}{\widehat{\mathit{y}}}-1\right)-{\mathit{P}}^{\prime }\text{diag}\left[\frac{y_i}{{\widehat{y}}_i^2}\right](\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}\right],$$ (18)

where

$$\mathit{F}\equiv {\mathit{P}}^{\prime }\text{diag}\left[\frac{y_i}{{\widehat{y}}_i^2}\right]\mathit{P}$$

and $\widehat{\mathit{y}}\equiv \mathit{P}\widehat{\mathit{x}}+\mathit{r}$. In high count situations we can approximate $\mathit{y}\approx \widehat{\mathit{y}}$, so (18) reduces to

$$\mathrm{\Delta }\widehat{\mathit{x}}\approx -{\left[\mathit{F}+\beta {\nabla }^{2}U(\widehat{\mathit{x}})\right]}^{-1}{\mathit{P}}^{\prime }\text{diag}\left[\frac{1}{{\widehat{y}}_i}\right](\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}.$$ (19)

The result shows that the error propagation from the system matrix depends on the prior function through $\beta {\nabla }^{2}U(\widehat{\mathit{x}})$. In general, a prior that encourages smoothness in the reconstructed image can reduce the error propagation. This is similar to the error propagation from the voxel sensitivity image [Qi and Huesman, 2004].

One application of (19) is to determine the minimum accuracy required for the system matrix. While the exact answer depends on the specific task, a reasonable requirement would be that the artifacts caused by the errors in the system matrix are small compared to the uncertainty caused by the Poisson noise in the data, i.e.,

$$E[(\mathrm{\Delta }\widehat{\mathit{x}})(\mathrm{\Delta }\widehat{\mathit{x}}{)}^{\prime }]<\alpha \mathrm{\Sigma },$$ (20)

where E denotes ensemble expectation, ∑ is the image covariance caused by the Poisson noise given the true system matrix $\overline{\mathit{P}}$, and a is a user-defined tolerance factor, e.g., 0.01.

From the results in [Fessler, 1996], we know that ∑ can be approximated by

$$\mathrm{\Sigma }\approx {\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}{\overline{\mathit{P}}}^{\prime }\mathrm{\hspace{0.17em} }\text{diag}\left[\frac{{\overline{y}}_i}{{\stackrel{⌣}{y}}_i^2}\right]\overline{\mathit{P}}{\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1},$$ (21)

where $\stackrel{⌣}{\mathit{x}}$ denotes the MAP reconstruction of the noise-free data $\overline{\mathit{y}}$ with $\overline{\mathit{P}}$,

$$\stackrel{⌣}{\mathit{F}}\equiv {\overline{\mathit{P}}}^{\prime }\mathrm{\hspace{0.17em} }\text{diag}\left[\frac{{\overline{y}}_i}{{\stackrel{⌣}{y}}_i^2}\right]\overline{\mathit{P}},$$

and $\stackrel{⌣}{\mathit{y}}\equiv \overline{\mathit{P}}\stackrel{⌣}{\mathit{x}}+\mathit{r}$.

To proceed, we assume that the artifacts caused by the modeling error are independent of the Poisson noise in the measurements. Thus, we can analyze $\mathrm{\Delta }\widehat{\mathit{x}}$ using noise-free data, in which case we have ${\widehat{\mathit{x}}}^{*}=\stackrel{⌣}{\mathit{x}}$. If we consider P as a random quantity, the expansion point of the first-order Taylor series approximation in (8) should be changed to $\overline{\mathit{P}}$, which essentially changes all $\widehat{\mathit{x}}$ to ${\widehat{\mathit{x}}}^{*}\left(=\stackrel{⌣}{\mathit{x}}\right)$ and all P to $\overline{\mathit{P}}$ in equation (19). Substituting the modified equation (19) and equation (21) into (20), we get

$$\begin{array}{l}E\left\{{\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}{\overline{\mathit{P}}}^{\prime }\text{diag}\left[\frac{1}{{\stackrel{⌣}{y}}_i}\right](\mathrm{\Delta }\mathit{P})\stackrel{⌣}{\mathit{x}}{\stackrel{⌣}{\mathit{x}}}^{\prime }(\mathrm{\Delta }\mathit{P}{)}^{\prime }\text{diag}\left[\frac{1}{{\stackrel{⌣}{y}}_i}\right]\overline{\mathit{P}}{\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}\right\}\\ <\alpha {\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}{\overline{\mathit{P}}}^{\prime }\text{diag}\left[\frac{{\overline{y}}_i}{{\stackrel{⌣}{y}}_i^2}\right]\overline{\mathit{P}}{\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}.\end{array}$$ (22)

A sufficient condition for (22) to hold is

$$E[(\mathrm{\Delta }\mathit{P})\stackrel{⌣}{\mathit{x}}{\stackrel{⌣}{\mathit{x}}}^{\prime }(\mathrm{\Delta }\mathit{P}{)}^{\prime }]<\alpha \text{diag}[{\overline{y}}_i].$$ (23)

Equation (23) is useful in practice to determine whether the system matrix is accurate enough for reconstruction. For example, when using a system matrix that is calculated using Monte Carlo simulations or is measured directly using a scanning point source, $E[(\mathrm{\Delta }\mathit{P})\stackrel{⌣}{\mathit{x}}{\stackrel{⌣}{\mathit{x}}}^{\prime }(\mathrm{\Delta }\mathit{P}{)}^{\prime }]$ can be estimated from the covariance of the forward projected sinogram. To satisfy the requirement in (23), the variance in the forward projection need be less than a times the statistical variance in the data. If no acceleration scheme is used in the Monte Carlo simulation, this essentially means that the total number of detected events in the forward projection should be more than 1/a times the total number of detections in the data set. A similar criterion may also be used in the situation where Monte Carlo simulation is used to calculate the forward and back projection at each iteration, e.g., [Kudrolli et al, 2002]. However, because the system matrix changes from iteration to iteration in this case, exact analysis is more difficult.

Another direct application of (23) is to determine the required accuracy for normalization and attenuation correction factors in PET. These factors are often measured using blank and transmission scans, in which noise is inevitable. Both factors can be written as a diagonal matrix, so we have

$$\mathrm{\Delta }\mathit{P}=\text{diag}\left[\frac{\mathrm{\Delta }{n}_i}{{\overline{n}}_i}\right]\overline{\mathit{P}},$$ (24)

where ${\overline{n}}_i$ and Δn_i denote the true correction (normalization or attenuation) factors and the errors in the measured correction factors, respectively.

Substituting (24) into (23) and using the approximation $\overline{\mathit{P}}\stackrel{⌣}{\mathit{x}}+\mathit{r}\approx \overline{\mathit{y}}$ results in

$$E\left\{\text{diag}\left[\frac{\mathrm{\Delta }{n}_i}{{\overline{n}}_i}\right](\overline{\mathit{y}}-\mathit{r})(\overline{\mathit{y}}-\mathit{r}{)}^{\prime }\text{diag}\left[\frac{\mathrm{\Delta }{n}_i}{{\overline{n}}_i}\right]\right\}<\alpha \text{diag}[{\overline{y}}_i].$$ (25)

Assuming Δn_i and Δn_j are independent for i ≠ j, we get

$$\frac{E[{(\mathrm{\Delta }{n}_i)}^2]}{{\overline{n}}_i^2}<\frac{\alpha {\overline{y}}_i}{{({\overline{y}}_i-r_i)}^2},\forall i.$$ (26)

A simpler but sufficient condition is

$$\frac{E[{(\mathrm{\Delta }{n}_i)}^2]}{{\overline{n}}_i^2}<\frac{\alpha }{{\overline{y}}_i},\forall i$$ (27)

which essentially requires the relative noise level in the correction factors to be less than α times of that in the original data.

2.3. Transmission Tomography

The theoretical result is also applicable to transmission tomography. Here we consider the transmission reconstruction from measurements that have independent Poisson distributions. We use x_j to denote the the attenuation coefficient in the jth pixel. The mean of the data, $\overline{\mathit{y}}$, is related to x by

$${\overline{y}}_i=b_i{e}^{-{[\mathit{Px}]}_i}+r_i,$$

where P_ij denotes the intersection length of the ith ray passing through the jth pixel, b_i denotes the number of emission from the transmission source along the ith measurement, and r_i denotes the additive background events in the ith measurement. For simplicity we focus on the case where r_i = 0. Thus, we have

$$h_i(z)=y_i\mathrm{\hspace{0.17em} }\text{log}(b_i{e}^{-z})-b_i{e}^{-z}-\text{log\hspace{0.28em}}{y}_i!$$ (28)

$${\dot{h}}_i(z)=b_i{e}^{-z}-y_i$$ (29)

$${\ddot{h}}_i(z)=-b_i{e}^{-z}$$ (30)

Substituting equations (29) and (30) into (12) yields the following error propagation expression for transmission tomography

$$\mathrm{\Delta }\widehat{\mathit{x}}\approx {\left[\mathit{F}+\beta {\nabla }^{2}U(\widehat{\mathit{x}})\right]}^{-1}[(\mathrm{\Delta }\mathit{P}{)}^{\prime }(\widehat{\mathit{y}}-\mathit{y})-{\mathit{P}}^{\prime }\mathrm{\hspace{0.17em} }\text{diag}[{\widehat{y}}_i](\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}],$$ (31)

where

$$\mathit{F}={\mathit{P}}^{\prime }\mathrm{\hspace{0.17em} }\text{diag}[{\widehat{y}}_i]\mathit{P}$$

and ${\widehat{y}}_i\equiv b_i{e}^{-{[\mathit{P}\widehat{\mathit{x}}]}_i}$. If we use the approximation $\mathit{y}\approx \widehat{\mathit{y}}$, equation (31) reduces to

$$\mathrm{\Delta }\widehat{\mathit{x}}\approx -{\left[\mathit{F}+\beta {\nabla }^{2}U(\widehat{\mathit{x}})\right]}^{-1}{\mathit{P}}^{\prime }\text{diag}[{\widehat{y}}_i](\mathrm{\Delta }\mathit{P})\widehat{\mathit{x}}.$$ (32)

We can also use the condition (20) to determine the required accuracy for transmission reconstruction. From [Fessler, 1996] we know that the covariance caused by Poisson noise in transmission reconstruction can be approximated by

$$\mathrm{\Sigma }\approx {\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1}\overline{{\mathit{P}}^{\prime }}\text{diag}[{\overline{y}}_i]\overline{\mathit{P}}{\left[\stackrel{⌣}{\mathit{F}}+\beta {\nabla }^{2}U(\stackrel{⌣}{\mathit{x}})\right]}^{-1},$$ (33)

where $\stackrel{⌣}{\mathit{x}}$ is the noisefree reconstruction, $\stackrel{⌣}{\mathit{F}}={\overline{\mathit{P}}}^{\prime }\text{diag}[{\stackrel{⌣}{y}}_i]\overline{\mathit{P}}$, and ${\stackrel{⌣}{y}}_i=b_i{e}^{-{[\overline{\mathit{P}}\stackrel{⌣}{\mathit{x}}]}_i}$. Substituting equations (32) and (33) into (20) and simplifying yields the following condition

$$E[(\mathrm{\Delta }\mathit{P})\stackrel{⌣}{\mathit{x}}{\stackrel{⌣}{\mathit{x}}}^{\prime }(\mathrm{\Delta }\mathit{P}{)}^{\prime }]<\alpha \text{diag}[\frac{1}{{\overline{y}}_i}].$$ (34)

3. Validation using Computer Simulations

Computer simulations have been conducted to validate the theoretical results for emission tomography. We simulate a single-ring small-animal PET scanner that consists of 240 scintillation detectors. The size of each scintillation crystal is 2 mm (transaxial) × 10 mm (radial). The field-of-view (FOV) is a circular region of 64 mm in diameter represented by 64×64 1-mm² pixels. A scaled Hoffman brain phantom is used (Fig. 1(a)). The activity concentrations in the gray matter, white matter, and CSF are 5, 1, and 0, respectively. The “true” system matrix is calculated using a ray-tracing technique with modeling of crystal penetration effect by subdividing each crystal into 36 small elements as described in [Huesman et al, 2000]. We add a uniform background (10% of true events) to model random and scattered events. The total number of detected events is about 0.1M except where noted otherwise. A preconditioned conjugated gradient MAP algorithm with a log-quadratic prior is used to reconstruct the image. The prior energy function is U(x) = ∑_j ∑_k∈Nj (x_j = x_k)², where N_j includes the four nearest neighbors of pixel j. Note that the results require only that the algorithm iterates to an effective convergence and are independent of the particular optimization algorithm. The exact expectation of the additive background r is used. A noisy reconstruction is shown in Fig. 1(b).

Figure 1.

(a) The scaled Hoffman brain phantom and (b) a noisy reconstruction with β = 100.

3.1. Validation of Equation (18)

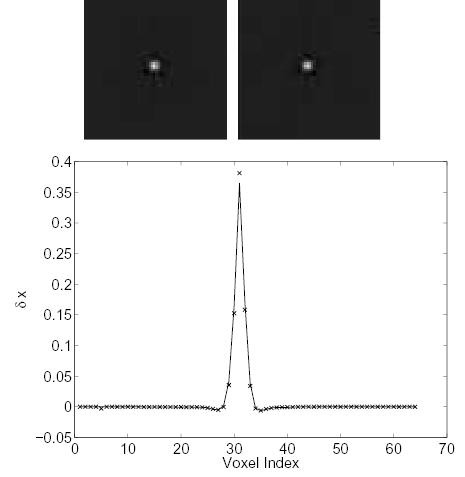
Figs. 2 and 3 show the changes in the reconstructed images when we decrease one row (i.e., a fixed LOR) of the system matrix by 50%. The theoretical predictions are computed using (18) with the reconstruction shown in Fig. 1b. The measured results are calculated from two independent reconstructions, i.e., reconstructions of the same noisy data using the “true” system matrix and the one with errors. Both results show a small increase in activity at the voxels close to the perturbed LOR. A slight decrease in activity at the voxels that are further away from the LOR is also noticed. Most importantly, the theoretical predictions match the measured results very well.

Figure 2.

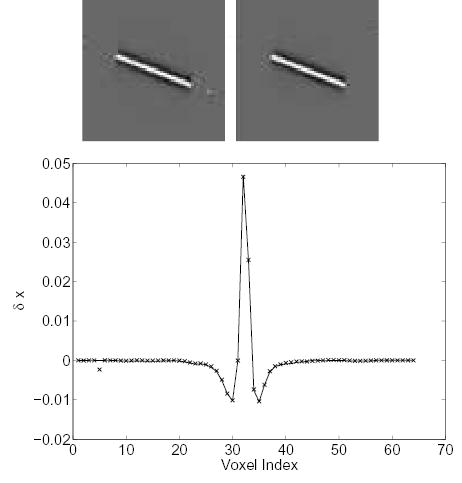
Comparison of the measured Δx and theoretically predicted Δx caused by a 50% perturbation along a center LOR. Top left: theoretically predicted Δx; top right: measured Δx; bottom: vertical profiles through the center of the theoretical (solid line) and the measured (‘×’) image.

Figure 3.

Comparison of the measured Δx and theoretically predicted Δx caused by a 50% perturbation along an off-center LOR. Top left: theoretically predicted Δx; top right: measured Δx; bottom: vertical profiles through the center of the theoretical (solid line) and the measured (‘×’) image.

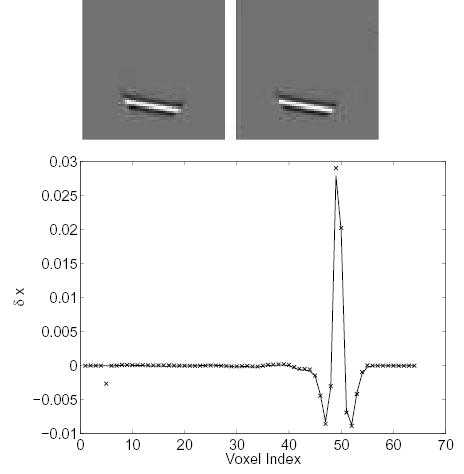
Figs. 4 and 5 show the changes in the reconstructed images when we decrease one column (i.e., a fixed voxel) of the system matrix by 50%. Without a prior, such perturbation would only increase the activity at this voxel. In our case, the effect is spread to neighboring voxels by the prior as shown by both theoretical calculation and Monte Carlo reconstructions.

Figure 4.

Comparison of the measured Δx and theoretically predicted Δx caused by a 50% perturbation along a column of the system matrix (a center voxel). Top left: theoretically predicted Δx; top right: measured Δx ; bottom: vertical profiles through the center of the theoretical (solid line) and the measured (‘×’) image.

Figure 5.

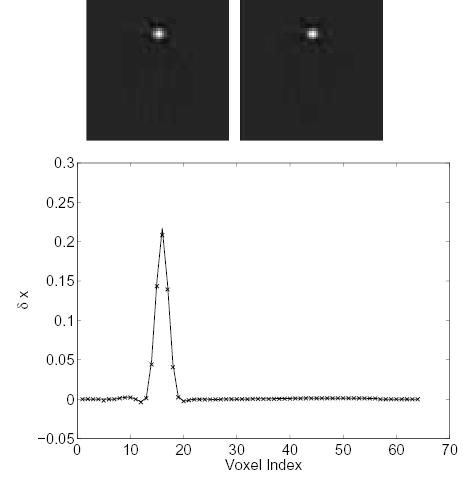
Comparison of the measured Δx and theoretically predicted Δx caused by a 50% perturbation along a column of the system matrix (an offset voxel). Top left: theoretically predicted Δx; top right: measured Δx; bottom: vertical profiles through the center of the theoretical (solid line) and the measured (‘×’) image.

Fig. 6 shows the changes in the reconstructed images when we add 20% zero-mean Gaussian noise to each nonzero element of the system matrix. Again, good agreement between the theoretical calculation and measured results is found.

Figure 6.

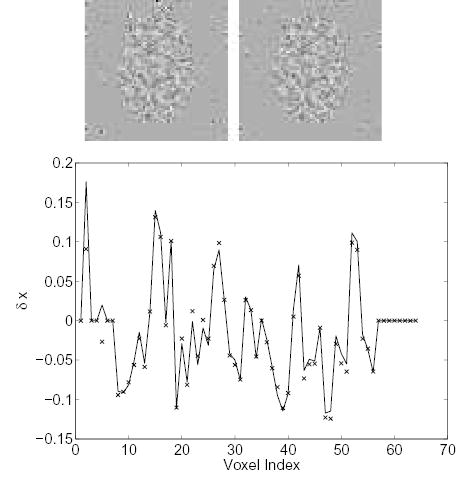
Comparison of the measured Δx and theoretically predicted Δx resulting from 20% white Gaussian noise in the system matrix. Top left: theoretically predicted Δx; top right: measured Δx; bottom: vertical profiles through the center of the theoretical (solid line) and the measured (‘×’) image.

3.2. Validation of Condition (23)

One of the contributions of this paper is the derivation of (23), which provides a guideline for determining the required accuracy of a system matrix. We test this condition at three different count levels, 0.1M, 1M, and 10M events. At each count level, we generate 50 independent data sets by adding pseudo-random Poisson noise. Each data set is reconstructed using both the “true” system matrix and a noisy system matrix with three different β values (β = 100, 10, 1). The resolution is measured by the full-width-at-half-maximum (FWHM) of the local impulse response function at the center of the FOV. The noisy system matrices are generated by adding 15% zero-mean Gaussian noise to each nonzero element of the “true” system matrix.

Table 1 shows the comparison of variations caused by Poisson noise and artifacts caused by noise in the system matrix. The variation caused by Poisson noise (denoted as “Poisson noise”) is measured by trace{∑}, where ∑ is the covariance matrix calculated from the 50 reconstructed images using the “true” system matrix. The level of the artifacts caused by noise in the system matrix is measured by the average of the mean squared error (MSE) between the reconstructed images using the “true” system matrix and noisy system matrices, which is equal to trace $\{E[(\mathrm{\Delta }\widehat{\mathit{x}})(\mathrm{\Delta }\widehat{\mathit{x}}{)}^{\prime }]\}$. The predicted MSE is calculated using $\mathrm{\Delta }\widehat{\mathit{x}}$ from equation (18).

Table 1.

Comparison of the variations caused by Poisson noise and system modeling errors. (See text for details.)

Total Counts	FWHM (β)	Poisson Noise	Measured MSE	Predicted MSE
0.1M	2.5 mm (100)	0.2068	0.1378	0.1254
	1.7 mm (10)	1.7722	1.1930	0.8883
	1.4 mm (1)	8.2431	6.7784	3.5624
1M	2.5 mm (100)	0.0211	0.0064	0.0063
	1.7 mm (10)	0.1988	0.0320	0.0320
	1.4 mm (1)	1.1999	0.4436	0.3393
10M	2.5 mm (100)	0.0021	0.0004	0.0004
	1.7 mm (10)	0.0201	0.0014	0.0014
	1.4 mm (1)	0.1289	0.0134	0.0140

The results show that when count level is high, the artifacts cause by system modeling error is small compared to Poisson noise. However, as count level decreases, the artifacts by the modeling error increases at a faster rate than that of Poisson noise. In low-noise reconstructions (high count or strong regularization), the theoretically predicted MSEs match the measured results very well. As noise level increases, the theoretical prediction breaks down. This is a limitation of the first-order Taylor series approximation that is used in the theoretical derivation.

To validate equation (23), we estimate the value of a by calculating the ratio of the second moments of $(\mathrm{\Delta }\mathit{P})\stackrel{⌣}{\mathit{x}}$ and $\overline{\mathit{y}}$. The maximum ratio is 1.05 and the average ratio is 0.22. All the results in Table 1 satisfy the worse case scenario a = 1.05. For high count data it is safe to use the average ratio instead of the maximum ratio.

3.3. Validation of Condition (27)

We generate noisy normalization factors using white Gaussian noise with unit mean and variance of 0.0025 (equivalent to the counting statistics of 400 events). We reconstruct 50 independent data sets with the ideal normalization factor and 50 noisy normalization factors (no other error is introduced to the system matrix). From these reconstructions we calculate the variations caused by Poisson noise and the variations caused by the noisy normalization factors.

Table 2 shows that the effect of noisy normalization factors (or attenuation correction factors) is independent of count level of the original data. When count level is at 0.1M (the maximum value in the sinogram is about 20), the effect of the noisy normalization factors is insignificant. However, when count level is at 10M (the maximum value in the sinogram is about 2000), the effect of the noisy normalization factors becomes greater than that of Poisson noise. This follows exactly the theoretical prediction in (27).

Table 2.

Comparison of the variations caused by Poisson noise and noise in normalization factors. (See text for details.)

Total Count	FWHM (β)	Poisson Noise	Measured MSE	Predicted MSE
0.1M	2.5 mm (100)	0.2130	0.0056	0.0056
	1.7 mm (10)	1.8158	0.0505	0.0519
	1.4 mm (1)	8.3067	0.2806	0.3199
1M	2.5 mm (100)	0.0214	0.0055	0.0055
	1.7 mm (10)	0.2015	0.0541	0.0545
	1.4 mm (1)	1.2078	0.3331	0.3511
10M	2.5 mm (100)	0.0021	0.0055	0.0055
	1.7 mm (10)	0.0201	0.0541	0.0542
	1.4 mm (1)	0.1296	0.3426	0.3546

4. Conclusions and Discussion

We have derived an analytical formula for calculating the error propagation from the system matrix to the final reconstructed image in iterative reconstruction. The theoretical expression has been used to determine the required accuracy of the system matrix in emission reconstruction. Computer simulation results show that the theoretical predictions match the measured results reasonably well at low-noise situations. The residual errors in the theoretical predication are caused mainly by the nonlinear property of the reconstruction algorithm, because we use the first-order Taylor series approximation. Using high-order approximations would improve the theoretical predictions, but expressions become more complicated quickly.