Understanding the Cortical Specialization for Horizontal Disparity

Abstract

Because the eyes are displaced horizontally, binocular vision is inherently anisotropic. Recent experimental work has uncovered evidence of this anisotropy in primary visual cortex (V1): neurons respond over a wider range of horizontal than vertical disparity, regardless of their orientation tuning. This probably reflects the horizontally elongated distribution of two-dimensional disparity experienced by the visual system, but it conflicts with all existing models of disparity selectivity, in which the relative response range to vertical and horizontal disparities is determined by the preferred orientation. Potentially, this discrepancy could require us to abandon the widely held view that processing in V1 neurons is initially linear. Here, we show that these new experimental data can be reconciled with an initial linear stage; we present two physiologically plausible ways of extending existing models to achieve this. First, we allow neurons to receive input from multiple binocular subunits with different position disparities (previous models have assumed all subunits have identical position and phase disparity). Then we incorporate a form of divisive normalization, which has successfully explained many response properties of V1 neurons but has not previously been incorporated into a model of disparity selectivity. We show that either of these mechanisms decouples disparity tuning from orientation tuning and discuss how the models could be tested experimentally. This represents the first explanation of how the cortical specialization for horizontal disparity may be achieved.

1 Introduction

Our remarkable ability to deduce depth from slight differences between the left and right retinal images appears to begin in primary visual cortex (V1), where inputs from the two eyes first converge and where many neurons are sensitive to binocular disparity (Barlow, Blakemore, & Pettigrew, 1967; Nikara, Bishop, & Pettigrew, 1968). Since the discovery of these neurons, it has always seemed obvious that their disparity tuning should reflect their tuning to orientation: a cell should be most sensitive to disparities orthogonal to its preferred orientation. As Figure 1 shows, this is a natural consequence of a linear-oriented filter preceding binocular combination. The fact that disparities in natural viewing are almost always close to horizontal, due to the horizontal displacement of our eyes, led to the expectation that cells tuned to vertical orientations should be the most useful for stereopsis, because such cells would be most sensitive to horizontal disparities (DeAngelis, Ohzawa, & Freeman, 1995a; Gonzalez & Perez, 1998; LeVay & Voigt, 1988; Maske, Yamane, & Bishop, 1986a; Nelson, Kato, & Bishop, 1977; Ohzawa & Freeman, 1986b).

Figure 1.

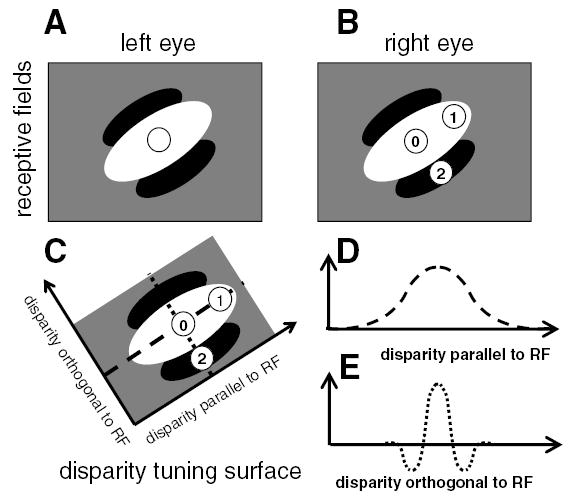
Existing models predict that neurons should be more sensitive to disparities orthogonal to their preferred orientation. (A,B) The receptive fields of a binocular neuron. The left and right eye receptive fields (RFs) are identical, both consisting of a single long ON region oriented at 45 degrees to the horizontal (shown in white) and flanked by OFF regions (black). We consider stimuli with three different disparities. In each case, the left eye’s image falls in the center of the left receptive field (circle in A). The different disparities occur because the right eye’s image falls at different positions for the three stimuli. This are labeled with the numbers 0–2 in B. (C) The disparities of the three stimuli are plotted in disparity space. Stimulus 0 has zero disparity; its images fall in the middle of the central ON region of the receptive field in each eye, and so it elicits a strong response. Stimulus 1 has disparity parallel to the receptive field orientation. Although its image is displaced in the right eye, its images still fall within the ON region in both eyes, so the cell still responds strongly to both stimuli. In consequence, the disparity tuning curve showing response as a function of disparity parallel to receptive field is broad (D, representing a cross-section through the disparity tuning surface along the dashed line). Conversely, stimulus 2 has the same magnitude of disparity, but in a direction orthogonal to the receptive field orientation. Its image in the right eye falls on the OFF flank of the receptive field (B), so the binocular neuron does not respond. This leads to a much narrower disparity tuning curve; the response falls off rapidly as a function of disparity orthogonal to the receptive field (E, representing a cross-section through the disparity tuning surface along the dotted line). This means that the neuron is more sensitive to disparity orthogonal to its preferred orientation, in the sense that its response falls off more rapidly as a function of disparity in this direction.

However, it has recently been demonstrated that the “obvious” premise was wrong. The response of V1 neurons was probed using random dot stereograms with disparity applied along different axes to obtain the cell’s firing rate as a function of the two-dimensional disparity of the stimulus. The resulting disparity tuning surfaces were generally elongated along the horizontal axis, independent of the cell’s preferred orientation (Cumming, 2002). Paradoxically, this means that V1 neurons are more sensitive to small changes in vertical than in horizontal disparity—precisely the opposite of the expected anisotropy. In this article, we consider why the observed anisotropy might be functionally advantageous for the visual system and then how individual cortical neurons may be wired up to achieve this.

We begin, in part A, by estimating the distribution of real two-dimensional disparities encountered in natural viewing. We show that while large vertical disparities do occur, they are extremely rare. The probability distribution of two-dimensional disparity is highly elongated along the horizontal axis, reflecting the much higher probability of large horizontal disparity compared to vertical disparity. We argue that the horizontal elongation observed in the disparity tuning of individual neurons may plausibly reflect the horizontal elongation of this probability distribution. This would be functionally useful because in stereopsis, the brain has to solve the correspondence problem: to match up features in the two eyes that correspond to the same object in space. The initial step in this process appears to be the computation, in V1, of something close to a local cross-correlation of the retinal images as a function of disparity (Fleet, Wagner, & Heeger, 1996). The cross-correlation function should peak when it compares points in the retinas that are viewing the same object in space. The problem faced by the brain is that not all peaks in the cross- correlation function correspond to real objects in space; there are a multitude of false matches where the interocular correlation is high by chance, even though no object is present at the corresponding position in space. To distinguish true matches from false, the brain has to consider the image over large scales and use additional constraints, such as the expectation that disparity generally varies smoothly across the image (Julesz, 1971; Marr & Poggio, 1976). The horizontal elongation of the probability distribution for two-dimensional disparity represents another important constraint. Because correct matches almost always have disparities very close to horizontal, local correlations between retinal positions that are separated vertically are likely to prove false matches (Stevenson & Schor, 1997). This may explain why the disparity-sensitive modulation of V1 neurons is abolished by small departures from zero vertical disparity: this property immediately weeds out a large number of false matches and simplifies the solution of the correspondence problem. Thus, although the global solution of the correspondence problem appears to be achieved after V1 (Cumming & Parker, 1997, 2000), the recently observed anisotropy (Cumming, 2002) may represent important preprocessing performed by V1.

We next, in parts B and C, address the puzzling issue of how this functionally useful preprocessing can be achieved by V1 neurons. In all existing models (Ohzawa, DeAngelis, & Freeman, 1990; Qian, 1994; Read, Parker, & Cumming, 2002), disparity selectivity is tightly coupled to orientation tuning, with the direction of maximum disparity sensitivity orthogonal to preferred orientation. This coupling arises as a direct result of orientation tuning at the initial linear stage (see Figure 1). It seems impossible to minimize disparity-sensitive responses to nonzero vertical disparities, independent of orientation tuning. Thus, at present, we have the undesirable situation that the best models of the neuronal computations supporting depth perception conflict with the best evidence that these computations do support depth perception (Uka & DeAngelis, 2002).

In this letter, we present two possible ways in which existing models can be simply modified so as to achieve horizontally elongated disparity tuning, regardless of orientation tuning. The first depends on position disparities between individual receptive fields feeding into a V1 binocular cell, the second on a form of divisive normalization. This demonstrates that the specialization for horizontal disparity exhibited by V1 neurons can be straightforwardly incorporated into existing models and is thus compatible with an initial linear stage.

2 Materials and Methods

2.1 The Probability Distribution of Two-Dimensional Disparity

In part A of the Results (section 3.1), we estimate the probability distribution of two-dimensional disparity encountered by the visual system within the central 15 degrees of vision.

2.1.1 Eye Position Coordinates

We specify eye position using Helmholtz coordinates, since these are particularly convenient for binocular vision (Tweed, 1997a, 1997b). In the Helmholtz system, eye position is specified by a series of rotations away from a reference position, in which the gaze is straight ahead. Starting with the eye in the reference position, we make a rotation through an angle T clockwise (from the eye’s point of view) about the reference gaze direction; then we make a rotation left through an angle H; then we make a rotation down through an angle V. Thus, the reference direction has H = V = T = 0 by definition. In general, the positions of the two eyes have 6 degrees of freedom, expressed by the angles H_L, H_R, V_L, V_R, T_L, T_R. However, we are interested only in the case where both eyes are fixated on a single point in space, so that the gaze lines intersect (possibly at infinity). This means that both eyes must have the same Helmholtz elevation, which we write V(= V_L = V_R), and positive or zero vergence angle D, defined by D = H_R − H_L. Specifying the fixation point further constrains H_L and H_R, leaving just 2 degrees of freedom, T_L and T_R. These describe the torsion state of the eyes, corresponding to the freedom of each eye to rotate about its line of sight without changing the fixation point. Donder’s law states that whenever the eyes move to look at a particular fixation point, specified by V, H_L, and H_R, they always adopt the same torsional state. So Helmholtz torsion can be expressed as a function of the Helmholtz elevation and azimuth: T_L(V, H_L, H_R), T_R(V, H_L, H_R). Current experimental evidence (Bruno & Van den Berg, 1997; Mok, Ro, Cadera, Crawford, & Vilis, 1992; Van Rijn & Van den Berg, 1993) suggests that the function T_R(V, H_L, H_R) has the form

$$tan\hspace{0.17em}{T}_{R/2}=tan\frac{V}{2}\left\{\frac{tan[{\lambda }_R+{\mu }_R(H_R-H_L)]-tan\hspace{0.17em}{H}_{R/2}}{1-tan{H}_{R/2}tan[{\lambda }_R+{\mu }_R(H_R-H_L)]}\right\},$$ (2.1)

where T_R/2 stands for T_R/2 and H_R/2 stands for H_R/2. The corresponding expression for the left eye’s torsion is obtained by interchanging L and R throughout. Estimates of μ range from 0.12 to 0.43 (Minken & Van Gisbergen, 1996; Mok et al., 1992; Somani, DeSouza, Tweed, & Vilis, 1998; Tweed, 1997b; Van Rijn & Van den Berg, 1993), and estimates of λ are around +2 degrees for the left eye and −2 degrees for the right (Bruno & Van den Berg, 1997). In our simulations, we use μ = 0.2 and |λ| = 2°.

2.1.2 The Retinal Coordinate System and Two-Dimensional Disparity

Next, we need a coordinate system for describing the position of images on the retinas. We assume that the retinas are hemispherical in shape. We define a Cartesian coordinate system (x, y) on the retina by projecting each retina onto the plane that is tangent to it at the fovea. The coordinates of a point P on the physical retina are given by the point where the line through P and the nodal point of the eye intersect this tangent plane. By definition, the fovea lies at the origin (0,0). We define the x-axis to be the retinal horizon, that is, the intersection of the horizontal plane through the fovea with the retina in its reference position. The y-axis is the retinal vertical meridian: the intersection of the sagittal plane through the fovea with the retina in its reference position.

Clearly, these axes change their orientation in space as the eyes move. However, we shall continue to refer to the x- and y-axes as the “horizontal” and “vertical” meridians, with the understanding that this terminology is based on their orientation when the eyes are in the reference position. We shall define the horizontal and vertical disparity of an object to be the difference between the x- and y-coordinates, respectively, of its images in the two retinas. Expressed in angular terms,

$$\begin{array}{l}\delta x=arctan\hspace{0.17em}\left(\frac{x_L}{f}\right)-arctan\hspace{0.17em}\left(\frac{x_R}{f}\right),\\ \delta y=arctan\hspace{0.17em}\left(\frac{y_L}{f}\right)-arctan\hspace{0.17em}\left(\frac{y_R}{f}\right),\end{array}$$ (2.2)

where f is the distance from the nodal point of the eye to the fovea.

2.1.3 The Epipolar Line

Given a particular point (x_L, y_L) in the left retina, the locus of possible matches in the right retina defines the right epipolar line. This depends not only on (x_L, y_L), but also on the position of the eyes. On our planar retina, the epipolar lines are straight but of finite extent. Two points on the epipolar line are the epipole, which is where the interocular axis intersects the tangent plane of the right retina, and the infinity point, which is the image in the right retina of the point at infinity that projects to (x_L, y_L) in the left retina. Written as a vector, these are, respectively,

$$q_0=\frac{f}{tan{H}_R}(-cos{T}_R,\hspace{0.17em}sin{T}_R),$$ (2.3)

and

$$\begin{array}{l}{q}_{\infty }=\frac{f}{[fcosD-x_{L}sinD\hspace{0.17em}\hspace{0.17em}cos{T}_L-y_{L}sinD\hspace{0.17em}sin{T}_L]}\\ \times \hspace{0.17em}(x_L[cosD\hspace{0.17em}\hspace{0.17em}cos{T}_R\hspace{0.17em}cos{T}_L+sin{T}_R\hspace{0.17em}sin{T}_L]\\ -y_L[cosDcos{T}_{R}sin{T}_L-sin{T}_{R}cos{T}_L]+fsinDcos{T}_R,\\ -x_L[cosDsin{T}_{R}cos{T}_L-cos{T}_{R}sin{T}_L]\\ +y_L[cosDsin{T}_{R}sin{T}_L+cos{T}_{R}cos{T}_L]\\ -fsinDsin{T}_R),\end{array}$$ (2.4)

where f is the distance from the nodal point of the eye to the fovea. We use bold type to denote a two-dimensional vector on the retina.

Not all points on the straight line through q₀ and q_∞ correspond to possible objects in space (we do not allow objects to be inside or behind the eyes). When the eye is turned inward, the epipolar line runs from the epipole q₀ to the infinity point q_∞. When the eye is turned outward, the epipolar line starts at the infinity point. Formally:

If H_R = 0:

the right-epipolar line is specified by the vector equation r = (x_R, y_R) = q₈ + βɛ, where β ranges from 0 to ∞, and

$$\begin{array}{l}\varepsilon =\frac{2If}{(x_{L}sin{H}_{L}cos{T}_L-y_{L}sin{H}_{L}sin{T}_L+fcos{H}_L)}\\ \times \hspace{0.17em}(-cos{H}_{R}cos{T}_R,\hspace{0.17em}sin{T}_R),\end{array}$$

where I is half the interocular distance.

If H_R ≠ 0: the right-epipolar line is r = q₀ + βɛ, where ɛ = q_∞ − q₀, and

$$\begin{array}{l}\text{if\hspace{0.17em}}\frac{sin{H}_R}{(fcosD-x_{L}sinDcos{T}_L+y_{L}sinDsin{T}_L)}>0,\\ \text{then\hspace{0.17em}}\beta \text{\hspace{0.17em}goes\hspace{0.17em}from\hspace{0.17em}}0\text{\hspace{0.17em}to\hspace{0.17em}}1;\\ \text{if\hspace{0.17em}}\frac{sin{H}_R}{(fcosD-x_{L}sinDcos{T}_L+y_{L}sinDsin{T}_L)}<0,\\ \text{then\hspace{0.17em}}\beta \text{\hspace{0.17em}goes\hspace{0.17em}from\hspace{0.17em}}1\text{\hspace{0.17em}to\hspace{0.17em}}\infty ;\end{array}$$ (2.5)

2.1.4 Distribution of Horizontal and Vertical Disparities for a Given Eye Posture

For a given eye posture, we sought the distribution of physically possible disparities for all objects whose images fall within an angle 15 degrees of the fovea in both retinas. For example, we consider an object whose image falls on (x_L, y_L) in the left retina and calculate the epipolar line in the right retina, as described above (see equations 2.3–2.5). We discard all points on the epipolar line that fall further than 15 degrees from the right eye fovea. With equation 2.1, we can then calculate the set of possible two-dimensional disparities (δ_x, δ_y) for all objects whose image in the left retina falls at (x_L, y_L), and whose image on the right retina falls within 15 degrees of the fovea. On disparity axes (δ_x, δ_y), this set forms an infinitely narrow line segment, which we convolved with an isotropic two-dimensional gaussian in order to obtain a smooth distribution.

We repeated this calculation for a set of 420 points (x_L, y_L) within the central 15 degrees region of the left retina and then redid the calculation the other way around: starting with a set of 420 points in the right retina and finding the epipolar lines in the left retina. The starting points (x, y) were equally spaced in latitude and longitude on the hemispherical retina: x = f tan φ cos θ, y = f tan φ sin θ, where θ covered the range from 0 to 360 degrees in steps of 18 degrees and φ ran from 0 to 15 degrees in steps of 0.75 degrees. For each starting point, we obtained another line segment on the disparity axes, and so gradually built up a picture of the distribution of possible disparities for the chosen eye position. The value of the angular disparities (δ_x, δ_y) so obtained does not depend on the interocular distance 2I or the eye’s focal length f individually, but only on the ratio I/f , which we took to be 3.

2.1.5 Distribution of Eye Postures

Finally, we wanted to find the mean distribution of disparity after averaging over likely eye positions. To do this, we repeated the above procedure for 1000 different randomly chosen eye positions. The eyes’ common Helmholtz elevation V, mean Helmholtz azimuth H_c, and the vergence angle D were drawn from independent gaussian distributions with mean 0 degree (for D, the absolute value was then taken, since D must be positive for fixation). The Helmholtz azimuths of the two eyes are given by H_L = H_c − D/2, H_R = H_c + D/2. The Helmholtz torsion in each eye, T_L and T_R, was then set according to equation 2.1. The disparity distribution for this eye position was then calculated as above.

2.2 Models of Disparity Tuning in V1 Neurons

In parts B and C of the Results (section 3), we investigate how existing models of disparity-selective V1 neurons can be modified to produce horizontally elongated disparity tuning surfaces, regardless of preferred orientation. Most of the results presented here use our model of V1 disparity selectivity (Read et al., 2002), which is a modified version of the stereo energy model (Ohzawa et al., 1990; Ohzawa, DeAngelis, & Freeman, 1997). As in the original energy model, disparity-selective cells are built from binocular subunits characterized by a receptive field in the left and right eye (see Figure 2A). Each binocular subunit (BS in Figure 2A) sums its inputs and outputs the square of this sum. However, whereas the original energy model is entirely linear until inputs from the two eyes have been combined, our version postulates that inputs from left and right eyes pass through a threshold before being combined at the binocular subunit. For instance, this could occur if the initial linear operation represented by the receptive field is performed in monocular simple cells (MS in Figure 2A). Because these cannot output a negative firing rate, they introduce a threshold before inputs from the two eyes are combined. This modification allows better quantitative agreement with the data in a number of respects. It was introduced to account for the weaker disparity tuning observed with anticorrelated stereograms (Cumming & Parker, 1997). It also naturally accounts for disparity-selective cells that do not respond to monocular stimulation in one of the eyes, which are not possible in the original energy model, and explains why the dominant spatial frequency in the Fourier spectrum of the disparity tuning curve is usually lower than the cell’s preferred spatial frequency tuning, even though the energy model predicts that these should be equal (Read & Cumming, 2003b).

Figure 2.

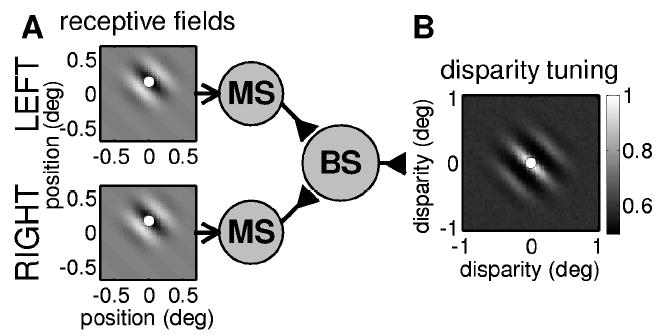
(A) Circuit diagram for our modified version of the energy model (Read et al., 2002). Binocular subunits (BS) are characterized by receptive fields in left and right eyes. The initial processing of the retinal images is linear, but input from left and right eyes is thresholded before being combined together. Here, this thresholding is represented by a layer of monocular simple cells (MS). In our simulations, the receptive field functions are two-dimensional Gabor functions (shown with gray scale: white = ON region, black = OFF region). The dots in the receptive field profiles mark the centers of the receptive fields, which are taken to be the peak of the gaussian envelope. (B) Disparity tuning surface for this binocular subunit. The gray scale indicates the mean firing rate of a simulated binocular subunit to 50,000 random dot patterns with different disparities: white = high firing rate (normalized to 1), gray = baseline firing rate obtained for binocularly uncorrelated patterns; black = low firing rate. The dot shows the difference between the receptive field centers, which is the position disparity of this binocular subunit (zero in this example).

All the models considered in this article have an initial linear stage in which we calculate the inner product of the retinal image I(x, y) with the receptive field function ρ(x, y) in that eye:

$$\upsilon ={\int }_{-\infty }^{+\infty }dx{\int }_{-\infty }^{+\infty }dy\hspace{0.17em}I(x,y)\rho (x,y).$$ (2.6)

In our modified version of the energy model (Read et al., 2002), the response of a binocular subunit is

$$B={[\mathrm{\Theta }({\upsilon }_L)+\mathrm{\Theta }({\upsilon }_R)]}^2,$$ (2.7)

where the subscripts L and R indicate left and right eyes, and Θ denotes a threshold operation: Θ(υ) = (υ − q) if υ exceeds some threshold level q, and 0 otherwise. In part C of the Results (section 3.3), the threshold q was set to zero (half-wave rectification). Since any given random dot pattern is as likely to occur as its photographic negative, the inner product in equation 2.6 is equally likely to be positive or negative. Thus, a threshold of zero implies that the monocular simple cell fired to only half of all random dot patterns. In part B of the Results, the threshold was raised above zero, such that the monocular simple cell fired to only 30% of all random dot patterns.

2.2.1 Inhibitory Input from One Eye

We also consider the case where input from one eye influences the binocular subunit via an inhibitory synapse. In the expression for the response of the binocular subunit, the inhibitory synapse is represented by a minus sign:

$$B={[Pos\left\{\mathrm{\Theta }({\upsilon }_L)-\mathrm{\Theta }({\upsilon }_R)\right\}]}^2,$$ (2.8)

where we have explicitly included half-wave rectification (Pos(x) = x if x > 0, and 0 otherwise) since it is now possible for the net input to the binocular subunit to be negative, and it should not fire in this case. A subunit of this type is disparity selective while still being “monocular” in that it does not respond to stimulation in the inhibitory eye alone. Many such cells are observed (Ohzawa & Freeman, 1986a; Poggio & Fischer, 1977; Read & Cumming, 2003a, 2003b).

2.2.2 The Original Energy Model

We also consider the response of the original energy model (Ohzawa et al., 1990). This assumes that each binocular subunit receives bipolar linear input from both eyes, so its response is

$$B={[{\upsilon }_L+{\upsilon }_R]}^2$$ (2.9)

This circuitry is sketched in Figure 8A.

Figure 8.

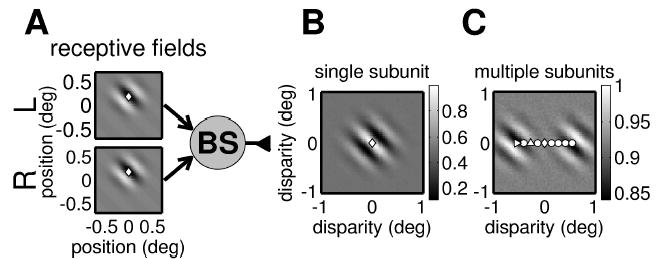
(A) Circuit diagram for a single binocular subunit from the original energy model (Ohzawa et al., 1990). In contrast to our modified version (see Figure 2), inputs from the two eyes are combined linearly (though the binocular subunit still applies an output nonlinearity of half-wave rectification and squaring). This results in more bandpass disparity tuning. (B) The side lobes in the disparity tuning surface shown here are much deeper than in Figure 2. This surface has almost no power at DC. As a consequence, when several binocular subunits with different horizontal position disparity combine to form a complex cell, their disparity tuning surfaces cancel out over most of the range (cf. Figure 9A). (C) The disparity tuning surface for a complex cell receiving input from 18 energy model binocular subunits whose position disparities are indicated by the symbols. Instead of being elongated horizontally as in Figure 7, all but the two end subunits are canceled out by their neighbors, so it has two separate regions of oscillatory response. This does not resemble the responses recorded from real cells.

2.2.3 Response Normalization

In part C of the Results (section 3.3), we consider the effect of incorporating a form of response normalization. This postulates that monocular inputs are gated by inhibitory zones outside the classical receptive field, before they converge on a binocular subunit (see Figure 3). The response of a binocular subunit is now

Figure 3.

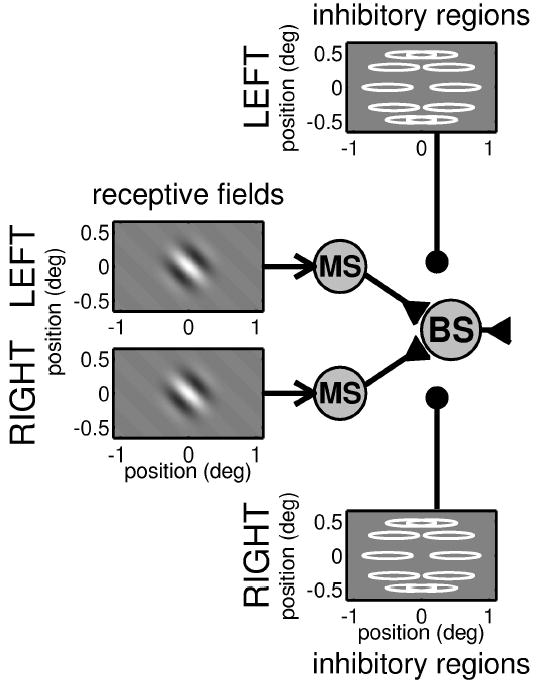
Circuit diagram for a binocular subunit in which the response from a classical receptive field is gated by input from inhibitory regions. As in Figure 2, monocular subunits, each characterized by a receptive field, feed into a binocular subunit. However, now the input from each eye may be suppressed, prior to binocular combination, by activity in horizontally elongated inhibitory regions. Excitatory connections are shown with an arrowhead, and quasi-divisive inhibitory input is shown with a filled circle. In the plots of the inhibitory regions, the gray scale shows several inhibitory zones in a ring around the receptive field in each eye.

$$B={[\mathrm{\Theta }({\upsilon }_L{z}_L)+\mathrm{\Theta }({\upsilon }_R{z}_R)]}^2$$ (2.10)

where the “gain factor” z describes the total amount of inhibition from the inhibitory zones. z ranges from 1 (inhibitory zones are not activated; output from monocular subunit is allowed through unimpeded) to 0 (inhibitory zones are highly activated: monocular subunit is silenced). To work out how much a particular retinal image activates the inhibitory zones, we calculate the inner product of the retinal image with each inhibitory zone’s weight function w(x, y) (analogous to a receptive field):

$$u={\int }_{-\infty }^{+\infty }dx{\int }_{-\infty }^{+\infty }dy\hspace{0.17em}I(x,y)w(x,y).$$

The weight functions are gaussians, which ensures that the inhibition is spatially broadband; this is designed to approximate the total input from a large pool of neurons with different spatial frequency tunings. In order to obtain the desired horizontally elongated disparity tuning surfaces, we postulate that the inhibitory zones are elongated along the horizontal axis (the elliptical contours in Figure 10A). This means that each inhibitory zone individually is orientation selective; however, we include multiple inhibitory zones, so arranged that their total effect is independent of orientation. Thus, the inhibition does not alter the orientation tuning of the original receptive field. The amount of inhibition contributed by each end zone is a sigmoid function of μ. The total inhibition from n zones is

Figure 10.

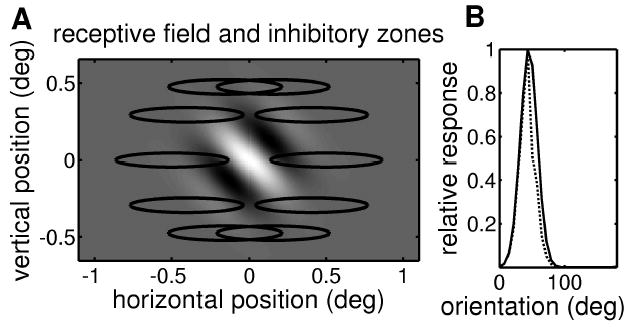
Horizontally elongated inhibitory end zones need not alter the orientation tuning. (A) Receptive field and inhibitory end zones. The gray scale shows the receptive field—a Gabor function in which a central ON region (white) is flanked by two OFF regions (black). The contours show the ten inhibitory end zones. Each inhibitory zone is a gaussian, and the contour marks the half-maximum. (B) Orientation tuning curve for the model with (dashed line) and without (solid line) gating by the inhibitory zones. This demonstrates that the horizontally elongated inhibitory zones do not alter the orientation tuning of the cell: it still responds best to a grating oriented at 45 degrees.

$$z=\frac{1}{n}\sum _{j=1}^n\hspace{0.17em}\frac{1}{1+exp[(\left|u_j\right|-c)/s]}.$$ (2.11)

The parameters c and s are chosen so that when u is small, the sigmoid function is 1, allowing monocular input to pass unimpeded, but as the magnitude of u increases, it falls to zero, meaning that more and more of the monocular input is blocked. This is qualitatively similar to divisive normalization (Heeger, 1992, 1993). c and s are small relative to the typical activation of each inhibitory zone, so that the sigmoid is less than half for 85% of the random dot patterns. We take the absolute value of |u| so that the inhibitory zones are activated by both bright and dark features.

In the simulation of Figure 10, we used 10 inhibitory zones, which were gaussians with standard deviations 0.31 degree in a horizontal direction and 0.04 degree vertically. The inhibitory zone centers were placed at 0.5 degree from the origin, at polar angles that are integer multiples of 36 degrees. As explained in section 3, these precise values are unimportant.

Again, the input from one eye can be purely subtractive inhibition; the output of the binocular subunit is then

$$B={\{Pos[\mathrm{\Theta }({\upsilon }_L{z}_L)-\mathrm{\Theta }({\upsilon }_R{z}_R)]\}}^2.$$ (2.12)

2.2.4 Receptive Fields

Model receptive fields are two-dimensional Gabor functions with isotropic gaussian envelopes of standard deviation 0.2 degree, and carrier frequency 2.5 cycles per degree. Spatial frequency and orientation tuning are experimentally observed to be similar in the two eyes (Bridge & Cumming, 2001; Ohzawa, DeAngelis, & Freeman, 1996; Read & Cumming, 2003b), so in our simulations, these are the same in both eyes. Left- and right-eye model receptive fields differ only in their position on the retina; none of the models in this article has phase disparity (although it would be easy to incorporate it).

2.2.5 Stimuli

Orientation tuning was assessed using sinusoidal luminance grating stimuli with a spatial frequency of 2.5 cycles per degree. Disparity tuning was assessed using random dot stereograms with dot-density 25%, as in the relevant experimental studies (cf. Cumming, 2002). The model response varies depending on the pattern of dots in the individual random dot stereogram. We therefore show the mean response, averaged over 50,000 random dot patterns generated with different seeds. This simulation was repeated for every combination of horizontal and vertical stimulus disparity on a two-dimensional grid, so as to obtain the model’s disparity tuning surface (analogous to the one-dimensional disparity tuning curve obtained when disparity is applied along a single axis). All simulated disparity tuning surfaces are shown normalized, so that 1 is the largest mean response at any disparity.

The random dot patterns used dots of 2 × 2 pixels. The size of the image and model retina was either 41×41 pixels representing 1.4°×1.4° (30 pixels per simulated degree; see part B of the Results, section 3.2) or 221 × 131 pixels representing 2.2° × 1.3° (100 pixels per simulated degree; see part C of the Results, section 3.3). For part C, the monocular-suppression model, a higher resolution was needed since the disparity tuning is suppressed at large disparities, so we need to be able to study the disparities around zero in more detail. All simulations were performed in Matlab 6.1.

3 Results

3.1 A: The Probability Distribution of Two-Dimensional Disparity

Stereopsis appears to be a phenomenon mainly of central vision; stereoscopic thresholds rise sharply for eccentric stimuli. We therefore consider only the central 15 degrees of cyclopean vision (i.e., the region of space projecting within 15 degrees of the fovea in both retinas). Obviously, 30 degrees is an upper bound for the disparity of any object in the central 15 degrees of vision. Most points on the retina will be associated with much smaller disparities; the precise distribution depends on the position of the eyes. To find the distribution for a given eye position, we have to consider each point P_L on the left retina in turn. For each P_L, we find the set of points P_R in the right retina that are possible physical correspondences for P_L. This is the epipolar line, and because we are restricting ourselves to central vision, we take only that portion of the epipolar line that lies within 15 degrees of the fovea. This gives us a set of possible disparities that could be associated with the point P_L. So every point in the left retina gives us a set of possible disparities. If we repeat this for all points in both retinas, we obtain the set of all the physical correspondences that are possible within the central visual field for this eye position (see section 2).

Figure 4A shows the probability distribution of retinal disparity for the eye position specified by a Helmholtz elevation V of 15 degrees, mean Helmholtz azimuth H_c of 15 degrees, and vergence D of 10 degrees. That is, the eyes are converged and looking down and off to the left. Note that the range of the horizontal axis is 10 times wider than that of the vertical axis. The dotted contour line marks the extent of possible physical correspondences. Outside this boundary, the probability density is zero; that is, for the given eye position, there can be no physical correspondences with that disparity. For this eye position, the maximum vertical disparity is 2.3 degrees, but this occurs with a horizontal disparity of 20 degrees, far too large for fusion. If we restrict ourselves to horizontal disparities within Panum’s fusion limit, δx < |0.5|°, the maximum vertical disparity is around 1 degree. The solid contour line marks the median; that is, 50% of possible physical correspondences fall within the solid line. Within this boundary, the range of vertical disparities is even smaller.

Figure 4.

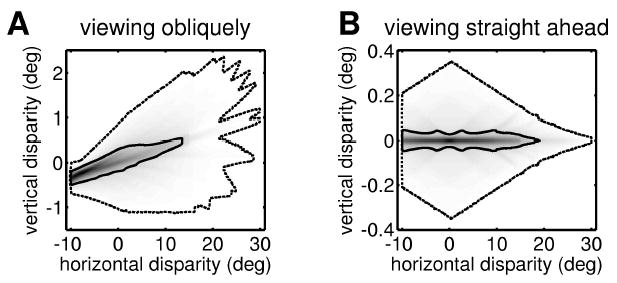
The probability distribution of horizontal and vertical disparities for a vergence angle of 10 degrees. (A) Helmholtz elevation V = 15 degrees, mean Helmholtz azimuth H_c = 15 degrees. (B) Helmholtz elevation V = 0 degree, mean Helmholtz azimuth H_c = 0 degree. In each case, the outer dotted contour marks the limit of possible disparities (beyond this contour, the probability density is zero). In A, this contour is only approximate: its irregularities reflect the relatively small number of retinal positions investigated. The solid contour marks the median (50% of randomly chosen possible correspondences lie within this iso-probability contour). In A, the SD of the isotropic gaussian used for smoothing was 0.04 degree; in B, it was 0.01 degree. The width of the distribution’s central ridge is limited by this smoothing.

Figure 4A demonstrates that large, vertical disparities can occur. But in fact, during natural viewing, it must be relatively uncommon to have the eyes elevated as much as 15 degrees and turned as much as 15 degrees to the side. We flick our eyes around a scene, but we do not usually spend a long time directing our eyes eccentrically; if that became necessary, we would move our head or the object of interest so that it could be viewed with H_c ~ V ~ 0°, where large, vertical disparities are even rarer. Figure 4B shows the distribution of retinal disparity for H_c = V = 0° with the same vergence as before, D = 10 degrees. Now, the largest vertical disparity is 0.35 degree. As before, the solid contour line encloses 50% of the possible physical correspondences. While this contour extends to horizontal disparities as large as 15 degrees, it never reaches a vertical disparity as large as 0.05 degree. Of course, which physical correspondences actually occur depends on the scene being viewed. But since there are far more possible correspondences with vertical disparities less than 0.1 degree, it seems reasonable to assume that with the given eye position (D = 10 degrees, H_c = V = 0 degree), it would be rare for a natural scene to contain an object with a vertical disparity more than 0.1 degree. In contrast, with this eye position, extremely large horizontal disparities are common.

To estimate the incidence of vertical disparities experienced by the visual system, we need to find the disparity distribution averaged not only over retinal position, as in Figure 4, but over all eye positions. For simplicity, we assume that H_c, V, and D are independently and normally distributed with mean zero (for D, since fixation requires a positive vergence angle, we use only the positive half of the gaussian). Figure 5 shows the resulting distributions for two different sets of values for the standard deviations of these distributions. In these plots, we have homed in on the small range of horizontal disparities that can actually be fused rather than the full range of possible horizontal disparities. Note that again the range of the horizontal axis is 20 times that of the vertical. In Figure 5A, gaze direction is assumed to be fairly tightly distributed about H_c = V = 0 degree (with a standard deviation of 10 degrees), while vergence is generally small (mean 2.4 degrees, SD 1.8 degrees). Figure 5B gives more weight to eccentric and converged gaze (the standard deviation of H_c and of V is 20 degrees, meaning that the person spends 5% of his or her time gazing more than 40° off to the side, while the vergence angle D has mean 6.4 degrees, SD 4.8 degrees, meaning that the person spends 20% of the time looking at objects closer than about 34 cm). These distributions are chosen to reflect opposite extremes of behavior, to demonstrate that our conclusions do not depend critically on the assumptions made about the distribution of eye position during normal viewing. The only critical assumption is that binocular eye movements are coordinated such that the gaze lines always intersect.

Figure 5.

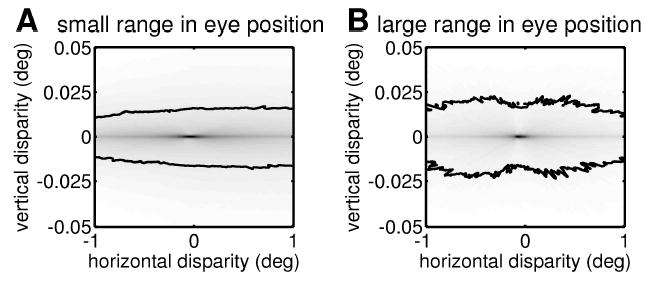
The distribution of horizontal and vertical disparities for normal viewing, averaged over 1000 random eye positions. Helmholtz elevation V and mean Helmholtz azimuth Hc are picked from a gaussian with mean 0 degree and SD either 10 degrees (A) or 20 degrees (B). To obtain vergence D, a random number is picked from a gaussian with mean 0 degree and SD either 3 degrees (A) or 8 degrees (B), and then vergence is set to the absolute value of this number. The resulting vergence distribution has a mean 2.4 degrees (A) or 6.4 degrees (B), and SD 1.8 degrees (A) or 4.8 degrees (B). The contour line marks the median for the section of the probability distribution shown (50% of randomly chosen possible correspondences with |δx| < 0.5 and |δy| < 0.05 lie within this iso-probability contour).

Under both sets of assumptions, the most striking feature in Figure 5 is the extreme narrowness of the disparity distributions in the vertical dimension (especially given the much larger scale on the vertical axis): less than 0.01 degree in both cases. At first sight, this extreme narrowness is hard to reconcile with Figure 4A, where the probability distribution peaks for −0.5° < δy < 0°. The solution is that the plots in Figure 5 represent the average of many plots like those shown in Figure 4. These all have a rodlike structure, with the orientation of the rod depending on the particular eye posture. But all the rods pass close to zero disparity. Thus, when we average over all eye postures, we end up with a strong peak close to zero disparity. This peak is stronger in Figure 5B, where the gaze and vergence are more variable. The rods are thus more widely dispersed, and we end up with a more pronounced peak at their common intersection. In Figure 5A, the eyes are assumed to stay fairly close to primary position, and so the rods are almost all close to horizontal. The averaged distribution is thus more elongated horizontally. The slight bias toward crossed (positive) disparities particularly evident in Figure 5A stems from an obvious geometric reason: the amount of uncrossed disparity, −δx, can never exceed the vergence angle D. (This restriction is visible as a sharp boundary in Figure 4.) No such restriction exists for crossed disparity. We began this discussion by restricting ourselves to central vision—the central 15 degrees around the fovea. If we widen this to the central 45 degrees—essentially the entire retina—then obviously larger disparities, both horizontal and vertical, become possible. However, the shape of the disparity distribution remains highly elongated horizontally (not shown).

This analysis has shown that independent of the precise assumptions made, the distribution of two-dimensional disparity experienced by the visual system in natural viewing is highly elongated. Large, horizontal disparities are far more likely to be encountered than vertical disparities of the same magnitude. We would therefore expect disparity detectors in V1 to be tuned to a considerably wider range of horizontal than vertical disparities. Following conflicting reports in earlier studies (Barlow et al., 1967; Joshua & Bishop, 1970; von der Heydt, Adorjani, Hanny, & Baumgartner, 1978), recent experimental evidence shows that this is indeed the case. Cumming (2002) extracted a single preferred two-dimensional disparity for each of 60 neurons and found that the distribution of this preferred disparity was horizontally elongated, with an SD of 0.225 degree in the horizontal direction and only 0.064 degree vertically. This observation is simple to incorporate within existing models: for example, if a cell’s preferred disparity reflects the position disparity between its receptive field locations in the two eyes, then the horizontally elongated distribution means that there is greater scatter in the horizontal than in the vertical location of the two eyes’ receptive fields. However, Cumming also found that the disparity tuning for individual neurons was horizontally elongated, independent of their orientation tuning. While this too makes sense in view of the extreme horizontal elongation of the disparity distribution shown in Figure 5, it presents problems for existing models of individual neurons. In the next section, we explain why and investigate how these models can be altered so as to reconcile them with the data.

In existing physiological models of disparity selectivity, tuning to two-dimensional binocular disparity must reflect the monocular tuning to orientation. This is illustrated in Figure 2, which sketches the circuitry underlying our model of disparity selectivity. In this example, the left and right eye receptive fields are oriented at 45 degrees to the horizontal (see Figure 2A). The disparity tuning surface (see Figure 2B) is approximately the cross-correlation of the two receptive fields (the thresholds prior to binocular combination in our model mean that it is not exactly the cross- correlation, but the approximation is accurate enough to be helpful). It is therefore elongated along the same axis as the receptive field. This means that as we move away from the cell’s preferred disparity along an axis orthogonal to the preferred orientation, the response falls off rapidly, whereas it falls off only slowly along an axis parallel to the preferred orientation. In this sense, therefore, the cell is most sensitive to disparities applied orthogonal to its preferred orientation. The challenge is to find a way of making the cell most sensitive to vertical disparity, while keeping its oblique orientation tuning. We consider two possible mechanisms that achieve this.

3.2 B. Multiple Binocular Subunits with Horizontal Position Disparity

Tuning to nonzero disparity may arise if the left and right eye receptive fields differ in their position on the retina, or in the arrangement of their ON and OFF subregions. In recent years, there has been intense debate about the relative contribution of the two mechanisms, known as position and phase disparity (Anzai, Ohzawa, & Freeman, 1997, 1999; DeAngelis, Ohzawa, & Freeman, 1991; DeAngelis et al., 1995a; Fleet et al., 1996; Ohzawa et al., 1997; Prince, Cumming, & Parker, 2002; Tsao, Conway, & Livingstone, 2003; Zhu & Qian, 1996). Both mechanisms predict a disparity tuning surface elongated along the preferred orientation of the cell, and thus preclude the experimentally observed specialization for horizontal disparity. However, all previous analysis has assumed that position and phase disparity is the same for all binocular subunits feeding into a given complex cell. Here, we relax this assumption and show that this breaks the relationship between disparity tuning surface and orientation tuning, allowing a specialization for horizontal disparity independent of orientation selectivity.

In Figure 2A, the left and right eye receptive fields are identical and occupy corresponding positions on the retina. The receptive fields are represented by Gabor functions; the dot indicates the receptive field center, which is in the same place in each retina. Thus, the disparity tuning surface has its peak at zero disparity (the dot in Figure 2B). If the receptive fields were offset from one another, they would have a position disparity, and the peak of the disparity tuning surface would be offset accordingly.

We now consider a complex cell that sums the outputs of several binocular subunits that differ in their horizontal position disparity. Figure 6A shows the centers of the left eye receptive fields for 18 binocular subunits that all feed into the same complex cell. (For comparison, one receptive field is indicated with contour lines.) The gray scale shows the sum of the gaussian envelopes for all 18 subunits, which is almost circularly symmetrical. Thus, no anisotropy is visible when the cell is probed monocularly.

Figure 6.

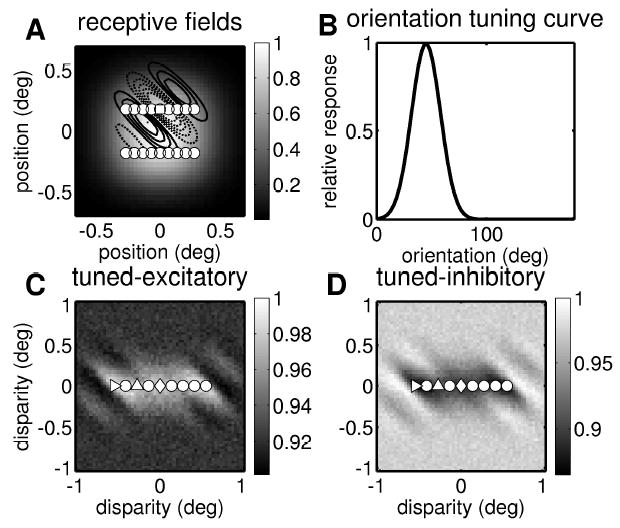
Response properties for a multiple subunit complex cell. (A) Monocular receptive field envelope. The gray scale shows the sum of the gaussian envelopes for all 18 receptive fields in one eye. The dots indicate the center of the receptive fields. The square is the center of the receptive field shown in Figure 2 (marked here with contour lines; solid lines show ON regions and broken lines OFF regions). (B) Orientation tuning curve. This shows the mean response of the complex cell to drifting grating stimuli at the optimal spatial frequency, as a function of the grating’s orientation. The preferred orientation is 45 degrees, reflecting the structure of the individual receptive fields. (C) Disparity tuning surface. This shows the mean response of the complex cell to random dot stereograms as a function of two-dimensional disparity. The disparity tuning surface is clearly elongated along the horizontal axis. The responses have been normalized to one, as indicated with the scale bar. The superimposed dots show the position disparities of the individual binocular subunits; the 18 subunits have 9 different disparities. The circuitry for three subunits is sketched in Figure 7; the position disparity for the three subunits shown there is here indicated with matching symbols. In the top subunit in Figure 7, the receptive fields in the two eyes are identical; this subunit therefore has zero position disparity (the diamond at (0,0)). The middle subunit in Figure 7 has receptive fields at different positions in each retina. It therefore has a horizontal position disparity, marked with a triangle pointing up. The bottom subunit in Figure 7 has an even larger horizontal position disparity, marked with a triangle pointing right. The tuned-excitatory disparity tuning surface shown here is the sum of 18 disparity tuning surfaces like that in Figure 2, but offset from one another horizontally. Thus, although the individual tuning surfaces were elongated along an oblique axis, the resulting disparity tuning surface is elongated horizontally. (D) Disparity tuning surface for a tuned-inhibitory complex cell. This was obtained with exactly the same receptive fields and subunits as in C, except that now, one out of each pair of monocular subunits made an inhibitory synapse onto the binocular subunit (see equation 2.8).

The disparity tuning of the complex cell depends on how pairs of monocular receptive fields are wired together into binocular subunits. We choose to pair together receptive fields that have the same vertical position on the retina but differ in their horizontal position. This means that the binocular subunits all have zero vertical position disparity but differ in their horizontal position disparity. Three examples are shown in Figure 7; the position disparity for these three subunits are indicated with different symbols in Figure 6C. For example, the top subunit in Figure 7, marked with a diamond, has zero position disparity, whereas the bottom subunit in Figure 7, marked with a triangle, has a position disparity of −0.6 degree. Because of the horizontal scatter of the subunits, the disparity tuning surface of the complex cell (see Figure 6C) is elongated along the horizontal axis, even though the monocular receptive field envelope is isotropic (see Figure 6A), and the preferred orientation remains at 45 degrees (see Figure 6B), reflecting the individual receptive fields. This demonstrates that disparity tuning and orientation tuning can be decoupled in a cell that receives input from multiple subunits with different position disparities.

Figure 7.

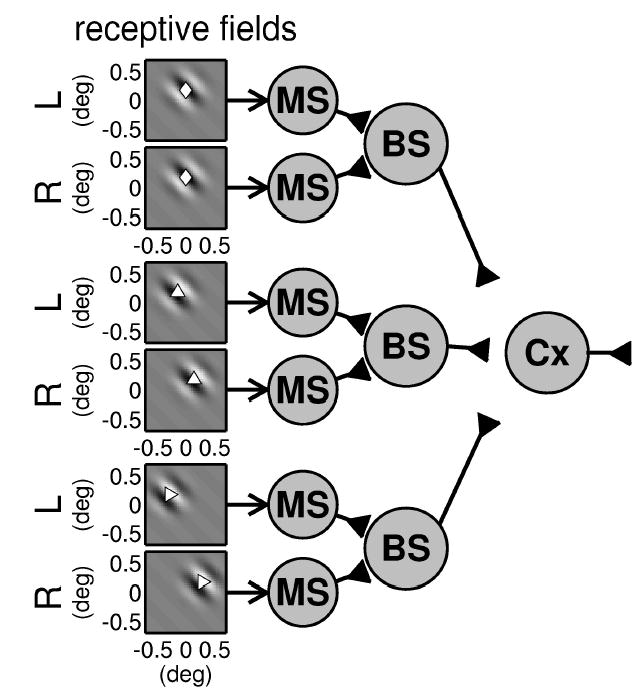
Circuit diagram indicating how multiple binocular subunits (BS) can be combined to yield a complex cell whose disparity tuning surface is elongated along the horizontal axis. Our model complex cell receives input from 18 binocular subunits, of which 3 are shown. The gray scale plots on the left show the monocular receptive field functions for monocular simple cells (MS). These are combined into binocular subunits (BS); note that the monocular simple cells apply an output threshold prior to binocular combination. The centers of the receptive field envelopes are shown with the symbols used to identify these disparities in Figure 6. As shown by the positions of these symbols, the three subunits have different horizontal position disparities (0 degree, −0.3 degree, −0.6 degree) and no vertical disparity. The receptive field phase is chosen randomly for each subunit, but within each subunit, it is the same for each eye.

In Figure 7, all the binocular subunits receive excitatory input from the monocular subunits feeding into them, and the left and right receptive fields for each subunit are in phase. This results in a “tuned-excitatory” type of disparity tuning surface (Poggio & Fischer, 1977), in which the cell’s firing rate rises above the baseline level for range of preferred disparities (see Figure 6C). If for each subunit one eye sends excitatory input and the other inhibitory (Read et al., 2002), then we obtain a “tuned-inhibitory” complex cell, whose firing rate falls below the baseline for a particular range of disparities (see Figure 6D). The position disparity of the individual subunits works in exactly the same way as before, so this cell’s disparity tuning surface is also elongated along the horizontal axis. Thus, this model works for both tuned-excitatory and tuned-inhibitory cells.

3.2.1 Energy Model Subunits Tend to Cancel Out

In the simulations above, we used our modified version of the stereo energy model (Ohzawa et al., 1990) because this is in better quantitative agreement with experimental data than the original energy model (Read & Cumming, 2003b; Read et al., 2002). As we shall see, this modification is also key to the success of the multiple-subunit model shown in Figures 7 and 6.

The receptive fields in the example cells in Figures 2 and 7 were chosen to be similar to the type of receptive fields derived from reverse correlation mapping (DeAngelis et al., 1991; DeAngelis, Ohzawa, & Freeman, 1995b; Jones & Palmer, 1987; Ohzawa et al., 1996). They are spatially bandpass, containing several ON and OFF subregions and little power at DC. In the energy model, bandpass receptive fields must yield bandpass disparity tuning curves (i.e., curves with several peaks and troughs). One problem for the energy model is that multiple peaks are not often seen in experimental disparity tuning curves. These are frequently close to gaussian in shape, with only weak side lobes, even when the spatial frequency tuning is bandpass. That is, real disparity tuning curves seem to be more lowpass than predicted from the energy model. This discrepancy has been noted by various authors (Ohzawa et al., 1997; Prince, Pointon, Cumming, & Parker, 2002), and quantified in detail by us (Read & Cumming, 2003b). Our modification to the energy model, introducing thresholds prior to binocular combination, helps fix this problem by removing side lobes from the disparity tuning curves, making them more low-pass and in better agreement with experimental data (Read & Cumming, 2003b). It turns out that this reduction of the side lobes is also what enables us to construct a horizontally elongated disparity tuning surface by combining multiple subunits with different horizontal position disparities.

To see why, consider what happens without the monocular thresholds. Figure 8A shows the circuit diagram of a binocular subunit according to the original energy model; the key feature is that bipolar input from the two eyes is combined linearly. The disparity tuning surface for this subunit is shown in Figure 8B. Note that the central peak is flanked by two deep troughs where firing falls well below baseline, so the surface as a whole has very little power at DC (compare Figure 8B to Figure 2B, which shows the equivalent surface for our modified version). As a result, when we add together several copies of such disparity tuning surfaces, most of the power cancels out, leaving a highly unrealistic tuning surface containing two distinct regions of modulation (see Figure 8C). To see why this happens, consider Figure 9A. The thin, broken lines show five hypothetical disparity tuning curves (in one dimension for clarity) that have no power at DC, because their deep side troughs have the same area as their central peak. When the five offset curves are averaged (heavy line), the peak of one subunit is canceled out by the side troughs of the two adjacent subunits, so that the response averages out to the baseline level everywhere except at the two ends, where the subunits have only one neighbor. In Figure 9B, the five disparity tuning curves are gaussians, representing the effect of a high threshold before binocular combination (Read & Cumming, 2003b). Because there are no inhibitory side lobes, cancellation does not occur, and the resultant disparity tuning curve (heavy curve) is above baseline for an extended range. In our simulations, the threshold was set such that each monocular simple cell fired on average for 3 out of every 10 random- dot patterns; for comparison, this figure would be 5 out of 10 for a threshold at zero (half-wave rectification). This does not entirely remove the side lobes (see Figure 2), but has enough of an effect to prevent cancellation. Thus our modification, introduced for quite different reasons, also enables us to obtain horizontally elongated disparity tuning surfaces by combining multiple subunits with horizontal position disparities. For bandpass receptive fields, this is not possible in the energy model, although it is possible for receptive fields with a substantial DC response.

Figure 9.

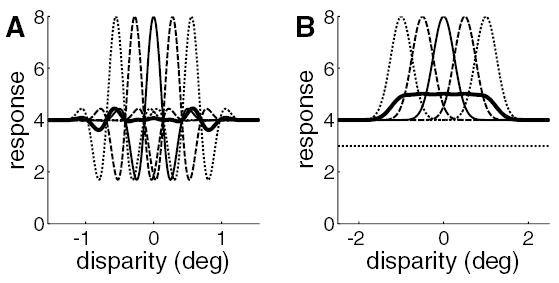
Problems encountered in combining subunits tuned to different disparities. Thin, broken curves: hypothetical disparity tuning curves from five binocular subunits. They are identical in form but offset from one another horizontally. Heavy curve: the mean of the thin curves. (A) These binocular subunits have bandpass disparity tuning (like those obtained from the original energy model). The thin curves have near-zero DC component, since the central peak is nearly equal in area to the two side troughs. When the subunits are combined, their disparity tuning curves cancel out over most of the range, leaving an oscillatory region at each end. This does not resemble real disparity tuning curves. (B) These binocular subunits have low-pass disparity tuning (like those obtained from our modified version of the energy model). Now, combining many subunits tuned to different disparities results in a broadened disparity tuning curve resembling experimental results. However, the disparity tuning is weakened. Whereas the tuning curves for individual subunits (thin lines) have amplitude equal to their baseline, the amplitude for the combination (heavy line) is only 25% of the baseline. This problem could be solved by imposing a final output threshold on the complex cell. If the region of the plot below the dotted line could be removed by an output threshold, then the amplitude of the disparity tuning curve would be a larger fraction of the new baseline.

3.2.2 An Additional Output Threshold is Needed

Figure 9B also highlights a problem with this multiple-subunit model as it stands. Summing multiple subunits inevitably reduces the amplitude of the modulation with disparity. In Figure 9B, the individual disparity tuning curves have amplitude equal to the baseline response, while the amplitude of the averaged curve (black) is just 20% of the baseline. This effect is apparent on examining the scale bars in Figure 6: the amplitude of the disparity tuning is only about 5% of the baseline (the response at large disparities, where the random dot patterns in the two eyes are effectively uncorrelated). In an experiment, a cell with such weak modulation would probably not even pass the initial screening for disparity selectivity. This problem can be solved if we postulate that the complex cell applies an output threshold: that is, it fires only when its inputs exceed a certain value (cf. the dotted line in Figure 9B). For the tuned-excitatory model, it would be equally valid to postulate that the necessary threshold is applied by the individual binocular subunits. However, for tuned-inhibitory cells, the threshold must be applied by the complex cell that sums the individual subunits (this is apparent on redrawing Figure 9B with tuned-inhibitory tuning curves).

3.3 C. Monocular Suppression from Horizontally Elongated Inhibitory Zones

We now turn to an alternative way of decoupling disparity and orientation tuning. A well-known feature of V1 neurons is that they can be inhibited by activity outside their classical receptive field (Cavanaugh, Bair, & Movshon, 2002; Freeman, Ohzawa, & Walker, 2001; Gilbert & Wiesel, 1990; Jones, Wang, & Sillito, 2002; Maffei & Fiorentini, 1976; Sillito, Grieve, Jones, Cudeiro, & Davis, 1995; Walker, Ohzawa, & Freeman, 1999, 2000, 2002). Phenomena such as end stopping, side stopping, and cross-orientation inhibition have been explained by suggesting that individual V1 neurons are subject to a form of gain control from the rest of the population, for example, by divisive normalization (Carandini, Heeger, & Movshon, 1997; Heeger, 1992, 1993). Yet existing models of disparity selectivity ignore these aspects of V1 neurons’ behavior. We now extend our model (Read et al., 2002) to include these effects. We postulate that inputs from each eye are suppressed by activity from inhibitory zones prior to binocular combination. We shall show that if the individual inhibitory zones are elongated horizontally on the retina, the disparity tuning surface will be horizontally elongated. If there are several inhibitory zones arranged isotropically, the total inhibition is independent of orientation. Thus, this horizontal elongation in disparity tuning is achieved without altering the cell’s orientation selectivity.

3.3.1 Monocular Suppression Can Decouple Disparity and Orientation Tuning

As before, we consider a binocular subunit with identical obliquely oriented receptive fields in left and right eyes. However, now the monocular inputs are gated by inhibitory zones before being combined in a binocular subunit. This is sketched in Figure 3. If the retinal image does not stimulate the inhibitory zones, the inhibitory synapses in Figure 3 are inactive, and the output of the monocular simple cell is passed to the binocular subunit just as in the previous model. But if the retinal image stimulates the inhibitory zones, the inhibitory synapses become active, and the firing rate of the monocular cell is reduced or even silenced (see section 2 for details). This is very similar to the divisive normalization proposed to explain non-specific suppression and response saturation (Carandini et al., 1997; Heeger, 1992, 1993; Muller, Metha, Krauskopf, & Lennie, 2003): the firing rate of a fundamentally linear neuron is suppressed by activity in a “normalization pool” of cortical neurons. In the simple model presented here, the horizontal elongation of the individual inhibitory zones, chosen in order to obtain horizontally elongated disparity tuning surfaces, means that they are tuned to horizontal orientation. This is a side effect of the computationally cheap way we have chosen to implement divisive normalization by a pool of neurons: in a full model, each inhibitory zone would represent input from a multitude of sensors tuned to different spatial frequencies and orientations, so that the response of each inhibitory zone individually would be independent of orientation. Equally, it would be possible to construct the surround such that it was sensitive to orientations other than horizontal. So long as the region over which these subunits are summed remains horizontally elongated, it would still produce the desired effect on disparity tuning. In this way, it would be possible to construct a model using the same principles that matched the reported orientation selectivity of surround suppression (Cavanaugh et al., 2002; Levitt & Lund, 1997; Muller et al., 2003). However, the simple model presented here is designed to be nonspecific in that the suppression contributed by all the inhibitory zones together is independent of orientation. This means that the suppression in our model affects the disparity tuning while leaving the orientation tuning unchanged.

One way of achieving this is to place the inhibitory zones in a ring around the original receptive field, as shown in Figure 10A, so that while the individual inhibitory zones are horizontally elongated, the total inhibitory region is roughly isotropic. Figure 10B shows the orientation tuning curves obtained with no suppression (solid curve) and after including the effect of suppression from the inhibitory end zones (broken curve). Despite the horizontal orientation of each inhibitory zone individually, the cell still responds best to a luminance grating aligned at 45 degrees. The ring pattern is consistent with experimental evidence indicating that suppressive regions are located all around the receptive field (Walker et al., 1999). In fact, as far as disparity tuning to random dot patterns is concerned, similar results are obtained no matter where the inhibitory zones are placed, provided that the overall arrangement is not tuned to orientation. We also ran our simulations with inhibitory end zones placed at the top and bottom of the original receptive field (not shown), and obtained essentially the same results. Similarly, the gaps between the inhibitory zones in Figure 10 are not important. We chose a sparse arrangement of inhibitory zones so that the location of the individual zones would be clear; in fact, the same results are obtained with a much denser array of overlapping inhibitory zones forming a complete ring around the original receptive field (not shown).

Although the inhibitory zones have little effect on orientation tuning, they have a profound effect on the two-dimensional disparity tuning observed with random dot stereograms. Figure 11A shows the disparity tuning surface that would be obtained from this binocular subunit in the absence of inhibitory zones. It is, as expected, elongated along an oblique axis corresponding to the orientation tuning. Figures 11B and 11C show the disparity tuning surface after incorporating inhibition from the ten inhibitory zones (in Figure 11B, for the same range of disparities as in Figure 11A, and in Figure 11C, focusing in on a smaller range of disparities). Comparing Figures 11A and 11B, it is apparent that the original disparity tuning surface has been greatly reduced. Suppression from the inhibitory zones has removed or weakened the cell’s responses to most disparities away from the preferred disparity (zero, in this example), especially to disparities with significant vertical components. However, the response to horizontal disparities has been relatively spared. This is especially clear in Figure 11C, where we focus in on the smallest disparities. What remains of the disparity tuning surface is now elongated along a near-horizontal axis.

Figure 11.

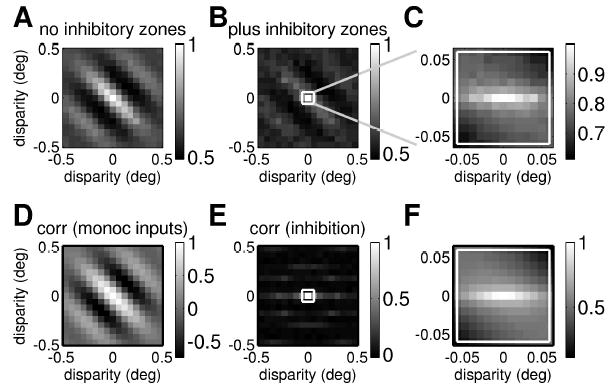
Monocular suppression by horizontally oriented inhibitory regions can result in a horizontally elongated disparity tuning surface. (Top row) Disparity tuning surface with and without monocular suppression. (A) Disparity tuning surface for a single binocular subunit without any suppression from inhibitory zones, as sketched in Figure 2 (equation 2.7, with the threshold set at zero so that Θ represents half-wave rectification). (B, C) Disparity tuning surface for the same binocular subunit after incorporating monocular suppression from inhibitory zones prior to binocular combination, as sketched in Figure 3 (see equation 2.10; again Θ represents half-wave rectification). At large scales (B), some trace of the original oblique structure remains, but in the central region where sensitivity to disparity is strongest (shown expanded in C), the structure is horizontal. (Bottom row) Correlation between left and right eye inputs as a function of disparity. (D) Correlation between output of classical receptive fields in left and right eyes (see equation 2.6). (E) Correlation between total inhibition from end zones in left and right eyes (see equation 2.11). (F) Correlation between output of classical receptive fields after inhibition from end zones.

3.3.2 The Monocular Suppression Vetoes Vertical-Disparity Matches

The inhibitory zones effectively veto local correlations with vertical disparities. Functionally, this would be useful since such correlations are likely to be false matches, which will only hamper a solution of the correspondence problem. Yet at first sight, it is hard to understand how this can occur. In our model, the inhibition is purely monocular: the inhibitory zones receive input from only one eye and suppress the response only in that eye. How, then, can they detect interocular correlation for vertical disparities in order to suppress it?

To understand this, we first note that the output of an ordinary binocular subunit (without gating from inhibitory zones) depends on the correlation between the terms from left and right eyes, which depends on disparity. If we plot the correlation between the inputs from left and right eyes, before normalization by the inhibitory zones, as a function of horizontal and vertical disparity, the resulting correlation surface has the same orientation as the receptive fields (see Figure 11D). Similarly, the correlation between the suppressive input from the inhibitory zones in left and right eyes is oriented along the same axis as the inhibitory zones, that is, horizontally (see Figure 11E). It was to achieve this result that we made the inhibitory zones horizontally elongated. Regions of weaker correlations at disparities corresponding to the separation between nearby inhibitory zones are also visible.

Finally, Figure 11F homes in on the same small range of disparities as in Figure 11C and shows the correlation between left and right eye inputs, after suppression from the inhibitory zones. In order for these to be tightly correlated, we need strong correlation between both the left and right receptive field inputs and the left and right eye inhibition. Thus, Figure 11F can be thought of as the product of Figures 11D and 11E. For disparities with a significant vertical component in Figure 11F, the lack of correlation in the inhibitory zone responses (see Figure 11E) has largely canceled out the correlation between the inputs from the receptive fields (see Figure 11D). The original obliquely oriented correlation function has been weakened, leaving a band of high correlation for small horizontal disparities. This horizontally elongated correlation translates into the horizontally elongated disparity tuning surface we saw earlier (see Figure 11C). Figure 12 shows that this works for tuned-inhibitory cells (see equation 2.12) too. Thus, end stopping can decouple disparity tuning from orientation tuning, for both tuned-excitatory and tuned-inhibitory cells. This basic idea has been suggested before (Freeman & Ohzawa, 1990; Maske et al., 1986a; Maske, Yamane, & Bishop, 1986b), but no one has previously developed a quantitative model and examined its properties.

Figure 12.

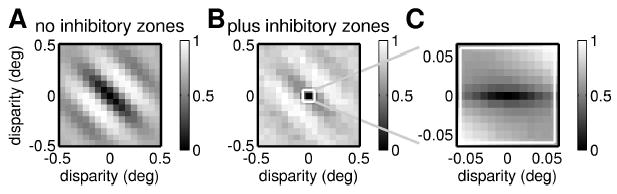
Monocular suppression by horizontally oriented inhibitory regions can also yield a tuned-inhibitory disparity tuning. As for Figures 11A to 11C, but for a model incorporating a tuned-inhibitory synapse, so the disparity is of the tuned-inhibitory type.

4 Discussion

Because our eyes are displaced horizontally, most disparities we encounter are horizontal. We have quantified this by producing estimates of the probability distribution of two-dimensional disparity encountered during natural viewing, making plausible assumptions for the distribution of eye posture. The results are independent of the precise assumptions used and show clearly that the probability distribution of experienced disparity is highly elongated along the horizontal axis. Psychophysically, this anisotropy mirrors our different sensitivities to horizontal and vertical disparity (Stevenson & Schor, 1997). Physiologically, it is reflected in V1 at two different levels. At the population level, there is a wider scatter in the horizontal than in the vertical component of preferred disparities (Barlow et al., 1967; Cumming, 2002; DeAngelis et al., 1991). At the level of individual cells, disparity tuning surfaces are usually elongated along the horizontal axis, regardless of orientation tuning (Cumming, 2002).

While the specialization at the population level was expected and is straightforward to incorporate into existing models, the specialization found in individual cells is at first sight extremely surprising. It is not only incompatible with all existing models of the response properties of disparity-tuned cells; it is the exact opposite of the behavior previously predicted to be functionally useful for stereopsis. Many workers have argued that cells mediating stereopsis should be most sensitive to horizontal disparity; their firing rate should change more steeply as a function of horizontal than of vertical disparity (DeAngelis et al., 1995a; Gonzalez & Perez, 1998; LeVay & Voigt, 1988; Maske et al., 1986a; Nelson et al., 1977; Ohzawa & Freeman, 1986b). Given the expectation that the direction of maximum disparity sensitivity would be orthogonal to the cell’s preferred orientation, this led to the expectation that cells tuned to vertical orientations should be most useful for stereopsis, since these were expected to be the most sensitive to horizontal disparity. It was therefore puzzling why real disparity-tuned cells occur with the full range of preferred orientations, with no obvious tendency to prefer vertical orientations. The recent discovery that the direction of maximum disparity sensitivity is in fact independent of orientation tuning (Cumming, 2002) would have satisfactorily solved this puzzle if it had not been for the fact that the direction of maximum disparity sensitivity was found to be vertical rather than horizontal. From the conventional point of view, this anisotropy of individual V1 neurons looks more like a specialization for vertical than for horizontal disparity. It is important, therefore, before we discuss how we have been able to reproduce the horizontally elongated disparity tuning surfaces of V1 neurons, to consider why this anisotropy occurs. Armed with hindsight and recent experimental evidence, we shall argue that the previous expectations were flawed and attempt to suggest plausible reasons that the observed anisotropy is in fact a useful specialization for horizontal disparity.

The previous expectation of vertically elongated disparity tuning surfaces was based on the fact that these are most sensitive to horizontal disparity. Yet given that stereo information is usually thought to be represented in the activity of a whole population of sensors tuned to different disparities, this is not particularly relevant. The sensitivity with which the population encodes horizontal disparity is not limited by the sensitivity of the individual sensors. It is not possible, therefore, to deduce the shape of the individual disparity tuning surfaces from the need for sensitivity to horizontal disparity. A population of sensors with either horizontally elongated or vertically elongated surfaces would be equally capable of achieving high sensitivity to horizontal disparity.

Imagine a population of neurons whose disparity tuning surfaces are isotropic (equally sensitive to vertical and horizontal disparity). If the scatter of center positions (preferred disparity) is equal in vertical and horizontal directions, the population carries equivalent information concerning the two disparity directions. The population response could be made more sensitive to horizontal than vertical disparity by reducing the scatter in the horizontal direction. However, the population would show such sensitivity over a narrower range of horizontal than vertical disparities. For simple pooling over a population of independent disparity detectors, there is a trade-off between the range of disparity encoded in any one direction and the sensitivity to small changes, regardless of the shape of individual filters.

That said, the horizontal displacement of the eyes does place constraints on the maximum useful extent of the individual disparity tuning surfaces. There is no point in having any one filter encompass a larger range than is required of the population. As our simulation of the probability distribution of the two-dimensional disparities encountered during normal viewing demonstrates, large, vertical disparities are rare in comparison to large, horizontal disparities. The iso-probability contours (see Figures 4 and 5) span a greater range of horizontal than vertical disparities. Suppose that the brain ignores disparities outside a certain iso-probability contour and that this is the functional reason that we cannot fuse large disparities outside Panum’s fusional limit: such large disparities are too rare to be worth encoding. The range of disparities to be encoded in each direction places an upper limit on the useful extent of an individual cell’s disparity tuning surface in that direction. Due to the horizontally elongated shape of the iso-probability contours, this upper limit is much lower in the vertical direction than in the horizontal direction. While this does not prove that individual disparity tuning surfaces must be horizontally elongated (it would be theoretically possible to cover the desired horizontally elongated range with vertically elongated disparity sensors), it nevertheless suggests that horizontally elongated surfaces may be more likely than vertically elongated ones.

The characteristic feature of horizontally elongated disparity tuning surfaces is that they continue responding to features across a range of horizontal disparities, while their response falls quickly back to baseline if the vertical disparity changes. This may be useful, given that features with significant vertical disparity are likely to be “false matches.” There is some evidence that the brain does not explicitly search for nonzero vertical disparities when solving the stereo correspondence problem. If the eyes are staring straight ahead (more precisely, are in primary position), then there are no vertical disparities, and the epipolar line of geometrically possible matches for a given point in the other retina is parallel to the horizontal retinal meridian. When the eyes move, the epipolar lines shift on the retina, so they are not in general exactly horizontal. However, rather than recompute the position of the epipolar lines every time the eyes move, the brain seems to approximate epipolar lines by horizontally oriented search zones of finite vertical extent. The search zones are horizontal because the epipolar lines are usually close to horizontal, while their finite vertical width allows for the fact that nonzero vertical disparities do occur. Computationally, this strategy is an enormous saving. The cost is that when the eyes adopt an extreme position that gives rise to vertical disparities larger than the vertical width of the search zones, matches are not found and the correspondence problem cannot be solved (Schreiber, Crawford, Fetter, & Tweed, 2001). If this theory is correct, the horizontally elongated disparity tuning surfaces in V1 (Cumming, 2002) may be a neural correlate of the psychophysics reported by Schreiber et al. (2001). The vertical extent of the search zones should then be determined by the vertical width of the disparity tuning surface and the scatter in preferred vertical disparity. The tolerance of vertical disparity estimated from Cumming’s (2002) data is ~0.4 degree at eccentricities between 2 and 9 degrees, while the psychophysics suggests that vertical disparities of ~0.7 degree should be tolerated at 3 degrees eccentricity (Schreiber et al., 2001; Stevenson & Schor, 1997). Given the uncertainties, these are in reasonable agreement.

Of course, nonzero vertical disparities do sometimes occur, especially when the eyes are looking up, down, or off to one side, and there is evidence that they influence perception (first shown by Helmholtz, 1925). Thus, the brain must presumably contain sensors that detect vertical disparity. However, the relative rarity of vertical disparities in perceptual experience suggests that these sensors should be correspondingly sparse. This may explain why vertical disparities appear to influence perception at a more global level, being integrated across the whole image, whereas horizontal disparities appear to act more locally, contributing to a local depth map (Rogers & Bradshaw, 1993, 1995; Stenton, Frisby, & Mayhew, 1984).

The above arguments give some insight into the functional constraints underpinning V1’s observed specialization for horizontal disparity at both the population level and the level of individual cells. The next problem is how to reconcile the individual cell specialization—the horizontally elongated disparity tuning surfaces—with existing models of disparity tuning, in which disparity tuning surfaces must be elongated parallel to the preferred orientation. Thanks to a multitude of electrophysiological, psychophysical, and mathematical studies, stereopsis is one of the best-understood perceptual systems. Our understanding of the early stages of cortical processing is encapsulated in the famous energy model of disparity selectivity, which has successfully explained many aspects of the behavior of real cells (Cumming & Parker, 1997; Ohzawa et al., 1990, 1997). Although it has long been known that there are quantitative discrepancies between the energy model and experimental data (Ohzawa et al., 1997; Prince, Cumming et al., 2002; Prince, Pointon et al., 2002; Read & Cumming, 2003b), the decoupling of disparity and orientation observed in real cells (Cumming, 2002) violates a key energy model prediction in a dramatic, qualitative way. This forces us to reconsider the model’s most fundamental assumptions, such as the underlying linearity (Uka & DeAngelis, 2002). This initial linear stage has been a cornerstone of a whole class of models, not only of disparity selectivity but of V1 processing in general.

Fortunately, as we demonstrate in this article, it turns out that the existing models can be fairly readily modified to allow the observed separation of disparity and orientation tuning. We present two possible ways of solving the problem: (1) multiple subunits with different horizontal position disparities and (2) monocular suppression from inhibitory zones. Both yield horizontally elongated disparity tuning surfaces—the first by extending the response to a wider range of horizontal disparities and the second by preventing response to any but a narrow range of vertical disparities. Both involve further modifications of the energy model, building on previous work in which we introduced a threshold prior to binocular combination (Read et al., 2002). The models are not necessarily alternative possibilities; some combination of the two may occur. For instance, complex cells in V1 may represent the sum of multiple subunits with different horizontal position disparities, with the monocular inputs to each subunit gated by horizontally elongated inhibitory zones.

4.1 Position versus Phase Disparity

The multiple subunit model relies on horizontal position disparities to achieve horizontally elongated disparity tuning surfaces. Phase disparities alone could not achieve this because differences in receptive field phase produce disparities only along an axis orthogonal to the cell’s preferred orientation. Of course, phase disparities could occur alongside the position disparities postulated here. Furthermore, phase disparities may be important in producing the wider range of preferred disparities along the horizontal than along the vertical axis which is observed at the population level (Anzai et al., 1999; Cumming, 2002; DeAngelis et al., 1991, 1995a).

4.2 Model Tests and Predictions

When postulating new physiological models, it is important to consider how they could be tested and falsified. One important point is that, at least as developed here, the multiple subunit model works only for complex cells. The model would respond to all phases of a grating stimulus at the optimum spatial frequency, since as the grating moves, it simply passes from one of the multiple subunits to the next. Thus, the observation of simple cells with horizontally elongated disparity tuning surfaces would present difficulties for the multiple subunit model. It would require a rather contrived relationship between the phase of a subunit’s receptive field and its position within the array of subunits.

Since the monocular suppression model achieves horizontally elongated disparity tuning by postulating horizontally elongated inhibitory regions, the obvious way of testing this model appears to be to see if suppressive zones in real cells are horizontally elongated. However, if there are several suppressive zones, as in our simulations, this could be difficult to establish. For example, in our simulations, the inhibitory zones are arranged in a ring. An experimental determination of the regions where stimuli exerted a suppressive effect would discover a halo of suppression around the receptive field center. In fact, this halo is made up of many horizontally elongated components, but this might not be apparent experimentally. Thus, it is hard to test this feature of the model.

Importantly, both models predict that with appropriately chosen stimuli, the horizontally elongated disparity tuning should vanish, and the coupling between disparity tuning and preferred orientation should reemerge. For example, the monocular suppression model predicts that when the disparate stimulus is a single dot, the two-dimensional disparity tuning should be elongated along the cell’s preferred orientation, as in the energy model. This is because—at least if the inhibitory zones do not substantially overlap the classical receptive field—when the dot stimulus activates the inhibitory zones, it is already largely outside the classical receptive field, so further monocular suppression has little effect. The disparity tuning is therefore elongated along the preferred orientation, as it would be in a model without horizontally elongated inhibitory zones. In contrast, random dot patterns—and most natural stimuli—activate both the receptive field and the inhibitory regions at the same time, allowing the inhibitory zones to suppress the response to vertical disparities. In this context, it is interesting to note that Pack, Born, and Livingstone (2003), using a single disparate dot stimulus, did not report the specialization for horizontal disparity found by Cumming (2002); in their data, in both V1 and MT, disparity tuning appeared to agree well with direction tuning. Our monocular suppression model explains how this apparent discrepancy could be due to the different stimuli used. It would thus be valuable to test disparity tuning in the same cell with both a disparate dot stimulus and with random-dot patterns.

The multiple subunit model still shows a horizontally elongated disparity tuning surface when probed with a single dot stimulus, as with random dot patterns. However, with suitable stimuli, the disparity tuning of this model too can be made to reveal the oriented structure of the receptive fields. For example, consider extended one-dimensional noise stimuli (“bar codes”). The disparity of such a stimulus is effectively one-dimensional: disparities applied parallel to the bar code have no effect, so all disparities can be reduced to their component orthogonal to the bar code. Now consider a stimulus made up of two such bar codes superimposed—one aligned with the cell’s preferred orientation and the other orthogonal to it. Any disparity can be resolved into a component parallel to the preferred orientation (which would affect only the orthogonal bar code), and a component orthogonal to the preferred orientation (which would affect only the parallel bar code). Thus, disparity would effectively be applied only along the two axes orthogonal and parallel to the cell’s preferred orientation. The disparity tuning is therefore elongated along this axis. This is not just an inevitable consequence of the stimulus, but reflects the underlying linearity of the models presented in this article. If V1 neurons implement more sophisticated nonlinearities than proposed here, they could potentially show horizontally elongated disparity tuning surfaces even with this crossed bar code stimulus. Thus, experiments with this stimulus could be a powerful way of probing the computations performed by V1 neurons.

5 Conclusion

This work provides the first explanation of the newly observed specialization for horizontal disparity in V1. It demonstrates that although this observation initially seemed completely at odds with all previous models, it can in fact be fairly straightforwardly incorporated into existing models of disparity selectivity. This represents an important step forward in our understanding of how cortical circuitry is specialized for binocular vision.