Statistical and Bayesian approaches to RNA secondary structure prediction

Abstract

Prediction of RNA secondary structure is a fundamental problem in computational structural biology. For several decades, free energy minimization has been the most popular method for prediction from a single sequence. In recent years, the McCaskill algorithm for computation of partition function and base-pair probabilities has become increasingly appreciated. This paradigm-shifting work has inspired the developments of extended partition function algorithms, statistical sampling and clustering, and application of Bayesian statistical inference. The performance of thermodynamics-based methods is limited by thermodynamic rules and parameters. However, further improvements may come from statistical estimates derived from structural databases for thermodynamics parameters with weak or little experimental data. The Bayesian inference approach appears to be promising in this context.

INTRODUCTION

RNA molecules are involved in some of the cell’s most fundamental processes that include catalysis, pre-mRNA splicing and RNA editing, and regulation of transcription and translation. To a large degree, the function of a regulatory RNA molecule is determined by its structure. Computational methods for modeling RNA secondary structure provide useful initial models for solving the tertiary structure by crystallography or nuclear magnetic resonance (NMR). The problem of computational prediction of secondary structure for a single RNA sequence dates back to the early 1970s (Tinoco et al. 1971). Free energy minimization has been the most popular method for such prediction. A review of the developments of this paradigm for RNA folding can be found elsewhere (Zuker 2000). The partition function approach by McCaskill enables rigorous computation of base-pair probabilities and heat capacity (McCaskill 1990). In recent years, there has been increasing interest in ensemble-base approaches that extend the pioneering work of McCaskill. This review is focused on discussing these recent developments. The Bayesian statistical inference approach has proven to be highly valuable for numerous computational biology problems. A Bayesian framework is outlined for tackling the problem of statistical estimation of thermodynamic parameters using RNA structure databases. Here the single sequence problem is the primary concern. Reviews of methods based on covariation analysis of homologous RNAs can be found elsewhere (Zuker 2000; Gardner and Giegerich 2004).

FREE ENERGY MINIMIZATION PARADIGM

In structural computational biology, free energy minimization for prediction of macromolecular folding is a long-established paradigm. It assumes that, at equilibrium, the solution to the underlying molecular folding problem is unique, and that the molecule folds into the lowest energy state. Also implicitly assumed is that the free energies of individual structural motifs are additive. This paradigm has been the foundation for prediction of RNA secondary structure for over three decades (Tinoco et al. 1971; Nussinov and Jacobson 1980; Zuker and Stiegler 1981; Mathews et al. 1999, 2004). Other applications include protein folding (Anfinsen 1973; Abagyan 1993) and transmembrane helix packing (Pappu et al. 1999). For RNA secondary structure prediction, free energy parameters for basic structural motifs are estimated or extrapolated from chemical melting experiments (Xia et al. 1998; Mathews et al. 1999, 2004). The discrete optimization problem is ill conditioned, in that the prediction is sensitive to small changes in the energy parameters (Zuker 2000; Layton and Bundschuh 2005). Furthermore, there is substantial uncertainty in the energy parameters, particularly for loops. For these reasons, efficient algorithms have been developed for not only computing the minimum free energy (MFE) structure, but also for generating a heuristic set of suboptimal structures (Zuker and Stiegler 1981; Mathews et al. 1999, 2004). An alternative approach computes all suboptimal foldings within an energy increment above the MFE (Wuchty et al. 1999). The exponential growth in the number of these foldings motivated recent development of the RNAshapes method for the efficient representation of the near-optimal foldings (Giegerich et al. 2004). The complete suboptimal approach addresses the low-energy end of the unweighted energy landscape. Neither approach guarantees an unbiased representation of the Boltzmann-weighted ensemble. The free energy minimization algorithm (Zuker and Stiegler 1981) and the algorithm for computing suboptimal structures (Wuchty et al. 1999) have been extended for two or more interacting RNAs (Andronescu et al. 2005). For the simple Nussinov–Jacobson energy model of constant base-pair energies (Nussinov and Jacobson 1980), an efficient algorithm has been developed for computation of the number of structures with k fewer base pairs than the maximum number (Clote 2005). Free energy minimization algorithms have also been developed to include certain types of pseudoknots (Rivas and Eddy 1999; Reeder and Giegerich 2004), but applications are limited to short or moderate-length sequences, depending on the time complexity and the memory requirement of the particular algorithm. A list of the programs for implementing these algorithms is presented by Table 1 ▶.

TABLE 1.

RNA folding programs based on free energy minimization

Name	Functionsa	URL
mfold	Folding of single and interacting nucleic acids	http://www.bioinfo.rpi.edu/applications/mfold
RNAstructure	Window software for RNA folding and oligo design	http://rna.urmc.rochester.edu/rnastructure.html
Vienna RNA package	Optimal and complete suboptimal folding	http://www.tbi.univie.ac.at/~ivo/RNA
RNAshapes	Abstract shape representation of Vienna suboptimal foldings	http://bibiserv.techfak.uni-bielefeld.de/rnashapes
pknotsRG	Folding including a class of simple pseudoknots	http://bibiserv.techfak.uni-bielefeld.de/pknotsrg
PKNOTS	Folding including a class of pseudoknots	http://selab.wustl.edu/cgi-bin/selab.pl?mode=software
RNALOSS	Locally optimal folding	http://clavius.bc.edu/~clotelab/RNALOSS

^aOnly directly relevant functions are listed.

PARTITION FUNCTION APPROACH

In a drastic departure from free energy minimization, the partition function approach pioneered by McCaskill (1990) laid the foundation for statistical characterizations of the equilibrium ensemble of RNA secondary structures. In particular, base-pair probabilities can be calculated. Similar to its MFE counterpart, the algorithm for computing partition function and base-pair probabilities is cubic and requires quadratic storage. The significance of base-pair probabilities has been further demonstrated in two recent studies. For base pairs in the MFE structure, those with higher probabilities have higher predictive accuracy measured by positive predictive value (Mathews 2004). The positive predictive value is the percentage of base pairs in the predicted structure that are in the structure determined by comparative sequence analysis. Thus, base-pair probabilities provide measures of confidence for MFE predictions. That study was based on a new partition function algorithm that accommodates coaxial stacking and more recent energy parameters. Furthermore, base-pair probabilities are found to be less affected by uncertainties in energy parameters than is the MFE structure (Layton and Bundschuh 2005). The McCaskill algorithm has also been extended to include a class of pseudoknots (Dirks and Pierce 2003, 2004). Like the partition function, the mean and variance (and any moments in general) of the Boltzmann-weighted free energy distribution can be calculated, and these ensemble characteristics are reported to be useful for distinguishing biological sequences from random sequences (Miklos et al. 2005). A partition function algorithm for k-point mutants of an RNA sequence has recently been described (Clote et al. 2005). For modeling the hybridization of two nucleic acid molecules, the Zuker group was the first to compute partition function and base-pair probabilities (Dimitrov and Zuker 2004). These developments are indicative of the recent surge in interest in the ensemble-based approaches. Table 2 ▶ presents a list of programs for implementing the partition function algorithms and the extensions below with comprehensive Turner free energy parameters.

TABLE 2.

RNA folding programs for characterizing Boltzmann ensemble of RNA secondary structures, using comprehensive Turner free energy parameters

Name	Functionsa	URL
Sfold	Statistical sampling and clustering, and rational design of nucleic acids	http://sfold.wadsworth.org; http://www.bioinfo.rpi.edu/applications/sfold
RNAstructure	Partition function and base-pair probabilities	http://rna.urmc.rochester.edu/rnastructure.html
Vienna RNA package	Partition function and base-pair probabilities	http://www.tbi.univie.ac.at/~ivo/RNA
NUPACK	Partition function and base-pair probabilities including a class of pseudoknots	http://www.acm.caltech.edu/~niles/software.html

^aOnly directly relevant functions are listed.

STATISTICAL SAMPLING APPROACH

In the traceback step of an RNA folding algorithm, base pairs are generated one at a time according a chosen principle (e.g., energy minimization or probabilistic sampling as discussed below) to form a secondary structure. The longstanding problem of a statistical representation of probable foldings can be addressed by a sampling extension of the partition function approach (Ding and Lawrence 2003). In the traceback step, the conditional probabilities computed with partition functions are used to sample a new base pair or unpaired base(s), given partially formed structure. Thus, the essence of the sampling algorithm is stochastic trace-back. This algorithm generates a sample of secondary structures in proportion to their Boltzmann weights, guaranteeing a statistical representation of the Boltzmann-weighted ensemble.

A statistical sample of the ensemble allows sampling estimates of the probabilities of any structural motifs, from the simplest elements of base pair and unpaired base, to loops of various types, to more complex structures consisting of stems and loops that may be of special interest in a given application. In particular, probability profiling of single-stranded regions in RNA secondary structure is directly applicable to the rational design of mRNA-targeting nucleic acids (Ding and Lawrence 2001, 2003, 2005; Ding 2002; Ding et al. 2004). The Boltzmann-weighted density of states (BWDOS) (Ding and Lawrence 2003) characterizes the weighted energy landscape, whereas a density-of-states algorithm (Cupal et al. 1997), applicable only to short sequences, describes the unweighted landscape. A structure sample can also be used for computation of other characteristics of the Boltzmann ensemble. For example, the mean and the variance of the free energy distribution can be estimated by a sample, whereas exact calculations require laborious algorithm development (Miklos et al. 2005). In principle, a sampling extension can also be developed for a partition function algorithm including pseudoknots. In this case, base-pair probabilities can be estimated by a sample, and the estimates should closely approximate those computed by a high-order algorithm (Dirks and Pierce 2004).

A sample of moderate size drawn from the ensemble of an enormous number of possible structures is sufficient to guarantee statistical reproducibility in the estimates of typical sampling statistics. The reproducibility is best demonstrated when two independent samples do not have a single structure in common (Ding and Lawrence 2003). These seemingly surprising observations are fully expected for an exact sampling algorithm.

In a recent study on both structural RNAs and mRNAs (D. Mathews, pers. comm.), base-pair probabilities estimated by the following three methods were compared to those computed by the partition function approach (McCaskill 1990; Mathews 2004): (1) the heuristic set of suboptimal foldings from the mfold program (Zuker 1989), (2) the complete suboptimal foldings (Wuchty et al. 1999), and (3) statistical sampling (Ding and Lawrence 2003). The same thermodynamic parameters and energy functions (Mathews et al. 2004) are used in implementing all these methods. These three methods generate different sets of structures, while the partition function approach does not generate a single structure. However, the partition function method does offer exact base-pair probabilities for the Boltzmann ensemble. Thus, to assess how well a set of structures represents the Boltzmann ensemble, the estimates of the base-pair probabilities using this set can be compared with the exact probabilities.

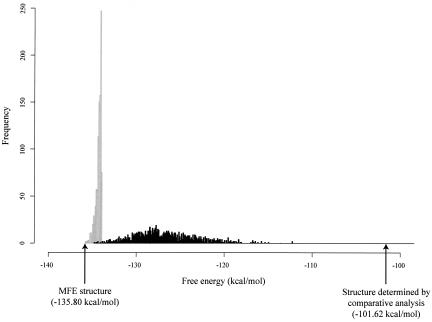
It was found from this study that the sampling method makes far better estimates than do the other two methods. In particular, a small sample of only 100 structures performs far better than does a complete set of suboptimal structures within 2 kT of the lowest free energy structure. The improvement by sampling is over an order of magnitude, as measured by the square root of the mean square deviation (RMSD). The major reason for this result is that, for sequences of several hundred bases or longer, the near-optimal foldings constitute only a small portion of the Boltzmann ensemble. This is illustrated in Figure 1 ▶ for an RNase P sequence; there is little overlap between the BWDOS for a sample of 1000 structures and the unweighted density of states for the 1000 structures with the lowest energies. Another reason for the above result is that there exist “entropic clusters” in the ensemble (Ding and Lawrence 2003). In such a cluster, each structure has a much higher energy (lower probability) than does the MFE; however, the cluster will be represented in a sample simply as a result of the sheer huge number of structures in the cluster, so that the cluster has a substantial probability (sum of probabilities of individual structures in the cluster).

FIGURE 1.

The energy distribution of the 1000 lowest energy structures (gray bars, i.e., the partial density of states for free energy below −133.90 kcal/mol, 1.9 kcal/mol above the MFE) and the energy distribution of 1000 sampled structures (black bars, i.e., the density of states of the weighted ensemble) for Heliobacterium chlorum RNase P RNA of 342 nt in length (GenBank accession U64881). The structure determined by comparative analysis is from the RNase P database (Brown 1999) and does not contain pseudoknotted base pairs. For a comparison based on the same implementation of the thermodynamic rules, all other structures here and the free energies of all the structures were computed with the Vienna package (Hofacker 2003).

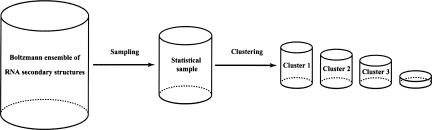
CLUSTER REPRESENTATION OF BOLTZMANN ENSEMBLE

In the sampled ensemble, distinct structural clusters were observed (Ding and Lawrence 2003). This observation suggests that the Boltzmann ensemble can be efficiently represented by clusters. An automated clustering procedure and tools have recently been developed for this purpose (Chan et al. 2005; Ding et al. 2005; Y. Ding, C.Y. Chan, and C.E. Lawrence, in prep.). The procedure returns three to four clusters on average. Another advantage of clustering is that the centroid structure, as the single best representative of the cluster, can be easily identified with little computational cost. The centroid of any set of structures is defined as the structure in the whole ensemble that has the shortest total distance to structures in the set. For the base-pair distance between two structures, the centroid is simply the structure formed by all base pairs having a frequency >0.5 in the structure set (Ding et al. 2005). The clusters together with their probabilities (estimated by frequencies in the sample), and their centroids, present a complete and efficient statistical characterization of the Boltzmann ensemble (Fig. 2 ▶). Similar to the reproducibility of ensemble-level sampling statistics (Ding and Lawrence 2003), the clusters and centroids are also statistically reproducible from one sample to another, even when the two independent samples do not share a single structure (Y. Ding, C.Y. Chan, and C.E. Lawrence, in prep.). It was a surprising finding that the centroid of the sampled ensemble and the best cluster centroid make structural predictions that are substantially improved over the MFE predictions (Ding et al. 2005), a result that further validates ensemble-based approaches.

FIGURE 2.

Efficient representation of the Boltzmann ensemble of secondary structures for an RNA molecule by clusters identified from a statistically representative sample of structures. The size or probability of a cluster is estimated by the frequency of occurrence of the cluster in the sample, and a representative of the cluster is its centroid structure (Ding et al. 2005).

In a recent comparison between mRNAs and structural RNAs (Y. Ding, C.Y. Chan, and C.E. Lawrence, in prep.), similarity was observed for the number of clusters and the energy gap between the MFE structure and the sampled ensemble. However, for structural RNAs, there are more high-frequency base pairs in both the Boltzmann ensemble and the clusters, and the clusters are more compact. Thus, clustering provides a new method for detecting differences between structural and nonstructural RNAs and between biological RNA sequences and random sequences (Y. Ding, C.Y. Chan, and C.E. Lawrence, in prep.).

BAYESIAN STATISTICAL INFERENCE APPROACH

Since the early 1990s, Bayesian methods have been applied to a wide range of problems in the burgeoning fields of bioinformatics and genomics. The Bayesian Revolution (Beaumont and Rannala 2004; Eddy 2004) can be partly credited to the conceptual simplicity of the Bayesian approach (as opposed to the difficulties of the classic, frequentist approach; Gelman et al. 1997) and partly to advances in computing power.

Bayesian inference paradigm

Bayesian inference methods treat all quantities in a problem as random variables. A Bayesian method starts with the specification of a joint distribution of all quantities of interest. Basic probability rules are applied to derive the posterior distributions of the unknown quantities, given the observed data. Inferential statements are made rigorously from these posterior distributions (Gelman et al. 1997). While these posterior distributions are usually easy to write down, they require intensive computations that have become feasible only with advancing computational power. The Bayesian method has been successfully used in regulatory motif search (Lawrence et al. 1993; Thompson et al. 2003), sequence alignment (Zhu et al. 1998), and sequence segmentation (Liu and Lawrence 1999), and it has the potential to provide a powerful solution to the general problem of missing data in the analysis of biopolymer sequences (Liu and Lawrence 1999). Excellent textbooks on Bayesian analysis are available (Berger 1985; Gelman et al. 1997; Carlin and Louis 2000; Liu 2001; Jaynes 2003). The motivation for and the framework of the Bayesian methodology are outlined below.

The focus of all statistics is on making inferences. The concept of statistical inference closely follows the dictionary definition of inference: “the process of deriving a conclusion from fact and/or premise”. In statistics the facts are the observed data, the premise is represented by a probabilistic model of the system of interest, and the conclusions concern unobserved quantities. In classical statistics, inferences are made by finding point estimates of unknown variables, with maximum likelihood estimates being the most common type of estimates. Uncertainty is addressed by setting confidence limits on these estimates. Bayesian statistics has a more ambitious goal: to find the probability distribution of all unknown variables after considering the data. The full process of a typical Bayesian analysis can be described as consisting of three main steps: (1) setting up a full probability model that includes all of the variables, so as to capture the relationships among these variables; (2) summarizing the findings for particular quantities of interest, by appropriate posterior distributions; and (3) evaluating the appropriateness of the model and suggesting improvements (Gelman et al. 1997).

A standard procedure for carrying out Step 1 is to first write down the likelihood function, i.e., the probability of the observed data given the unknowns, and multiply it by a prior distribution, i.e., a distribution for all of the unobserved variables (typically, unknown parameters). Let y denote the observed data, and θ, the unobserved parameter. The joint probability distribution is represented as joint = likelihood * prior, i.e.,

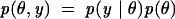where the prior distribution on θ, p(θ), reveals what is known about the parameter without the knowledge of the data; p(y | θ) is often denoted as l(θ | y), and is referred to as the likelihood in classical statistics that is based on a model of the underlying process.

Bayesian inference is drawn by examination of the probability of all possible values of the parameter, after consideration of the data. Accordingly, Step 2 is completed by obtaining the posterior distribution, i.e., the conditional distribution of the parameter, given the data, through the application of Bayes’s Theorem to the joint distribution:

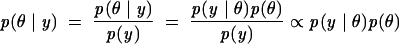where the posterior distribution p(θ | y) tells us what is known about θ, given knowledge of the data. Thus, the primary tasks of Bayesian analysis are to develop a model for p(θ,y) and to perform computation necessary to summarize p(θ | y). The computation of the marginal likelihood p(y) is typically the most challenging part of the Bayesian analysis. The popular Gibbs sampler and related Monte Carlo methods can aid Bayesian computation (Liu 2001).

Bayesian inference can not only be readily applied to any probability model, but it can also avoid the difficulties of asymptotic inferences for interval estimates that are encountered by classical statistics. It provides a satisfactory way of explicitly introducing and keeping track of assumptions about prior knowledge or ignorance. When no or minimal prior information is available about the parameter, a noninformative prior can be considered in the application of the Bayesian machinery for making inferences. Typically, a uniform density giving equal weight to all possible values of the parameter is used for this purpose. For a continuous parameter defined on an infinite interval, the uniform density is referred to as an improper prior because it does not integrate to 1. Use of an improper prior can lead to a proper posterior distribution, but caution must be exercised in interpretation of the results (Gelman et al. 1997). In this case, the posterior mode is the maximum likelihood estimate, because the posterior distribution is proportional to the likelihood function. In many situations, noninformative prior Bayesian inference could be argued to be the single most powerful method of statistical analysis (Berger 1985).

Applications to RNA structure predictions

From the perspective of statistical mechanics, the secondary structure of an RNA sequence is a random variable that follows the Boltzmann equilibrium distribution. From a full Bayesian viewpoint, the Boltzmann equilibrium distribution is, in fact, a conditional probability distribution, given the RNA sequence data and the thermodynamic parameters (Ding and Lawrence 2003). The Bayesian inference approach was first applied to the RNA folding problem for a single sequence (Ding and Lawrence 1999). In this application, the set of random variables includes the primary sequence data (observed), the unknown secondary structure and number of destabilizing loops, and free energy parameters. Based on the stacking energy model and noninformative priors, the Bayesian algorithm returns posterior distributions for the number of destabilizing loops, stacking energy matrices, and secondary structures. In particular, the idea of generating a statistically representative sample of RNA secondary structures after partition function calculation was presented for the first time.

The Bayesian approach has also been applied to the prediction of the common secondary structure for homologous sequences (Knight et al. 2004). This procedure works on a reduced structural space, by considering a set of foldings based on thermodynamic predictions made by the RNAsubopt program of the Vienna package (Hofacker 2003). Posterior inference is performed using Bayes’s Theorem, given thermodynamic predictions, alignment (mutual information) and chemical mapping information, and under the assumptions of uniform prior for the structures in the reduced space, and conditional independence for data from different sources. The alternative of modeling the full structure space, as considered for the one-sequence problem (Ding and Lawrence 1999), appears to be much more challenging to implement for the multiple-sequence problem.

STATISTICAL ESTIMATION OF THERMODYNAMIC PARAMETERS

In terms of free energy, the sampled ensemble can be much closer to the structure determined by comparative analysis than are the MFE structure and the near-optimal structures (Fig. 1 ▶); nevertheless, there is much room for improvement. If the free energy function were complete, and if all thermodynamic parameters were accurate, the biological structure could often be expected to have the lowest energy. However, the thermodynamics parameters for RNA, for which thermodynamics is arguably best studied among macromolecules, are incomplete. In particular, extrapolations for large loops are currently necessary. Thus, any free-energy-based algorithm is limited by the parameters used.

Structure predictions might be improved through kinetic modeling of RNA folding (Doshi et al. 2004), and through improvements in the accuracy of the free energy model. While the set of experimental parameters is expected to continue to improve, an alternative is to statistically estimate the parameters, by taking advantage of RNA structure databases (Larsen and Zwieb 1991; Brown 1999; Cannone et al. 2002; Rosenblad et al. 2003; Zwieb et al. 2003; Sprinzl and Vassilenko 2005). This strategy was first considered by Michael Zuker in the 1990s. In numerous presentations (including the 2003 Computational RNA Workshop in Benasque, Spain), Zuker described “pseudo energy rules” for base-pair stacking and small structural motifs that are derived by computing the ratio of the observed frequencies over the expected frequencies from random background. Essentially based on the same framework, the published statistical energies for base-pair stacking are in excellent agreement with the well-studied experimental energies (Dima et al. 2005), suggesting the potential of such “knowledge-based” approaches to improve estimates of energies for loops and other secondary structural motifs.

The idea of estimating energy parameters with known structural information does follow the way a Bayesian thinks about a problem. It has been shown that the primary sequence data, the secondary structure, and the free energy parameters can be described together through Bayesian statistical modeling (Ding and Lawrence 1999). Like the relationships among pressure, volume, and absolute temperature for an ideal gas of a fixed number of moles, inference on any variable can be made from the knowledge of the other two variables. Analogously, databases containing secondary structural information can be used to make inferences on the thermodynamic parameters. The accuracy of the estimates obviously rests on the assumption that the structural information from comparative analysis is reliable. For 16S and 23S ribosomal RNAs, comparative analysis identifies nearly all of the base pairs present in the crystal structures, but also predicts some base pairs that are absent in the crystal structures (Cannone et al. 2002).

For statistical inference, independence of observations simplifies the formulation of a probability model, in particular, the likelihood function. Correlated observations complicate the analysis. For the problem of multiple sequence alignment, two methods have been proposed to address the issue of sequence correlation (or redundancy) due to similarity among related sequences. One approach is to recruit diversified sequences so as to minimize correlation. This approach is not objective and results in loss of information, and automation is essential as data sets grow (Vingron and Sibbald 1993). Another approach is to use a sequence weighting scheme that assigns higher weights to more distantly related sequences, based on the distance between a sequence and an ancestral or generalized sequence (Luthy et al. 1994; Thompson et al. 1994); alternatively it can assign weights based on the diversity observed at each position in the alignment (Henikoff and Henikoff 1994). Conceptually, inferences for thermodynamic parameters can be performed for any sequence in a database or for a set of sequences. It is advantageous to pool information from diverse sequences, for improved accuracy in the estimates.

The Turner parameter values can be used for prior specification, e.g., uniform priors on intervals centering at Turner values. The prior specification is the first step of Bayesian statistical inference. For the posterior distribution of a parameter, a global peak is very interesting. If the peak is near the Tuner parameter value, this indicates that the Turner parameter is supported by the structural data used. If the peak is away from the Turner value, this suggests that the value can be corrected by the posterior mode. If the posterior is flat on the interval, this may mean that there remains substantial uncertainty about the parameter so that a much larger data set may be necessary for an estimate with improved accuracy. Alternatively, a flat posterior may suggest that the parameter is not important, if predictions are not sensitive to changes in this parameter.

For the large number of free energy parameters, the high dimensionality of the estimation problem will pose computational challenges. To reduce dimensionality, a “divide and conquer” strategy can be considered that focuses on one class of motifs when energies of other motifs are considered to be reliable and thus are assumed to be known. For example, for estimating the parameters for multibranched loops, tRNA sequences (with the implications of modified bases taken into consideration as further discussed below) may be considered and it can be assumed that the energies for base-pair stacking and small loops are known and accurate. The values of the estimated energies for prediction improvement can be assessed by the positive predictive values and sensitivity for MFE structure and centroids computed with these estimates. The sensitivity for a predicted structure is the percentage of base pairs in the structure determined by comparative sequence analysis that are also present in the predicted structure.

It is well understood that modified nucleotides (Rozenski et al. 1999) present problems for structure predictions for tRNAs. Some of the modified nucleotides either cannot form the correct set of hydrogen bonds or cannot stack (D. Mathews, pers. comm.). These nucleotides can be handled by forcing them to be unpaired for folding, and a list of such nucleotides has been published (Mathews et al. 1999). Other modified nucleotides can still form canonical pairs, but with a high likelihood of altered strength for every nucleotide (D. Mathews, pers. comm.). For these nucleotides, their energetic contributions may also be estimated by applying the Bayesian framework, with an appropriate assembly of tRNA sequences that contain a particular modification of interest.

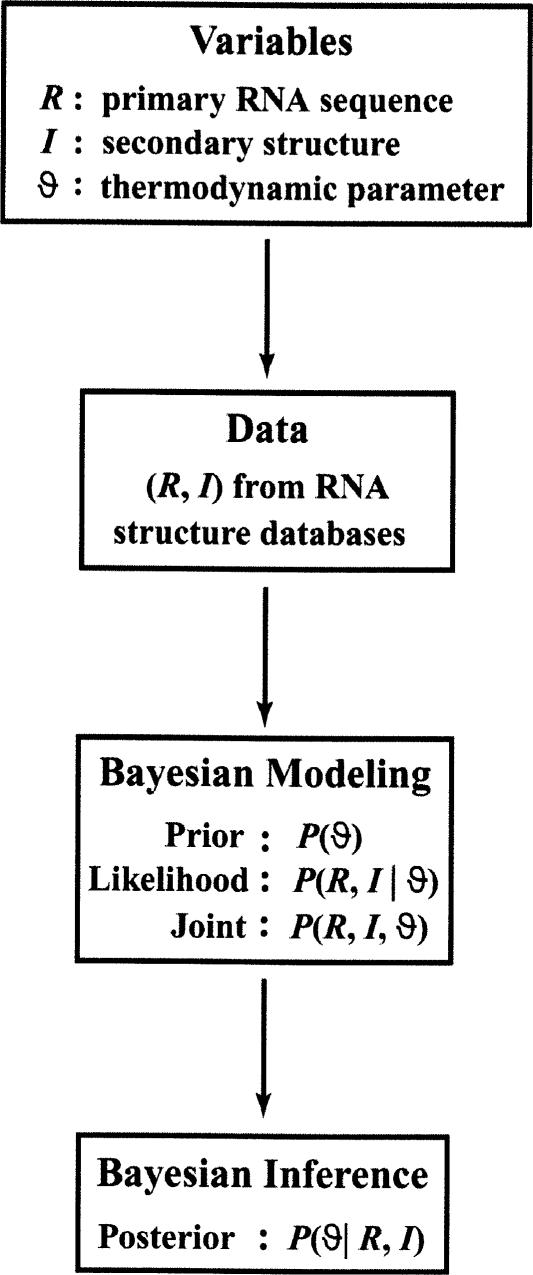
The Bayesian inference process is illustrated in Figure 3 ▶ for the simplest case of one sequence, one structure, and one parameter. For multiple sequences and parameters, the construction of the likelihood must take into account multiple observations (e.g., through the assumption of independence), and posterior inference can generally be facilitated by Gibbs sampler and related Monte Carlo methods (Liu 2001). In some cases, e.g., in discrete modeling of the base-pair stacking parameters (Ding and Lawrence 1999), the marginal likelihood can be exactly computed.

FIGURE 3.

The Bayesian inference framework for estimating a thermodynamic parameter, with the use of RNA structure databases. The essence of the Bayesian viewpoint is that both the data and the parameter are random variables. Here, the primary RNA sequence R and the known secondary structure I are data available from RNA structure databases, and ϑ is the unknown thermodynamic parameter. Based on a likelihood function constructed with an appropriate model and a prior distribution on the parameter, the joint probability distribution of all variables will allow Bayesian inference to be drawn about the thermodynamic parameter, through the posterior distribution of ϑ given the data, i.e., P(ϑ | R, I).

CONCLUSIONS

The paradigm-shifting work by McCaskill has inspired the recent developments of extended partition function algorithms for modeling single molecular folding and hybridization of two nucleic acid molecules, sampling extension, and clustering representation of sampled ensemble. These methods enable characterizations of the equilibrium structure ensemble that are not possible with the use of free energy minimization.

Computational solution of a macromolecular folding problem requires two components: sufficiently complete and accurate free energies and a procedure to find the minimum of the energy function (Abagyan 1993). The energy model is incomplete for RNA secondary structure. The ensemble is important to consider even in the ideal case of the complete energy model, because macromolecular folding may not always be governed by the Anfinsen hypothesis of lowest energy state (Anfinsen 1973). For RNA, in the rugged energy landscape, it might be possible that one of the structural clusters approximately represents an energy well that is utilized in folding to the native structure, while the others could be associated with kinetic traps and metastable (misfolded) states that can be involved in an RNA conformational switch.

In the post-genomic era, the Bayesian approach has proven to be highly useful to address uncertainties in large, noisy biological data sets (Eddy 2004). The Bayesian inference approach appears to be well suited to the problem of estimating thermodynamic parameters from RNA structure databases. The application of Bayesian methods to computational RNA problems lags behind the applications of these methods to sequence analysis and other genetic problems (Beaumont and Rannala 2004). The potential of the highly flexible Bayesian framework is worthy of full exploration in the era of RNAomics.