Stronger control of ATP/ADP by proton leak in pancreatic β-cells than skeletal muscle mitochondria

Abstract

Pancreatic beta cells respond to rising blood glucose concentrations by increasing their oxidative metabolism, which leads to an increased ATP/ADP ratio, closure of K_ATP channels, depolarization of the plasma membrane potential, influx of calcium and the eventual secretion of insulin. Such a signalling mechanism implies that the ATP/ADP ratio is flexible in beta cells (β-cells), which is in contrast with other cell types (e.g. muscle and liver) that maintain a stable ATP/ADP poise while respiring at widely varying rates. To determine whether this difference in flexibility is accounted for by mitochondrial peculiarities, we performed a top-down metabolic control analysis to quantitatively assess how ATP/ADP is controlled in mitochondria isolated from rat skeletal muscle and cultured beta cells. We show that the ATP/ADP ratio is more strongly controlled (approx. 7.5-fold) by proton leak in beta cells than in muscle. The comparatively high importance of proton leak in beta cell mitochondria (relative to phosphorylation) is evidenced furthermore by its relatively high level of control over membrane potential and overall respiratory activity. Modular-kinetic analysis of oxidative phosphorylation reveals that these control differences can be fully explained by a higher relative leak activity in beta cell mitochondria, which results in a comparatively high contribution of proton leak to the overall respiratory activity in this system.

INTRODUCTION

The global incidence of type 2 diabetes is rising rapidly as 300 million people, mostly young adults, are projected to be affected by the year 2025 [1]. Multiple organ sites are involved in the occurrence of the high blood glucose levels associated with this disease; defects in the insulin responsiveness of skeletal muscle and liver are responsible for insulin resistance, whereas defects in the function of pancreatic beta cells (β-cells) account for its final progression to hyperglycemia [2]. Evidently, a fundamental understanding of beta cell function will be necessary to appreciate fully how type 2 diabetes arises.

When blood glucose levels rise, beta cells increase their oxidative metabolism, which leads to an increased mitochondrial protonmotive force and cytoplasmic ATP/ADP ratio, closure of ATP-sensitive potassium channels, depolarization of the plasma membrane potential, influx of calcium and the eventual secretion of insulin [3]. Interestingly, the glucose-induced increases in the protonmotive force and the cytoplasmic ATP/ADP poise are fundamentally different from that in other cell types such as liver or muscle, where regulatory feedback loops ensure that the response of these parameters to substrate supply is not as pronounced [4]. The unique character of beta cells is often attributed to their particular hexokinase isoenzyme, ‘glucokinase’ [5]. Because of its exceptionally high control on glycolytic flux, this enzyme is thought to govern the ATP/ADP ratio and insulin secretion almost exclusively [6]. However, the effects of glucose on the protonmotive force [7] and potential constraints imposed by mitochondrial metabolism on insulin secretion [8] are largely ignored in this view of events.

Mitochondria play an essential role in GSIS (glucose-stimulated insulin secretion). This is demonstrated directly by the observation that beta cells depleted of mitochondrial DNA (i.e. lacking functional mitochondria) do not exhibit GSIS [9,10]. In addition, the importance of mitochondria is indicated by several lines of circumstantial evidence: UCP2 ablation, which improves efficiency of ATP synthesis, increases GSIS [11]; acute overexpression of lactate dehydrogenase, which disadvantages mitochondrial oxidation of pyruvate, impairs GSIS [12] and inhibition of the sodium-calcium exchanger, which increases mitochondrial metabolism, potentiates GSIS [13]. Furthermore, it is becoming increasingly clear that the development of type 2 diabetes is associated with mitochondrial dysfunction [2,14–16].

Given the pivotal position of mitochondria in GSIS, we hypothesized that the relatively high flexibility of the ATP/ADP ratio in beta cells may be accounted for, at least partly, by mitochondrial peculiarities. Clearly, this would not be the case if this poise was controlled exclusively by glucokinase. To distinguish between these different scenarios, we performed a modular, or top-down, metabolic control analysis of respiration using mitochondria isolated from either cultured beta cells or rat skeletal muscle. Metabolic control analysis [17–20] is a powerful systems biology tool that allows a quantitative description of the strength of the control over biological system properties exerted by the individual components of the system. We conducted a top-down control analysis [21] to examine the distribution of control over the ATP/ADP ratio in the two types of mitochondria, and modular kinetic analysis [22] to reveal which system-kinetic characteristics caused the observed differences in control.

In the present study we show that the proton leak across the mitochondrial inner membrane exerts more control over the ATP/ADP ratio in mitochondria from beta cells than in those from muscle. This difference can be fully explained by the higher relative proton leak in beta cell mitochondria.

MATERIALS AND METHODS

Mitochondria

Skeletal muscle mitochondria were isolated from female Wistar rats (6–10 weeks old) as described previously [23], using defatted BSA. Beta cell mitochondria were prepared from cultured INS-1E cells grown as described previously [24]. Each of 4 trays (500 cm², Nunclon™) were seeded at 2.5×10⁵ cells·ml⁻¹ and allowed to reach approx. 90% confluence. Following two washes with ice-cold buffer containing 0.25 M sucrose, 20 mM Hepes (pH 7.4), 2 mM EGTA, 10 mM KCl, 1.5 mM MgCl₂ and 0.1% (w/v) defatted BSA (referred to as SHE), cells were scraped off the trays and harvested in SHE by centrifugation at 350 g (10 min, 4 °C). Cell pellets were resuspended in 5 ml of SHE supplemented with a protease-inhibitor cocktail (Calbiochem) and then homogenized using a glass homogenizer. Subsequent to 15-fold dilution in supplemented SHE and removal of cell debris (3 min centrifugation at 1100 g followed by filtration through muslin), mitochondria were pelleted by centrifugation at 12000 g (11 min, 4 °C). This procedure gave good quality mitochondria (respiratory control ratio with succinate approx. 3) and yielded typically 10 mg of mitochondrial protein per 500 cm² tray.

Respiratory flux, membrane potential and ATP/ADP

Oxygen consumption was measured at 37 °C using a Clark-type electrode (Rank Brothers, Cambridge, U.K.) calibrated with air-saturated medium comprised of 0.115 M KCl, 10 mM KH₂PO₄, 3 mM Hepes (pH 7.2), 1 mM EGTA, 2 mM MgCl₂, and 0.3% (w/v) defatted BSA, assumed to contain 406 nmol atomic oxygen·ml⁻¹ [25]. Simultaneously with respiratory activity, Δψ (mitochondrial membrane potential) was measured using an electrode sensitive to the lipophilic TPMP (triphenyl-methylphosphonium) cation [26]. Mitochondria were incubated at 0.35 mg·ml⁻¹ (muscle) or 0.9 mg·ml⁻¹ (beta cells) in the presence of 350 ng·ml⁻¹ nigericin to collapse ΔpH and 4 μM rotenone to inhibit complex I. The TPMP⁺-sensitive electrode was calibrated with sequential additions of TPMP⁺ up to 2 μM and 4 mM succinate was then added to initiate respiration. Experiments were terminated with 1.5 μM FCCP (carbonyl cyanide p-trifluoromethoxyphenylhydrazone), allowing correction for any small baseline drift. Δψ values were calculated from the distribution of TPMP⁺ across the mitochondrial inner membrane using a binding correction factor of 0.4 mg of protein·μl⁻¹.

The extra-mitochondrial ATP/ADP ratio was determined using a luciferase-based assay [27]. Samples were quenched with ice-cold extraction buffer containing 3% (v/v) perchloric acid, 2 mM EDTA and 0.5% (v/v) Triton X-100 (final concentrations). After denatured protein was spun-down, the supernatants were neutralized with buffer containing 2 M KOH, 2 mM EDTA and 50 mM Mops [3-(N-morpholino)-2-hydroxypropanesulphonic acid] (20:6, v/v), vortexed and then centrifuged to pellet the KClO₄ precipitate. ATP assays were performed in Tris-acetate buffer (pH 7.8) containing 15 μM luciferin and 0.12 μg of luciferase (Sigma, U.K.), using an AutoLumatPlus luminometer (Berthold Technologies, U.K.). Standards were prepared in quenching buffer and neutralized the same way as the samples. Samples lacking mitochondria were included to confirm all ATP was recovered. ADP contents were estimated by subtracting measured ATP from added ATP.

Modular kinetics

Mitochondrial oxidative phosphorylation can be divided conceptually into modules that establish Δψ and those that dissipate it. The kinetic behaviour of a ‘Δψ-producer’ can be established by specific modulation of a ‘Δψ-consumer’ and reciprocally, the behaviour of a consumer is revealed upon modulation of a producer [22]. Oxygen consumption and Δψ were measured simultaneously using mitochondria that were incubated in the presence of 350 ng·ml⁻¹ nigericin, 4 μM rotenone, 0.7 μg·ml⁻¹ oligomycin (to inhibit the phosphorylation system) and 4 mM succinate. State 4 respiratory activity was titrated with either malonate (up to 0.5 mM) or FCCP (up to 0.8 μM). Expression of the oxygen uptake rates observed in successive steady states, as a function of the concomitant Δψ values, revealed the kinetic responses of proton leak (malonate titration) and the respiratory chain (FCCP titration) to Δψ.

Metabolic control analysis

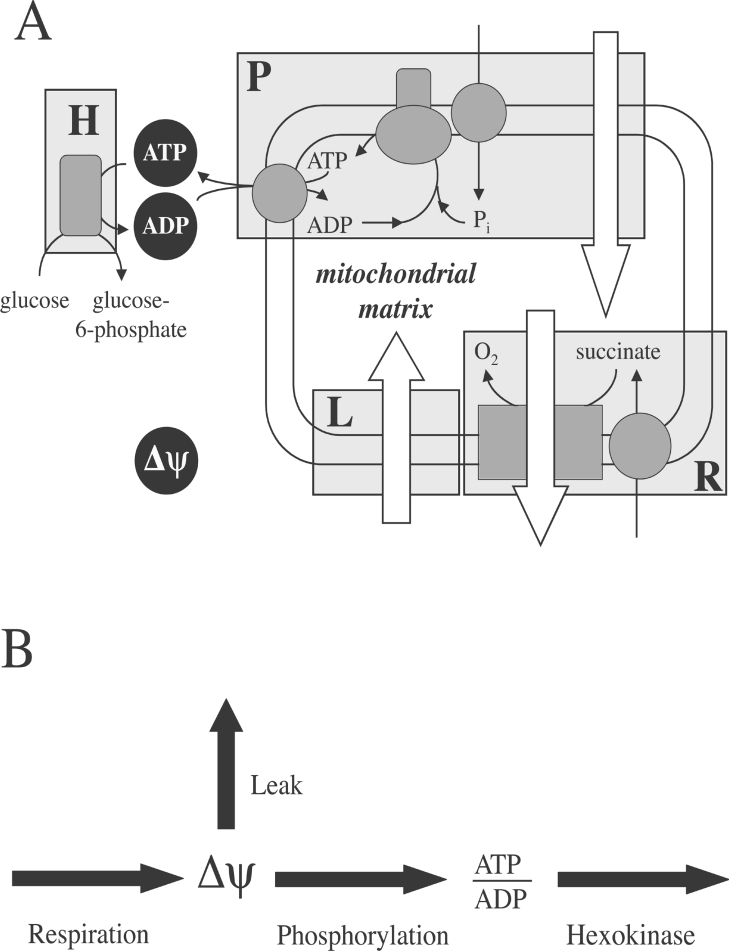
An introduction to top-down metabolic control analysis has been provided previously [21]. We simplified our experimental system conceptually to comprise four enzymatic modules that communicate through two metabolic intermediates, Δψ and the extra-mitochondrial ATP/ADP ratio (Figure 1). Experiments were performed with isolated mitochondria respiring succinate under phosphorylating conditions in the presence of nigericin and rotenone. Succinate is transported into the mitochondrial matrix by the dicarboxylate carrier and subsequently oxidized by the respiratory chain. The net result of these processes (the respiration module) is the establishment of Δψ, which is dissipated by proton-leak reactions (the leak module) and the activity of the phosphorylation apparatus, which includes the phosphate carrier, the ATP synthase and the adenine nucleotide translocase (the phosphorylation module). To allow the system to reach a steady state, 1.6 units·ml⁻¹ hexokinase (yeast enzyme from Sigma) was added to consume ATP (the hexokinase module); state 3 respiration was initiated by addition of 100 μM ATP and 20 mM glucose. The mitochondrial sample prepared from beta cells appeared to exhibit endogenous hexokinase activity (results not shown). Because the hexokinase isoenzyme found in beta cells (glucokinase) exhibits a K_1/2 for ATP that is comparable with that of the yeast enzyme (compare [28] with [29]), it was deemed justifiable to exploit this activity as the ATP-consuming module in beta cell experiments.

Figure 1. Mitochondrial oxidative phosphorylation from a top-down perspective.

As explained fully in the Materials and methods section, 4 enzymatic units – respiration (R), leak (L), phosphorylation (P) and hexokinase (H) – communicate through two metabolic intermediates, Δψ and extra-mitochondrial ATP/ADP. Open arrows in (A) represent proton translocation across the mitochondrial inner-membrane.

Control of the experimental system is fully described by sixteen control coefficients: 4 overall flux; 8 concentration; 4 fluxratio control coefficients. These coefficients were calculated, following a matrix-based approach [30] from elasticity coefficients (quantifying the responsiveness of modules to intermediates) and the ratio of fluxes through separate system branches. If a module was exclusively sensitive to Δψ, its kinetic behaviour to this intermediate was modelled mathematically using Kaleidagraph 3.6.4 (Synergy Software). The derivative of the obtained rate equation (see legend, Figure 2), together with the steady state Δψ and flux through the particular module, were used to calculate the elasticity coefficient. If a module was sensitive to both Δψ and the ATP/ADP ratio, the respective elasticity coefficients were calculated from the changes in steady state flux and intermediate concentrations observed upon a double modulation of the respiratory system; a single modulation sufficed when a module was only sensitive to the ATP/ADP ratio [4]. Calculations were performed using Microsoft Excel X.

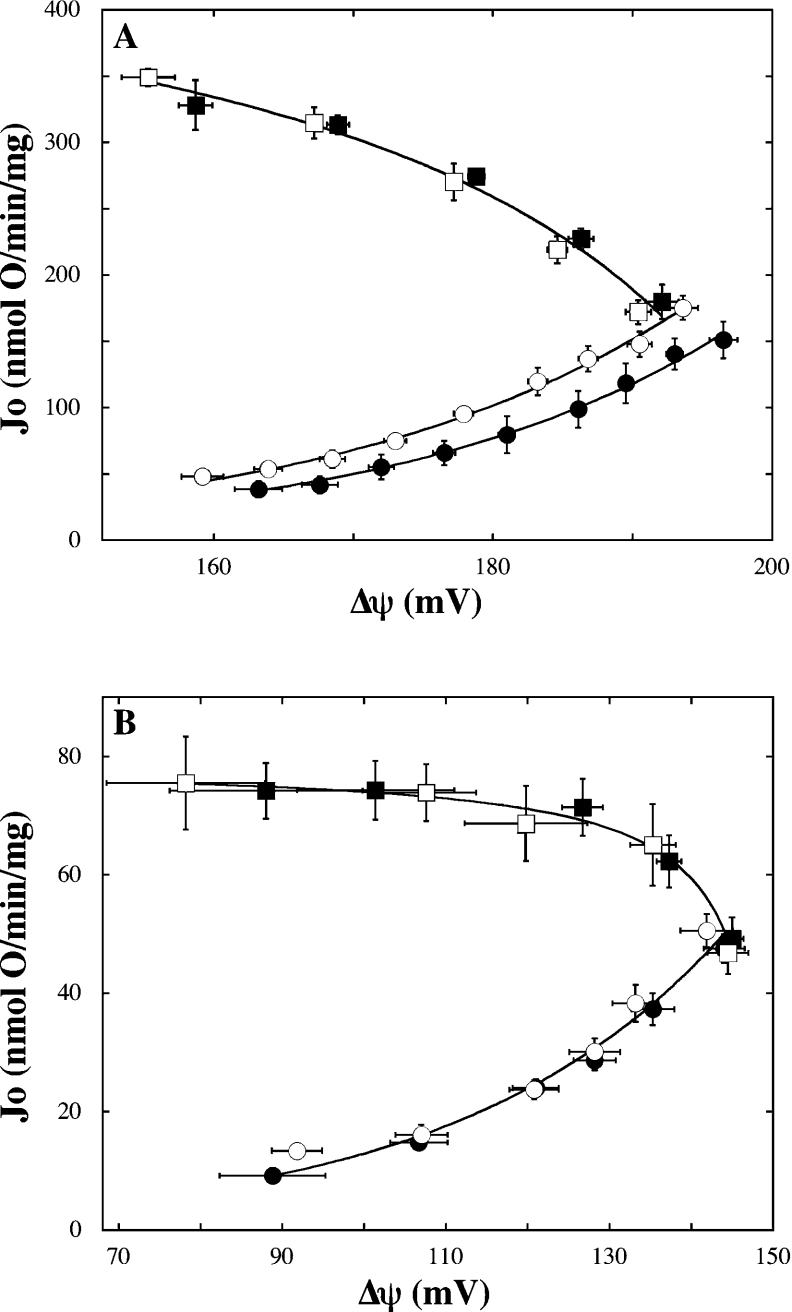
Figure 2. Sensitivity of respiration and leak to ATP/ADP.

The kinetic dependency of respiration (squares) and leak (circles) on Δψ was determined in mitochondria from muscle (A) and beta cells (B) in the exclusive presence of 0.15 mM ATP (filled symbols) or 0.15 mM ADP (open symbols). Respiration and leak data were fitted mathematically to hyperbolic [Jo=(αΔψ+β)/(γΔψ+1)] and exponential (Jo=αe^βΔψ) equations respectively where Jo is the rate of oxygen uptake/mg of protein, α, β and γ are fit parameters. Correlation coefficients of all models were equal to or exceeded 0.99. Data points and error bars represent mean±S.E.M. of 6 (leak, both systems), 3 (respiration, muscle), 7 (respiration-ADP, beta cells) or 10 (respiration-ATP, beta cells) independent mitochondrial samples.

Statistics

Error associated with calculated elasticity and control coefficients was determined using a Monte Carlo method [31]. Steady state parameters were simulated 500 times, assuming they were normally distributed with a mean equal to that of the experimental repeats and a standard deviation equal to the standard error of the experimental mean. Data reflecting the kinetic relations of the leak and respiration modules to Δψ were not simulated: the mathematical fit parameters describing these relations were fixed (legend of Figure 2). To obtain an indication of error, the median of a given set of simulated coefficients was compared with the corresponding coefficient calculated from the averaged experimental data. Furthermore, the probability was determined that the true value of a coefficient is opposite in sign to that obtained from the averaged experimental data [4]. This probability (P) is given by the percentage of simulated values of different sign to that calculated from the averaged experimental data. Differences between medians of equivalent sets of muscle and beta cell simulations were assessed for significance by Wilcoxon-Mann–Whitney rank sum tests using Kaleidagraph 3.6.4 (Synergy software). All other procedures were performed using Microsoft Excel X.

RESULTS

Testing assumptions

Figure 1(A) shows oxidative phosphorylation divided into four modules connected by two intermediates, and Figure 1(B) shows a simplified representation, which assumes that ATP/ADP has no influence on respiration or leak. These assumptions were tested. First, the elasticity of leak to the extra-mitochondrial ATP/ADP ratio might not be zero, given that basal proton leak depends on adenine nucleotide translocator content [32], that fatty acid-dependent uncoupling by this carrier is inhibited by ATP or ADP [33] and that UCP (uncoupling protein)-mediated leak is sensitive to purine nucleoside di- and tri-phosphates [34]. Secondly, the elasticity of respiration to the ATP/ADP poise might not be zero, as the activity of some respiratory complexes is regulated by adenine nucleotides [35,36]. To address this matter, we determined respiration and leak kinetics in the presence of either exclusively ATP or ADP (i.e. the ATP/ADP ratio approximates infinity or zero respectively). It is evident from Figure 2 that the dependence of respiration on Δψ is unaffected by the ATP/ADP ratio in mitochondria from either muscle (Figure 1A) or beta cells (Figure 1B), confirming that its elasticity to this ratio is indeed zero in both systems. Similarly, the kinetic behaviour of leak appears to be insensitive to changes in the ATP/ADP poise in beta cell mitochondria (Figure 2B). In muscle, leak activity in the exclusive presence of ADP is higher than that observed in the sole presence of ATP at all Δψ values measured (Figure 2A). These differences are not observed in the presence of CAT (carboxyatractyloside), a specific inhibitor of the adenine nucleotide translocator (results not shown), and indicate potential regulation of leak in muscle by the ATP/ADP ratio.

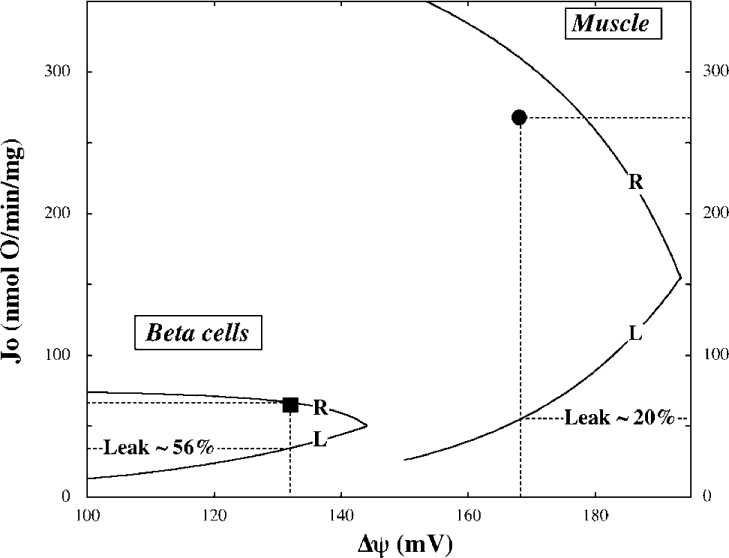
Contribution of leak to respiration

During state 3 oxidation of succinate, muscle mitochondria reach a steady state, in which oxygen is consumed at 268 nmol·min⁻¹·(mg of protein)⁻¹, the established Δψ is 168 mV and the ATP/ADP ratio is 0.17 (Table 1). Under the same conditions, mitochondria from beta cells respire at a considerably lower rate (65 nmol·min⁻¹·mg⁻¹), achieve a lower Δψ (132 mV), but exhibit a higher ATP/ADP poise (0.55). From the dependencies of leak activity on Δψ (Figure 2) it is possible to calculate leak rates in these steady states and furthermore, to determine the extent to which these contribute to overall oxygen consumption. Although the absolute steady state leak rate in beta cells is lower than that in muscle [36±2.8 versus 54±2.6 nmol·min⁻¹·(mg of protein)⁻¹], it is clear from Figure 3 that its contribution to respiration is nearly three times higher, 0.56±0.05 versus 0.20±0.007.

Table 1. Steady state parameters.

Oxygen uptake rate (Jo), Δψ and the ATP/ADP ratio were measured with mitochondria incubated in the presence of 4 mM succinate, 20 mM glucose, 100 μM ATP and, in the case of muscle 1.6 units·ml⁻¹ hexokinase. The resultant steady state (labelled none) was perturbed by partial inhibition of the respiration module with 15 and 100 μM malonate for muscle and beta cell mitochondria respectively. In separate experiments, the same steady state was modulated by partial inhibition of the hexokinase module by lowering the amount of enzyme added to 0.018 unit·ml⁻¹ (muscle) or by including 3.9 mM glucose 6-phosphate in the reaction medium (beta cells). The presented data are the mean±S.E.M. of n independent mitochondrial samples.

	Jo (nmol of O·min−1·mg−1)		Δψ (mV)		ATP/ADP ratio
Inhibited module	Mean	n	Mean	n	Mean	n
Muscle
None*	268±6.8	16	168±1.2	16	0.17±0.02	3
Respiration	189±5.7	11	157±0.9	11	0.15±0.02	3
Hexokinase	199±5.6	9	176±2.7	9	3.69±1.67	3
Beta cells
None*	65±2.2	15	132±2.3	15	0.55±0.14	6
Respiration	31±2.9	7	102±4.6	7	0.43±0.09	6
Hexokinase	42±1.2	3	134±2.4	3	1.27±0.75	3

* None represents steady state kinetics.

Figure 3. Contribution of proton leak to overall respiratory activity.

Curves representing the kinetic dependencies of leak (L) and respiration (R) on Δψ are the same as those describing the experimental data shown in Figure 2, except for the muscle leak curve which describes the combined data obtained in the presence of either ATP or ADP. Steady state parameters, determined during state 3 oxidation of succinate in mitochondria from muscle (●) and beta cells (■), were taken from Table 1. Leak contribution (%) was calculated from 15–16 independent experiments. Note that partitioning of flux for control analysis was calculated from the averaged experimental data shown in Table 1.

Elasticities of system modules to Δψ and ATP/ADP

Given the lack of responsiveness of respiration (both systems) and leak (beta cells only) to changes in the ATP/ADP ratio (Figure 2), the elasticities of these modules to Δψ can be calculated from their respective kinetic responses to this intermediate (see Materials and methods section). Other elasticities are determined by steady state perturbations, inhibiting either the respiration or the hexokinase module specifically. It is evident from Table 1 that inhibition of respiration results in a decreased oxygen uptake rate and in decreased values of Δψ and the ATP/ADP ratio, whereas inhibition of hexokinase lowers the respiratory activity, but causes increases in both Δψ and the ATP/ADP poise. The relative changes in steady state fluxes and intermediates, caused by this double modulation of the system, allows calculation of the elasticities of phosphorylation (both muscle and beta cells) and leak (muscle only) to both Δψ and the ATP/ADP ratio (see Materials and methods section). Assuming that hexokinase is unresponsive to Δψ, its elasticity to the ATP/ADP poise can be calculated from the steady state changes that result from specific inhibition of respiration (Table 1).

Table 2 shows that elasticities calculated from averaged experimental data agree reasonably well with the medians of the simulated elasticity coefficients, which all differ statistically significantly between beta cell and muscle mitochondria (P<0.0001). The most substantial difference concerns the elasticity of phosphorylation to ATP/ADP, which is approx. 18–19 times higher, in absolute terms, in beta cells than in muscle. Furthermore, respiration, leak, and phosphorylation are all less responsive to changes in Δψ in beta cells. In line with the kinetic data shown in Figure 2(A), the responsiveness of leak in muscle to changes in ATP/ADP is relatively small.

Table 2. Elasticities of system modules to Δψ and ATP/ADP.

Elasticity coefficients were calculated from averaged experimental data or represent the medians of 500 simulated data sets. The elasticities of respiration (muscle and beta cells) and leak (beta cells only) to the ATP/ADP ratio were shown experimentally to be zero (Figure 2), whereas that of hexokinase to Δψ was assumed as zero.

	Elasticity coefficient
	Δψ			ATP/ADP
Module	Experimental	Simulated	P*	Experimental	Simulated	P*
Muscle
Respiration	−1.81	−1.80	<0.1	0
Leak	5.50	5.50	<0.1	0.006	0.006	3
Phosphorylation	4.20	4.19	0.4	−0.030	−0.030	3
Hexokinase	0			2.34	2.35	<0.1
Beta cells
Respiration	−1.10	−1.10	<0.1	0
Leak	4.05	4.05	<0.1	0
Phosphorylation	2.62	2.61	2.4	−0.637	−0.548	13
Hexokinase	0			2.04	2.03	1.2

* Error is indicated by the percentage of simulated values (P) that had an opposite sign to the experimental value.

Relatively strong control of leak in beta cells

The control structure of the system defined in Figure 1 can be calculated from the flux ratio derived from Figure 3 and the elasticity coefficients given in Table 2. As in the case for elasticities, control coefficients calculated from the averaged experimental data are in tolerable agreement with the medians of the simulated values (Table 3), which all differ significantly (P<0.0001) between muscle and beta cells.

Table 3. Control of mitochondrial respiration under phosphorylating conditions.

The presented coefficients quantify the control exerted by the respective system modules on ATP/ADP (C^ATP/ADP), Δψ (C^Δψ), overall respiratory flux (C^J) and the ratio of leak and phosphorylation fluxes (C^L/P). Control values were calculated from averaged experimental data or represent the medians of 500 simulated data sets.

	Control value
	Muscle			β cells
Module	Experimental	Simulated	P*	Experimental	Simulated	P*
CATP/ADP
Respiration	0.292	0.292	<0.1	0.230	0.230	1.2
Leak	−0.017	−0.017	<0.1	−0.129	−0.129	1.2
Phosphorylation	0.148	0.148	0.4	0.296	0.305	3.6
Hexokinase	−0.423	−0.423	0.2	−0.397	−0.406	3.2
CΔψ
Respiration	0.166	0.166	<0.1	0.235	0.235	<0.1
Leak	−0.010	−0.010	<0.1	−0.132	−0.132	<0.1
Phosphorylation	−0.154	−0.154	0.4	−0.079	−0.076	2.4
Hexokinase	−0.002	−0.002	2.6	−0.025	−0.022	9.4
CJ
Respiration	0.701	0.701	<0.1	0.740	0.740	<0.1
Leak	0.018	0.018	<0.1	0.146	0.146	<0.1
Phosphorylation	0.278	0.278	0.4	0.087	0.090	2.4
Hexokinase	0.004	0.004	2.6	0.027	0.027	9.4
CL/P
Respiration	0.053	0.053	0.2	0.239	0.240	<0.1
Leak	0.234	0.234	<0.1	0.362	0.362	<0.1
Phosphorylation	−0.283	−0.283	0.4	−0.459	−0.455	2.4
Hexokinase	−0.003	−0.003	2.6	−0.143	−0.134	9.4

* Error is indicated by the percentage of simulated values (P) that had an opposite sign to the experimental value.

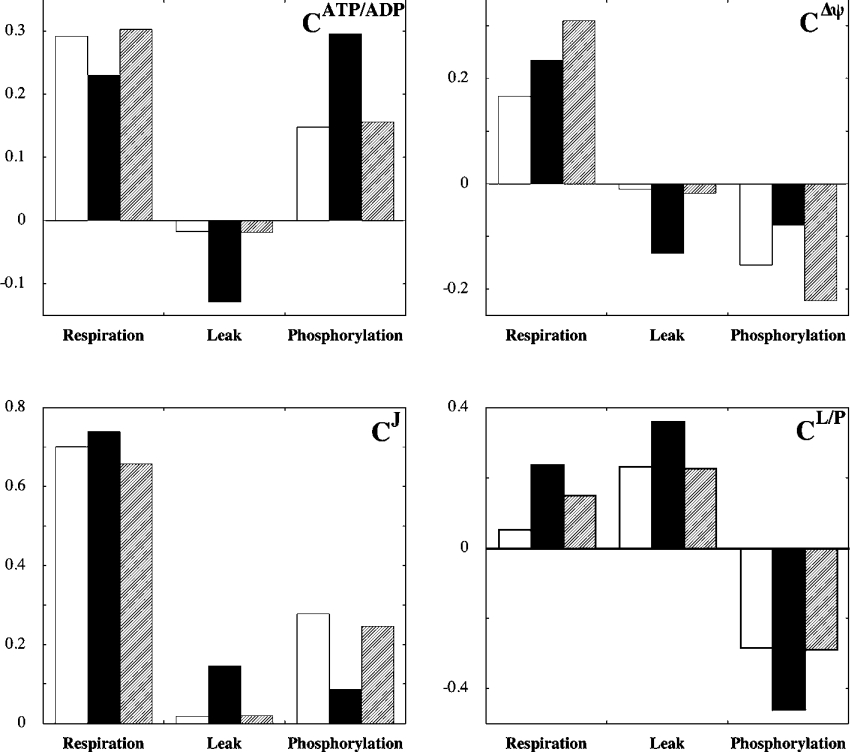
The main message to be taken from the coefficients listed in Table 3 is that relative control by leak and phosphorylation – on any system property – differs between muscle and beta cell mitochondria: the importance of leak is significantly higher in beta cell mitochondria. Most importantly, it is evident that leak exerts substantially more control, in absolute terms, on the ATP/ADP ratio in beta cells than in muscle (approx. 7.5 fold). Control over this ratio by phosphorylation is also higher in beta cells, but not nearly as much (approx. 2 fold). This clearly supports our hypothesis that the relatively high flexibility of the ATP/ADP ratio in beta cells may be accounted for, at least partly, by mitochondrial particularities. Control exerted by leak over Δψ is approx. 13 fold greater in beta cells than in muscle, whereas control over Δψ by phosphorylation is approx. 50% lower. The relative importance of leak in beta cells is evidenced furthermore by the observation that it assumes a significant share of control over total respiratory flux (C^J=0.15), which is at the expense of phosphorylation. In muscle on the other hand, flux is controlled almost exclusively by respiration and phosphorylation.

Besides the fact that leak plays a comparatively important role in beta cell mitochondria, it can be observed from Table 3 that respiration also controls several properties of this system differently. Although the ATP/ADP ratio in beta cells is controlled less (approx. 20%) by respiration, both Δψ and particularly partitioning of flux are controlled more strongly (approx. 40% and 4.5 fold respectively).

Leak determines beta cell control

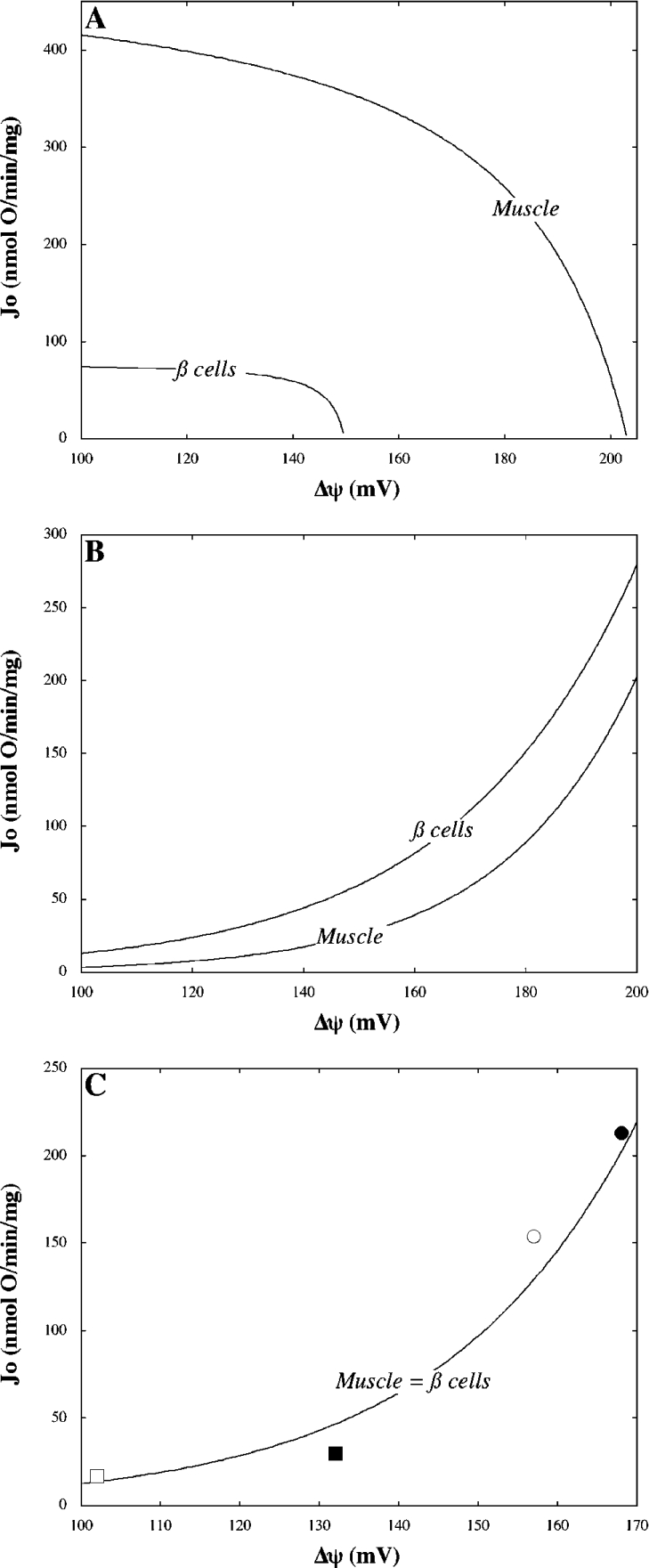
To determine where control differences between muscle and beta cell mitochondria arise, the kinetic behaviour of system modules that interact with Δψ were compared directly. From Figure 4(A) it is evident that the activity of respiration is considerably lower (>5.5 fold) at any Δψ in beta cells than in muscle. In principle, this could be interpreted to indicate a relatively low purity of the mitochondrial beta cell sample. The activity of leak, however, is approx. 2 fold higher at any Δψ value in beta cells (Figure 4B), weakening the argument for such an explanation. Furthermore, it appears from Figure 4(C) that the kinetic behaviour of phosphorylation does not differ significantly between systems; although limited as to number and range, the steady states obtained in beta cells and muscle are described reasonably well by a single exponential model.

Figure 4. Modular kinetics.

Models representing respiration (A) and leak (B) kinetics with respect to Δψ were taken from Figure 3 and extrapolated to allow direct comparison between beta cells and muscle. Steady state phosphorylation activities (C) in muscle (circles) and beta cell (squares) mitochondria were calculated by subtracting leak activities (B) from overall state 3 respiratory activities shown in Table 1; filled symbols represent uninhibited steady states whereas open symbols reflect the states achieved upon specific partial inhibition of respiration. Combined data were fitted to a single exponential equation (correlation coefficient=0.97).

A consequence of the observed modular-kinetic differences (Figures 4A and 4B) is that the contribution of leak to the overall respiratory activity is nearly 3 fold higher in mitochondria from beta cells than in those from muscle (compare Figure 4 with Figure 3). As shown by the data presented in Figure 5, the partitioning of flux between leak and phosphorylation modules has a major effect on the distribution of control: recalculating the beta cell control coefficients with the flux ratio changed to the value observed in muscle annuls virtually all differences between the two systems. The only exceptions are the control exerted by respiration over Δψ and to a lesser extent, over the flux ratio.

Figure 5. The effect of flux partitioning on distribution of control.

Control coefficients quantifying control of ATP/ADP (C^ATP/ADP), Δψ (C^Δψ), overall respiratory flux (C^J) and of the ratio of leak and phosphorylation fluxes (C^L/P). Values were calculated from averaged experimental data and represent control strengths in muscle (open bars) and beta cell (filled bars) mitochondria (compare Figure 5 with Table 3). Hatched bars represent beta cell control coefficients that were recalculated with the ratio of leak and phosphorylation activities changed to the level observed in muscle.

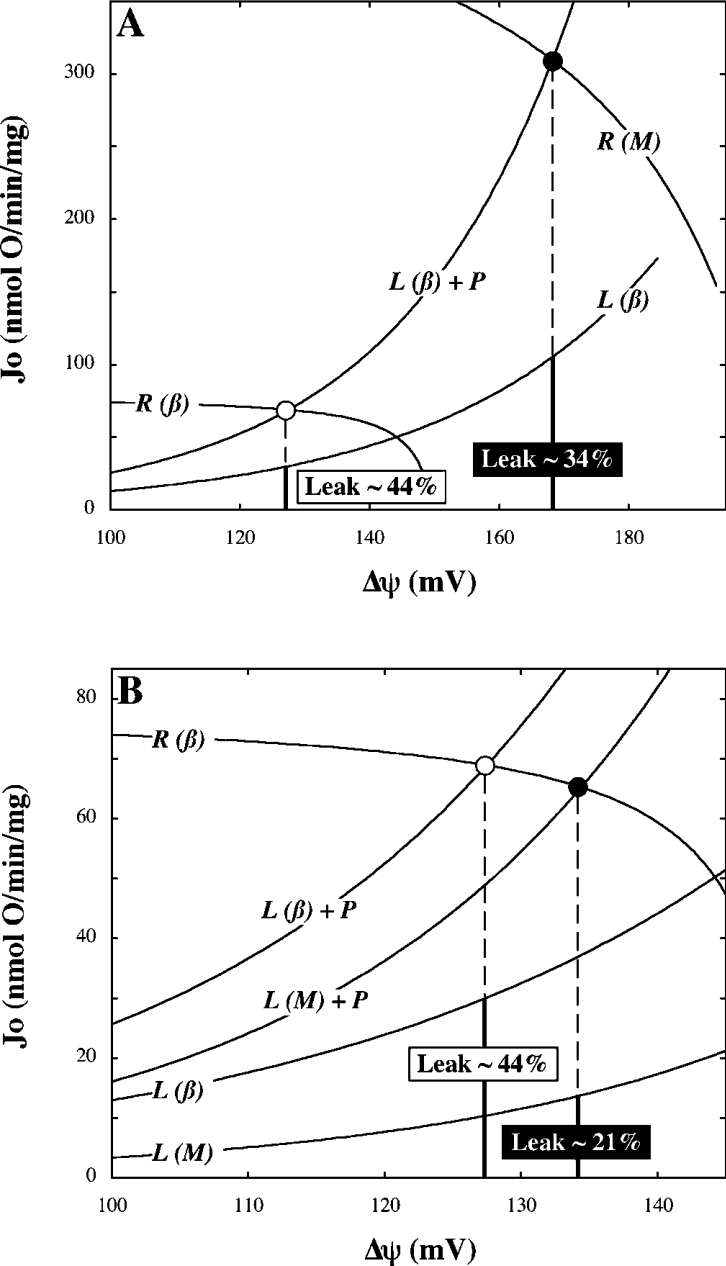
Given the impact of flux partitioning on the distribution of control, it is of interest to consider which modular-kinetic property specific to beta cell mitochondria – low respiration or high leak – accounts most for the relatively high contribution from leak in this system. To address this matter, we modelled the kinetic interplay between Δψ-establishing and Δψ-dissipating system modules in beta cell mitochondria (Figure 6). The model predicted a contribution of leak to overall state 3 respiratory activity of approx. 44% (Figure 6), which is lower than that experimentally observed (Figure 3). This discrepancy results from the slight difference between the phosphorylation activity modelled and that calculated from experimental data [Figure 4C, compare the curve with the steady state (■)]. Nonetheless, it is clear that the predicted contribution from leak falls to approx. 34% when the kinetic behaviour of respiration is changed to its muscle counterpart (Figure 6A). This fall is far more substantial when leak kinetics are changed to their muscle equivalent (Figure 6B). In the latter scenario, the predicted proportion of state 3 repiratory activity accounted for by leak (approx. 21%) is almost identical to the value observed experimentally in muscle (compare Figure 6 with Figure 3). We therefore conclude that leak is the main determinant of flux partitioning, and consequently the distribution of control, in isolated beta cell mitochondria.

Figure 6. Modelled kinetic interaction between Δψ-establishing and Δψ-dissipating modules.

Curves describe the kinetic behaviour of respiration (R) and leak (L) with respect to Δψ as measured in muscle (M) and beta cell (β) mitochondria (compare with Figures 4A and 4B). Total Δψ-dissipating activity (L+P) was modelled by summation of the phosphorylation (Figure 4C) and respective leak curves. The intersect of the curves labelled R(β) and L(β)+P models the steady state achieved in beta cells oxidizing succinate in state 3 (compare with Table 1, ○). (A) and (B) respectively, predict how this state shifts when respiration or leak kinetics are altered to the relationships observed in muscle (●). Percentages indicate the contribution of leak to overall respiration in the respective modelled states.

DISCUSSION

The results reported in this paper highlight the relative strength of ‘systems’ approaches to answer questions of biomedical relevance. By studying oxidative phosphorylation as a whole, we have demonstrated that the ATP/ADP ratio is controlled more strongly by proton leak in mitochondria from cultured beta cells than in those from skeletal muscle. This outcome supports our initial hypothesis that the relatively high flexibility of this poise in beta cells may be accounted for, at least partly, by mitochondrial peculiarities and highlights mitochondrial proton conductance as a good potential regulatory step over ATP/ADP and GSIS in beta cells.

The importance of ATP/ADP as a signal in GSIS has been firmly established [37–40], indeed it has been suggested that this ratio is regulated by mitochondrial coupling mechanisms [41]. However, our results are the first to provide direct quantitative information regarding mitochondrial control of the ATP/ADP ratio (Table 3). The results reveal categorically that not only ATP/ADP, but all other system properties assessed (i.e. Δψ, overall respiratory flux and flux partitioning) are controlled differently in mitochondria from cells in which the phosphorylation potential does (beta cells) or does not (muscle) respond to changes in substrate supply.

From modular-kinetic analysis of the experimental data (Figures 4–6) it transpires that the control structure of beta cell mitochondria is determined predominantly by leak activity. This activity is relatively high, which means that the contribution of proton leak to the overall state 3 respiratory activity is nearly 3 fold higher in beta cells than in muscle (Figure 3).

Consequently, the ATP/ADP ratio is controlled comparatively strongly by both leak and phosphorylation (Table 3). It thus appears that the efficiency of mitochondrial energy conservation exerts a relatively high degree of control on the phosphorylation potential in beta cells. This agrees well with results from work performed on mice deficient in UCP2 [11], an uncoupling protein that lowers the efficiency of oxidative phosphorylation [34]. Ablation of UCP2 results in higher pancreatic islet ATP levels and increased GSIS, which indicates that this protein exerts negative control on the ATP/ADP ratio and insulin secretion [11].

What accounts for the observed differences in leak between beta cell and muscle mitochondria is presently unclear. It is unlikely that the relatively high leak activity in beta cell mitochondria is mediated by UCP, since the activity is not affected by the ATP/ADP ratio (Figure 2B) or indeed by the presence or absence of adenine nucleotides (results not shown). The adenine nucleotide translocase is equally unlikely to be responsible, since the mitochondrial content of this carrier is approx. 9 fold less in beta cells than muscle; besides which, beta cell leak is insensitive to CAT (results not shown). It is conceivable, however, that differences in surface area and/or fatty acid composition of the mitochondrial inner membrane may explain the different leak activities [42], although these parameters were not measured. Another explanation for the observed differences could be that the preparation of mitochondria may have affected the mitochondrial inner membranes from beta cells and muscle differently. To address this matter, the control of ATP/ADP is currently being investigated in intact beta cells.

The outcome of our control analysis challenges the notion that GSIS is controlled exclusively by glucokinase [5], a common view based on the observation that this enzyme exerts high control on glycolysis [6]. Although the importance of glucokinase is beyond doubt, as evidenced by its pivotal role in controlling blood glucose homoeostasis [5,43], a complementary role of mitochondrial respiration in GSIS is likely. In other words, it is not merely the supply of substrate that governs the ATP/ADP ratio; the efficiency by which energy is conserved provides an additional mechanism of control. A regulatory relationship between substrate supply and energy transduction is also suggested by the strength of control that is exerted by respiration on the ratio of leak and phosphorylation fluxes, which is substantially higher in beta cells than in muscle (Table 3).

It has been shown previously that activation of UCP2 by endogenously produced mitochondrial superoxide impairs GSIS in pancreatic islets. Given that obesity and hyperglycemia increase both mitochondrial superoxide production and UCP2 expression in beta cells [11,44], an important role for UCP2 in the pathogenesis of beta cell dysfunction and the development of type 2 diabetes has been suggested [2,34,45]. Although this may be correct, the evolved function of UCP2 in beta cells remains unclear. The relatively high level of control exerted by leak on all properties of mitochondrial oxidative phosphorylation that we assessed (Table 3), would indeed suggest that UCP2-mediated uncoupling could be important physiologically, perhaps to co-ordinate the appropriate response of beta cells to continuous changes in nutrient supply (compare with [46]). Obviously, caution should be taken when drawing physiological conclusions from in vitro experiments, although it is encouraging in this respect that the distribution of control of oxidative phosphorylation in whole cells (hepatocytes) was found to be similar to that in isolated mitochondria (liver) [47]. In any case, our detailed mitochondrial control analysis has yielded specific predictions that are readily testable in more complex experimental systems.

In conclusion, we have shown that the control structure of mitochondrial respiration in beta cells is comprehensively different from that in muscle, which is predominantly due to a relatively high contribution of proton leak to the overall respiratory activity. The results imply that the phosphorylation potential in beta cells is controlled to a significant extent by the efficiency of mitochondrial energy conservation. This demonstrates clearly that the relatively high flexibility of the ATP/ADP ratio is likely to be a systemic property of beta cells that emerges from the interaction of multiple cellular processes.