Shannon Information Theoretic Computation of Synonymous Codon Usage Biases in Coding Regions of Human and Mouse Genomes

Abstract

Exonic GC of human mRNA reference sequences (RefSeqs), as well as A, C, G, and T in codon position 3 are linearly correlated with genomic GC. These observations utilize information from the completed human genome sequence and a large, high-quality set of human and mouse coding sequences, and are in accord with similar determinations published by others. A Shannon Information Theoretic measure of bias in synonymous codon usage was developed. When applied to either human or mouse RefSeqs, this measure is nonlinearly correlated with genomic, exonic, and third codon position A, C, G, and T. Information values between orthologous mouse and human RefSeqs are linearly correlated: mouse = 0.092 + 0.55 human. Mouse genes were consistently placed in genomic regions whose GC content was closer to 50% than was the GC content of the human ortholog. Since the (nonlinear) information versus percent GC curve has a minimum at 50% GC and monotonically increases with increasing distance from 50% GC, this phenomenon directly results in the low slope of 0.55. This appears to be a manifestation of an evolutionary strategy for placement of genes in regions of the genome with a GC content that relates synonymous codon bias and protein folding.

[The following individuals kindly provided reagents, samples, or unpublished information as indicated in the paper: D. Church and D. Maglott.]

In a seminal study comparing human and rodent coding and noncoding sequences, Makalowski and Boguski (1998) clearly showed that synonymous substitution rates were very high, close to rates for substitutions in 5′ and 3′ untranslated regions. In sharp contrast, nonsynonymous substitution rates were about five-fold slower. This high rate of synonymous substitution might be expected to lead to a rather homogeneous distribution of synonymous codons. On the other hand, there are patterns of synonymous codon usage that are indicative of nonrandomness (for review, see Li 1997, pp. 196–202). Relying heavily on cited work by Sharp et al. (1988), Sharp and Li (1986), Ikemura (1981), Kimura (1983), and other researchers, this review shows that, in unicellular organisms, genes whose protein products are highly expressed preferentially utilized synonymous codons that corresponded to the most abundant tRNA species. In contrast, genes whose protein products are not highly expressed are more or less promiscuous in their usage of synonymous codons.

There is a comprehensive body of literature documenting the universal existence and nature of codon usage bias within and between many organisms. Professor Paul Sharp kindly shared an informal historical perspective (detailed references are given in the Results section): The earliest studies started around mid 1980's with the work of Ikemura and colleagues, and a number of other major groups continued this tradition in ongoing efforts that continue very energetically to the present time. A common focus of this work is the determination of the relationship of the nucleotide composition of codon position 3 and the local genomic nucleotide composition. Often this information has been used to elucidate alternative hypotheses relevant to mechanisms or pathways of genomic evolution.

I show here that an information theoretic value (in the sense of Shannon 1948) can be computed for each coding sequence based upon its usage of synonymous codons. As described here briefly and in Methods in full detail, Shannon Information for synonymous codon usage is computed as the double sum,

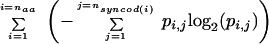where n_aa is the number of distinct amino acids, n_syncod(i) is the number of synonymous codons for amino acid i, and p_i,j is the probability of synonymous codon j for amino acid i. This information value can be used to describe the diversity of codon usage within individual coding sequences and for the genome as a whole, to compare diversity between multiple organisms, and to develop models of coding sequence evolution. For example, comparison of results for mouse and human genomes shows that there is a linear correlation of information values between orthologous mouse and human mRNA reference sequences, following the regression equation: mouse = 0.092 + 0.55 human. Mouse genes were consistently placed in genomic regions whose GC content was closer to 50% than was the GC content of the human ortholog. Since the (nonlinear) information versus percent GC curve has a minimum at 50% GC and monotonically increases with increasing distance from 50% GC, this phenomenon directly results in the low slope of 0.55. This appears to be a manifestation of an evolutionary strategy for placement of genes in regions of the genome with a GC content that relates synonymous codon bias and protein folding. This analysis indicates the potential utility of the information theoretic measure for whole genomic comparison of synonymous codon usage.

RESULTS

Relationship of Percent GC in Coding Sequences of Genes and Percent GC in Human Genome

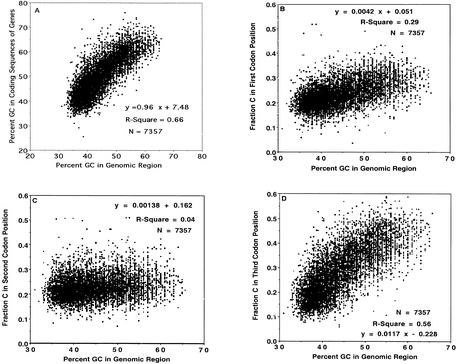
There is a positive linear relationship between percent GC in coding sequences of genes and the percent GC in the genomic region containing the gene (Fig. 1A). These observations, which utilize a large number of high-quality sequences and information derived from the completed human genome sequence, are in accord with a vast body of results published during the last two decades (Ikemura et al. 1983; Ikemura 1985; Aota and Ikemura 1986; Bulmer 1987; Filipski et al. 1987; Mouchiroud et al. 1987; Muto and Osawa 1987; Ikemura and Aota 1988; Sharp et al. 1988; Marin et al. 1989; Ikemura et al. 1990; Ikemura and Wada 1991; Lloyd and Sharp 1993; Sharp et al. 1993; Kliman and Hey 1994; Sharp and Matassi 1994; Stenico et al. 1994; Sharp et al. 1995; Andersson and Sharp 1996; Table 7.10 of Li 1997; Lafay and Sharp 1999; Bernardi 2000a; Cruveiller et al. 2000; Lafay et al. 2000; Sueoka and Kawanishi 2000; Grocock and Sharp 2001; Knight et al. 2001). There is a small contribution to this phenomenon from codon 1 (Fig. 1B), a negligible contribution from codon 2 (Fig. 1C), and a substantial contribution from codon 3 (Fig. 1D). These relationships are similar for all four individual nucleotides (Table 1), with A and T exhibiting negative rather than positive correlations (figures not shown). Nucleotide frequency of each codon position (position 1: G > A > C > T; position 2: A > T > C > G; position 3: C > G > T > A) is in accord with the quantitation given by Karlin and Mrázek (1996).

Figure 1.

Relationship of (A) percent GC in coding sequences of genes, (B) fraction C in first codon position, (C) fraction C in second codon position, and (D) fraction C in third codon position to percent GC in genomic region of human sequences.

Table 1.

Statistical Results for Linear Regression Analysis of Codon Nucleotide Composition in Relationship to Percent GC in Human Genomic Regions

Slopes
Nucleotide	Codon position
1	2	3
A	−0.0039	−0.00282	−0.0102
C	0.0042	0.00138	0.0117
G	0.00162	0.00195	0.0084
T	−0.00192	−0.00051	−.0100
Intercepts
Nucleotide	Codon position
1	2	3
A	0.45	0.45	0.66
C	0.051	0.162	−0.228
G	0.243	0.100	−0.090
T	0.258	0.291	0.66
R-Square values
Nucleotide	Codon position
1	2	3
A	0.29	0.10	0.60
C	0.29	0.04	0.56
G	0.06	0.10	0.56
T	0.11	0.004	0.62

Relationship of Human Nucleotide Content and Information (bits)

As described here briefly and in Methods in full detail, Shannon Information for synonymous codon usage is computed as the double sum

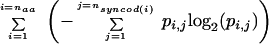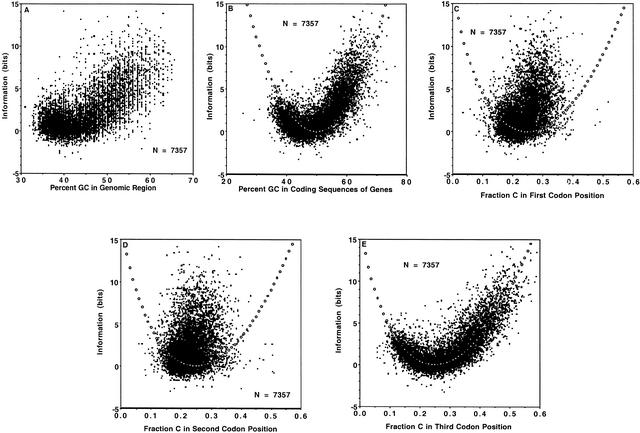
where n_aa is the number of distinct amino acids, n_syncod(i) is the number of synonymous codons for amino acid i, and p_i,j is the probability of synonymous codon j for amino acid i. There is a nonlinear relation between information in the coding region of a gene and the percent GC in the genomic region containing the gene (Fig. 2A). This relationship becomes visually clearer when the percent GC in the coding portion of the gene rather than in the genomic region is used (Fig. 2B). The shape is reminiscent of the plot of uncertainty versus probability for two variables (see, e.g., Hamming 1980; Tom Schneider, “Information Theory Primer with an Appendix on Logarithms,” www.lecb.ncifcrf.gov/∼toms/paper/primer): The shape in Figure 2B is rescaled and inverted, since this was measured for much more than two variables, and this is a plot of information rather than uncertainty. There is no contribution to this shape from the C content of codon 1 (Fig. 2C) or codon 2 (Fig. 2D); the major if not only source of contribution is from codon 3 (Fig. 2E). Similar results were obtained for G, and the mirror for A and T (not shown).

Figure 2.

Relationship of information (bits) and percent GC, in (A) genomic regions of human sequences; and relationship of information (bits) and C content in (B) coding sequences of human genes, (C) first codon position for human sequences, (D) second codon position for human sequences; and (E) third codon position for human sequences. Open circles indicate theoretical fit to the information function.

As described here briefly and in Methods in full detail, given a scatter plot of information versus the probability of one (of several) variables, the effective number of variables can be estimated as n_effective = 1/p_min, where n_effective is the effective number of variables and p_min is the value of p at which the information achieves a minimum. For the data in Figure 2B, the minimum in the scatter plot occurs close to 50% GC; therefore, as described in Methods, n_effective = 1/0.5 = 2. The fit of the theoretical curve for 2 variables (Equation 5) was rather poor: the minimum for the measured data occurs at approximately 45% GC rather than exactly at the position of the theoretical minimum at 50% GC; also, the theoretical curve tends to underestimate the bulk of the information values for GC ≥50%. On the other hand, for Figure 2E, the minimum in the scatter plot occurs close to fraction C in codon position 3 = 0.25; therefore, n_effective= 1/0.25 = 4. The fit to the theoretical curve for four variables (Equation 6) appears to be better than that in Figure 2B: the minima for both the measured data and the theoretical curve coincide at 0.25, and the theoretical curve comes close to running through the middle of the measured data. As analyzed in detail in the Discussion, the measured data in Figure 2C,D deviate markedly from the theoretical curve.

Identification of “Rare” Codon Usage and Relationship to Information Value

For reference, the nucleotide triplets for each synonymous codon for each amino acid are numbered and tabulated (Table 2). The positions of numerical values (codon frequencies) in Tables 3–7 correspond to the positions in reference Table 2. The results in Table 3 are in excellent agreement with those in the gold standard tabulation (Nakamura 1998; www.kazusa.or.jp/codon/cgi-bin/showcodon.cgi?species=Homo+sapiens+[gbpri]). The codon frequencies for the pooled 10,862 human RefSeqs were normalized for the pooled total (Table 3) and for each individual amino acid (Table 4). Visual inspection of Table 4 indicates that there are no amino acids that have extremely rarely used codons which might be expected to be involved in translational control. Moderately rarely used codons were identified by dividing each codon frequency in Table 4 by the maximum frequency for the corresponding amino acid (Table 5). The rank order of the pooled and sorted rarely used codons is indicated in parentheses for values ≤0.50. The most rarely used codon is codon 3 of leucine (CTA) with a ratio of 0.181 relative to codon 4 of leucine (CTG).

Table 2.

Positional Correspondence of Condons for Subsequent Tables

Amino acid	Codon number
1	2	3	4	5	6
PHE	TTT	TTC
LEU	CTT	CTC	CTA	CTG	TTA	TTG
ILE	ATT	ATC	ATA
MET	ATG
VAL	GTT	GTC	GTA	GTG
SER	TCT	TCC	TCA	TCG	AGT	AGC
PRO	CCT	CCC	CCA	CCG
THR	ACT	ACC	ACA	ACG
ALA	GCT	GCC	GCA	GCG
TYR	TAT	TAC
HIS	CAT	CAC
GLN	CAA	CAG
ASN	AAT	AAC
LYS	AAA	AAG
ASP	GAT	GAC
GLU	GAA	GAG
CYS	TGT	TGC
TRP	TGG
ARG	CGT	CGC	CGA	CGG	AGA	AGG
GLY	GGT	GGC	GGA	GGG

Table 3.

Pooled Synonymous Codon Frequencies for 10862 Human RefSeqs Normalized by Pooled Totals

Amino acid	Codon number
1	2	3	4	5	6
PHE	0.017	0.020
LEU	0.013	0.019	0.007	0.039	0.008	0.013
ILE	0.016	0.021	0.007
MET	0.022
VAL	0.011	0.014	0.007	0.028
SER	0.015	0.017	0.012	0.004	0.012	0.019
PRO	0.018	0.020	0.017	0.007
THR	0.013	0.019	0.015	0.006
ALA	0.019	0.028	0.016	0.007
TYR	0.012	0.015
HIS	0.011	0.015
GLN	0.012	0.034
ASN	0.018	0.020
LYS	0.025	0.033
ASP	0.023	0.026
GLU	0.030	0.040
CYS	0.010	0.012
TRP	0.012
ARG	0.005	0.010	0.006	0.011	0.012	0.011
GLY	0.011	0.023	0.017	0.016

Table 7.

Synonymous Codon Frequencies for RefSeq NM_002246 Relative to Pooled Synonymous Codon Frequencies for 10862 Human RefSeqs

Amino acid	Codon number
1	2	3	4	5	6
PHE	0.000	1.868
LEU	0.180	1.620	0.000	1.621	0.000	0.183
ILE	0.000	2.113	0.000
MET	1.000
VAL	0.000	1.237	0.000	1.528
SER	0.000	1.692	0.203	3.785	0.000	1.640
PRO	0.000	1.247	0.360	4.405
THR	0.144	1.315	0.000	4.278
ALA	0.000	1.325	0.256	3.942
TYR	0.000	1.801
HIS	0.000	1.726
GLN	0.000	1.360
ASN	0.000	1.894
LYS	0.000	1.760
ASP	0.193	1.717
GLU	0.000	1.757
CYS	0.000	1.839
TRP	1.000
ARG	0.000	3.494	0.302	1.174	0.000	0.343
GLY	0.319	2.167	0.208	0.653

Table 4.

Pooled Synonymous Codon Frequencies for 10862 Human RefSeqs Normalized by Amino Acid Totals

Amino acid	Codon number
1	2	3	4	5	6
PHE	0.465	0.535
LEU	0.132	0.191	0.072	0.397	0.078	0.130
ILE	0.364	0.473	0.162
MET	1.000
VAL	0.182	0.236	0.118	0.464
SER	0.185	0.215	0.149	0.056	0.154	0.240
PRO	0.288	0.321	0.278	0.113
THR	0.247	0.353	0.283	0.117
ALA	0.266	0.399	0.230	0.104
TYR	0.445	0.555
HIS	0.421	0.579
GLN	0.265	0.735
ASN	0.472	0.528
LYS	0.432	0.568
ASP	0.471	0.529
GLU	0.431	0.569
CYS	0.456	0.544
TRP	1.000
ARG	0.084	0.188	0.014	0.206	0.208	0.201
GLY	0.165	0.340	0.253	0.242

Table 5.

Ratio to Maximum and Rank Ordering of Rare Codons Computed from Pooled Synonymous Codon Frequencies for 10,862 Human RefSeqs

Amino acid	Codon number
1	2	3	4	5	6
PHE	0.869	1.000
LEU	0.332 (8)	0.481 (14)	0.181 (1)	1.000	0.196 (2)	0.327 (6)
ILE	0.770	1.000	0.342 (9)
MET	1.000
VAL	0.392 (12)	0.509	0.254 (4)	1.000
SER	0.771	0.896	0.621	0.233 (3)	0.642	1.000
PRO	0.897	1.000	0.866	0.352 (10)
THR	0.700	1.000	0.802	0.331 (7)
ALA	0.667	1.000	0.576	0.261 (5)
TYR	0.802	1.000
HIS	0.727	1.000
GLN	0.361 (11)	1.000
ASN	0.894	1.000
LYS	0.761	1.000
ASP	0.890	1.000
GLU	0.757	1.000
CYS	0.838	1.000
TRP	1.000
ARG	0.404 (13)	0.904	0.548	0.990	1.000	0.966
GLY	0.485 (15)	1.000	0.744	0.712

Analyses were performed for two arbitrarily selected RefSeqs, NM_000065 (Homo sapiens complement component 6; Table 6) with a low information value (0.00 bits), and NM_002246 (Homo sapiens potassium channel, subfamily K, member 3; Table 7), with a high information value (16.12 bits). These analyses are described in detail in the Discussion.

Table 6.

Synonymous Codon Frequencies for RefSeq NM_000065 Relative to Pooled Synonymous Codon Frequenceies for 10862 Human RefSeqs

Amino acid	Codon number
1	2	3	4	5	6
PHE	1.435	0.623
LEU	1.110	0.693	1.430	0.630	1.893	1.696
ILE	1.267	0.704	1.264
MET	1.000
VAL	1.276	1.183	1.771	0.602
SER	1.365	0.841	1.775	0.215	1.094	0.502
PRO	0.969	0.870	1.506	0.205
THR	1.373	0.695	1.335	0.323
ALA	1.222	0.876	1.412	0.000
TYR	1.083	0.934
HIS	1.627	0.545
GLN	1.643	0.769
ASN	1.186	0.833
LYS	1.369	0.720
ASP	1.133	0.881
GLU	1.516	0.609
CYS	1.199	0.833
TRP	1.000
ARG	0.509	0.681	1.117	0.414	1.843	1.163
GLY	0.917	0.624	1.618	0.940

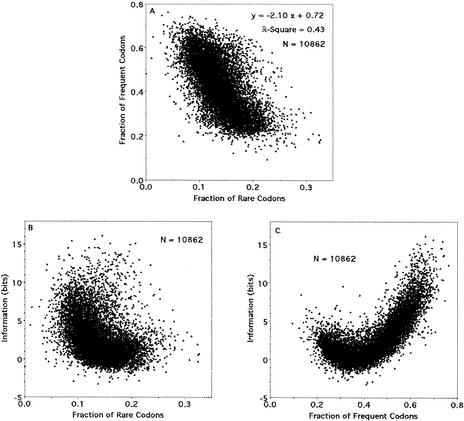
The fraction of frequent codons is inversely linearly related to the fraction of rare codons (Fig. 3A). However, this observation may not entirely reflect a biologically relevant relationship, since a sequence that contains, for example, a frequent codon fraction of 0.80 can contain at most a rare codon fraction of 0.20, so that at least a portion of the inverse relationship may be attributable to a mathematical constraint rather than to biological selection.

Figure 3.

(A) Relationship of frequent codons and rare codons, (B) relationship of information (bits) and rare codons, and (C) relationship of information (bits) and frequent codons for human sequences.

The information value exhibits a nonlinear relationship to the fraction of rare codons (Fig. 3B), reminiscent of the relationship of the information value to A or T in codon position 3 (not shown). The information value exhibits a nonlinear relationship to the fraction of frequent codons (Fig. 3C), reminiscent of the relationship of the information value to C (Fig. 2E) or G (not shown) in codon position 3. The details of the individual and the large-scale information values analyses are presented in the Discussion.

Comparison with Mouse

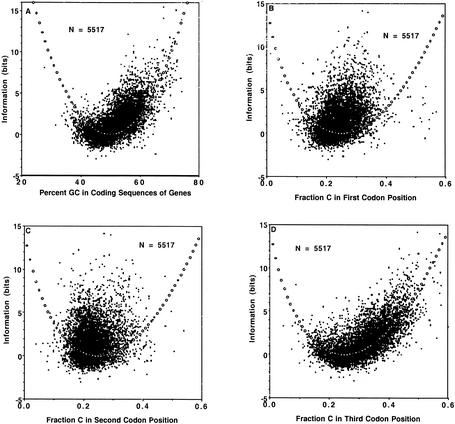
The relationship of mouse nucleotide content and information values (Fig. 4A–D) was very similar to those for human (Fig. 2B–E). The comments above regarding the theoretical curve fits for human apply similarly to mouse, and are analyzed in detail in the Discussion.

Figure 4.

Relationship of information (bits) and percent GC, in (A) coding sequences of mouse genes; and relationship of information (bits) and C content in (B) first codon position for mouse sequences, (C) second codon position for mouse sequences, and (D) third codon position for mouse sequences. Open circles indicate theoretical fit to the information function.

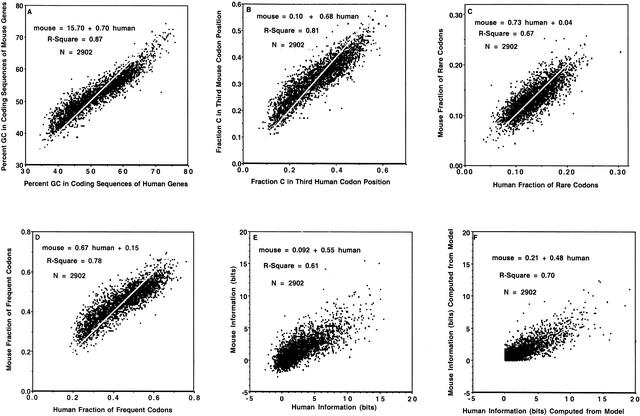
Linear regression analysis for 2902 mouse versus human orthologous RefSeq pairs (D. Maglott, pers. comm.) showed linear correlations for percent GC in coding sequences of genes (Fig. 5A). This was also true for the composition of all four nucleotides at all three codon positions (Table 8; Fig. 5B); similar analyses have been published by Mouchiroud and Bernardi (1993) and Bernardi (2000b) for orthologous pairs of genes in several species.

Figure 5.

Relationship of (A) percent GC in coding sequences (white line through data points indicates identity: GC in mouse = GC in human), (B) fraction C in third codon position (white line through data points indicates identity: fraction C in codon position 3 in mouse = fraction C in codon position 3 in human), (C) fraction of rare codons, (D) fraction of frequent codons, (E) information (bits), and (F) model-computed information (bits) in orthologous mouse and human sequences.

Table 8.

Linear Regression Results for Mouse versus Human Orthologous RefSeq Codon Nucleotide Composition

Slopes
Nucleotide	Codon position
1	2	3
A	0.88	0.95	0.67
C	0.87	0.95	0.68
G	0.92	0.91	0.65
T	0.92	0.97	0.61
Intercepts
Nucleotide	Codon position
1	2	3
A	0.011	0.005	0.019
C	0.010	0.004	0.033
G	0.008	0.006	0.034
T	0.005	0.002	0.028
R-Square values
Nucleotide	Codon position
1	2	3
A	0.92	0.94	0.82
C	0.91	0.92	0.81
G	0.90	0.89	0.74
T	0.89	0.95	0.73

The mouse and human orthologs also exhibited a linear relationship for both fraction of rare (Fig. 5C) and fraction of frequent (Fig. 5D) codons. The implications of this observation are analyzed in detail in the Discussion.

The information values for orthologous mouse and human RefSeqs were linearly correlated (Fig. 5E), following the regression equation: mouse = 0.092 + 0.55 human. This relationship could be modeled quite closely (Fig. 5F) by substituting the fraction C in codon position 3 (i.e., each point in Fig. 5B) for “p” in Equation 6, for both mouse and human. This allowed a transformation from “fraction C orthologous pairs” (fraction C in third human codon position, fraction C in third mouse codon position) to “model information orthologous pairs” (human information computed from model, mouse information computed from model). The regression equation for the model fit (i.e., the scatter plot of “model information orthologous pairs;” Fig. 5F) was similar to that for the measured data (Fig. 5E): mouse = 0.21 + 0.48 human.

DISCUSSION

Relationship of Percent GC in Coding Sequences of Genes and Percent GC in Human Genome

The positive correlation between percent GC in coding sequences of genes and the percent GC in the genomic region containing the gene (Fig. 1A) is somewhat surprising: the number of nucleotides in coding sequences is generally a small fraction of the number of nucleotides in the genomic region spanning the gene, since in human the introns are much longer than the exons, and the 20 kb window used in computing the genomic percent GC adds even more nonexonic sequence at the termini of the spanning genomic region. Thus, it is highly unlikely that the genomic percent GC is numerically a consequence of the coding sequence percent GC. The same argument would apply even more strongly to the correlation with fraction C (Fig. 1D; Table 1) or G in the third codon position. There is simply not enough G or C in one codon position to substantially affect the genomic GC content. By logical elimination, it is likely that the same factor(s) from which genomic regions of different characteristic percent GC arose also caused the correlation with the third codon position. The second codon position was not subject to this factor (Fig. 1C), since this position is instrumental in determining the identity of the amino acid, so that strong functional constraints would completely override the tendency toward GC bias. These same constraints are apparently present, but not as strongly, in the first codon position (Fig. 1B). In fact, this position has a minor characteristic of a wobble position in that there are synonymous substitutions in codon position 1 for leucine and arginine (see Methods). Although there are no such synonymous substitutions in codon position 2 for leucine and arginine, it should be mentioned that the combination of positions 1 and 2 could be regarded as a wobble position for serine (TCT/AGT and TCC/AGC), but this type of “concerted” synonymous substitution would have no effect on the A, C, G, or T content of any of the three codon positions.

Relationship of Human Nucleotide Content and Information (bits)

A fundamental observation is that the information value is nonlinearly correlated with GC content (and, since AT = 1 – GC, also with AT content) in the genome (Fig. 2A) and in the coding sequence (Fig. 2B), and with the A, C, G, or T content in the third codon position (Fig. 2E). This observation can be understood by considering the GC content in the coding sequence (Fig. 2B): as percent GC or AT approaches the maximal value (that is, as the percent GC or AT increases or decreases from 50%), there are fewer choices of synonymous codons available, so that the information tends towards a relatively high value. Because of the linear correlation of GC content in the coding sequence with GC content in the genomic region (Fig. 1A) and with A, C, G, and T in codon position 3 (Fig. 1D), these also “inherit” the nonlinear relation between information value and GC content in the coding sequence.

This phenomenon is the biological analogy of the probabilistic argument leading to the nonlinear relationship in the plot of uncertainty versus probability for two variables (see, e.g., Hamming 1980; Tom Schneider, “Information Theory Primer with an Appendix on Logarithms,” www.lecb.ncifcrf.gov/∼toms/paper/primer). As the probability deviates either positively or negatively from 50%, the information approaches its maximum value. The biological observation is all the more important in that the nonlinear relationship is present for codon position 3 (Fig. 2E), but not for codon positions 1 (Fig. 2C) or 2 (Fig. 2D). The high quality of the theoretical fit for codon position 3 (Fig. 2E) indicates that the choice of codon position 3 and therefore of synonymous codons is under, at most, quite modest biological constraint, and is governed primarily by probabilistic and statistical considerations. On the other hand, the deviation from the theoretical fit for codon positions 1 and 2 (Fig. 2C,D) indicates that the choice of codon positions 1 and 2 are under severe biological constraint (i.e., the identity of the amino acid) that causes a marked deviation from what would be expected if based solely upon probabilistic and statistical considerations. If the choice of synonymous codons were under biological constraint, then Figure 2E would look like Figure 2C,D, and the data in Figure 2E would not correspond to the theoretical fit. The lower quality of the theoretical fit for percent GC in coding sequences (Fig. 2B) relative to the theoretical fit for fraction C in codon position 3 (Fig. 2E) is easily explained by the fact that the former is “contaminated” by including codon positions 1 and 2, which exhibit a very poor fit (Fig. 2B,C).

The conclusion that synonymous codon choice is under, at most, quite modest biological constraint appears to be inconsistent with the classical findings in unicellular organisms that genes whose protein products are highly expressed are under a strong biological constraint, in that they preferentially use the most frequent codons (see above). This general conclusion is supported by examination of certain specific classes of proteins that are considered to be highly expressed. For example, within the set of human RefSeqs studied here, 106 were identified as coding for ribosomal proteins. The mean ± standard deviation for the information value, fraction of rare codons, and fraction of frequent codons are 2.60 ± 2.35, 0.13 ± 0.04, and 0.43 ± 0.11, respectively; these values are very similar to those for various sets of housekeeping genes (not shown). The corresponding values for the complete set of human RefSeqs are 2.63 ± 2.81, 0.14 ± 0.03, and 0.44 ± 0.12. Thus the highly expressed ribosomal proteins and housekeeping gene products are statistically similar to the complete set of genes. When the highly expressed ribosomal proteins and housekeeping gene products are removed from the complete set, the resulting set, which is specifically diminished in genes for highly expressed proteins, has corresponding values of 2.42 ± 2.63, 0.14 ± 0.04, and 0.42 ± 0.12. Thus the highly expressed ribosomal proteins and housekeeping gene products are statistically similar to the set of genes which is specifically diminished in genes for highly expressed proteins. In summary, in contrast to the unicellular organisms, human does not appear to preferentially utilize frequent codons for genes with highly expressed protein products.

In addition, plots that are analogous to those in Figures 2 and 3, but in which only the genes for highly expressed proteins are included, are visually identical to the corresponding plots in Figures 2 and 3. Thus, there is no evidence that these genes are more highly constrained than the general population of genes.

Identification of “Rare” Codon Usage and Relationship to Information Value

An obvious hypothesis for explaining the existence of some sequences with a high information value is that these sequences use a preponderance of “rare” codons for translational control. However, “rare” codons are in fact rare or nonexistent (Table 5). The rarest codon is codon 3 of leucine, and this is used at 18.1% the frequency of the maximally used codon 4 of leucine.

It is notable that the codon with the maximum usage for each amino acid usually has C (or, less often, G) in codon position 3. It is also notable that the four four-codon families which have C in codon position 2 (i.e., serine, proline, threonine, and alanine, if we momentarily ignore the two “extra” serine codons that contain G in codon position 2) all contain a codon (codon 4 in all four cases) that is identified as a “rarely used” codon. It is perhaps somewhat surprising that these four codons all contain G in position 3, given the comment above concerning codons with maximum usage.

Two RefSeqs were arbitrarily chosen for manual examination. NM_000065 (information = 0.00 bits) and NM_002246 (information = 16.12 bits) are representatives of coding sequences with low and high information, respectively. NM_000065 (Table 6; computed as the ratios of the codon frequencies for the sequence to the corresponding entries in Table 3) exhibits a modest amount of deviation from the pooled pattern, with the exception of a low usage of the four rare-usage codons mentioned above (codon 4 for serine, proline, threonine, and alanine). However, NM_000065 fully utilizes other rare-usage codons, such as codons 3, 5, and 6 of leucine.

In stark contrast, NM_002246 (Table 7) is extremely reluctant to use codons 1, 3, or 5 of any amino acid, and strongly overutilizes the rare-usage codon 4 for serine, proline, threonine, and alanine. However, NM_002246 frequently utilizes codon 2 of all amino acids, which is almost invariably the codon with maximum usage (Table 6) for each amino acid.

The relationship between information values and the fraction of frequent codons within a sequence (Fig. 3C) is reminiscent of the relationship between information values and fraction C in codon position 3 (Fig. 2E). In fact, most of the frequent codons in multicodon amino acids have C in codon position 3 (Table 5), so this similarity is expected. As a consequence of the inverse linear correlation between the fraction of rare and the fraction of frequent codons (Fig. 3A), the mirror-image type behavior is expected for the fraction of rare codons (Fig. 3B).

Comparison with Mouse

The relationship of mouse nucleotide content and information values (Fig. 4A–D) was very similar to that for human (Fig. 2B–E), and the comments for human sequences concerning each codon position equally apply to mouse. Again, the comments regarding the human theoretical fits equally apply to mouse.

Linear regression analysis for 2902 mouse versus human orthologous RefSeq pairs showed linear correlations for the composition of all four nucleotides at all three codon positions (Table 8). As expected, the slopes are closest to unity and the R-Square values are generally highest for codon position 2, since this position is the most constrained by the functional requirement for the identity of the amino acid. The opposite is true for codon position 3, which has the most flexibility in terms of synonymous substitutions notwithstanding the fact that codon position 3 has the most flexibility in terms of synonymous substitution, the R-Square values are still very high.

Despite the rather high rate of synonymous divergence between rodent and human (Makalowski and Boguski 1998), there is a linear correlation in the information values for human/mouse orthologs (Fig. 5E), following the regression equation: mouse = 0.092 + 0.55 human. The fact that the slope is substantially less than unity is the direct result of the relationship of fraction C in codon position 3 for mouse versus human (Fig. 5B): when the theoretical model for information versus p (Equation 6) is applied to the data in Figure 5B, the resulting model scatter plot (Fig. 5F) is similar to the measured scatter plot (Fig. 5E).

In fact, it is easy to see that the relationship between mouse and human information (Fig. 5E) is a direct consequence of a special property of the relationship of fraction C in mouse versus human (Fig. 5B): when fraction C in human is approximately 0.25, there is a transition relative to the line of identity (white line through the data points) such that fraction C in mouse exceeds that in human below this transition point, and such that fraction C in human exceeds that in mouse above this transition point. Thus, for orthologous pairs, the distance from 0.25 of fraction C in humans is remapped in mouse such that the distance from 0.25 is smaller in mouse than in human. The nonlinear relationship governing the data in Fig. 2E indicates that this remapping leads to a smaller information value in mouse, since the information value is at a minimum at 0.25 and it increases as fraction C moves away, either positively or negatively, from 0.25. It is indeed remarkable that the transition in the fraction C data occurs almost exactly where the information minimum occurs.

This effect does not occur as an isolated phenomenon. The fraction C in codon position 3 is strongly dependent upon percent GC in the coding sequence (Fig. 1D). It is no surprise that the same phenomenon occurs for percent GC in coding sequences at approximately 50% GC in human (Fig. 5A). The discussion relating to fraction C in the preceding paragraph also applies here in relationship to percent GC in coding sequences. Because percent GC in coding sequences is, in turn, strongly dependent upon percent GC in genomic region (Fig. 1A), it is clear that there is a chain linking (1) placement of a gene within a genomic region of a given GC composition, (2) GC composition of the coding sequence, (3) fraction C in codon position 3, and (4) information value.

This same effect is present in the relationship of fraction of frequent (Fig. 5D) but not fraction of rare (Fig. 5C) codons. Again, the transition for frequent codons occurs at approximately the same position as does the information value minimum (Fig. 3C). The effect is to remap the human fraction of frequent codons to a mouse value that is closer to that for the information minimum. In essence, mouse does not utilize the full dynamic range that human does in modulating frequent codon usage. It is not clear at this time whether there is a significance to the absence of this effect for fraction of rare codons.

These observations suggest that, for a given organism, evolution may place a given gene in a region of a particular GC content so as to adjust the information to the appropriate value for that gene in that organism. The concept of “appropriate value” for information is based upon the idea that the information value of a protein-coding gene is largely determined by the GC content of the genomic region in which the gene is embedded, perhaps through the intermediacy of the genomic GC content upon the composition of codon position 3. This is important because other important properties of the gene may themselves be determined through the intermediacy of the composition of the information value. A specific example of this is the composition of frequent and rare codons. However, the role of the information value may well extend to determining other properties of the gene that are important for adequate functionality. Placement of the gene in this manner is a strategy that utilizes the already existing mechanism for isochore maintenance to robustly maintain the appropriate information value, and consequently to maintain the appropriate composition of rare and frequent codons (Fig. 3B,C). This strategy is particularly economical, since it utilizes the already existing mechanism for isochore maintenance; it is particularly robust, since it requires only that the information values follow the theoretical curve (Figs. 2E and 4D), which is the expected “maximum entropy” behavior for an ensemble that is not subject to external constraints. In contrast, maintenance of the identity of the amino acid requires costly external constraints, since codon positions 1 and 2 deviate substantially from the theoretical curve (Figs. 2C,D and 4B,C).

Postulating an evolutionary strategy of gene placement requires a slight modification of the conclusion that “the choice of codon position 3 and therefore of synonymous codons is under, at most, quite modest biological constraint, and is governed primarily by probabilistic and statistical considerations.” While it is still true that the choice of synonymous codons is governed primarily by probabilistic and statistical considerations, it is not quite true that the choice of synonymous codons is under, at most, quite modest biological constraint. There is a subtle constraint, namely that the gene was placed in a genomic region of a particular GC content.

Furthermore, is there any significance to controlling the fraction of rare and of frequent codons via the relationship with information value (Fig. 3B,C)? Unlike unicellular organisms, it does not appear that translation is regulated in human by synonymous codon choice. On the other hand, in mammals, but not in E. coli, there is a relationship between synonymous codon choice and protein structure (Tao and Dafu 1998). Presumably, this indicates that in mammals, folding and structure of the nascent polypeptide in the ribosome complex are under the control of synonymous codon choice. This can explain why human does not exhibit the correlation between protein expression level and synonymous codon choice: synonymous codon choice is utilized in human for control of protein folding rather than for regulation of translation.

These results and analyses indicate the potential utility of the information theoretic measure for interpretation of whole genomic comparison of synonymous codon usage, and for the inference of evolutionary mechanisms.

METHODS

Coding Sequences

Reference mRNA sequences (RefSeqs; Pruitt et al. 2000; Pruitt and Maglott 2001) for human and mouse were downloaded from www.ncbi.nlm.nih.gov on March 2, 2001 and March 16, 2001, respectively. These files contained 10,995 and 5623 sequences, respectively. The sequences in these files were converted to FASTA format and were truncated to include only protein-coding region. After removal of sequences that contained symbols other than A, C, G, or T, there were 10,862 and 5517 sequences, respectively, that were used for subsequent analyses.

Human Genomic GC Content

The GC content of the genomic region (NCBI public genome build 22 in effect March, 2001) spanning each RefSeq was determined from Spidey (Wheelan, Church, and Ostell 2001) alignments. Each contig containing a Spidey hit was partitioned into adjacent 20 kb segments, and the GC content was computed for each segment. Finally, the average GC content for the adjacent genomic segments spanning each RefSeq was computed.

Computation of Fraction A, C, G, and T in Codon Positions 1, 2, and 3

For each coding sequence, the fraction F_n,p of nucleotide n ∈ {A,C,G,T} in codon position p ∈ {1,2,3} was computed as

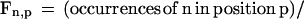1

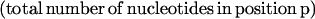Computation of Pooled Codon Frequencies and Identification of “Rare” Codons

For the pooled coding sequences from a given organism (Tables 3–5 for human), the number of occurrences of each codon was tabulated. The synonymous codon frequencies were computed by dividing the number of occurrences of each synonymous codon either by the pooled total over all the amino acids or, for a given amino acid, by the sum of the number of occurrences of synonymous codons for that amino acid. In order to identify “rare” codons (which may be important in translational control), for each amino acid the codon frequency of each synonymous codon was divided by the codon frequency of the codon with the highest codon frequency. These ratios for all the codons for all the amino acids were then pooled and sorted. The rank order of all ratios ≤0.50 was assigned, with the codon having the lowest ratio over all amino acids and all codons designated as “1” in the rank ordering.

Computation of Rare and Frequent Codon Fractions

For an examination of the relationship of rare codons, frequent codons, and information values, rare codons were defined as the 15 codons identified as rare in Table 5, and frequent codons were defined as those with a value of 1.000 in Table 5, with the exception of the codons of methionine and tryptophan, which have only one codon. Fractions of rare and frequent codons were computed by dividing the number of rare or frequent codons, respectively, by the total number of codons in the sequence.

In mouse, the rare and frequent codon computations were based upon the tabulation of (Nakamura 1998; www.kazusa.or.jp/codon/cgi-bin/showcodon.cgi?species=Mus+muscalus+[gbrod]). The results (not shown) were essentially identical to those for human (Table 5).

Computation of Information (bits)

The method developed by Schneider et al. (1986) to compute the information content of binding sites was adapted to compute the information of an individual protein-coding nucleotide sequence with respect to usage of synonymous codons. Very briefly, in the method developed by Schneider, multiple alignment of N sequences results in n aligned columns representing a protein binding site. For each column, the information value is computed. Finally, the overall information value for the binding site is computed by adding the information values for each of the n columns. The ability to perform this addition is not trivial; it is a direct consequence of the additivity property of information values (Hamming 1980; Tom Schneider, “Information Theory Primer with an Appendix on Logarithms,” www.lecb.ncifcrf.gov/∼toms/paper/primer). The additivity property requires that the information values be statistically independent, as is expected to be the case here.

There is a direct analogy between the method developed here for computation of the information of an individual protein-coding nucleotide sequence with respect to usage of synonymous codons, and for computation of the information of a protein (e.g., a transcription factor) binding site using multiple alignment of related sequences (Schneider et al. 1986): in the method developed here, each coding sequence (RefSeq) is the analogy of a binding site. Each of the (encoded) amino acids is the analogy of one column in the DNA multiple alignment. A synonymous codon is the analogy of A, C, G, or T in the DNA multiple alignment. Computation of the information value for a single (encoded) amino acid is the analogy of computing the information for a given column of the multiple alignment. Computation of the overall information value for a sequence by adding the information values for each of the (encoded) amino acids is the analogy of computing the overall information value for the binding site by summing the information values for each of the columns in the DNA alignment example.

This information measure for a given sequence (R_sequence) was computed as the difference between the overall uncertainty H_g (with respect to a set of sequences of which the given sequence is a member; the subscript “g” is intended to indicate “global” or “genomic”) and the uncertainty for the given sequence H_s (the subscript “s” is intended to indicate a “single” sequence) after applying the “Approximate method” for small sample size as described in the Appendix of Schneider et al. (1986). The general form for uncertainty H is

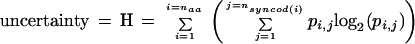2

where n_aa is the effective number of amino acids (in this case equal to 23 as described below), n_syncod(i) is the number of synonymous codons for amino acid i, and p_i,j is the probability of synonymous codon j for amino acid i. For the overall uncertainty H_g, p_i,j is computed over the entire set of sequences for the given organism (it is important to emphasize that p_i,j is the actually measured frequency distribution and NOT based upon a prior assumption of uniform distribution), whereas for each individual sequence, the computation of p_i,j is restricted to the codons for that one sequence to give H_s. This measures the diversity of synonymous codon usage within the given sequence. The general form for information is

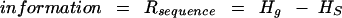3

This is an analogy to information by Shannon (Shannon 1948; Schneider et al. 1986).

The effective number of amino acids is 23, since the codons for leucine, serine, and arginine were each divided into two disjoint sets such that only codon position 3 substitutions were counted as possibly being synonymous. This approach introduces a slight error, since in fact there are several instances where codon position 1 substitutions might be synonymous (two for leucine (CTA/TTA and CTG/TTG), zero for serine, and two for arginine (CGA/AGA and CGG/AGG)). This slight error is not expected to alter any of the conclusions here. There are no cases where position two substitutions might be synonymous.

Fitting the Information Function Using a Theoretical Model

For the simple case of two independent variables, the uncertainty versus probability curve has a maximum at p = 0.50 (Hamming 1980; Tom Schneider, “Information Theory Primer with an Appendix on Logarithms,” www.lecb.ncifcrf.gov/∼toms/paper/primer), or, equivalently, the information versus probability curve has a minimum at p = 0.50. In general, for n independent variables, the uncertainty achieves a maximum and the information achieves a minimum when the probabilities of all n variables are equal to one another (Hamming 1980), and therefore, since the p values must sum to unity, when each is equal to 1/n. Conversely, given a scatter plot of information versus the probability of one variable, the effective number of variables can be estimated as

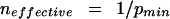4

where n_effective is the effective number of variables and p_min is the value of p at which the information achieves a minimum.

For the data examined here, n_effective is either 2 or 4 (see Results). In the instances where n_effective = 2, with the exception of a scale factor, there are no free parameters (that is, there are zero degrees of freedom) in fitting a theoretical curve to the scatter plot: one of the degrees of freedom is used up by the constraint that the two p values must sum to unity, and the other degree of freedom is used up by the fact that one of the p values is used as the x coordinate in the scatter plot.

In the theoretical curve, H_g should be attributed a value that results from making the weakest possible assumption. This assumption is that the overall uncertainty is as high as possible. This condition will be met if all p values are equal. In this case, Equation 2 for H_g is given as log2(n_effective) =log2(2) = 1. Thus, the data in the scatter plot will be fit to the theoretical curve (according to Equations 2 and 3):

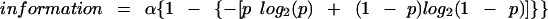5

where the scale factor α is obviously the only adjustable parameter.

In the instances where n_effective = 4, in addition to the scale factor, there are now two free parameters. As just described for n_effective = 2, H_g is now given as log2(n_effective) =log2(4) = 2. For the sake of clarity, assume that the four probability values are p₁, p₂, p₃, and p₄. Further assume that p₁ is to be used as the x axis and that p₄ is constrained by the relationship p₁ + p₂ + p₃ + p₄ = 1, so that p₂ and p₃ are the adjustable parameters (subject to the constraint that p₂ + p₃ ≤ 1 − p₁). In practice, an alternative simpler approach to performing the fitting was used here: p₂, p₃, and p₄ were each set to be equal to (1 − p₁)/3, so that the scale factor was the only adjustable parameter. This approach worked well, and it was neither justifiable nor useful to adjust additional free parameters. In this case, (after algebraic simplification) information was given by

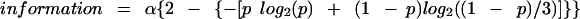6

In Figure 2C, D, and E, only the data in Figure 2E matched a theoretical curve for information (Equation 6). Therefore, the value for α was determined by fitting to data in Figure 2E, and then this same value for α was used to generate the theoretical curves in Figure 2C and D, in order to show the large deviation of the data in Figure 2C and D from the theoretical curve. This was also true for Figure 4B, C, and D.

WEB SITE REFERENCES

www.kazusa.or.jp/codon/cgi-bin/showcodon.cgi?species=Homo+sapiens+[gbpri]

www.lecb.ncifcrf.gov/∼toms/paper/primer

www.ncbi.nlm.nih.gov