Surface crystallization of supercooled water in clouds

Abstract

The process by which liquid cloud droplets homogeneously crystallize into ice is still not well understood. The ice nucleation process based on the standard and classical theory of homogeneous freezing initiates within the interior volume of a cloud droplet. Current experimental data on homogeneous freezing rates of ice in droplets of supercooled water, both in air and emulsion oil samples, show considerable scatter. For example, at −33°C, the reported volume-based freezing rates of ice in supercooled water vary by as many as 5 orders of magnitude, which is well outside the range of measurement uncertainties. Here, we show that the process of ice nucleus formation at the air (or oil)-liquid water interface may help to explain why experimental results on ice nucleation rates yield different results in different ambient phases. Our results also suggest that surface crystallization of ice in cloud droplets can explain why low amounts of supercooled water have been observed in the atmosphere near −40°C.

For almost 200 years, persistent (liquid) fogs have been observed at temperatures well below the frost point, and there has been a continued vigorous interest in understanding why, and how far, water droplets can supercool in the atmosphere. The presence of heterogeneous ice nuclei in supercooled water droplets has been shown to be necessary for glaciating clouds at temperatures above about −30°C (1). However, ice particle number densities in clouds below −30°C are often observed to exceed the ice nuclei number densities (2–7). This finding suggests that, in clouds, some supercooled water droplets freeze homogeneously.

The conversion of supercooled water droplets and/or droplets of aqueous salt solutions into ice below −30°C can occur anywhere in the atmosphere from the surface layer (resulting in ice fogs) (8) to the upper troposphere (in cirrus clouds) (4–6). In addition, ice freezing in the polar stratosphere has been shown to occur via a homogeneous nucleation process (9, 10). Therefore, it is important to elucidate the actual physical process by means of which clouds glaciate in the atmosphere, particularly at cold temperatures and in situations where ice nuclei become less abundant and less effective in promoting the freezing of cloud droplets into ice (1).

Radiative properties of ice clouds and their subsequent effect on climate depend strongly on the size of the cloud particles (11), a property closely linked to the rate at which ice particles in the cloud nucleate and grow. In addition, the rates of chemical reactions, which occur in cloud droplets or on cloud surfaces, depend on the phase of the cloud particle (12). Thus it is important to be able to predict under what set of environmental conditions supercooled cloud droplets freeze into ice. Other significant natural processes, which are affected by the physical state of clouds, include lightning (13) and precipitation. The occurrence of lightning can increase the concentration of reactive nitrogen oxides in air, thereby affecting the rate of gas-phase chemical processes (14). Finally, the amount of precipitation reaching the ground (under many circumstances) is influenced by the in-cloud rate of glaciation of liquid water into ice.

Thermodynamics and Kinetics of the Crystallization Process

The first theoretical description of crystallization of supercooled water droplets into ice was presented in 1939 by Volmer (15). In that study a classical volume-based nucleation rate theory was used, i.e., an ice nucleus was assumed to form only within a droplet volume. The theory of homogeneous freezing of pure water droplets has remained nearly unchanged in the last 60 years, and the current theory (1), commonly used in atmospheric science studies, still relies on Volmer's assumption (15).

In principle, the homogeneous freezing of a supercooled liquid water droplet occurs when an ice nucleus forms either inside or on the surface of the droplet. Although the formation of a single nucleus is sufficient to crystallize a supercooled water droplet, the nucleation rate (J_V) is often expressed as the number of nuclei formed in unit time in unit volume of liquid solution (1). Similarly, J_S can be defined as the number of critical nuclei formed per unit time on unit surface area of the liquid solution. Thus, the total number of nuclei formed in a unit volume of air in unit time can be written as

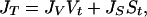where V_t and S_t are the total collective volume and collective surface area, respectively, of all of the droplets in a unit volume of air. At this point, it should be emphasized that Volmer's assumption of volume-based nucleation (15) can only be meaningful if J_VV_t≫ J_SS_t. Below, we present intuitive thermodynamic arguments to suggest why, for the ice–water–air system, the second term in Eq. 1 may be the dominant term in the atmosphere. In later sections, analysis of existing experimental data leads to the conclusion that ice nucleation in supercooled water droplets may, in many instances, be a surface-based process, i.e., a process in which the second term in Eq. 1 is dominant.

In a recent paper (16) we presented a thermodynamic theory for the reversible work of formation of a crystal nucleus in a supercooled single-component melt. The thermodynamic analysis was rigorous but the systems to which it was applied were modeled to conform to the so-called “capillarity approximation” in which both surface adsorption and the dependence of surface tension on curvature are ignored. However, for single-component systems, nucleation theories based on the capillarity approximation have been reasonably successful. We evaluated and compared the work of nucleus formation at the melt surface to that within its bulk. For surface nucleation to dominate over bulk-volume nucleation, the work of crystal nucleus formation in the former mode should be less than that in the latter mode. On the basis of the thermodynamic analysis in ref. 16, and when the ambient is the system vapor, this condition will be satisfied when the following inequality holds:

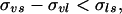where the surface tensions σ_vs, σ_vl, and σ_ls refer to the vapor-solid, vapor-liquid(melt), and liquid(melt)-solid interfaces, respectively. Eq. 2 is also the condition for the partial wetting (nonzero contact angle) of a solid by its melt.

The theory developed in ref. 16 and its result, Eq. 2, do not require the volumes or shapes of the respective nuclei for the surface and volume modes to be the same. Nor do they require the surface tension of every face of the crystalline nucleus to be the same. However, if it is assumed that they are the same, it is possible to sketch a nonrigorous but intuitive argument for the validity of Eq. 2, one that provides physical insight into the basis of the equation. When a crystalline nucleus forms within the volume of a drop, assume that every face of the crystal exhibits a surface or interfacial tension σ_sl characteristic of a solid-liquid interface. As indicated above, this surface tension may vary from face to face, but for simplicity assume that it does not. If the crystal is nucleated at the surface of the drop, then at least one of its faces is a solid-vapor surface with a surface tension that may be denoted by σ_vs. Normally σ_vs > σ_ls so that it might appear that the work of formation of the nucleus in the bulk is less than that at the surface where at least one face of the crystalline nucleus has the surface tension σ_vs rather than the smaller σ_ls. However, this simple conclusion is faulted by the omission of another simple fact. This is the fact that when a crystal face is formed at the liquid-vapor interface, the surface tension σ_vl of this pre-existing interface is lost. Thus it is not σ_vs that replaces the σ_ls, characteristic of the face when immersed in the liquid, but rather the effective surface tension σ_eff = σ_vs − σ_vl and the inequality that should be considered is σ_eff < σ_ls or σ_vs − σ_vl < σ_ls if surface nucleation is to be favored. This last condition is just Eq. 2, which is what we wanted to prove. Our rough proof is predicated on the assumption that the crystal has exactly the same size and habit in the surface mode of nucleation as in the bulk mode, an assumption that is most likely not the case, but our rough argument is supported by the more rigorous theory of ref. 16.

The idea of surface freezing is also supported by several kinds of independent evidence. For example, Cahn (17) has performed a statistical thermodynamic analysis, which indicates that perfect wetting below the critical temperature should usually not occur. Thus according to Cahn's analysis the inequality in Eq. 2 is in general satisfied for most single-component systems. Furthermore, molecular dynamics simulations (18–20) of the crystallization process in small clusters, containing neat substances, indicate that the crystalline nucleus in molten single-component liquid clusters tends to form at or very near the surface layer. Thus, the assumption that crystal nucleation at the surface may be thermodynamically the favored mode is supported by additional theory (17) and computer simulation experiments (18–20).

Optical studies (21) on the surface melting of ice show that water only partially wets the ice surface even at 0°C. Thus, according to the above arguments (16, 17), ice nucleation on the surface should be thermodynamically favored over that in the bulk. An increase in temperature can often cause a wetting transition, where partial wetting is transformed into complete wetting (22). If this occurs, then nucleation in the bulk may be thermodynamically favored over that on the surface. In the atmosphere, ice clouds always form below 0°C. Thus, because below 0°C water only partially wets the ice surface (21), homogeneous nucleation of ice crystals may potentially occur at cloud droplet surfaces. Nevertheless, as far as we know, all laboratory data on ice nucleation, in either supercooled water (1, 23–28) or in droplets of dilute aqueous solution (9, 10, 29–32), have been analyzed under the assumption that ice nucleation took place in the interior volume and not on the surface of supercooled droplets (i.e., in the analysis the second term in Eq. 1 was set to zero).

Sometimes the freezing of droplets is studied by dispersing them in an oil bath in which they do not dissolve. If the ambient is not the system vapor but rather an oil, then even though the full system no longer consists of a single component, it is likely that Eq. 2 will still represent the condition under which surface nucleation will be favored. Thus in the case of an oil bath, Eq. 2 should be slightly modified to read

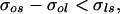where the subscript o refers to the oil phase. Because the surface tensions of the melt and the oil can be of comparable magnitude (33), the inequality in Eq. 3 may not always be satisfied, in which case the dominant mode of crystal nucleation in droplets will be the volume process. Thus we should expect to see varying droplet-freezing rates in varying ambients, and the observation of such variations may be taken as a strong signature of a freezing process occurring on the surface.

Another strong indicator of surface crystallization can be found in the freezing of different size droplets immersed in the same ambient bath. In this case, a strong variation of nucleation rate with droplet size distribution can only be the result of surface nucleation. For example, the collective volume of the droplets can be spread over a population of either numerous small particles (in the submicron range) or of a few larger ones (in the supermicron range). Both droplet distributions will have the same total volume but very different surface areas. If nucleation occurs on the surface, then the former distribution, with a much higher surface-to-volume ratio, will freeze at a faster rate. On the other hand, if nucleation occurs in the volume, then both distributions will freeze at the same rate. Thus studies of crystallization rates in the same ambient bath, using different droplet size distributions, can provide useful information regarding the mode of the nucleation process.

Before re-examining laboratory data on the nucleation of ice crystals, it is important to re-emphasize the point made in connection with Eq. 3 regarding the differences between freezing rates measured in oil (9, 23–25, 29) and air (26–28, 30–32). In oil ambients, depending on the oil and surfactant materials used, there could be cases where volume-based nucleation can become thermodynamically more favorable than the surface process. However, such a preference has no relevance to the atmosphere where water droplets and/or aqueous solution droplets are suspended freely in the air while surfactant materials are probably not present in significant enough quantities to alter droplet surface properties.

Interpretation and Analysis of Laboratory Ice Freezing Rates

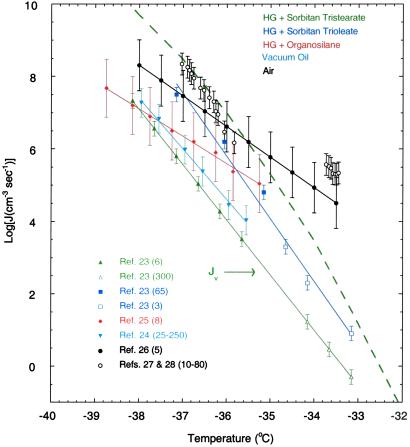
The symbols in Fig. 1 represent raw laboratory data on ice nucleation rates, reported as volume processes in units of cm⁻³⋅s⁻¹. These data refer to measurements on ice nucleation rates in supercooled water droplets suspended in various ambient oil phases (23–25) as well as in air (26–28). The analysis of these data in the present section indicates that, in oils, the nucleation of ice can be either volume or surface based, whereas in air it can only be surface based. Features of the data that allow us to draw these conclusions are the following:

Fig 1.

Homogeneous volume-based freezing nucleation rates of ice in supercooled water. Symbols and solid lines give raw laboratory data and least-square fits to these data. Note that the least-square fit line to the data presented by open circles (27, 28) is omitted for clarity. The numbers in parentheses give the droplet size range in units of μm. The dashed line gives the homogeneous freezing rate provided by Pruppacher and Klett (1). The error bars show the reported range of measurement uncertainties.

(i) Strong dependence of the reported volume-based ice nucleation rates on both the properties of the ambient phase and the droplet size distribution (suggesting surface-based nucleation);

(ii) Independence of the reported volume-based ice nucleation rates on both the properties of the ambient phase and the droplet size distribution (suggesting volume-based nucleation).

Fig. 1 exhibits laboratory rates, measured and analyzed under the assumption that the ice nucleation process was solely volume based (23–28). The droplet ambients in these experiments were oils [heptane grease (HG) + various surfactants or vacuum oil (VO)] and air. In the HG experiments, different surfactants were used in the formation of emulsions of droplets of supercooled water in oil. The results of the volume-based classical homogeneous nucleation rate theory, provided by Pruppacher and Klett (1), is also shown as a dashed line. Solid lines in Fig. 1 are least-square fits to the corresponding data. Error bars are also shown. The numbers in parentheses indicate the size or the size range in microns of the droplets used in each set of measurements.

What stands out most in Fig. 1 is the pronounced lack of coincidence between experiments performed in different ambients. As indicated above, this by itself is a signature of a surface-based process, or at least of a surface process in some ambients and a volume process in others. For example, at −33°C, the nucleation rates, reported as volume based, vary by as many as 5 orders of magnitude, which is well outside the range of measurement uncertainties suggested by the error bars. The experimental data also show different temperature dependencies (different slopes) in different ambient phases. This is most pronounced for the curves associated with the squares [HG + sorbitan triolate (STO)] and diamonds (HG + organosilane), and suggests that, in the corresponding ambients, nucleation was surface based. On the other hand, the curves passing through the inverted triangles (VO) and triangles [HG + sorbitan tristearate (STS)], not only lie close to one another, but have similar slopes. Also shown in Fig. 1 are the data for droplets in air (circles). If one assumes that bulk properties of water do not vary as droplets are immersed in different ambient phases (this assumption implies that the oils used in the emulsion experiments were pure and surfactants were completely water insoluble), it is reasonable to conclude that ice nucleation occurred at the water-ambient phase interface in the cases corresponding to the circles, squares, and diamonds in Fig. 1. On the other hand, the close proximity and similar slopes of the curves marked by inverted triangles (VO) and triangles (STS) suggests that, in these ambients, nucleation was volume based. We note that the line provided by Pruppacher and Klett (1) does not provide a good fit to the overall experimental data shown.

In the cases of the ambients, STS (Fig. 1, triangles) and VO (Fig. 1, inverted triangles), the reported volume-based nucleation rates form perfect straight lines despite factors of 50 and 10 changes, respectively, in the size of the water droplets used. The corresponding surface-to-volume ratios of the various particles were vastly different, and yet the observed ice nucleation rates were not affected. This finding strongly suggests that the nucleation rates in the droplets in these two oils were mainly volume based. As discussed above, volume-based nucleation could occur in some oil ambients when the inequality in Eq. 3 is not satisfied. Assuming that the ice freezing rates in STS were mainly volume based, an approximate formula for this rate process can be obtained by fitting the classical volume-based rate theory to the STS data in Fig. 1 (line labeled J_v). This classical expression is given by (34)

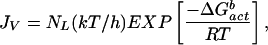where J_V is the ice nucleation rate in units of cm⁻³⋅s⁻¹, N_L is the molecular water concentration per cm³ of solution (≈3.35 × 10²² water molecules per cm³ of pure water), k and h are the Boltzmann and Planck constants, respectively, T is the Kelvin temperature, R is the ideal gas constant (cal⋅mol⁻¹⋅K⁻¹), and ΔG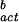 (= −394.22 + 1.805 T) (kcal⋅mol⁻¹) is the free energy of nucleus formation in bulk water. It is interesting to note that the rate of freezing to ice in bulk water, based on data obtained in STS (Fig. 1, J_V line), lies below the line provided by Pruppacher and Klett (1) for this process (Fig. 1, dashed line).

The reported volume-based freezing rates for STO in Fig. 1 show different slopes for droplets of different size and, unlike the STS and VO results, the experimental points within their error bars do not overlap the least-square fit. Furthermore, the rates with STO as a surfactant are roughly an order of magnitude larger than those measured with STS in the same laboratory. Based on these facts, the observed rates with STO were very likely affected by the properties of the oil–water interface at which ice nucleation took place. The rate of ice nucleation with organosilane exhibits yet a completely different slope than those observed with any of the other oil samples. Again, the most likely explanation is the occurrence of ice nucleation at the oil–water interface.

Clearly, the rates of ice nucleation in droplets in air (Fig. 1, circles) are higher than those observed in the experiments with droplets in oil. In addition, given the demonstrated fact that water can wet ice only partially (21), it seems reasonable on an a priori basis that, in droplets in air, the nucleation of ice is mainly surface based and is described primarily by the second term in Eq. 1. However, we note that ice nucleation rates (Fig. 1, open circles) in charged particles (27, 28), levitated in an electric field, are larger than those measured in cloud chambers (Fig. 1, filled circles) (26). Also, the experimental data from the levitation studies (Fig. 1, open circles) do not fit a single line with a single slope over the narrow temperature range of −37 to −34°C. We do not have an explanation for this observed behavior. In a future paper we plan to qualitatively determine how the kinetics and thermodynamics of the crystallization process are affected by the external conditions present in levitation-type experiments. For example, the surface tension of a charged droplet in a constant electric field is not uniform. At any point on the surface, the surface tension would depend on the angle between the external electric field and the radius vector (drawn from the center of the droplet).

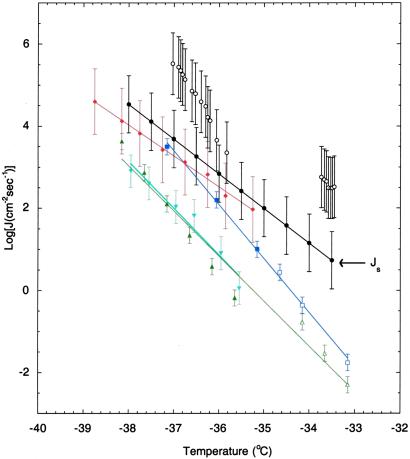
Assuming that the freezing rates of supercooled water in air are surface based, the volume-based rates in Fig. 1 can be replotted as surface rates in Fig. 2 by using the relation (35)

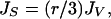where r is the droplet radius in cm. Note that in deriving Eq. 5 it is assumed that water droplets are monodispersed. Furthermore, only the results from cloud chamber studies (Fig. 2, filled circles) were used in obtaining a parameterized function for ΔG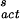 (see below). An approximate relation for the rate of ice nucleus formation (J_S in units of cm⁻²⋅s⁻¹) on the surface in air is (35)

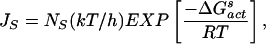where N_S is the number of water molecules per cm² of surface [≈10¹⁵ water molecules per cm² of surface (33)], and ΔG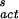 (= −218.2 + 1.0338 T) (kcal⋅mol⁻¹) is the free energy of nucleus formation on the surface. The latter quantity is obtained by fitting Eq. 6 to the line labeled J_S in Fig. 2.

Fig 2.

Homogeneous surface-based freezing nucleation rates in supercooled water. Eq. 5 was used to convert the reported volume-based rates, shown in Fig. 1, into surface-based rates. Symbols and color charts are defined in Fig. 1. Note that the error bars on open circles are larger than those shown in Fig. 1 because no information is given in refs. 27 and 28 on the size of particles used for each individual experiment. Thus we have extended the length of the error bar to account for the effect of variation in the droplet size range on the rate of the surface nucleation process.

Converting the reported volume-based rates in Fig. 1 to surface-based rates, and plotting the results in Fig. 2, leads to a somewhat dramatic inversion of behavior in various curves. For example, the STO results in Fig. 1 do not really fit a single line with a single slope, but they do fit a single straight line in Fig. 2. On the other hand, the STS results that fit a single straight line in Fig. 1 no longer fit a single line in Fig. 2. The simple explanation is that the STO process is surface based and therefore the corresponding data are made consistent when represented as a surface-based result, while on the other hand, the STS process is volume based so that the corresponding data are made inconsistent by representation as a surface-based process in Fig. 2. It is impressive that the data for the STO process form such a perfect straight line in Fig. 2, despite the fact that they encompass a 20-fold variation in droplet size.

The foregoing suggests that, in the interpretation of experimental results on the freezing of supercooled water droplets, it is important to recognize that, depending on the experimental conditions, ice nucleation rates may involve either the first or the second term in Eq. 1. The current homogeneous freezing rate theory (1) is incapable of explaining the wide range of nucleation rates measured in the laboratory, probably, because it fails to account for the important process of surface nucleation in droplets.

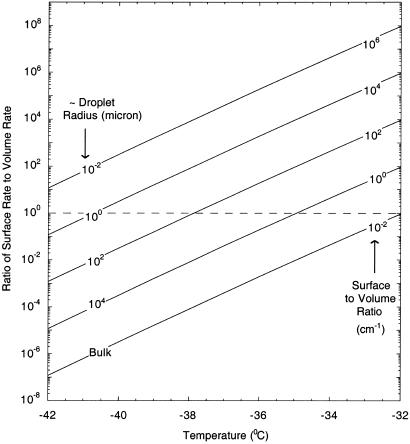
As argued above, thermodynamics can favor ice nucleus formation on the drop surface over that within the drop volume. However, the overall rate of crystal formation also depends on the surface-to-volume ratio of drops as well as the kinetic factors given in Eqs. 4 and 6 (N_L ≈ 3.35 × 10²² and N_S ≈ 10¹⁵). In Fig. 3 the ratio of surface nucleation rate (J_SS_t) to volume nucleation rate (J_VV_t) is shown for different assumptions of surface-to-volume ratio, using Eqs. 4 and 6 for supercooled water. Above the dashed line in Fig. 3, the surface-based process is dominant. In general, surface nucleation is favored over volume nucleation when supercooled water drops are smaller and temperatures are higher. Over the temperature range shown in Fig. 3, when the sample size approaches the bulk limit, the bulk process is dominant. However, it should be emphasized that the rate expressions derived in this article (Eqs. 4 and 6) for the freezing of supercooled water are crude, and more experimental and theoretical investigation is needed to obtain more accurate expressions for both processes. The main goal of this study is to indicate that surface nucleation cannot be ignored as a possible mechanism, in many cases, when interpreting experimental data on the freezing of supercooled water droplets. Whichever mechanism dominates, the laboratory data, as we have shown, is ambiguous on the issue of surface versus volume nucleation and is in fact biased toward the surface mechanism. Clearly, more focused laboratory investigations along with sophisticated coupled nucleation-growth algorithms are needed to better quantify how surface nucleation can affect the overall rate of the crystallization process in droplets.

Fig 3.

Variation in the ratio of surface freezing rate to volume freezing rate in supercooled water as a function of temperature.

In a separate paper (35) laboratory crystallization rates of nitric acid dihydrate (NAD), in concentrated solutions of aqueous nitric acid, were analyzed. It was concluded that, in this binary system, the crystalline NAD nucleus most likely formed at the droplet surface. Thus it is also likely that, in the atmosphere, the nucleation of ice in binary systems, such as aqueous droplets of H₂SO₄ and (NH₄)₂SO₄, also occurs at the droplet surface. In fact, the surface-based nucleation mechanism may help to explain why, in aqueous droplets, the measured freezing temperature of ice in solution differs when oil (9, 29) or air (30–32) ambients are used because the same behavior is also observed with the nucleation of ice in supercooled water (Fig. 1).

Based on the analysis of kinetic data on the freezing of dilute aqueous solution droplets into ice, obtained by using oil emulsions, Koop et al. (29) have recently suggested that ice nucleation rates in the atmosphere are independent of the nature of the solute. It is clear from the analysis presented here that freezing rates measured in oil ambients are not applicable to the atmosphere because different interfaces are respectively involved. Cziczo and Abbatt (30) have also noted that the freezing rates of ice in solution reported by Koop et al. (29), for many solutions of aqueous droplets immersed in various ambient oil baths, are inconsistent with those measured for the same systems in the air (30–32).

Supercooled Water Cloud Observations in the Atmosphere

This article and the development of its theme would be incomplete without addressing the evidence, gleaned from direct observations in the atmosphere, that surface-based nucleation of ice does take place in cloud droplets. We discuss such evidence in the present section.

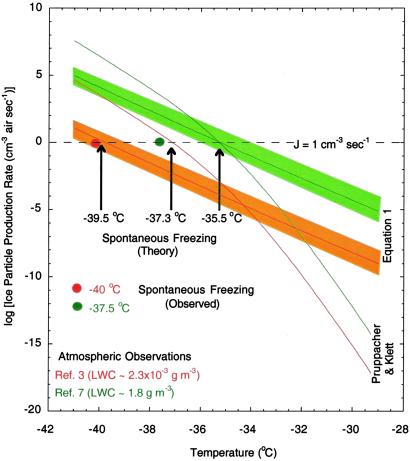
Until recently, only a few isolated supercooled water cloud observations have shown that water in the atmosphere, in small amounts, can remain liquid down to near −40°C (2, 3). A recent study (7), however, has also shown that even large amounts of liquid water can remain supercooled in clouds down to temperatures below about −37.5°C. In Fig. 4 nucleation rates calculated by Pruppacher and Klett (1) and this work (Eq. 1) are shown for two assumptions of liquid water content, i.e., for both small and large water contents. Spontaneous freezing (glaciation) in the atmosphere will occur when J = 1 cm⁻³⋅s⁻¹. For small amounts of liquid water (≈0.002 g⋅m⁻³) (3), Pruppacher and Klett (1) and rate expressions in this work predict that glaciation will occur near −37.3 and −39.6°C, respectively. Small amounts of supercooled water were observed in aircraft observations (2, 3) near −40°C. Thus, only rates obtained based on Eq. 1 can account for the existence of supercooled water in the atmosphere down to such low temperatures. For large amounts of liquid water (≈1.8 g⋅m⁻³) (7), where droplets are usually large, both theoretical formulations (Pruppacher and Klett in ref. 1 and Eq. 1) predict that glaciation will occur near −35.7°C, which is about 2°C warmer than what Rosenfeld and Woodley (7) concluded based on their recent aircraft observations. Thus neither theory can explain how supercooled water in such large amounts could have persisted in air down to −37.5°C (7). Nevertheless, at −37.5°C, where glaciation (J = 1 cm⁻³⋅s⁻¹) (7) was reported in the field, freezing rates (J = 10² cm⁻³⋅s⁻¹) based on Eq. 1 are much closer to the observations than freezing rates (J = 10⁴ cm⁻³⋅s⁻¹) provided by Pruppacher and Klett (1) formulations. Perhaps the difference of 2°C between the calculated and observed temperature of glaciation may be related to temperature and/or water-content measurement uncertainties that are not discussed in the Rosenfeld and Woodley study (7). For example, it has been shown, in wind tunnel experiments (36), that droplet and air temperatures inside a wind tunnel are often different due to water evaporation and/or condensation processes. We note that Rosenfeld and Woodley (7) only reported the ambient air temperature and therefore the true droplet temperature, which controls the rate of the ice nucleation process, could have been slightly different from the ambient air temperature. Overall, because the results obtained based on Eq. 1 can predict the onset of glaciation in a cloud of small water content (2, 3), it is hard to explain why the theory should fail in predicting the onset in a cloud of large water content (7). However, it is difficult to compare these observations (7) directly to the theory because the comparisons may still overlap within the range of both data and model uncertainties.

Fig 4.

Ice particle production rates in the atmosphere as a function of temperature and liquid water content. The shaded areas show the range of uncertainties in surface rate predictions based on error bars shown in Fig. 2 for the J_S line. The liquid water range used in the calculations varies from 2.3 × 10⁻³ (low) to 1.8 (high) g⋅m⁻³ and is constrained by aircraft observations (3, 7). A monodisperse size distribution with a mode diameter of 5 and 17 μm was used in the calculations to obtain liquid water surface areas in air for low and high water content measurements, respectively. Arrows mark temperatures at which each theory predicts spontaneous freezing of ice will occur in the atmosphere. Symbols mark temperatures where spontaneous ice freezing was observed in the field.

Concluding Remarks

The results presented in this work question the general validity of applying the conventional classical volume-based homogeneous nucleation rate theory for studying droplet phase transformation processes in both the atmosphere and the laboratory. Even in a simple system, such as pure water, there is evidence that ice nucleus formation may occur at the air–droplet interface. In addition, a recent study (35) seems to show that the freezing of aqueous nitric acid solution droplets also takes place at the droplet surface. Because more complicated droplet systems (37) containing acid, salt, and organic material exist in the atmosphere, it is unlikely that crystal nucleus formation in such systems would follow a simple classical nucleation volume-based rate theory.

Recent studies indicate that the surface of an aqueous particle is often enriched in low surface tension components such as molecular nitric acid (38, 39) and organic materials (40–42). This surface adsorption effect in complex particle systems, which exist in the atmosphere, can have a 2-fold effect. First, it is clear from Eqs. 2 and 3 that such surface enrichments (38–42) will make it more difficult for an ice nucleus to form at the surface layer of an aqueous droplet as compared with that of a pure water droplet. Second, the same surface adsorption effect can enrich the composition of the surface layer to a level where multicomponent solid phases can nucleate and grow. For example, we have suggested (35) that the observed enrichment of molecular nitric acid (38, 39) at the surface layer of an aqueous nitric acid solution droplet may lead to crystallization of hydrates of nitric acid at the droplet surface. Similarly, organic species in aerosols, which are often enriched at the surface layer (40–42), may nucleate to form condensable (or perhaps crystalline) species at or very near the surface layer of the particle. Thus many, and perhaps the majority, of phase transformations in atmospheric droplets may indeed be surface-based and not volume-based rate processes.

The fact that atmospheric droplets may begin to crystallize at their surfaces rather than within their volumes is intriguing. Anthropogenic emissions, which are sometimes rich in low surface tension components, can eventually condense either on pre-existing particles or nucleate from the gas phase to form new particles. Thus, it is reasonable to expect that such variations in aerosol composition, caused by human activities, can change the rate of surface crystallization in the atmosphere. Such processes affect the Earth's climate and atmospheric composition. Therefore, it is important to understand the basic physical process by which atmospheric particles change their phase.

Abbreviations

• HG, heptane grease

• STO, sorbitan triolate

• VO, vacuum oil

• STS, sorbitan tristearate