The average distances in random graphs with given expected degrees

Abstract

Random graph theory is used to examine the “small-world phenomenon”; any two strangers are connected through a short chain of mutual acquaintances. We will show that for certain families of random graphs with given expected degrees the average distance is almost surely of order log n/log d̃, where d̃ is the weighted average of the sum of squares of the expected degrees. Of particular interest are power law random graphs in which the number of vertices of degree k is proportional to 1/k^β for some fixed exponent β. For the case of β > 3, we prove that the average distance of the power law graphs is almost surely of order log n/log d̃. However, many Internet, social, and citation networks are power law graphs with exponents in the range 2 < β < 3 for which the power law random graphs have average distance almost surely of order log log n, but have diameter of order log n (provided having some mild constraints for the average distance and maximum degree). In particular, these graphs contain a dense subgraph, which we call the core, having n^{c/log log n} vertices. Almost all vertices are within distance log log n of the core although there are vertices at distance log n from the core.

In 1967, the psychologist Stanley Milgram (1) conducted a series of experiments that indicated that any two strangers are connected by a chain of intermediate acquaintances of length at most six. In 1999, Barabási et al. (2) observed that in certain portions of the Internet any two web pages are at most 19 clicks away from one another. In this article, we will examine average distances in random graph models of large complex graphs. In turn, the study of realistic large graphs provides directions and insights for random graph theory.

Most of the research papers in random graph theory concern the Erdős–Rényi model 𝒢_p, in which each edge is independently chosen with probability p for some given p > 0 (see ref. 3). In such random graphs the degrees (the number of neighbors) of vertices all have the same expected value. However, many large random-like graphs that arise in various applications have diverse degree distributions (2, 4–7). It is therefore natural to consider classes of random graphs with general degree sequences.

We consider a general model G(w) for random graphs with given expected degree sequence w = (w₁, w₂, … , w_n). The edge between v_i and v_j is chosen independently with probability p_ij, where p_ij is proportional to the product w_iw_j. The classical random graph G(n, p) can be viewed as a special case of G(w) by taking w to be (pn, pn, … , pn). Our random graph model G(w) is different from the random graph models with an exact degree sequence as considered by Molloy and Reed (8, 9), and Newman, Strogatz, and Watts (10, 11). Deriving rigorous proofs for random graphs with exact degree sequences is rather complicated and usually requires additional “smoothing” conditions because of the dependency among the edges (see ref. 8).

Although G(w) is well defined for arbitrary degree distributions, it is of particular interest to study power law graphs. Many realistic networks such as the Internet, social, and citation networks have degrees obeying a power law. Namely, the fraction of vertices with degree k is proportional to 1/k^β for some constant β > 1. For example, the Internet graphs have powers ranging from 2.1 to 2.45 (see refs. 2 and 12–14). The collaboration graph of mathematical reviews has β = 2.97 (see www.oakland.edu/∼grossman/trivia.html). The power law distribution has a long history that can be traced back to Zipf (15), Lotka (16), and Pareto (17). Recently, the impetus for modeling and analyzing large complex networks has led to renewed interest in power law graphs.

In this article, we will show that for certain families of random graphs with given expected degrees, the average distance is almost surely (1 + o(1)) log n/logd̃. Here d̃ denotes the second-order average degree defined by d̄ = ∑ w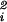/∑ w_i, where w_i denotes the expected degree of the ith vertex. Consequently, the average distance for a power law random graph on n vertices with exponent β > 3 is almost surely (1 + o(1))log n/logd̃. When the exponent β satisfies 2 < β < 3, the power law graphs have a very different behavior. For example, for β > 3, d̃ is a function of β and is independent of n but for 2 < β < 3, d̃ can be as large as a fixed power of n. We will prove that for a power law graph with exponent 2 < β < 3, the average distance is almost surely O(log log n) (and not log n/log d̃) if the average degree is strictly greater than 1 and the maximum degree is sufficiently large. Also, there is a dense subgraph, that we call the core, of diameter O(log log n) in such a power law random graph such that almost all vertices are at distance at most O(log log n) from the core, although there are vertices at distance at least c log n from the core. At the phase transition point of β = 3, the random power law graph almost surely has average distance of order log n/log log n and diameter of order log n.

Definitions and Statements of the Main Theorems

In a random graph G ∈ G(w) with a given expected degree sequence w = (w₁, w₂, … , w_n), the probability p_ij of having an edge between v_i and v_j is w_iw_jρ for ρ = (1/∑_i w_i). We assume that max_i w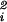 < ∑_i w_i so that the probability p_ij = w_iw_jρ is strictly between 0 and 1. This assumption also ensures that the degree sequence w_i can be realized as the degree sequence of a graph if w_is are integers (18). Our goal is to have as few conditions as possible on the w_is while still being able to derive good estimates for the average distance.

First, we need some definitions for several quantities associated with G and G(w). In a graph G, the volume of a subset S of vertices in G is defined to be vol(S) = ∑_v∈Sdeg(v), the sum of degrees of all vertices in S. For a graph G in G(w), the expected degree of v_i is exactly w_i and the expected volume of S is Vol(S) = ∑_i∈S w_i. In particular, the expected volume of G is Vol(G) = ∑_i w_i. By the Chernoff inequality for large deviations (19), we have

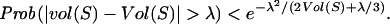For k ≥ 2, we define the kth moment of the expected volume by Vol_k(S) = ∑_vi∈S w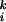 and we write Vol_k(G) = ∑_i w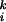. In a graph G, the distance d(u, v) between two vertices u and v is just the length of a shortest path joining u and v (if it exists). In a connected graph G, the average distance of G is the average over all distances d(u, v) for u and v in G. We consider very sparse graphs that are often not connected. If G is not connected, we define the average distance to be the average among all distances d(u, v) for pairs of u and v both belonging to the same connected component. The diameter of G is the maximum distance d(u, v), where u and v are in the same connected component. Clearly, the diameter is at least as large as the average distance. All of our graphs typically have a unique large connected component, called the giant component, which contains a positive fraction of edges.

The expected degree sequence w for a graph G on n vertices in G(w) is said to be strongly sparse if we have the following:

• (i)  The second order average degree d̃ satisfies 0 < log d̃ ≪log n.

• (ii)  For some constant c > 0, all but o(n) vertices have expected degree w_i satisfying w_i ≥ c. The average expected degree d = ∑_i w_i/n is strictly greater than 1, i.e., d > 1 + ɛ for some positive value ɛ independent of n.

The expected degree sequence w for a graph G on n vertices in G(w) is said to be admissible if the following condition holds, in addition to the assumption that w is strongly sparse.

• (iii)  There is a subset U satisfying: Vol₂(U) = (1 + o(1))Vol₂(G) ≫ (Vol₃(U)logd̃log log n/d̃logn).

The expected degree sequence w for a graph G on n vertices is said to be specially admissible if i is replaced by i′ and iii is replaced by iii′:

• (i′)  log d̃ = O(log d).

• (iii′)  There is a subset U satisfying Vol₃(U) = O(Vol₂(G))(d̃/logd̃), and Vol₂(U) > dVol₂(G)/d̃.

In this article, we will prove the following:

Theorem 1.

For a random graph G with admissible expected degree sequence (w₁, … , w_n), the average distance is almost surely (1 + o(1))(logn/logd̃).

Corollary 1.

If np ≥ c > 1 for some constantc, then almost surely the average distance of G(n, p) is (1 + o(1))(log n/lognp), provided (log n/log np) goes to infinity as n → ∞.

The proof of the above corollary follows by taking w_i = np and U to be the set of all vertices. It is easy to verify in this case that w is admissible, so Theorem 1 applies.

Theorem 2.

For a random graph G with a specially admissible degree sequence (w₁, … , w_n), the diameter is almost surelyΘ(log n/logd̃).

Corollary 2.

If np = c > 1 for some constantc, then almost surely the diameter of G(n, p)is Θ(log n).

Theorem 3.

For a power law random graph with exponent β > 3 and average degree d strictly greater than1, almost surely the average distance is (1 + o(1))(log n/logd̃) and the diameter is Θ(log n).

Theorem 4.

Suppose a power law random graph with exponent β has average degree d strictly greater than 1 and maximum degreem satisfying log m ≫ log n/log log n. If 2 < β < 3, almost surely the diameter is Θ(log n) and the average distance is at most (2 + o(1))(log log n/log(1/(β − 2))). For the case ofβ = 3, the power law random graph has diameter almost surely Θ(log n) and has average distance Θ(log n/log log n).

Neighborhood Expansion and Connected Components

Here we state several useful facts concerning the distances and neighborhood expansions in G(w). These facts are not only useful for the proofs of the main theorems but also are of interest on their own right. The proofs can be found in ref. 20.

Lemma 1.

In a random graph G in G(w)with a given expected degree sequence w = (w₁, … , w_n), for any fixed pairs of vertices (u, v), the distance d(u, v)between u and v is greater than ⌊(log Vol(G) − c)/logd̃⌋ with probability at least 1 − (w_uw_v/d̃(d̃ − 1))e^−c.

Lemma 2.

In a random graph G ∈ G(w), for any two subsets S and T of vertices, we have

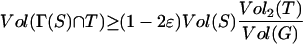with probability at least 1 − e^−c where Γ(S) = {v : v ∼ u ∈ S and v ∉ S}, providedVol(S) satisfies

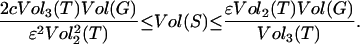Lemma 3.

For any two disjoint subsets S and T withVol(S) Vol(T) > cVol(G),we have

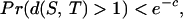where d(S, T) denotes the distance betweenS and T.

Lemma 4.

Suppose that G is a random graph on nvertices so that for a fixed value c, G haso(n) vertices of degree less than c and has average degree d strictly greater than 1. Then for any fixed vertex v in the giant component, if τ = o(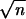), then there is an index i₀ ≤ c₀τ so that with probability at least1 − (c₁τ^3/2/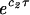),we have

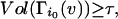where c_is are constants depending only on c and d, whileΓ_i(S) = Γ(Γ_i−1(S)) fori > 1 and Γ₁(S) = Γ(S).

We remark that in the proofs of Theorem 1 and Theorem 2, we will take τ to be of order (log n/logd̃). The statement of the above lemma is in fact stronger than what we will actually need.

Another useful tool is the following result on the expected sizes of connected components in random graphs with given expected degree sequences (21).

Lemma 5.

Suppose that G is a random graph inG(w) with given expected degree sequencew. If the expected average degree d is strictly greater than 1, then the following holds:

• (i)  Almost surelyG has a unique giant component. Furthermore, the volume of the giant component is at least (1 − (2/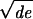) + o(1))Vol(G) if d ≥ (4/e) = 1.4715 … , and is at least (1 − (1 + log d)/d + o(1))Vol(G) ifd < 2.

• (ii)  The second largest component almost surely has size O(log n/log d).

Proof of Theorem 1

Suppose G is a random graph with an admissible expected degree sequence. From Lemma 5, we know that with high probability the giant component has volume at least Θ(Vol(G)). From Lemma 5, the sizes of all small components are O(log n). Thus, the average distance is primarily determined by pairs of vertices in the giant component.

From the admissibility condition i, d̃ ≤ n^ɛ implies that only o(n) vertices can have expected degrees greater than n^ɛ. Hence we can apply Lemma 1 (by choosing c = 3ɛlog n, for any fixed ɛ > 0) so that with probability 1 − o(1), the distance d(u, v) between u and v satisfies d(u, v) ≥ (1 − 3ɛ − o(1))log n/logd̃. Here we use the fact that log Vol(G) =log d + log n = (1 + o(1))log n. Because the choice of ɛ is arbitrary, we conclude the average distance of G is almost surely at least (1 + o(1))log n/logd̃.

Next, we want to establish the upper bound (1 + o(1))⋅ (log Vol(G)/logd̃) for the average distance between two vertices u and v in the giant component.

For any vertex u in the giant component, we use Lemma 4 to see that for i₀ ≤ Cɛ(logn/logd̃), the i₀ boundary Γ_i0(v) of v satisfies

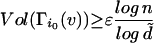with probability 1 − o(1).

Next, we use Lemma 2 to deduce that Vol(Γ_i(u)) will grow roughly by a factor of (1 − 2ɛ)d̃ as long as Vol(Γ_i(u)) is no more than 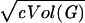(by choosing c = 2log log n). The failure probability is at most e^−c at each step. Hence, for i₁ ≤ log(c Vol(G))/(2log(1 − 2ɛ)d̃) more steps, we have Vol(Γ_i0+i1(v)) ≥ 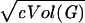with probability at least 1 − i₁e^−c = 1 − o(1). Here i₀ + i₁ = (1 + o(1))(log n/2 logd̃). Similarly, for the vertex v, there are integers i′₀ and i′₁ satisfying i′₀ + i′₁ = (1 + o(1))(logn/(2 logd̃)) so that Vol(Γ_i′0+i′1(v)) ≥ 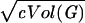holds with probability at least 1 − o(1).

By Lemma 3, with probability 1 − o(1) there is a path connecting u and v with length i₀ + i₁ + 1 + i′₀ + i′₁ = (1 + o(1))(log n/logd̄). Hence, almost surely the average distance of a random graph with an admissible degree sequence is (1 + o(1))(log n/logd̄).

The proof of Theorem 2 is similar to that of Theorem 1 except that the special admissibility condition allows us to deduce the desired bounds with probability 1 − o(n⁻²). Thus, almost surely every pair of vertices in the giant components have mutual distance O(logn/logd̃). We remark that it would be desirable to establish an upper bound (1 + o(1)) logn/logd̃ for the diameter. However, we can only deduce the weaker upper bound because of the traveoff for the required probability 1 − o(n⁻²) by using Lemma 4.

Random Power Law Graphs

For random graphs with given expected degree sequences satisfying a power law distribution with exponent β, we may assume that the expected degrees are w_i = ci^{−1/(β−1)} for i satisfying i₀ ≤ i < n + i₀. Here c depends on the average degree and i₀ depends on the maximum degree m, namely, c = β − 2/(β − 1)dn^(1/β−1), i₀ = n(d(β − 2)/m(β − 1))^β−1.

The power law graphs with exponent β > 3 are quite different from those with exponent β < 3 as evidenced by the value of d̃ (assuming m ≫ d).

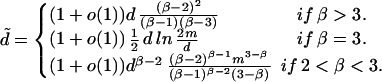For the range of β > 3, it can be shown that the power law graphs are both admissible and especially admissible. [One of the key ideas is to choose U in condition iii or iii′ to be a set U_y = {v :deg(v) ≤ y} for an appropriate y independent of the maximum degree m. For example, choose y to be n^1/4 for β > 4, to be 4 for β = 4 and to be log n/(log d log log n) for 3 < β < 4.] Theorem 3 then follows from Theorems 1 and 2.

The Range 2 < β < 3

Power law graphs with exponent 2 < β < 3 have very interesting structures that can be roughly described as an “octopus” with a dense subgraph having small diameter as the core. We define S_k to be the set of vertices with expected degree at least k. (We note that the set S_k can be well approximated by the set of vertices with degree at least k.)

We note that the power law distribution is not especially admissible for 2 < β < 3. Thus Theorem 2 can not be directly used. Here we outline the main ideas for the proof of Theorem 4.

Sketch of Proof for Theorem 4

We define the core of a power law graph with exponent β to be the set S_t of vertices of degree at least t = n^{1/log log n}.

Claim 1:

The diameter of the core is almost surely O(log log n). This follows from the fact that the core contains an Erdős–Renyi graph G(n′, p) with n′ = cnt^1−β and p = t²/Vol(G). From ref. 3, this subgraph is almost surely connected. Using a result in (22), the diameter of this subgraph is at most (log n′/log pn′) = (1 + o(1))(log n/((3 − β) log t)) = O(log log n).

Claim 2:

Almost all vertices with degree at least log n are almost surely within distance O(log log n) from the core. To see this, we start with a vertex u₀ with degree k₀ ≥ log^Cn for some constant C = (1.1/((β − 2)(3 − β))). By applying Lemma 3, with probability at least 1 − n⁻³, u₀ is a neighbor of some u₁ with degree k₁ ≥ (k₀/log^Cn)^1/(β−2)s. We then repeat this process to find a path with vertices u₀, u₁, … , u_s, and the degree k_s of u_s satisfies k_s ≤ (k₀/log^Cn)^1/(β−2)s with probability 1 − n⁻². By choosing s to satisfy log k_s ≥ log n/log log n, we are done.

Claim 3:

For each vertex v in the giant component, with probability 1 − o(1), v is within distance O(log log n) from a vertex of degree at least log^Cn. This follows from Lemma 4 (choosing τ = c log log log n and the neighborhood expansion factor c′ log log log n).

Claim 4:

For each vertex v in the giant component, with probability 1 − o(n⁻²), v is within distance O(log n) from a vertex of degree at least O(log n). Thus with probability 1 − o(1), the diameter is O(log n).

Combining Claims 1–3, we have derived an upper bound O(log log n) for the average distance. [By a similar but more careful analysis (20), this upper bound can be further improved to c log log n for c = (2/log(1/(β − 2))).] From Claim 4, we have an upper bound O(log n) for the diameter.

Next, we will establish a lower bound of order log n. We note that the minimal expected degree in a power law random graph with exponent 2 < β < 3 is (1 + o(1))(d(β−2)/(β−1)). We consider all vertices with expected degree less than the average degree d. By a straight-forward computation, there are about (β−2)/(β−1)^β−1n such vertices. For a vertex u and a subset T of vertices, the probability that u has only one neighbor that has expected degree less than d and is not adjacent to any vertex in T is at least

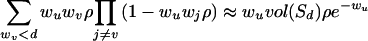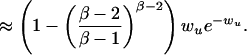Note that this probability is bounded away from 0, (say, it is greater than c for some constant c). Then, with probability at least n^−1/100, we have an induced path of length at least log n/(100log c) in G. Starting from any vertex u, we search for a path as an induced subgraph of length at least log n/(100 log c) in G. If we fail to find such a path, we simply repeat the process by choosing another vertex as the starting point. Since S_d has at least ((β−2)/(β−1))^β−1n vertices, then with high probability, we can find such a path. Hence the diameter is almost surely Θ(log n).

For the case of β = 3, similar arguments show that the power law random graph almost surely has diameter of order log n but the average distance is Θ(log n/logd̃) = Θ(log n/log log n).

Summary

When random graphs are used to model large complex graphs, the small-world phenomenon of having short characteristic paths is well captured in the sense that with high probability, power law random graphs with exponent β have average distance of order log n if β > 3, and of order log log n if 2 < β < 3. Thus, a phase transition occurs at β = 3 and, in fact, the average distance of power law random graphs with exponent 3 is of order log n/log log n. More specifically, for the range of 2 < β < 3, there is a distinct core of diameter log log n so that almost all vertices are within distance log log n from the core, while almost surely there are vertices of distance log n away from the core.

Another aspect of the small-world phenomenon concerns the so-called clustering effect, which asserts that two people who share a common friend are more likely to know each other. However, the clustering effect does not appear in random graphs and some explanation is in order. A typical large network can be regarded as a union of two major parts: a global network and a local network. Power law random graphs are suitable for modeling the global network while the clustering effect is part of the distinct characteristics of the local network.

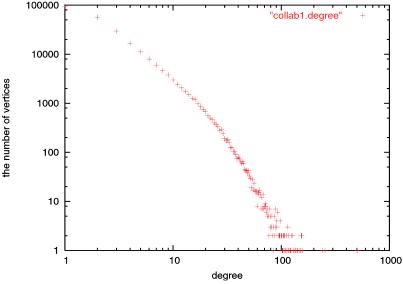
Based on the data graciously provided by Jerry Grossman (Oakland University, Rochester, MI), we consider two types of collaboration graphs with roughly 337,000 authors as vertices. The first collaboration graph G₁ has about 496,000 edges with each edge joining two coauthors. It can be modeled by a random power law graph with exponent β₁ = 2.97 and d = 2.94 (see Fig. 1 and 2). The second collaboration graph G₂ has about 226,000 edges, each representing a joint paper with exactly two authors. The collaboration graph G₂ corresponds to a power law graph with exponent β₂ = 3.26 and d = 1.34.Theorem 3 predicts that the value for the average distance in this case should be 9.89 (with a lower order error term). In fact, the actual average distance in this graph is 9.56 (www.oakland.edu/∼grossman/trivia.html).

Fig 1.

The power law degree distribution of the collaboration graph G₁.

Fig 2.

An induced subgraph of the collaboration graph G₁.