The Brownian Web

Abstract

Arratia, [Arratia, R. (1979) Ph.D. thesis (University of Wisconsin, Madison) and unpublished work] and later Toth and Werner [Toth, B. & Werner, W. (1998) Probab. Theory Relat. Fields111, 375–452] constructed random processes that formally correspond to coalescing one-dimensional Brownian motions starting from every space-time point. We extend their work by constructing and characterizing what we call the Brownian Web as a random variable taking values in an appropriate (metric) space whose points are (compact) sets of paths. This leads to general convergence criteria and, in particular, to convergence in distribution of coalescing random walks in the scaling limit to the Brownian Web.

Construct random paths in the plane, as follows (1). Take the square lattice consisting of all points (m, n) with m, n integers and rotate it by 45 degrees resulting in all points (i, j) with i, j integers and i + j even. Imagine a walker at spatial location i at time j deciding to move right or left at unit speed between times j and j + 1 if the outcome of a fair coin toss is heads (Δ_i,j = +1) or tails (Δ_i,j = −1), with the coin tosses independent for different space-time points (i, j). Fig. 1 depicts a simulation of the resulting paths.

Fig. 1.

Coalescing random walks in discrete time; the horizontal coordinate is space and the vertical coordinate is time.

The path of a walker starting from y₀ at time s₀ is the graph of a simple symmetric one-dimensional random walk, Y_y0,s0(t). At integer times, Y_y0,s0(t) is the solution of the simple stochastic difference equation,

0.1

Note that the paths of distinct walkers starting from different (y₀, s₀)s are automatically coalescing; i.e., they are independent of each other until they coalesce (i.e., become identical) upon meeting at some space-time point.

After rescaling to spatial steps of size δ and time steps of size δ², a single rescaled random walk (say, starting from 0 at time 0) Y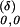(t) = δY_0,0(δ⁻²t) converges as δ → 0 to a standard Brownian motion B(t). More precisely, by the Donsker invariance principle (2), the distribution of Y 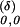on the space of continuous paths converges weakly as δ → 0 to standard Wiener measure.

The invariance principle is also valid for continuous time random walks, where the move from i to i ± 1 takes an exponentially distributed time (see the discussion after Remark 2.2 for more details). In continuous time, coalescing random walks are at the heart of Harris's graphical representation of the (one-dimensional) voter model (3) and their scaling limits arise naturally in the physical context of (one-dimensional) aging (4). Like for a single random walk, finitely many rescaled coalescing walks in discrete or continuous time (with rescaled space-time starting points) converge in distribution to finitely many coalescing Brownian motions. In this paper, we present results concerning the convergence in distribution of the collection of the rescaled coalescing walks from all the uncountably many starting points; detailed proofs will be published elsewhere.

Our results come in two parts: (a) characterization (and construction) of the limiting object, which we call the standard Brownian Web (BW), and (b) general convergence criteria, which are then applied to coalescing random walks.

A key ingredient of the characterization and construction (see Theorem 1.1) is the choice of a space for the BW; this is the BW analogue of the space of continuous paths for Brownian motion. The convergence criteria and application (see Theorems 2.1 and 2.3 below) are the BW analogues of Donsker's invariance principle. Like Brownian motion itself, we expect that the BW and its variants (see, e.g., Remark 1.4) will be quite ubiquitous as scaling limits, well beyond the context of coalescing random walks (and our sufficient conditions for convergence); one situation where this occurs is for two-dimensional “Poisson webs” (P. A. Ferrari, L.R.G.F., and X. Y. Wu, unpublished work).

Much of the construction of the BW (but without characterization or convergence results) was already done in the groundbreaking work of Arratia (ref. 1 and unpublished work; see also refs. 5 and 6) and then in work of Tóth and Werner (7) (see also ref. 8 and unpublished work of B. Tsirelson). It should be noted that the BW was not the central object in the work of ref. 7 but rather served there as the main ingredient in the construction of the “true self-repelling motion.” Arratia, Tóth, and Werner all recognized that in the limit δ → 0 there would be (nondeterministic) space-time points (x, t) starting from which there are multiple limit paths and they provided various conventions (e.g., semicontinuity in x) to avoid such multiplicity. Our main contribution vis-a-vis construction is to accept the intrinsic nonuniqueness by choosing an appropriate metric space in which the BW takes its values. Roughly speaking, instead of using some convention to obtain a process that is a single-valued mapping from each space-time starting point to a single path from that starting point, we allow multi-valued mappings; more accurately, our BW value is the collection of all paths from all starting points. This choice of space is very much in the spirit of earlier work (9–11) on spatial scaling limits of critical percolation models and spanning trees, but modified for our particular space-time setting; the directed (in time) nature of our paths considerably simplifies the topological setting compared to refs. 9–11.

The Donsker invariance principle implies that the distribution of any continuous (in the sup-norm metric) functional of Y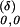 converges to that for Brownian motion. The classic example of such a functional is the random walk maximum, sup_0≤t≤1Y(t). An analogous example for coalescing random walks is the maximum over all rescaled walks starting at (or passing through) some vertical (time-like) interval, i.e., the maximum value (for times t ∈ [s, 1]) over walks touching any space-time point of the form (0, s) for some s ∈ [0, 1]. In this case, the functional is not quite continuous for our choice of metric space, but it is continuous almost everywhere (with respect to the BW measure), which is sufficient.

BW: Characterization

We begin by defining three metric spaces: (ℝ̄², ρ), (Π, d), and (ℋ, d_ℋ). The elements of the three spaces are, respectively, points in space-time, paths with specified starting points in space-time, and collections of paths with specified starting points. The BW will be an (ℋ, ℱ_ℋ)-valued random variable, where ℱ_ℋ is the Borel σ-field associated to the metric d_ℋ.

(ℝ̄², ρ) is the completion (or compactification) of ℝ² under the metric ρ, where

1.1

ℝ̄² may be thought as the set of (x, t) in [−∞, ∞] × [−∞, ∞] with all points of the form (x, −∞) identified [and similarly for (x, ∞)]. More precisely, it is the image of [−∞, ∞] × [−∞, ∞] under the mapping

1.2

For t₀ ∈ [−∞, ∞], let C[t₀] denote the set of functions f from [t₀, ∞] to [−∞, ∞] such that Φ(f(t), t) is continuous. Then define

1.3

where (f, t₀) ∈ Π then represents a path in ℝ̄² starting at (f(t₀), t₀). For (f, t₀) ∈ Π, we denote by f̂ the function that extends f to all [−∞, ∞] by setting it equal to f(t₀) for t < t₀. Then we take

1.4

(Π, d) is a complete separable metric space.

Let now ℋ denote the set of compact subsets of (Π, d), with d_ℋ the induced Hausdorff metric, i.e.,

1.5

(ℋ, d_ℋ) is also a complete separable metric space.

Before stating our characterization theorem for the BW, we need some definitions. For an (ℋ, ℱ_ℋ)-valued random variable W̄ (or its distribution μ), we define the finite dimensional distributions of W̄ as the induced probability measures μ_{(x1,t1;…;xn,tn)} on the subsets of paths starting from any finite deterministic set of points (x₁, t₁), … , (x_n, t_n) in ℝ². There are several ways in which the BW can be characterized; they differ from each other primarily in the type of extra condition required beyond the finite-dimensional distributions. The characterization of the next theorem, or more precisely a variant discussed later in Remark 1.3, is the one most directly suited to the convergence results of the next section; alternative characterizations in which the extra condition is either a type of Doob separability property (see, e.g., chapter 3 of ref. 12) or a minimality property are discussed in Remark 1.2. For the next theorem, we also define, for t ≥ 0 and a ≤ b, the ({0, 1, … , ∞}-valued) random variable η(t₀, t; a, b) as the number of distinct points in ℝ × {t₀ + t} that are touched by paths in W̄ that also touch some point in [a, b] × {t₀}.

Theorem 1.1.

There is an(ℋ, ℱ_ℋ)-valued random variable W̄whose distribution μ is uniquely determined by the following two properties:

• (i)  its finite-dimensional distributions are those of coalescing Brownian motions (with unit diffusion constant), and

• (ii)  for −∞ < t₀ < ∞, 0 < t < ∞, −∞ < a ≤ b < ∞,

  1.6

Remark 1.2.

Implicit in condition i of the theorem is that starting from any deterministic point, there is almost surely only a single path in W̄. Condition ii can be replaced by the separability property that there is a deterministic dense countable set 𝒟 of space-time starting points, such that almost surely, W̄ is the closure in (Π, d) of the set of paths starting from the points of 𝒟. Alternatively, ii can be replaced by the minimality property that any W′ satisfying i stochastically dominates W̄ (where K₁ ≥ K₂ means that K₁ ⊇ K₂ for K₁, K₂ ∈ ℋ). It should be noted that (ℋ, ℱ_ℋ)-valued random variables, satisfying condition i but not condition ii or its separability/minimality alternatives, can occur naturally. Such a process (closely related to the Double BW of Remark 1.4 below), where the counting variable η is infinite with strictly positive probability, will be studied elsewhere and shown to arise as the scaling limit of stochastic flows, extending earlier work of Piterbarg (13).

Sketch of Proof of Theorem 1.1.

The construction of the BW (i.e., the existence of such a W̄) begins as in Arratia's unpublished work and ref. 7 with the construction of a set W of coalescing Brownian paths starting from a deterministic dense countable set 𝒟 of space-time starting points. This skeleton W = {W̃₁, W̃₂, … , } is a random subset of Π that is constructed by deterministically ordering the points of 𝒟 as (x₁, t₁), (x₂, t₂), … , then defining W_j = (x_j + B_j(t − t_j), t_j) ∈ Π where the B_js are independent standard Brownian motions, and finally using the ordering to inductively define W̃_j ∈ Π by following W_j until it meets some W̃_k with k < j after which point it follows W̃_k.

The next several steps of the construction are to show that the closure W̄ in (Π, d) of this BW-skeleton is compact, that the distribution of W̄ does not depend on the choice of 𝒟 or its ordering, and that W̄ satisfies i and ii of Theorem 1.1 above. The compactness can be proved in a number of ways; one of these is to verify a condition, as in 2.1 below, but with μ_δ replaced by the distribution of {W̃₁, … , W̃_m} and the sup over δ replaced by a sup over m (and then argue as at the beginning of the proof of Theorem 2.1 below, eventually invoking the Arzelà–Ascoli theorem). To verify the said condition, one argues as in the last two paragraphs of the proof of Theorem 2.3. The argument actually involves only a single bound like 2.6, which is obtained in the same way as in the proof of Theorem 2.3. We remark that by considering the quantity g̃(t, u), as in 2.1, but with u = t^ξ, one can show not just compactness of W̄, but also Hölder continuity with any exponent ξ < ½ for all the paths of W̄.

The lack of dependence of the distribution on the choice of 𝒟 or its ordering follows fairly directly after verifying property i for W̄. Property i itself follows by a trapping argument about a deterministic point (x̄, t̄) (and similarly for finitely many points) and any sequence (x̄_i, t̄_i) = (x_j(i), t_j(i)) from 𝒟 converging to (x̄, t̄) as i → ∞: that [even if j(i) is nondeterministic and regardless of whether t_j(i) > t̄ or t_j(i) ≤ t̄] for large i, W̃_j(i) is (with probability very close to one) trapped between W̃_k and W̃_k′ for deterministic k, k′ with x_k < x̄ < x′_k, t_k < t̄, t_k′ < t̄, x_k and x′_k close to x̄ and t_k, t_k′ even closer to t̄ so that W̃_j(i) (with probability very close to one) quickly coalesces with both W̃_k and W̃_k′; thus W̃_j(i) converges almost surely as i → ∞ to a path [independent of the specific sequence (x̄_i, t̄_i)] that is distributed as a Brownian motion starting from (x̄, t̄).

Verifying property ii is somewhat indirect. First, one shows that the random variable η for our constructed W̄ is almost surely finite with a finite mean, which, by the translation invariance in space and time that results from the lack of dependence on 𝒟, must be of the form Λ(b − a, t). Second, the specific evaluation of Λ as given on the right side of 1.6 is carried out. As the explicit expression for Λ will not actually be used in our convergence results of the next section (see Remark 1.3), we can and will use those convergence results in the evaluation of Λ.

The first part of the verification of ii is a consequence of an inequality,

1.7

where Θ(b − a, t) is the probability that two independent Brownian motions starting at a distance b − a apart at time zero will have met by time t (which itself can be expressed in terms of a single Brownian motion). The inequality in 1.7 is first derived for finite subsets {W̃₁, W̃₂, … , W̃_m} of the skeleton, and thus for the whole skeleton. For the (whole skeleton and its) closure W̄, the equality in 1.7 is seen to be valid by choosing the countable set 𝒟 so that its first two points are (a, t₀) and (b, t₀). Then the inequality is extended to W̄ from the skeleton by a limit/approximation argument that uses that {K ∈ ℋ : η̃(K) ≥ k} is open in (ℋ, d_ℋ), where η̃ is the modification of η that counts points in ℝ × {t₀ + t} touched by paths in K that touch (a − ɛ̃₁, b + ɛ̃₁) × {t₀ + ɛ̃₂} and start earlier than t₀ + ɛ̃₂.

The second part of the verification of ii, in which Λ is explicitly evaluated, is a consequence of all the following: a result of Bramson and Griffeath (14) on the large-time asymptotics of mean interparticle distance in coalescing random walks, the conversion of that result by standard arguments to asymptotics for the mean of the rescaled random walk version of the counting variable η, convergence of the distribution of η in the scaling limit (see Remark 2.2), and finally the analogue of 1.7 for coalescing walks (see 2.5), which implies uniform integrability of η as δ → 0 and hence convergence of the mean of η.

It remains to show that conditions i and ii for a measure μ′ on (ℋ, ℱ_ℋ) together imply that μ′ equals the distribution μ of the constructed BW W̄. Let us denote by X′ the (ℋ, ℱ_ℋ)-valued random variable distributed by μ′ and by η′ the counting random variable appearing in condition ii for μ′. Choose some deterministic dense countable subset 𝒟 and consider the countable collection W* of paths of X′ starting from 𝒟. By condition i, W* is equidistributed with our constructed Brownian skeleton W (based on the same 𝒟) and hence the closure W̄* of W* in (Π, d) is a subset of X′ that is equidistributed with our constructed BW W̄. To complete the proof, we will use condition ii to show that X′∖W̄* is almost surely empty by using the fact that the counting variable η* for W̄* already satisfies condition ii since W̄* is distributed as a BW. If X′∖W̄* were nonempty (with strictly positive probability), then there would have to be some rational t₀, t, a, b for which η′ > η*. But then

1.8

for some rational t₀, t, a, b and so condition ii for η′ would not be valid for that t₀, t, a, b.

Remark 1.3.

The proof of Theorem 1.1 makes clear that the idea behind conditions i and ii together implying uniqueness of the distribution is that i implies sufficiently many paths and ii implies no extraneous ones. Thus condition i can be weakened to the existence of a subset of paths distributed as the coalescing Brownian motions of the skeleton W (for any deterministic dense countable 𝒟) and condition ii can also be modified, e.g., by replacing the equality in 1.6 by an inequality (≤) and by replacing an (in)equality for the mean by one for the distribution. Similarly, in applying our characterization results to obtain convergence criteria as we do in Theorem 2.1, an explicit expression for the mean as given in the right side of 1.6 or an explicit expression for the distribution is not needed; i.e., to verify that an X′ is equidistributed with our explicitly constructed BW W̄, condition ii for the η′ of X′ can be replaced by the condition that the distribution of η′ equals (or only is stochastically dominated by) the distribution of the η of W̄.

Remark 1.4.

In the graphical representation of Harris for the one-dimensional voter model (3), coalescing random walks forward in time and coalescing dual random walks backward in time (with forward and backward walks not crossing each other) are constructed simultaneously (see, e.g., the discussion in ref. 4). The simultaneous construction of forward and (dual) backward Brownian motions was emphasized in refs. 7 and 8 and their approach and results can be applied to extend both our characterization and convergence results to the Double BW, which includes simultaneously the forward BW and its dual backward BW. We note that in the double BW, the η of 1.6 equals 1 + η^dual, where η^dual is the number of distinct points in [a, b] × {t₀} touched by backward paths that also touch ℝ × {t₀ + t}.

Remark 1.5.

As in ref. 7, space-time points (x, t) can be characterized by the number of locally disjoint paths m_in (respectively, m_out) of the BW entering (respectively, leaving) that point from earlier (respectively, to later) times. The corresponding dual BW characterization has m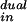 = m_out − 1 and m 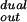= m_in + 1. Generic (e.g., deterministic) points have (m_in, m_out) = (0, 1). Almost surely, there are nongeneric points of type (0, 2), (0, 3), (1, 1), (1, 2) and (2, 1) but no others. We note that as in ref. 7, ruling out points of higher type uses improvements of 1.7 for k > 2. Type (2, 1) (resp., (0, 3)) points are those where coalescing (respectively, dual coalescing) occurs. Type (1, 2) points are particularly interesting in that the single incident path continues along exactly one of the two outward paths, with the choice determined intrinsically rather than by some convention.

Convergence to the BW

Let X_δ be an (ℋ, ℱ_ℋ)-valued random variable indexed by δ ∈ (0, 1], with distribution μ_δ. We present criteria sufficient to insure convergence in distribution as δ → 0 of X_δ to the BW W̄, in the setting where the X_δs have coalescing paths; for simplicity, we will not present here more general criteria that do not require the coalescing property. We next introduce the various conditions on μ_δ that together will imply convergence.

The first condition will guarantee tightness of the μ_δs. Let R(x₀, t₀; u, t) denote the rectangle [x₀ − u/2, x₀ + u/2] × [t₀, t₀ + t] in ℝ². We call {x₀ ± u/2} × [t₀, t₀ + t] its right and left boundaries. For t, u > 0, define A_t,u(x₀, t₀) to be the event (in ℱ_ℋ) that K (in ℋ) contains a path touching both R(x₀, t₀; u/2, t) and (at a later time) the left or right boundary of the bigger rectangle R(x₀, t₀; u, 2t); see Fig. 2. Our tightness condition is

2.1

Our second condition will guarantee a weakened version of i in Theorem 1.1 (see Remark 1.3) for any limit μ of μ_δ. Let 𝒟 be any deterministic countable dense set of points in ℝ². The condition concerns the existence for each δ > 0 and y ∈ 𝒟 of measurable (on the probability space of X_δ) single-path valued random variables θ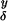(ω) ∈ X_δ(ω):

Fig. 2.

Schematic diagram of a path causing the unlikely event A_t,u(x₀, t₀) to occur.

(I₁) There exist such θ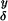 ∈ X_δ satisfying: for any deterministic y₁, … , y_m ∈ 𝒟, θ, … , θ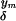 converge in distribution as δ → 0 to coalescing Brownian motions (with unit diffusion constant) starting at y₁, … , y_m.

Our next two conditions will together guarantee (when X_δ is coalescing) a version of ii in Theorem 1.1 (see Remark 1.3). For 0 < t < ∞,

2.2

2.3

Theorem 2.1.

Suppose X_δ for 0 < δ ≤ 1 are (ℋ, ℱ_ℋ)-valued random variables with coalescing paths. If T₁, I₁, B₁and B₂all hold, then the distributions μ_δof X_δconverge weakly as δ → 0 to the distributionμ_W̄ of the standard BW.

Sketch of Proof of Theorem 2.1.

We first explain why T₁ implies tightness. Let g_δ(t, u) denote the sup over x₀, t₀ of μ_δ(A_t,u) as in 2.1. This represents an upper bound on the μ_δ-probability that there is some path (f, t*) passing through some point (x′, t′) = (f(t′), t′) in the deterministic (u/2) × t rectangle R(x₀, t₀; u/2, t) located at any (x₀, t₀), such that for some t" ∈ [t′, t′ + t] the spatial increment |f(t") − f(t′)| ≥ u even though the time increment is ≤ t. Now take a large L × T space-time rectangle centered at the origin and cover it with O(LT/(ut)) (u/2) × t small rectangles. We see that (LT/u)g̃(t, u) represents an upper bound on the μ_δ-probability (for any δ) that some path has |f(t") − f(t′)| ≥ u while t" − t′ ≤ t with (f(t′), t′) anywhere in the L × T region.

We next choose sequences u_n → 0, L_n → ∞, T_n → ∞ and then t_n → 0 sufficiently rapidly that (L_nT_n/u_n)g̃(t_n, u_n) is summable. Now moving to the compactified space-time ℝ̄² (and using the notation of 1.2), it follows that there are sequences φ_n, ψ_n → 0 so that for large enough n, with μ_δ-probability close to one (for any δ), |Ψ(t") − Ψ(t′)| ≤ ψ_n implies Φ(f(t"), t") − Φ(f(t′), t′)| ≤ φ_n. This equicontinuity with probability close to one (for any δ) combined with a version of the Arzelà–Ascoli theorem leads to the paths, as elements of (Π, d), belonging to a compact subset K_ɛ̃ of (Π, d) with μ_δ-probability ≥ 1 − ɛ̃ (for any δ), which implies tightness because the collection of compact subsets of K_ɛ̃ is itself a compact set in (ℋ, d_ℋ).

Tightness implies that every subsequence of μ_δ has a sub-subsequence converging weakly to some μ. To complete the proof, we need to show that any such μ equals μ_W̄. To do this, we will show that μ satisfies the two characterization properties of Theorem 1.1, as modified in Remark 1.3. Combining condition I₁ with convergence in distribution (along a subsequence) of X_δ to some X distributed by μ, we see that we can realize X on some probability space so that it contains paths starting from the points of 𝒟 distributed as coalescing Brownian motions. This is just the desired (weakened version of) property i in Theorem 1.1. Indeed, this shows that X contains an X′ that has the BW distribution.

To complete the proof we use conditions B₁ and B₂. Note first that by limit/approximation arguments these two conditions (without the lim sup over δ) are valid with μ replacing μ_δ. For fixed t₀, t, a, b, we now consider M + 1 equally spaced points, z_j = (a + j(b − a)/M, t₀) for j = 0, … , M. For the random X we will denote the counting variable η(t₀, t; a, b) by η, and the corresponding variable for X′ by η′. We also want to count the number of points on ℝ × {t₀ + t} that are touched by paths of X that also touch {z₀, … , z_M} and we will denote these variables for X and X′ by η_M and η′_M. Of course, η ≥ η_M and η ≥ η′_M. By condition B₁ (for μ) applied to small intervals about each of the z_j's, it follows that η_M = η′_M almost surely. Applying condition B₂ (for μ) to the M spatial intervals [z_j−1, z_j] of length ɛ = (b − a)/M, and using the coalescing (or at least noncrossing) property of X that it inherits from the X_δs, it follows that

2.4

Thus P(η > η′) = 0 so that the distribution of η′ is stochastically dominated by (and hence equal to) the distribution of η. This gives the desired (modified version of) property ii in Theorem 1.1 and completes the proof.

Remark 2.2.

The arguments used in the proof of Theorem 2.1 also show that under the same four conditions T₁, I₁, B₁, and B₂, the counting random variables η_δ(t₀, t; a, b) for X_δ converge in distribution to the BW counting variable η_W̄(t₀, t; a, b). If one also has uniform integrability as δ → 0, then the means converge to the mean of η_W̄.

To apply Theorem 2.1 to random walks, we begin by precisely defining Y (respectively, Ỹ), the set of all discrete (respectively, continuous) time coalescing random walks on ℤ. The sets of rescaled walks, Y^(δ) and Ỹ^(δ), are then obtained by the usual rescaling of space by δ and time by δ². The (main) paths of Y are the discrete-time random walks Y_y0,s0, as described in the Introduction and shown in Fig. 1, with (y₀, s₀) = (i₀, j₀) ∈ ℤ × ℤ arbitrary except that i₀ + j₀ must be even. Each random walk path goes from (i, j) to (i ± 1, j + 1) linearly. In addition to these, we add some boundary paths so that Y will be a compact subset of Π. These are all the paths of the form (f, s₀) with s₀ ∈ ℤ ∪ {−∞, ∞} and f ≡ ∞ or f ≡ −∞. Note that for s₀ = −∞ there are two different paths starting from the single point at s₀ = −∞ in ℝ̄².

The continuous time Ỹ can be defined similarly, except that here y₀ is any i₀ ∈ ℤ and s₀ is arbitrary in ℝ. Continuous time walks are normally seen as jumping from i to i ± 1 at the times T ∈ (−∞, ∞) of a rate one Poisson process. If the jump is, say, to i + 1, then our polygonal path will have a linear segment between (i, T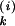) and (i + 1, T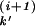), where T 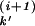is the first Poisson event at i + 1 after T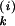. Furthermore, if 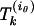< s₀ < then there will be a constant segment in the path before the first nonconstant linear segment. If s₀ =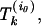 then we take two paths: one with an initial constant segment and one without.

Theorem 2.3.

Each of the collections of rescaled coalescing random walk paths,Y^(δ) (in discrete time) andỸ^(δ) (in continuous time) converges in distribution to the standard BW as δ → 0.

Sketch of Proof of Theorem 2.3.

By Theorem 2.1, it suffices to verify conditions T₁, I₁, B₁, and B₂. We will save the tightness condition T₁ for last as it is the messiest to verify, at least in the continuous time case of Ỹ^(δ).

Condition I₁ is basically a consequence of the Donsker invariance principle, as already noted in the Introduction. Conditions B₁ and B₂ follow from the coalescing walks version of the inequality of 1.7, which is

2.5

Taking the sup over a and the lim sup over δ and using standard random walk arguments produces an upper bound of the form C_k(ɛ/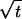)^k−1 that yields B₁ and B₂ as desired.

It remains to verify T₁. We will sketch the arguments for the continuous time Ỹ^(δ); the discrete time Y^(δ) is easier and corresponds to a portion of the continuous time arguments. As in the proof of Theorem 2.1, we denote by g_δ(t, u) the sup over x₀, t₀ of μ_δ(A_t,u), where μ_δ now denotes the distribution of Ỹ^(δ). For the continuous time case (and for u ≤ 1 and 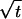much smaller than u), we will obtain a δ-independent bound on g_δ(t, u) that will yield T₁ by first obtaining, as we explain below, separate upper bounds in three regions of δ-values that depend on t, u:

2.6

2.7

2.8

Together, these bounds (with D₀ chosen appropriately) yield

2.9

which gives T₁ as desired.

The first region of δ-values corresponds to a spatial interval of width 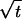being multiple lattice spacings δ wide and a spatial interval of width u being multiple 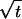-intervals wide. The bound 2.6 comes about because the event A_t,u is prevented if between the small rectangle and both the left and right boundaries of the larger rectangle (see Fig. 2), there is a random walk path that stays within some spatial 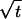-interval between times t₀ and t₀ + 2t. The second region corresponds to two (or more) spatial lattice sites between the small rectangle and the left (or right) boundary of the larger rectangle. The bound here arises because A_t,u can only occur if every one of those lattice sites on the left (or else every one on the right) has at least one Poisson process occurrence during [t₀, t₀ + 2t]. The third bound comes from preventing A_t,u by not having the Poisson occurrences at adjacent spatial lattice sites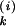, T and T, too close together in time. This completes our sketch of the proof.

Abbreviations

• BW, Brownian Web