Guiding neuronal growth with light

Abstract

Control over neuronal growth is a fundamental objective in neuroscience, cell biology, developmental biology, biophysics, and biomedicine and is particularly important for the formation of neural circuits in vitro, as well as nerve regeneration in vivo [Zeck, G. & Fromherz, P. (2001) Proc. Natl. Acad. Sci. USA 98, 10457–10462]. We have shown experimentally that we can use weak optical forces to guide the direction taken by the leading edge, or growth cone, of a nerve cell. In actively extending growth cones, a laser spot is placed in front of a specific area of the nerve's leading edge, enhancing growth into the beam focus and resulting in guided neuronal turns as well as enhanced growth. The power of our laser is chosen so that the resulting gradient forces are sufficiently powerful to bias the actin polymerization-driven lamellipodia extension, but too weak to hold and move the growth cone. We are therefore using light to control a natural biological process, in sharp contrast to the established technique of optical tweezers [Ashkin, A. (1970) Phys. Rev. Lett. 24, 156–159; Ashkin, A. & Dziedzic, J. M. (1987) Science 235, 1517–1520], which uses large optical forces to manipulate entire structures. Our results therefore open an avenue to controlling neuronal growth in vitro and in vivo with a simple, noncontact technique.

Many of the chemical cues that control neuronal growth during the development of an organism have been identified, although their interplay is rather complex (1–4). These biochemical signals eventually address the actin cytoskeleton, which advances the leading edge of a growth cone, known as the lamellipodium, through polymerization of new actin filaments and interactions with molecular motors (5–7). This understanding of neuronal growth is the basis for ongoing efforts to form defined neuronal network architectures, which can be interfaced with artificial structures such as semiconductors (8, 9), and to achieve successful nerve regeneration. In both cases, alternative approaches to complex guidance cues have been explored. On artificial substrates, such as silicon wafers, nerves have been directed by topographically structured surfaces (10) or by selectively patterning the substrate with materials that act as adhesives for nerves (11, 12). Damaging tensions, however, often rip apart the neuronal structures formed on the substrate due to the tendency of axons to straighten and stiffen with time. Thus, only small random neuronal networks have been successfully built in contact with semiconductor structures (13). There also have been reports of guiding neurons with electrodes (14, 15), but the specific impact of induced electrophoresis effects is not well understood (16, 17). In vivo, various types of guidance channels (18, 19) are used to repair neuronal damage of the peripheral nerve system. Fiber-based optical guidance may offer an alternative for aided regeneration of peripheral nerves. For the more complex situation of spinal cord injuries, stem cell approaches may be more viable (20). With this background, it is clear that optical nerve guidance is an important alternative to existing methods of nerve guidance.

Over the past 30 years, lasers have been used to manipulate objects ranging from atoms to μm-sized beads or biological cells (21–24). One-beam gradient traps, also known as optical tweezers, have been used successfully for a variety of biological experiments in which cells, organelles, or beads, attached to biological objects as tiny handles, have been held and moved (25–28). Single polymers have been micromanipulated with light (29, 30) and polymer solutions have been patterned with a laser (31). The results reported in this article show that lasers can be used to actually control a natural biological process and can address the long-standing goal of controlling neuron growth.

Cell Culture

We used PC12 cells, a rat neuron precursor cell line, stimulated to spread with neuronal growth factor (5 × 10⁻⁵ mg/ml), and NG108 cells, an immortalized mouse neuroblastoma rat glioma hybrid cell line. Cells were cultured in medium at 37°C (PC12: 85% RPMI-1640, 10% horse serum, 5% FBS; NG108: 90% DMEM, 10% FBS) (32, 33). Cells and media were purchased from the American Type Culture Collection. Cells under optical direction were grown for up to 4 h on plain cover glasses for NG108 cells and either plain or laminin-coated cover glasses for PC12 cells. Cells adhered to these cover glasses were integrated into a temperature-controlled sample chamber to assure continuing cell viability. Because no differences were observed between experiments with normal cell medium and cell medium that was pH-stabilized through addition of 10 mM Hepes we concluded that pH effects can be neglected although the sample's pH was not actively controlled. This finding is not surprising because the measured changes in medium without Hepes were <5% during the observation time.

Optical Guidance Methods

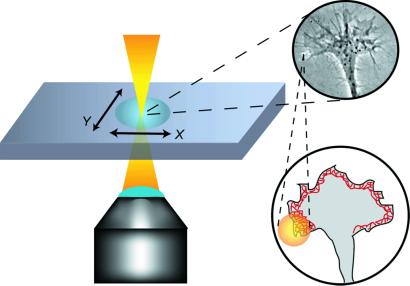
Control over the extending growth cone was achieved with a Ti:sapphire laser (λ = 800 nm). The laser light was guided and focused through the beam pathway of an inverted confocal microscope (Zeiss LSM 410) equipped with a ×63 objective (Zeiss Plan Neofluar, Ph3, numerical aperture = 1.25), which allowed us simultaneously to image the growth cone in phase contrast (Fig. 1). No particular efforts were made to achieve a tightly focused beam as is typically required for optical tweezers (34). We varied the spot size diameter in the plane of the lamellipodium between ≈2 and 16 μm and directly measured the power after the microscope objective from 20 to 120 mW. Whereas the variation in beam diameters <4 μm was achieved by optically defocusing the beam, the larger spot sizes were simulated by scanning the beam at a frequency of ≈0.1 Hz along the desired area of the growth cone's leading edge. Scanning at a frequency faster than intracellular processes generated an illuminated band along the lamellipodial outline. This process is beneficial for guiding larger areas of the lamellipodium, because it combines the sharper optical gradient of a smaller spot with an artificially larger spatial coverage. To achieve optical guidance, the beam was interactively steered with the confocal scanning microscope or by moving the microscope stage relative to the sample with an xy-piezo stage (Physik Instrumente, Berlin). We placed approximately one-fourth to one-half of the beam image on the lamellipodium, with the remainder of the spot placed ahead of the leading edge.

Fig 1.

Experimental setup for the optical guidance of growing neurons. A laser spot (⊘ = 2–16 μm, power = 20–120 mW, λ = 800 nm) was placed with partial overlap in front of an actively extending growth cone. The overlap area was chosen in the direction of the preferred growth and to cover the actin cortex, which directly underlies the plasma membrane and drives the advancement of the leading edge of the nerve.

Heating effects caused by absorption of the laser beam, which could influence the cell's biochemical reactions, play a minor role because the steady-state temperature increase is estimated to be only a few degrees. The rate of actin nucleation is relatively insensitive to small temperature changes ≈37°C, although the rate can drastically change at lower temperatures (35, 36). Although small heating enhances actin polymerization, it is not restricted to the area of the laser spot, due to thermal conductivity. We can therefore exclude heating as the cause of controlled optical guidance. Because the neuronal cells maintained their viability and growth after guiding, we also conclude that no significant radiation damage occurred.

Results

The observed optical guidance of neurons is a robust effect, successful for both rat and mouse neuronal cell lines and a broad range of laser powers. For our experiments, we chose actively ruffling lamellipodia, which were vigorously extending and sufficiently separated from the cell body and other axons to be clearly defined. Successfully biased growth is characterized by a lamellipodia extension in the radius of influence (approximately three laser beam radii) that grows toward the beam center. Subsequent extensions into the radius of influence are not considered to be new events here if no beam parameters (size, power, position, direction angle) have changed.

Our laser beam, asymmetrically positioned to the left or right of the leading edge of a growth cone, clearly affects advancing nerves (Fig. 2). The laser spot determines the active area of lamellipodia extension. We observe that the extending lamellipodia grow into the focus of the laser beam in 35 of 44 experiments. This is in 79.5% of all cases. Experiments where normally advancing growth cones are visible in the same field of view as optically guided neurons indicate that the laser increases the rate at which the nerve's leading edge advances (Fig. 3). Because growth cones extend discontinuously and two well-defined advancing growth cones in the field of view are rarely observed, a precise quantification of the effect was not possible. Nevertheless, from the time series in Fig. 3 we are able to estimate the trend that the lamellipodia extension rate increases from 7 ± 3 μm/h to 37.5 ± 22.5 μm/h.

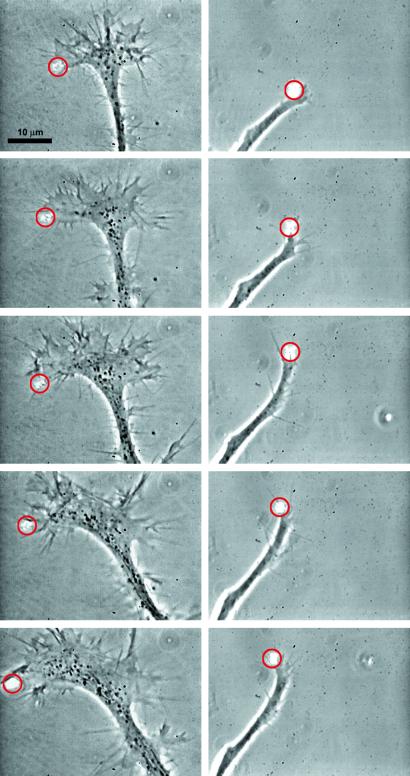
Fig 2.

Time sequences of optically guided turns of neurons and optically enhanced neuronal growth. Optically induced turns are shown for a time period of 40 min (Left) and 20 min (Right). The time interval between successive pictures is 10 min (Left) and 5 min (Right). The power of the laser spot is 100 mW (Left) and 60 mW (Right), and a red circle indicates the position of the laser spot (see Movies 1 and 2, which are published as supporting information on the PNAS web site, www.pnas.org). Optical control was achieved for extensive flat growth cones (Left) as well as for small, tube-like growth cones (Right). Before the laser altered the direction of the growth cone, the nerve was growing upward (Left) or to the right side (Right). The growth direction changes on the order of 90° under optical guidance. Note that the apparent change growth direction appears to be smaller because the axon straightens into the new direction.

Fig 3.

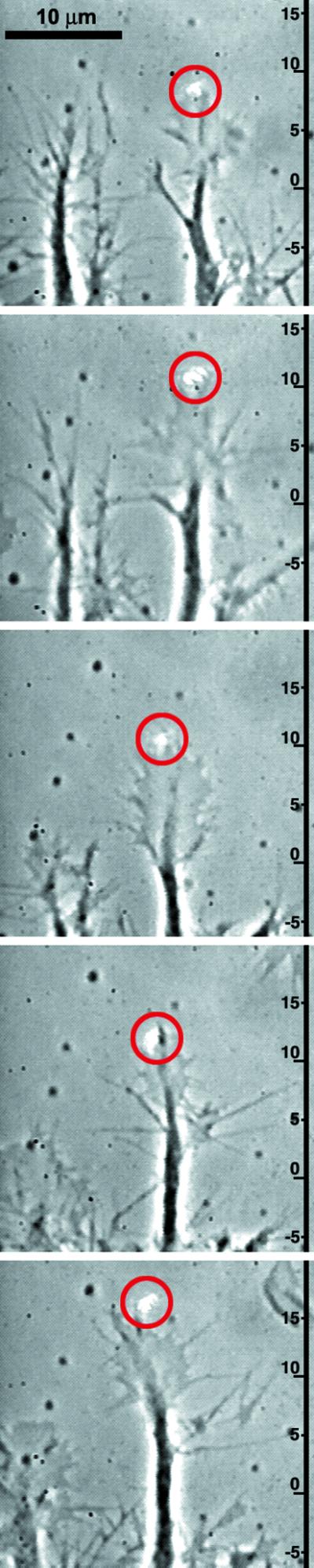
The parallel extension of two growth cones, one optically guided (right) and one normally growing, illustrates the increase in the speed of growth cone extension in the presence of a 20-mW laser spot (red circle) (see Movie 3, which is published as supporting information on the PNAS web site). The time interval between successive pictures is 10 min. The reference marks on the left are spaced in 5-μm steps.

The biased growth events are transient, lasting a few minutes. However, their cumulative effect leads to permanent results. Continuous optical guidance of the spreading growth cone results in controlled turns. We define a turn as a persistent change of growth direction that tracks the path of the laser spot for at least three radii of influence. The change in direction was chosen to be between 30° and 90° from the initial direction of growth. In these experiments, the laser spot is continuously positioned sufficiently in front of the leading edge to ensure uninterrupted extension and to prevent the leading edge from filling the entire laser spot. The laser guidance speed is limited by the extension speed of the cone. We observe successfully guided turns as successions of controlled lamellipodia extensions in 17 of 20 experiments. This finding means that optically guided turns were achieved with a success rate of 85.0% whereas in control experiments with an imaginary laser spot the success rate for apparent optically guided turns is only 20% in 10 experiments. The control experiments use fictitious radiation times and time intervals between trials that both agree with real optically guided turns. Our results are clearly statistically significant. The Fisher–Yates test, which is used for experiments with a small number of tests and controls, gives a P value of 0.097% for our optically guided turn experiments (a value below the standard confidence level of 5% is considered to be statistically significant). The P value denotes the probability to get an 85% success rate by chance in control experiments.

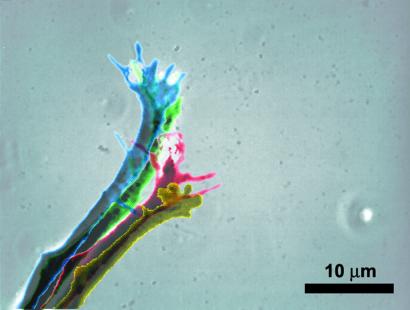
An overlay of the shapes of an optically guided neuron reveals the direct impact of the laser beam on lamellipodia structure as well as an indirect, temporally delayed turn of the axonal stump (Fig. 4). The area radiated by the beam promptly responds with the extension of a lamellipodium and with an accumulation of filopodia in the beam area. The induced turn does not appear as large as the true change in direction because the axonal stump behind the growth cone slowly straightens in the new direction of lamellipodia extension. The directional change of the leading edge can be on the order of 90°, as can be seen in Figs. 2 and 4. Thus, optically guided growth cones are able to drastically change their direction of movement if the axon behind the lamellipodia is allowed to turn in the new direction of growth cone extension. Because the high rigidity of the axon favors low curvatures (i.e., no curves and bends), it is preferable to guide a neuron in a fashion that allows the axonal stump to straighten, relaxing high curvatures. Optical guidance avoids high tensions due to bending, yielding a substantial but gradual turn.

Fig 4.

Superposition of the shapes of an actively extending growth cone under optical guidance. The same growth cone is shown in Fig. 2 Right. The progressing time is coded by the following series of colors: yellow (t = 0 min), red (t = 5 min), green (t = 10 min), and blue (t = 20 min). Two effects are clearly visible: stimulated by the laser, the small growth cone extends to the top of the picture in a pronounced lamellipodia structure with noticeable filopodia; the axonal stump, which does not actively participate in the growth process, changes its orientation by pointing more toward the top of the picture. Thus, the laser spot is able to induce significant changes in growth direction if the following axon can relax and avoid bends.

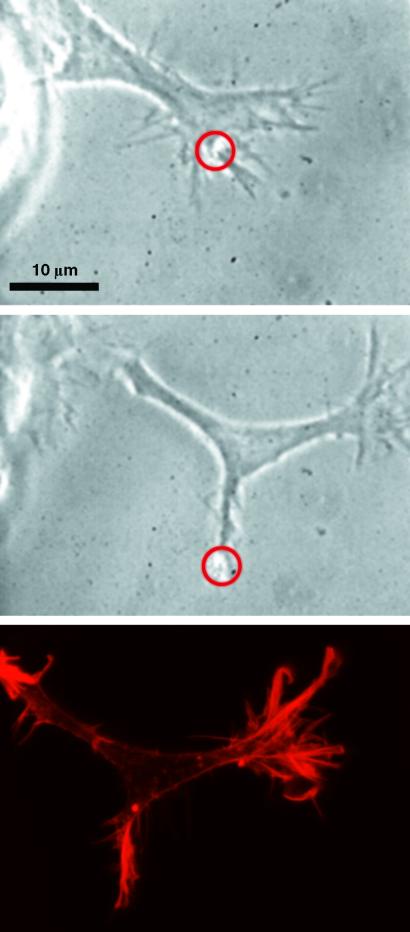
In some cases where the angle of directed growth is large with respect to the original growth direction, the laser beam induced a bifurcation of the growth cone (Fig. 5). This allows us to compare the underlying structure of the actin cytoskeleton in optically guided and normally developed lamellipodia. The narrower shape of the optically guided growth cone is not significant because we observe small and large growth cones during both normal, as well as optically guided, growth. For both growth cones, we find prominent structures of filamentous actin, which are absent in the main body of the growth cone, when visualized by rhodamine-phalloidin staining (which only binds to actin filaments). Actin bundles, originating from the filopodia and the filamentous actin cortex directly underlying the plasma membrane, are also visible. Because these two structures are key to lamellipodia extension, an essential prerequisite for the expansion of the leading edge is the transport of actin monomers (G-actin) to the front of the cell to provide for the polymerization of new actin filaments (37).

Fig 5.

Optically induced bifurcation of a growth cone. A growth cone, which is growing to the upper right, sprouts off an extension to the lower right under the influence of the beam marked by a circle. The last picture displays the distribution of actin filaments by rhodamine-phalloidin staining. Actin filaments are clearly accumulated at the areas of lamellipodia extension.

Discussion

At the chosen power levels of the laser, we are not able to detach the growth cone from the substrate and move it around by steering the focus of the laser beam. Therefore, we do not use the gradient forces of our optical trap in the conventional fashion, whereby the tweezing effect of the trap is used to move an entire structure. We conclude that our laser spot influences the general actin-based processes for growth cone extension when we optically guide turns. Because these intracellular processes are not completely understood, it is difficult to fully explain the molecular basis of optical guidance. Nevertheless, the optical forces interact with the proteins of the cytoplasm. Because the larger filamentous structures of the cytoplasm are crosslinked and coupled to the plasma membrane by focal adhesions, the optical forces can only exert a tension on these structures, but cannot move them. However, globular proteins and small oligomeric structures are free to move in the cytoplasm, and thus the optical forces can impact their diffusive behavior. The smallest forces are felt by globular proteins and are a lower bound for this effect.

The laser beam, placed just outside the growth cone, creates an intensity gradient for the globular proteins of the cytoplasm, such as actin monomers, and they feel a weak optical dipole force. This force is directed toward the center of the laser spot. In the electromagnetic field of the laser E, the force on an induced electric dipole p = αE is given by (38)

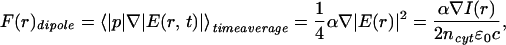where α is the polarizability of the protein experiencing the dipole force, n_cyt = 1.37 is the refractive index of the cytoplasm (39), ɛ₀ is the dielectric constant, and c is the speed of light. I(r) represents the Gaussian intensity profile of the laser beam. The corresponding dipole potential (i.e., the attractive energy toward the center of the laser beam) is

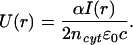We estimated α for G-actin, which we needed to calculate F_dipole and U, using the Clausius–Mosotti equation (40)

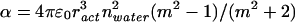(r_act = 3 nm is the radius of an actin monomer, n_water is the refractive index of water, m = n_act/n_water). With a refractive index for actin of n_act = 1.59 (41–43) we obtain for G-actin (as well as other proteins of similar size within the cell) a polarizability of ≈6.5 × 10⁻³⁷ Cm²/V.

With a laser power of 60 mW focused to a beam radius of 1.5 μm, Eq. 2 yields a potential well depth of U = 1.5 × 10⁻²⁴ J = 3.6 × 10⁻⁴ k_BT (k_B Boltzmann's constant, T = 310 K the cell temperature, k_BT thermal energy). Because polarizability increases with molecular size, small actin oligomers (fragments of actin filaments) will experience a deeper potential well than actin monomers. These fragments originate in the depolymerization of the actin cortex toward the interior of the growth cone. Nevertheless, this potential well remains smaller than the thermal energy k_BT and thus is much too weak to function as optical tweezers because Brownian diffusion can overcome its trapping power.

A significant portion of the cytoplasmic proteins, including G-actin, undergo Brownian motion within the cell, and their diffusive transport to the leading edge of a lamellipodium is essential for cell motility. By approximating the dipole force F_dipole with a spatially constant force equaling the dipole force at half the radius of the laser spot, a drift velocity caused by the dipole force toward the center of the laser beam can be estimated. This drift velocity biases diffusion of cytoplasmic proteins toward the laser. The drift velocity, v_Drift, satisfies

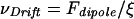with ξ = k_BT/D (D is the diffusion coefficient). The diffusion coefficient D of a globular macromolecule of the size of G-actin in the cytoplasm is ≈2.5 × 10⁻¹¹ m²/s (44). Based on these parameters and Eqs. 1 and 4, we predict a drift velocity of 26 μm/h for actin monomers, which is very close to growth rates of an active growth cone observed in the experiments. Dipole forces create even higher drift velocities for fragments of actin filaments. We therefore propose that the optical gradient enhances actin polymerization at the leading edge by pooling actin monomers and providing nucleation seeds in the form of actin filament fragments. The resulting locally enhanced actin polymerization promotes a turn of the lamellipodium in the direction of optically increased actin density. Optical forces that distend the membrane might also allow actin monomers to flow into new extensions. Furthermore, although they cannot move the crosslinked actin cortex, the optical forces do pull on this actin network and relieve pressure at the rearward cortex-microtubule junction, thus enhancing pressure-dependent microtubule polymerization (45). In summary, we conjecture that weak optical dipole forces could be used to control biological growth processes such as growth cone extension. The molecular basis of this optical guidance is complex and may rely on a combination of all of the optically induced processes discussed above.

Conclusion

We have shown that weak optical dipole forces can be used to bias the molecular process of cell motility so that we can guide neuronal growth. Because we influence lamellipodia extension, a process essential for all motile cells, optical guidance may be extended as a general cell guidance method and provide an investigative tool to understand the underlying processes of cell motility. Moreover, we hope that optical guidance will allow us to form controlled neuronal structures in vitro, and we can also imagine that optical guidance could find applications in nerve repair in vivo.