Large-scale molecular dynamics simulations of general anesthetic effects on the ion channel in the fully hydrated membrane: The implication of molecular mechanisms of general anesthesia

Abstract

Interactions of volatile anesthetics with the central nervous system are characterized by low yet specific binding affinities. Although neurotransmitter-gated ion channels are considered the primary anesthetic targets, the mechanism of action at the molecular level remains elusive. We consider here the theoretical implications of channel dynamics on anesthetic action in a simplified membrane-channel system. Large-scale 2.2-ns all-atom molecular dynamics simulations were performed to study the effects of halothane, a clinical anesthetic, on a gramicidin A (gA) channel in a fully hydrated dimyristoyl phosphatidylcholine membrane. In agreement with experimental results, anesthetics preferentially target the anchoring residues at the channel–lipid–water interface. Although the anesthetic effect on channel structure is minimal, the presence of halothane profoundly affects channel dynamics. For 2.2-ns simulation, the rms fluctuation of gA backbone in the lipid core increases from ≈1 Å in the absence of anesthetics to ≈1.5 Å in the presence of halothane. Autocorrelation analysis reveals that halothane (i) has no effect on the subpicosecond librational motion, (ii) prolongs the backbone autocorrelation time in the 10- to 100-ps time scale, and (iii) significantly decreases the asymptotic values of generalized order parameter and correlation time of nanosecond motions for the inner but not the outer residues. The simulation results discount the viewpoint of a structure–function paradigm that overrates the importance of structural fitting between general anesthetics and yet-unidentified hydrophobic protein pockets. Instead, the results underscore the global, as opposed to local, effects of anesthetics on protein dynamics as the underlying mechanisms for the action of general anesthetics and possibly of other low-affinity drugs.

The mechanisms of general anesthesia remain poorly understood. The first successful public demonstration using ether to end surgical pain also marked the beginning of a painstaking search for the molecular understanding of this medical wonder. For more than a century, thinking has been directed to one of the two putative target sites: the lipid portion of neuronal membranes (1–3) or the hydrophobic pockets in certain crucial excitable proteins (4–6). The lipid theory postulates that general anesthetics cause a generalized perturbation to neuronal membranes through nonspecific interactions, whereas the protein theory contends that anesthetics must bind specifically to a set of appropriate molecular dimensions on the membrane proteins to produce the effect. Recent attempts have also been made to colligate the lipid effects with lipid–matrix-mediated modulations of membrane protein function without the binding of a receptor (7–9). Nevertheless, intensive studies along these lines have not revealed an unequivocal mechanism for the action of general anesthetics.

Nearly all investigations to date at the molecular level are based on inferences from studies of functional sensitivity. Although relating the sensitivity to the mode of action is debatable (10), the potential link between the two offers a reasonable interpretation of some in vitro measurements that are otherwise difficult to put into physiological perspective. By contrasting sensitivity and insensitivity, recent mutagenesis studies (5, 11) were able to pinpoint, in vastly complicated ligand-gated receptors, individual amino acids that are responsible for the sensitivity. The popular idea that anesthetics must occupy some “hydrophobic pockets” to produce anesthesia has prompted important questions, such as whether the mutation sites are part of the anesthetic binding sites, and whether the binding pockets are specific enough to warrant the design of novel anesthetic molecules that are devoid of any side effects. High-resolution structural analyses (12) have recently been made to answer some of these questions.

It has long been recognized that anesthetic binding, particularly when volatile anesthetics are involved, cannot be viewed as stationary (13–16). Rapid binding kinetics, along with the fact that a huge number of structurally diverse anesthetics can produce similar effects, seems to suggest that a “one-size-fits-all” anesthetic pocket is not plausible. This has led to the viewpoint of a multisite multimechanism mode of action and the abandonment, although not without question, of the unitary theory of general anesthesia.

Because of the critical role of ion channels in synaptic transmission, we have investigated the theoretical implications of ion channel dynamics on anesthetic action. We believe that anesthetic molecules exert their action on all proteins through a common molecular mechanism of modulating protein dynamics, not necessarily by fitting into structurally compatible pockets but by becoming an integral part of amphipathic domains where they can either disrupt the association of the channel with its surrounding or facilitate the formation of structured water clusters within the protein or at deep levels of protein–lipid interface where the water presence is normally scarce and brief. In doing so, they alter the functional characteristics of protein motion and thereby change the protein function.

In this study, we used large-scale molecular dynamics simulation to investigate the dynamical behaviors of a transmembrane channel in the absence and presence of volatile anesthetic molecules. The gramicidin A (gA) channel was chosen as a convenient model, because the high-resolution structure of this channel has been solved by NMR (17, 18) and thus can be used as the starting structure for simulation (19, 20). In addition, we have accumulated an extensive amount of experimental data about anesthetic effects on this channel and found that the channel conductance can be modulated by anesthetics but not by structurally similar molecules devoid of anesthetic effects (15), suggesting the theoretical relevance of the model to anesthetic action. We also found that anesthetics, but not nonanesthetics (or nonimmobilizers), can interact specifically with the amphiphilic-anchoring tryptophan residues of gA channel at the lipid-water interface and that this interaction requires the channel conformation in the membranous environment (14, 15, 21). These experimental results are the essential premise for the initial setup of the simulation system.

Methods

Preparation of Simulation Systems.

namd2 (22) and x-plor (23) were used for preparing the gA channel in a preequilibrated dimyristoyl phosphatidylcholine (DMPC) membrane, consisting of 200 DMPC lipid molecules fully hydrated with n_w = 27.4 water molecules per lipid (24). The structural and coordinate files of gA ( from the Protein Data Bank) and the preequilibrated DMPC membrane were merged with the geometric centers of the channel and membrane superimposed. The channel axis is parallel to the membrane normal. The lipid and water molecules whose atoms are within 1.6 Å from any atoms of the gramicidin were removed. A cylinder of TIP3 water was used to fill the pore of the channel, with any water molecules within 1.4 Å from the channel atoms deleted. The final system contains one gA channel (an N-to-N dimer of two β^6.3 helices of 15 aa each), 182 lipid molecules, and 5,538 TIP3 water molecules. The system was first energy minimized by using a simple velocity-quenching scheme with heavy atoms of the gA channel constrained with a force constant of 999 kcal/mol/Ų, so that the NMR-determined structure remains stable. The minimized system then underwent constant number of atoms, pressure, and temperature (NPT) dynamic equilibration for an additional 1,400 ps at 310 K and 1 bar, with a stepped decrease in gA constraint over the initial 380 ps from 999 to 0 kcal/mol/Ų (free dynamics). Ten halothane molecules, parameterized by ab initio calculation (25–27), were placed at locations consistent with predictions from our experimental studies, as detailed below. The initial docking of halothane was done manually by first imposing a random rotation on the halothane molecules and then placing them in the transiently formed voids in the equilibrated gA–membrane system. Acceptance criteria for the initial docking were that all atoms in halothane were at least 1 Å away from any atoms in gA and lipid molecules and that the coordinates of halothane atoms did not overlap with any of the water molecules. The system with halothane was subjected to additional energy minimization and equilibration without constraints by using the conjugate gradient and line-search algorithm (28) until the total energies were stabilized.

Molecular Dynamics Simulations.

After the preparation procedures, two NPT simulations were carried out in parallel for 2.2 ns each in the presence and absence of 10 halothane molecules. All simulations were carried out on the T3E parallel computer at the Pittsburgh Supercomputing Center by using the NAMD2 program. The Nosé–Hoover method with Langevin dynamics for temperature control (29, 30) and Langevin piston pressure for barostat fluctuation control were used to maintain the temperature and pressure at 305 K (32°C) and 1 bar, respectively. The periodic boundary condition was imposed in a flexible cell of dimension 80 × 80 × 60 ų with water wrapping. The time step was 1 fs, with energies and trajectories being stored every 0.5 and 1 ps, respectively. Local interactions, including bonded interactions and short-range van der Waals and electrostatic interactions, were calculated in every time step. The cutoff distance for the van der Waals interactions was 12 Å, with the pair list distance extended to 14 Å. The long-range full electrostatic interactions were evaluated every four time steps by using the particle mesh Ewald (PME) method with a PME tolerance of 10⁻⁶ and a PME interpolation order of 4. For all simulations, the Shake routine was used to restrain all bonds between hydrogen and its parent atom to a tolerance of 10⁻⁵ Å.

Data Analysis.

All analyses of energies and trajectories of the simulated systems were performed on SGI Octane workstations (Silicon Graphics, Mountain View, CA) by using local scripts developed within the vmd software environment (31). Standard procedures for rms deviations and fluctuations (RMSF) were used. For evaluating the channel's internal motions to estimate the generalized order parameter, S², the trajectory frames were first superimposed onto an optimal common frame of reference to remove any translational and rotational motions and then calculated by using (32):

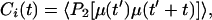where μ(t′)μ(t′ + t) is the projection of a unit vector pointing along a given backbone or side chain vector at time t′ onto itself at a later time t′ + t, P₂(x) is the second Legendre polynomial, and the brackets denote a time average over the trajectory. The generalized order parameter is given by:

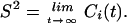For molecular dynamics simulations with a finite time length of T, S² can be computed by using:

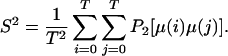We analyzed the time dependence of the autocorrelation for the internal motion using the extended model-free formulism (32–35):

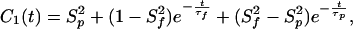where S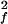 and τ_f are the amplitude and correlation time of the subpicosecond decay due to librational motion, and S and τ_p are the amplitude and correlation time for the local N—H bond anisotropic diffusion in the picosecond range. Different from globular proteins with independent isotropic tumbling, transmembrane helical channels have a second internal motion related to anisotropic helical tumbling in the membrane. We included the contribution of this second internal motion by considering an order parameter S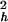 and a correlation time τ_h (36):

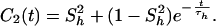The total internal autocorrelation function will then become:

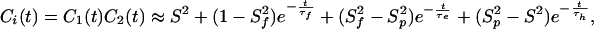where S²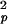 = SS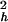, τ_e = τ_pτ_h/(τ_p + τ_h), and approximations were made by assuming 1/τ_f ≫ 1/τ_h and 1/τ_p ≫ 1/τ_h.

Differences in S² between two parallel simulations in the presence and absence of halothane reflect changes in the motional characteristics of the channel and consequent changes in the conformational entropy. The upper bound for the change in entropy and the Gibbs' free energy can be estimated from order parameters by (37, 38):

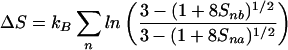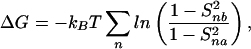where k_B is the Boltzmann constant, and S_nx is the order parameter for the nth vector in the absence (x = a) and presence (x = b) of halothane.

Results and Discussion

Dynamic Distribution of Anesthetics in Membrane.

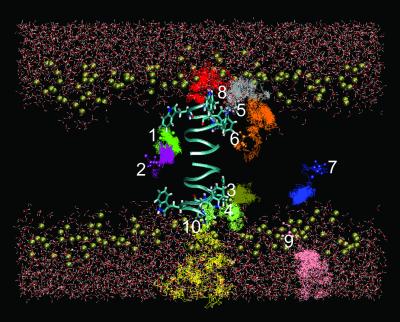
It is not yet feasible to fully simulate anesthetic equilibration in a biological membrane by all-atom simulations (e.g., ≈39,000 atoms in the present study) with the currently existing computing power, and this is not the purpose of the present study. The initial locations for halothane molecules were selected on the basis of prior experimental knowledge about the halothane distribution in the membrane, so that different microenvironments could be properly sampled, as shown in Fig. 1. Of 10 halothane molecules, six (halothane 1–6) are within the cutoff distance from the channel at different depths in the membrane, two (halothane 7 and 9) are at least 1 Å more than the pair-list distance (14 Å) away from the channel, and the remaining two (halothane 8 and 10) are near the channel entrances. Three halothane molecules (halothane 8–10) are placed in the water phase near the lipid head groups. These initial halothane arrangements also conform with the large lipid–water partition coefficient for halothane and qualitatively agree with the NMR prediction of volatile anesthetic distribution in the lipid bilayers (14, 15, 39).

Fig 1.

Halothane trajectories over the 2.2-ns all-atom simulations in a channel-membrane system, consisting of a gA channel (cyan ribbon showing the backbone), 182 dimyristoyl phosphatidylcholine lipids (showing only the phosphorus atoms as gold spheres to mark the interface of the membrane), and 5,538 water molecules. The initial halothane positions, which are chosen based on the prior knowledge of equilibrated halothane distribution in membrane, are marked by the licorice drawing. Notice the tendency of halothane 3–8 to move toward the membrane interface. Halothane 1 and 2 form a pair and behave differently from the others.

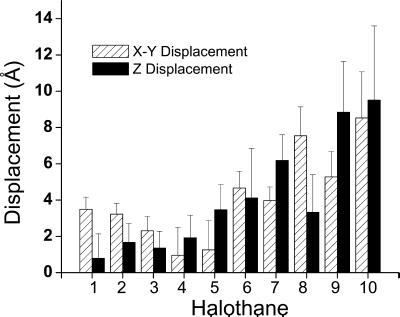
Redistribution of halothane occurred over the 2.2-ns simulation, despite the near equilibrating state of the initial setup. Fig. 1 shows the side view of halothane trajectories over the 2.2-ns simulation with 1-fs time steps and 1-ps sampling intervals. Although the simulation time is significantly shorter than the characteristic time for thermal equilibration, a statistically significant tendency of anesthetic redistribution in membrane is nevertheless discernable from the collective behavior of 10 halothane molecules in our 2.2-ns simulations. Fig. 2 shows the lateral (perpendicular to the membrane normal direction) and longitudinal (in membrane normal direction) displacements of the mean halothane positions averaged over the 2.2-ns trajectories relative to the initial positions. The error bars indicate the SD of all recorded positions in the corresponding trajectories. Clearly, the halothane molecule placed in the water phase (halothane 8, 9, and 10) had the largest displacements and overall SD. Of those initially placed in the tail region of the membrane (halothane 1, 2, 6, and 7), two (halothane 6 and 7) showed a clear tendency to move to the lipid–water interface with large longitudinal movements. Three halothane molecules (3, 4, and 5) placed in the channel–lipid–water interface had relatively small overall displacements, suggesting that halothane molecules populate more favorably in these regions. Taken together, the results of halothane distribution over the 2.2-ns all-atom simulation are in excellent agreement with our NMR finding that volatile anesthetics are accessible to the aqueous phase and preferentially target the membrane interface (39–41).

Fig 2.

Mean displacements for the 10 halothane molecules relative to their initial positions in the direction parallel (solid bar) and perpendicular (hatched bar) to the membrane normal. Molecular numbering is the same as shown in Fig. 1. Error bars show the standard deviations of the trajectories in the corresponding directions. See text for details.

Pairing of Anesthetics as a Nonanesthetic.

The intriguing behavior of halothane molecules 1 and 2 is worth scrutinizing further. Instead of migrating to and localizing at the membrane interface where general anesthetic action is believed to be, these two halothane molecules formed a pair and stabilized each other through electrostatic interaction in a grove at the lipid–channel interface deep in the lipid bilayer (Fig. 3). This interesting finding has significant implications. The pairing shown in Fig. 3 partially cancels the dipole moment of the halothane molecules, making them favor the apolar lipid tail region. Although molecules with dipole moments are not necessarily anesthetics, it has been found that permanent or inducible dipole moments are important for anesthetic action (40). Molecules that are nonanesthetics (nonimmobilizers) but are structurally similar to their anesthetic counterparts often have virtually zero dipole moment. We learned in our previous NMR experiments that nonanesthetic molecules prefer the lipid tail region to the lipid–water interface (39). The different tendency in the distribution of halothane 1 and 2 from that of other halothane molecules seems to suggest that the pairing of two anesthetics can render them indistinguishable from a nonanesthetic molecule. An inference from this is that at a given anesthetizing concentration, a significant portion of anesthetic molecules might be in an inactive pool (behaving like nonanesthetics) to maintain adequate equilibrium anesthetic concentrations at the critical target sites.

Fig 3.

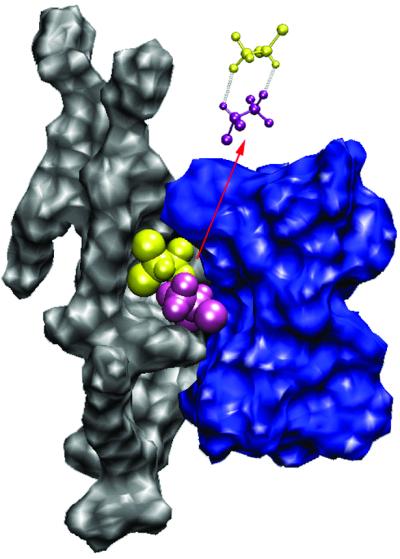
Pairing of two halothane molecules by electrostatic interaction results in nonanesthetic-like behavior. The dipole moments of halothane 1 and 2 (yellow and purple) are partially cancelled to stabilize each other in a hydrophobic grove at the interface of lipid (gray) and gA channel (blue) deep in the dilayer. The pairing occurs during the first ≈100 ps and lasts to the end of the 2.2-ns simulation.

Specific Halothane Interaction with Anchoring Tryptophan Side Chains.

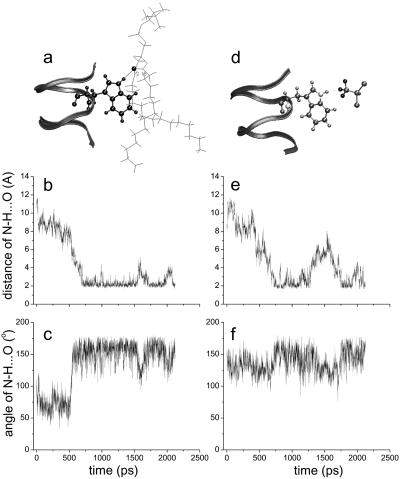
The preferential and stable distribution of halothane molecules at the channel–lipid–water interface increases the probability of halothane molecules interacting with residue side chains in this region. The simulation reveals that the indole amide hydrogen atoms form stable hydrogen bonds with the phosphate oxygen in the lipid head region or the fatty acid oxygen near the glycerol bridge, depending on the depths of the indoles in the membrane (Fig. 4a). These hydrogen bonds last for nanoseconds in the absence of halothane (Fig. 4 b and c) and are disrupted more frequently in the presence of a nearby halothane molecule (Fig. 4 e and f). Presumably, the disruption is due to the replacement of hydrogen bonds between tryptophan and lipid by those between the indole amide hydrogen and the fluorine in halothane (Fig. 4d). It should be noted that the hydrogen bonding between anesthetic molecules and the channel is transient, lasting only a few hundred picoseconds in a 2.2-ns simulation (Fig. 4 e and f). Nevertheless, the strong interactions between halothane and the tryptophan indoles affect the interactions of indoles with lipid head groups. For transmembrane ion channels, a reoccurring feature is that amphipathic residues at membrane interface act either as the anchoring points to stabilize channels across the membrane, or the hinge points to provide allosteric linkage for gating. gA serves as an excellent model for this, because each gA channel has four tryptophans (W9, -11, -13, and -15) at each end to anchor a channel dimer.

Fig 4.

The anchoring tryptophan side chains interact specifically with the lipid surrounding by hydrogen bonding, as exemplified in a for a hydrogen bonding between W-9 indole amide hydrogen with fatty acid oxygen of the glycerol bridge. A hydrogen bond is considered formed when the H…O distance (b and e) is <3.1 Å and N—H… O angle (c and f) is >146° (46). In the absence of halothane (b and c), hydrogen bonding between tryptophan and lipids lasts over nanosecond, whereas in the presence of halothane (e and f), hydrogen bonding is more frequently broken as a result of transient hydrogen bonding between indole amide hydrogen and fluorine in halothane, as shown in d.

The ability of the tryptophan indole hydrogen to form hydrogen bonds with lipid head groups is an important interaction for stabilizing the channel in the membranes. It has been found (42, 43) that the orientations of tryptophan indole rings and their interaction with the lipid–water surrounding have profound effects on channel conductance. Moreover, changes in the dipole moments of tryptophan affect channel function significantly (44). Our previous NMR studies showed that volatile anesthetics, but not the structurally similar nonanesthetics, could cause concentration-dependent shifts of the indole amide proton resonance (21) and could alter the Na⁺ transport (15). Disrupting the association of anchoring residues of the channel at the membrane surface can affect the entire channel motion, as revealed by the systematic change in the backbone fluctuations of the channel.

Profound Effect of Halothane on Channel Dynamics.

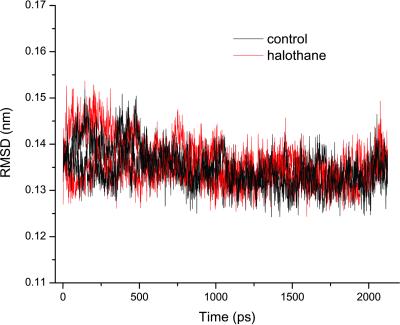
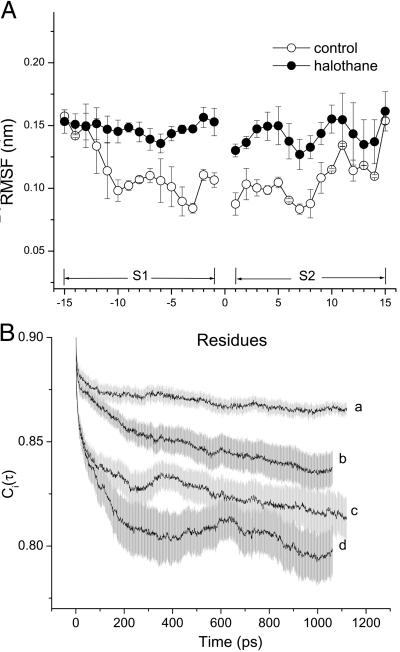
NMR structural analysis showed that general anesthetics at physiologically relevant concentrations had minimal effects on gA structures (21, 45). The same conclusion can be drawn from the 2.2-ns simulations in the presence and absence of halothane. Fig. 5 shows the rms deviation of the backbone C_α over the 2.2-ns simulations; the values are small and well overlapped for the two parallel simulations, suggesting that no halothane effects on the channel backbone structure are measurable. However, the presence of halothane profoundly affects channel dynamics. Fig. 6A compares the RMSF of the backbone C_α atoms in the absence and presence of halothane. Under control conditions without halothane, the RMSF profile varies with the depth of the residues in the membrane. Backbone RMSF for residues near the two ends of the channel is about 50% larger than for those deep in the membrane tail region (≈1.5 vs. ≈1 Å). This variation in C_α RMSF profile reflects the difference between the motional characteristics of the channel surroundings at the membrane interface and in the more ordered lipid tail region. In the presence of halothane, RMSF profile along the channel is equalized: it is increased in the center while it remains at the background level near the two ends. It is worth noting that, although anesthetics interact specifically with side chains of the anchoring residues in the membrane interfacial region, the largest RMSF change occurs in the membrane center where halothane is less populated. Moreover, although the distribution of halothane in the immediate vicinity of the two segments is asymmetrical, the increase in RMSF is nearly symmetrical along the channel. These findings strongly suggest that anesthetics exert a global rather than local effect on transmembrane channel dynamics. No discernable change in RMSF for the end residues indicates that the movement of water molecules, which penetrate into the membrane head region, dominates background fluctuation, and the addition of mobile anesthetic molecules does not further enhance the preexisting strong fluctuations.

Fig 5.

Halothane has minimal effects on gA channel structure, as revealed here by the small and well overlapped rms deviations of the backbone C_α in the absence and presence of halothane.

Fig 6.

Comparison of the dynamics of gA channel in the absence and presence of halothane: (A) RMSF for the C_α carbons along the channel, and (B) the autocorrelation functions of the backbone N—H bond orientation. For display clarity, the autocorrelation functions are pooled and averaged separately for inner residues (residues 1–8, a, without halothane; and b, with halothane) and outer anchoring tryptophan residues along with the leucine spacers (residues 9–15, c, without halothane; and d, with halothane). For the 2.2-ns simulations, the RMSF is dominated by the motions on the nanosecond time scale. On this time scale, halothane significantly enhanced the motion of the inner residues of the channel. See text and Table 1 for details.

The time dependence of the channel dynamics is depicted in Fig. 6B for the autocorrelation function of the backbone N—H bonds. For display clarity, the autocorrelation for residues 1–8 in the lipid tail region and for the four anchoring tryptophans along with the “spacer” leucines at the membrane interface (i.e., residues 9–15) are separately pooled and averaged. The ranges of variation within each group are shown by the standard errors. Clearly, halothane profoundly affects overall channel dynamics. Table 1 summarizes the parameter from nonlinear least-squares fitting by using Eq. 6. The subpicosecond decays have S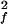 values of 0.88–0.89 for the inner residues and 0.87–0.88 for the outer residues, with a narrow range of τ_f. Thus, the librational motion is not affected by the halothane. On the 10- to 100-ps time scale, which is well sampled in the 2.2-ns simulations, halothane significantly lowered the S 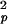values and at the same time prolonged the effective correlation time τ_e from 24 to 83 ps for the inner residues and from 29 to 74 ps for the outer residues. For the nanosecond motions, halothane greatly decreased the asymptote values of the order parameter and shortened the correlation time from ≈1.3 to 0.8 ns for the inner residues. In contrast, the outer residue motions on the nanosecond time scale were not strongly affected by halothane.

Table 1.

Parameters of autocorrelation function in the presence and absence of halothane

Parameters	Residues 1–8		Residues 9–15
	Control	Halothane	Control	Halothane
S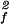	0.8899  ± 0.0005	0.8821  ± 0.0003	0.8736  ± 0.0009	0.871  ± 0.001
τf, ps	0.36  ± 0.02	0.41  ± 0.02	0.51  ± 0.03	0.56  ± 0.06
S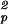	0.8758  ± 0.0002	0.8654  ± 0.0009	0.8390  ± 0.0004	0.813  ± 0.002
τe, ps	24  ± 2	83  ± 6	29  ± 1	74  ± 4
S2	0.856  ± 0.002	0.826  ± 0.002	0.786  ± 0.006	0.780  ± 0.020
τh, ps	1,318  ± 162	800  ± 71	1,865  ± 305	1,817  ± 1,968

^*Significantly different from the corresponding values in the control simulation (P < 0.05).

The seemingly opposite halothane effects on the pico- and nanosecond correlation times (Table 1) actually both reflect an enhancement in channel dynamics after the addition of halothane. The correlation time in the picosecond range (τ_e) can be attributed to the anisotropic diffusion of individual N—H bonds within a cone with the vertex on the nitrogen. As shown by many NMR relaxation measurements of protein dynamics, an increase in τ_e and a decrease in S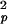 indicate a larger amplitude of diffusive motion. On the nanosecond time scale, the shortening of τ_h is a result of an increased anisotropic helical tumbling of the channel in the membrane. Because a gA channel is formed by unique head-to-head dimerization in the membrane interior with four anchoring tryptophan residues at each end of membrane interface, the halothane effects on shortening the nanosecond correlation time (τ_h) are more profound for the inner than for the anchoring residues. The reduced S² values in the presence of halothane also confirm that halothane disorders the channel.

The asymptotic values of S² can be used to estimate the upper bound of ΔS and ΔG in the motion of gA channel backbone due to halothane. At the simulation temperature of 305 K, Eqs. 7 and 8 yield: TΔS = 2.34 kcal/mol and ΔG = −2.19 kcal/mol, which gives an enthalpy change of mere 0.15 kcal/mol. These results reconfirm that the action of halothane on the gA channel is predominantly entropic (dynamics), with negligible enthalpy (structure) contributions.

The finding that the pattern of change in channel dynamics is globally affected and remotely coupled to the site of direct anesthetic interaction has profound implications in the protein theory of general anesthesia. Ample evidence suggests direct modulation of protein function by general anesthetics, yet potency additivity exhibited by structurally diverse anesthetic molecules argues against the idea that additivity is the result of cooccupation or competitive displacement by different anesthetics at the same sites. The simulation results presented in this study offer an alternative viewpoint: that the functionally significant changes in dynamics at various sites in a protein are governed predominantly by the protein's intrinsic susceptibility to the environment-controlled dynamical modulations. As long as the modulators (anesthetics) are present (not necessarily at the same sites), the global change in dynamics will occur and will be additive, leading to the corresponding functional changes. Specifically for the gA channel, the targeted interaction of halothane with the anchoring tryptophan residues at the membrane interface results in symmetrical dynamic changes along the channel near the locations where dimerization occurs. The inner residues in the membrane tail region are intrinsically more susceptible to the global changes in the anisotropic helical tumbling than are the four anchoring tryptophan residues. The functionality of the gA channel is characterized by ion transport, which depends on the hopping from one end of the channel to the other of the partially dehydrated ions bound to the channel entrances. It is conceivable that alteration of the dynamical characteristics of the channel can strongly influence the hopping process. A more flexible channel on the time scale of hopping is likely to increase the unidirectional transport rate. It has been found experimentally that volatile anesthetics can indeed enhance the Na⁺ transport across the gramicidin channel (15).

The functional consequences of anesthetic modulation of channel dynamics are not necessarily the same on different time scales. Halothane enhances backbone N—H bond diffusion on all residues along the gA channel in the 10- to 100-ps time range but shortens the correlation time of the inner residues only on the nanosecond time scale. The latter time scale is clearly more important for the function (ion transport) of the gA channel. For more complicated receptor channels, the influence of general anesthetics on channel dynamics can be more complicated and possibly results in both enhancement and suppression of ion transport, depending on the conformational states of the channels. Whether a given change in protein dynamics has any functional significance depends on the characteristic time with which the protein carries out a particular function. This viewpoint offers a unitary explanation for different anesthetic action on a diverse range of proteins and protein functions. A testable hypothesis of the molecular mechanism of general anesthesia based on protein dynamics can thus be stated:

For all proteins, multiple conformers coexist dynamically, and general anesthetics can shift the equilibrium among different conformation states. When anesthetic modulations of the global dynamics of a given protein create “conformation resonance,” in which all multiple equilibrating conformers are locked into one dominating conformation having dynamical characteristic time significant for the protein function, then the function carried out by the protein will be changed. The functional state can be either “on resonance,” leading to anesthetic-induced potentiation, or “off resonance,” leading to anesthetic-induced inhibition.

In summary, large-scale molecular dynamics simulations reveal a clear tendency for general anesthetics to target anchoring residues of the gramicidin channel at the membrane–water interface, resulting in a global change in channel dynamics. The anesthetic-induced dynamic changes differed on different time scales. Only the dynamic changes with characteristic time matching that of the protein function can potentially contribute to the action of general anesthetics.

Abbreviations

• gA, gramicidin A

• RMSF, rms fluctuations