Coupling of protein motions and hydrogen transfer during catalysis by Escherichia coli dihydrofolate reductase

Abstract

The enzyme DHFR (dihydrofolate reductase) catalyses hydride transfer from NADPH to, and protonation of, dihydrofolate. The physical basis of the hydride transfer step catalysed by DHFR from Escherichia coli has been studied through the measurement of the temperature dependence of the reaction rates and the kinetic isotope effects. Single turnover experiments at pH 7.0 revealed a strong dependence of the reaction rates on temperature. The observed relatively large difference in the activation energies for hydrogen and deuterium transfer led to a temperature dependence of the primary kinetic isotope effects from 3.0±0.2 at 5 °C to 2.2±0.2 at 40 °C and an inverse ratio of the pre-exponential factors of 0.108±0.04. These results are consistent with theoretical models for hydrogen transfer that include contributions from quantum mechanical tunnelling coupled with protein motions that actively modulate the tunnelling distance. Previous work had suggested a coupling of a remote residue, Gly¹²¹, with the kinetic events at the active site. However, pre-steady-state experiments at pH 7.0 with the mutant G121V-DHFR, in which Gly¹²¹ was replaced with valine, revealed that the chemical mechanism of DHFR catalysis was robust to this replacement. The reduced catalytic efficiency of G121V-DHFR was mainly a consequence of the significantly reduced pre-exponential factors, indicating the requirement for significant molecular reorganization during G121V-DHFR catalysis. In contrast, steady-state measurements at pH 9.5, where hydride transfer is rate limiting, revealed temperature-independent kinetic isotope effects between 15 and 35 °C and a ratio of the pre-exponential factors above the semi-classical limit, suggesting a rigid active site configuration from which hydrogen tunnelling occurs. The mechanism by which hydrogen tunnelling in DHFR is coupled with the environment appears therefore to be sensitive to pH.

INTRODUCTION

It has long been accepted that electrons can be transferred in chemical reactions by quantum mechanical tunnelling with energies of activation deriving from heavy-atom motions [1]. However, only recently have several cases of hydrogen tunnelling been described where the probability of tunnelling was modulated by environmental dynamics and protein motions [2–15]. Several theoretical models that incorporate environmental motions have been developed to describe hydrogen transfer reactions [5,16–19]. The model proposed by Kuznetsov and Ulstrup [19] and developed further by Knapp and Klinman [5,13] for enzymatic transformations, which separates the faster e⁻ and H co-ordinates from the environmental co-ordinate, distinguishes between passive motions that influence the probability of the formation of an active site configuration conducive to hydride transfer, and active protein motions that modulate the tunnelling distance and hence the reaction rate.

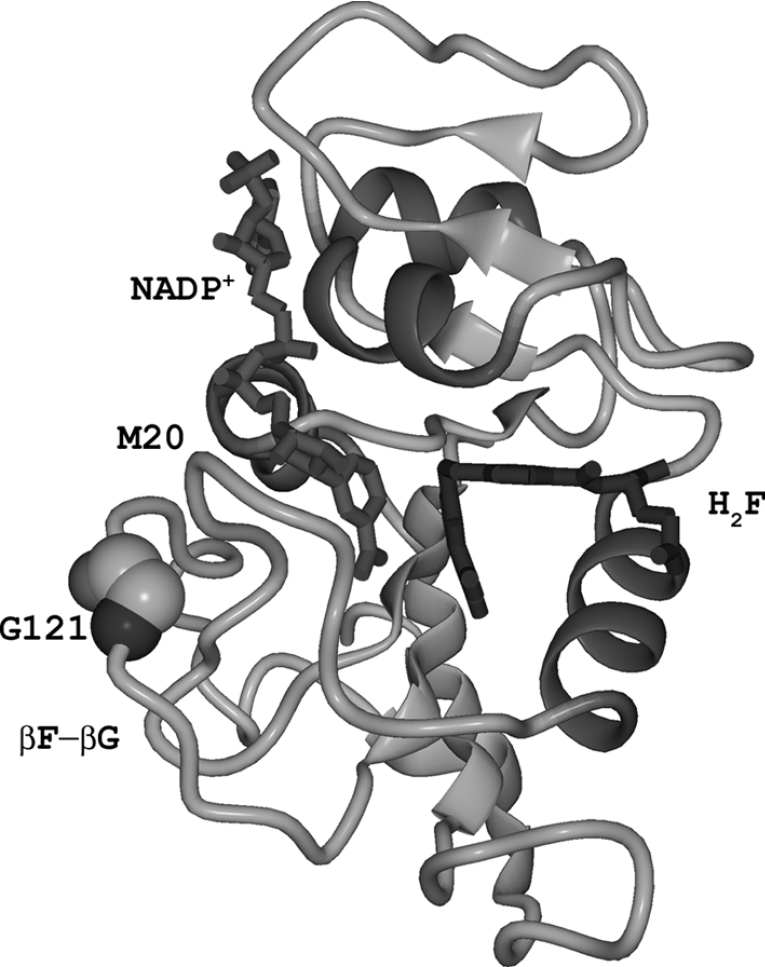
DHFR (dihydrofolate reductase) has long served as a paradigm for the study of issues relating to enzyme structure, dynamics and catalysis. DHFR catalyses the reduction of H₂F (7,8-dihydrofolate) to H₄F (5,6,7,8-tetrahydrofolate) with the concurrent oxidation of NADPH. DHFR is essential for maintaining intracellular levels of H₄F, a cofactor involved in the biosynthesis of several amino acids, purines and thymidylate. DHFR from Escherichia coli is a monomeric enzyme comprising an eight-stranded β-sheet and four α-helices connected by flexible loop regions (Figure 1). The M20, βF-βG and βG-βH loops have been implicated in catalysis [20]. In the reactive ternary complex, when both H₂F and NADPH are bound, the M20 loop adopts the closed conformation, which is stabilized through hydrogen bonds between residues in the M20 and the βF-βG loops [21]. The backbone atoms of the βF-βG loop display high dynamic mobility in NMR relaxation experiments, which has been interpreted to suggest a connection between the dynamic properties and the catalytic behaviour of DHFR [22–25].

Figure 1. Structure of DHFR from E. coli bound to NADP⁺ and H₂F.

The PDB file 1RA2 [21] was used to generate the diagram. The βF-βG and the M20 loops as well as the position of the catalytically important loop residue Gly¹²¹ are indicated.

The complete kinetic scheme for DHFR from E. coli has been determined [26,27]. The reaction rate is strongly dependent on the pH of the solution. The chemical step, in which the pro-R hydrogen is transferred from C-4 of NADPH to C-6 of H₂F and N-5 of the substrate is protonated, is characterized by a single pK_a of approx. 6.5 with a rate variation of almost two orders of magnitude. This pK_a can most likely be attributed to protonation of the substrate in the ternary enzyme complex [28]. At physiological pH, the overall rate of the conversion of H₂F into H₄F is limited by product release, while the chemical step is fast and essentially irreversible [26]. However, at pH values of 9.5 and above, hydrogen transfer is much slower and fully rate-determining.

Several computational studies using combined QM/MM (quantum mechanical and molecular mechanical) and free-energy perturbation approaches have shed some light on the mechanism of the hydride transfer step in DHFR catalysis [28–35]. QM/MM simulations and genomic sequence analysis identified a network of hydrogen bonds and van der Waals interactions in DHFR from E. coli between the surface βF-βG loop and the active site that may influence protein dynamics and promote catalysis [18,36]. Replacement of Gly¹²¹, a highly mobile residue located in the middle of the βF-βG loop over 19 Å (1 Å=0.1 nm) from the active site (Figure 1), with valine or leucine slowed the hydride transfer rate dramatically and weakened binding of NADPH [37]. Experimental and theoretical results suggested that this reduction in the rate of hydride transfer was due to significant differences in the stability of the tertiary structural elements surrounding the site of the mutation [22,33,38].

Two previous experimental studies suggested a coupling between protein dynamics and DHFR catalysis. Pre-steady-state measurements with DHFR from Thermotoga maritima indicated that protein fluctuations were coupled with hydride transfer which at low temperature displayed a significant contribution from tunnelling [8]. Steady-state experiments at the non-physiological pH value of 9, where hydride transfer is largely rate-determining for the E. coli enzyme, suggested a relatively rigid active site geometry and hydride transfer by extensive tunnelling, modulated by passive dynamics [2].

Here, we report measurements of the hydride transfer catalysed by DHFR from E. coli and the G121V-DHFR mutant, in which valine replaced the loop residue Gly¹²¹. While hydride transfer was slowed by almost two orders of magnitude in the mutant at physiological pH, hydrogen transfer was actively coupled with the environment for both proteins. The mechanism by which hydrogen transfer coupled with the environment was dependent on pH.

MATERIALS AND METHODS

Substrates and cofactors

H₂F was prepared by dithionite reduction of folate (Sigma) as described previously [39]. NADPH was purchased from Sigma. NADPD ((4R)-[²H]NADPH) was prepared by reduction of NADP⁺ (Sigma) using the NADP⁺-dependent alcohol dehydrogenase from Thermoanaerobium brokii (Sigma) and purified by anion-exchange chromatography on Mono Q™ HR 5/5 (Amersham Biosciences). NADPH and NADPD concentrations were determined spectrophotometrically using a molar absorption coefficient (ϵ) at 339 nm of 6200 M⁻¹·cm⁻¹. Similarly, the concentration of H₂F was measured assuming an ϵ of 28000 M⁻¹·cm⁻¹ at 282 nm for pH 7.4.

Protein purification

BL21(DE3) Star (Stratagene) cells were used for the production of DHFR from E. coli and its G121V mutant from a pET11c derived plasmid (Novagen) containing the respective coding regions essentially as described in [38]. Cells were grown in LB (Luria–Bertani) medium containing 0.27 mM ampicillin at 37 °C to an optical density at 600 nm of 0.6. Expression was induced by the addition of isopropyl β-thiogalactoside to a final concentration of 0.4 mM. Cells were harvested by centrifugation and resuspended in lysis buffer [25 mM potassium phosphate, pH 7.0, 0.5 M NaCl, 1 mM EDTA, 10%, v/v, glycerol and 1 mM DTT (dithiothreitol)]. The suspension was sonicated for 5 min on ice and centrifuged at 50000 g for 45 min. The supernatant was applied to a methotrexate column (10 ml; Sigma) pre-equilibrated with lysis buffer. The resin was extensively washed (∼300 ml) with the same buffer and elution of bound protein was achieved with 100 mM sodium borate (pH 8.3), 0.5 M NaCl, 10% glycerol and 3 mM folic acid. The eluted protein was dialysed extensively against 10 mM potassium phosphate (pH 7.0) containing 1 mM DTT. The dialysate was applied to a DEAE-Sepharose column (20 ml; GE Healthcare) previously equilibrated with 10 mM potassium phosphate (pH 7.0) containing 1 mM DTT and 5 mM EDTA. The bound protein was eluted with a gradient from 0 to 1 M NaCl in potassium phosphate (pH 7.0), 5 mM EDTA and 1 mM DTT and dialysed to remove salt. The protein concentrations were measured spectrophotometrically assuming an ϵ of 31100 M⁻¹·cm⁻¹ at 280 nm and by titration with methotrexate.

Pre-steady-state kinetic measurements

Pre-steady-state kinetic experiments were performed on an Applied Photophysics stopped-flow spectrophotometer essentially as described before [8]. Hydride transfer rates were measured following the fluorescence resonance energy transfer from the protein to reduced NADPH in potassium phosphate for optimal pH stability over the temperature range. The sample was excited at 292 nm and the emission was measured using an output filter with a cut-off at 400 nm. In a typical experiment for DHFR, the enzyme (40 μM, final concentrations) was preincubated with NADPH or NADPD (20 μM) in 100 mM potassium phosphate (pH 7.0) and 100 mM NaCl for at least 15 min to avoid hysteresis. The reaction was started by rapidly mixing with H₂F (200 μM) in the same buffer. For G121V-DHFR, the enzyme (20 μM) was preincubated with NADPH or NADPD (10 μM) and the experiments were run as above. The hydride transfer rates did not change when the concentration of NADPH was reduced to 5 μM or doubled to 20 μM.

Steady-state kinetic measurements

All steady-state kinetic experiments were performed in MTEN buffer (50 mM MES buffer, 25 mM Tris, 25 mM ethanolamine and 100 mM NaCl) at pH 9.5. The pH was carefully adjusted at the experimental temperature with the relevant calibration buffers [borate (pH 10; Fisher Chemicals) and phosphate (pH 7; Fisher Chemicals)] at that temperature. DHFR (50 nM) was preincubated with NADPH/NADPD (50 μM) for 10 min at the experimental temperature prior to the addition of excess H₂F (100 μM) to initiate the reaction. The steady-state rate was determined from the linear decrease in the absorbance of the reduced cofactor at 340 nm with time using a molar absorbance change for the DHFR reaction of 11800 M⁻¹·cm⁻¹ [40]. Each data point was measured at least six times.

RESULTS AND DISCUSSION

Temperature dependence of hydride transfer and KIEs (kinetic isotope effects) for DHFR catalysis

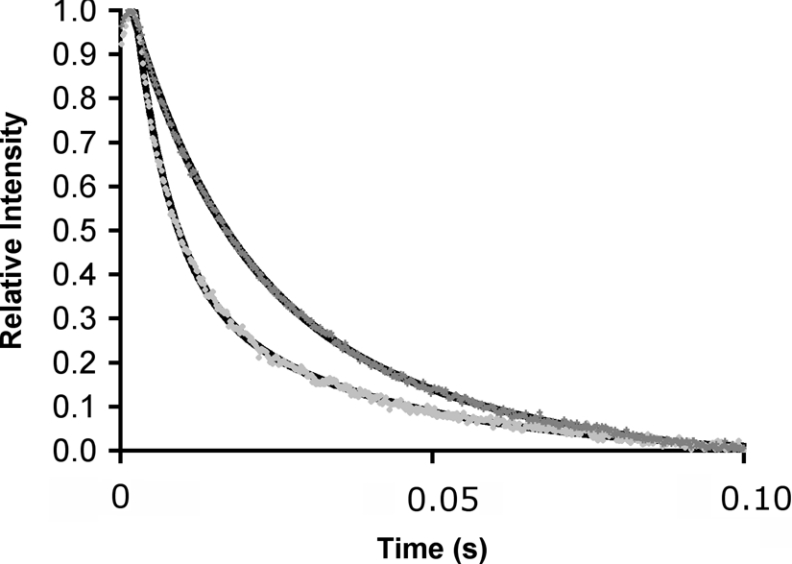
The rate of hydride transfer (k_H) from NADPH to H₂F was measured at pH 7 and 25 °C in single-turnover experiments by monitoring fluorescence resonance energy transfer from DHFR to the reduced cofactor in the presence of excess enzyme [26,37]. The decrease of the fluorescence intensity was best described by a double exponential (Figure 2). The rate constant of the slow step (∼6.5 s⁻¹) was independent of the concentration of NADPH and did not depend on whether NADPH or NADPD was used as the cofactor. It most likely represented the slow release of cofactor and/or product. At 25 °C, the rapid decrease in fluorescence intensity preceding this slow step occurred with a first-order rate constant of 203.7±7.4 s⁻¹ (see Supplementary Table 1 at http://www.BiochemJ.org/bj/394/bj3940259add.htm) in good agreement with previously published values of 220 s⁻¹ [26,37] and 222.8±1.3 s⁻¹ [8]. The slight variation is most likely a consequence of the different buffers used in these experiments. In the experiments reported here potassium phosphate was used because of its good pH stability over wide ranges of temperature. When NADPD was used as the cofactor, the rate constant was reduced to 75.1±5.4 s⁻¹, resulting in a KIE of 2.7±0.2. This value was identical with the value of 2.8 that has been predicted computationally [31] and the published experimental value of 2.9±0.2 at ambient temperature [41].

Figure 2. Fluorescence energy transfer during DHFR catalysis.

Measurement of the rate of H- (light grey dots) and D- (dark grey) transfer catalysed by DHFR in a single turnover experiment measured by stopped-flow fluorescence resonance energy transfer from DHFR to the reduced cofactor at 25 °C. The relative intensity of fluorescence above 400 nm was measured after excitation at 292 nm. The fits to a double-exponential model for decreasing fluorescence intensity are also indicated. DHFR was preincubated with NADPH or NADPD and the reaction started through the addition of H₂F. Final concentrations were: DHFR, 40 μM; reduced cofactor, 20 μM and H₂F, 200 μM. The dead time of the experiments was approx. 0.002 s.

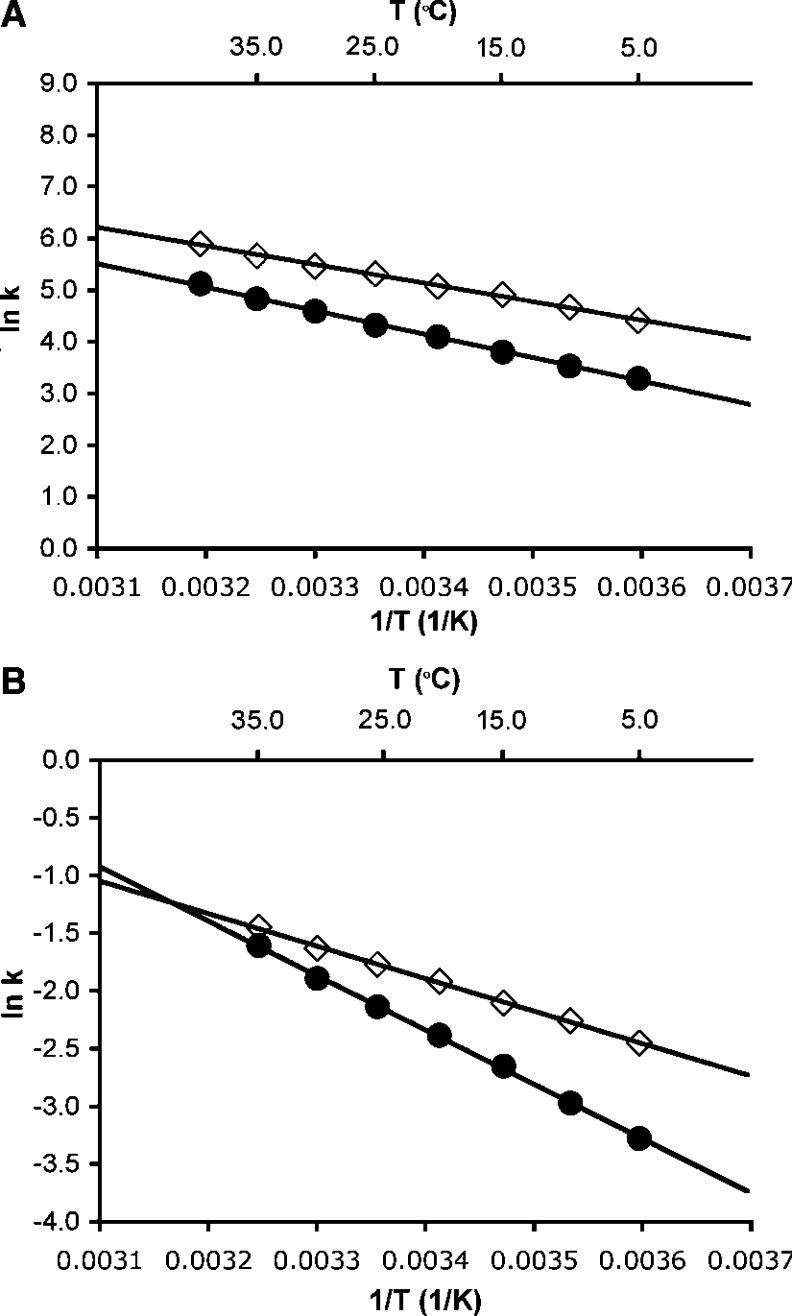
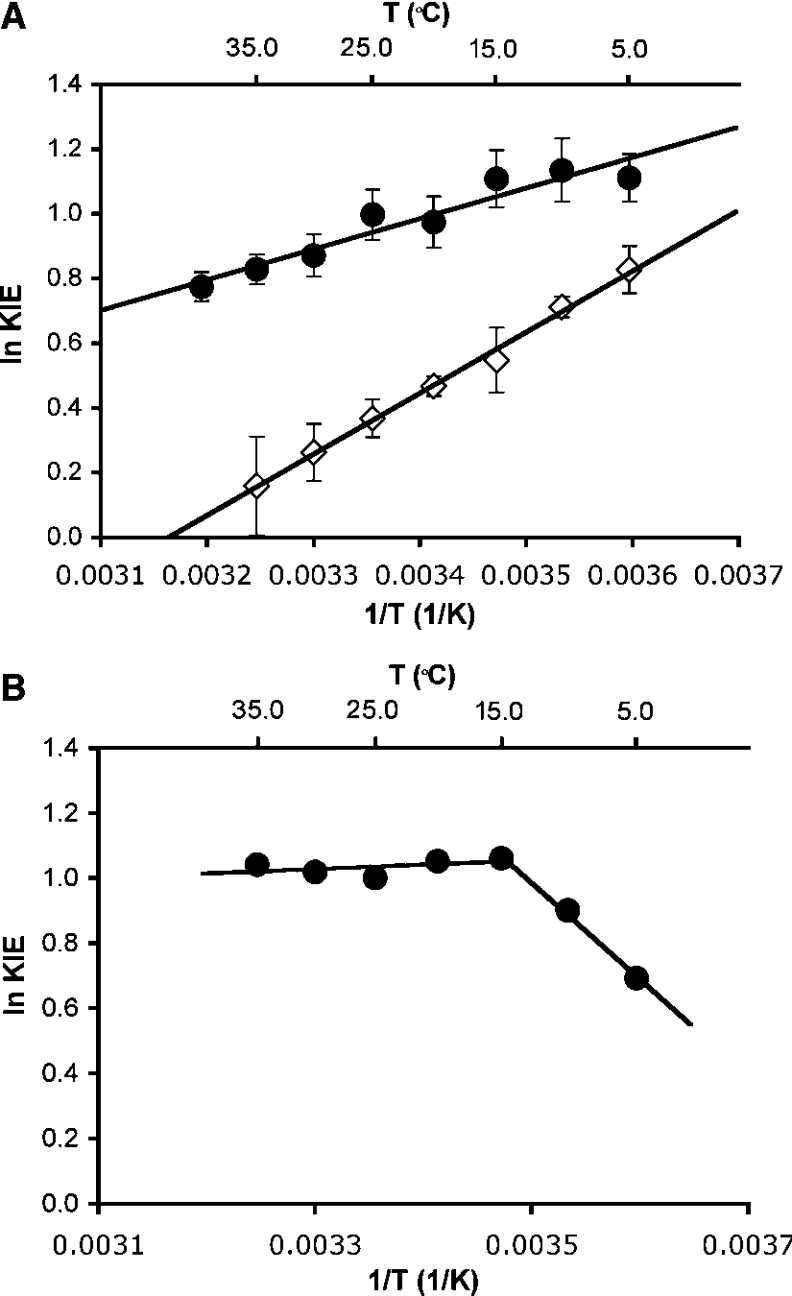
To evaluate whether hydride transfer during catalysis by DHFR was coupled to protein motions, the rate of the chemical step was measured at pH 7.0 as a function of the temperature between 5 and 40 °C for both ¹H (H)- and ²H (D)-transfer. The temperature dependence of the rates was fitted to the empirical Arrhenius equation (ln k=ln A−E_A/RT, where k is a first-order rate constant, A is the pre-exponential factor and E_A is the experimental activation energy) to obtain the activation energy and the pre-exponential factor (Figure 3). The reaction rates showed a relatively strong dependence on the temperature, resulting in activation energies of E_A^H of 29.9±0.6 kJ·mol⁻¹ and E_A^D of 37.7±0.7 kJ·mol⁻¹, leading to an inverse pre-exponential factor A_H/A_D of 0.108±0.04 (A_H=3.3±0.8×10⁷ s⁻¹; A_D=3.07±0.81×10⁸ s⁻¹). The activation energy for H-transfer reported here was very similar to that measured previously in a different buffer but under identical conditions otherwise (28.2±0.9 kJ·mol⁻¹) [8]. The relatively large difference in the activation energies for H- and D-transfer led to a temperature dependence of the primary KIEs (Figure 4). The KIE varied from 3.0±0.2 at 5 °C to 2.2±0.2 at 40 °C. The inverse ratio of the pre-exponential factors, which was well below the lower limit for the semi-classically calculated value of 0.71 [2,42], suggested a contribution from quantum mechanical tunnelling. Within a model of tunnelling through a rigid barrier, the temperature-dependent KIEs together with the observed values for A_H/A_D and E_A^H/D suggest a moderate amount of tunnelling [43]. Two recent computational studies of hydrogen transfer during catalysis by DHFR from E. coli suggested that the barrier for hydrogen transfer was significantly lowered through the inclusion of quantum mechanical effects [31,36]. Garcia-Viloca et al. [31] obtained an overall quantum mechanical correction of 13.4 kJ·mol⁻¹ to the classical activation energy for hydrogen transfer. Most of this correction was attributed to quantization of nuclear vibrations, while only 2.9 kJ·mol⁻¹ derived from hydrogen tunnelling. From the inverse ratio of the pre-exponential factors measured here, a previously proposed static model would predict moderate hydrogen tunnelling [43,44]. However, within the formalism of this model, elevated KIEs would be predicted in contrast with the rather small values measured here. The hydride transfer reaction catalysed by DHFR can therefore only be described adequately if protein motions coupled with hydrogen transfer are taken into account. Several theoretical approaches to hydrogen transfer models have been proposed that treat the hydrogen co-ordinates as fully quantum mechanical and incorporate various degrees of heavy atom motions to modulate the tunnelling barrier [16,17,45–47]. In one such model, a distinction was made between motions that actively modulate the tunnelling barrier and passive motions that merely help bring the substrates into reactive configurations (reviewed in [5,13]). This model predicts that when active dynamic motions are dominant and generate a temperature-dependent tunnelling distance, the KIEs become so temperature-dependent that the ratio of the pre-exponential factors is inverse. The experimentally observed inverse A_H/A_D and the temperature dependence of the KIEs suggest that at pH 7.0, DHFR actively modulates the tunnelling distance and hence the reaction rates [48]. Such active motions result in temperature-dependent KIEs and an inverse ratio of the pre-exponential factors, because the ideal tunnelling distance is different for the two isotopes. Such actively promoted tunnelling has been called rate-promoting vibrations [14,49,50], environmentally coupled tunnelling [13,43], and vibrationally enhanced ground state tunnelling [51]. The results reported here may also support the recent proposal of a correlation of changes in structural characteristics within DHFR from E. coli along the reaction pathway of hydrogen transfer through a network of hydrogen bonds and van der Waals interactions spanning the entire enzyme [18].

Figure 3. Arrhenius plots for H- and D-transfer during DHFR and G121V-DHFR catalysis at pH 7.0.

Temperature dependence of the H- (◇) and D-transfer (●) rate constants for the reactions catalysed by DHFR (A) and G121V-DHFR (B) is shown. Each data point is the average of at least six measurements; the error bars are obscured by the symbols. Fitting the average rate value for every temperature to the Arrhenius equation yields the following parameters: DHFR, E_A^H=29.9±0.6 kJ·mol⁻¹, A_H=3.3±0.8×10⁷ s⁻¹ and E_A^D=37.7±0.6 kJ·mol⁻¹, A_D=3.07±0.80×10⁸ s⁻¹; G121V-DHFR, E_A^H=23.3±0.3 kJ·mol⁻¹, A_H=2.2±0.2×10³ s⁻¹ and E_A^D=39.0±0.6 kJ·mol⁻¹, A_D=8.1±2.0×10⁵ s⁻¹.

Figure 4. Temperature dependence of the KIEs for H- and D-transfer from NADPH/NADPD to H₂F.

(A) Results from pre-steady-state measurements at pH 7.0 for catalysis by DHFR (●) and G121V-DHFR (◇). The best fit through the data yielded ΔE_A^H/D of 7.83±0.98 kJ·mol⁻¹ and A_H/A_D of 0.109±0.043 for DHFR and ΔE_A^H/D of 15.83±0.44 kJ·mol⁻¹ and A_H/A_D of 0.0024±0.0004 for G121V-DHFR. (B) Steady-state measurements for DHFR catalysis at pH 9.0 and 5.0. The best fit through the data between 15 and 35 °C is indicated and yields ΔE_A^H/D of 1.11±0.79 kJ·mol⁻¹ and A_H/A_D of 1.81±0.19.

Steady-state kinetics of DHFR at pH 9.5

In a previous study, the temperature dependence of the deuterium and tritium isotope effects at pH 9.0, which was measured under steady-state conditions, also revealed environmentally coupled hydrogen transfer [2]. However, in contrast with the results presented here, for H-transfer at pH 7.0, the KIEs were independent of temperature. The rates for hydride transfer in DHFR catalysis have been shown to decrease steeply with increasing pH [26]. However, the rate of product release, which is rate-determining at physiological pH, is pH-independent; hence hydride transfer becomes rate limiting at elevated pH and, at pH 9.5 and above, the steady-state rate reflects the rate of the chemical step only [2,26]. Since at pH 9.0 the chemical step is not fully rate-determining, hydride transfer rates were measured under steady-state conditions at pH 9.5 to exclude kinetic complexity at pH 9.0 as a basis for the observed difference in the temperature dependence of transfer at elevated and physiological pH. We have therefore determined the temperature dependence of the steady-state turnover rates for the reduction of H₂F with NADPH and NADPD during DHFR catalysis at pH 9.5 [26] from the decrease in the absorbance at 340 nm due to the oxidation of the cofactor. At 25 °C, the rates for H- and D-transfer were 0.927±0.012 and 0.341±0.008 s⁻¹, resulting in a KIE of 2.72±0.1 (see Supplementary Table 2 at http://www.BiochemJ.org/bj/394/bj3940259addd.htm). The KIE measured here was essentially identical to that calculated in a previous study [KIE (H/D)=2.92±0.076] from the measured H/T and D/T KIEs at pH 9.0 [2].

Within the temperature range of 15 and 35 °C the KIEs remained constant within the error of the experiment (Figure 4), while below 15 °C the KIEs decreased sharply. Fitting the KIEs between 15 and 35 °C to the Arrhenius equation resulted in a very small difference in the activation energy for H- and D-transfer (ΔE_A^H/D=1.11±0.79 kJ·mol⁻¹) and an isotope effect for the pre-exponential factor A_H/A_D of 1.81±0.19, larger than the upper semi-classical limit of 1.41 [42]. A similar temperature dependence and enhanced KIE for the pre-exponential factors had been observed previously for the H/T and D/T KIEs at pH 9.0 [2]. A larger value for A_H/A_D of 4.0±1.5 has been reported previously in steady-state experiments at pH 9.0 [2]. While an A_H/A_D ratio outside the semi-classical range has widely been accepted as an indication for quantum mechanical tunnelling, a recent computational study resulted in a ratio of pre-exponential factors of 1.9 [52], identical within error with the results reported here. Interestingly, a larger value was obtained when the tunnelling contributions were omitted.

The temperature-independent KIEs at elevated pH were in sharp contrast with the strong temperature dependence of the KIEs at pH 7 and suggested a relatively rigid active site configuration from which hydrogen transfer occurs with a contribution from environmentally coupled hydrogen tunnelling. Within the model linking catalysis and dynamics proposed by Klinman and co-workers [43], the elevated value for A_H/A_D together with the temperature-independent KIEs suggested contributions from passive dynamics that do not actively modulate the tunnelling distance. This is in sharp contrast with the behaviour of DHFR at physiological pH, where hydrogen transfer is facilitated by active modulation of the tunnelling barrier. It is interesting to point out in this context that a recent computational study of DHFR catalysis revealed a small but significant temperature variation of the KIEs as a consequence of two competing temperature effects [53]. It is perhaps not surprising that in such a system the temperature dependence varies with reaction conditions.

DHFR has evolved an active site structure that is organized to support hydrogen tunnelling and to use active dynamics to promote hydrogen transfer at physiological pH. Relatively small increases in the pH of the solution, however, lead to a stiffening of the active site that no longer allows DHFR to actively promote hydrogen transfer, resulting in a reduction of the reaction rate by more than one order of magnitude. Interestingly, at pH 9.5, DHFR displays a temperature dependence of the reaction rates similar to that of the structurally more rigid DHFR from the thermophilic bacterium T. maritima [8]. Both enzymes appear to rely on passive motions only to generate active site configurations conducive to hydrogen transfer. In addition, the hydride transfer rates for the thermophilic DHFR at pH 7 and for the mesophilc DHFR at pH 9.5 were similar in the experimentally accessible temperature range [8,39]. These observations may suggest an evolutionary pattern in which catalysis progressed from a relatively rigid active site structure of DHFR from the ancient thermophile T. maritima to a more flexible and kinetically more efficient structure in E. coli that actively promotes hydrogen transfer at physiological pH.

Temperature dependence of hydride transfer and KIEs for catalysis by G121V-DHFR

Although residue 121 in the βF-βG loop of DHFR is on the exterior of the protein and approx. 19 Å from the centre of the enzyme, experimental studies have shown that mutations of Gly¹²¹ can reduce the rate of hydride transfer by up to 163-fold [20,37]. Together with NMR and computational studies, these results have been interpreted as evidence for the existence of a network of coupled dynamic motions that include residues in exterior loops of DHFR and promote hydride transfer [18]. It has been postulated that mutation of Gly¹²¹ disrupts this network of coupled motions leading to the observed reduction in the reaction rate and altered dynamic properties of the enzyme [52]. The rate of the hydride transfer from NADPH to H₂F catalysed by G121V-DHFR was measured at pH 7.0 in pre-steady-state experiments. The decrease in the fluorescence intensity was best described by a double exponential. A first event was observed that occurred with a rate constant of approx. 3.5 s⁻¹ at 25 °C and did not show a KIE when NADPD replaced NADPH. This process had previously been interpreted as a conformational change associated with a rearrangement of the reduced nicotinamide ring into the enzyme's active site [20]. Surprisingly, this fast isotopically insensitive step had not been observed under similar conditions in a previous study of G121V-DHFR catalysis, perhaps due to the different buffers used in the two studies [37]. This initial step was followed by a slow decrease in the fluorescence intensity, the rate of which did not change when the concentration of NADPH was varied. The slow step was therefore most likely due to the oxidation of the cofactor that occurred with a first-order rate constant of 0.171±0.004 s⁻¹ at 25 °C (see Supplementary Table 3 at http://www.BiochemJ.org/bj/394/bj3940259add.htm). This rate constant is somewhat lower than that published previously [37], most likely as a consequence of the different reaction conditions. In the present study, potassium phosphate, which shows little variation of pH with changing temperature, was used rather than the amine-based MTEN buffer. At 25 °C, a KIE of 1.450±0.042 was measured when NADPD was used instead of NADPH.

Similar to the wild-type enzyme, a relatively strong temperature dependence of the hydride transfer rates and the KIEs was observed between 5 and 35 °C (Figures 3 and 4). The rates increased almost 3-fold in the temperature range leading to activation energies of E_A^H of 23.3±0.3 and E_A^D of 39.0±0.6 kJ·mol⁻¹ for H- and D-transfer respectively. The activation energy for H-transfer catalysed by G121V-DHFR was smaller than that measured for the wild-type, indicating that the reduced catalytic efficiency of the mutant was a consequence of a smaller pre-exponential factor (A_H=2.2±0.2×10³ s⁻¹; A_D=8.1±2.0×10⁵ s⁻¹). The difference in activation energies (ΔE_A=E_A^H−E_A^D) of −15.7 kJ·mol⁻¹ was twice that observed for wild-type DHFR, leading to more strongly inverse pre-exponential factors A_H/A_D of 0.0025±0.0007. These data are consistent with a model in which the reaction occurred with a significant contribution from quantum mechanical tunnelling coupled with active dynamic motions.

The results presented here indicate that, while replacing residue 121 in DHFR with valine leads to a significant reduction in the rate of hydrogen transfer, the general mechanism by which the reaction is coupled with the environment is unaltered, at least in a qualitative sense. Molecular dynamics, CD and fluorescence experiments had suggested that the reduced catalytic efficiency of the mutant may arise from structural effects on the overall fold of the protein [38]. NMR experiments indicated that in G121VDHFR the closed conformation, in which hydrogen transfer occurs in the wild-type, was destabilized [22]. Geometric constraints imposed by the bulky isopropyl group in G121V-DHFR may be transmitted to the active site to produce a lower number of active site configurations favourable for hydride transfer. In agreement with this explanation, a computational study by Thorpe and Brooks [33] suggested that H₂F and NADPH populate preferentially a region of configuration space of DHFR that is conducive to the reaction, while substrate and cofactor become trapped in unproductive configurations in G121V-DHFR. The results presented here indicate, however, that once NADPH and H₂F are bound in the reactive configuration, both mutant and wild-type actively promote hydride transfer.

The reduced catalytic efficiency of G121V-DHFR was mainly a consequence of the significantly reduced pre-exponential factors. The Eyring interpretation of the temperature dependence of the reaction rates relates activation energy and pre-exponential factor to activation enthalpy and entropy, Δη‡ and ΔS‡. The activation enthalpies and entropies for hydride transfer by DHFR and G121V-DHFR were obtained by fitting the temperature dependence of the reaction rates to the Eyring equation [k/T=k_B/h exp (ΔS‡/R) exp(−ΔH‡/RT), where k is a first-order constant, k_B the Boltzmann constant and h the Planck constant; R is the universal gas constant]. While the activation enthalpy favoured hydride transfer by G121V-DHFR by 6.3±0.2 kJ·mol⁻¹, the activation entropy strongly favoured the reaction catalysed by the wild-type enzyme. An increase in the activation entropy (−TΔS‡) for the mutant indicated that a significantly higher molecular reorganization was required to reach the transition state in G121V-DHFR (TΔS‡_G121V=−56.4±0.8 kJ·mol⁻¹) than in the wild type enzyme (TΔS‡_WT=−32.9±0.8 kJ·mol⁻¹).

In summary, our results suggest that the mechanism by which hydrogen transfer in DHFR is coupled with protein fluctuations, depends on the pH of the environment. Under physiological conditions, DHFR increases the reaction rate through optimization of the coupling of environmental dynamics with quantum mechanical tunnelling. Only relatively small changes in pH lead to a stiffening of the active site and a loss of active promotion of hydrogen transfer. On the other hand, the mechanism is relatively robust towards mutation of residue 121, the identity of which is known to be critical for efficient hydride transfer. Like in the wild-type enzyme, the tunnelling distance is modulated by active dynamics in the kinetically compromised mutant G121V-DHFR. The reduced hydride transfer rates of this mutant are therefore not the consequence of altered dynamics, but most likely of geometric constraints [33,38] that lead to a higher entropic cost for the formation of active site conformations conducive to the reaction.