Stereochemistry and Position-Dependent Effects of Carcinogens on TATA/TBP Binding

Abstract

The TATA-box binding protein (TBP) is required by eukaryotic RNA polymerases to bind to the TATA box, an eight-basepair DNA promoter element, to initiate transcription. Carcinogen adducts that bind to the TATA box can hamper this important process. Benzo[a]pyrene (BP) is a representative chemical carcinogen that can be metabolically converted to highly reactive benzo[a]pyrene diol epoxides (BPDE), which in turn can form chemically stereoisomeric BP-DNA adducts. Depending on the TATA-bound adduct's location and stereochemistry, TATA/TBP binding can be decreased or increased. Our previous study interpreted the location-dependent effect in terms of conformational freedom and major-groove space available to BP. Here we further explore specific structural changes of the TATA/TBP complex to help interpret the stereochemical effect in terms of the flexibility of the TATA bases that frame the intercalated adduct. Thermodynamic analyses using molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) yield large standard deviations, which make the computed binding free energies the same within the error bars and point to current limitations of free energy calculations of large and highly charged systems like DNA/protein complexes.

INTRODUCTION

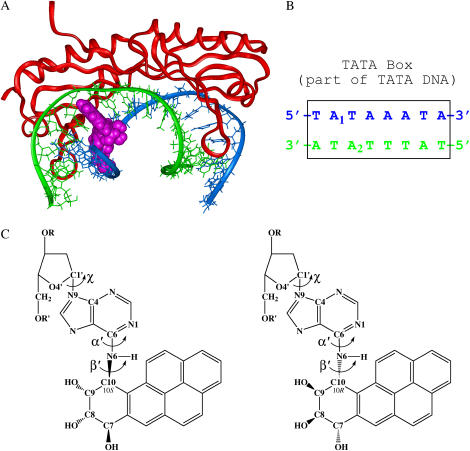
Transcription in eukaryotes involves a large range of RNA polymerases, transcription factors, and other agents (1–3). The TATA-box binding protein (TBP), a component of transcription factor II D, is required by all eukaryotic RNA polymerases for correct initiation of transcription of ribosomal, messenger, small nuclear, and transfer RNAs (4). TBP has a phylogenically conserved 180-residue core segment, which contains two imperfect direct repeats and supports the protein's biological activities. Upon binding to the TATA box—an A/T-rich 8-basepair (bp) DNA in the DNA promoter region (5)—TBP causes local compaction of the TATA box, unwinding, and severe bending, which in turn results in a widened minor groove and a compressed major groove (6) (see Fig. 1). Specifically, TBP's two phenylalanines insert into the first and last base steps of the TATA box, kinking the DNA locally by 52° and 39°, respectively (6). The kinks are accompanied by another pair of phenylalanines, which form extensive van der Waals contacts with the second and seventh basepairs of the TATA box.

FIGURE 1.

TATA/TBP/BP complex. (A) Complex of TBP (red) bound to a BP-modified 16-bp TATA DNA (blue and green) after a 2.32-ns molecular dynamics simulation. The BP-adenine adduct is pink (spacefilling view) and is positioned at site A₁. (B) TATA box, in the center of the TATA DNA, is shown with the A₁ and A₂ BP-adenine adduct locations. (C) Stereoisomeric BP-adenine adducts: 10S(+)-trans-anti-(BP)-N⁶-dA (left) and 10R(−)-trans-anti-(BP)-N⁶-dA (right).

Our previous molecular dynamics (MD) study (7) showed that 12 hydrogen bonds form between TBP and the central two basepairs of the TATA box and another seven between TBP and the backbone of the rest of the TATA box residues (including two strong interactions at the two ends). Ingeniously, these hydrogen bonds and extensive hydrophobic interactions stabilize the complex's kinks as well as the TATA/TBP binding (see hydrogen bond contribution in (8)), therefore allowing the normal Watson-Crick basepairings to be maintained, despite the severely bent TATA DNA.

The TATA/TBP binding and transcription initiation can be affected if the TATA box is damaged by chemical carcinogens. For example, DNA is often affected by benzo[a]pyrene (BP), a chemical carcinogen in the class of polycyclic aromatic hydrocarbons that is a ubiquitous component of environmental pollutants, like automobile exhaust, tobacco smoke, and food contaminants (9–11). BP can be metabolically activated to highly reactive benzo[a]pyrene diol epoxide (BPDE) molecules, which in turn can form BP-DNA adducts (12). If unrepaired by cellular DNA repairing machinery, these adducts can lead to transcription blocking (13,14) or to carcinogenic mutations if bypassed (9,15–19).

BPDE has two enantiomers (Fig. 1): (+)-(7R,8S,9S,10R)-7,8-dihydroxy-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene and (−)-(7S,8R,9R,10S)-7,8-dihydroxy-9,10-epoxy-7,8,9,10-tetrahydrobenzo[a]pyrene. They can react with adenines in DNA to form stereoisomeric 10S(+) and 10R(−)-trans-anti-(BP)−N⁶-dA covalent DNA adducts, respectively (9,20–22). High-resolution NMR solution studies (23–26) show that BP has conformational preferences in these two adducts: it is classically intercalated between DNA basepairs, instead of being exposed in the solvent-accessible major or minor groove of the DNA duplex (thus, the hydrophobic pyrenyl moiety of BP can be buried within the duplex). BP resides on the 3′-side of the modified adenine in the 10S(+) adduct and on the 5′-side in the 10R(−) adduct.

An experimental study by Rechkoblit and co-workers (27) has shown that the TATA/TBP binding affinity can be decreased or slightly increased (Table 1) by the BP-adenine adducts in the TATA box, depending on the adduct location (A₁ or A₂) and stereochemistry (10S(+) or 10R(−)), as shown in Fig. 1. The combination of the adduct location and stereochemistry leads to four systems studied by the experimental work: 10S(+)-trans-(A₁), 10R(−)-trans-(A₁), 10S(+)-trans-(A₂), and 10R(−)-trans-(A₂). The first two systems (BP at A₁) were found to increase slightly the TATA/TBP binding affinity, while the other two (BP at A₂) decrease the binding affinity (Table 1). The adduct stereochemistry plays a minor role for changing the binding affinity; the 10R(−) stereoisomer at both locations shows stronger TATA/TBP binding affinity than the 10S(+) stereoisomer.

TABLE 1.

Experimental equilibrium constants K° and binding free energies ΔG° of TBP bound to BP-modified and unmodified TATA DNA duplexes

TATA DNA	K°	ΔG° (kcal/mol)	ΔΔG° (kcal/mol)
Unmodified	1.18 × 108	−10.23	0.00
10S(+)-trans-(A1)	1.33 × 108	−10.30	−0.07
10R(−)-trans-(A1)	1.82 × 108	−10.47	−0.24
10S(+)-trans-(A2)	5.71 × 107	−9.84	0.39
10R(−)-trans-(A2)	8.00 × 107	−10.02	0.21

K° and ΔG° are derived from Rechkoblit et al. (27). ΔΔG° is the relative binding free energy of a BP-modified system compared to the unmodified one. Experimental temperature is 277.15 K.

Our previous MD simulation study (7) interpreted the effect of the adduct location on TATA/TBP binding in terms of the conformational freedom and major-groove space available to BP due to the hydrogen bonds and phenylalanine insertions at the TATA/TBP interface. That is, we found that BP at A₁ can easily adopt an intercalated orientation between DNA bases or a major-groove orientation in the DNA major groove without much distortion of the TATA or TBP backbone; on the other hand, the A₂ location does not allow BP to easily adopt either orientation without distorting the backbones.

Here we further study the effect of the adduct location on TATA/TBP binding by examining the adduct-dependent structural changes of the TATA/TBP complex. We also interpret the effect of the adduct stereochemistry on TATA/TBP binding. To derive the thermodynamic effects of BP modifications and to correlate the TATA/TBP complex's structural changes with energetics, we perform free energy analyses on all systems.

METHODS

Initial structures

With InsightII (Accelrys, San Diego, CA), we construct the initial TATA/TBP/BP structure by combining the crystal structure of TATA/TBP complex (Protein DataBank ID: 1CDW) (6) and the NMR structure of a BP-modified DNA structure (PDB ID: 1AGU) (26). The TATA DNA has the same length (16 bp) as that in the 1CDW PDB structure, but the initial structure is remodeled to match the experimental sequence (see below; the TATA box is underlined). Sequence remodeling is conducted on the DNA bases only (not on sugars or backbone) and causes only one contact change between the DNA and TBP, as shown in Appendix S1 in the Supplementary Material. The remodeled structure contains 32 DNA residues (#1–32) and 179 TBP residues (#33–211) with the BP covalently binding to the DNA.

For each combination of the adduct location (A₁ or A₂) and stereochemistry (10S(+) or 10R(−)), we determine the best orientation of the adduct in its TATA/TBP/BP complex structure based on its four low-energy domains (I, II, III, and IV; see Table 2) (28). These domains, defined by the three torsion angles in Fig. 1, account for the conformational preferences of the two stereoisomeric adducts: BP is classically intercalated and residing on the 3′-side of the modified adenine in the 10S(+) adduct and on the 5′-side in the 10R(−) stereoisomer. The best orientation we find produces the minimal steric collision between the adduct and the TATA/TBP complex.

TABLE 2.

Low-energy conformational domains of 10S(+) and 10R(−)-trans-anti-(BP)-N⁶-dA adducts

			β′ (°) (C6-N6-C10(BP)-C9(BP))
Domain	χ (°) (O4′-C1′-N9-C4)	α′ (°) (N1-C6-N6-C10(BP))	(+) adduct	(−) adduct
I	0–60	0 ± 35	−90 ± 40	90 ± 40
II	180–360	0 ± 35	−90 ± 40	90 ± 40
III	180–360	180 ± 35	−90 ± 40	90 ± 40
IV	0–60	180 ± 35	−90 ± 40	90 ± 40

A total of 11 initial structures of BP-modified TATA/TBP complexes are constructed; an unmodified complex is used as reference. In total, the 12 starting structures are listed in Table 3 (see also Fig. 3 and Table 5 of Zhang et al. (7)) along with their BP-adenine adduct's domains (I, II, III, or IV) and BP's orientations (intercalated between DNA bases or exposed to DNA major groove). The initial structure of free TBP is then taken from the PDB structure of the TBP-DNA complex, by removing the DNA, and then removing the crystal water molecules that are more than 10 Å away from TBP. The remaining water molecules are retained as they may be important for TBP. The initial structure of each free TATA DNA is taken from its corresponding TATA/TBP complex structure by removing TBP, counterions, and water molecules after the complex has been minimized with a water box and counterions (see Energy Minimization and MD Simulation, below). Therefore, totally 25 systems are simulated, including 12 TATA/TBP complexes, 12 free TATA DNA, and one free TBP (Table 3), as required for the thermodynamic analyses.

TABLE 3.

Simulated systems and simulation lengths

12 TATA/TBP complexes (2.32 ns each)	12 free TATA DNA (3.34 ns each)	1 free TBP (2.32 ns)
Unmodified	Unmodified
10S(+)-trans-(A1): II (int*)	10S(+)-trans-(A1): II
10S(+)-trans-(A1): III (MG†)	10S(+)-trans-(A1): III
10R(−)-trans-(A1): II (MG†)	10R(−)-trans-(A1): II
10R(−)-trans-(A1): III (int*)	10R(−)-trans-(A1): III
10R(−)-trans-(A1): IV (MG†)	10R(−)-trans-(A1): IV	Free TBP
10S(+)-trans-(A2): III (int*)	10S(+)-trans-(A2): III
10S(+)-trans-(A2): III-2‡ (MG†)	10S(+)-trans-(A2): III-2
10S(+)-trans-(A2): IV (int*)	10S(+)-trans-(A2): IV
10R(−)-trans-(A2): I (MG†)	10R(−)-trans-(A2): I
10R(−)-trans-(A2): III (int*)	10R(−)-trans-(A2): III
10R(−)-trans-(A2): IV (MG†)	10R(−)-trans-(A2): IV

^*BP is initially intercalated between DNA bases.

^†BP is initially exposed to DNA major groove.

^‡The second possible conformation of this adduct in domain III.

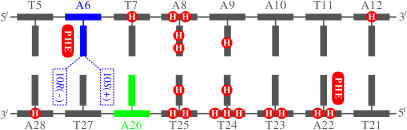
FIGURE 3.

Diagram of major TATA/TBP interactions and possible intercalation orientations of BP at A₁ (A6). The TATA box residues are shown in gray, with A6 (A₁) and A26 (A₂) highlighted in blue and green, respectively. Each DNA residue is represented by one horizontal bar as backbone and one vertical bar as base. The major TATA/TBP interactions include hydrogen bonds (white H letters on red background) and phenylalanine insertions (white PHE letters on red background). Possible intercalation orientations of BP at A₁ (A6) are shown with dashed boxes, and the stereochemistry of the BP-adenine adducts (10S(+), 10R(−)) are labeled in the dashed boxes. The relatively weak interactions (hydrophobic interactions and water-mediated hydrogen bonds) are not diagramed.

TABLE 5.

Binding free energies from triplet-trajectory analysis

System	G(TATA/TBP)	G(TATA)	ΔG	ΔΔG
Unmodified	−15176 ± 44	−7008 ± 23	−34 ± 58	0
10S(+)-trans-(A1): II	−15086 ± 41	−6942 ± 20	−10 ± 55	+24
III	−15108 ± 32	−6952 ± 21	−22 ± 49	+12
10R(−)-trans-(A1): II	−15087 ± 40	−6942 ± 20	−11 ± 54	+23
III	−15130 ± 40	−6957 ± 19	−39 ± 54	−5
IV	−15069 ± 41	−6929 ± 23	−6 ± 56	+28
10S(+)-trans-(A2): III	−15143 ± 34	−6971 ± 20	−38 ± 50	−4
III-2	−15123 ± 38	−6964 ± 22	−25 ± 53	+9
IV	−15103 ± 45	−6979 ± 21	10 ± 58	+44
10R(−)-trans-(A2): I	−15101 ± 40	−6930 ± 23	−37 ± 55	−3
III	−15131 ± 44	−6953 ± 22	−44 ± 58	−10
IV	−15110 ± 42	−6956 ± 19	−20 ± 55	14

G(TATA/TBP) is the free energy of a TATA/TBP complex, G(TATA) is the free energy of corresponding free TATA DNA, ΔG is the binding free energy between TBP and TATA DNA, and ΔΔG is the relative binding free energy of a BP-modified TATA/TBP complex compared to the unmodified one. The free energy of free TBP G(TBP) is −8134 ± 30 kcal/mol. Underlined are the lowest energy in each of the four combinations of carcinogen location (A₁ or A₂) and stereochemistry (10S(+) or 10R(−)). All energies have the unit of kcal/mol and are shown in both average and standard deviation (except ΔΔG).

Force field

The force-field parameters of the TATA DNA and the TBP protein are assigned using the Cornell et al. (29) force field with parm98 parameter set (30). The missing partial charges and three bond angles of the BP-adenine adducts are computed using our partial charge protocol (see Appendix), based on the RESP approach (31–33) in AMBER (34), and according to chemically similar bond angles in the parm98; these computed force-field parameters are listed in Appendix S2 in the Supplementary Material.

Energy minimization and MD simulation

Energy minimization and MD simulations were performed in AMBER 6 (34). Energy minimization eliminates unfavorable van der Waals contacts in the initial structures. Each system is then solvated with a rectangular box of TIP3 water molecules (35) and counterions (neutralizing the system and reproducing the experimental ionic strength). Energy minimization is performed again to eliminate van der Waals collisions due to the addition of water molecules and counterions. MD simulations then follow with four equilibration stages (heating, constant pressure I, constant pressure II, final equilibration) and one production dynamics stage (7). Equilibration focuses on the solvent while production dynamics collects structural changes of the solute. The simulations employ the leap-frog Verlet algorithm (36) with a time step of 2 fs. Electrostatic interactions are computed using the particle-mesh Ewald method (37,38).

For each of the 12 TATA/TBP systems, energy minimization on the initial structure is performed with 400 steps of steepest descent (SD) followed by 400 steps of conjugate gradient (CG). The system is then solvated with a rectangular box of TIP3 water molecules that extends 10.0 Å from the solute and contains 37 Na⁺ and 23 Cl⁻ for neutralizing the system and mimicking the experimental ionic strength of 130 mM. To relax the added solvent, the entire system is minimized again using 50 steps of SD followed by 5000 steps of CG. The four equilibration stages take 460,000 steps (920 ps) and the production dynamics stage takes 700,000 steps (1400 ps); the total length of the trajectory is then 2.32 ns. More details of the energy minimization and MD simulation of the 12 TATA/TBP systems are described in Zhang et al. (7).

For the free TBP, a water box is added with a buffer size of (12.0, 10.0, 10.0) Å. The buffer size in the X direction is larger than those in the Y and Z directions because TBP may expand in this direction without bound DNA. Then 14 Na⁺ and 30 Cl⁻ are added to neutralize the system and satisfy the experimental ionic strength (130 mM). The free TBP system undergoes the same procedure of minimizations and dynamics as those TATA/TBP systems (7) and has a trajectory length of 2.32 ns too.

For the 12 corresponding free TATA DNA systems, each DNA is taken from its corresponding TATA/TBP complex after the complex is minimized with a water box and counterions. The TBP, counterions, and all water molecules are then removed. Each DNA is minimized using 400 steps of SD followed by 400 steps of CG with a 1.0 kcal/mol restraint on the DNA's non-end atoms. A water box is added with a buffer size of (10.0, 15.0, and 10.0) Å. The larger buffer in the Y direction allows for the possibility that the bent DNA may become straight during dynamics. Thirty Na⁺ are then added to neutralize the system. Minimization follows using 50 steps of SD and 5000 steps of CG with a 50.0 kcal/mol restraint only on DNA. The 12 DNA systems undergo fewer steps of equilibration stages because these systems have less solvent than those of the TATA/TBP complex systems. The numbers of equilibration steps are: 10,000 (heating), 20,000 (constant pressure simulation I), 20,000 (constant pressure simulation II), and 20,000 (final equilibration). More steps of production dynamics (1,600,000) were used to allow the bent DNA to become stable. The length of each TATA DNA trajectory is 3.34 ns.

Molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) free energy analyses

Molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) (39–42) is a free energy evaluation methodology that has been employed in a variety of applications (see Discussion). The MM-PBSA free energy is estimated from molecular mechanical energy E_MM, solvation free energy G_SOL, and vibrational, rotational, and translational entropies S,

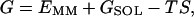(1)

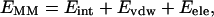(2)

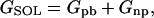(3)

where T is the temperature; E_int is internal energy, E_int = E_bond + E_angle + E_dihedral, the sum of bond, angle, and dihedral energies; E_vdw is van der Waals energy; E_ele is electrostatic energy; G_pb is the electrostatic solvation free energy, computed from the finite difference Poisson-Boltzmann method in the DelPhi program (43,44); G_np is nonpolar solvation free energy, G_np = γSASA + b, γ = 0.00542 kcal/Ų, b = 0.92 kcal/mol, and SASA is the solvent-accessible surface area, which is estimated using Sanner's algorithm implemented in the MSMS software (45); and the solute entropy S is approximated with normal mode analysis (46) using the Nmode module in AMBER 7 (47). The MM-PBSA free energy computations are conducted in AMBER 7 (47).

Binding free energies can be computed from triplet-trajectory analysis or single-trajectory analysis. Triplet-trajectory analysis involves computing free energies for the complex (TATA/TBP) as well as for the free ligand (TATA DNA) and the free receptor (TBP) after they are simulated, respectively (three trajectories); the respective binding free energy is the free energy of the complex minus the free energies of the free ligand and the free receptor. This method is theoretically accurate but computationally expensive. Single- rather than triplet-trajectory analysis only uses the trajectory of the complex; the binding free energy is thus expressed as the free energy of the complex minus the free energies of the bound ligand and the bound receptor in the complex. This method is faster but does not consider possible ligand and receptor conformational changes going from their free states to the bound states. We employ both methods for proper assessment. In addition, we employ a computationally inexpensive analysis method by calculating only the local molecular mechanics interaction energies between the TATA DNA and TBP residues that are within 5 Å from the carcinogen.

Triplet-trajectory analysis

For each TATA/TBP complex and for the free TBP, the last 600-ps trajectory of the production dynamics stage is used for free energy analyses: 60 snapshots at a 10-ps interval for computation of enthalpy (H = E_MM + G_SOL) and 10 snapshots at 60-ps interval for computation of entropy. For each free TATA DNA, the last 1600-ps trajectory of the production dynamics stage is used for free energy analyses: 80 snapshots at a 20-ps interval for computation of enthalpy and 10 snapshots at a 160-ps interval for computation of entropy. The normal mode entropy analyses are estimates and computationally expensive, so only 10 snapshots are selected for the analyses. (With 50 snapshots for the unmodified DNA system, we obtained the nearly identical entropy as in the 10-snapshot analysis; therefore we use the more computationally feasible 10-snapshot entropy analysis for all systems.)

Single-trajectory analysis

For each TATA/TBP complex and its bound TATA DNA and bound TBP, the last 600-ps trajectory of the production dynamics stage of the complex is used for free energy analyses: 60 snapshots at a 10-ps interval for computation of enthalpy and 10 snapshots at 60-ps interval for computation of entropy.

Temperature T is set to 277.15 K to mimic the experimental temperature (27). For calculating E_MM, the dielectric constant is set to 1.0. For calculating G_SOL, the salt concentration is set to 0.13 M to mimic the experimental ionic strength (27); the internal dielectric constant is set to 1.0 and external to 80.0. For calculating entropy, each structure is minimized using the conjugate gradient method with a distance-dependent dielectric constant (ɛ = 4R, where R is the interatomic distance) until the root-mean-square of the elements in the gradient vector was <10⁻⁴ kcal/mol/Å. Its entropy is then computed and averaged on all the 10 minimized structures.

RESULTS

Structural changes of TATA/TBP complex due to BP modifications

In our previous study (7), we ranked the structural distortions of the TATA DNA backbones and the TBP backbones of the BP-modified systems compared to the unmodified one as follows: minimal distortions for the 10R(−) stereoisomer at A₁, moderate distortion for the 10S(+) stereoisomer at A₁, and greatest distortions for the two stereoisomers at A₂. We also interpreted this adduct-location-dependent effect in terms of conformational freedom and major-groove space available to BP due to the hydrogen bonds and phenylalanine insertions at the TATA/TBP interface: at A₂, BP cannot easily intercalate between the DNA bases and has a smaller space in the DNA major groove (7).

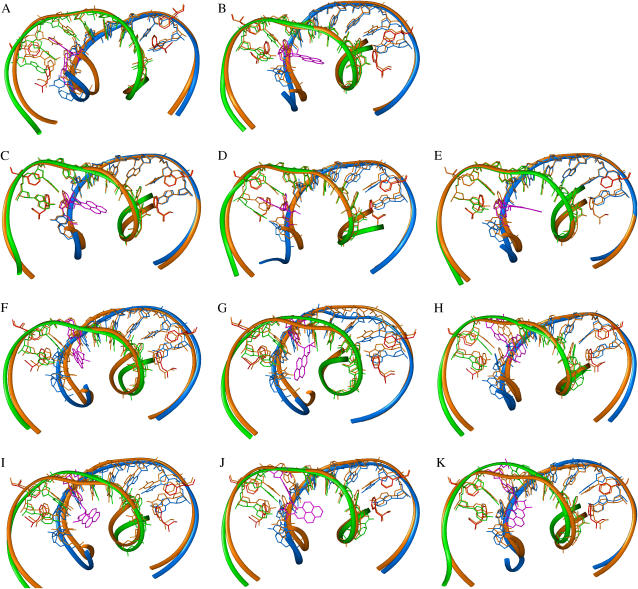
To examine the specific BP-induced structural changes of the TATA/TBP complex, we visualize these changes by superimposing each BP-modified complex on the unmodified one in Fig. 2. The structural changes are summarized in Table 4. These structural changes are consistent with our RMSD analyses (7): BP at A₂ distorts the TATA/TBP complex, while BP at A₁ nearly conserves the complex, and agree with the experimental finding (27) that BP at A₂ decreases the TATA/TBP binding affinity while BP at A₁ slightly increases the binding affinity. The slight increase of binding affinity by BP at A₁ suggests that the ease of intercalation by BP at A₁ increases the stacking energy in the severely bent TATA DNA and stabilizes the overall binding between TATA and TBP. (Although we remodeled the DNA sequence and our systems had limited simulation time, BP has been stabilized early in simulations in all BP-modified systems; in Appendix S3 in the Supplementary Material, BP's three torsion angles (χ, α′, β′) as a function of simulation time are plotted for the first BP-modified system 10S(+)-trans-(A₁): II.)

FIGURE 2.

Superimposition of BP-modified and unmodified TATA/TBP complexes. Both structures are averaged over the last 600 ps of production dynamics. The DNA strands are blue and green in the BP-modified complex and orange in the unmodified complex; the BP-adenine adduct is pink; TBP residues are not shown except four phenylalanines; the four phenylalanines are red in the BP-modified complex and orange in the unmodified complex; hydrogens are not shown. The two phenylalanines (Phe-162 at the second left and Phe-71 at the second right) insert and kink the DNA at A6 (A₁) and A22 (A₂); the other two phenylalanines reside over T11 and A27 and are stabilized by van der Waals interactions. (A) 10S(+)-trans-(A₁): II versus unmodified. (B) 10S(+)-trans-(A₁): III versus unmodified. (C) 10R(−)-trans-(A₁): II versus unmodified. (D) 10R(−)-trans-(A₁): III versus unmodified. (E) 10R(−)-trans-(A₁): IV versus unmodified. (F) 10S(+)-trans-(A₂): III versus unmodified. (G) 10S(+)-trans-(A₂): III-2 versus unmodified. (H) 10S(+)-trans-(A₂): IV versus unmodified. (I) 10R(−)-trans-(A₂): I versus unmodified. (J) 10R(−)-trans-(A₂): III versus unmodified. (K) 10R(−)-trans-(A₂): IV versus unmodified.

TABLE 4.

Structural changes of TATA/TBP complex due to BP modifications

System	Fig.	Phenylalanines* of TBP	TATA DNA	BP
10S(+)-trans-(A1): II	2 A	Phe-162† is pushed back to TBP by 1.65 Å; the rest are stable.	Backbone in the TATA region is pushed toward TBP; the remaining part remains stable.	Hydroxyls are in the solvent-accessible DNA major groove; hydrophobic aromatic rings are intercalated between DNA bases.
III	2 B	All stable.	Backbone in the TATA region is pushed slightly toward TBP; the remaining part remains stable.	Exposed to the solvent-accessible DNA major groove.
10R(−)-trans-(A1): II	2 C	All stable.	Backbone is reserved; all TATA residues (except A1) are positionally identical with those from the unmodified system.	Exposed to the solvent-accessible DNA major groove.
III	2 D	All stable.	Backbone in the TATA region is pushed slightly toward TBP; the remaining part remains stable.	Hydroxyls are in the solvent-accessible DNA major groove; hydrophobic aromatic rings are intercalated between DNA bases.
IV	2 E	All stable.	Backbone is perfectly conserved; all TATA residues (except A1) are positionally similar to those from the unmodified system.	Exposed to the solvent-accessible DNA major groove.
10S(+)-trans-(A2): III	2 F	All pushed back to TBP.	Backbone is distorted.	Hydroxyls are in the solvent-accessible DNA major groove; hydrophobic aromatic rings are partly intercalated between DNA bases.
III-2	2 G	All moved slightly.	Backbone is severely distorted.	Hydroxyls are in contact with the central TATA box; hydrophobic aromatic rings are in the DNA major groove, but are close to the beginning of the TATA box.
IV	2 H	All pushed back to TBP.	Backbone around A2 is distorted; backbone in the TATA region is pushed slightly toward TBP.	Hydroxyls are in the solvent-accessible DNA major groove; hydrophobic aromatic rings are distorted.
10R(−)-trans-(A2): I	2 I	Phe-162 is pushed back to TBP by 1.88 Å; the rest are moved slightly.	Backbone is distorted; A2 is largely stretched to allow bulky BP to stay in DNA major groove.	Exposed to the solvent-accessible DNA major groove.
III	2 J	Phe-162 is pushed back to TBP by 1.32 Å; the rest are slightly pushed back toward TBP.	Backbone is slightly distorted; thymine (downstream of A1) loses its Watson-Crick hydrogen bonds.	Exposed to the solvent-accessible DNA major groove; the only system in which BP's orientation changes during MD: from intercalated to major-groove form.
IV	2 K	All moved slightly.	Backbone is distorted, especially at the A2 residue; thymine (downstream of A1) loses its Watson-Crick hydrogen bonds; glycosidic torsion χ of the thymine (upstream of A2) is rotated by 23.7°.	Exposed to the solvent-accessible DNA major groove.

^*Referring to the four phenylalanines that interact with the TATA DNA and are shown in red in Fig. 2.

^†Referring to the phenylalanine that inserts the first basepair step of the TATA box.

Stereochemical effect of BP at A₁ on TATA/TBP binding

The experimental work (27) showed that the TATA/TBP binding affinity changes are also dependent on the stereochemistry of the BP-adenine adducts (Table 1). Of the two adducts, the 10R(−) stereoisomer gives more favorable binding affinity changes than the 10S(+) stereoisomer at both A₁ and A₂. However, as shown here, it is difficult for BP at A₂ to adopt either the intercalated orientation or the major-groove orientation. Thus, we interpret here the stereochemistry-dependent effect of BP at A₁ on TATA/TBP binding. BP at A₁ can adopt both the intercalated orientation and major-groove orientation. In the former arrangement, the hydrophobic pyrenyl moiety of BP is buried between DNA bases and forms favorable stacking interactions between the aromatic moiety and DNA bases; in the latter orientation, the hydrophobic moiety will be exposed to the hydrophilic solvent-accessible major groove. Thus the intercalated orientation is favored and represents the major population in the BP-modified TATA/TBP complex solution. This is also consistent with the experimental result that BP at A₁ slightly increases TATA/TBP binding (due to the favorable stacking interaction in the intercalated orientation).

High-resolution NMR solution studies (23,24,26) show that intercalated BP resides on the 3′-side of the modified adenine in the 10S(+) adduct and on the 5′-side in the 10R(−) adduct. This agrees with our simulations of the two systems with BP at A₁ adopting the intercalated orientation: 10S(+)-trans-(A₁): II (Fig. 2 A) and 10R(−)-trans-(A₁): III (Fig. 2 D).

We diagram the positions of the two stereoisomeric adducts in Fig. 3; the 10S(+) BP intercalates between DNA residues T27 and A26 (A₂), and the 10R(−) BP between A28 and T27. We also diagram the major TATA/TBP interactions in the figure for interpreting the stereochemistry-dependent effect. The major interactions between TBP and the TATA box include hydrogen bonds and phenylalanine insertions computed from the last 600-ps production dynamics simulation of the unmodified TATA/TBP complex (7). The two phenylalanines kink the DNA at A6 (A₁) and A22.

For the 10S(+) BP, the bulky aromatic rings intercalating between the bases of T27 and A26 (A₂) require more space between these two bases. Thus the bases of T27 and A26 are pushed to their 3′ side and 5′ side, respectively. T27's base lacks hydrogen bonds with TBP or with its 3′-side neighbor A28's base; thus T27's base has the flexibility required to be pushed to its 3′ side. A26's base has no hydrogen bonds with TBP either but its 5′-side neighbor T25's base has one, making the pushing of A26's base to its 5′ side relatively difficult. For the 10R(−) BP between A28 and T27, the intercalation is relatively easy. A28's base has no hydrogen bonds with TBP and neither do its 3′-side neighbors (outside the 8-bp TATA box; not diagramed); thus A28's base can be pushed to its 3′ side. T27's base also has some flexibility to be pushed to its 5′ side because T27's base or its 5′-side neighbor (A26's base) has no hydrogen bonds with TBP.

Thus, we have interpreted the stereochemistry-dependent of BP at A₁ in terms of the flexibility of the TATA bases that frame the intercalated adduct due to the hydrogen bonds between the TATA box and TBP. It is relatively more easy for the 10R(−) BP to adopt the intercalated orientation than the 10S(+) BP, as found experimentally (Table 1). Note that the above analysis does not consider the Watson-Crick hydrogen bonds, as each basepair in the TATA box maintains two. Although the binding affinity difference due to the stereochemistry is very small (−10.30 vs. −10.47 kcal/mol; see the binding free energies in Table 1), our simulations together with structural analyses have helped interpret the small stereochemistry-dependent effect of BP modification at A₁ on TATA/TBP binding.

Binding free energy analyses

The experimental binding free energies are derived from the experimental equilibrium constants (27) and listed in Table 1. The derivation procedure is described in Appendix S4 in the Supplementary Material. We compute the theoretical binding affinities from our MD trajectories mainly using the following two methods: triplet-trajectory analysis and single-trajectory analysis. The other method (local molecular mechanics interaction analysis) yields large variations in the interaction energies (Appendix S5 in the Supplementary Material) and is thus unable to interpret the global binding affinity differences shown in Table 1.

Triplet-trajectory analysis

Analyses based on separate trajectories are theoretically more accurate for deriving binding free energies, since the conformational changes of the TATA/DNA and TBP upon binding are considered. Although the free TBP and DNA are initially taken from the complexes (see Methods), their free energies have stabilized during the simulation time in which the free energies are computed, as shown in Appendix S6 in the Supplementary Material. Table 5 shows the free energies G(TATA/TBP) of TATA/TBP complexes, free energies G(TATA) of corresponding free TATA DNA, free energy G(TBP) of free TBP, binding free energies ΔG between TATA DNA and TBP, and relative binding free energies ΔΔG of the BP-modified TATA/TBP complexes compared to the unmodified complex. We see that the ΔG values are dominated by G(TATA/TBP) and have relative binding free energies ΔΔG ranging from −10 to 44 kcal/mol. The ΔΔG values are within the standard deviations of ΔG (49–58 kcal/mol), which means all systems have nearly the same binding free energy. This agrees with the experimental binding free energies that have less than 1 kcal/mol differences (Table 1). However, the computed standard deviations are also too large to distinguish the binding free energies from one another.

Single-trajectory analysis

Table 6 provides the results from the single-trajectory analysis. The molecular mechanics energy changes ΔE_MM are dominated by the electrostatic energy changes ΔE_ele, and the solvation free energy changes ΔG_SOL are dominated by the electrostatic solvation free energy changes ΔG_pb. The binding free energies ΔG are not dominated by any one term, and their standard deviations (12–18 kcal/mol) are much smaller than those from the triplet-trajectory analysis (49–58 kcal/mol; Table 5). Most ΔΔG values are within the standard deviations of ΔG. If we consider only the systems that have the lowest relative binding free energy (underlined in the last column of Table 6) in each of the four combinations of adduct location (A₁ or A₂) and stereochemistry (10S(+) or 10R(−)), their relative binding free energies are much closer (7, 7, 5, and 10 kcal/mol) and well within their standard deviations. This small spread in magnitude is consistent with the experimental binding free energy differences (<1 kcal/mol; Table 1).

TABLE 6.

Binding free energies from single-trajectory analysis

System	ΔEele	ΔEvdw	ΔEMM	ΔGnp	ΔGpb	ΔGSOL	ΔH	−TΔS	ΔG	ΔΔG
Unmodified	−6721 ± 108	−199 ± 6	−6920 ± 107	−11 ± 0.4	6793 ± 98	6782 ± 98	−138 ± 11	67 ± 13	−71 ± 17	0
10S(+)-trans-(A1): II	−6540 ± 79	−197 ± 6	−6737 ± 80	−11 ± 0.3	6609 ± 83	6598 ± 83	−139 ± 17	75 ± 6	−64 ± 18	7
III	−6472 ± 78	−201 ± 7	−6672 ± 81	−11 ± 0.3	6554 ± 74	6543 ± 74	−129 ± 10	77 ± 14	−52 ± 18	19
10R(−)-trans-(A1): II	−6579 ± 62	−199 ± 5	−6777 ± 62	−11 ± 0.3	6656 ± 56	6645 ± 56	−132 ± 9	78 ± 9	−54 ± 13	17
III	−6508 ± 79	−205 ± 6	−6713 ± 82	−11 ± 0.3	6591 ± 76	6580 ± 76	−133 ± 8	69 ± 10	−64 ± 18	7
IV	−6599 ± 74	−198 ± 7	−6797 ± 74	−11 ± 0.3	6676 ± 68	6665 ± 68	−132 ± 9	70 ± 8	−62 ± 12	9
10S(+)-trans-(A2): III	−6566 ± 128	−198 ± 7	−6764 ± 131	−11 ± 0.3	6642 ± 119	6631 ± 119	−133 ± 14	70 ± 6	−63 ± 15	8
III-2	−6471 ± 152	−202 ± 7	−6673 ± 154	−11 ± 0.4	6551 ± 138	6540 ± 138	−133 ± 17	67 ± 5	−66 ± 18	5
IV	−6589 ± 76	−201 ± 7	−6790 ± 78	−11 ± 0.4	6670 ± 71	6659 ± 71	−131 ± 10	76 ± 10	−55 ± 14	16
10R(−)-trans-(A2): I	−6534 ± 90	−197 ± 5	−6731 ± 90	−11 ± 0.2	6607 ± 83	6596 ± 83	−135 ± 10	74 ± 7	−61 ± 12	10
III	−6656 ± 62	−194 ± 7	−6850 ± 61	−11 ± 0.4	6733 ± 57	6712 ± 57	−138 ± 8	83 ± 11	−55 ± 14	16
IV	−6588 ± 75	−209 ± 6	−6797 ± 77	−12 ± 0.4	6679 ± 70	6667 ± 70	−130 ± 10	75 ± 15	−55 ± 18	16

ΔE_ele, ΔE_vdw, and ΔE_int (zeros; not shown) are electrostatic energy, van der Waals energy, and internal energy changes. ΔE_MM is the molecular mechanics energy change and ΔE_MM = ΔE_ele + ΔE_vdw + ΔE_int. G_np and ΔG_pb are nonpolar and electrostatic solvation free energy changes. ΔG_SOL is solvation free energy change and ΔG_SOL = ΔG_np + ΔG_pb. ΔH is enthalpy change and ΔH =ΔE_MM + ΔG_SOL. T is the absolute temperature and ΔS is the entropy change. ΔG is the binding free energy and ΔG = ΔE_MM + ΔG_SOL − TΔS. ΔΔG is the relative binding free energy of a BP-modified system compared to the unmodified one. Underlined are the lowest energy in each of the four combinations of carcinogen location (A₁ or A₂) and stereochemistry (10S(+) or 10R(−)). All energies have the unit of kcal/mol and are shown in both average and standard deviation (except ΔΔG). Although ΔH =ΔE_MM + ΔG_SOL, the large standard deviations of ΔE_MM and ΔG_SOL do not lead to large standard deviations of ΔH, which means fluctuations of these two terms are mostly canceled out.

Therefore, both the triplet-trajectory analysis and the single-trajectory analysis reproduce the experimental relative binding free energies within the computed standard deviations. However, these standard deviations are large especially in the (theoretically more accurate) triplet-trajectory analysis. We analyze this problem in details in Discussion.

DISCUSSION

Geacintov and co-workers (27) have shown that TATA/TBP binding affinity is altered with a bulky BP present in the TATA box and that the binding affinity decreases or slightly increases depending on the location and stereochemistry of the BP-adenine adduct. Although the changes of binding affinity are <1.0 kcal/mol, our MD studies help interpret such small changes in terms of conformational freedom and major-groove space available to BP due to the hydrogen bonds and phenylalanine insertions at the TATA/TBP interface. That is, our structural and flexibility analyses revealed that BP at A₂ has difficulty to adopt either intercalated or major-groove orientation without distorting the TATA and TBP backbones. For BP at A₁, both orientations are easily adopted. Furthermore, the 10R(−) stereoisomer at A₁ can more easily adopt the intercalated orientation due to the larger flexibility of the two DNA bases, between which the BP is intercalated (BP in the 10R(−) stereoisomer thus has larger conformational freedom). Thus, MD simulations, together with structural analyses, help relate atomic-level structure/flexibility effects to global binding effects.

MM-PBSA has been applied to studying binding free energies between protein and small ligand (48–57), protein and protein (58–62), protein and peptide (63,64), small molecule and small molecule (65,66), RNA and peptide (67), RNA and small ligand (68), DNA and small ligand (69), and protein and RNA (70). To the best of our knowledge, our case is the first MM-PBSA binding free energy study between protein and DNA. Though our free energy calculations reproduce the experimental relative binding free energies within the computed standard deviations, these standard deviations are large, especially in the theoretically more accurate triplet-trajectory analysis, which considers the conformational changes of the ligand (TATA DNA) and the receptor (TBP) upon binding. Wang and co-workers underscore several sources of error in MM-PBSA: the force field, MD sampling, solvation free energy estimate of PBSA, and the entropy estimated by normal mode analyses (54). They also suggest that the MM-PBSA approach may not work as well in calculating the absolute binding free energy for charged ligands as for neutral systems (54). In the following, we focus on discussing the two error sources—MD sampling and electrostatic solvation free energy.

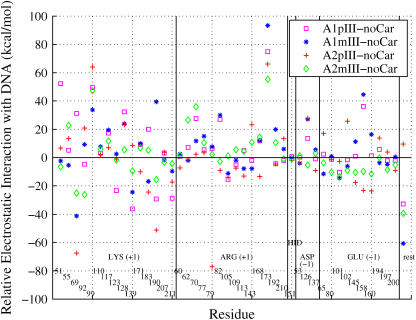
Although experimental results are condition-dependent, they are averaged in time and space for many molecular systems. In contrast, a MD trajectory only mimics behavior of one molecule within a limited time span in the large thermally accessible conformation space. This causes large standard deviations in the free energy evaluation. Fig. 4 shows relative TATA/TBP electrostatic interaction energies of four BP-modified systems compared to the unmodified one. The wide variations of interactions between the TBP residues and the TATA/DNA indicate that there are large random movements by the flexible TBP residues. Large fluctuations in binding free energies are also reported in a recent protein-ligand association free-energy study by Swanson and co-workers (53). These fluctuations explain why freezing the atoms outside binding regions yields good binding free energies for large systems (54,56). Without freezing, two trajectories for the same molecule may produce two quite different binding free energies. For example, one trajectory of our 10S(+)-trans-(A₂): III complex produces a −63 kcal/mol binding free energy and another gives −75 kcal/mol, although they are within the standard deviations of 15 kcal/mol. (Please note that freezing may not be appropriate if the frozen parts should undergo conformational changes upon binding.) Increasing MD sampling to overcome large energy fluctuations remains difficult due to the high cost of MD simulations and free-energy analyses of large systems.

FIGURE 4.

Relative electrostatic interaction energies of TBP residues with TATA DNA. Each spot indicates the relative TBP residue/DNA electrostatic interaction energy of a carcinogen-modified system compared to the unmodified one (noCar). The four carcinogen-modified systems are 10S(+)-trans-(A₁): III (A1pIII); 10R(−)-trans-(A₁): III (A1mIII); 10S(+)-trans-(A₂): III (A2pIII); and 10R(−)-trans-(A₂): III (A2mIII). The energies are averaged over the last 600 ps of production dynamics. The TBP residues are listed in six groups separated by vertical lines: positively charged (+1 e) lysine (LYS); positively charged (+1 e) arginine (ARG); neutral histidine (HID); negatively charged (−1 e) aspartic acid (ASP); negatively charged (−1 e) glutamic acid (GLU); and the rest are residues. All the groups, except the last one, are also provided with residue numbers.

The electrostatic solvation free energy G_pb (main part of solvation free energy) obtained by solving the Poisson-Boltzmann equation (PBE) is another large error source in MM-PBSA. One reason is that the implicit treatment of water and counterions in the PBE is still a step away from describing the atomic-level explicit solvent environment. Wagoner and Baker find that polar solvation forces generated by PBE systematically overestimate the magnitude of the explicit solvent forces (71) (their work also shows that SASA-based nonpolar forces have no significant correlation with nonpolar explicit solvent forces). Another reason stems from uncertainty regarding dielectric constants. The solute dielectric constant ɛ_in, which we set to its vacuum value of 1.0, can vary over a wide range (1.0–20.0) according to different studies (discussed in (72)). However, the variation in ɛ_in has a dramatic effect on the electrostatic solvation free energies G_pb. For example, G_pb of our 10R(−)-trans-(A₁): III complex is −8518 kcal/mol if ɛ_in = 1.0, and −2019 kcal/mol if ɛ_in = 4.0. In a comprehensive review (73), Schutz and Warshel conclude that the dielectric constant is not a universal constant but a parameter that depends on the model used. The more explicit the model, the smaller the dielectric constant that is needed. The dielectric constant can be as small as 1.0 if all contributions are treated explicitly and accurately, including protein permanent dipole, protein reorganization energy, and water penetration, etc. We also note that the solvent dielectric constant ɛ_out, which we set to 80, is dependent on temperature (74).

In sum, developing a more accurate and faster free energy calculation method still is a distance away. Our TATA/TBP systems are both large (211 residues) and highly charged (−30 e on the DNA), which makes our systems difficult for binding free-energy evaluation. The large standard deviations may also be partly caused by the limited trajectories and timescales in our simulations (one 2.32-ns trajectory for each of the 12 TATA/TBP complexes and the free TBP; one 3.34-ns trajectory for each of the 12 free TATA DNA) due to the large set and sizes of the systems and limited computing resources available. Still, despite these limitations, both the triplet-trajectory analysis and the single-trajectory analysis produce the relative binding free energies (Table 5 and Table 6) consistent with the experimental values (Table 1) within the computed standard deviations. Thus, structurally distinct molecules may have similar binding free energies. The single-trajectory analysis (Table 6) yields much smaller standard deviations than the triplet-trajectory analysis (Table 5) because fewer random movements (Fig. 4) are introduced in the former, which actually only calculates the interactions at the TATA/TBP interfaces. This is similar to the case in which freezing the atoms outside the binding regions can give better binding free energies for large systems (54,56). Therefore, besides improvements in the MM-PBSA methodology, future binding free energy calculations of DNA/protein complexes require longer simulation time, multiple trajectories for each system, and restraints on noninterface residues (if they do not undergo conformational changes upon binding). Employing multiple trajectories for each system can also help to identify the timescale limitation on a system due to the deficiencies in force fields and simulation protocols (75,76).

CONCLUSION

This study reveals the specific position and stereochemistry-dependent structural changes of the TATA/TBP complex due to BP binding to the TATA box. Together with our former analyses (7), we can interpret the location-dependent effect and stereochemistry-dependent effect (for BP at A₁) of BP modifications on TATA/TBP binding in terms of the conformational freedom and major-groove space available to BP due to the hydrogen bonds and phenylalanine insertions at the TATA/TBP interface. Thermodynamic analyses using MM-PBSA produce large standard deviations, which make the computed binding free energies the same within the error bars. Although it agrees with the experimental binding free energy differences (<1 kcal/mol), it suggests the need for MM-PBSA methodology improvements and better sampling for evaluating binding free energies of large and highly charged systems like DNA/protein complexes. More generally, the unraveled structures and interactions in these studies can help investigate how transcription initiation may be affected by a bulky BP chemically binding to the TATA box.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.

SCHEME 1.

APPENDIX: PROCEDURE OF COMPUTING PARTIAL CHARGES OF CARCINOGEN-MODIFIED B-DEOXYNUCLEOTIDES

Step 1: Build two molecules (InsightII)

To make our partial charges compatible with AMBER's force field (29), we calculate partial charges of the following two molecules, similar to the way AMBER (34) does. Finally we will combine the partial charges of these two molecules in Step 5. We use InsightII (Accelrys) to build these two molecules.

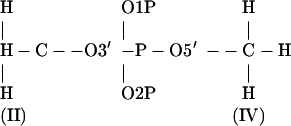
Nucleoside with carcinogen

Cap 5′ and 3′-end (no phosphate group).

Set dihedral angles:

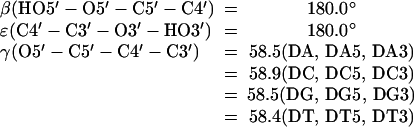No bumps.

Dimethylphosphate (DMP)

Set dihedral angles:

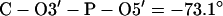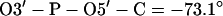(Cieplak et al. (33) used positive dihedral angles. But in regular A- and B-DNA, these dihedral angles are negative, i.e., (g−, g−) conformation.)

No bumps.

Step 2: Optimize geometry on each molecule (Gaussian)

The geometry optimization of both molecules will be performed in next step as the electrostatic potentials (ESP) are calculated simultaneously in Gaussian (77). The time of Gaussian calculation with optimization option will be quite long (∼1 week) on the nucleoside with carcinogen. (The optimized structures can be used for building topology files for AMBER, if one needs to do molecular dynamics.) If you want to calculate the partial charges on a specific structural conformation, you may skip this step.

Step 3: Calculate electrostatic potential (ESP) on each molecule (Gaussian)

How to build Gaussian input files can be found in the Gaussian Manual (77). Following are a few parameters which have to be set in Gaussian input files:

• Route section (HF/6-31G*, ESP output, optimization; remove “opt” if you want to calculate the partial charges on a specific structural conformation): # HF/6-31G* pop = (minimal,mk) opt maxdisk = 134217728 iop(6/33 = 2).

• Charge = 0 (nucleoside with carcinogen, if carcinogen has zero charge), or = −1 (dimethylphosphate).

• Spin multiplicity = N_up+1 (N_up is the number of unpaired electrons; ground state).

Step 4: Check interactions in optimized structures (InsightII)

Gaussian does not know where bonds, angles, and dihedral angles are if we do not tell in the input files. So the optimized structures may have unreasonable interactions. We use InsightII to check bumps in the optimized structures. If all the interactions are reasonable, we can go to next step. Otherwise, we have to restart from Step 1 (or the current optimized structures) by manually adjusting the structures to avoid further unreasonable interactions.

Step 5: Calculate partial charges of both molecules together (RESP)

Now we need to combine ESP of these two molecules to calculate the partial charges of the carcinogen modified nucleotide within two stages of AMBER's RESP. See AMBER Manual (34) for how to build the input files for RESP. The partial charges of the phosphate group (P, O1P, and O2P) will be taken from the dimethylphosphate (DMP).

First stage

Charge constraints:

• I + II = 0 (DX5, X = A, C, G, or T. Partial charge of O3′ will be taken from DMP), or III + IV = 0 (DX3, Partial charge of O5′ will be taken from DMP), or I + II = III + IV = 0 (DX, Partial charges of O3′ and O5′ will be taken from DMP).

• O1P, O2P in phosphate group are equivalenced.

• H in NH₂ groups are equivalenced.

• Hyperbolic restraints with a force constant a = 0.0005 are applied to all heavy atoms, and hydrogens are not restrained.

Second stage

• CH₂ and CH₃ in nucleoside are refit; other atoms' charges are kept.

• Hyperbolic restraints with a force constant a = 0.001 are applied to only the carbons of CH₂ and CH₃ in nucleoside, and hydrogens are not restrained.

• H in CH₂ or CH₃ in nucleoside are equivalenced.

Notes

The final total charge of the carcinogen modified nucleotide will be exactly −1.0000 for DX types (X = A, C, G, or T), if the carcinogen has zero charge. This procedure can be easily applied to A-deoxynucleotides and A-ribonucleotides with Cieplak et al. (33). PERL programs and a sample are available at http://monod.biomath.nyu.edu/∼qzhang/Research.htm.