Force Unfolding Single RNAs

Abstract

We develop a continue time Monte Carlo algorithm to simulate single RNAs unfolded by a time-dependent external force on the secondary structure level. Two recent unfolding RNA experiments carried out by Bustamante group are mainly investigated. We find that, in contrast to popular two-state assumption about the RNAs free energy landscape along the molecular extension, the molecules used in the experiments do not present apparent energy barriers. The strong cooperative folding and unfolding transitions of the RNAs observed in the experiments and in our simulations arise from the interaction of the molecules and the light trap. In addition, we also investigate the properties of Jarzynski's remarkable equality, whose experimental test has received considerable attention.

INTRODUCTION

RNA folding, which includes thermodynamic and dynamic folding, is one of the central problems in biophysics. Many experimental techniques have been applied in the RNA folding, such as x-ray crystallograph, NMR spectroscopy, etc. Recently, single-molecule manipulation techniques developed in the past decade provide a novel way to solve the important problem (1–3). Their common principle is to exert an external force on single molecules, and then to record the molecular end-to-end extensions (force-extension curves). Compared to the conventional methods that only yield time-averaged snapshots of RNA structures, current single-molecule technique is able to track RNA folding and unfolding trajectories on a single-molecule level in real time (1). These experiments may shed new light on the RNA folding problem. Until now, RNAs investigated by this technique include simple secondary structure units of RNA (1), complex tertiary structural ribozyme (2), and 1540-base long 16S ribosomal RNA with pseudoknots (3).

The single RNAs manipulation experiments address a challenging issue for theorists: whether or how can we make use of the known secondary structural RNA knowledge to explain or predict the phenomena observed in the experiments? Many theoretical efforts have been devoted to understanding this issue (4–8). However, these theories or models are too simple to be useful in real experiments; free energy data about RNA secondary structures obtained by thermodynamic experiments (9) were often neglected. Moreover, they just only studied equilibrium behaviors. The intriguing nonequilibrium phenomena were not investigated seriously. Computational simulation should be a good choice to overcome these shortcomings. But we noted that, compared to enormous simulations for force unfolding proteins (10–13), simulations for RNAs were few (3) although the biological importance of the latter is the same as the former. Recently we proposed a continuous time Monte Carlo (CTMC) method to simulate force unfolding single RNAs to fill this gap (14,15). We mainly focused on thermodynamic and kinetic behaviors of single RNAs under a constant mechanical force. Our simulation particularly calculated folding and unfolding rate constants at different forces, and the results agreed with the experiment very well. Unfortunately, the method cannot correctly account for the fact that in many real experiments, e.g., the mixed ensembles that we are concerned with here, the mechanical force is often time-dependent (1,16). In our initial simulations, a rough velocity estimation v = δx/δt was used (15), where δx is the displacement of a light trap after a dwell time δt. The major problem of the approximation is that we cannot uniquely choose δx and δt except that the ratio between them is a constant. Hence, nonequilibrium behaviors simulated by the method may be problematic. In this paper, we will show that this flaw could be naturally solved by a time-dependent CTMC approach.

The organization of the article is as follows. In the next section, we simply review our previous force unfolding single RNAs model, and then show how to extend it to the time-dependent force cases using the time-dependent CTMC method. Because the thermodynamic quantities, such as the free energy differences are necessary in the discussion of nonequilibrium behaviors, an exact partition function method for the mixed ensemble with vanishing velocity of light trap (6) is reformulated. In the Results section, we first study the RNA unfolding thermodynamics with the simulation and the partition function method to confirm the correctness of the simulation. In the following part, we investigate the kinetics of RNAs, which includes the force-extension curves in far-from equilibrium, the free energy reconstruction from nonequilibrium data, and a comparison of three free energy estimators. Finally we give our conclusion.

MODEL AND METHOD

Force unfolding RNA model

Same with the experiments (1,16), our discussion is restricted to RNA secondary structures. The mixed ensemble is sketched in Fig. 1. The position of the center of the light trap is moved according to a time-dependent relationship z(t) = z_o + vt, where z(t) is the distance between the centers of the light trap and the bead held by the micropipette, z_o is the offset at time t = 0, and v is the constant velocity. We suppose that the changes of the extensions of RNA and the handle proceed along one direction, and the physical effect of the beads is negligible. Any state of the system at time t then can be specified with three independent quantities, the extension of the RNA x^ss, the end-to-end distance of the handle x^ds, and the RNA secondary structure S, i.e., the system in i-state at time 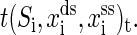Here x^tw is not included because the sum of individual extensions satisfies the constraint condition,

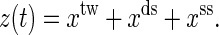(1)

FIGURE 1.

Sketch of the mixed ensemble and the native states of the RNA molecules P5ab, P5abcΔA, and P5abc studied in this work. The molecules are attached between the two beads (larger black points) with a RNA:DNA hybrid handle (black dashed curves). The center of the light trap is moved with velocity v. The total distance at time t is z(t) = x^tw + x^ds + x^ss.

Hence, unfolding of single RNA proceeds in space

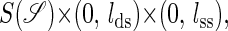(2)

where 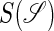is the set of all secondary structures of a given RNA sequence 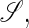l_ds, and l_ss are the contour lengths of the handle and the RNA molecule, respectively. To describe the RNA unfolding as a time-ordered series of the conformations in the space, a relation M, which specifies whether two conformations are accessible from each other by an elementary “move” must be reasonably defined. We proposed the following move set (15),

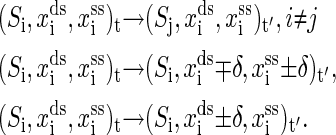(3)

The first kind of move is removal or insertion of single basepair while fixing the extensions x^ds and x^ss. The other two kinds are to, respectively, move the positions of the end of the handle and the end of single-stranded RNA with a small displacement δ, while the secondary structure is fixed simultaneously. Given the system state i at time t, the whole energy of it can be written as

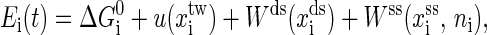(4)

where 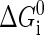is the free energy obtained from folding the RNA sequence into the secondary structure S_i, and the last three terms are the elastic energies of the optical trap, the handle, and the single-stranded part of the RNA, respectively (15). The light trap here is simply assumed to be a harmonic potential with a spring constant k_tw. The loading rate then is k_twv.

Time-dependent CTMC algorithm

Given the conformational space, the RNA unfolding is modeled as a Markov process in it. Previous works (14,15,17) have demonstrated that CTMC simulation (18) was an excellent approach toward the stochastic process. As a variant of the standard Monte Carlo method, CTMC method is very efficient and fast because of lacking of waiting times due to rejection. Moreover, the “time” in the method could be real if the transition probabilities were calculated by first principles or empirically. Because we are considering time various external force, a time-dependent CTMC is essential (19).

The key formula in the time-dependent CTMC is that, given the system at i-state at current time t, the probability density p(j, t′|i, t) that the next state is j and occurs at time t′ is

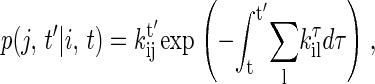(5)

where k^τ_ik is transition probability from the i-state to the neighboring k-state at time τ (19), and the sum is over all neighbors of the current state. According to Eq. 5, the time t′ for the next state to occur then can be obtained by solving equation,

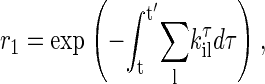(6)

where r₁ is a uniform random number in the interval [0, 1]. For a time-independent situation, Eq. 6 reduces to the most common expression (15)

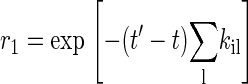(7)

The next state j is chosen if another uniform random number satisfies

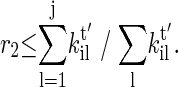(8)

For general k^τ_ik, solving Eq. 6 often requires time-consuming numerical integration and root finding. Here we simply assume that they have symmetric expressions, rule (20)

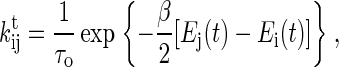(9)

where β = 1/k_BT, k_B is the Boltzmann constant, T is the temperature, and τ_o scales the time axis of the unfolding process. In addition to that, the transition probabilities obey the detailed balance condition locally in time (21,22), we find that the complicated formula of the right side of Eq. 6 has an analytical expression if the light trap is a harmonic potential. Great effort spent in the numerical integration therefore can be completely avoided.

Partition function method in equilibrium

If the moving velocity of the light trap vanishes, an exact partition function method can calculate the molecular average extension and the average force at a given distance z (6). The method is an extension of the partition function method proposed for RNA secondary structural prediction (23). Different from the experimental measurement of the free energy with slow pulling velocity (quasiequilibrium process) (16), we obtain the equilibrium information by this exact method. Considering coincidences of formulas and new physical quantities needed here, we rewrite the formulas proposed by Gerland et al. (6).

The central idea of the exact method is that the partition function over all secondary structures of a given RNA can be calculated by dynamic programming (23). Given the partition function Q(i, j, m) on the sequence segment [i, j] with exterior bases m, its recursion formula is given by,

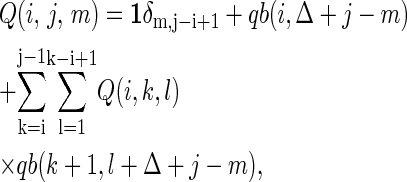(10)

where Δ = 2, the partition function qb(i, j) on the sequence segment [i, j] for which the i and j bases are paired; Vienna Package 1.4 provides the calculation codes (24).

Let the partition function of the RNA molecule with n nucleotides at extension x (including the handle) be Z_n(x). Then the function can be written as

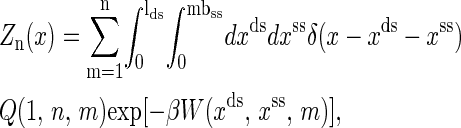(11)

where

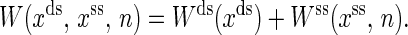(12)

The molecular free energy landscape along x then is

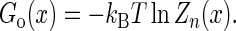(13)

To calculate the average force 〈f〉 and the average extension 〈x〉 at given distance z, we first have to calculate the free energy G(z) of the whole partition function 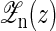including the light trap by

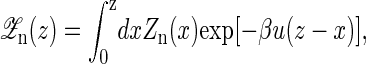(14)

and

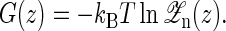(15)

Hence the 〈f〉 and 〈x〉 are, respectively, given by

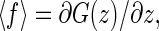(16)

and 〈x〉 = z − 〈f〉/k_tw.

Parameters and measurement

We carry out simulations at the experimental temperature T = 298 K (1,16). The elastic parameters used here are: the persistence length of the handle P_ds = 53 nm, l_ds = 320 nm, b_ss = 0.56 nm, Kuhn length of single-stranded part of RNAs K_ss = 1.5 nm, and k_tw = 0.2 pN/nm. We use the single-stranded DNA parameters for the single-stranded part of RNAs because they have similar chemical structures. The displacement δ = 1 Å. The free energy parameters for the RNA secondary structures are from the Vienna Package 1.4 (24) in standard salt concentrations [Na⁺] = 1 M and [Mg²⁺] = 0 M. In addition to the standard Watson-Crick basepairs (AU and CG), GU basepair is allowed in our simulations. Formation of isolated basepairs is forbidden because of their instability. The instant force f_i(t) acting on the RNA molecule at i-state is calculated by

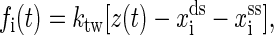(17)

and the instant molecular extension is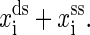

RESULTS

Single RNAs thermodynamics

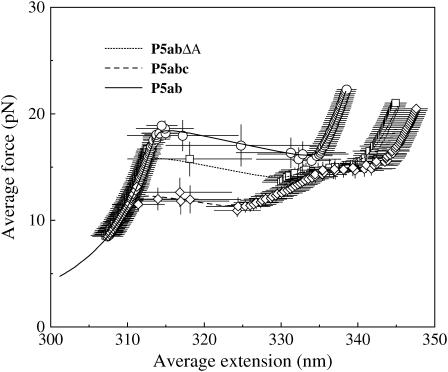
A comparison between our simulation in equilibrium and the partition function method is necessary to directly confirm correctness of our method. We simulate the average force-extension curves of the three RNA molecules in Fig. 1 with standard approach: average physical quantity A is calculated according to

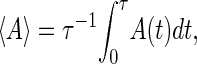(18)

where τ = 10⁶; see the symbols in Fig. 2. We let τ₀ = 1 for convenience here. The force-extension curves obtained by the exact method are plotted with different kinds of curves in the same figure. We can see that these two independent calculations agree very well.

FIGURE 2.

Comparison of the exact (lines) and the simulation (symbols) force-extension curves in equilibrium for P5ab, P5abcΔA, and P5abc in the mixed ensemble.

Although the two methods agree with each other well, the values of the unfolding forces have apparent discrepancies with the experimental measurements. For example, in the absence of Mg²⁺ the values are 13.3, 11.3, and 8.0 pN for P5ab, P5abcΔA, and P5abc molecules in the mixed ensemble, respectively (1). It is not unexpected because we do not take account the effect of ionic concentration in our model. Hence, we choose a reasonable ionic correction of RNA free energies (25). Unfortunately, we still do not get good results; see Table 1. There are two possible causes leading to such discrepancies. One is that the ionic correction or free energy parameters for RNA are not precise enough to be used in the force unfolding cases. The other is that polymer elastic parameters are not good enough. We prefer the latter to the former. In addition to RNA free energy measured and tested for almost 40 years, the persistent length of small ssDNA in ionic environment is still debatable (28). For instance, we calculate the unfolding forces of the three molecules with K_ss = 2.2 nm and indeed find that they are closer to the experimental values. As a further demonstration, we also list other values measured in previous experiments and compare them with theoretical predictions in the same table.

TABLE 1.

The unfolding forces f_u of the different molecules under different experimental conditions

Molecule	Temperature (K)	Na+ (mM)	Mg2+ (mM)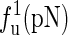
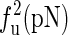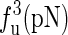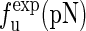P5abc	298	250	0	12.2	11.4	10.0	7.0–11.0
poly(dA-dU)	293	150	0	12.3	11.0	9.3	9.0
P5abcΔA	298	250	0	15.8	14.8	13.2	11.4 ± 0.5
P5abcΔA	298	250	10	–	15.4	13.8	12.7 ± 0.3
P5ab	298	250	0	18.4	17.4	15.7	13.3 ± 1.0
P5ab	298	250	10	–	18.0	16.2	14.5 ± 1.0
CG hairpin	293	150	0	25.8	24.4	22.4	17.0
poly(dC-dG)	293	150	0	25.1	23.8	21.7	20.0

The experimental data are from the published lectures (1,26,27). The theoretical values are from the exact partition function method; 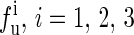represent the unfolding forces without the ionic correction, with the ionic correction on the free energy, and with the ionic and the Kuhn length corrections, respectively. We do not show the P5abc unfolding force for it is not reversible in Mg²⁺ due to the presence of tertiary interactions.

Single RNAs kinetics

Force-extension curves

If one knows the force-extension curves in equilibrium, a way to check whether the unfolding proceeds in equilibrium or not is to see the coincidence of unfolding trajectories and equilibrium curves. Otherwise we have to check the coincidence of folding and unfolding trajectories. Fig. 3 A shows such an example: P5ab is stretched with the velocity v = 5 × 10⁻³ Å from the offset z_o = 350 nm to z = 450 nm, and then relaxed with the same velocity. Here the dimension of the velocity is distance instead of distance/time for the dimensionless τ₀ = 1 assumed at the beginning. Apparently, the trajectories are not coincident, i.e., force-hysteresis, which indicates that the molecule is driven from thermodynamic equilibrium occurs.

FIGURE 3.

(A) One of the time trajectories of unfolding (right arrow) and refolding (left arrow) for P5ab with velocity 5 × 10⁻³ Å. Force hysteresis is observed. (B) The force-extension curves simulated by approximation velocity approach (15): δx = 10 Å, the dwell time δt = 10⁵, hence the pulling velocity is 1 × 10⁻⁴ Å. (C) With the same velocity, the unfolding force-extension curves simulated by the time-dependent CTMC. We can see that the approximation approach works well if smaller dwell time chosen. The less noisy of the former is from a time-average in the dwell time (15). (D) The force-extension curves simulated by the current approach; the pulling velocity is 1 × 10⁻⁵ Å in this case. The smooth curves in these panels are the exact force-extension curves of the molecules in equilibrium.

Until now we did not point out what values of the velocity correspond to equilibrium or a near-equilibrium situation. It is necessary for in the real experiments, the equilibrium information, e.g., free energy differences, is obtained by a slow pulling velocity (16). To solve the problem, we unfold the three RNA molecules with two slower velocities, 1 × 10⁻⁴ and 1 × 10⁻⁵ Å. Because enormous data would be generated if the time trajectories were fully recorded, we only show the data per unit times 10⁵ and 10⁶ (see Fig. 3, C and D). For the faster velocity, we find that, except P5ab case, the unfolding forces for the others do not equal the equilibrium values, whereas for the slower case, the curves of simulations agree with the exact curves. It means that the unfolding of the three molecules with the later velocity has been in near equilibrium regime. In addition, two features in Fig. 3 D are of interest to us: 1), compared with the curves obtained by the time averaging in equilibrium, the curves recorded at time points are very rough even before and after the unfolding; and 2), although the whole extension z(t) monotonically increases with time, the extensions of the molecules may still jump between two distinct values, such as P5ab and P5abc molecules. Indeed, similar phenomena were also observed in the experiment (1). They indicate the fluctuations of the extensions and RNA structures under the external force. We have known from the experiments (1,16) that P5abc unfoldings are near-equilibrium and far from equilibrium at the loading rates 2–5 and 34–52 pN/s, respectively (similar values for P5abcΔA). Our simulations showed that the unfoldings of the same molecule are, respectively, near-equilibrium and far from equilibrium at the loading rates k_tw10⁻⁵/τ₀ and k_tw10⁻⁴/τ₀. Let them equate to the experimental loading rates; correspondingly, we then estimate the constant τ_o ≈ 10⁻⁷s. We will scale the time with this parameter in the following. The timescale obtained in this work is very different from previous τ_o ≈ 10⁻⁵s (15), which was from the simulations in the constant force ensemble. A possible cause is that a different kinetic move set was used therein.

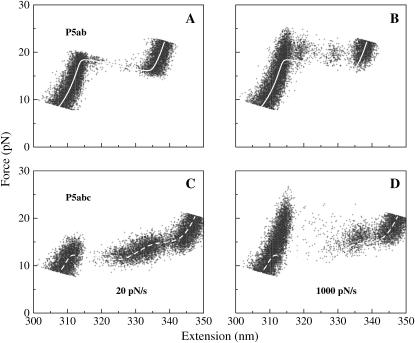
Fig. 4 shows 100 trajectories with two loading rates, 20 and 1000 pN/s for P5ab and P5abc molecules. The trajectories are stretched from the same offset z_o = 350 nm after thermal equilibrium until the terminal extension z = 450 nm. For both the loading rates, below and above the unfolding forces, the force-extension curves are dominated by the double-stranded handle. But the values of the unfolding forces apparently fluctuate and dependent on the rates and molecular types. When the pulling speed is faster, or the loading rate is larger (1000 pN/s), the average unfolding force increases correspondingly. This phenomenon has been theoretically predicted earlier (29). We note that at the same loading rate, the trajectories of P5ab are closer to its equilibrium force-extension curve than the trajectories of P5abc. It means that the relaxing process of the former is faster than the latter. This fact has also been observed in the experiment (1).

FIGURE 4.

Unfolding trajectories of P5ab (A,B) and P5abc (C,D) with loading rates 20 and 1000 pN/s. Curves (superposition of 100 curves per figure) are represented by 100 points with the equal time interval. For clarity we do not connect them with lines. The white curves in these panels are the exact force-extension curves of the molecules in equilibrium.

Free energy reconstruction

Recently, Hummer and Szabo (30) extended the remarkable Jarzynski equality (21) to extract unperturbed molecular free energy landscape G_o(x) along the molecular extension x by the following expression

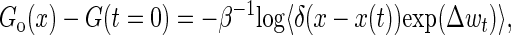(19)

where Δw_t = w_t − k_tw(x(t) − vt)²/2, G(t = 0) is the free energy of the whole system in equilibrium at initial time, and

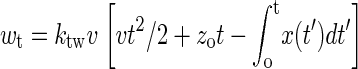(20)

It is interesting to construct the free energy landscapes of the real RNA molecules. Equation 19 implicates that the free energy landscape can be reconstructed just by one stretching. But considering that for finite stretching trajectories, we only sample a small window around the molecular equilibrium position at the whole extension z(t). Therefore, a weighted histogram method was proposed (30),

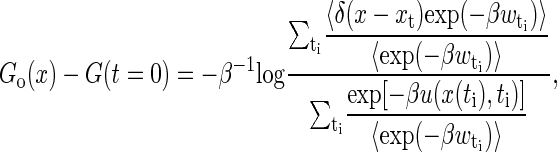(21)

where the sum is over many time slices t′, and the average is over the repeated trajectories at each given time slice. For each trajectory, we choose the discrete time t_i = iΔt, i = 1, ···, 100, here Δt = 10/v, i.e., the time moving the light trap 1 nm (or every point in Fig. 4).

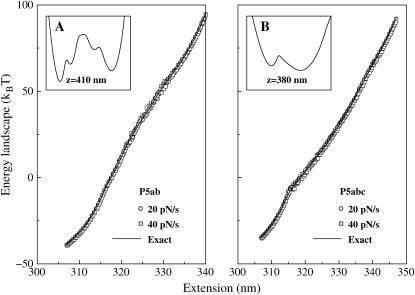
Fig. 5 shows the finally reconstructed free energy landscapes for the two molecules at two loading rates 20 and 40 pN/s. The exact free energy landscapes obtained by the partition function method are also plotted there. We see that the precisions of the reconstructions are satisfactory. We also note that the landscapes are unexpectedly trivial: neither of them presents apparent energy barrier. Ritort et al. (31) have investigated Jarzynski's equality by modeling RNA molecules as a two-level system with an intermediate barrier. Our calculations contradict their assumption. The strong unfolding-refolding cooperativity observed in the experiments (1,16) and in our simulations actually arises from the interaction of the RNA molecules and the light trap; the addition of their potentials is a two-level system (see the respective insets in the figure). Therefore, the two-level system, although it is a good approximation in the RNA folding study, should not be simply copied to the force unfolding cases.

FIGURE 5.

Comparison of the free energy landscapes of the two molecules P5ab and P5abc reconstructed from the Jarzynski equality and the exact landscapes calculated from the partition function method. The loading rates are 20 and 40 pN/s, and the number of trajectories for each case is 1000. The insets are the free energy landscapes of the whole systems composed of the RNA molecules and the light trap, which are from the partition function method. Note that we do not show the scales of the extensions and free energies.

Free energy difference estimators

In addition to Jarzynski's equality (JE), there are two other common estimators of the free energy difference: the mean work (MW) and the fluctuation-dissipation theorem estimators (FD) (32). Similar to the experiment (16), a comparison among the three estimators using our simulation should be interesting. Instead of the molecular free energies, we will use the whole free energies (the molecules and the light trap) for simplicity. Their definitions are:

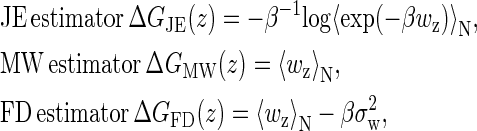where

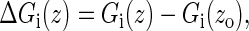(22)

i = MW, FD, and JE, and σ_w is the standard deviation of the work distribution (32) (we here replace time t by the whole extension z due to the linear relation between them). To get an intuitive observation about the estimators, we calculate the free energy differences between the estimators and the exact free energies,

(23)

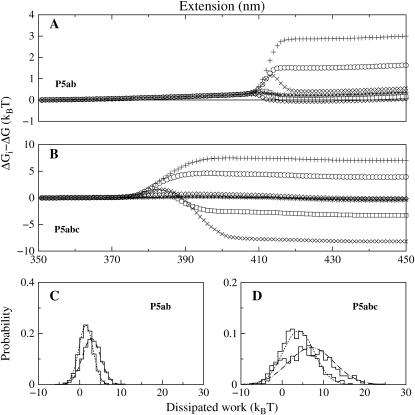
The differences of P5ab and P5abc with the loading rates 20 and 40 pN/s, respectively, are shown in Fig. 6, A and B, and N = 1000.

FIGURE 6.

(A,B) The differences between the three free energy estimators and the exact energies for P5ab and P5abc at two loading rates 20 (solid symbols) and 40 pN/s (crossed symbols): MW (circle and plus sign), FD (square and multiplication sign), and JE (diamond and star); here N = 1000. (C, D) Histograms of the dissipated works at extension z = 430 nm for P5ab and P5abc molecules at the two loading rates. The solid lines are Gaussian functions with mean and variance from the same data set, the dotted lines are for 20 pN/s, and the dashed lines are for 40 pN/s.

There are two common features in the figure. First, the free energy differences for each estimator are not uniform along the molecular extension. For example for JE estimator, the differences are maximum around the unfolding extensions such as 415 nm for P5ab. We conclude that nonequilibrium behaviors of the same molecule are not uniform along its extension, even if the RNA is unfolded with the same loading rate. Then for both the molecules, the JE estimator is always better than the MW at any loading rates. For the P5ab case, the FD estimator is more or less better than the JE at the extension z > 415 nm. This trend is more apparent as P5ab is unfolded with smaller loading rate 20 pN/s. In contrast, the JE estimator for P5abc is superior to the FD estimator over the entire extension range at the two loading rates.

These interesting observations can be understood from the distributions of the dissipated works

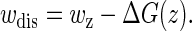(24)

Fig. 6, C and D, show the histograms at a given distance z = 430 nm, respectively. We find that for P5ab cases at the loading rates, the distributions agree well with Gaussian functions whose means and variances are obtained from the same data. This agreement is not unexpected: When a system is in the near-equilibrium regime, it always has a Gaussian dissipated work distribution, and in particular, an important equality, (32)

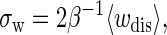(25)

holds (in our data set σ_w = 2.86 (k_BT)² and 〈w_dis〉 = 1.57 k_BT). Indeed, the force-extension curves of P5ab at lower rates have implicated this conclusion (see Fig. 3 A); whereas for the P5abc cases, we cannot obtain similar results because the system is driven far from equilibrium at the given loading rates (see Fig. 6 D).

Because the above analysis is carried out at a given N-value over a specific data set, we do not consider the errors caused by the value of N and the difference of samples. Gore et al. (33) have studied the issues in the large N limit and in the near-equilibrium regime. Our simulations also demonstrate correctness of their conclusions (F. Liu, unpublished data).

CONCLUSION

In this work, we improve our previous stochastic model to correctly take into account the time-dependent force by using the time-dependent CTMC method. We mainly consult with two recent RNA force unfolding experiments carried out by the Bustamante group (1,16). The simple RNA thermodynamic and kinetic properties under mechanical forces have been investigated. Combined with our previous effort for the constant force ensemble, our results show that, in contrast to protein cases, using the single polymer elastic theory and the RNA secondary structure free energy knowledge, we can successively simulate various behaviors of force unfolding RNAs under different experimental setups from equilibrium to far-from equilibrium. We hope that our simulations would be more useful in RNA unfolding studies in the future.