Abstract
The reversal potential of GABAA receptor channels is known to be less negative than the resting membrane potential under some cases. Recent electrophysiological experiments revealed that a GABAergic unitary conductance with such a depolarized reversal potential could not only prevent but also facilitate action potential generation depending on the timing of its application relative to the excitatory unitary conductance. Using a two-dimensional point neuron model, we simulate the experiments regarding the integration of unitary conductances, and execute bifurcation analysis. Then we extend our analysis to the case in which the neuron receives two kinds of periodic input trains—an excitatory one and a GABAergic one. We show that the periodic depolarizing GABAergic input train can modulate the output time-averaged firing rate bidirectionally, namely as an increase or a decrease, in a devil's-staircase-like manner depending on the phase difference with the excitatory input train. Bifurcation analysis reveals the existence of a wide variety of phase-locked solutions underlying such a graded response of the neuron. We examine how the input time-width and the value of the GABAA reversal potential affect the response. Moreover, considering a neuronal population, we show that depolarizing GABAergic inputs bidirectionally modulate the amplitude of the oscillatory population activity.
INTRODUCTION
GABA (γ-aminobutyric acid), one of the principal neurotransmitters in the vertebrate central nervous system, is classically considered to have inhibitory effects in mature animals. However, the value of the reversal potential of GABAA receptor channels is known to possibly be less negative than the resting membrane potential, though it is still lower than the firing threshold, in mature neocortical pyramidal cells (1), as well as fast spiking cells (2) or striatal spiny neurons (3). Moreover, in hippocampal cultures and slices, it was recently shown that GABAergic stimulation combined with postsynaptic spiking results in the long-term increase of the GABAA reversal potential (4). Gulledge and Stuart showed that, due to such a depolarized value of the reversal potential, GABAergic unitary conductances could, depending on the timing of their application relative to the excitatory unitary conductance, facilitate action potential generation (5).
Although several experiments have indirectly demonstrated this paradoxical excitatory action of GABA (6,7), its functional relevance has not been thoroughly examined. We used a two-dimensional point neuron model to explore the possible roles of depolarizing GABAergic conductances on the neuronal input-output relationship, and we suggested that a highly fluctuating depolarizing GABAergic conductance would achieve discriminative firing rate modulation (8). This modulation decreases the firing rate if and only if it has a considerable temporal correlation with the fluctuating glutamatergic conductance. In this article, we explore other aspects of the depolarizing GABAergic inputs using the same Wilson's two-dimensional neuron model. Specifically, we examine transient unitary and periodic waveforms of depolarizing GABAergic inputs. First, we show through a numerical simulation that Wilson's neuron model with α-function unitary conductances qualitatively reproduces the experimental results of Gulledge and Stuart (5), that GABAergic unitary inputs temporally adjacent to glutamatergic unitary inputs have inhibitory effects whereas GABAergic inputs more advanced in time have excitatory effects. We perform a bifurcation analysis of the model using periodic inputs with long periods as substitutes for transient unitary inputs. We then examine neural responses to periodic glutamatergic and GABAergic inputs whose periods are in the range of the cortical γ-oscillation. We explore through a numerical simulation and bifurcation analysis how the input time-width, or the temporal jitter on the compound input, and the value of the GABAA reversal potential affect the response characteristics of the neuron. Finally, we discuss the implications for the strategy of neuronal coding.
METHODS
Neuron model
We use the single-compartment model of a neocortical neuron proposed by Wilson (9,10):
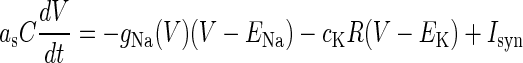 |
(1) |
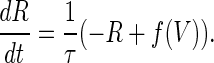 |
(2) |
Here, V (mV) is the membrane potential (inside against outside); R is the inactivation variable that qualitatively represents the conductance of the potassium channels; 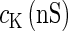 is a certain constant;
is a certain constant; 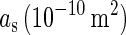 is the area of the axon hillock and the initial segment;
is the area of the axon hillock and the initial segment; 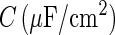 is the membrane capacitance per unit area;
is the membrane capacitance per unit area; 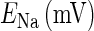 and
and 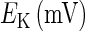 are the respective reversal potentials of sodium and potassium channels;
are the respective reversal potentials of sodium and potassium channels; 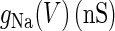 is the steady-state voltage-dependent sodium conductance; f(V) is the voltage dependence of the potassium channels, including both the delayed-rectifier channels and the A-current channels; and
is the steady-state voltage-dependent sodium conductance; f(V) is the voltage dependence of the potassium channels, including both the delayed-rectifier channels and the A-current channels; and 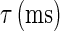 is the time constant of the inactivation variable. The forms of the functions
is the time constant of the inactivation variable. The forms of the functions 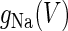 and f(V), as well as the values of other parameters, were determined by Wilson (10) as
and f(V), as well as the values of other parameters, were determined by Wilson (10) as 
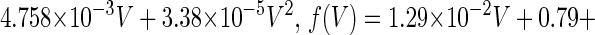
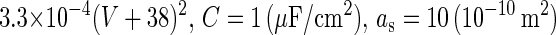 (that is, equal to
(that is, equal to 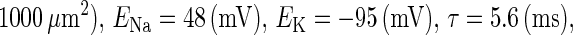 and
and 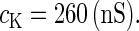 The area can be calculated from other defined values.
The area can be calculated from other defined values.  in Eq. 1 represents the following current through synaptic channels:
in Eq. 1 represents the following current through synaptic channels:
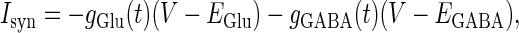 |
(3) |
where 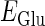 and
and 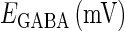 represent the reversal potentials of the channels coupled with non-NMDA glutamate receptors and GABAA receptors, respectively;
represent the reversal potentials of the channels coupled with non-NMDA glutamate receptors and GABAA receptors, respectively; 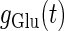 and
and 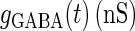 represent the corresponding total time-dependent synaptic conductances. NMDA and GABAB receptors are not considered in this article. Although Wilson's neuron model usually generates action potentials with similar shapes, sometimes it generates a wave form of the membrane potential that is difficult to classify into either an action potential or a subthreshold fluctuation. To work around such a case, we set a critical value of the membrane potential to V = 0 (mV): we regard that the neuron generates an action potential if the membrane potential passes through this V = 0 (mV) from below, otherwise a membrane potential transient is regarded as a subthreshold fluctuation.
represent the corresponding total time-dependent synaptic conductances. NMDA and GABAB receptors are not considered in this article. Although Wilson's neuron model usually generates action potentials with similar shapes, sometimes it generates a wave form of the membrane potential that is difficult to classify into either an action potential or a subthreshold fluctuation. To work around such a case, we set a critical value of the membrane potential to V = 0 (mV): we regard that the neuron generates an action potential if the membrane potential passes through this V = 0 (mV) from below, otherwise a membrane potential transient is regarded as a subthreshold fluctuation.
Reversal potentials
In this article, we are primarily interested in the case in which the GABAA reversal potential lies between the resting membrane potential and the firing threshold. Thus we set the standard value of the GABAA reversal potential of Wilson's model at −64 mV, which is more depolarized than the resting potential (−75.4 mV) but more hyperpolarized than the steady-state firing threshold (−58.2 mV) of the model, and is at nearly the same proportional level as in the Gulledge-Stuart experiments (5). Please refer to Morita et al. (8) for detailed information. In some analyses, we test the effects of varying the GABAA reversal potential. The reversal potential of the non-NMDA glutamate receptor channel is set to 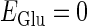 (mV) throughout this article.
(mV) throughout this article.
Bifurcation analysis
Consider the following general representation of n-dimensional nonautonomous differential equations:
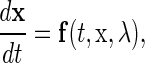 |
(4) |
where 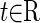 denotes time;
denotes time; 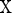 denotes the state variables in
denotes the state variables in 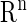 ; and
; and 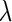 denotes the parameters in
denotes the parameters in 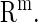 We represent a solution of Eq. 4 with an initial condition
We represent a solution of Eq. 4 with an initial condition 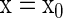 at
at 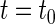 as
as 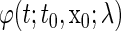 for all t. If
for all t. If 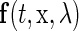 is a periodic function with respect to t with a period T such that
is a periodic function with respect to t with a period T such that
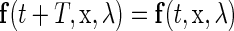 |
(5) |
is satisfied for all 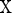 and
and 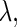 we can define the Poincaré, or stroboscopic map S from the state space
we can define the Poincaré, or stroboscopic map S from the state space 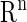 into itself as follows:
into itself as follows:
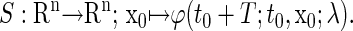 |
(6) |
The study of the periodic solution of Eq. 4 is topologically equivalent to the study of a fixed point of the map S. Let 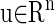 be a fixed point of S:
be a fixed point of S:
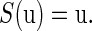 |
(7) |
Then the characteristic equation of the fixed point 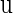 is defined by
is defined by
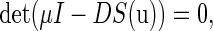 |
(8) |
where I is the n × n identity matrix, and 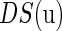 denotes the derivative of S with respect to the state variables. The solutions of Eq. 8 are the characteristic multipliers at the fixed point
denotes the derivative of S with respect to the state variables. The solutions of Eq. 8 are the characteristic multipliers at the fixed point 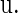 The codimension-one bifurcations that could occur in Eq. 4 are the saddle-node (tangent) bifurcation, the period-doubling bifurcation, and the Neimark-Sacker bifurcation, which is the discrete analog of the Andronov-Hopf bifurcation. These bifurcations occur when one of the characteristic multipliers, i.e., the solutions of Eq. 8, is
The codimension-one bifurcations that could occur in Eq. 4 are the saddle-node (tangent) bifurcation, the period-doubling bifurcation, and the Neimark-Sacker bifurcation, which is the discrete analog of the Andronov-Hopf bifurcation. These bifurcations occur when one of the characteristic multipliers, i.e., the solutions of Eq. 8, is
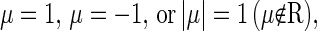 |
(9) |
respectively. Each case in Eq. 9 describes a specific relationship among the system's parameters 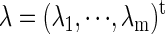 corresponding to each type of bifurcation. Therefore, if we fix all the parameters except for two, for example
corresponding to each type of bifurcation. Therefore, if we fix all the parameters except for two, for example 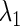 and
and 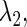 we can define, although theoretically, the relationship between
we can define, although theoretically, the relationship between 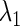 and
and 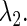 The curve representing this function on the
The curve representing this function on the  plane is called a bifurcation curve, of which we show many examples. In practice, though, because usually neither Eq. 7 nor Eq. 8 can be solved analytically, they require numerical solution. Specifically, we fix all but one, say
plane is called a bifurcation curve, of which we show many examples. In practice, though, because usually neither Eq. 7 nor Eq. 8 can be solved analytically, they require numerical solution. Specifically, we fix all but one, say 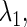 parameters, and then numerically solve Eqs. 7 and 8 as a simultaneous equation for
parameters, and then numerically solve Eqs. 7 and 8 as a simultaneous equation for 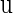 and
and 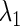 using the Newton method (11). Next, we slightly change the value of one of the other parameters, say
using the Newton method (11). Next, we slightly change the value of one of the other parameters, say 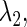 and then repeat the same procedure so as to obtain a new
and then repeat the same procedure so as to obtain a new 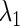 value. Repeating this procedure while gradually changing the value of
value. Repeating this procedure while gradually changing the value of 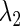 will yield a
will yield a  bifurcation curve. To execute the Newton method for Eqs. 7 and 8, we need to know the first- and the second-order derivatives of S with regard to
bifurcation curve. To execute the Newton method for Eqs. 7 and 8, we need to know the first- and the second-order derivatives of S with regard to 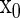 and
and 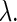 To do so, we numerically solve variational equations for them using the Runge-Kutta method. How to execute them, especially when the system's initial condition is partially reset to produce an α-function during each period, as is the case in this article, was described before (12,13).
To do so, we numerically solve variational equations for them using the Runge-Kutta method. How to execute them, especially when the system's initial condition is partially reset to produce an α-function during each period, as is the case in this article, was described before (12,13).
Mutual information
To quantify the amount of information transfer between the input signal, or the phase difference of the periodic glutamatergic and GABAergic inputs, and the output signal, or the time-averaged firing rate of a neuron, we calculate the mutual information between them. However, because we deal with deterministic, rather than stochastic, dynamics in most cases, simultaneous probability of the input signal and the output signal is equal to 0 unless multistability appears, from its usual definition, and thus the mutual information in its naive definition is simply equal to the information entropy of the output signal, except for some constant corresponding to the information entropy of the input signal, for which we assume the uniform distribution. To obtain a more meaningful definition of the mutual information, therefore, we adopt some coarse-graining of the input signal, or the phase difference, so that the simultaneous probabilities become positive. Specifically, we calculated the output firing rates for 250 uniformly distributed points in the whole range of the input phase difference (time difference), i.e., 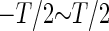 (see below for details). Subsequently, we divided the whole range of the input signal into 25 bins, each of which contains 10 points where the output firing rates are calculated, and regarded the distributions of the output firing rates in individual bins as their “probability distributions”. We also divided the whole range of the output signal, 0 ∼ 40 (Hz), into 20 bins, and then calculate the simultaneous probabilities and mutual information. Because this value depends on the way of dividing the range of the input signal into the bins, we took an average of the values of the mutual information over all the possible shifts about the division into the bins.
(see below for details). Subsequently, we divided the whole range of the input signal into 25 bins, each of which contains 10 points where the output firing rates are calculated, and regarded the distributions of the output firing rates in individual bins as their “probability distributions”. We also divided the whole range of the output signal, 0 ∼ 40 (Hz), into 20 bins, and then calculate the simultaneous probabilities and mutual information. Because this value depends on the way of dividing the range of the input signal into the bins, we took an average of the values of the mutual information over all the possible shifts about the division into the bins.
Simulation and numerical calculation
We numerically solved the ordinary differential equations described as Eqs. 1 and 2 by the fourth-order Runge-Kutta method for the right panel of Fig. 4 a and the lower panels of Figs. 5 a and 6 a. Other calculations and simulations were done by MATLAB (The MathWorks, Natick, MA) (14) using a built-in function “ode23”, except for Figs. 9 and 10 that were calculated using the forward Euler method with a time step of 0.01 ms. To obtain dependence of the firing rate of the neuron model on the time difference between two sorts of glutamatergic and GABAergic periodic input trains, we calculated the time-averaged firing rate for 1000 ms for 250 uniformly distributed points in the whole range of the time difference, i.e., 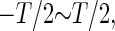 for Figs. 4 f, 5 b, 6 b, and 8 a. As for the population activity, at first we calculated the “population sum of activity”, that is, the number of neurons, out of the total 100 neurons, that fire in each 1 ms time bin, as shown in the lower panels of Fig. 10, a and b. Then we performed fast Fourier transformation on the population sum of activity vector for 1000 ms with the 1-ms time bin using a MATLAB built-in function “fft” for the right panels of Fig. 10, a and b.
for Figs. 4 f, 5 b, 6 b, and 8 a. As for the population activity, at first we calculated the “population sum of activity”, that is, the number of neurons, out of the total 100 neurons, that fire in each 1 ms time bin, as shown in the lower panels of Fig. 10, a and b. Then we performed fast Fourier transformation on the population sum of activity vector for 1000 ms with the 1-ms time bin using a MATLAB built-in function “fft” for the right panels of Fig. 10, a and b.
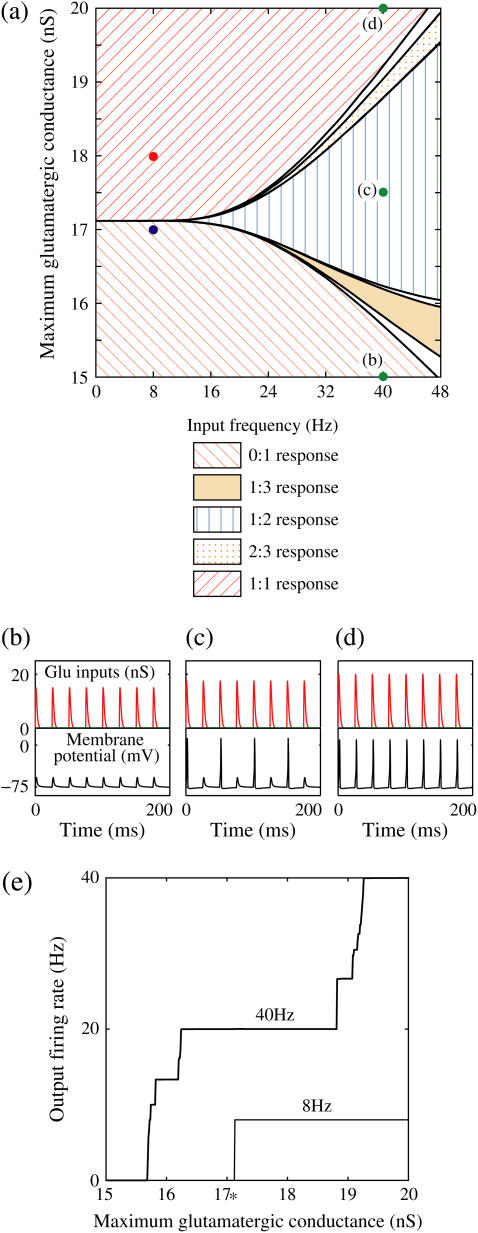
FIGURE 4.
Neuronal responses to periodic glutamatergic and GABAergic inputs of γ-frequency: simulation and bifurcation analysis. (a) The left panel shows the numerically calculated bifurcation sets with respect to Δt and 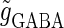 under the fixed parameters T = 25 (ms),
under the fixed parameters T = 25 (ms), 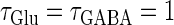 (ms), and
(ms), and 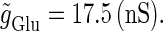 Solid and dashed lines indicate numerically calculated saddle-node and period-doubling bifurcation curves, respectively. The right panel is a corresponding result by explicit simulation of Eqs. 1 and 2 using the Runge-Kutta method; different colors indicate solutions with different periods. The colors listed right below indicate the periods of the solution: the numbers under the colors indicate how many input cycles are included in the period of the solution. These colors are commonly used throughout this article. (b–e) Glutamatergic and GABAergic synaptic conductances indicated by red solid and green dotted lines, respectively (top panels), and resulting wave forms of the membrane potential (bottom panels) at the locations in the 0:1 (b), 1:2 (c), 2:3 (d), and 1:1 (e) phase-locked regions, as indicated by red circles in panel a. (f) The relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs
Solid and dashed lines indicate numerically calculated saddle-node and period-doubling bifurcation curves, respectively. The right panel is a corresponding result by explicit simulation of Eqs. 1 and 2 using the Runge-Kutta method; different colors indicate solutions with different periods. The colors listed right below indicate the periods of the solution: the numbers under the colors indicate how many input cycles are included in the period of the solution. These colors are commonly used throughout this article. (b–e) Glutamatergic and GABAergic synaptic conductances indicated by red solid and green dotted lines, respectively (top panels), and resulting wave forms of the membrane potential (bottom panels) at the locations in the 0:1 (b), 1:2 (c), 2:3 (d), and 1:1 (e) phase-locked regions, as indicated by red circles in panel a. (f) The relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs 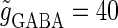 (nS). The firing rate was calculated by numerically solving Eqs. 1 and 2 for 1000 ms.
(nS). The firing rate was calculated by numerically solving Eqs. 1 and 2 for 1000 ms.
FIGURE 5.
Neuronal responses to periodic glutamatergic and GABAergic inputs of γ-frequencies in the case when the input time-width is 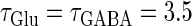 (ms). (a) The top panel shows the numerically calculated bifurcation sets with respect to Δt and
(ms). (a) The top panel shows the numerically calculated bifurcation sets with respect to Δt and 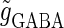 under the fixed parameters T = 25 (ms),
under the fixed parameters T = 25 (ms), 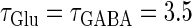 (ms), and
(ms), and 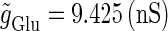 that gives a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs. Solid and dashed lines indicate numerically calculated saddle-node and period-doubling bifurcation curves, respectively. The bottom panel is a corresponding result by explicit simulation of Eqs. 1 and 2 using the Runge-Kutta method. (b) The relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs
that gives a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs. Solid and dashed lines indicate numerically calculated saddle-node and period-doubling bifurcation curves, respectively. The bottom panel is a corresponding result by explicit simulation of Eqs. 1 and 2 using the Runge-Kutta method. (b) The relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs 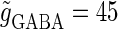 (nS).
(nS).
FIGURE 6.
Neuronal responses to periodic glutamatergic and GABAergic inputs of γ-frequencies in the case when the input time-width is 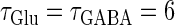 (ms).
(ms). 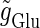 is fixed to
is fixed to 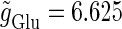 (nS) that gives a 1:2 phase-locked response in the absence of GABAergic inputs, and
(nS) that gives a 1:2 phase-locked response in the absence of GABAergic inputs, and 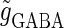 is fixed to
is fixed to 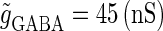 in panel b.
in panel b.
FIGURE 9.
Effects of small temporal fluctuations of timings, durations, and amplitudes of the periodic inputs on the phase-to-rate transformation. To test the effects of temporal fluctuations, we added Gaussian noise on the parameters 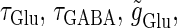 and
and 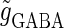 with standard deviations of 5% of the original parameter values. (a) The phase-to-rate transformation when
with standard deviations of 5% of the original parameter values. (a) The phase-to-rate transformation when 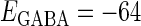 (mV) and
(mV) and 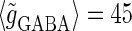 (nS) without (the gray line) and with (the black line) fluctuations. (b) The phase-to-rate transformation when
(nS) without (the gray line) and with (the black line) fluctuations. (b) The phase-to-rate transformation when 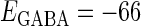 (mV) and
(mV) and 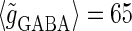 (nS) without (the gray line) and with (the black line) fluctuations. In both panels a and b, T = 25 (ms),
(nS) without (the gray line) and with (the black line) fluctuations. In both panels a and b, T = 25 (ms), 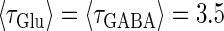 (ms), and
(ms), and 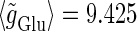 (nS), realizing a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs and of fluctuation on glutamatergic inputs.
(nS), realizing a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs and of fluctuation on glutamatergic inputs.
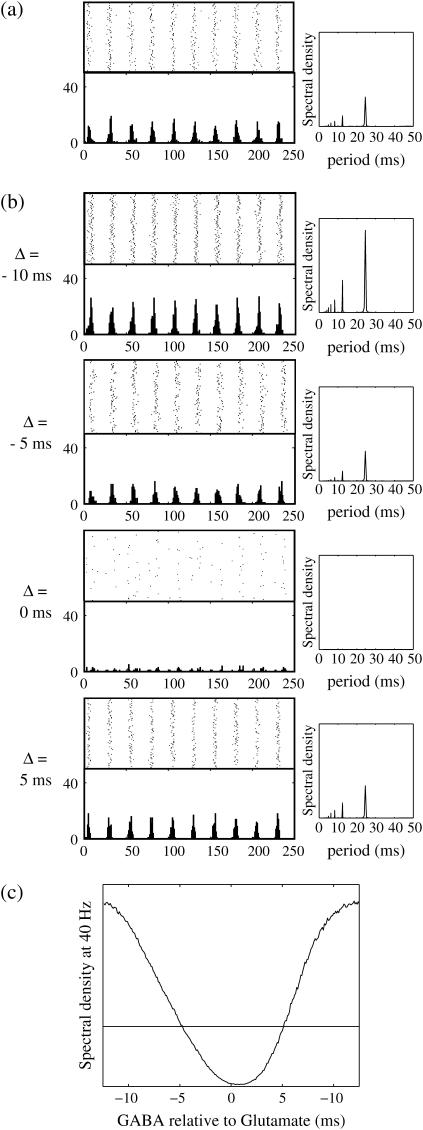
FIGURE 10.
Phase-to-amplitude transformation by a population of neurons. (a) Raster plot (upper left panel) and histogram (lower left panel) of a neuronal population composed of 100 neurons receiving the common 40 Hz glutamatergic input train with 5% of independent fluctuation on its amplitude, timing, and duration, in the absence of GABAergic inputs. The parameters are T = 25 (ms), 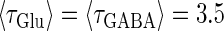 (ms), and
(ms), and 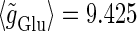 (nS), giving a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs and also without fluctuation on glutamatergic inputs. The right panel shows the power spectrum (vertical axis) versus the period (horizontal axis) obtained by fast Fourier transformation. (b) Raster plots, histograms, and Fourier spectra of 100 neurons receiving 40 Hz glutamatergic input train and depolarizing GABAergic trains with
(nS), giving a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs and also without fluctuation on glutamatergic inputs. The right panel shows the power spectrum (vertical axis) versus the period (horizontal axis) obtained by fast Fourier transformation. (b) Raster plots, histograms, and Fourier spectra of 100 neurons receiving 40 Hz glutamatergic input train and depolarizing GABAergic trains with 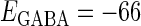 (mV) and
(mV) and 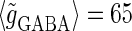 (nS), both of which contain 5% of fluctuations on their amplitudes, timings, and durations. Four cases are shown: the temporal difference between glutamatergic input and GABAergic input is, from top to bottom, −10, −5, 0, and 5 ms. (c) Dependence of the power spectrum of the population activity at 40 Hz on the time difference between glutamatergic and GABAergic periodic input trains. The horizontal black line indicates the value in the absence of GABAergic inputs for comparison.
(nS), both of which contain 5% of fluctuations on their amplitudes, timings, and durations. Four cases are shown: the temporal difference between glutamatergic input and GABAergic input is, from top to bottom, −10, −5, 0, and 5 ms. (c) Dependence of the power spectrum of the population activity at 40 Hz on the time difference between glutamatergic and GABAergic periodic input trains. The horizontal black line indicates the value in the absence of GABAergic inputs for comparison.
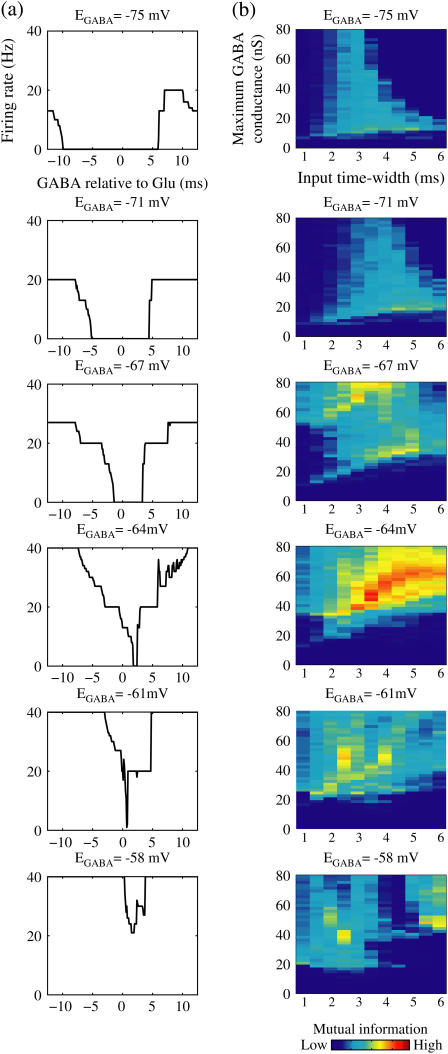
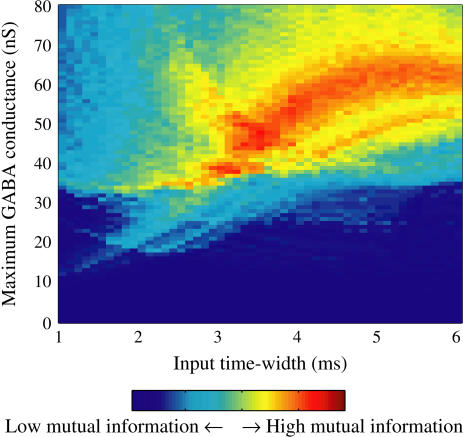
FIGURE 8.
Effects of change in the value of the GABAA reversal potential on the neuronal response to periodic glutamatergic and GABAergic inputs. (a) The relationships between the time difference Δt (ms) and the neuronal firing rate for the different values of the GABAA reversal potential indicated. The GABAA reversal potential is varied from 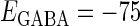 (mV) (top panel), which is equal to the resting potential of Wilson's model, to
(mV) (top panel), which is equal to the resting potential of Wilson's model, to 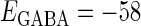 (mV) (bottom panel), which is equal to the firing threshold. The time-widths of the glutamatergic and GABAergic inputs are fixed to
(mV) (bottom panel), which is equal to the firing threshold. The time-widths of the glutamatergic and GABAergic inputs are fixed to 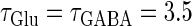 (ms). The maximum amplitude of the glutamatergic inputs is fixed so that the neuron shows a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs, and the maximum amplitude of the GABAergic inputs is fixed to be
(ms). The maximum amplitude of the glutamatergic inputs is fixed so that the neuron shows a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs, and the maximum amplitude of the GABAergic inputs is fixed to be 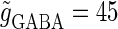 (nS). (b) The dependence of the mutual information (see Methods for details) between the input phase difference and the output firing rate on the input time-width (the horizontal axis) and the maximum amplitude of the GABAergic inputs (the vertical axis) when the value of the GABAA reversal potential is systematically varied from
(nS). (b) The dependence of the mutual information (see Methods for details) between the input phase difference and the output firing rate on the input time-width (the horizontal axis) and the maximum amplitude of the GABAergic inputs (the vertical axis) when the value of the GABAA reversal potential is systematically varied from 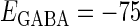 (mV), the resting potential, to
(mV), the resting potential, to 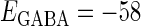 (mV), the firing threshold. The color represents the amount of mutual information as indicated by the color bar at the bottom.
(mV), the firing threshold. The color represents the amount of mutual information as indicated by the color bar at the bottom.
RESULTS
Excitatory and inhibitory actions of GABAergic unitary conductance simulation
First, we examine whether Wilson's model can reproduce timing-dependent excitatory and inhibitory actions of GABAergic unitary inputs observed in the experiments by Gulledge and Stuart (5). In their conductance injection (dynamic-clamp) experiments, the time courses of the glutamatergic unitary conductance and the GABAergic conductance were, respectively, represented by a mixture of two or three exponential functions. Using the same unitary conductance functions, we have shown that Wilson's model can quantitatively well reproduce their experimental results (8). However, in many experimental and modeling studies, the time courses of the unitary conductances are fitted or modeled by α-functions. Because we are interested in the qualitative rather than quantitative nature, we use the mathematically simpler α-functions as follows (see Fig. 1 a):
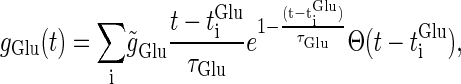 |
(10) |
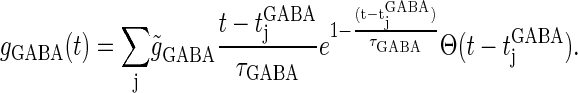 |
(11) |
Here, 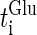 and
and 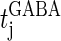 are the onset times of the ith glutamatergic unitary conductance and the jth GABAergic one, respectively;
are the onset times of the ith glutamatergic unitary conductance and the jth GABAergic one, respectively; 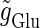 and
and 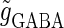 are the maximum values of the single glutamatergic and GABAergic unitary conductances, respectively;
are the maximum values of the single glutamatergic and GABAergic unitary conductances, respectively; 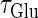 and
and 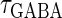 are the time constants of the α-functions representing the durations from the onsets to the time when they reach the maximums;
are the time constants of the α-functions representing the durations from the onsets to the time when they reach the maximums; 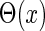 represents a Heaviside step function such that
represents a Heaviside step function such that 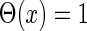 if
if 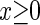 and
and 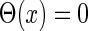 otherwise.
otherwise.
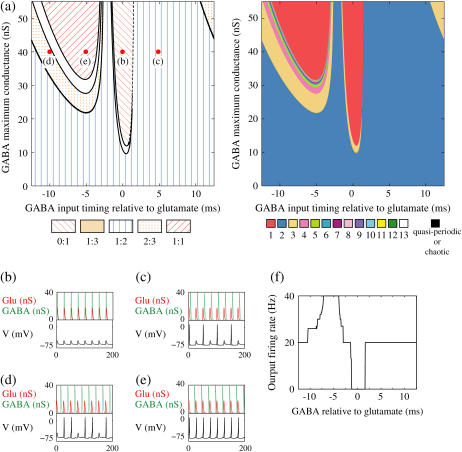
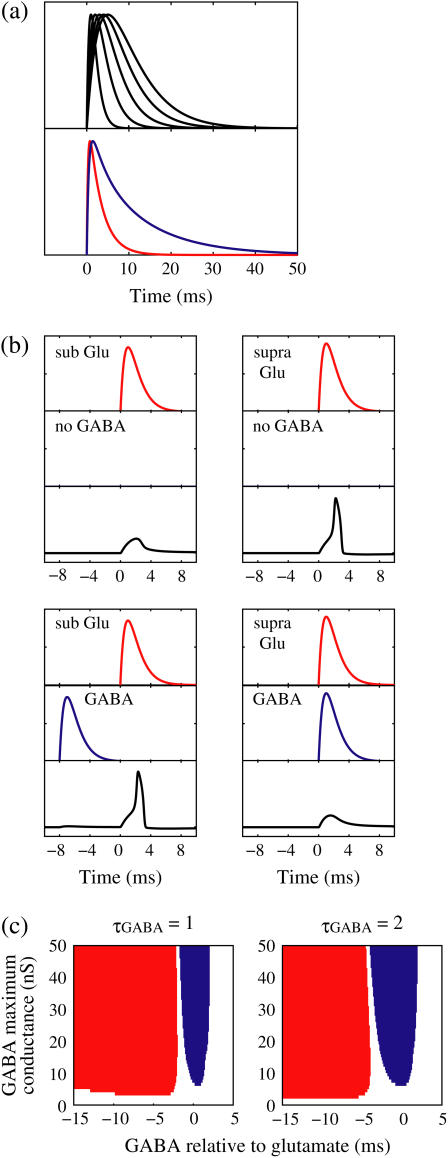
FIGURE 1.
Excitatory and inhibitory actions of GABA: simulation results. (a) The top panel shows the wave forms of the α-functions represented by Eq. 10 or Eq. 11 with various time constants: 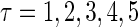 from the left to the right. For comparison, the bottom panel shows the wave forms of glutamatergic (red line) and GABAergic (blue line) synaptic conductances in the Gulledge-Stuart experiments (5) fitted by differences of two or three exponentials. (b) Reproduction of the Gulledge-Stuart experiments using Wilson's neuron model and the α-function synaptic inputs. Top, middle, and bottom traces in each panel represent glutamatergic synaptic inputs, GABAergic synaptic inputs, and the membrane potentials, respectively. (Left column) A subthreshold glutamatergic input cannot evoke an action potential by itself (top), but a GABAergic input preceding the subthreshold glutamatergic input by 8 ms facilitates action potential generation (bottom). (Right column) A suprathreshold glutamatergic input can evoke an action potential (top), but a GABAergic input coincident with the suprathreshold glutamatergic input prevents action potential generation (bottom). (c) Summary of the excitatory or inhibitory actions for
from the left to the right. For comparison, the bottom panel shows the wave forms of glutamatergic (red line) and GABAergic (blue line) synaptic conductances in the Gulledge-Stuart experiments (5) fitted by differences of two or three exponentials. (b) Reproduction of the Gulledge-Stuart experiments using Wilson's neuron model and the α-function synaptic inputs. Top, middle, and bottom traces in each panel represent glutamatergic synaptic inputs, GABAergic synaptic inputs, and the membrane potentials, respectively. (Left column) A subthreshold glutamatergic input cannot evoke an action potential by itself (top), but a GABAergic input preceding the subthreshold glutamatergic input by 8 ms facilitates action potential generation (bottom). (Right column) A suprathreshold glutamatergic input can evoke an action potential (top), but a GABAergic input coincident with the suprathreshold glutamatergic input prevents action potential generation (bottom). (c) Summary of the excitatory or inhibitory actions for 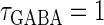 (ms) (left panel) and
(ms) (left panel) and 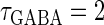 (ms) (right panel). The horizontal axis shows the timing of a GABAergic input relative to a glutamatergic input (ms). The vertical axis represents the maximum conductance of a GABAergic input (
(ms) (right panel). The horizontal axis shows the timing of a GABAergic input relative to a glutamatergic input (ms). The vertical axis represents the maximum conductance of a GABAergic input (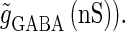 Red indicates the region where a GABAergic input has a facilitatory action; that is, where it evokes an action potential in cooperation with a subthreshold
Red indicates the region where a GABAergic input has a facilitatory action; that is, where it evokes an action potential in cooperation with a subthreshold 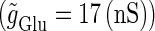 glutamatergic input. Blue indicates the region where a GABAergic input has an inhibitory action; that is, it prevents action potential generation by a suprathreshold (
glutamatergic input. Blue indicates the region where a GABAergic input has an inhibitory action; that is, it prevents action potential generation by a suprathreshold (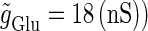 glutamatergic input. White indicates the region where a GABAergic input has no action in the above sense.
glutamatergic input. White indicates the region where a GABAergic input has no action in the above sense.
We numerically analyze the interaction of a single glutamatergic and a GABAergic unitary conductance represented by the α-functions with 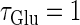 (ms) and
(ms) and 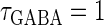 (ms), respectively. In this setting, a single glutamatergic unitary conductance cannot evoke an action potential if its maximum (
(ms), respectively. In this setting, a single glutamatergic unitary conductance cannot evoke an action potential if its maximum (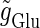 ) is 17 nS, but can do so if
) is 17 nS, but can do so if 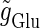 is 18 nS. We use these values as the subthreshold and the suprathreshold input, respectively. If a single GABAergic unitary conductance in cooperation with the subthreshold
is 18 nS. We use these values as the subthreshold and the suprathreshold input, respectively. If a single GABAergic unitary conductance in cooperation with the subthreshold 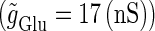 glutamatergic input evokes an action potential, it is said to have an excitatory action. On the other hand, if a single GABAergic unitary conductance inhibits spike generation by the suprathreshold
glutamatergic input evokes an action potential, it is said to have an excitatory action. On the other hand, if a single GABAergic unitary conductance inhibits spike generation by the suprathreshold 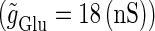 glutamatergic input, it is said to have an inhibitory action. We examine under what conditions GABAergic unitary conductances have excitatory or inhibitory actions. For example, a GABAergic unitary conductance that precedes a subthreshold glutamatergic input by 8 ms facilitates action potential generation (the left column of Fig. 1 b), whereas another GABAergic unitary conductance coincident with a suprathreshold glutamatergic input prevents spike generation (the right column of Fig. 1 b). As summarized in the left panel of Fig. 1 c, a GABAergic unitary conductance with the same time constant and the same maximum value as the associated subthreshold glutamatergic unitary conductance has an excitatory action if it arrives ∼2 ms or more before the glutamatergic input. On the other hand, a GABAergic unitary conductance appears to have an inhibitory action if it arrives within ∼ ± 2 ms of the glutamatergic input. In this way, Wilson's model with the depolarized GABAA reversal potential can qualitatively reproduce the experimental results of Gulledge and Stuart (5) that GABAergic unitary conductances that are temporally adjacent to glutamatergic inputs have inhibitory effects whereas earlier GABAergic inputs have excitatory effects.
glutamatergic input, it is said to have an inhibitory action. We examine under what conditions GABAergic unitary conductances have excitatory or inhibitory actions. For example, a GABAergic unitary conductance that precedes a subthreshold glutamatergic input by 8 ms facilitates action potential generation (the left column of Fig. 1 b), whereas another GABAergic unitary conductance coincident with a suprathreshold glutamatergic input prevents spike generation (the right column of Fig. 1 b). As summarized in the left panel of Fig. 1 c, a GABAergic unitary conductance with the same time constant and the same maximum value as the associated subthreshold glutamatergic unitary conductance has an excitatory action if it arrives ∼2 ms or more before the glutamatergic input. On the other hand, a GABAergic unitary conductance appears to have an inhibitory action if it arrives within ∼ ± 2 ms of the glutamatergic input. In this way, Wilson's model with the depolarized GABAA reversal potential can qualitatively reproduce the experimental results of Gulledge and Stuart (5) that GABAergic unitary conductances that are temporally adjacent to glutamatergic inputs have inhibitory effects whereas earlier GABAergic inputs have excitatory effects.
Though the temporal borderline that divides the excitatory and inhibitory actions of GABAergic unitary conductances is ∼2 ms before the onset of the glutamatergic input in our above simulation, this boundary is located at ∼5.8 ms in the experiments by Gulledge and Stuart (5). This quantitative difference may come from the fact that the GABAergic unitary conductance in our simulation, which is the α-function with the time constant 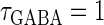 (ms) as described above, decays much faster than the one in their experiments, whose decaying time course is represented by the mixture of two exponentials with time constants of 3.2 and 12.3 ms (the blue line in the lower panel in Fig. 1 a). The inhibitory effect of GABAergic unitary conductances that are temporally adjacent to glutamatergic inputs is due to so-called shunting inhibition: the GABAergic conductance effectively shunts the current through the coinciding glutamatergic conductance. Therefore, the shunting effect of our faster decaying GABAergic conductance would be weaker than that in the experiments by Gulledge and Stuart. To confirm this idea, we examine the effects of GABAergic unitary conductances with a longer time constant of decay,
(ms) as described above, decays much faster than the one in their experiments, whose decaying time course is represented by the mixture of two exponentials with time constants of 3.2 and 12.3 ms (the blue line in the lower panel in Fig. 1 a). The inhibitory effect of GABAergic unitary conductances that are temporally adjacent to glutamatergic inputs is due to so-called shunting inhibition: the GABAergic conductance effectively shunts the current through the coinciding glutamatergic conductance. Therefore, the shunting effect of our faster decaying GABAergic conductance would be weaker than that in the experiments by Gulledge and Stuart. To confirm this idea, we examine the effects of GABAergic unitary conductances with a longer time constant of decay, 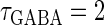 (ms). As shown in the right panel of Fig. 1 c, the borderline in this case is about 4 ∼ 5 ms before the onset of the glutamatergic input, which is closer to the result of Gulledge and Stuart. On the other hand, the facilitatory effect of depolarizing GABAergic unitary conductances that precede glutamatergic inputs results from the fact that membrane charging lasts still after the conductance change is terminated due to the membrane capacity. Therefore, the membrane capacitance, and the membrane time constant, would affect the duration for which the facilitatory effect sustains. In Wilson's model that we have used, the system's time constant τ reflects the membrane capacitance. Decreasing τ generally tends to shift the onset time of the facilitatory effect of the GABAergic input later, i.e., closer to the glutamatergic input (results not shown). Although the dependence of the excitatory and inhibitory actions on the strength of the GABAergic unitary conductance has not been examined in the experiments by Gulledge and Stuart (5), according to these simulation results, the temporal borderline has a negative slope (Fig. 1 c), indicating that as the strength of the GABAergic unitary conductance increases, the shunting effect is more enhanced than the excitatory effect of depolarization.
(ms). As shown in the right panel of Fig. 1 c, the borderline in this case is about 4 ∼ 5 ms before the onset of the glutamatergic input, which is closer to the result of Gulledge and Stuart. On the other hand, the facilitatory effect of depolarizing GABAergic unitary conductances that precede glutamatergic inputs results from the fact that membrane charging lasts still after the conductance change is terminated due to the membrane capacity. Therefore, the membrane capacitance, and the membrane time constant, would affect the duration for which the facilitatory effect sustains. In Wilson's model that we have used, the system's time constant τ reflects the membrane capacitance. Decreasing τ generally tends to shift the onset time of the facilitatory effect of the GABAergic input later, i.e., closer to the glutamatergic input (results not shown). Although the dependence of the excitatory and inhibitory actions on the strength of the GABAergic unitary conductance has not been examined in the experiments by Gulledge and Stuart (5), according to these simulation results, the temporal borderline has a negative slope (Fig. 1 c), indicating that as the strength of the GABAergic unitary conductance increases, the shunting effect is more enhanced than the excitatory effect of depolarization.
Bifurcations associated with the excitatory and inhibitory actions of GABAergic unitary conductance
Next, we examine the dynamics of the interaction between a glutamatergic and a GABAergic unitary conductance through bifurcation analysis. Because it is generally difficult to compute the bifurcation sets for a dynamical system with such a transient time-varying driving force, we examine the dynamics of the interaction between periodic glutamatergic and GABAergic input trains as an approximation, assuming that their period is substantially longer than the system's intrinsic time constant (τ = 5.6 (ms)).
At first, let us consider the case where the neuron receives a periodic glutamatergic input train in the absence of GABAergic inputs. Specifically, we assume that 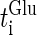 in Eq. 10 is periodic with period T (ms), that is,
in Eq. 10 is periodic with period T (ms), that is, 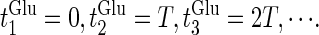 We numerically calculate bifurcation sets with respect to the frequency (1/T) and the maximum conductance
We numerically calculate bifurcation sets with respect to the frequency (1/T) and the maximum conductance  for fixed values of the time constant
for fixed values of the time constant  (ms) (see Methods for details). Fig. 2 a shows such bifurcation curves in the
(ms) (see Methods for details). Fig. 2 a shows such bifurcation curves in the 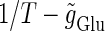 parameter plane in the case with
parameter plane in the case with 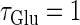 (ms). Solid lines indicate saddle-node bifurcation curves obtained numerically. There are two predominant regions, occupying large portions of this
(ms). Solid lines indicate saddle-node bifurcation curves obtained numerically. There are two predominant regions, occupying large portions of this 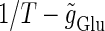 parameter plane, where the periodic solution has the same period (T (ms)) as the periodic driving force (
parameter plane, where the periodic solution has the same period (T (ms)) as the periodic driving force (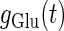 ). In the upper region, the amplitude of this periodic solution is larger than the value V = 0 (mV), which was the critical value expediently set as action potential threshold (see Methods for details), as shown in Fig. 2 d. Therefore, in this region the neuron generates a single action potential on every cycle, with the firing frequency 1000/T (Hz), and thus it is called a 1:1 phase-locked response. On the other hand, in the lower region, the amplitude of the periodic solution is smaller than the value V = 0 (mV), as shown in Fig. 2 b, so that it may well be regarded as a subthreshold oscillation without action potentials. Therefore, in this region the neuron generates no action potential, i.e., the frequency is 0 (Hz), and thus it is called a 0:1 phase-locked state. As shown in Fig. 2 a, between these 1:1 and 0:1 phase-locked states, there are several regions separated from each other by a series of saddle-node bifurcation curves. Among them, the most predominant region is the middlemost one. In this region, the period of the solution is twice the period of the driving force, and the state variable V passes through the value V = 0 (mV) once every two cycles of the driving force, as shown in Fig. 2 c. Therefore, the firing rate is 1000/2T (Hz), and this is called a 1:2 phase-locked state. The other regions correspond to various kinds of solutions whose periods are some rational multiples of the period of the driving glutamatergic input train.
). In the upper region, the amplitude of this periodic solution is larger than the value V = 0 (mV), which was the critical value expediently set as action potential threshold (see Methods for details), as shown in Fig. 2 d. Therefore, in this region the neuron generates a single action potential on every cycle, with the firing frequency 1000/T (Hz), and thus it is called a 1:1 phase-locked response. On the other hand, in the lower region, the amplitude of the periodic solution is smaller than the value V = 0 (mV), as shown in Fig. 2 b, so that it may well be regarded as a subthreshold oscillation without action potentials. Therefore, in this region the neuron generates no action potential, i.e., the frequency is 0 (Hz), and thus it is called a 0:1 phase-locked state. As shown in Fig. 2 a, between these 1:1 and 0:1 phase-locked states, there are several regions separated from each other by a series of saddle-node bifurcation curves. Among them, the most predominant region is the middlemost one. In this region, the period of the solution is twice the period of the driving force, and the state variable V passes through the value V = 0 (mV) once every two cycles of the driving force, as shown in Fig. 2 c. Therefore, the firing rate is 1000/2T (Hz), and this is called a 1:2 phase-locked state. The other regions correspond to various kinds of solutions whose periods are some rational multiples of the period of the driving glutamatergic input train.
FIGURE 2.
Neuronal responses to periodic glutamatergic inputs in the absence of GABAergic inputs: simulation and bifurcation analysis. (a) The bifurcation diagram of the case with only glutamatergic input calculated with respect to two parameters, the frequency 1/T indicated by the horizontal axis and the maximum conductance 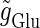 indicated by the vertical axis, under the fixed value of the time constant
indicated by the vertical axis, under the fixed value of the time constant 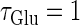 (ms). Solid lines indicate saddle-node bifurcation curves. Different phase-locked solutions are indicated by different symbols as shown below the figure. These symbols are used throughout this article. The blue spot and the red spot indicate the parameter values used as the subthreshold and suprathreshold inputs for bifurcation analyses (see text for details). (b–d) Glutamatergic input conductances (top panels) and resulting wave forms of the membrane potential (bottom panels) at the three points on the
(ms). Solid lines indicate saddle-node bifurcation curves. Different phase-locked solutions are indicated by different symbols as shown below the figure. These symbols are used throughout this article. The blue spot and the red spot indicate the parameter values used as the subthreshold and suprathreshold inputs for bifurcation analyses (see text for details). (b–d) Glutamatergic input conductances (top panels) and resulting wave forms of the membrane potential (bottom panels) at the three points on the 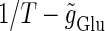 parameter plane indicated by green circles in panels a–d correspond to 0:1, 1:2, and 1:1 phase-locked solutions, respectively. (e) The relationship between the
parameter plane indicated by green circles in panels a–d correspond to 0:1, 1:2, and 1:1 phase-locked solutions, respectively. (e) The relationship between the 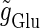 (the maximum conductance of the driving glutamatergic input) and the output firing frequency for the T = 25 (ms) (i.e., 40 Hz) and the T = 125 (ms) (i.e., 8 Hz) cases calculated from numerical simulation of Eqs. 1 and 2. The asterisk indicated the critical strength of the glutamatergic inputs for T = 125 (ms) (i.e., 8 Hz).
(the maximum conductance of the driving glutamatergic input) and the output firing frequency for the T = 25 (ms) (i.e., 40 Hz) and the T = 125 (ms) (i.e., 8 Hz) cases calculated from numerical simulation of Eqs. 1 and 2. The asterisk indicated the critical strength of the glutamatergic inputs for T = 125 (ms) (i.e., 8 Hz).
Fig. 2 e shows the relationship between the maximum conductance of the driving glutamatergic input 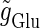 and the output firing frequency for T = 25 (ms) (i.e., 40 Hz) and T = 125 (ms) (i.e., 8 Hz) cases calculated from numerical simulation of Eqs. 1 and 2. In the case with T = 25 (ms) (40 Hz), as the input magnitude
and the output firing frequency for T = 25 (ms) (i.e., 40 Hz) and T = 125 (ms) (i.e., 8 Hz) cases calculated from numerical simulation of Eqs. 1 and 2. In the case with T = 25 (ms) (40 Hz), as the input magnitude 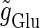 increases, the output firing frequency increases in a devil's-staircase-like manner. Such a response of a neuron to a periodic input has been observed in many experiments and extensively analyzed (15–20). The longest plateau in the relationship between the input magnitude
increases, the output firing frequency increases in a devil's-staircase-like manner. Such a response of a neuron to a periodic input has been observed in many experiments and extensively analyzed (15–20). The longest plateau in the relationship between the input magnitude 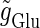 and the output firing frequency at 20 Hz, which is half the input frequency 40 Hz, corresponds to the region where the 1:2 phase-locked solution exists. On the other hand, in the case with T = 125 (ms) (8 Hz), the relationship between the input magnitude
and the output firing frequency at 20 Hz, which is half the input frequency 40 Hz, corresponds to the region where the 1:2 phase-locked solution exists. On the other hand, in the case with T = 125 (ms) (8 Hz), the relationship between the input magnitude 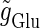 and the output firing frequency appears to be almost a single step function rather than a staircase. This means that the solution of Eqs. 1 and 2 has almost always the same period T = 125 (ms) as that of the driving glutamatergic input train. The 1:1 phase-locked solution exists when the input magnitude
and the output firing frequency appears to be almost a single step function rather than a staircase. This means that the solution of Eqs. 1 and 2 has almost always the same period T = 125 (ms) as that of the driving glutamatergic input train. The 1:1 phase-locked solution exists when the input magnitude 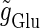 is larger than a critical point indicated by the asterisk in Fig. 2 e, whereas the 0:1 phase-locked solution, representing failure to generate any spikes, exists below the critical point. Therefore, each cycle could be regarded as practically independent because the period T = 125 (ms) of the glutamatergic input train is much longer than the system's intrinsic time constant (τ = 5.6 (ms)). Indeed, the critical amount of
is larger than a critical point indicated by the asterisk in Fig. 2 e, whereas the 0:1 phase-locked solution, representing failure to generate any spikes, exists below the critical point. Therefore, each cycle could be regarded as practically independent because the period T = 125 (ms) of the glutamatergic input train is much longer than the system's intrinsic time constant (τ = 5.6 (ms)). Indeed, the critical amount of 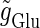 that separates the 1:1 and 0:1 phase-locked states (asterisk in Fig. 2 e) lies between
that separates the 1:1 and 0:1 phase-locked states (asterisk in Fig. 2 e) lies between 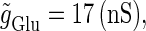 which was found to be subthreshold in the simulation in the previous section, and
which was found to be subthreshold in the simulation in the previous section, and 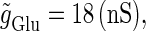 which was suprathreshold, indicating that the bifurcation analysis of a neuron receiving the periodic glutamatergic input train with a long period like T = 125 (ms) produces results almost identical to the simulation results for the transient inputs described in the previous section. Therefore, we use this T = 125 (ms) case for bifurcation analysis as a substitute for the original situation in the experiments by Gulledge and Stuart where the neuron receives transient, rather than periodic, inputs.
which was suprathreshold, indicating that the bifurcation analysis of a neuron receiving the periodic glutamatergic input train with a long period like T = 125 (ms) produces results almost identical to the simulation results for the transient inputs described in the previous section. Therefore, we use this T = 125 (ms) case for bifurcation analysis as a substitute for the original situation in the experiments by Gulledge and Stuart where the neuron receives transient, rather than periodic, inputs.
We next consider a periodic GABAergic input train in addition to the glutamatergic one. Specifically, we assume that 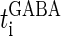 in Eq. 11 has the same long period T = 125 (ms) as the glutamatergic input train, but with a time difference Δtms, that is,
in Eq. 11 has the same long period T = 125 (ms) as the glutamatergic input train, but with a time difference Δtms, that is, 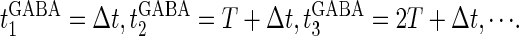 Note that
Note that 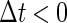 means that the GABAergic inputs arrive
means that the GABAergic inputs arrive 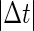 ms before the glutamatergic inputs. Here, as in the previous section, the time constants of the synaptic conductances are fixed at
ms before the glutamatergic inputs. Here, as in the previous section, the time constants of the synaptic conductances are fixed at 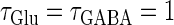 (ms). In this setting, we numerically calculate bifurcation sets with respect to the time difference Δt and the maximum GABAergic conductance
(ms). In this setting, we numerically calculate bifurcation sets with respect to the time difference Δt and the maximum GABAergic conductance 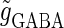 (nS) (see Methods for details) for either the subthreshold
(nS) (see Methods for details) for either the subthreshold 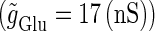 or the suprathreshold
or the suprathreshold 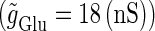 glutamatergic input, indicated by the blue or the red spot in Fig. 2 a, respectively.
glutamatergic input, indicated by the blue or the red spot in Fig. 2 a, respectively.
Fig. 3 a shows the bifurcation sets on the 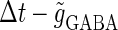 parameter plane for the
parameter plane for the 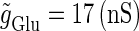 subthreshold glutamatergic input. Solid lines in Fig. 3 a indicate saddle-node bifurcation curves obtained numerically. As shown in the figure, there are two wide regions on the parameter plane. One region, including the horizontal line where there is no GABAergic input
subthreshold glutamatergic input. Solid lines in Fig. 3 a indicate saddle-node bifurcation curves obtained numerically. As shown in the figure, there are two wide regions on the parameter plane. One region, including the horizontal line where there is no GABAergic input 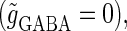 corresponds to the 0:1 phase-locked solution that has the same period T = 125 (ms) as the glutamatergic input train, and whose amplitude is small so that the neuron fails to generate spikes. The other region, indicated by shadow in Fig. 3 a, corresponds to the 1:1 phase-locked solution that also has the same period T = 125 (ms) as the glutamatergic input train, but whose amplitude is large enough so that the neuron can be regarded as generating action potentials. According to Fig. 3 a, these two wide regions appear to be divided by a saddle-node bifurcation curve indicated as the solid line. According to bifurcation analysis, however, there actually exist a large, possibly infinite, number of bifurcation curves separating the two regions. Bifurcation analysis shows that if the time difference Δt is in a certain range, for example
corresponds to the 0:1 phase-locked solution that has the same period T = 125 (ms) as the glutamatergic input train, and whose amplitude is small so that the neuron fails to generate spikes. The other region, indicated by shadow in Fig. 3 a, corresponds to the 1:1 phase-locked solution that also has the same period T = 125 (ms) as the glutamatergic input train, but whose amplitude is large enough so that the neuron can be regarded as generating action potentials. According to Fig. 3 a, these two wide regions appear to be divided by a saddle-node bifurcation curve indicated as the solid line. According to bifurcation analysis, however, there actually exist a large, possibly infinite, number of bifurcation curves separating the two regions. Bifurcation analysis shows that if the time difference Δt is in a certain range, for example 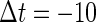 (ms), as the magnitude of the GABAergic input
(ms), as the magnitude of the GABAergic input 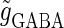 increases from
increases from 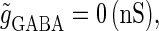 a saddle-node bifurcation occurs on the 0:1 phase-locked solution. On the other hand, bifurcation analysis also shows that if the time difference Δt is the same
a saddle-node bifurcation occurs on the 0:1 phase-locked solution. On the other hand, bifurcation analysis also shows that if the time difference Δt is the same 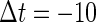 (ms), as the magnitude of the GABAergic input
(ms), as the magnitude of the GABAergic input 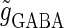 decreases from a large value, for example
decreases from a large value, for example 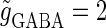 (nS), another saddle-node bifurcation occurs on the 1:1 phase-locked solution. Although these two saddle-node bifurcations are distinct, they are so close to each other that they are almost overlapped and thus appear to be a single bifurcation curve in Fig. 3 a. Comparing Fig. 1 c with Fig. 3 a, it can be said that the boundary of the region where GABAergic unitary conductances have excitatory actions, which is indicated by red in Fig. 1 c, corresponds to the closely packed bifurcation curves indicated by the single curve in Fig. 3 a between the 0:1 phase-locked region and the 1:1 phase-locked one.
(nS), another saddle-node bifurcation occurs on the 1:1 phase-locked solution. Although these two saddle-node bifurcations are distinct, they are so close to each other that they are almost overlapped and thus appear to be a single bifurcation curve in Fig. 3 a. Comparing Fig. 1 c with Fig. 3 a, it can be said that the boundary of the region where GABAergic unitary conductances have excitatory actions, which is indicated by red in Fig. 1 c, corresponds to the closely packed bifurcation curves indicated by the single curve in Fig. 3 a between the 0:1 phase-locked region and the 1:1 phase-locked one.
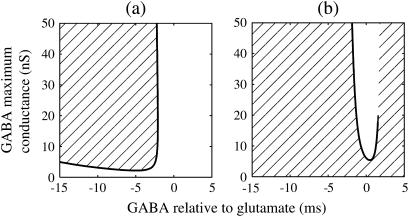
FIGURE 3.
Bifurcations associated with the excitatory and inhibitory actions of GABA. The bifurcation diagrams were calculated with respect to two parameters, the time (phase) difference Δt between glutamatergic and GABAergic inputs, indicated by the horizontal axis, and the maximum conductance 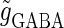 of the GABAergic inputs, indicated by the vertical axis. The time constants are fixed at
of the GABAergic inputs, indicated by the vertical axis. The time constants are fixed at 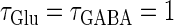 (ms), and the periods are fixed at T = 125 (ms) (i.e., 8 Hz), which approximates the situation of the transient inputs (see text). The maximum conductance of the glutamatergic inputs is fixed either at the subthreshold value
(ms), and the periods are fixed at T = 125 (ms) (i.e., 8 Hz), which approximates the situation of the transient inputs (see text). The maximum conductance of the glutamatergic inputs is fixed either at the subthreshold value 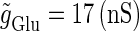 in panel a or the suprathreshold value
in panel a or the suprathreshold value 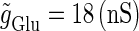 in panel b. Solid lines represent numerically calculated saddle-node bifurcation curves. The shadowed areas represent the regions where the 1:1 phase-locked solution representing full firing of the neuron exists whereas the white areas represent the regions where the 0:1 phase-locked solution representing no firing of the neuron exists. There is a short dashed line just above the solid line in panel b, though too short to be clearly visible, which indicates a period-doubling bifurcation curve. Note that there is no bifurcation curve above the end of this dashed line, indicating that the 1:1 phase-locked solution continuously changes into the 0:1 phase-locked solution here.
in panel b. Solid lines represent numerically calculated saddle-node bifurcation curves. The shadowed areas represent the regions where the 1:1 phase-locked solution representing full firing of the neuron exists whereas the white areas represent the regions where the 0:1 phase-locked solution representing no firing of the neuron exists. There is a short dashed line just above the solid line in panel b, though too short to be clearly visible, which indicates a period-doubling bifurcation curve. Note that there is no bifurcation curve above the end of this dashed line, indicating that the 1:1 phase-locked solution continuously changes into the 0:1 phase-locked solution here.
Fig. 3 b shows the bifurcation sets on the 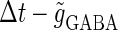 parameter plane for the
parameter plane for the 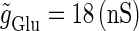 suprathreshold glutamatergic input. Solid lines in Fig. 3 b again indicate saddle-node bifurcation curves obtained numerically. There are again two wide regions on the parameter plane. The shadowed region, including the horizontal line of Fig. 3 b where there is no GABAergic input
suprathreshold glutamatergic input. Solid lines in Fig. 3 b again indicate saddle-node bifurcation curves obtained numerically. There are again two wide regions on the parameter plane. The shadowed region, including the horizontal line of Fig. 3 b where there is no GABAergic input 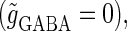 corresponds to the 1:1 phase-locked solution that has the same period T = 125 (ms) as the glutamatergic input train, and whose amplitude is large enough to be regarded as action potentials of the neuron. The white region in Fig. 3 b, on the other hand, corresponds to the 0:1 phase-locked solution that also has the same period T = 125 (ms) as the glutamatergic input train, but whose amplitude is small meaning failure to generate spikes. Bifurcation analysis suggests that there exist between these two regions multiple bifurcation curves, which again, however, are so densely packed that they appear to be a single line in Fig. 3 b. Comparing Fig. 1 c with Fig. 3 b, it can be said that the boundary of the region where GABAergic unitary conductances have inhibitory actions, that is the boundary of the blue region in Fig. 1 c, could be characterized as the closely packed bifurcation curves indicated by the single line in Fig. 3 b between the 0:1 phase-locked region and the 1:1 phase-locked one.
corresponds to the 1:1 phase-locked solution that has the same period T = 125 (ms) as the glutamatergic input train, and whose amplitude is large enough to be regarded as action potentials of the neuron. The white region in Fig. 3 b, on the other hand, corresponds to the 0:1 phase-locked solution that also has the same period T = 125 (ms) as the glutamatergic input train, but whose amplitude is small meaning failure to generate spikes. Bifurcation analysis suggests that there exist between these two regions multiple bifurcation curves, which again, however, are so densely packed that they appear to be a single line in Fig. 3 b. Comparing Fig. 1 c with Fig. 3 b, it can be said that the boundary of the region where GABAergic unitary conductances have inhibitory actions, that is the boundary of the blue region in Fig. 1 c, could be characterized as the closely packed bifurcation curves indicated by the single line in Fig. 3 b between the 0:1 phase-locked region and the 1:1 phase-locked one.
In this way, in both the 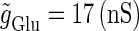 and
and 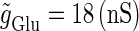 cases with a long-period periodic input, the boundary of the excitatory and inhibitory effects of the GABAergic unitary conductances can be characterized as the closely packed bifurcation curves between the 0:1 and 1:1 phase-locked regions.
cases with a long-period periodic input, the boundary of the excitatory and inhibitory effects of the GABAergic unitary conductances can be characterized as the closely packed bifurcation curves between the 0:1 and 1:1 phase-locked regions.
Neuronal responses to glutamatergic and GABAergic periodic input trains with γ-frequency
As we have shown above, the boundaries of the facilitatory and inhibitory actions of the depolarizing GABAergic unitary conductances are characterized by densely packed series of many bifurcations. Such crowding of the bifurcation curves might be related to the fact that the period of the inputs we have assumed in the previous section is so long that each cycle is almost independent, because in the absence of GABAergic inputs, all the bifurcation curves converge in the limit of infinite period, as shown in Fig. 2 a. Therefore it could be expected that the intervals of such bifurcation curves broaden if the period of the inputs becomes shorter. In the following, we examine how bifurcation curves are arranged on the parameter plane, and in consequence, how the neuronal response changes, when the period of the glutamatergic and GABAergic input trains is shorter, specifically in the range of the cortical γ-oscillation.
First, though, the neurophysiological significance of examining such situations should be presented. In the real cerebral cortex of the animal, periodic glutamatergic and GABAergic inputs to a single postsynaptic neuron would come from synchronized oscillatory activities of two distinct preneuronal populations, one of which is glutamatergic whereas the other is GABAergic. Such pairs of neuronal groups—for example, the pyramidal cells and the fast spiking cells—are widely observed in the neocortex and the hippocampus of the behaving animal's brain, and are considered to be associated with γ- and/or θ-oscillations (21,22). Therefore, examining neural responses to such periodic glutamatergic and GABAergic inputs in the frequency range of γ- and/or θ-oscillations should be important in considering the functional relevance of synchronized oscillatory neural activities. Especially, from the viewpoint of neural coding theory, we focus on how the time difference between these two oscillatory activities affects, or is transformed into, the output neuronal time-averaged firing rate.
In a similar fashion to the previous section, let us consider periodic glutamatergic and GABAergic input trains having the same period T(ms) but a time difference Δt (ms). Period T is now assumed to be T = 25 (ms), corresponding to 40 Hz, which is typical for cortical γ-oscillations. The time constants are assumed to be the same as in the previous sections: 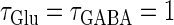 (ms). Thus, there are three parameters left to be determined: the maximum conductance of the glutamatergic input
(ms). Thus, there are three parameters left to be determined: the maximum conductance of the glutamatergic input 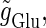 that of the GABAergic input
that of the GABAergic input 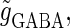 and the time difference (Δt). Because we are interested in the effects of the GABAergic inputs on the neuronal response, here we fix the strength of the glutamatergic input and then perform the bifurcation analysis about the remaining parameters
and the time difference (Δt). Because we are interested in the effects of the GABAergic inputs on the neuronal response, here we fix the strength of the glutamatergic input and then perform the bifurcation analysis about the remaining parameters 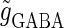 and Δt on the GABAergic inputs. Specifically, we fix the maximum conductance of the glutamatergic input to be
and Δt on the GABAergic inputs. Specifically, we fix the maximum conductance of the glutamatergic input to be 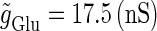 so that a 1:2 phase-locked solution, which means 20 Hz firing, exists as shown in Fig. 2 c. Then we numerically calculate bifurcation sets with respect to Δt and
so that a 1:2 phase-locked solution, which means 20 Hz firing, exists as shown in Fig. 2 c. Then we numerically calculate bifurcation sets with respect to Δt and 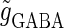 (see Methods for details).
(see Methods for details).
The left panel of Fig. 4 a shows the bifurcation diagram on the 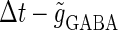 parameter plane. The predominant region including the horizontal line where there is no GABAergic input (
parameter plane. The predominant region including the horizontal line where there is no GABAergic input (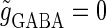 ) is that of the 1:2 phase-locked solution, an example spike train of which is shown in Fig. 4 c, representing 20 Hz firing. There exist two regions in the
) is that of the 1:2 phase-locked solution, an example spike train of which is shown in Fig. 4 c, representing 20 Hz firing. There exist two regions in the 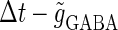 parameter plane in which the solution has the same period as the driving forces: the 0:1 phase-locked region corresponding to 0 Hz (see Fig. 4 b) and the 1:1 phase-locked region corresponding to 40 Hz (see Fig. 4 e). In this way, the firing rate of the neuron entrained by the periodic glutamatergic input train can be decreased to 0 Hz, but also can be increased up to the twice as the original value, depending on the timing and the strength of the periodic GABAergic input train. In other words, depolarizing GABAergic inputs can have both excitatory and inhibitory effects at the level of the time-averaged firing rate, as well as at the level of the generation of single action potentials, according to their strength and the temporal relationship with the glutamatergic inputs. As shown in Fig. 4 a, there are some gaps between those 1:2, 0:1, or 1:1 phase-locked regions. Numerical calculation of bifurcation sets revealed that there exist a large number of bifurcation curves of saddle-node and period-doubling types in such spaces, only some of which are drawn in the figure. Different regions divided by such bifurcation curves correspond to different types of phase-locked solutions, and therefore, different values of the firing rates. For example, the dotted region in Fig. 4 a indicates the region in which a 2:3 phase-locked solution, as shown in Fig. 4 d, corresponding to 27 Hz firing, exists. Fig. 4 f shows the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs:
parameter plane in which the solution has the same period as the driving forces: the 0:1 phase-locked region corresponding to 0 Hz (see Fig. 4 b) and the 1:1 phase-locked region corresponding to 40 Hz (see Fig. 4 e). In this way, the firing rate of the neuron entrained by the periodic glutamatergic input train can be decreased to 0 Hz, but also can be increased up to the twice as the original value, depending on the timing and the strength of the periodic GABAergic input train. In other words, depolarizing GABAergic inputs can have both excitatory and inhibitory effects at the level of the time-averaged firing rate, as well as at the level of the generation of single action potentials, according to their strength and the temporal relationship with the glutamatergic inputs. As shown in Fig. 4 a, there are some gaps between those 1:2, 0:1, or 1:1 phase-locked regions. Numerical calculation of bifurcation sets revealed that there exist a large number of bifurcation curves of saddle-node and period-doubling types in such spaces, only some of which are drawn in the figure. Different regions divided by such bifurcation curves correspond to different types of phase-locked solutions, and therefore, different values of the firing rates. For example, the dotted region in Fig. 4 a indicates the region in which a 2:3 phase-locked solution, as shown in Fig. 4 d, corresponding to 27 Hz firing, exists. Fig. 4 f shows the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs: 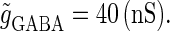 As shown in the figure, the firing rate, which is originally 20 Hz in the absence of the GABAergic inputs, changes from 0 to 40 Hz according to the time difference between the glutamatergic and GABAergic periodic input trains. In other words, it can be said that the information about the time difference between these two periodic input trains is, at least partially, transformed into an increase or decrease of the firing rate of the neuron that receives them.
As shown in the figure, the firing rate, which is originally 20 Hz in the absence of the GABAergic inputs, changes from 0 to 40 Hz according to the time difference between the glutamatergic and GABAergic periodic input trains. In other words, it can be said that the information about the time difference between these two periodic input trains is, at least partially, transformed into an increase or decrease of the firing rate of the neuron that receives them.
Effects of input time-widths
So far we have fixed the time constants 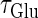 and
and 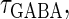 which are the peak times of the unitary conductances, or the “input time-widths”, to
which are the peak times of the unitary conductances, or the “input time-widths”, to 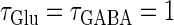 (ms). Because in a neuronal network in the brain, periodic inputs most likely come from a presynaptic neural population that is in a state of synchronized oscillation, these input time-widths can be considered to represent also the degree of their synchronization: a small
(ms). Because in a neuronal network in the brain, periodic inputs most likely come from a presynaptic neural population that is in a state of synchronized oscillation, these input time-widths can be considered to represent also the degree of their synchronization: a small 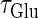 or
or  value would mean high temporal precision of presynaptic neuronal firings (6). Hence, changing the input time-widths
value would mean high temporal precision of presynaptic neuronal firings (6). Hence, changing the input time-widths 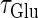 and
and 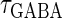 would correspond to changing the degree of synchronization of presynaptic neural activities. Here we test how the neuronal response is affected by changing the input time-widths
would correspond to changing the degree of synchronization of presynaptic neural activities. Here we test how the neuronal response is affected by changing the input time-widths  and
and 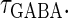
At first, we test the 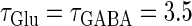 (ms) case. We fix the maximum conductance of the glutamatergic input
(ms) case. We fix the maximum conductance of the glutamatergic input 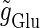 so that the neuron fires at 20 Hz in the absence of GABAergic inputs. Specifically, we fix
so that the neuron fires at 20 Hz in the absence of GABAergic inputs. Specifically, we fix 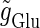 to the mean value of the range corresponding to 1:2 phase-locked solutions. Then we numerically calculate bifurcation sets with respect to the time difference Δt (ms) and the maximum GABAergic conductance
to the mean value of the range corresponding to 1:2 phase-locked solutions. Then we numerically calculate bifurcation sets with respect to the time difference Δt (ms) and the maximum GABAergic conductance 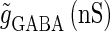 (see Methods for details). The top panel of Fig. 5 a shows the bifurcation diagram on the
(see Methods for details). The top panel of Fig. 5 a shows the bifurcation diagram on the 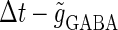 parameter plane for
parameter plane for 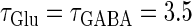 (ms). The predominant region including the horizontal line where there is no GABAergic input (
(ms). The predominant region including the horizontal line where there is no GABAergic input (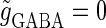 ) is that of the 1:2 phase-locked solution representing 20 Hz firing, as in the
) is that of the 1:2 phase-locked solution representing 20 Hz firing, as in the 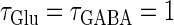 (ms) case shown in Fig. 4 a. Also like in the
(ms) case shown in Fig. 4 a. Also like in the 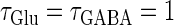 (ms) case, there is a relatively large region corresponding to the 1:1 phase-locked solution of 40 Hz firing. The 0:1 phase-locked solution can also be found although it is considerably shifted upward, i.e., toward the direction of larger GABAergic inputs, compared with the
(ms) case, there is a relatively large region corresponding to the 1:1 phase-locked solution of 40 Hz firing. The 0:1 phase-locked solution can also be found although it is considerably shifted upward, i.e., toward the direction of larger GABAergic inputs, compared with the 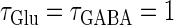 (ms) case. Notably, in the widened gap between the 1:2 phase-locked region and the 0:1 phase-locked one, as well as in the also widened gap between the 1:2 phase-locked region and the 1:1 phase-locked one, a large number of different regions clearly appear. Because these different regions are separated by bifurcation curves, they correspond to different types of solutions, and therefore, usually to different firing rates. Fig. 5 b shows the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs:
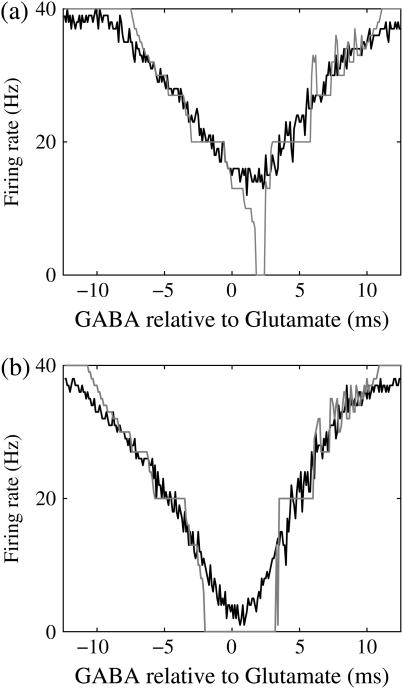
(ms) case. Notably, in the widened gap between the 1:2 phase-locked region and the 0:1 phase-locked one, as well as in the also widened gap between the 1:2 phase-locked region and the 1:1 phase-locked one, a large number of different regions clearly appear. Because these different regions are separated by bifurcation curves, they correspond to different types of solutions, and therefore, usually to different firing rates. Fig. 5 b shows the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs: 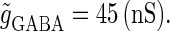 As shown in Fig. 5 b, the relationship appears to be a devil's-staircase-like shape, though there exist irregular ups and downs in the region with positive Δt. Such a staircase-like graded response means that the input time differences between the glutamatergic and GABAergic periodic input trains are transformed into finer values of the output firing rate than in the
As shown in Fig. 5 b, the relationship appears to be a devil's-staircase-like shape, though there exist irregular ups and downs in the region with positive Δt. Such a staircase-like graded response means that the input time differences between the glutamatergic and GABAergic periodic input trains are transformed into finer values of the output firing rate than in the 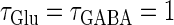 (ms) case, in which almost all time differences are transformed into one of the four predominantly appearing values: 0, 20, 27, and 40 Hz. In terms of neural coding, the transformation from the input time difference into the output firing rate is more informative in the
(ms) case, in which almost all time differences are transformed into one of the four predominantly appearing values: 0, 20, 27, and 40 Hz. In terms of neural coding, the transformation from the input time difference into the output firing rate is more informative in the 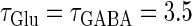 (ms) case than in the
(ms) case than in the 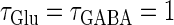 (ms) case.
(ms) case.
In this way, a lower precision of preneuronal synchronization would be better than a higher one for an informative neuronal coding transformation. Further decreasing the precision of preneuronal synchronization, however, again reduces the quality of the coding transformation as follows. Fig. 6 a (top panel) and b, respectively, show the bifurcation sets on the 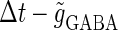 parameter plane and the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs:
parameter plane and the relationship between the time difference Δt (ms) and the neuronal firing rate for a fixed value of the maximum conductance of the GABAergic inputs: 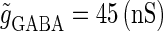 for
for 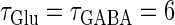 (ms). Although there again exist a large number of different regions on the
(ms). Although there again exist a large number of different regions on the 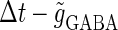 parameter plane and the overall characteristic looks similar to that of the
parameter plane and the overall characteristic looks similar to that of the 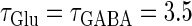 (ms) case shown in Fig. 5 a, the 0:1 phase-locked solution representing no firing of the neuron moves toward much larger values of the GABAergic conductance than in the
(ms) case shown in Fig. 5 a, the 0:1 phase-locked solution representing no firing of the neuron moves toward much larger values of the GABAergic conductance than in the 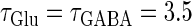 (ms) case. This recession of the 0:1 phase-locked region means that inhibitory effects of the depolarizing GABAergic inputs become apparently weaker as the time-widths
(ms) case. This recession of the 0:1 phase-locked region means that inhibitory effects of the depolarizing GABAergic inputs become apparently weaker as the time-widths  and
and 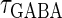 become larger. This result may be naturally understandable because inhibitory effects of the depolarizing GABAergic inputs are due to shunting so that even a brief transient is sufficient and further increasing
become larger. This result may be naturally understandable because inhibitory effects of the depolarizing GABAergic inputs are due to shunting so that even a brief transient is sufficient and further increasing 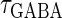 provides no more inhibitory effect. The facilitatory effect, in contrast, results from enhanced charging of the membrane capacitor when
provides no more inhibitory effect. The facilitatory effect, in contrast, results from enhanced charging of the membrane capacitor when 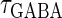 increases. The weakened inhibitory effects then result in the decrease of the range of the output firing rate change shown in Fig. 6 b, compared with the
increases. The weakened inhibitory effects then result in the decrease of the range of the output firing rate change shown in Fig. 6 b, compared with the 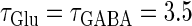 (ms) case shown in Fig. 5 b with the same strengths of GABAergic inputs. Such decrease then would cause greater information loss. To estimate the amount of information loss in the transformation from the input phase difference to the output firing rate, we compute the mutual information between the input signal, or the phase difference, and the output signal, or the firing rate, defined through coarse-graining (see Methods for details) for different values of the GABAergic conductance (
(ms) case shown in Fig. 5 b with the same strengths of GABAergic inputs. Such decrease then would cause greater information loss. To estimate the amount of information loss in the transformation from the input phase difference to the output firing rate, we compute the mutual information between the input signal, or the phase difference, and the output signal, or the firing rate, defined through coarse-graining (see Methods for details) for different values of the GABAergic conductance (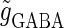 ) and the time constant of the α-functions (
) and the time constant of the α-functions (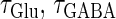 ). The maximum value of the glutamatergic conductance (
). The maximum value of the glutamatergic conductance (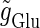 ) was fixed so that a 1:2 phase-locked solution representing 20 Hz firing exists in the absence of the GABAergic inputs. Fig. 7 shows the mutual information for various input time-widths (
) was fixed so that a 1:2 phase-locked solution representing 20 Hz firing exists in the absence of the GABAergic inputs. Fig. 7 shows the mutual information for various input time-widths (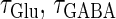 ) and various values of the strength of the GABAergic inputs (
) and various values of the strength of the GABAergic inputs (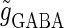 ). As shown in the figure, the mutual information takes large values around
). As shown in the figure, the mutual information takes large values around 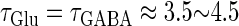 (ms) with
(ms) with 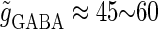 (nS). Therefore, this range of the input time-widths, which represents the degree of the presynaptic neuronal synchrony as previously described, can be said to be the optimum value for maximizing the information transfer from the input phase difference to the output firing rate.
(nS). Therefore, this range of the input time-widths, which represents the degree of the presynaptic neuronal synchrony as previously described, can be said to be the optimum value for maximizing the information transfer from the input phase difference to the output firing rate.
FIGURE 7.
The mutual information (see Methods for details) between the input phase difference and the output firing rate for various input time-widths (the horizontal axis) and maximum amplitudes of the GABAergic inputs (the vertical axis). The period of the inputs is fixed to T = 25 (ms), and the maximum amplitude of the glutamatergic inputs are fixed to 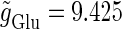 (nS), which gives a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs.
(nS), which gives a 1:2 phase-locked response, i.e., 20 Hz firing in the absence of GABAergic inputs.
Effects of the value of the GABAA reversal potential
So far we have fixed the value of the GABAA reversal potential at 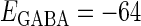 (mV), which is consistent with the experimental results of Gulledge and Stuart (5) (see Methods for details). We here examine how changing the value of the GABAA reversal potential affects the neuronal response to periodic glutamatergic and GABAergic inputs. Fig. 8 a shows how the neuronal response to the 40-Hz periodic glutamatergic and GABAergic inputs changes when the value of the GABAA reversal potential is varied from
(mV), which is consistent with the experimental results of Gulledge and Stuart (5) (see Methods for details). We here examine how changing the value of the GABAA reversal potential affects the neuronal response to periodic glutamatergic and GABAergic inputs. Fig. 8 a shows how the neuronal response to the 40-Hz periodic glutamatergic and GABAergic inputs changes when the value of the GABAA reversal potential is varied from 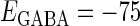 (mV) (top panel of Fig. 8 a), which is equal to the resting potential of Wilson's model, to
(mV) (top panel of Fig. 8 a), which is equal to the resting potential of Wilson's model, to 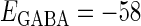 (mV) (bottom panel of Fig. 8 a), which is equal to the firing threshold of the model. As shown in Fig. 8 a, the phase difference between glutamatergic and GABAergic periodic inputs is transformed into a graded response of the neuronal firing rate, regardless of the values of the GABAA reversal potential. However, there are also differences. When the GABAA reversal potential is equal to the neuronal resting potential (top panel of Fig. 8 a), GABAergic inputs cannot increase the firing rate but only decrease it from 20 Hz regardless of the timing relative to glutamatergic inputs. On the other hand, when the GABAA reversal potential is equal to the firing threshold (bottom panel of Fig. 8 a), GABAergic inputs cannot decrease the firing rate but only increase it. It is only when the GABAA reversal potential is in an appropriate range between the resting potential and the firing threshold (see the third and fourth panels of Fig. 8 a) that modulating the firing rate toward both directions is possible. Fig. 8 b shows the dependence of the mutual information (see Methods for details) between the input phase difference and the output firing rate on the input time-width and the maximum amplitude of the GABAergic inputs when the value of the GABAA reversal potential is systematically valued from
(mV) (bottom panel of Fig. 8 a), which is equal to the firing threshold of the model. As shown in Fig. 8 a, the phase difference between glutamatergic and GABAergic periodic inputs is transformed into a graded response of the neuronal firing rate, regardless of the values of the GABAA reversal potential. However, there are also differences. When the GABAA reversal potential is equal to the neuronal resting potential (top panel of Fig. 8 a), GABAergic inputs cannot increase the firing rate but only decrease it from 20 Hz regardless of the timing relative to glutamatergic inputs. On the other hand, when the GABAA reversal potential is equal to the firing threshold (bottom panel of Fig. 8 a), GABAergic inputs cannot decrease the firing rate but only increase it. It is only when the GABAA reversal potential is in an appropriate range between the resting potential and the firing threshold (see the third and fourth panels of Fig. 8 a) that modulating the firing rate toward both directions is possible. Fig. 8 b shows the dependence of the mutual information (see Methods for details) between the input phase difference and the output firing rate on the input time-width and the maximum amplitude of the GABAergic inputs when the value of the GABAA reversal potential is systematically valued from 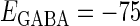 (mV), the resting potential, to
(mV), the resting potential, to 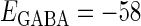 (mV), the firing threshold. As shown in this figure, the neuronal coding transformation is optimal within a narrow range of values for the GABAA reversal potential, around
(mV), the firing threshold. As shown in this figure, the neuronal coding transformation is optimal within a narrow range of values for the GABAA reversal potential, around 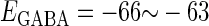 (mV), between the resting potential and the firing threshold.
(mV), between the resting potential and the firing threshold.
DISCUSSION
Although how information is coded in the brain is still elusive, it has been postulated that there are two basic coding schemes: firing-rate coding and temporal-spike coding (23–27). The former can be further classified into population rate coding and time-averaged rate coding. The brain seems to use one of them according to regions, types of information, or other circumstances. Therefore, there may be mechanisms of coding transformation between them. As we have shown, when a neuron receives two kinds of periodic inputs, a glutamatergic input train and a GABAergic one, the phase difference between these inputs is encoded into a graded response of the time-averaged firing rate (Figs. 4 f, 5 b, and 6 b). This could be a mechanism of the coding transformation. Admittedly, such transformation is possible regardless of the value of the GABAA reversal potential (Fig. 8), e.g., if the magnitude of 40 Hz periodic glutamatergic inputs is tuned so that the neuron gives 1:1 phase-locked response in the absence of GABAergic inputs, purely shunting GABAergic inputs with the reversal potential equal to the resting potential can modulate the firing rate over the entire range, that is, from 0 to 40 Hz (results not shown). However, the purely shunting GABAergic inputs usually only decrease the time-averaged firing rate. On the other hand, the depolarizing GABAergic inputs are able to both increase and decrease it, as we have shown (Fig. 8 a), enabling another kind of neural computation. Most recently, Stiefel and colleagues experimentally proved that a GABAergic input with such an intermediate value of the GABAA reversal potential can either increase or decrease the probability of the next spike generation depending on its timing relative to the phase of the oscillatory driving current (28). This study may be consistent with their results.
We have shown that increasing the time-widths of the input waveforms, by which we have intended to represent decreasing the precision of the presynaptic spikes, smoothes the transformation from the input phase difference to time-averaged firing rate, thus improving the information transfer (Fig. 7). Increasing the time-widths, however, may not be sufficient to represent the impreciseness of the spikes. Specifically, although we have assumed that all these parameters are deterministically fixed, it would be more natural that the parameters other than 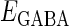 and 1/T are accompanied by some degree of temporal fluctuations. To examine the effects of such variability, we performed simulations in which parameters
and 1/T are accompanied by some degree of temporal fluctuations. To examine the effects of such variability, we performed simulations in which parameters 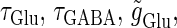 and
and 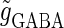 are accompanied by Gaussian noise whose standard deviations are 5% of the original parameter values. As shown in Fig. 9 a, adding such small amounts of fluctuations smoothes the phase-to-rate transformation, and thereby improves the associated information transfer. When the value
are accompanied by Gaussian noise whose standard deviations are 5% of the original parameter values. As shown in Fig. 9 a, adding such small amounts of fluctuations smoothes the phase-to-rate transformation, and thereby improves the associated information transfer. When the value 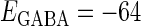 (mV), as in Fig. 9 a, there is a much wider range where GABAergic inputs act facilitatory than the range where GABAergic inputs have an inhibitory action. A slightly hyperpolarized GABAA reversal potential,
(mV), as in Fig. 9 a, there is a much wider range where GABAergic inputs act facilitatory than the range where GABAergic inputs have an inhibitory action. A slightly hyperpolarized GABAA reversal potential, 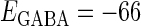 (mV), together with the same degree of small temporal fluctuations could achieve almost ideally smooth and evenly bidirectional firing-rate modulation, as shown in Fig. 9 b.
(mV), together with the same degree of small temporal fluctuations could achieve almost ideally smooth and evenly bidirectional firing-rate modulation, as shown in Fig. 9 b.
So far we have examined responses, or specifically, time-averaged firing rates of a single neuron receiving periodic inputs. Because there is increasing evidence that population coding is used in at least some parts of the cerebral cortex, here we discuss it with regard to our situation. Let us consider 100 mutually unconnected neurons receiving 40 Hz glutamatergic and GABAergic inputs with fluctuations (of 5%) on their timings, durations, and amplitudes. If such fluctuations are statistically independent over the population as well as over trials, the population-averaged activity is expected to be consistent with the trial-averaged activity (29), and practically we calculated the latter by simulation. The mean magnitude of the glutamatergic inputs are so tuned as to give 1:2 phase-locked response in the absence of GABAergic inputs and also without fluctuations on the timing, duration, and amplitude. Actually, there are fluctuations in inputs as just described, and therefore the response varies from neuron to neuron, resulting in the nearly 40 Hz population activity shown in Fig. 10 a. When GABAergic inputs with a depolarized reversal potential 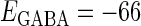 (mV) are added, the population activity is still nearly 40 Hz periodic (Fig. 10 b). However, its amplitude, that is, the power spectral density at 40 Hz, varies with the input time (phase) difference. In other words, the input phase difference is transformed into the amplitude of the output periodic population activity, as shown in Fig. 10 c. Note that the phase of the population activity, contrary to the amplitude, is hardly affected by the input phase difference, as shown in the bottom panels of Fig. 10, a and b. This is because different amplitudes of the population activity come from different types of phase-locked states, e.g., 1:2, 2:3, etc., of single neurons, but the spike timing in each input period does not largely change. Also note that such phase-to-amplitude transformation would be possible with purely shunting GABAergic inputs, but bidirectional modulation of the amplitude is enabled only when the GABAA reversal potential is more depolarized than the resting potential.
(mV) are added, the population activity is still nearly 40 Hz periodic (Fig. 10 b). However, its amplitude, that is, the power spectral density at 40 Hz, varies with the input time (phase) difference. In other words, the input phase difference is transformed into the amplitude of the output periodic population activity, as shown in Fig. 10 c. Note that the phase of the population activity, contrary to the amplitude, is hardly affected by the input phase difference, as shown in the bottom panels of Fig. 10, a and b. This is because different amplitudes of the population activity come from different types of phase-locked states, e.g., 1:2, 2:3, etc., of single neurons, but the spike timing in each input period does not largely change. Also note that such phase-to-amplitude transformation would be possible with purely shunting GABAergic inputs, but bidirectional modulation of the amplitude is enabled only when the GABAA reversal potential is more depolarized than the resting potential.
Our analysis is based on Wilson's two-dimensional neuron model. There are two directions in terms of refinement of the neuron model: one is increasing the number of types of ion channels as well as representing more details of their gating dynamics, and the other is considering spatial inhomogeneity of the membrane potential. Both of these points could affect the results in this study. High dimensionality generally could enrich the types of possible bifurcations, and could induce complex responses including multistability and chaos more easily. More specifically, it is known that slow voltage-dependent potassium current (M-current), which causes spike frequency adaptation, would qualitatively alter the phase responses of the neuron, namely, change its infinitesimal phase-response-curve from type I to type II (30,31). Consequently, a neuron having such adaptation potassium current might show a response like rebound facilitation to appropriately timed GABAergic inputs with a hyperpolarized reversal potential. Other than this, time delay and low-pass filtering effects of dendrites, as well as their possible active properties, could also greatly affect the results, especially considering that the majority of glutamatergic synapses are located on the dendritic spines. These points should be addressed with detailed neuron models, making use of simulation software such as NEURON (32), and compared with results in real living neurons via the dynamic clamp (conductance injection) technique (33,34).
Acknowledgments
The authors thank Prof. H. Fujii for valuable discussions and Prof. T. Yoshinaga for giving help on numerical calculation of bifurcation sets.
This study is partially supported by Grant-in-Aid No. 17022012 for Scientific Research on Priority Areas System study on higher-order brain functions from the Ministry of Education, Culture, Sports, Science and Technology of Japan. K.M. is supported by Research Fellowships for Young Scientists (No. 10834) from Japan Society for the Promotion of Science.
References
- 1.Kaila, K., J. Voipio, M. Pasternack, P. Paalasmaa, and R. A. Deisz. 1993. The role of bicarbonate in GABAA receptor-mediated IPSPs in rat neocortical neurons. J. Physiol. 464:273–289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Martina, M., S. Royer, and D. Pare. 2001. Cell-type-specific GABA responses and chloride homeostasis in the cortex and amygdala. J. Neurophysiol. 86:2887–2895. [DOI] [PubMed] [Google Scholar]
- 3.Wilson, C. J., and Y. Kawaguchi. 1996. The origins of two-state spontaneous membrane potential fluctuations of neostriatal spiny neurons. J. Neurosci. 16:2397–2410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Woodin, M. A., K. Ganguly, and M. M. Poo. 2003. Coincident pre- and postsynaptic activity modifies GABAergic synapses by postsynaptic changes in Cl− transporter activity. Neuron. 39:807–820. [DOI] [PubMed] [Google Scholar]
- 5.Gulledge, A. T., and G. J. Stuart. 2003. Excitatory actions of GABA in the cortex. Neuron. 37:299–309. [DOI] [PubMed] [Google Scholar]
- 6.Grande, L. A., G. A. Kinney, G. L. Miracle, and W. J. Spain. 2004. Dynamic influences on coincidence detection in neocortical pyramidal neurons. J. Neurosci. 24:1839–1851. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wirth, C., and H. R. Luscher. 2004. Spatiotemporal evolution of excitation and inhibition in the rat barrel cortex investigated with multielectrode arrays. J. Neurophysiol. 91:1635–1647. [DOI] [PubMed] [Google Scholar]
- 8.Morita, K., K. Tsumoto, and K. Aihara. 2005. Possible effects of depolarizing GABAA conductance on the neuronal input-output relationship: a modeling study. J. Neurophysiol. 93:3504–3523. [DOI] [PubMed] [Google Scholar]
- 9.Wilson, H. R. 1999. Simplified dynamics of human and mammalian neocortical neurons. J. Theor. Biol. 200:375–388. [DOI] [PubMed] [Google Scholar]
- 10.Wilson, H. R. 1999. Spikes, decisions, and actions. Oxford University Press, Oxford, UK.
- 11.Kawakami, H. 1984. Bifurcation of periodic responses in forced dynamic nonlinear circuits: computation of bifurcation values of the system parameters. IEEE. Trans. CAS. 31:248–260. [Google Scholar]
- 12.Yoshinaga, T., and H. Kawakami. 1995. Bifurcation in a BVP equation with periodic impulsive force. Proc. NOLTA. 95:331–334. [Google Scholar]
- 13.Yoshinaga, T., Y. Sano, and H. Kawakami. 1999. A method to calculate bifurcations in synaptically coupled Hodgkin-Huxley equations. Int. J. Bifurcat. Chaos. 9:1451–1458. [Google Scholar]
- 14.Reference deleted in proof.
- 15.Nagumo, J., and S. Sato. 1972. On a response characteristic of a mathematical neuron model. Kybernetik. 10:155–164. [DOI] [PubMed] [Google Scholar]
- 16.Guttman, R., L. Feldman, and E. Jakobsson. 1980. Frequency entrainment of squid axon membrane. J. Membr. Biol. 56:9–18. [DOI] [PubMed] [Google Scholar]
- 17.Aihara, K., G. Matsumoto, and Y. Ikegaya. 1984. Periodic and non-periodic responses of a periodically forced Hodgkin-Huxley oscillator. J. Theor. Biol. 109:249–269. [DOI] [PubMed] [Google Scholar]
- 18.Aihara, K., T. Numajiri, G. Matsumoto, and M. Kotani. 1986. Structures of attractors in periodically forced neural oscillators. Phys. Lett. A. 116:313–317. [Google Scholar]
- 19.Matsumoto, G., K. Aihara, Y. Hanyu, N. Takahashi, S. Yoshizawa, and J. Nagumo. 1987. Chaos and phase locking in normal squid axons. Phys. Lett. A. 123:162–166. [Google Scholar]
- 20.Aihara, K., T. Takabe, and M. Toyoda. 1990. Chaotic neural networks. Phys. Lett. A. 144:333–340. [Google Scholar]
- 21.Freund, T. F. 2003. Interneuron diversity series: rhythm and mood in perisomatic inhibition. Trends Neurosci. 26:489–495. [DOI] [PubMed] [Google Scholar]
- 22.Klausberger, T., P. J. Magill, L. F. Marton, J. D. Roberts, P. M. Cobden, G. Buzsaki, and P. Somogyi. 2003. Brain-state- and cell-type-specific firing of hippocampal interneurons in vivo. Nature. 421:844–848. [DOI] [PubMed] [Google Scholar]
- 23.Gray, C. M., P. Konig, A. K. Engel, and W. Singer. 1989. Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. Nature. 338:334–337. [DOI] [PubMed] [Google Scholar]
- 24.Fujii, H., H. Ito, K. Aihara, N. Ichinose, and M. Tsukada. 1996. Dynamical cell assembly hypothesis: theoretical possibility of spatio-temporal coding in the cortex. Neural Netw. 9:1303–1350. [PubMed] [Google Scholar]
- 25.Shadlen, M. N., and W. T. Newsome. 1998. The variable discharge of cortical neurons: implications for connectivity, computation, and information coding. J. Neurosci. 18:3870–3896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Masuda, N., and K. Aihara. 2002. Bridging rate coding and temporal spike coding by effect of noise. Phys. Rev. Lett. 88:248101. [DOI] [PubMed] [Google Scholar]
- 27.Masuda, N., and K. Aihara. 2003. Duality of rate coding and temporal coding in multilayered feedforward networks. Neural Comput. 15:103–125. [DOI] [PubMed] [Google Scholar]
- 28.Stiefel, K. M., V. Wespatat, B. Gutkin, F. Tennigkeit, and W. Singer. 2005. Phase dependent sign changes of GABAergic synaptic input explored in-silicio and in-vitro. J. Comput. Neurosci. 19:71–85. [DOI] [PubMed] [Google Scholar]
- 29.Masuda, N., and K. Aihara. 2003. Ergodicity of spike trains: when does trial averaging make sense? Neural Comput. 15:1341–1372. [DOI] [PubMed] [Google Scholar]
- 30.Ermentrout, B., M. Pascal, and B. Gutkin. 2001. The effects of spike frequency adaptation and negative feedback on the synchronization of neural oscillators. Neural Comput. 13:1285–1310. [DOI] [PubMed] [Google Scholar]
- 31.Gutkin, B. S., G. B. Ermentrout, and A. D. Reyes. 2005. Phase-response curves give the responses of neurons to transient inputs. J. Neurophysiol. 94:1623–1635. [DOI] [PubMed] [Google Scholar]
- 32.Hines, M. L., and N. T. Carnevale. 1997. The NEURON simulation environment. Neural Comput. 9:1179–1209. [DOI] [PubMed] [Google Scholar]
- 33.Robinson, H. P., and N. Kawai. 1993. Injection of digitally synthesized synaptic conductance transients to measure the integrative properties of neurons. J. Neurosci. Methods. 49:157–165. [DOI] [PubMed] [Google Scholar]
- 34.Sharp, A. A., M. B. O'Neil, L. F. Abbott, and E. Marder. 1993. Dynamic clamp: computer-generated conductances in real neurons. J. Neurophysiol. 69:992–995. [DOI] [PubMed] [Google Scholar]