Abstract
A fundamental step in the replication of a viral particle is the self-assembly of its rigid shell (capsid) from its constituent proteins. Capsids play a vital role in genome replication and intercellular movement of viruses, and as such, understanding viral assembly has great potential in the development of new antiviral therapies and a systematic treatment of viral infection. In this article, we assume that nucleation is the underlying mechanism for self-assembly and combine the theoretical methods of the physics of equilibrium polymerization with those of the classical nucleation to develop a theory for the kinetics of virus self-assembly. We find expressions for the size of the critical capsid, the lag time, and the steady-state nucleation rate of capsids, and how they depend on both protein concentration and binding energy. The latter is a function of the acidity of the solution, the ionic strength, and the temperature, explaining why capsid nucleation is a sensitive function of the ambient conditions.
INTRODUCTION
There is little doubt that the assembly of virus capsids from the coat proteins is a thermodynamic process, if not for all then certainly for a large class of virus (1–7). Indeed, for many viruses, including Hepatitis B virus (HBV), Human Papilloma virus (HPV), Cowpea Chlorotic Mottle virus, Brome Mosaic virus, Broad Bean Mottle virus, Sindbis virus, and Tobacco Mosaic virus (TMV), the coat proteins spontaneously form capsids in aqueous solution under the right conditions of concentration, salinity, pH, and temperature (4,8–14). Often these capsids have a morphology identical to that of the native virion, but nonnative structures may emerge too (9). Although still poorly understood, the phenomenon of capsid polymorphism was recently explained in terms of a conformational switching of the coat proteins (2,7).
Plausibly, the main driving force for capsid assembly is the hydrophobic interaction between apolar patches on the coat proteins (4,15–18), which has to be strong enough to overcome the Coulomb repulsion between the net electrical charge on them (15,16,18,19). Other types of interaction may also contribute to the stability of virus capsids, of which the most prominent are the complexation with the oppositely charged genome (real or synthetic) (9,11,20,21), and hydrogen bonds or salt bridges involving, e.g., Caspar carboxylate pairs on neighboring coat proteins (1,3,22). The strength of the net attractive interaction between the coat proteins inferred from equilibrium assembly studies are remarkably weak (4,23), however, and thought to prevent the growing capsids from becoming kinetically trapped (24,25).
Kinetic studies of icosahedral capsids (and procapsids) suggest that their assembly does not occur in a single step but follows a cascade of lower-order reactions (10,24–26). Experimental data and computer simulations point at nucleation-and-growth as the prevailing assembly mechanism (27–29), the kinetics of which is sensitive to the ambient conditions. These conditions determine whether the docking of coat proteins onto partially complete capsids is reversible or (effectively) irreversible. The latter should be the case if the quenching is (in some sense) deep or the bonding strong, albeit for different reasons so (27). For relatively weak bonding, coat proteins attaching to the growing capsid are presumably able to rearrange themselves and to find a state of a local equilibrium, arguably a crucial requirement for the completion of well-formed capsids (28).
If the interactions between the virus coat proteins are not strong and if they are initially freely dissolved, we would expect the classical nucleation picture to (approximately) hold, bearing in mind that capsid assembly is believed to be akin to crystallization and to micelle formation (6). This implies that there must be thermodynamically unfavorable intermediate states that produce a kinetic bottleneck to the formation of the capsids (30–32). If so, capsid assembly kinetics should be sigmoidal and characterized by a lag time before a significant production of capsids is reached. This has indeed been observed in assembly studies of HPV capsids (10) and of phage P22 (26) procapsids in the presence of scaffolding subunits, and arguably so in studies on CCMV and HBV under mild quenching conditions (24,25).
Experimental observations on HBV assembly kinetics can described qualitatively by a reaction cascade model put forward by Zlotnick and collaborators (25,27), the governing set of equations of which have so far only been solved numerically. Since the model is similar in spirit to theoretical models for surfactant micelle assembly (30) and the homogeneous nucleation of crystals (31), it should be possible to apply notions from either field to capsid formation and provide qualitative predictions without explicitly solving the rate equations. Here, we do exactly that by invoking classical nucleation theory for a simplified version of the model, valid in the limit where kinetic trapping does not occur and conditions of local equilibrium are observed. Our nucleation-and-growth model is consistent with the energy landscape picture of the minimal model of capsomer interaction presented in (33). A better understanding of the capsid nucleation kinetics could be instrumental in the design of antiviral drugs that interfere with the polymerization pathway (34).
The theory we present in this article allows for a quantification of the quench depth in terms of supersaturation of the coat proteins relative to a critical capsid concentration (15). It explains how the steady-state nucleation rate and the lag time can be influenced by varying the concentration of coat protein, the ionic strength, the temperature, and the pH. We put forward that the differences in the scaling of the nucleation rate with concentration found for coat proteins of different viruses might be due to the unusual nucleation of (quasi two-dimensional) objects of fixed size. It suggests that more extensive experimentation is necessary, spanning a larger range of concentration than hitherto done to ascertain that the observed nonuniversal behavior is caused by differences in coat protein structure (10,24–26). Finally, the theory also provides a natural explanation for the hysteresis observed in assembly and disassembly experiments (35), an issue we address in more detail elsewhere.
The remainder of this article is organized as follows. In the first section, entitled Equilibrium Theory of Virus Capsid Assembly, we recapitulate the statistical theory of the supramolecular assembly of spherical (icosahedral) capsid shells (15,36–38), formulated slightly differently from the usual theory of micellization, but in fact equivalent to it (20,39). We confirm that capsid formation is indeed reminiscent of a first-order phase transition and that capsid formation must always be nucleated. In the next section, Classical Nucleation Theory of Capsids, we apply the classical nucleation theory to spherical shells that, for simplicity, we presume to be incompressible. We calculate the steady-state nucleation rate as well as the lag time, and find it to be a nonuniversal function of the actual concentration and the critical capsid concentration of the equilibrium state the system attempts to approach. In the last two sections, Discussion and Conclusions, we discuss our findings and their implications, and summarize our conclusions.
EQUILIBRIUM THEORY OF VIRUS CAPSID ASSEMBLY
Let F denote the Helmholtz free energy of an aqueous solution of N-coat protein building blocks in a volume V. The building blocks self-assemble into capsids of fixed aggregation number q ≫ 1. We do not specify the kind of building block: depending on the species they may be monomers, dimers, or even pentamers or hexamers of the actual coat proteins (5). Partially formed capsids are stable only in very small amounts for reasons intimated in the Introduction and elaborated below, so we ignore these for now (36). Incorporating them in the equilibrium theory would make the mathematics more cumbersome, but does not alter our conclusions in any significant way (see Appendix A). Hence, we assume that there are an as-yet-unknown number of N1 free monomers and of Nq fully formed capsids.
Within a mean-field approximation, the free energy is the sum of an ideal free energy of mixing of the free monomers and capsids, and a free energy accounting for the interactions between proteins bound in the individual capsids. We ignore other types of (nonbonded) interaction between the various species, because, at the level of a (Flory-type) mean-field theory, these do not couple to the self-assembly (40). The reason is that the associated excess free energy is a function of the overall concentration of material only, not how this material is distributed over monomeric and polymeric species.
We thus write (40)
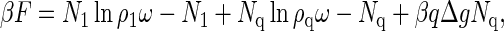 |
(1) |
where ρi = Ni/V denotes the number density of the component with i = 1, q is the aggregation number, and β = 1/kBT is the reciprocal of the thermal energy with kB Boltzmann's constant and T the absolute temperature. A particular derivation of Eq. 1 is given in Appendix A. In Eq. 1, the quantity Δg ≤ 0 is the effective, mean binding free energy of a single subunit, tacitly assuming that it is a quantity averaged over all q monomer units of a fully formed capsid. (Recall that in icosahedral capsids the coat proteins do not have identical but quasi-equivalent local environments (5).) We present a phenomenological estimate for the free energy of binding in Appendix B, and merely note that because interaction energies between pairs of protein are of the order of a few kBT (18,41,42), this amounts to binding energies |Δg| of 10–20 kBT. (For HBV, Δg was found to be closer to −20 than to −10 kBT (4,15).) The reference volume, ω, is of the order of the volume of a solvent molecule, so for all intents and purposes, ρiω < 1 may be interpreted as a mole fraction in a description that implicitly includes the background solvent as part of the system (43). As noted in Appendix A, the size of a solvent molecule must be the smallest relevant physical length scale in the problem because we have tacitly integrated it out of our description.
The equilibrium distribution of proteins over the assembled and disassembled states follows by minimization of the free energy subject to the conservation of mass, N = N1 + qNq. Putting (∂F/∂N1)N,V,β = 0 results to
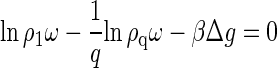 |
(2) |
or
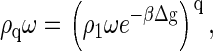 |
(3) |
which is the familiar law of mass action. Equation 3 establishes a relation between equilibrium concentration of capsids and free protein subunits. For very low concentration of proteins, 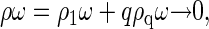 most subunits remain free in the solution, i.e.,
most subunits remain free in the solution, i.e., 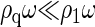 and ρω ≈ ρ1ω. However, since ρqω must always be smaller than unity, it is clear that ρ1ω can never exceed the quantity eβΔg. Thus,
and ρω ≈ ρ1ω. However, since ρqω must always be smaller than unity, it is clear that ρ1ω can never exceed the quantity eβΔg. Thus,
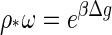 |
(4) |
is a critical density, equivalent to the critical micelle concentration in surfactant solutions (39). This critical capsid density depends not only on the type of coat proteins but also on the physical conditions of the solution, i.e., on the temperature, ionic strength, acidity, and so on. See the Appendix B. From Eqs. 3 and 4, we deduce that the transition from the monomer to the capsid-dominated regime becomes sharp in the limit where q → ∞, because in that case qρq = ρ − ρ* if ρ ≥ ρ* and ρq = 0 if ρ ≤ ρ*.
Interestingly, capsid assembly resembles a phase transition, provided we let q → ∞. As may be verified straightforwardly, the heat capacity per monomer, 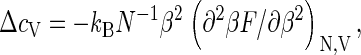 calculated from Eqs. 1–4, exhibits a jump from ΔcV = 0 to
calculated from Eqs. 1–4, exhibits a jump from ΔcV = 0 to 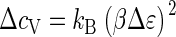 when the critical density ρ* crosses the monomer density ρ from above, where Δɛ is the capsid binding energy (enthalpy). Such a jump is typical of a phase transition in a mean-field theory (44), but cannot help distinguish between a first- or second-order transition. Note that for finite q there is no discontinuity, but the heat capacity is sharply peaked—in fact, allowing for an accurate measurement of ρ* and therefore of Δg (17). We refer to Appendix C for details.
when the critical density ρ* crosses the monomer density ρ from above, where Δɛ is the capsid binding energy (enthalpy). Such a jump is typical of a phase transition in a mean-field theory (44), but cannot help distinguish between a first- or second-order transition. Note that for finite q there is no discontinuity, but the heat capacity is sharply peaked—in fact, allowing for an accurate measurement of ρ* and therefore of Δg (17). We refer to Appendix C for details.
An important quantity in the development of the classical nucleation theory is the difference between the chemical potential of free protein subunits in the metastable solution and bound proteins in the capsids. The chemical potential of the free protein subunits in solution is
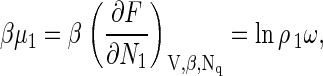 |
(5) |
and similarly, the chemical potential of a capsid is
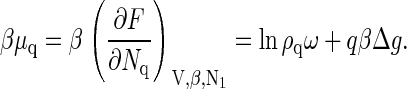 |
(6) |
It can be easily shown (see Appendix A) that the optimal distribution of proteins over the assembled and disassembled states, given by Eq. 2, corresponds to the condition μ1 = μq/q. In other words, the equilibrium condition is determined by the requirement that the chemical potential of a subunit in the capsid, μq/q, be equal to that of a subunit in solution μ1. If we consider an initial state in which no capsids and only monomers are dispersed in the solution, that requirement translates into
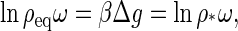 |
(7) |
which determines the concentration of free subunits ρeq at which, from a purely equilibrium perspective, capsid self-assembly will set in. It is worth noticing that this coexistence concentration ρeq coincides with the critical capsid density, defined by Eq. 4.
We shall be needing Eqs. 5 and 6 in the theory presented in the next section.
CLASSICAL NUCLEATION THEORY OF CAPSIDS
With a first-order phase transition it is often possible to quench an initially stable phase (e.g., a vapor, liquid, or solution) through the thermodynamic condition of coexistence sufficiently rapidly, so that the transition does not immediately occur and the phase becomes metastable. Quenching does not necessarily involve a change in temperature; it may, for example, involve a rapid change of pressure or any other intensive variable that characterizes the system. The metastable system may then be relatively slowly converted to a stable one that contains the initial phase (the mother phase) and a new phase. The dynamic process by means of which this is achieved usually involves nucleation (already referred to in the Introduction). A particularly simple example of the conversion from metastability to stability is the condensation of a vapor from an initial state of supersaturation to coexistence with its corresponding liquid at the equilibrium or saturation pressure.
The relative slowness of the conversion is due to a free energy barrier (discussed in Introduction) which the system must surmount in the process. The basic theory of the rate of conversion, especially at the molecular level, is very difficult, and after many years is still a work in progress. However, considerable quantitative success has been achieved by appealing to a modelistic approach (classical theory of nucleation) in which the intermediate states of the conversion are treated as coarse-grained renormalized versions of the detailed molecular states. Take, e.g., the example of the condensation of a supersaturated (metastable) vapor into a liquid. Normally it will proceed via fluctuations that produce clusters of molecules that eventually grow into liquid drops. In the coarse-grained classical theory, the smallest clusters are then modeled as liquid drops that have the uniform density and the surface tension of the bulk liquid and a sharp interface with the vapor.
Within the model, thermodynamics shows that the free energy of formation of a cluster containing n molecules may be expressed as (31,32)
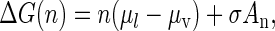 |
(8) |
in which μl is the chemical potential per molecule in the drop, as if all of its material were at the pressure outside of the drop, while μv is the chemical potential in the vapor. The value σ is the surface tension of the drop and An is its surface area. Since the vapor is supersaturated, its chemical potential exceeds that of the liquid and the first term on the right of Eq. 8 is negative, while the second term is positive. However, when n is small, the absolute value of the first term is smaller than that of the second which, through its dependence on An, increases only as n2/3. As a result, at small values of n, ΔG increases as n increases but at larger values the negative first term (the volume term that varies directly as n) overtakes the surface term and causes ΔG to decrease. A maximum, representing the free energy barrier, is thus produced.
Cluster growth is described by a sequence of reversible kinetic steps involving the gain and loss of single molecules. With the aid of the principle of detailed balance the flux of clusters through size space (n-space) may be described by a Fokker-Planck equation (31,32). The actual rate of nucleation (rate of drop formation) is determined by the rate (nucleation rate) at which clusters cross the top of the barrier. Indeed, the cluster at the top of the barrier is the condensation nucleus since it can grow spontaneously with a decrease of free energy. When the barrier and its curvature are large enough, the crossing rate can be determined by a steepest-descents integration (involving only clusters in the neighborhood of the nucleus) of the Fokker-Planck equation that leads to an Arrhenius-like expression for the nucleation rate that contains the barrier height in the exponential factor. The preexponential factor contains the so-called Zeldovich factor which, among other things, accounts for the concentration of nuclei being less than the equilibrium value that would obtain if clusters were not allowed to grow appreciably beyond the nucleus size.
Turning to capsid assembly, we will, as promised, model the process as a nucleation phenomenon. Using the framework of nucleation theory, capsids, complete or partially formed, will be treated as clusters of proteins or capsomers. The capsid self-assembly does not set in, in general, at the equilibrium concentration predicted by Eq. 4, mainly due to the presence of a free energy barrier. When the concentration of proteins exceeds a critical value, the chemical potential of proteins in a capsid becomes smaller than in solution, and this difference is, in fact, the thermodynamic driving force for the capsid formation. Some differences from the standard approach of classical nucleation theory (31,32) are that clusters have a maximum size and that, since the capsid consists only of a two-dimensional structure, surface tension will be replaced by a line or rim tension. Rim tension contributions will only appear in incomplete capsids. The rim proteins have fewer contacts with their neighboring protein resulting into a higher free energy. Other subtleties will be ignored. For example, in Eq. 8, μl is the chemical potential that a molecule in the drop would have if the interior of the drop were at the pressure outside of the drop. An equivalent subtlety would be expected in the capsid chemical potential, but we will ignore it to keep the model as simple as possible.
Here, we consider an initial state in which the capsid subunits are molecularly dispersed, and a final state in which a finite fraction of the subunits has assembled into capsids. Following the standard ideas of classical nucleation theory, we can then propose a thermodynamic expression—very similar to Eq. 8—for the free energy of formation of a partially formed capsid consisting of n units. Provided that the capsids have a fixed radius of curvature R (i.e., the radius of the capsid) even when incomplete, and that the shell is laterally incompressible, the Gibbs free energy ΔG of a growing capsid in contact with the metastable host dispersion becomes equal to (31)
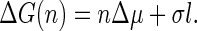 |
(9) |
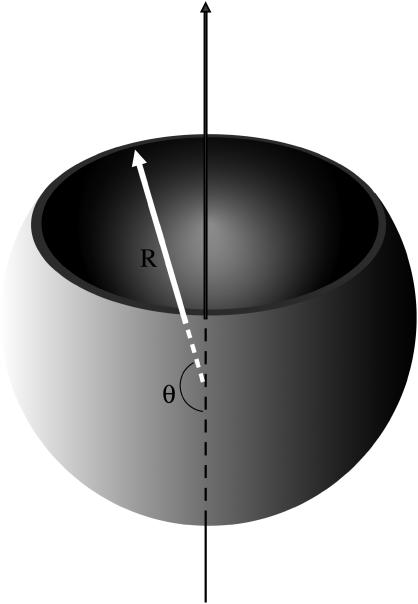
Here Δμ is the difference between the chemical potentials of the protein subunits in the stable assembled and metastable disassembled states; l is the contour length of the rim; and σ is the energy cost per unit length associated with the rim (and it is in this sense, similar to a line tension). As in the case of CNT, we will resort to a quasi-continuum approach. We assume that a partially formed capsid is a spherical cap characterized by an angle θ (see Fig. 1). From simple geometry, n = q(1 − cos θ)/2, and the length of the rim is l = 2πR sin θ. We can also express, l, in terms of the number of units n as
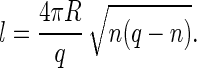 |
(10) |
FIGURE 1.
Representation of the continuum model of a partially formed capsid. R denotes the radius of the capsid and θ is the angle that characterizes the degree of completion of the capsid.
Accordingly, the free energy of formation becomes ΔG(θ) = Δμq(1 − cos θ)/2 + 2πRσ sin θ, or in terms of the number of units in the partially formed capsid,
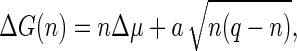 |
(11) |
where
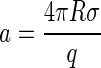 |
(12) |
is a measure of the rim energy. The first term in Eq. 11 promotes the formation of capsids, while the second term is responsible for the barrier exhibiting nucleation of capsids. The presence of the rim free energy is, in fact, also the reason for partially complete capsids to be strongly suppressed in equilibrium so that they can be approximately ignored in an equilibrium description. (Numerical studies confirm this (36).)
To calculate the barrier height, we locate the maximum of the Gibbs free energy Eq. 11. Let Γ ≡ −Δμ/a be a dimensionless measure of the supersaturation or quench depth. By setting 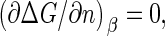 we find for the barrier height
we find for the barrier height
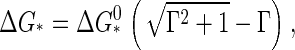 |
(13) |
with 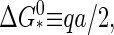 and for the critical nucleus size
and for the critical nucleus size
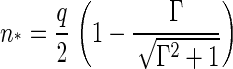 |
(14) |
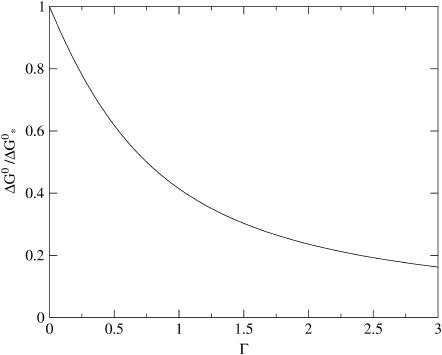
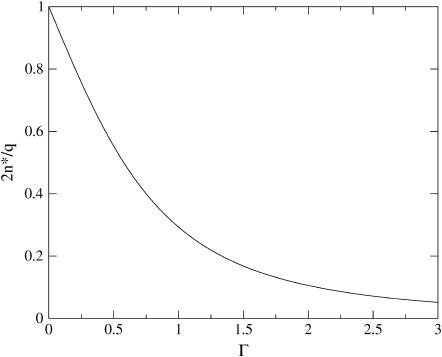
We have plotted both quantities in Figs. 2 and 3, showing (as expected) a monotone decrease of both the barrier height and the size of critical nucleus with increasing supersaturation Γ. We postpone a more detailed discussion of our findings to the next section, where we also translate the theoretical parameter Γ into a more practical one.
FIGURE 2.
The capsid nucleation barrier, ΔG*, scaled to its maximum value at the critical density,  as a function of the dimensionless supersaturation Γ as defined in the main text.
as a function of the dimensionless supersaturation Γ as defined in the main text.
FIGURE 3.
Ratio of the critical capsid nucleus, n*, and the aggregation number of a complete capsid q as a function of the dimensionless supersaturation Γ.
As noted previously, the barrier height is the principal determinant of the nucleation rate because of the unfavorable Boltzmann weight ρ exp (− βΔG*) of the critical nucleus that acts as a kinetic bottleneck. Within a Becker-Döring type of kinetics where single monomers sequentially attach or detach, the steady-state nucleation rate per unit volume, J, can be found to obey the Zeldovich form (31),
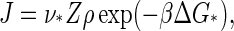 |
(15) |
with ν* the so-called jump-frequency that is a function of the diffusivity of the free monomers, and
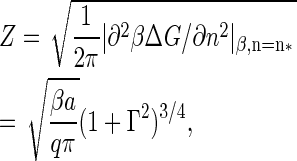 |
(16) |
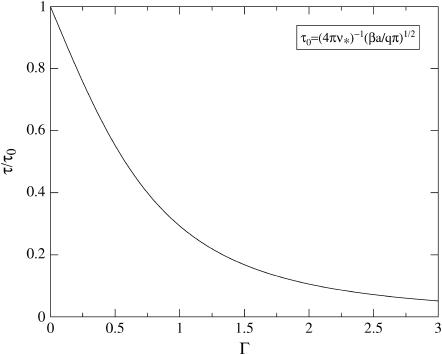
the Zeldovich factor that accounts for the survival time of the critical nucleus. Without derivation we also simply quote the estimate for the lag time, τ, before reaching steady-state nucleation (31,32)
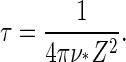 |
(17) |
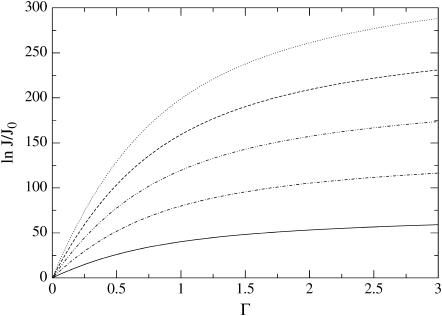
Our predictions for the nucleation rate, Eq. 15, and for the lag time, Eq. 17 are plotted in Figs. 4 and 5. The nucleation rate increases, while the lag time decreases, with increasing supersaturation. This agrees with experimental observation, and with results of numerical model calculations (25,27,28).
FIGURE 4.
Nucleation rate J for a T = 3 virus capsid with q = 180, scaled to its minimum value J0 as a function of the dimensionless supersaturation Γ. Shown are results for different dimensionless binding free energies |βΔg| = 5,10,15,20,25 (from bottom to top).
FIGURE 5.
The lag-time τ scaled to its maximum value τ0 at the critical density, as a function of the dimensionless supersaturation Γ.
The theory developed in this section is quite general and can, in principle, be applied to any type of model for the effective interaction between capsid structural units. Indeed, its main ingredients, Δμ and σ, can be expressed in terms of the protein density, ρ, and the interaction energy, Δg. Based on the equilibrium theory developed in the previous section “Equilibrium Theory of Virus Capsid Assembly”, the difference in chemical potentials in the limit q ≫ 1 becomes
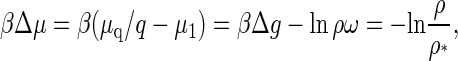 |
(18) |
where we have considered an initial state in which no capsids and only free subunits are dispersed in the solution. A very simple estimate of the line tension is σ = − cΔg/r0, where c denotes the number of bonds that a rim protein has fewer than a core protein, and r0 is the effective diameter of a unit. If, for simplicity, we assume that the structural units can be approximated as disks of effective diameter r0, and further assume full coverage of the spherical surface of a fully formed capsid, then we have 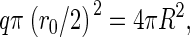 or
or 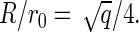 Therefore, we can estimate the value of a as
Therefore, we can estimate the value of a as
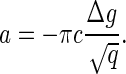 |
(19) |
In more general terms, the value of a would be given by 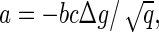 where b is a geometrical factor related to the shape of the subunits and the structure (T number) of the capsids. It is important to stress again that ρ* and therefore Δg are experimentally accessible quantities (4,15).
where b is a geometrical factor related to the shape of the subunits and the structure (T number) of the capsids. It is important to stress again that ρ* and therefore Δg are experimentally accessible quantities (4,15).
DISCUSSION
The key quantities in a nucleation process are the barrier height and critical nucleus size, given in our case by Eqs. 13 and 14. In this section we will analyze in more detail these expressions and relate them with physical and experimentally measurable quantities. Let us first analyze the behavior upon the value of the quench depth. For shallow quenches with 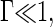 we find n*/q ∼ (1/2)−(1/2) Γ +… and
we find n*/q ∼ (1/2)−(1/2) Γ +… and 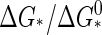 ∼1 − Γ + ···. For deep quenches, implying strong supersaturation Γ ≫ 1, we have n*/q ∼(1/4) Γ−2 ≪ 1 and
∼1 − Γ + ···. For deep quenches, implying strong supersaturation Γ ≫ 1, we have n*/q ∼(1/4) Γ−2 ≪ 1 and 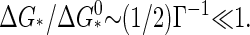 So, the critical nucleus is large, up to half the size of a complete capsid if the quench is shallow. Its size rapidly decreases with increasing supersaturation, shrinking to approximately a monomer size if
So, the critical nucleus is large, up to half the size of a complete capsid if the quench is shallow. Its size rapidly decreases with increasing supersaturation, shrinking to approximately a monomer size if 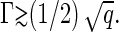 The free energy barrier also reduces in magnitude with increasing supersaturation, ultimately to become of the order of the thermal energy, in which case the nucleation process becomes dominated by kinetic effects represented by the preexponential factor.
The free energy barrier also reduces in magnitude with increasing supersaturation, ultimately to become of the order of the thermal energy, in which case the nucleation process becomes dominated by kinetic effects represented by the preexponential factor.
The above theory is similar to that for the nucleation of a macroscopic phase, as in the crystallization of a solid or the condensation of a vapor. In classical nucleation theory, one finds that n* = 32πυ2χ−3/3 and 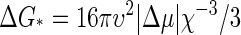 provided the nuclei are spherical with υ is the volume of a molecule and χ = − Δμ/σ, where σ is the surface tension of the stable phase (31). Apart from a different scaling of the various quantities with the thermodynamic driving force βΔμ, the main difference between capsid nucleation and the nucleation of a macroscopic phase is that in capsid assembly neither the nucleation barrier nor the critical nucleus size diverge when the supersaturation becomes vanishingly small, i.e., when βΔμ → 0. The reason is that, in a way, the novel phase grows on the surface of a sphere of fixed size, where both reduced dimensionality and finite size modify the predictions of classical theory.
provided the nuclei are spherical with υ is the volume of a molecule and χ = − Δμ/σ, where σ is the surface tension of the stable phase (31). Apart from a different scaling of the various quantities with the thermodynamic driving force βΔμ, the main difference between capsid nucleation and the nucleation of a macroscopic phase is that in capsid assembly neither the nucleation barrier nor the critical nucleus size diverge when the supersaturation becomes vanishingly small, i.e., when βΔμ → 0. The reason is that, in a way, the novel phase grows on the surface of a sphere of fixed size, where both reduced dimensionality and finite size modify the predictions of classical theory.
The upper limit to the barrier height 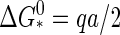 for capsid nucleation may not be infinite, but it is still very large. A simple order-of-magnitude estimate of the height is
for capsid nucleation may not be infinite, but it is still very large. A simple order-of-magnitude estimate of the height is 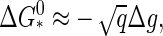 with |Δg| ≈ 10–20 kBT and q ≈ 60–180 for the smaller viruses with a T number less than or equal 3 (23). (Here, we presume that the building blocks are single coat proteins—this does not need be the case in practice (5).) Hence, we expect barrier heights in the range 70–140 kBT for the smaller viruses at weak supersaturation.
with |Δg| ≈ 10–20 kBT and q ≈ 60–180 for the smaller viruses with a T number less than or equal 3 (23). (Here, we presume that the building blocks are single coat proteins—this does not need be the case in practice (5).) Hence, we expect barrier heights in the range 70–140 kBT for the smaller viruses at weak supersaturation.
To clarify what shallow and deep quenches precisely are in the context of capsid nucleation, we rewrite the supersaturation parameter Γ = − Δμ/a in terms of quantities that are measurable in an actual experiment, even if this is true only in principle. For our choice of assembly conditions, where no capsids are present in the initial (metastable) state, we have
 |
(20) |
where we have made use of Eqs. 18 and 19. Note that Eqs. 13 and 20 show that the deeper we quench into the capsid-dominated regime, the larger the value of Γ, and the lower is the free energy barrier. In other words, the larger the final fraction of protein assembled into capsids, the swifter will have been the kinetics of nucleation. Again, this is in accord with experimental observation on HBV, HPV, P22 procapsids, and CCMV (10,24–26). From Eq. 20 we are also able to conclude that the critical nucleus size is reduced to the order of a monomer for ρ/ρ* ≈ exp(−βΔg/2), which is of the order of 102–104.
It is now clear that the height of the nucleation barrier, ΔG* as well as the rate of nucleation, J, and the lag time, τ, are functions of the ratio of the logarithms of the actual and the critical concentrations, and of the critical concentration after the quench. For example, for deep quenches we find the following simplified relation for the nucleation barrier
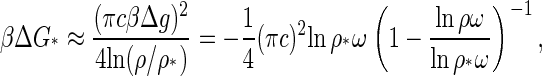 |
(21) |
where we have inserted Eq. 20 as well as the relation 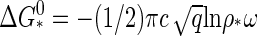 into the asymptotic behavior of Eq. 13. Similar expressions may be obtained for the nucleation rate and the lag time from Eqs. 15 and 17. We are led to conclude that capsid nucleation kinetics must be nonuniversal, for it depends not only on some measure of the relative quench depth but also on the binding energy, Δg, and the geometry of the capsid subunits. The averaged binding energy Δg, or equivalently, the location of the critical concentration depends on the type of virus coat protein, the ionic strength, the pH, the temperature, and so on. See, e.g., the Appendix B.
into the asymptotic behavior of Eq. 13. Similar expressions may be obtained for the nucleation rate and the lag time from Eqs. 15 and 17. We are led to conclude that capsid nucleation kinetics must be nonuniversal, for it depends not only on some measure of the relative quench depth but also on the binding energy, Δg, and the geometry of the capsid subunits. The averaged binding energy Δg, or equivalently, the location of the critical concentration depends on the type of virus coat protein, the ionic strength, the pH, the temperature, and so on. See, e.g., the Appendix B.
Finally, it is worth mentioning that not only capsid assembly but also capsid disassembly can be described in the context of classical nucleation theory (31). We will analyze the interesting problem of disassembly and of hysteresis elsewhere in detail, and only mention that the rate of disassembly is different from that of assembly because the critical nuclei have different Boltzmann weights. (Even if the barrier to nucleation were the same, in a disassembly experiment, the number of critical nuclei is on the order of the aggregation number of the complete capsid—which is smaller than in an assembly experiment at equal concentration, because in that case, the monomer density ρ entering the nucleation rate Eq. 15 must be replaced by the capsid density ρq ≤ ρ/q ≪ ρ.)
CONCLUSIONS
By combining an equilibrium theory of virus capsid assembly and homogeneous nucleation theory, we have obtained predictions that reproduce the main features of assembly kinetics of empty virus capsids under mild quenching conditions as found in experiment and in numerical simulation.
We find that both the lag time and the steady-state nucleation rate of capsids are functions of the protein concentration and of the critical capsid concentration. The latter quantity depends on the type of virus coat protein as well as on the ambient conditions of ionic strength, pH, and temperature through the impact that these have on the strength of the interactions between the coat proteins. Hence, a useful interpretation of capsid assembly (or disassembly) data does not seem possible unless either the critical capsid concentrations or the average binding energies are known.
Matters are compounded by the lack of a universal scaling of either the lag time or the nucleation rate with the concentration of coat protein. This suggests that the different power laws found for the nucleation rates of coat proteins of different viruses (10,24–26) need not be entirely caused by differences in the protein structure, but may also be due to differences in the quenching conditions. Experiments spanning a larger range of concentrations than thus far performed are required to resolve this issue.
Finally, capsid nucleation experiments in the presence of genome seem to follow different kinetics from that seen in the absence of genome. Since the genomes form complexes with capsid proteins, it may be possible to study this phenomenon theoretically from the perspective of heterogeneous nucleation theory (45). Work along these lines is currently underway.
Acknowledgments
The authors have benefited from many helpful discussions with Professor William Gelbart.
This work was supported by grants No. NSFCHE-03013563 and No. NSFCHE04-00363. D.R. acknowledges support by the Ministerio de Ciencia y Tecnologia of Spain through the Ramon y Cajal program.
APPENDIX A: FREE ENERGY OF A CAPSID SOLUTION
In this Appendix we provide more insight into the mean-field expression for the Helmholtz free energy F given in Eq. 1. There are many ways to set up a mean-field theory, but here we choose to invoke a cell model of the subject system, consisting of a renormalized background solvent within which coat proteins and partially formed capsids are dissolved. In this description, intermolecular potentials between proteins and proteins, on the one hand, and capsids and proteins, on the other, become potentials of mean force (actually free energies). The sizes of the cells are chosen so that, at one time, only the center of mass of a single protein or capsid fragment can occupy a cell. Since the solvent enters the description only implicitly, a natural cell size would be the size of a solvent molecule. (For a more detailed discussion, the reader is referred to (43).) In effect, we will deal with solutions of proteins and capsids so dilute that they may be considered to form an ideal solution within the background solvent.
The number of particles containing n coat proteins will be denoted by Nn, whereas the number of cells will be denoted by M, and it is given by
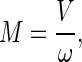 |
(A1) |
where V is the total volume of the system and ω is the volume of a cell. If the total number of protein molecules in the system is N, the conservation condition, Eq. A2,
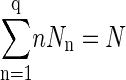 |
(A2) |
applies, where q represents the number of coat proteins in a fully formed capsid. The internal partition function of a particle will be denoted by 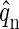 and the partition function of a particle confined to a cell will then be given by
and the partition function of a particle confined to a cell will then be given by
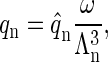 |
(A3) |
where Λn ≪ ω1/3 is the thermal De Broglie wavelength
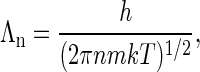 |
(A4) |
in which h is Planck's constant and m is the mass of a coat protein. Then 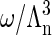 is the translational partition function of the particle confined to a cell. With these various definitions the partition function of the protein system in the renormalized background may be written as
is the translational partition function of the particle confined to a cell. With these various definitions the partition function of the protein system in the renormalized background may be written as
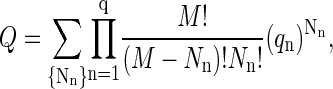 |
(A5) |
where the sum is over {Nn} representing all particle size distributions that satisfy Eq. A2. The combinatorial factor in this equation represents the number of distinguishable configurations of the particles over cells, whereas the product of qn-values reflects the fact that the particles in the protein system are in dilute enough concentration such that interactions between them can be ignored.
The structure of Q should be self-evident. As usual, we shall be content with representing Q by its maximum term and the equilibrium distribution of Nn by the distribution corresponding to that maximum term. That distribution, subject to Eq. A2, is easily found by the method of undetermined multipliers to be
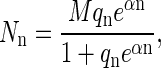 |
(A6) |
where α is the undetermined multiplier. Note that qn can be expressed, in standard canonical ensemble form, as
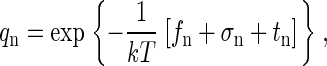 |
(A7) |
where fn is the internal free energy of the particle, σn is line-tension free energy of an incomplete capsid, and tn is the translational free energy of the particle within a cell. Thus,
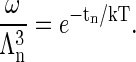 |
(A8) |
Note that tn is negative, reflecting the increased entropy of a freely moving (within ω) particle.
The free energy of the protein system is
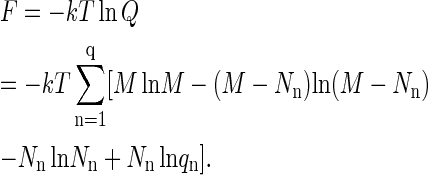 |
This equation is obtained by taking the logarithm of the maximum term in Eq. A5. Note that, using M = (M − Nn) + Nn, it can be expressed as
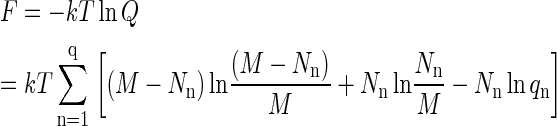 |
(A9) |
In the case that Nn/M ≪ 1, i.e., when the protein solution is dilute, the first term in square brackets on the right of Eq. A9 can be expanded in powers of Nn/M, keeping the linear term, to yield
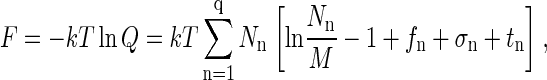 |
(A10) |
where Eq. A7 has also been used. Defining
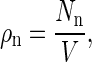 |
we finally obtain
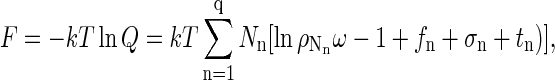 |
(A11) |
which would be identical to Eq. 1 if the only terms in the sum were those for n = 1 and n = q. Note that σ1 = σq = 0 for free proteins and fully formed capsids. In Eq. 1, Δg = (fq + tq)/q and f1 + t1 has been set equal to zero, making Δg an excess free energy relative to the internal free energy of a free monomer that, in principle, includes contributions also from conformational changes of the coat proteins upon assembly. It should also be emphasized that Eq. 1 is restricted to a dilute solution and that ω is essentially a cell volume of the order of the volume of a solvent molecule.
Finally, by expressing the chemical potential μn of a particle of size n in terms of α, the undetermined multiplier can be determined. Thus
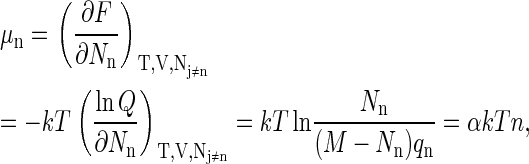 |
(A12) |
or
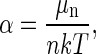 |
(A13) |
thus determining α. From Eq. A13 we obtain
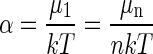 |
(A14) |
or
 |
(A15) |
which is the law of mass action. Eq. A6 now becomes
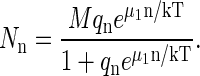 |
(A16) |
This distribution was evaluated numerically for a particular capsid assembly model some time ago by Zlotnick (36). If partially formed capsids are suppressed, Eq. A16 leads to Eq. 3, because in the dilute limit, 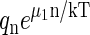 ≪ 1.
≪ 1.
APPENDIX B: A SIMPLE MODEL FOR THE CAPSID BINDING STRENGTH
Here, we briefly review the phenomenological binding free energy of capsid proteins that does not rely on the concept of conformational switching recently put forward by two of us (15). For an extensive discussion the reader is referred to the original publication. Presuming that hydrophobic interactions drive the assembly of virus capsids (4,16,18) and that the electrostatic repulsion between the coat proteins oppose it (15,19), we must have
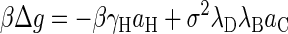 |
(B1) |
at the level of a Debye-Hückel approximation (39). In Eq. B1, γH and aH denote the surface tension and surface area of the apolar patches on the proteins buried upon assembly, σ the net surface charge density of the water-exposed parts of the proteins, and aC their surface area. Absorbed in aH and aC are unknown geometrical constants of order unity. The electrostatic lengths λB and λD are, respectively, the Bjerrum and the Debye screening lengths defined below. Eq. B1 quite accurately describes the temperature, ionic strength, and concentration dependence of the assembly of HBV coat protein when inserted into the theory described in the section Equilibrium Theory of Virus Capsid Assembly (15). Additional contributions may be necessary, e.g., when Caspar pairs contribute to the stability of the virus, such as in Tobamo viruses (22) and in CCMV (1). An extended version of Eq. B1 that includes the effects of Caspar pairs has recently been shown to semiquantitatively describe the stability of TMV (W. K. Kegel and P. van der Schoot, unpublished), a rodlike virus.
The Bjerrum length λB = βe2/4πE is the distance over which the (unscreened) electrostatic interaction between two unit charges equals the thermal energy, where E denotes the dielectric permittivity of the medium (in our case water) and e the unit charge. The Debye length 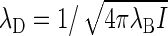 measures the scale over which electrostatic interactions are screened by the presence of salt ions, with
measures the scale over which electrostatic interactions are screened by the presence of salt ions, with 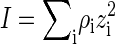 the ionic strength of the solution containing a number density ρi of ions of zi unit charge (40). For 1:1 electrolytes,
the ionic strength of the solution containing a number density ρi of ions of zi unit charge (40). For 1:1 electrolytes, 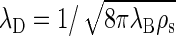 in terms of the number density of added salt ρs. This reduces at equal concentration to
in terms of the number density of added salt ρs. This reduces at equal concentration to 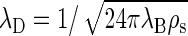 for a 1:2 electrolyte and to
for a 1:2 electrolyte and to 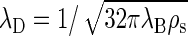 for a 2:2 electrolyte.
for a 2:2 electrolyte.
It is now immediately clear how the concentration of added salt and the pH impact on the binding free energy and hence on the critical capsid concentration given in Eq. 4. At fixed temperature, βΔg becomes increasingly negative with increasing ionic strength I and with decreasing net surface charge σ, shifting the critical concentration ρ* to lower values. The ionic strength increases with increasing concentration of added salt, or, at constant salt, with increasing valence of added ions. Both predictions are in agreement with measurements on the coat proteins of TMV, HBV, and CCMV (1,9,13,14,46,47). The net charge increases with increasing pH relative to the isoelectric point, which for the coat proteins of most viruses is (well) below 7, so assembly should be inhibited with increasing pH > 7. This is also in agreement with measurements on TMV, HBV, and CCMV (1,9,13,14,46,47).
APPENDIX C: HEAT CAPACITY OF A CAPSID SOLUTION
The mean binding energy (enthalpy) per coat protein, ɛ, can be calculated from the free energy according to 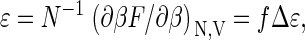 where Δɛ ≡ (∂βΔg/∂β)V is the energy (enthalpy) of a bound monomer and f = qρq/ρ. The heat capacity per protein thus becomes
where Δɛ ≡ (∂βΔg/∂β)V is the energy (enthalpy) of a bound monomer and f = qρq/ρ. The heat capacity per protein thus becomes
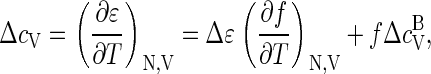 |
(C1) |
with 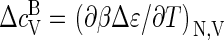 as the heat capacity associated with the bound state of a protein in a capsid that includes the contribution from the so-called breathing or phonon modes. If the proteins are harmonically bound to the capsid, we expect
as the heat capacity associated with the bound state of a protein in a capsid that includes the contribution from the so-called breathing or phonon modes. If the proteins are harmonically bound to the capsid, we expect 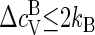 since the capsid may be viewed as a quasi two-dimensional crystal (48). Because estimates of Δɛ/kBT are typically of order 10, we must conclude that the contribution
since the capsid may be viewed as a quasi two-dimensional crystal (48). Because estimates of Δɛ/kBT are typically of order 10, we must conclude that the contribution 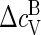 stemming from the breathing modes of the capsids are subdominant.
stemming from the breathing modes of the capsids are subdominant.
Inserting Eqs. 3 and 4 into Eq. C1, we find
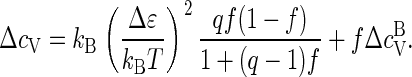 |
(C2) |
In the limit q → ∞, this expression simplifies to
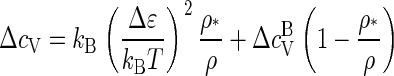 |
(C3) |
for ρ ≥ ρ*, and to ΔcV = 0 for ρ ≤ ρ*, since f = 1 − ρ*/ρ if ρ ≥ ρ* and f = 0 otherwise. Hence, the heat capacity jumps from ΔcV = 0 to ΔcV = kB(Δɛ/kBT)2 at ρ = ρ*, showing that we are indeed dealing with a phase transition. The jump is typical of mean-field theories (44).
Remarkably, the leading contribution to the enthalpy of binding comes from the hydrophobic effect. From Eq. B1 we obtain
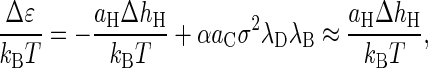 |
(C4) |
where ΔhH is the surface excess enthalpy of the hydrophobic patches on the coat proteins. In water of near-room-temperature, the constant α has a value of −0.14, and the second approximate equality is valid for ionic strengths in excess of, say, 0.01 M. We refer to Kegel and van der Schoot (15) for a more detailed discussion.
References
- 1.Bancroft, J. B. 1970. The self-assembly of spherical plant viruses. Adv. Virus Res. 16:99–134. [DOI] [PubMed] [Google Scholar]
- 2.Bruinsma, R. F., W. M. Gelbart, D. Reguera, J. Rudnick, and R. Zandi. 2003. Viral self-assembly as a thermodynamic process. Phys. Rev. Lett. 90:248101-1–248101-4. [DOI] [PubMed] [Google Scholar]
- 3.Caspar, D. L. D. 1963. Assembly and stability of the Tobacco Mosaic Virus particle. Adv. Protein Chem. 18:37–121. [DOI] [PubMed] [Google Scholar]
- 4.Ceres, P., and A. Zlotnick. 2002. Weak protein-protein interactions are sufficient to drive assembly of Hepatitis B virus capsids. Biochemistry. 41:11525–11531. [DOI] [PubMed] [Google Scholar]
- 5.Chiu, W., R. M. Burnett, and R. L. Garcea. 1997. Structural Biology of Viruses. Oxford University Press, Oxford.
- 6.McPherson, A. 2005. Micelle formation and crystallization as paradigms for virus assembly. Bioessays. 27:447–458. [DOI] [PubMed] [Google Scholar]
- 7.Zandi, R., D. Reguera, R. F. Bruinsma, W. M. Gelbart, and J. Rudnick. 2004. Origin of icosahedral symmetry in viruses. Proc. Natl. Acad. Sci. USA. 101:15556–15560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zandi, R., and D. Reguera. 2005. Mechanical properties of viral capsids. Phys. Rev. E. 72:021917-1–021917-12 . [DOI] [PubMed] [Google Scholar]
- 9.Adolph, K. W., and P. J. G. Butler. 1976. Assembly of a spherical plant virus. Philos. Trans. R. Soc. Lond. B Biol. Sci. 276:113–122. [DOI] [PubMed] [Google Scholar]
- 10.Casini, G. L., D. Graham, D. Heine, R. L. Garcea, and D. T. Wu. 2004. In vitro Papillomavirus capsid assembly analyzed by light scattering. Virology. 325:320–327. [DOI] [PubMed] [Google Scholar]
- 11.Hiebert, E., J. B. Bancroft, and C. E. Bracker. 1968. The assembly in vitro of some small spherical viruses, hybrid viruses and other nucleoproteins. Virology. 34:492–508. [DOI] [PubMed] [Google Scholar]
- 12.Da Poian, A. T., A. C. Oliveira, and J. L. Silva. 1995. Cold denaturation of an icosahedral virus. The role of entropy in virus assembly. Biochemistry. 34:2672–2677. [DOI] [PubMed] [Google Scholar]
- 13.Klug, A. 1999. The Tobacco Mosaic Virus particle: structure and assembly. Phil. Trans. Roy. Soc. London B. 354:531–535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wingfield, P. T., S. J. Stahl, R. W. Williams, and A. C. Steven. 1995. Hepatitis core antigen produced in Escherichia coli: subunit composition, conformational analysis, and in vitro capsid assembly. Biochemistry. 34:4919–4932. [DOI] [PubMed] [Google Scholar]
- 15.Kegel, W. K., and P. van der Schoot. 2004. Competing hydrophobic and screened-Coulomb interactions in Hepatitis B virus capsid assembly. Biophys. J. 86:3905–3913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Smith, C. E., and M. A. Lauffer. 1967. Polymerization-depolymerization of Tobacco Mosaic Virus protein VI: light scattering studies. Biochemistry. 6:2457–2465. [DOI] [PubMed] [Google Scholar]
- 17.Sturtevant, J. M., G. Velicelebi, R. Jaenike, and M. A. Lauffer. 1981. Scanning calorimetric investigation of the polymerization of the coat proteins of tobacco mosaic virus. Biochemistry. 20:3792–3800. [DOI] [PubMed] [Google Scholar]
- 18.Tsai, C.-J., S. L. Lin, H. J. Wolfson, and R. Nussinov. 1997. Studies of protein-protein interfaces: a statistical analysis of the hydrophobic effect. Protein Sci. 6:53–64. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dell'Orco, D., W.-F. Xue, and S. Linse. 2005. Electrostatic contributions to the kinetics and thermodynamics of protein assembly. Biophys. J. 88:1991–2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.van der Schoot, P., and R. Bruinsma. 2005. Electrostatics of an RNA virus. Phys. Rev. E. 70:61928-1–61928-12. [DOI] [PubMed] [Google Scholar]
- 21.Speir, J. A., S. Mushi, G. Wang, T. S. Baker, and J. E. Johnson. 1995. Structures of the native and swollen forms of CCMV determined by x-ray crystallography and cryo-electron microscopy. Structure. 3:63–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang, H., A. Planchart, and G. Stubbs. 1997. Caspar carboxylates: the structural basis of Tabomovirus disassembly. Biophys. J. 74:633–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zlotnick, A. 2003. Are weak protein-protein interactions the general rule in capsid assembly? Virology. 315:269–274. [DOI] [PubMed] [Google Scholar]
- 24.Zlotnick, A., R. Aldrich, J. M. Johnson, P. Ceres, and M. J. Young. 2000. Mechanism of capsid assembly for an icosahedral plant virus. Virology. 277:450–456. [DOI] [PubMed] [Google Scholar]
- 25.Zlotnick, A., J. M. Johnson, P. W. Wingfield, S. J. Strahl, and D. Andres. 1999. A theoretical model successfully identifies features of Hepatitis B Virus capsid assembly. Biochemistry. 38:14644–14652. [DOI] [PubMed] [Google Scholar]
- 26.Prevelige, P. E., Jr., D. Thomas, and J. King. 1993. Nucleation and growth phases in the polymerization of coat and scaffolding subunits into icosahedral procapsid shells. Biophys. J. 64:824–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Endres, D., and A. Zlotnick. 2002. Model-based analysis of assembly kinetics for virus capsids or other spherical polymers. Biophys. J. 83:1217–1230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Rapaport, D. C. 2004. Self-assembly of polyhedral shells: a molecular dynamics study. Phys. Rev. E. 70:051905, 1–13. [DOI] [PubMed]
- 29.Schwartz, R., P. W. Schorr, P. E. Prevelige, Jr., and B. Berger. 1998. Local rules simulation of the kinetics of virus capsid self-assembly. Biophys. J. 75:2626–2636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Aniansson, E. A. G., and S. N. Wall. 1974. On the kinetics of step-wise micelle association. J. Phys. Chem. 78:1024–1030. [Google Scholar]
- 31.Kashchiev, D. 2000. Nucleation. Butterworth-Heinemann, Oxford, UK.
- 32.Wu, D. T. 1997. Nucleation theory. Solid State Phys. 50:37–187. [Google Scholar]
- 33.Wales, D. J. 2005. The energy landscape as a unifying theme in molecular science. Phil. Trans. Roy. Soc. A. 363:357–377. [DOI] [PubMed] [Google Scholar]
- 34.Prevelige, P. E. 1998. Inhibiting virus-capsid assembly by altering the polymerisation pathway. Trends Biotechnol. 16:61–65. [DOI] [PubMed] [Google Scholar]
- 35.Singh, S., and A. Zlotnick. 2003. Observed hysteresis of virus capsid assembly is implicit in kinetic models of assembly. J. Biol. Chem. 278:18249–18255. [DOI] [PubMed] [Google Scholar]
- 36.Zlotnick, A. 1994. To build a virus capsid. An equilibrium model of the self-assembly of polyhedral protein complexes. J. Mol. Biol. 241:59–67. [DOI] [PubMed] [Google Scholar]
- 37.Endres, D., M. Miyahara, P. Moisant, and A. Zlotnick. 2005. A reaction landscape identifies the intermediates critical for self-assembly of virus capsids and other polyhedral structures. Protein Sci. 6:1518–1525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Johnson, J. M., J. H. Tange, Y. Nyame, D. Willitts, and A. Zlotnick. 2005. Regulating self-assembly of spherical oligomers. Nano Lett. 4:765–770. [DOI] [PubMed] [Google Scholar]
- 39.Israelachvili, J. 1992. Intermolecular and Surface Forces. Academic Press, London.
- 40.van der Schoot, P. 2005. Theory of supramolecular polymerization. In Supramolecular Polymers, 2nd Ed. A. Ciferri, editor. CRC Press, Boca Raton, FL.
- 41.Jiang, L., Y. Gao, R. Mao, Z. Lia, and L. Lai. 2002. Potential of mean force for protein-protein interaction studies. Proteins Struct. Funct. Gen. 46:190–196. [DOI] [PubMed] [Google Scholar]
- 42.Reddy, V. S., P. Natarajan, B. Okerberg, K. Li, K. Damodaran, R. T. Morton, C. L. Brooks III, and J. E. Johnson. 2001. Virus particle explorer (VIPER), a website for virus capsid structures and their computational analyses. J. Virol. 75:11943–11947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Reiss, H., W. K. Kegel, and J. Groenewold. 1996. Length scale for configurational entropy in microemulsions. Ber. Bunsenges. Phys. Chem. 100:279–295. [Google Scholar]
- 44.Goldenfeld, N. 1992. Lectures on phase transitions and the renormalization group. Addison-Wesley, Reading, MA.
- 45.Johnson, J. M., D. A. Willits, M. J. Young, and A. Zlotnick. 2004. Interaction with capsid protein alters RNA structure and the pathway for in vitro assembly of Cowpea Chlorotic Mottle virus. J. Mol. Biol. 335:455–464. [DOI] [PubMed] [Google Scholar]
- 46.Choi, Y., S. G. Park, J. Yoo, and G. Jung. 2005. Calcium ions affect the HBV core assembly. Virology. 332:454–463. [DOI] [PubMed] [Google Scholar]
- 47.Stray, S. J., P. Ceres, and A. Zlotnick. 2004. Zinc ions trigger conformational change and oligomerization of Hepatitis B Virus capsid protein. Biochemistry. 43:9989–9998. [DOI] [PubMed] [Google Scholar]
- 48.Landau, L. D., and E. M. Lifshitz. 1980. Statistical Physics, Part 1. Pergamon, Oxford, UK.