Clustering of the SOM easily reveals distinct gene expression patterns: results of a reanalysis of lymphoma study

Abstract

Background

A method to evaluate and analyze the massive data generated by series of microarray experiments is of utmost importance to reveal the hidden patterns of gene expression. Because of the complexity and the high dimensionality of microarray gene expression profiles, the dimensional reduction of raw expression data and the feature selections necessary for, for example, classification of disease samples remains a challenge. To solve the problem we propose a two-level analysis. First self-organizing map (SOM) is used. SOM is a vector quantization method that simplifies and reduces the dimensionality of original measurements and visualizes individual tumor sample in a SOM component plane. Next, hierarchical clustering and K-means clustering is used to identify patterns of gene expression useful for classification of samples.

Results

We tested the two-level analysis on public data from diffuse large B-cell lymphomas. The analysis easily distinguished major gene expression patterns without the need for supervision: a germinal center-related, a proliferation, an inflammatory and a plasma cell differentiation-related gene expression pattern. The first three patterns matched the patterns described in the original publication using supervised clustering analysis, whereas the fourth one was novel.

Conclusions

Our study shows that by using SOM as an intermediate step to analyze genome-wide gene expression data, the gene expression patterns can more easily be revealed. The "expression display" by the SOM component plane summarises the complicated data in a way that allows the clinician to evaluate the classification options rather than giving a fixed diagnosis.

Background

The development and progression of cancer is accompanied by complex changes in the patterns of gene expression. That can be revealed by DNA microarrays analysis [1]. However, to reliably identify expression patterns associated with tumor type, prognosis or therapy, hundreds of samples need to be studied, and powerful data mining tools are needed. Microarray experiments are generally performed without a priori hypothesis. Therefore, the data mining tools have to be developed that reveal a maximum of information to generate new hypotheses [9] with minimal supervision. Hierarchical clustering is a frequently used method [2-4], but has a number of shortcomings [5,6]. Notably, the most important genes defining the branches of the clustering tree are not readily recognized, and important patterns can be lost due to the deterministic nature of clustering or the high dimensionality of data. To solve this problem, we propose a two-level analysis [14] for the study of complex gene expression data. This analysis summarizes the data by the SOM component plane, and then clusters the SOM to investigate the feature gene expression patterns. The SOM reduces the dimensionality of the data, and thereby allows to easy display the data and reveal the gene expression patterns. The visual inspection of the gene expression patterns in each single case, and comparison of those patterns between the different cases allows identifying common patterns in gene expression that may have been lost by directly applying hierarchal clustering to the data. In addition, by K-means clustering of the SOM, genes that have similar expression patterns, and might therefore be functionally related, may be identified.

To test the power of this two-level approach, we applied it to the analysis of a publicly available gene expression data set of non-Hodgkin's lymphomas, including mostly diffuse large B-cell lymphoma (DLBCL), follicular lymphoma (FL) and chronic lymphocytic leukaemia (CLL). K-means clustering of the SOM readily identifies four distinct gene expression profiles: germinal center related, proliferation, inflammatory and plasma cell differentiation related gene expression patterns. All identified gene expression patterns are correlated with clinical survival analysis.

Results

The expression data [10] were filtered and preprocessed as described and subjected to SOM. Davies-Bouldin index was used to find the optimum number of 12 clusters in K-means clustering of the SOM [14]. Figure 1b shows the K-means clustering of SOM with map size (22 × 14), where the number of map units M = 5 N^0.5, N is the number of genes; after M has been determined, the map size is determined by setting the ratio between column number and row number of map units equal to the ratio of two biggest eigenvalues of the training data, and their product is as close to M as possible [11]. Each hexagonal node of SOM is a prototype vector representing local averages of the data, and the nearby nodes have similar prototype vectors. The genes included in each cluster can be found in the supplement [13].

Figure 1.

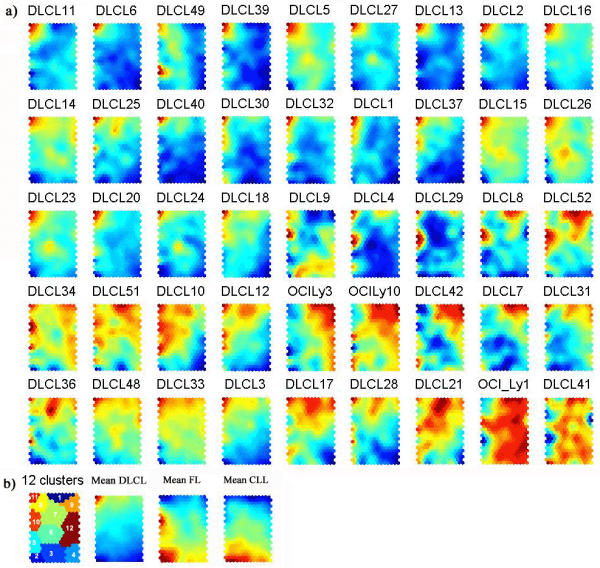
Classification of samples by SOM analysis and K-means clustering. SOM component planes are shown for a) 42 DLBCL samples and three DLBCL cell lines (OCILy3, OCILy10 and OCILy1). SOM map size is (22 × 14) and the color scale of SOM component plane represented the mean ratio in each map node, and red indicates high expression, blue indicates low expression. See supplementary information for full data. b) K-means clustering of SOM, mean SOM component planes for DLBCL, FL and CLL. The cluster numbers are given, and the genes contained within each SOM node and K-means cluster are listed in the web supplement [13], selected genes from clusters 10, 11 and 1, 7, 9 are listed in table 1.

Through the proposed two-level approach, one may directly observe the gene expression pattern of different lymphoma subtypes, i.e. DLBCL, CLL and FL (figure 1b). As can be seen from figure 1a, DLBCL primarily showed four prominent gene expression patterns; distinguished by gene cluster 10, 11, 1 and the large group of clusters 7 and 9. More detailed illustrations of distinct gene expression patterns are shown in the supplement [13], summary of the genes included in these clusters are listed in Table 1. Cluster 10 contains genes were known to be expressed in germinal center B cells, such as FAK, WIP, CD10, CD27, CD38, FMR2, BCL-6 and BCL-7A. Cluster 11 contains genes specifically expressed by T-cells (a.o. CD3, CD2, TCR), NK cells (a.o. NK4), macrophages (a.o. CD14, CD63, CD64, CD115) and lymph node dendritic cells (a.o. S100). Also included are genes coding for chemokines and chemokine receptors (RANTES, BLC, IP10, SLC, FPR, STRL33.1 and MIP1), which play a major role in the chemoattraction of inflammatory cells. Furthermore DLBCL variably express genes in the adjacent clusters 1, 7 and 9 (figure 1a). Cluster 1 includes genes associated with proliferation (Ki67, cyclin A, BUB1, Cyclin B1, thymidine kinase) whereas clusters 7 and 9 include genes associated with cell survival (Bcl-XL, defender against cell death 1, Bfl-1, BAK, Bag-1, MCL1) and plasma cell differentiation (XBP-1, STAT3, IRF-4, ribosomal proteins) [10].

Table 1.

Selected genes grouped to cluster 1,7,9,10,11 of K-means clustering of SOM. Full list can be found in the web supplement [13].

Cluster No.	Clone ID	Gene Description
Cluster 1	100	Ki67 (long type)
	1287099	Survivin = apoptosis inhibitor = effector cell protease EPR-1
	108294, 1287528	XRCC9 = DNA repair protein
	950690, 824709	Cyclin A
	563130, 824060	Cyclin B1
	1288839, 325880	Tubulin-beta
	1240822, 588637	Actin = cytoskeletal gamma-actin
	683084	Cyclin E2
	1356512	Similar to MCM2 = DNA replication licensing factor
	703757	MPP1 = Putative M phase phosphoprotein 1
	1240595	Tubulin-alpha
	1341540, 781047	BUB1 = putative mitotic checkpoint protein ser/thr kinase
Cluster 7	789182	PCNA = proliferating cell nuclear antigen
	1288183, 235938	BAK = BCL-2 family member
	80592	Syndecan-1
	469256, 1322301	Bag-1 = Bcl-2 interacting anti-apoptotic protein = RAP46 = Glucocorticoid receptor-associated protein
	525540	BCL-3
	1338456, 364941	C-myc binding protein
	784012	40S ribosomal protein S21
	324144	Ribosomal protein S29
	1087015, 1240788	Ribosomal protein S9
	510395	Ribosomal protein S16
	272185	Ribosomal protein L27
	1335421	Similar to ribosomal protein L37a
	1368302	Ribosomal protein L32
Cluster 9	46778	BCL-XL
	814478, 1353675	A1 = Bfl-1 = GRs = Bcl-2 related protein
	270770, 1272196	IRF-4 = LSIRF = Mum1 = homologue of Pip = Lymphoid-specific interferon regulatory factor = Multiple myeloma oncogene 1
	1290353	Similar to TREB and X box binding protein 1
	145093	MCL1 = myeloid cell differentiation protein
Cluster 10	701606, 1286850, 200814	CD10 = CALLA = Neprilysin = enkepalinase
	1337241, 306139	BCL-7A
	1340526, 712395	BCL-6
	824476, 95093, 1350545	Spi-B transcription factor
	1335782, 13194072, 1338245	Oct-2 = lymphoid-specific octamer binding transcription factor = POU
	278808	Spi-1 = PU.1 = ets family transcription factor
	50214	CD86 = B7-2 = CD28 and CTLA-4 counter-receptor 2
Cluster 11	753794	BLC = BCA-1 = B lymphocyte chemoattractant BLC = CXC chemokine
	1326652	CD2
	245959	SDF-1 = Stromal cell-derived factor 1 = chemokine
	159946	CD14 = monocyte differentiation antigen
	1130062	CD3E antigen, epsilon polypeptide
	258802, 470615	CD64 = high affinity immunogobulin gamma FC receptor I A form precursor = FC-gamma
	377560	CD3 delta = T cell surface glycoprotein
	505569	T cell receptor beta chain
	23435, 1306024	CD11C = leukocyte adhesion protein p150,95 alpha subunit = integrin alpha-X
	1219244, 57, 1071581	RANTES = chemokine
	472180	S100 calcium binding protein A4 = Placental calcium binding protein = Calvasculin
	701290	C-C chemokine receptor 5 == CC CK5
	47509	Major histocompatibility complex, class II, DN alpha

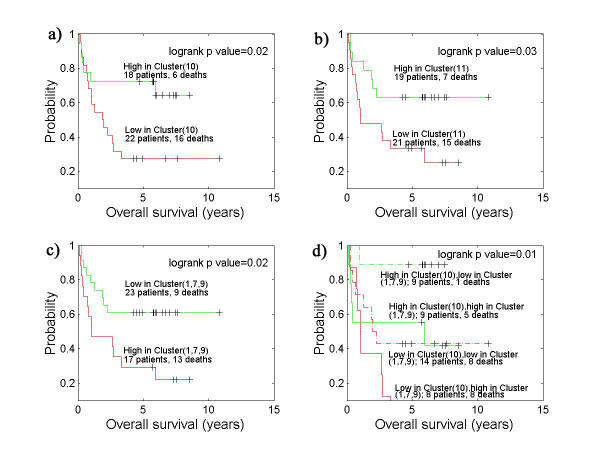
We subsequently regrouped the DLBCL based on the expression of each of the identified gene expression patterns and studied survival differences between the groups thus formed. We confirmed the better survival (figure 2a) for those cases expressing genes related to the germinal center (gene cluster 10) as reported by Alizadeh et al. We furthermore could show that there is a significant improved survival (figure 2b) of cases expressing genes related to inflammation (gene cluster 11). Equally, there is a significant reduced survival (figure 2c) of cases expressing genes related to cell proliferation, anti-apoptosis and plasma cell differentiation (clusters 1,7,9). Interestingly, there is also a significant difference in survival (figure 2d) obtained when cases are subdivided using a combination of gene expression patterns 10 and 1,7,9 in spite of the low number of cases. We were further intrigued by the clusters of genes in groups 7 and 9 that apparently were related to plasma cell differentiation and are frequently co-expressed with the genes in cluster 1 (cell proliferation). Hierarchical clustering of DLBCL using only genes in clusters 7 and 9 (figure 3) revealed an interesting pattern of mutually exclusive expressed genes, including many of which are of utmost importance for plasma cell differentiation (XBP-1, STAT3, IRF-4) as well as genes coding for ribosomal proteins, known to be highly expressed in plasma cells. Of interest are the two mutually exclusive patterns of plasma cell differentiation in DLBCL, suggesting either different pathways of plasma cell differentiation or different stages of differentiation.

Figure 2.

Clinically distinct DLBCL subgroups defined by gene expression profiling. a) Kaplan-Meier plot of overall survival of DLBCL patients grouped on the basis of gene expression profiling in K-means cluster 10. b) Kaplan-Meier plot of overall survival of DLBCL patients grouped on the basis of gene expression profiling in K-means cluster 11. c) Kaplan-Meier plot of overall survival of DLBCL patients grouped on the basis of gene expression profiling in K-means cluster (1,7,9). d) Kaplan-Meier plot of overall survival of DLBCL patients grouped on the basis of gene expression profiling in K-means cluster 10 and cluster (1,7,9).

Figure 3.

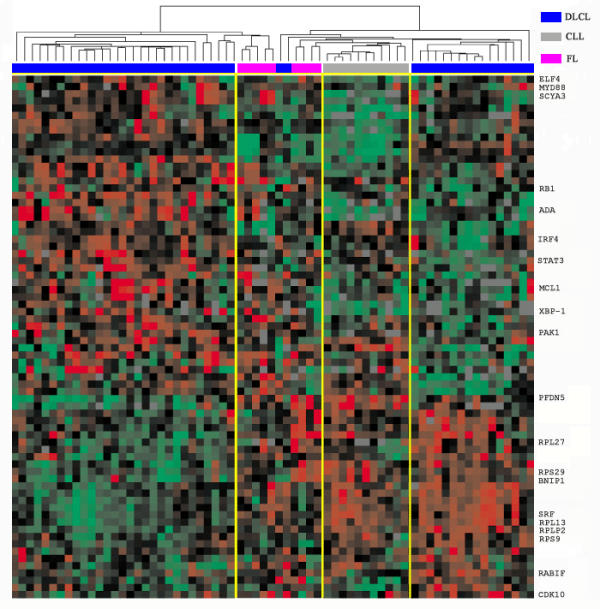
Selected genes from K-means clusters. Hierarchical clustering of 72 selected genes from K-means cluster 1, 7 and 9. Depicted are the measurements of gene expression from DLBCL, FL and CLL samples. The dendrogram is colour coded according to the category of sample studied (see upper right key). Each row represents a separate cDNA clone on the microarray and each column a separate mRNA sample. The squares presented represent the ratio of hybridisation of fluorescent cDNA probes prepared from each experimental mRNA sample to reference mRNA sample. These ratios are a measure of relative gene expression, and red indicates high expression, green indicates low expression and grey indicates missing or excluded data. See supplementary information for full data [13].

Figures 1b shows the mean SOM component planes of CLL and FL. Typically for CLL the genes in the whole lower part of the SOM are highly expressed while for FL the genes in the lower and middle left part of the SOM (cluster 10) are highly expressed. Therefore, the most prominent distinction between CLL and FL lies in the expression of genes that are characteristic of germinal center B cells (cluster 10), as has also been suggested by Alizadeh et al [10].

Discussion

When microarray measurements are presented in random order, the patterns of gene expression are impossible to discern by eye, and methods like hierarchical clustering are frequently used to sort the measurements in such a way that many patterns can easily be visualized, such as in figure 3. However, this method suffers from several shortcomings [14], of which the most important is the loss of information of potentially important patterns in a high dimensional gene space. Although the number of measured genes is large there may only be a few underlying gene components that account for most of the response variation; for example, only a few linear combinations of a subset of genes can account for nearly all of the expression variation among various tumor types. In such a situation, dimension reduction is needed to reduce the high dimensional gene space to a low dimensional gene component space; for instance, principal component analysis [18] and partial least squares [20] had been applied to the dimension reduction of microarray data. Thus, we proposed a two-level analysis, first to summarize the gene expression data by a large set of prototypes; then the prototypes are further combined to form the actual clusters in the next step. SOM is a suitable method for data reduction since it creates a set of prototype vectors representing the gene expression data and carries out a topology preserving the projection of the prototypes from the high-dimensional gene space into a low-dimensional map. To preserve the cluster structure of original data in a low-dimensional map, we can select as many prototype vectors as needed, where the number of prototypes equals 5 N^0.5 (N is the number of genes) [14]. The map follows the probability density function of the data and is very robust with regard to missing data points [7]. Furthermore, the component plane of SOM can be used as a visualization surface for showing different features of the SOM (and thus of the gene expression data), for example the cluster structure [14]. By clustering the SOM, a good insight into the cluster structure (and thus of the feature gene expression patterns) can be obtained.

We applied this two-level approach to the analysis of a set DLBCL samples that have previously been published. The inspection of the maps obtained through our analysis clearly reveals four major gene expression patterns. One pattern concerns genes expressed by germinal center B cells (cluster 10), the second could be called an 'inflammatory' pattern and relates to genes expressed by T-cells and macrophages (cluster 11). The third pattern is an extensive collection of genes involved in cell proliferation (cluster 1), which seems to be closely linked to the fourth pattern, anti-apoptosis and plasma cell differentiation-related genes (cluster 7, 9). This last pattern has not previously been described whereas the others were also discovered by Alizadeh et. al, by using hierarchical clustering only.

The survival data based on the grouping of cases according to the different gene expression patterns show that all these expression patterns were significantly correlated with survival (figure 2a, 2b, 2c). When the germinal center B cell gene expression pattern (cluster 10) is combined with the proliferation/anti-apoptosis/plasma cell differentiation pattern (cluster 1,7,9), thus yielding four groups (figure 2d), significant differences in survival are still seen notwithstanding the low number of cases. It is of particular interest that all but one of the cases expressing high levels of germinal center (cell) genes but low levels of proliferation/anti-apoptosis/plasma cell genes, have a survival beyond 5 years (figure 2d). This contrasts sharply with the cases expressing low levels of germinal center B cell genes but high levels of proliferation/anti-apoptosis and plasma cell differentiation genes of which none survive beyond 5 years. Although these data need to be confirmed in larger series of cases, a division of DLBCL according to expression of a combination of genes relating to the germinal center, proliferation, anti-apoptosis and plasma cell differentiation seems to be very relevant in predicting prognosis. Why the expressions of genes related to cell proliferation, anti-apoptosis and plasma cell differentiation are frequently co-expressed in DLBCL is not known and needs to be further investigated. It is apparent from our further analysis (figure 3) that there are two mutually exclusive patterns of gene expression related to plasma cell differentiation. One pattern contains the transcription factors IRF4 and XBP-1, which have both been shown to be important for plasma cell differentiation, as well as STAT3, which is part of the IL-6 signaling pathway involved in plasma cell differentiation [15-17]. The other pattern shows many unknown genes in addition to genes coding for ribosomal proteins. The latter suggests an expression pattern related to a later stage of plasma cell differentiation. These patterns are intriguing but more studies on normal plasma cell differentiation are needed in order for these plasmas to be fully understood.

In conclusion, we propose a two-level approach for the analysis of gene expression patterns, where the clustering analysis is carried out in a set of summarized prototype vectors created by SOM. By applying the current two-level approach to the DLBCL data set [10], the discovered gene expression patterns were consistent with the ones originally published. In addition, a novel pattern of gene expression related to plasma cell differentiation was revealed. Our results underscore the value of the two-level analysis for discovering gene expression patterns, and the method should be useful as a part of routine classification of clinical samples, when the suggested subdivision have been confirmed in large studies.

Methods

Sources of experimental data

All experimental data including the survival data of the lymphoma patients were obtained from the web supplement to the publication of Alizadeh et al. [10]http://llmpp.nih.gov/lymphoma/data.shtml.

Preprocessing of data

The data were cleaned before doing any data mining. This includes flagging and removal of bad measurements, i.e. measurements where the fluorescent intensity in one channel was less than 1.4 times the local background were discarded [10], and replacement of values for identical probes (same IMAGE number and gene) with the mean ratio. After cleaning the original data, we were left with values for 3906 genes from 96 samples, and these ratios were log 2 transformed.

Hierarchical clustering

Hierarchical clustering [12] is an agglomerative clustering usually having the following steps: 1) Initialization: assign each vector (the series of values from a single sample) to its own cluster. 2) Computation of the distance between all clusters. 3) Merging the two clusters that are closest to each other. Step 2 and 3 are repeated until there is only one cluster left. In this work, log 2 transformed ratios were median-centered before clustering, Pearson correlation was used as distance matrixes and the centered average linkage method was used for merging. Hierarchical clustering was applied to both rows and columns using the Cluster and Tree View software from Stanford [2].

Self-organizing map (SOM) and K-means clustering

The basic SOM [7] consists of m neurons located on a regular low-dimensional grid, usually 1- or 2- dimensional. The lattice of the grid is hexagonal. The basic SOM algorithm is iterative. Each neuron i has a d-dimensional prototype vector m_i= [m_i1, ..., m_id], d is the input vector dimension. Before the training phase, initial values are given to the prototype vectors and typically linear initialization was used. At each training step, a sample data vector x is randomly chosen from the training set. Distances between x and all the prototype vectors are computed. During training, the SOM behaves like a flexible net that folds onto the "cloud" formed by the training data. Because of the neighborhood relations, neighboring prototypes are pulled to the same direction, and thus prototype vectors of neighboring units resemble each other [11]. To inspect the cluster structure of the map, the SOM component plane (figure 1) was used to show the gene expression features of various tumor samples, and also the common gene expression patterns of each tumor type. Each component plane can be thought of as a slice of the map: it consists of the values of a single vector component in all map units. It is visualized as 2-dimensional color images, where the color of a map unit corresponds to its value. By visualizing the spread of values of that component and comparing component planes with each other, correlations are revealed as similar patterns in identical positions of the component planes. Based on overall view, it is easy to select interesting component combinations and map units for further investigation. To be able to more effectively study interesting groups of map units, methods to give good candidates for map unit clusters or groups are required. Thus, the trained prototype vectors m_i of SOM is further clustered by K-means clustering and combined to form the actual clusters, more detailed description of clustering of the SOM can be found in the early paper [14].

K-means clustering is a partition clustering, it classifies the data into k groups, which together satisfy the requirements of a partition: (1) Each group must contain at least one object. (2) Each object must belong to only one group. To select the best k among different partitions, each of these can be evaluated using some kind of validity index. In our calculations, we used the Davies-Bouldin index [11], which minimizes the ratio between within-cluster distance and between-cluster distance, indicating good clustering results for spherical clusters with low values. Because no unified theory for determining the number of clusters has been fully developed and accepted, the selection of optimal number of clusters remains as an active research field [19,21]. Thus, the Davies-Bouldin index used here is only a guideline to estimate the best clustering among the partitionings with different number of clusters. Some problems need to be noted when clustering the SOM by the K-means clustering, due to the properties of the algorithm: it not only searches for spherical clusters but also clusters with roughly equal number of samples, the non-spherical cluster could not be properly recognized as one cluster; and as the number of clusters is increased, the number of samples in clusters decreases, which makes the algorithm more sensitive to outliers. Therefore, we have to carefully verify the results obtained by K-means clustering [14].

In this work, SOM and K-means clustering were carried out by the SOM toolbox in MATLAB [11]. SOM was trained using batch version of the algorithm for raw expression data. All prototype vectors were linearly initialized in the subspace spanned by the two eigenvectors with greatest eigenvalues computed from the training data. The SOM was trained in two phases: a rough training with large initial neighborhood width and a fine-tuning phase with small initial neighborhood width. The neighborhood width decreased linearly to 1; neighborhood function was Gaussian. The training length of the two phases was 1 and 4 epochs and the initial neighborhood width 3 and 1, respectively.

Survival analysis

The statistical treatment of survival times is known as survival analysis. From a set of observed survival times from a sample of individuals we can estimate the proportion of the population of such people who would survive a given length of time in the same circumstances. The method yields a graph, the Kaplan-Merier survival curve, is drawn as a "step function" that changes at every distinct survival time. The time of survival observations are indicated by ticks on the survival curve, which shows at a glance the survival times of the surviving subjects (figure 2). To compare the survival experience of two or more groups of subjects we calculate the logrank test. The logrank test is a hypothesis test for testing the null hypothesis that the groups being compared are samples from the same population as regards survival experience, it involves calculating the observed and expected numbers of failures in separate time intervals, and summing these, comparing the results to a χ² distribution with k-1 degrees of freedom gives P value, where there are k groups of observations [9]. The plotting of Kaplan-Merier survival curves and logrank test of significance level P value were implemented in MATLAB.

Authors' contributions

Junbai wang carried out the data mining studies, performed microarray data analysis, implemented MATLAB code for survival analysis and drafted the manuscript. Jan Delabie carried out the biological studies of discovered gene expression patterns, participated in data analysis and drafted part of the manuscript. Hans Christian Aasheim and Erlend Smeland participated in validation of the microarray analysis. Ola Myklebost conceived of the study, and participated in its design and coordination.

Acknowledgements

This work was supported by the Norwegian Cancer Society http://www.kreft.no.