Mechanism of regulation of phosphate dissociation from actomyosin-ADP-Pi by thin filament proteins

Abstract

Regulation by calcium and myosin-S1 of the acceleration of the rate of phosphate release from myosin-ADP-inorganic phosphate (M-ADP-Pi) by the thin filament actin-tropomyosin (Tm)-troponin (Tn), was measured directly by using double mixing stopped-flow experiments with fluorescent phosphate binding protein. At low calcium and without rigor myosin-S1, saturating concentrations of thin filaments accelerate the rate of phosphate dissociation from M-ADP-Pi 8-fold, from 0.08 to 0.64 s⁻¹. If either myosin-S1 or calcium is bound to the thin filaments, phosphate release is a biphasic process in which the fast phase is the dissociation of Pi from actoTmTnM-ADP-Pi and the slow phase is limited by the hydrolysis of actoTmTnM-ATP to actoTmTnM-ADP-Pi. The maximum accelerations of the fast components by saturating thin filaments (relative to M-ADP-Pi alone) are: ≈200-fold, 16 s⁻¹ (calcium only); ≈400-fold, 30 s⁻¹ (EGTA and rigor S1); and ≈1,000-fold, 75 s⁻¹ (calcium and rigor S1). The maximum rate of phosphate dissociation attained with S1 and calcium bound to the thin filament is the same as for unregulated actin. Regulation of the rate of phosphate dissociation by calcium and myosin-S1 is partially explained by the model of Geeves [McKillop, D. F. and Geeves, M. A. (1993) Biophys. J. 65, 693–701], in which calcium and rigor S1 perturb the equilibria among three states of the thin filament (blocked, closed, and open). However, a quantitative description of the regulatory mechanism requires acceleration by calcium of an additional step of the mechanism, either phosphate dissociation or a preceding conformational change.

In striated muscle the constitutive activation of myosin by actin (1) is prevented by the actin binding proteins, tropomyosin (Tm) and troponin (Tn). These proteins assemble into the repeating units of the thin filament, which contains seven actin monomers, one Tn, and one Tm. Although the atomic-level structure of the thin filament is not yet available, the broad structural features are well established (2, 3). Tm lies end to end in the grove created by the helical strands of actin monomers. There is no direct interaction between adjacent Tn molecules that are bound to the underlying filament at regular intervals via two of three subunits, Tn-T and Tn-I. The third subunit, Tn-C, is the calcium sensor. Although there is only one Tn per regulatory unit, protein–protein contacts within the thin filament expand the range of any signal resulting from the binding of ligand (4–7).

How the structure of the thin filament is modified by ligand interaction has provided considerable insight into the mechanism of regulation. Despite the lack of a crystal structure, different conformations of the thin filament can be distinguished at low resolution (8). The three-state model (9), consistent with the interpretation of 3D reconstructions of electron micrographs (8), requires the formation of three different conformers produced by the binding of calcium and myosin-S1. In a resting muscle, Tn straddles actin and Tm, tethering the latter to the outside of the actin filament on subdomains 1 and 2. In this state the productive interaction of actin and myosin is said to be blocked. Calcium, which instigates a structural change in Tn (10–12), induces a new state in which Tm has moved toward subdomains 3 and 4 of actin, exposing a portion of the myosin binding site of the weak binding intermediates, myosin-ATP (M-ATP) and myosin-ADP-inorganic phosphate (M-ADP-Pi). Rigor myosin head attachment produces an additional shift in Tm, farther into the helical axis of the actin filament, and uncovers the entire myosin binding site. Although changes in the position of Tm on actin have long been of interest regulation is unlikely to be solely mediated by steric means (13, 14).

In addition, a fundamental question is yet to be answered. Which step(s) of the mechanism of actomyosin (AM)-ATP hydrolysis is (are) regulated? The mechanism of regulation of the interaction of the most physiologically relevant intermediates, M-ATP and M-ADP-Pi, with the thin filament has not been directly studied for technical reasons. A previous approach to the problem using a fluorescent nucleotide analogue observed a significant calcium dependence, 10- to 20-fold, in the rate of dissociation of products by thin filaments (15). The subsequent development of a fluorescent phosphate binding protein (PBP), capable of monitoring real-time phosphate fluxes, now permits direct measurement of phosphate dissociation kinetics (16). When this method was used to analyze unregulated AM it was found that: (i) phosphate release is enhanced some 1,000-fold by actin and (ii) cleavage of ATP is rate limiting at saturating concentrations of actin (17). The objective of the current work is to measure the rate of these processes in the presence of regulated actin.

Experimental Procedures

Materials.

“Bacterial” purine nucleoside phosphorylase, 7-methylguanosine, ATP, buffers, and salts were from Sigma. N-[2-(1-maleimidyl)ethyl]-7-(diethylamino)coumarin-3-carboxamide (MDCC) was obtained from Molecular Probes. Bacterial PBP containing a single (Ala-197–Cys) mutation was isolated as described (16). The PBP was expressed in Escherichia coli strain BW 24777, in which the PBP is under the control of a rhamnose promoter (18). This strain, provided to us by E. W. Taylor (University of Chicago), was transformed by W. Epstein (University of Chicago) with the plasmid pSN5182 developed by M. L. Webb (National Institute of Medical Research). Fluorescent PBP (MDCC-PBP) was prepared as described (16).

Proteins.

Actin, myosin, Tn, and Tm were prepared from rabbit skeletal muscle. The subfragment 1 was prepared from myosin with α-chymotrypsin by the method of Weeds and Taylor (19) except that 2 mg lima bean trypsin inhibitor per mg chymotrypsin rather than PMSF was used to inhibit α-chymotrypsin. The protein was column-purified on DEAE-52 cellulose. Fractions were pooled to obtain myosin-S1 containing only the A1 light chain component.

Tm, isolated by the method of Smillie (20) was used as a mixture of isoforms. Tn isolation was based on the method of Potter (21) but omitting the Cibacron blue-Sephacryl chromatography. Thin filaments were reconstituted from actin, Tn, and Tm that were separately dialyzed against 50 mM NaCl, 6 mM MgCl₂, 5 mM Mops, 1 mM DTT, pH 7.00. The final reconstituted mixture containing actin-Tn-Tm was dialyzed against 4.5 mM MgCl₂, 5 mM Mops, 1 mM DTT, pH 7.00, at 4°C. Protein concentrations were determined from A₂₈₀ of 1% (wt/vol) solutions: S1, 7.7; Tm, 3.3; Tn, 4.7; and actin, 11.5 after correction for light scattering (1.5 × A₃₂₀).

Kinetic Measurements.

Steady-state ATP hydrolysis was measured by colorimetric assay (22). Reconstituted thin filaments displayed at least a 15-fold calcium sensitivity of the rates of steady-state ATP hydrolysis (mole ratio of S1/actin = 1:70 to 1:120) under identical temperature and buffer conditions used for presteady-state assays except that the ATP concentration was 1 mM.

Chemical quench measurements were done by using a computer-controlled stepper-motor driven quench-flow apparatus as described (17).

Stopped-Flow Measurements.

Stopped-flow fluorescence experiments were performed by using a Kintek (Austin, TX) SF-2001 double mixing stopped-flow fluorimeter. The excitation light from a 75-W xenon lamp was selected by using a 0.125-m monochrometer (PTI, South Brunswick, NJ). Kinetic measurements of phosphate release were observed by using an excitation at 430 nm and emission >450 nm with a sharp cutoff filter. Three to four data traces of 500 points were averaged and the observed rate constants were obtained by fitting the data to one or two exponential terms by using the software package included with the Kintek stopped-flow. In most cases two different time bases of 250 data points each were selected that were appropriate for the rate constants being observed. Simulations and global fitting of the kinetic data seen in Fig. 4 were done by using the simplex algorithm contained in scientist (Micromath, Ogden, UT).

Fig 4.

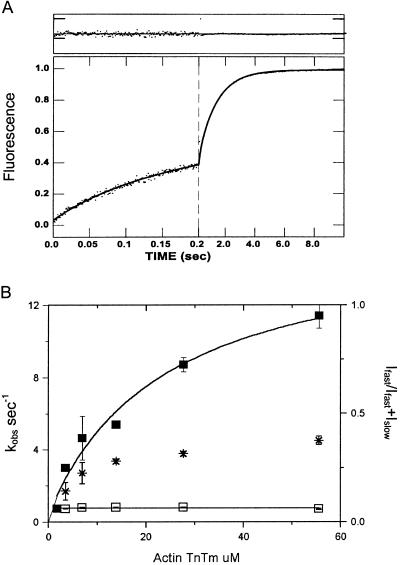
Phosphate dissociation from actoTmTn-myosin-S1A1-ADP-Pi at high calcium concentration with rigor myosin bound to the thin filaments. (A) Time course of phosphate release. Myosin-S1A1 was first mixed with a subsaturating amount of ATP, incubated for 1 s, and then mixed with reconstituted thin filaments containing CaCl₂. Final concentrations were the same as Fig. 3A except that 0.3 mM CaCl₂ replaced 0.3 mM EGTA. The line through the data is the best fit to a double exponential equation: I(t) = 0.68e^−45.4t + 0.32e^−5.2t + C₀. (B) Dependence of k_obs on thin filament concentration. Final concentrations were as above except for 2.7–55 μM regulated actin and [S1] = [actin]/7. The solid lines are observed rates of phosphate release fit to the equation k_obs = k/(1 + K/[actin]) in which K_app = 18 μM and k_−fastP = 77 s⁻¹ (fast phase, ▪) and K_app = 14 μM and k_−Pslow = 9.6 s⁻¹ (slow phase, □). The fraction of amplitude of the fast phase [I_fast/(I_fast + I_slow)] is indicated by *. Dashed lines are the theoretical curves simulated for the mechanism in Eq. 1.

The Kintek stopped-flow was fitted with 2-ml syringes in positions A and B and a 5-ml syringe in position C so that both mixes were approximately equivolume and to obtain a high concentration of thin filaments in the final mix. The very low ionic strength previously used in double mixing experiments to measure the rate of phosphate dissociation from AM-ADP-Pi and attached hydrolysis (17) could not be used here because the regulatory proteins do not remain bound to actin under these conditions. It was, however, desirable to keep the final ionic strength as low as possible to maintain high affinity of M-ATP and M-ADP-Pi for actin.

Experiments were performed by first mixing S1A1 (dialyzed in 5 mM Mops) with ATP (5 mM Mops, 1 mM MgCl₂). The resulting steady-state mixture was held in a delay line and, in a second mix, combined with thin filaments [5 mM Mops, 4.5 mM MgCl₂ + 0.5 mM CaCl₂ (high calcium) or 0.5 mM EGTA (low calcium)]. The dilution of the syringe contents was 2:9 for S1 and ATP and 5:9 for thin filaments, and the final concentration of MgCl₂ was 2.7 mM. All solutions were at pH 7.0 and 20°C and contained 5 μM fluorescent PBP and a “phosphate mop” consisting of 0.01 units/ml purine nucleoside phosphorylase and 0.1 mM 7-methylguanosine.

In previous experiments using unregulated actin (17), relatively high concentrations of myosin-S1 in excess to substrate (typically 8 μM myosin and 4 μM substrate) were used to be certain that all (>99%) of the substrate had bound to the myosin during the first mix. Because rigor heads bound to the thin filament activate the thin filament it was necessary to devise conditions that controlled the extent of rigor activation to investigate the effect of calcium binding. Experimental conditions were sought that would (i) maximize the amount of M-ATP and M-ADP-Pi and (ii) minimize the concentration of myosin and M-ADP (both of which can produce rigor activation) and ATP at the end of the first mix. Excess ATP is undesirable because any substrate not bound to myosin in the first mix will produce a slow kinetic phase from binding to, and hydrolysis by, AM after the second mix. We optimized conditions for the stopped-flow experiments by determining the composition of the myosin nucleotide intermediates in the delay line of the stopped-flow under identical conditions using rapid chemical quench (data not shown). For example, the hydrolysis of 1 μM ATP by a 10-fold excess of myosin-S1 was found to be biphasic and fit by amplitude and rate constants of 0.71 and 10.8 s⁻¹ for the phosphate burst and 0.29 and 0.08 s⁻¹ for the steady-state component. Based on simulations of the hydrolysis mechanism using these rate constants, the time course of the formation of reaction intermediates (M-ATP + M-ADP-Pi and M-ADP) indicate that optimal conditions were obtained after a delay time of 1 s between the first and second mix, when there was 9.00 μM M, 0.05 μM M-ADP, 0.29 μM M-ATP, and 0.66 μM M-ADP-Pi. The 1-s first mix used in these experiments was a compromise. Longer incubation times reduce the amount of myosin and ATP but increase M-ADP; shorter incubation times reduce the amount of M-ADP but increase the amount of myosin and ATP.

Results

Effect of Calcium Binding to the Thin Filament on the Rate of Dissociation of Phosphate from AM-ADP-Pi.

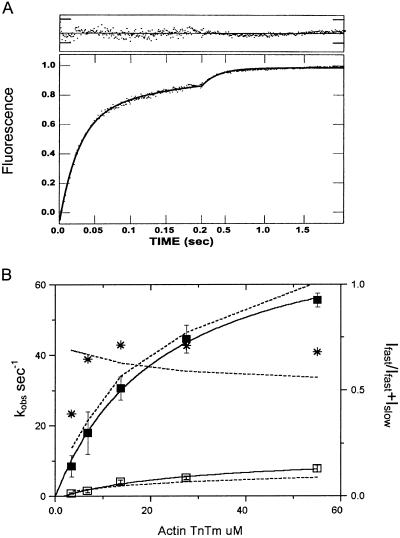
Equal concentrations of S1 and ATP are combined in the first mix and allowed to incubate for 1 s for ATP to be bound and hydrolyzed by the S1. In the second mix the S1-nucleotide complex is combined with thin filaments and the rate of dissociation of AM-bound phosphate is measured from the fluorescence enhancement because of the rapid binding of phosphate to PBP. At low calcium (0.3 mM EGTA), the fluorescence change is essentially single exponential: k_obs = 0.4 s⁻¹ (Fig. 1A). A more rapid component comprising <10% of the total amplitude was observed with some batches of regulatory proteins, which may reflect a small population of thin filaments with defective regulation (data not shown). No emission signal is observed >430 nm when PBP is omitted from all solutions, demonstrating that there is no significant light scattering contribution to the readings at this wavelength (data not shown). The dependence of the observed rate on thin filament concentration is shown in Fig. 1B. The dependence of k_obs on thin filament concentration is fit by a hyperbola with a maximum of 0.64 s⁻¹. This finding represents an ≈8-fold increase from the steady-state ATP hydrolysis rate in the absence of actin, which is equal to the extrapolated intercept at zero thin filament concentration. We were initially concerned that the activation of product release observed in these experiments could be caused by partial activation of the thin filament by a small amount of rigor S1 that was produced by: (i) S1 that had not bound ATP during the first mix, (ii) “dead heads,” damaged S1 that binds to actin but is not dissociated by ATP, or (iii) activation of the thin filament by S1 after the products ADP and Pi have dissociated. However, the observed rate of Pi release was unchanged by doubling the concentrations of S1 and ATP in the initial mix to 2 μM, which would have been expected to increase activation of the thin filament by all three of the mechanisms, had they been present.

Fig 1.

Phosphate dissociation from actoTmTn-myosin-S1A1-ADP-Pi at low calcium concentration. (A) Time course of phosphate release. Double mixing stopped-flow experiments using PBP were performed as described in Experimental Procedures. Equal concentrations (2 μM) of myosin-S1 and ATP were mixed, incubated for 1 s, and then mixed with reconstituted thin filaments containing EGTA. Final concentrations in the flow cell were: 0.44 μM myosin-S1, 0.44 μM nucleotide, 28 μM regulated actin, 0.3 mM EGTA, 2.7 mM MgCl₂, 5 mM Mops, 5 μM PBP, 0.1 mM 7-methylguanosine, 0.01 unit/ml purine nucleoside phosphorylase, pH 7, at 20°C. The solid line through the data is the best fit to a single exponential equation: I(t) = I_ae^−0.4t + C_o. (B) Dependence of k_obs on thin filament concentration. Conditions are as described for A except that the concentration of regulated actin varied from 2.7 to 55 μM. The observed rates of phosphate release are fit to the equation k_obs = k_−P/(1 + K_app/[actin]) + k_o in which K_app = 26 μM and k_−P = 0.64 s⁻¹ and k_o = 0.06 s⁻¹.

At high calcium (0.3 mM), the rate of phosphate dissociation is biphasic (Fig. 2A), an initial rapid increase (k_obs = 8.4 s⁻¹) is followed by a slower increase (k_obs = 0.8 s⁻¹). The dependence of the observed rates of the slow and fast components on thin filament concentration is shown in Fig. 2B. A fit of the fast component to a hyperbola gives a maximum rate of 16 s⁻¹ at saturating actin (Fig. 2B, filled symbols). The observed rate of the slow component, 0.8 s⁻¹, is independent of thin filament concentration (Fig. 2B, open symbols). These data show that the maximum rate of phosphate release at saturating thin filaments is increased ≈20-fold by calcium binding to the thin filament.

Fig 2.

Phosphate dissociation from actoTmTn-myosin-S1A1-ADP-Pi at high calcium concentration. (A) Time course of phosphate release. Equal concentrations (2 μM) of myosin-S1A1 and ATP were mixed, incubated for 1 s, and then mixed with reconstituted thin filaments containing CaCl₂. Final concentrations were identical to those of Fig. 1A except that 0.3 mM CaCl₂ replaced 0.3 mM EGTA. The solid line through the data is the best fit to a double exponential equation: I(t) = 0.33e^−8.4t + 0.67e^−0.81 + C₀. (B) Dependence of k_obs on thin filament concentration. Conditions are as described for A except that the concentration of regulated actin varied from 2.7 to 55 μM. The observed rates of the rapid phase of the phosphate release (▪) are fit to the equation k_obs = k_−Pfast/(1 + K_app/[actin]) in which K_app = 17.2 μM and k_−Pfast = 16 s⁻¹ (solid line). The observed rate constant of the slow phase (□) is essentially independent of actin concentration over the indicated range of protein concentrations with k_−Pslow = 0.8 ± 0.1 s⁻¹. The fraction of amplitude of the fast phase [I_fast/(I_fast + I_slow)] is indicated by *.

Effect of Rigor Myosin Head Binding to the Thin Filament on the Rate of Phosphate Dissociation from AM-ADP-Pi.

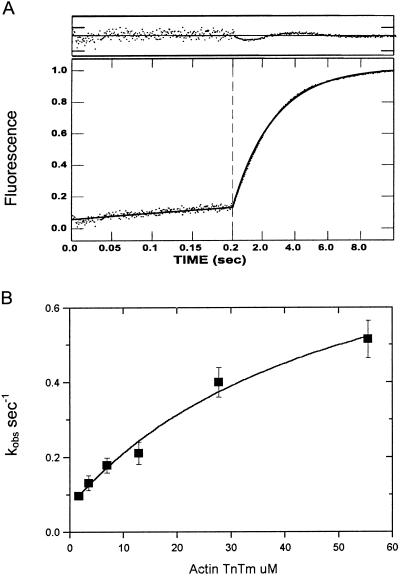
It has been known from both structural and steady-state kinetic data that thin filaments can be activated by myosin heads bound in rigor. To determine the effect of rigor heads on phosphate dissociation we have measured the rate of phosphate dissociation under conditions where excess myosin-S1 is available to produce rigor activation of the thin filaments. Fig. 3A shows the rate of phosphate dissociation observed after incubating 1 μM ATP with a 10-fold excess of myosin-S1 in the first mix and after 1-s mixing with thin filaments to obtain a final concentration of 28 μM actin in the thin filaments. Even at low calcium (0.3 mM EGTA) there is a rapid biphasic dissociation of phosphate from M-ADP-Pi. The dependence of the observed rate on thin filament concentration is shown in Fig. 3B. The S1 concentration was varied so as to maintain a constant ratio of 1 rigor S1 to each seven actin subunits after the second mix. The dependence of both slow and fast components increases with thin filament concentrations to maximum extrapolated rates of 5.4 and 29.6 s⁻¹.

Fig 3.

Phosphate dissociation from actoTmTn-myosin-S1A1-ADP-Pi at low calcium concentration with rigor myosin bound to the thin filaments. (A) Time course of phosphate release. Myosin-S1A1 was mixed with a subsaturating amount of nucleotide, incubated for 1 s, and then mixed with reconstituted thin filaments containing EGTA. Final concentrations were identical to those in Fig. 1A except that the myosin-S1A1 was 4.4 μM. The solid line through the data is the best fit to a double exponential equation: I(t) = 0.54e^−20.8t + 0.46e^−3.9t + C₀. (B) Dependence of k_obs on thin filament concentration. Final concentrations are as in A except for 2.7–28 μM regulated actin and [S1] = [actin]/7. The observed rates of phosphate release are fit to the equation k_obs = k_−Pfast/(1 + K_app/[actin]) in which K_app = 12.3 μM and k_−Pfast = 29.6 s⁻¹ (fast phase, ▪) and K_app = 9.5 μM and k_−Pslow = 5.4 s⁻¹ (slow phase, □). The fraction of amplitude of the fast phase [I_fast/(I_fast + I_slow)] is indicated by *.

High calcium produces an additional enhancement of both the slow and fast phases of the phosphate dissociation from rigor thin filaments (Fig. 4A). The dependence of the observed rate constants of the fast and slow phases of phosphate dissociation on thin filament concentration at a ratio of 1 rigor bound S1 per seven thin filament actin subunits is shown by the closed and open symbols, respectively, in Fig. 4B. The extrapolated rates at saturating thin filament concentration for the slow and fast components are 9.6 and 77 s⁻¹. Similar results were obtained when S1 was bound to the thin filaments (by mixing a 1:7 ratio of S1 to actin in a “T” mixer) 5–10 min before being used in a double mixing experiment in which there was no nucleotide free S1 arising from the first mix (data not shown). The maximum rate of the fast component at saturating concentration of thin filaments observed here is the same within experimental error as the value of 75 s⁻¹ previously measured with F-actin in the absence of regulatory proteins at lower ionic strength (17). These results show that the rate of phosphate dissociation from M-ADP-Pi bound to regulated actin that has been activated by rigor S1 and high calcium occurs at the same maximal rate as from M-ADP-Pi bound to unregulated actin. The amplitude of the fast component is 68% of the total amplitude, which is within experimental error of the 66% M-ADP-Pi measured by quench-flow. This finding indicates that the fast component is a measurement of phosphate dissociation from M-ADP-Pi binding to thin filaments and that the slower component is derived from M-ATP.

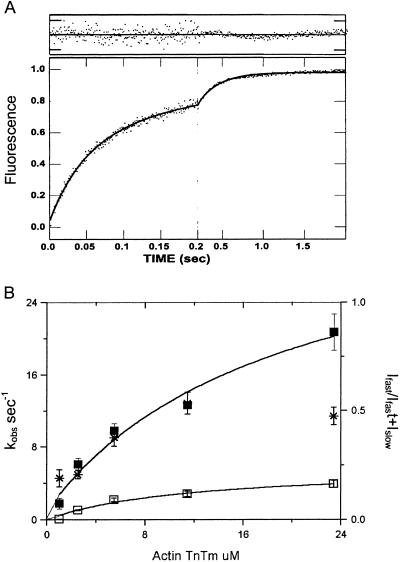
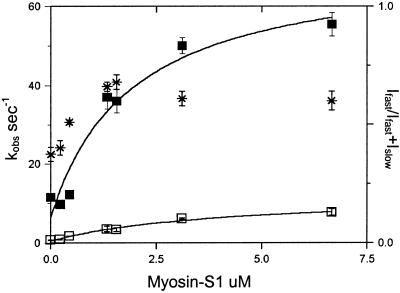
The fraction of thin filament actin sites required to obtain maximal activation of the thin filament was investigated by varying the ratio of myosin-S1 to actin. The dependence of the observed rates of slow and fast phases of phosphate dissociation on the ratio of rigor myosin-S1 to filaments is shown in Fig. 5. The data are fit by a curve in which half-maximal activation is obtained with 1 rigor S1 bound per ≈28 actin subunits or a stoichiometry of 1 S1 per ≈14 actin subunits to obtain maximal activation. These data compare with a measurement of 1 S1 per 10–12 actin subunits of actinTmTn at high calcium in the apparent cooperative unit, measured by Geeves and Lehrer (23). These results suggest a functional regulatory unit that is either longer than a single Tm molecule or one that comprises both sides of the thin filament.

Fig 5.

Dependence of the slow and fast components of Pi dissociation on the concentration of rigor myosin S1A1 bound to thin filament. The k_obs was obtained from experiments described as in Fig. 4A except that the final concentration of thin filament actin was 55 μM and myosin-S1 in excess of nucleotide as indicated. The observed rates of the slow and fast phases of the phosphate release are fit to the equation k_obs = k_−Pfast/(1 + K_app/[actin]) in which K = 1.78 μM and k_fast = 68 s⁻¹ for the fast phase (▪) and K_app = 2.7 μM and k_−Pslow = 11.1 s⁻¹ for the slow phase (□). The fraction of amplitude of the fast phase [I_fast/(I_fast + I_slow)] is indicated by *.

Discussion

We have directly measured the regulation by rigor S1 and calcium of thin filament activation of phosphate dissociation from M-ADP-Pi with a fluorescent PBP (16). It had been shown that the rate-limiting step of ATP hydrolysis by AM is attached hydrolysis (AM-ATP → AM-ADP-Pi) at saturating concentrations of F-actin (17). Although the data observed here with thin filaments are superficially quite similar to those obtained with pure actin there are some differences, which may be significant. Here the observed rate of the slow phase increases with thin filaments whereas it decreased with pure actin. The decrease observed with pure actin that paralleled the steady-state rate provided compelling evidence that the slow phase measured attached hydrolysis. The increase in k_obs of the slow phase observed with the concentration of thin filaments could theoretically be explained by a model in which the pathways of phosphate dissociation from M-ATP and M-ADP-Pi were parallel rather than sequential. In such a kinetic model, both slow and fast k_obs would depend on actin concentration, and the relative proportion of the amplitudes of the slow and fast phases would be independent of actin concentration. Such a model is difficult to reconcile with rapid binding and dissociation of M-ATP and M-ADP-Pi from thin filaments. However, actin is known to promote the dissociation of a significant fraction of ATP from M-ATP (24). The dissociated ATP must subsequently rebind to AM before it can be hydrolyzed and ultimately produces the product phosphate that dissociates from the active site. Moreover, the rate of ATP rebinding depends on the concentration of rigor myosin heads, which increases in parallel with the actin concentration in Fig. 4. We determined that such a model was feasible by globally fitting the data in Fig. 4 to a model shown in Eq. 1, in which binding of both M-ATP and M-ADP-P to thin filaments are faster than ligand binding or dissociation steps. This finding provides an explanation for why a lag is not observed for the binding step, which precedes phosphate dissociation (Figs. 1–4A).

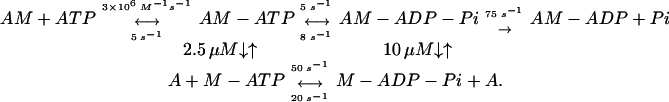Although best fits were obtained with the attached hydrolysis and rates of ATP dissociation of ≈5 s⁻¹, values between 2 and 10 s⁻¹ did not produce significantly worse fits provided that the two rate constants were equal within a factor of 2. The actin dependence of the simulation of the slow and fast components and the fractional amplitude are shown by the dashed lines through the data in Fig. 4. As was the case with pure actin, the rate measured for phosphate dissociation from actoTmTn-M-ADP-Pi is considerably faster than the steady-state rate and is therefore not the rate-limiting step of ATP hydrolysis by thin filament-regulated AM.

The rate of phosphate dissociation from M-ADP-Pi is accelerated by thin filaments (Figs. 1–4). The extent of the increase is regulated by binding of the ligands calcium and myosin-S1 to the thin filaments. The activation is the smallest under conditions of low calcium in the absence of rigor S1 (Fig. 1). Even under these suboptimal conditions, we have observed ≈8-fold enhancement at saturating concentrations of thin filaments. A similar extent of actin activation of products using ethenoATP was observed by Rosenfeld and Taylor (15). At saturating thin filament concentrations, high calcium and rigor myosin-S1 separately bound to the thin filaments, respectively, produce additional 22-fold (16 s⁻¹, Fig. 2) and 42-fold (29.6 s⁻¹, Fig. 3) increases in the rate of the rapid component of phosphate dissociation, relative to the rate (0.64 s⁻¹, Fig. 1) observed at low calcium without rigor myosin-S1. A combination of both rigor-bound myosin-S1 and high calcium is required for maximal acceleration of phosphate dissociation (Figs. 4 and 5). The maximal activation of phosphate dissociation from actoTmTn-M-ADP-Pi is >100-fold faster than the rate of phosphate dissociation produced by thin filaments at low calcium without rigor myosin heads and is identical within experimental error to that observed with pure actin.

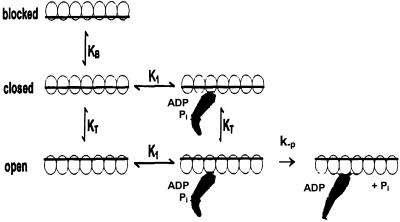
In the simplest steric blocking model of thin filament regulation, calcium binding to Tn regulated the position of the Tm between two positions on the actin filament. At low calcium the Tm covers the myosin binding site on actin whereas at high calcium the site is exposed. To account for equilibrium and kinetic data for the binding of strong binding myosin intermediates (myosin and M-ADP) to thin filaments, an expanded model was required in which calcium and myosin binding regulates the equilibrium constants between three different positions of the Tm on the actin: blocked, closed, and open as shown in Fig. 6 (25). In this model strong binding myosin intermediates (such as myosin and M-ADP) can bind only when Tm is in the open conformation. The closed conformation can bind weak binding myosin intermediates (M-ATP and M-ADP-Pi) but not the strong binding intermediates. The blocked conformation does not bind either weak or strong binding intermediates. The dependence of the observed rate of phosphate dissociation, k_obs, on thin filament concentration, [A], where K₁, K_T, K_B are in rapid equilibrium relative to the maximally activated rate of phosphate dissociation, k_−P, is given in the legend of Fig. 6. Calcium increases the equilibrium constant, K_B, between the blocked and closed conformations from 0.6 to >10 and K_T between the closed and open conformations from 0.06 to 0.2 but the equilibrium constants of two-step binding of myosin to actin are unchanged by calcium (26). The dependence of the observed rate of phosphate dissociation, k_obs, on thin filament concentration, [A], where K₁, K_T, K_B are in rapid equilibrium relative to the maximally activated rate of phosphate dissociation, k_−P, is given in the legend of Fig. 6. However, at the ionic strength and magnesium concentrations used in Figs. 1–4, K_B, the equilibrium constant between the blocked and open positions of Tm, is ≧1 even at low calcium (27). As a result the blocked state is essentially unpopulated and calcium-dependent changes in the fraction of the thin filament sites in the open state are almost entirely caused by changes in K_T (right side of Eq. 1). This finding is consistent with the lack of calcium dependence of myosin-S1 binding to thin filaments measured during steady-state ATP hydrolysis (28) and the small, ≈2-fold calcium dependence of apparent binding constants of M-ADP-Pi to thin filaments observed in Figs. 1–4 and summarized in Table 1, which indicate that K_B is ≧1 at low calcium. Rigor myosin-S1 bound to the thin filaments would be expected to increase the fraction of open thin filament sites to ≈1.0 and produce maximal activation of phosphate dissociation, independent of calcium concentration. The observed rate of phosphate dissociation from AM-ADP-Pi is the same within experimental error for thin filaments activated by high calcium and rigor myosin heads (77 s⁻¹, Fig. 1A) and by actin alone in the absence of regulatory proteins (17). In addition, the value of K_T = 0.2, measured under similar ionic conditions (26), predicts an observed maximum value of phosphate dissociation at high calcium in the absence of rigor-bound S1 of (0.2/1 + 0.2) × 77 s⁻¹ ≈ 13 s⁻¹, which is in good agreement with the observed value of 16 s⁻¹ measured in Fig. 2B. However, several other aspects of the three-state steric blocking model are not consistent with the data in Table 1. The observed increase of >20-fold in the rate of dissociation of phosphate from actinTmTn-M-ADP-Pi from low (0.64 s⁻¹) to high calcium (16 s⁻¹) requires a similar calcium dependence of K_T, which has only a 3-fold dependence on calcium (26). In addition, the maximum rate of phosphate dissociation is increased 2.5-fold by calcium (Figs. 2 and 5), even when the thin filament is already held in the open conformation by rigor S1. According to this model, binding of rigor myosin-S1 alone would be expected to increase the fraction of open thin filament sites to ≈1.0 and produce maximal activation of phosphate dissociation, independent of calcium concentration. Both the calcium sensitivity of the maximum rate in the presence of bound S1 and the inability of the dependence of K_T on calcium concentration to quantitatively account for the extent of regulation indicate that either phosphate dissociation (or the rate of the weak to strong conformational change after M-ADP-Pi binding to actin that limits phosphate dissociation) is the principal calcium-regulated step of the hydrolysis mechanism. This work provides direct evidence in support of the earlier steady-state measurements of Chalovich and Eisenberg (29) and kinetic studies by Rosenfeld and Taylor (15) that demonstrated the importance of calcium regulation of the rate of the product release steps.

Fig 6.

Three-state steric blocking model applied to the regulation of phosphate dissociation. K_B is the equilibrium constant between the blocked and closed states, K_T the equilibrium constant between the blocked and open states, K₁ the association constant of M-ADP-P_i binding to the open and closed states, and k_−P the rate constant of dissociation of phosphate from AM-ADP-Pi. The dependence of k_obs on k_−P, K₁, K_T, K_B, and [A] is: k_obs = k_−P/((1 + 1/K_T) + (1/K₁[A])(1 + (1/K_T)(1 + 1/K_B))) ≈ k_−PK_T/(1 + K_T) for K_B ≫1 and [A] ≫ K₁.

Table 1.

Summary of kinetic data

[Ca]	<10−7 M	>10−5 M	<10−7 M	>10−5 M
[Myosin]	0	0	1/7 [Actin]	1/7 [Actin]
Fast	0.64 s−1 (26 μM)	16 s−1 (17 μM)	30 s−1 (12 μM)	77 s−1 (18 μM)
Slow	na	0.8 s−1	5.4 s−1 (9.5 μM)	9.6 s−1 (14 μM)

^*[Myosin − S1] = 0 at t = 0.

^† [Myosin − S1]/[actin] = 1/7 at t = 0.

^‡ k_obs (s⁻¹) is for the maximal rate of phosphate dissociation for the slow and fast components at saturating thin filament concentrations in Figs. 1–4. The values in parentheses are the thin filament concentration required to obtain half the maximal observed rate.

^§ Data were fit to a single exponential. na, not available.

^¶ There is no dependence of k_obs of the slow component on thin filament concentration.

Abbreviations

• M-ADP-Pi, myosin-ADP-inorganic phosphate

• M-ATP, myosin-ATP

• PBP, phosphate binding protein

• Tm, tropomyosin

• Tn, troponin

• AM, actomyosin