A structural model for Alzheimer's β-amyloid fibrils based on experimental constraints from solid state NMR

Abstract

We present a structural model for amyloid fibrils formed by the 40-residue β-amyloid peptide associated with Alzheimer's disease (Aβ_1–40), based on a set of experimental constraints from solid state NMR spectroscopy. The model additionally incorporates the cross-β structural motif established by x-ray fiber diffraction and satisfies constraints on Aβ_1–40 fibril dimensions and mass-per-length determined from electron microscopy. Approximately the first 10 residues of Aβ_1–40 are structurally disordered in the fibrils. Residues 12–24 and 30–40 adopt β-strand conformations and form parallel β-sheets through intermolecular hydrogen bonding. Residues 25–29 contain a bend of the peptide backbone that brings the two β-sheets in contact through sidechain-sidechain interactions. A single cross-β unit is then a double-layered β-sheet structure with a hydrophobic core and one hydrophobic face. The only charged sidechains in the core are those of D23 and K28, which form salt bridges. Fibrils with minimum mass-per-length and diameter consist of two cross-β units with their hydrophobic faces juxtaposed.

Amyloid fibrils are filamentous structures, with typical diameters of ≈10 nm and lengths up to several micrometers, formed by numerous peptides and proteins with disparate sequences and molecular weights. Biomedical interest in amyloid fibrils arises from their occurrence in amyloid diseases (1), including Alzheimer's disease, type 2 diabetes, Huntington's disease, and prion diseases. Current interest in the molecular structures of amyloid fibrils additionally arises from fundamental questions regarding the molecular mechanism of amyloid formation and the nature of the intermolecular interactions that stabilize these structures for an extremely diverse class of polypeptides.

No high-resolution molecular structure of an amyloid fibril has yet been determined experimentally because amyloid fibrils are noncrystalline solid materials and are therefore incompatible with x-ray crystallography and liquid state NMR. X-ray fiber diffraction shows that amyloid fibrils contain cross-β structural motifs, i.e., extended β-sheets in which the β-strand segments run approximately perpendicular to, and the intermolecular hydrogen bonds run approximately parallel to, the long axis of the fibril (2, 3). Other molecular-level structural features of amyloid fibrils are not well established.

In the case of fibrils formed by the full-length β-amyloid peptide associated with Alzheimer's disease (Aβ), which ranges from 39 to 43 residues in length in vivo (4, 5), several molecular models have been proposed (6–10). These models exhibit many qualitative and quantitative differences, reflecting the paucity of experimental constraints. All of these models are inconsistent with recent measurements of ¹³C-¹³C nuclear magnetic dipole-dipole couplings (i.e., intermolecular distances) by solid state NMR (11–13), which imply an in-register parallel alignment of peptide chains within the cross-β motif in Aβ_1–40 and Aβ_1–42 fibrils (Aβ_m−n denotes residues m to n of Aβ). Earlier solid state NMR measurements showed the same in-register parallel alignment in Aβ_10–35 fibrils (14–16).

Here, we describe a molecular model for Aβ_1–40 fibrils that is based on solid state NMR and other experimental data. The NMR data include: (i) ¹⁵N and ¹³C chemical shifts and NMR linewidths determined from 2D ¹³C-¹³C and ¹⁵N-¹³C chemical shift correlation spectra of samples in which selected residues are uniformly ¹⁵N- and ¹³C-labeled, which serve to identify β-strand segments, non-β-strand segments, and disordered segments; (ii) constraints on backbone φ and ψ torsion angles obtained from measurements on doubly ¹³C-labeled fibril samples, which permit a quantitative characterization of non-β-strand conformations at certain sites; and (iii) recent measurements of intermolecular ¹³C-¹³C distances (11, 12). Additional experimental constraints on fibril dimensions and mass-per-length (MPL) are obtained from electron microscopy (EM) measurements. The model, which is derived by incorporation of the experimental constraints into an energy minimization procedure, reveals how amyloid fibrils with apparently favorable electrostatic and hydrophobic interactions can be constructed from the full-length Aβ peptide sequence.

Materials and Methods

Sample Preparation.

Peptides with the human Aβ_1–40 sequence DAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVV were synthesized, purified, and fibrillized from 0.25- to 1.0-mM solutions at pH 7.4 as described (11, 12). Fibrillized solutions were lyophilized for solid state NMR measurements. Typical solid state NMR samples were 10 mg. For EM, fibrillized solutions were diluted by a factor of 10–20 and negatively stained with uranyl acetate as described (11, 13).

The following samples were synthesized with uniform ¹⁵N and ¹³C labeling of the specified residues: SU7 (F19, V24, G25, A30, I31, L34, M35), SU6 (A2, D7, G9, Y10, V12, M35), SU5 (D23, K28, G29, I32, V36), and CU6 (K16, L17, V18, F19, F20, A21). The following samples were synthesized with ¹³C labels at the specified pairs of backbone carbonyl sites: DL1 (D23, V24), DL2 (V24, G25), DL3 (G25, S26), DL4 (K28, G29), and DL5 (G29, A30). The notations SUn, CUn, and DLn indicate “scattered uniform” labeling of n residues, “consecutive uniform” labeling of n residues, and the nth “double labeled” sample, respectively.

Solid State NMR Measurements.

For SUn and CUn samples, 2D ¹³C/¹³C chemical shift correlation spectra were acquired at a proton NMR frequency of 400.9 MHz and magic-angle spinning (MAS) frequencies of 21.7–23.3 kHz, using finite-pulse radio-frequency-driven recoupling (fpRFDR) mixing periods of 1.37–1.47 ms, as described (17, 18). 2D ¹⁵N/¹³C chemical shift correlation spectra were acquired at an MAS frequency of 9.0 kHz, using a frequency-selective ¹⁵N-¹³C cross-polarization technique with mixing periods of 1.2–2.5 ms, as described by Baldus et al. (19).

For DLn samples, constant-time fpRFDR (fpRFDR-CT) data were acquired at proton NMR frequencies of 400.9 and 399.2 MHz, using an MAS frequency of 20.0 kHz and with the parameters K = 3 and M + 2N = 96, in the notation of Ishii et al. (20) Double quantum chemical shift anisotropy (DQCSA) data were acquired as described (21), using an MAS frequency of 5.0 kHz and DQ preparation and mixing periods of 6.4 ms. Sensitivity of fpRFDR-CT and DQCSA measurements was enhanced by pulsed spin locking (22). 2D MAS exchange data were acquired at a proton NMR frequency of 599.1 MHz as described (23), using an MAS frequency of 3.78 kHz and 500-ms exchange periods.

NMR Data Analysis.

Backbone torsion angles were predicted from chemical shift data as follows: (i) the TALOS database (24) was used to generate best-fit functional dependences of ¹³C and ¹⁵N secondary shifts on φ and ψ (i.e., chemical shift surfaces); and (ii) for each seven-residue segment of Aβ_1–40, an exhaustive comparison with predicted chemical shifts for seven-residue segments in a nonredundant subset of protein structures in the Protein Data Bank (PDB) was conducted. For each PDB segment, a score was calculated according to the TALOS formula (24). The 10 most closely matching PDB segments were retained. The average φ and ψ values for these 10 segments, and the ranges of these values, are reported in Table 2.

Table 2.

Residue-specific φ and ψ backbone torsion angles (degrees) for Aβ_1–40 fibrils, predicted from ¹³C and ¹⁵N chemical shifts in Table 1 or determined from measurements on the doubly ¹³C-labeled DLn samples

Residue	φ, ψ from chemical shift set 1	φ, ψ from chemical shift set 2	φ, ψ from DLn samples
G9	−148 ± 11, 151 ± 15	−148 ± 11, 151 ± 15
Y10	−127 ± 9, 124 ± 9	−127 ± 9, 124 ± 9
V12	−119 ± 8, 124 ± 10	−119 ± 8, 124 ± 10
K16	−149 ± 12, 152 ± 8	−149 ± 12, 152 ± 8
L17	−150 ± 12, 143 ± 9	−150 ± 12, 143 ± 9
V18	−145 ± 9, 147 ± 11	−145 ± 8, 146 ± 12
F19	−144 ± 10, 141 ± 12	−144 ± 10, 139 ± 15
F20	−147 ± 9, 151 ± 11	−145 ± 11, 152 ± 13
A21	−137 ± 12, 143 ± 16	−127 ± 11, 141 ± 19
D23	−145 ± 16, 147 ± 16	−83 ± 13, 122 ± 22
V24	−103 ± 10, 117 ± 11	−100 ± 12, 114 ± 22	−145, 115
G25	−88 ± 30, 124 ± 33	−58 ± 48, 11 ± 74	−70, −40
S26			68, −65
K28	−134 ± 12, 152 ± 14	−151 ± 14, 156 ± 13
G29	−59 ± 50, 119 ± 58	−150 ± 18, 156 ± 14	−120, −125
A30	−138 ± 14, 157 ± 14	−144 ± 12, 145 ± 13	−165, 133
I31	−113 ± 16, 127 ± 12	−118 ± 15, 129 ± 11
I32	−123 ± 10, 146 ± 14	−127 ± 9, 147 ± 12
L34	−143 ± 9, 145 ± 17	−144 ± 8, 145 ± 16
M35	−141 ± 9, 138 ± 11	−141 ± 9, 138 ± 11
V36	−118 ± 8, 120 ± 11	−118 ± 8, 120 ± 11

^*First chemical shift value for each labeled site in Table 1.

^† Second chemical shift value for each labeled site in Table 1, where more than one value is observed.

Backbone torsion angles were determined from data on DLn samples by comparison with numerical simulations, using fortran programs that simulate the dependence of the data on φ and ψ (20, 21, 23). Simulations of fpRFDR-CT data were carried out for a four-spin system (two carbonyl labels on two parallel peptide chains). Simulations of DQCSA and 2D MAS exchange data were carried out for a two-spin system (two carbonyl labels on one chain). CSA principal values in simulations were determined experimentally from 1D MAS spectra (25).

Molecular Modeling.

The model in Fig. 4 was generated by energy minimization, using the CHARMm force field and algorithms contained in quanta 97 (Molecular Simulations, Waltham, MA), starting from an initial peptide conformation generated manually within molmol (26). Residues 1–8 were considered disordered and were omitted. For residues 9–23 and 31–40, initial φ and ψ values were taken from chemical shift predictions (set 1 in Table 2). For residues 24–30, initial φ and ψ values were taken from measurements on DLn samples. Where no experimentally derived values were available, φ and ψ were set to −140° and 140°, respectively. All ω angles were set to 180°. Signs of the φ and ψ values from DLn data (see below) were chosen to permit an approximate alignment of all backbone carbonyl C==O and amide N–H bonds along a single intermolecular hydrogen-bonding direction, as required by the cross-β structural motif. Five copies of the initial peptide conformation related by 5-Å displacements along the hydrogen-bonding direction were generated so that energy minimization would take place in the context of a five-stranded cross-β structure. Energy minimization included bond, angle, dihedral, improper, and van der Waals energy terms, but not electrostatic energy. The in-register parallel alignment within the cross-β motif was enforced by distance constraints between backbone carbonyl oxygens of each residue k and the backbone amide hydrogen of residue k + 1 of a neighboring chain, producing the 4.8-Å backbone-backbone distance seen in diffraction data (3, 27, 28). Torsion angle constraints were included with the target values described above and with force constants that resulted in typical deviations of less than 10° from the target values in the energy-minimized structure. For N27 and K28, torsion angle force constants were reduced by a factor of 20, reflecting the absence of experimental constraints.

Fig 4.

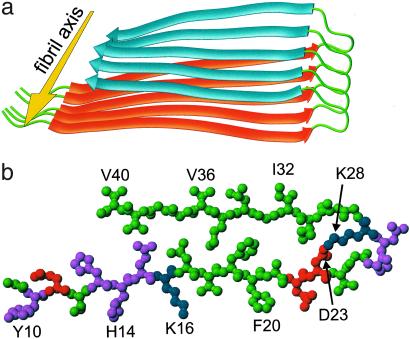
Structural model for Aβ_1–40 fibrils, consistent with solid state NMR constraints on the molecular conformation and intermolecular distances and incorporating the cross-β motif common to all amyloid fibrils. Residues 1–8 are considered fully disordered and are omitted. (a) Schematic representation of a single molecular layer, or cross-β unit. The yellow arrow indicates the direction of the long axis of the fibril, which coincides with the direction of intermolecular backbone hydrogen bonds. The cross-β unit is a double-layered structure, with in-register parallel β-sheets formed by residues 12–24 (orange ribbons) and 30–40 (blue ribbons). (b) Central Aβ_1–40 molecule from the energy-minimized, five-chain system, viewed down the long axis of the fibril. Residues are color-coded according to their sidechains as hydrophobic (green), polar (magenta), positive (blue), or negative (red).

An initial stage of energy minimization, using only the constraints described above, resulted in a structure consisting of two separate, parallel β-sheets, created by residues 9–24 and 30–40, with a net bend angle of ≈60° between them due to non-β-strand conformations at G25, S26, and G29. Additional intramolecular distance constraints were then applied between Cγ of D23 and Nζ of K28 (see below), between Cζ of F19 and Cα of G33, and between Nɛ of Q15 and Cα of G37, with target distances of 4.5 Å. A second stage of energy minimization resulted in a bend angle of ≈180°, i.e., a double-layered β-sheet structure. In the final stage of energy minimization, distance constraints between F19 and G33 and between Q15 and G37 were removed. The double-layered structure was maintained by van der Waals interactions between sidechains of the two β-sheets. Final torsion angles of the central peptide chain agree with target values to within an rms deviation of 4.1° for φ and 6.7° for ψ, with the largest deviations being 11° for φ and 15° for ψ (except for a deviation of 28° for ψ of N27). All ω values are within 6° of 180°. No unrealistic distortions of bond angles or steric clashes are observed.

Results

Fibril Dimensions and Morphologies.

Fig. 1a shows representative EM images of Aβ_1–40 fibrils. Fibrils exhibit a diversity of morphologies, often with a periodic modulation in diameter suggesting a twist about the long axis. Similar morphologies have been reported previously for Aβ and other amyloid fibrils, in both EM and atomic force microscope images (29–31). The narrowest Aβ_1–40 fibrils have diameters of 50 ± 10 Å.

Fig 1.

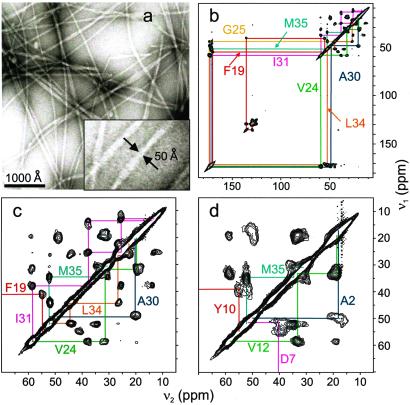
(a) Transmission electron microscope images of negatively stained amyloid fibrils after 14-day incubation of a 0.5 mM Aβ_1–40 solution. A 3× expansion (Inset) shows fibrils with the smallest diameters observed. (b) 2D ¹³C-¹³C chemical shift correlation spectrum of Aβ_1–40 fibril sample SU7, showing resonance assignment paths for the seven uniformly ¹⁵N- and ¹³C-labeled residues in this sample. (c) Expansion of the aliphatic region of the 2D spectrum of SU7. (d) Aliphatic region of the 2D ¹³C-¹³C chemical shift correlation spectrum of Aβ_1–40 fibril sample SU6.

Characterization of Structural Order.

Fig. 1 b and c shows the 2D ¹³C-¹³C chemical shift correlation spectrum of Aβ_1–40 fibril sample SU7 (see Materials and Methods for sample descriptions). Strong crosspeaks in the spectrum connect the chemical shifts of directly bonded, labeled carbon sites. The crosspeaks are readily assigned based on the chemical structures and known ¹³C chemical shift ranges of the amino acid sidechains. ¹³C NMR linewidths determined from the full-width at half height of the crosspeaks are 1.5–2.5 ppm for fibrillized SU7. Fig. 1d shows a portion of the 2D ¹³C-¹³C correlation spectrum of Aβ_1–40 fibril sample SU6. Linewidths for M35 are the same in SU6 and SU7, but significantly broader lines (3.0–5.5 ppm) are observed for labeled carbon sites of A2, D7, G9, and Y10 in SU6.

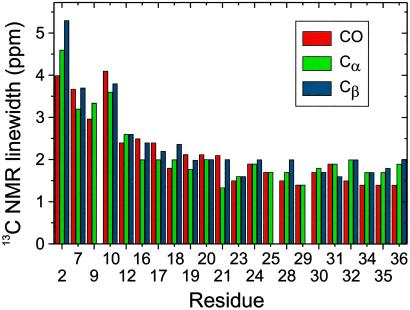
¹³C NMR linewidths for CO, Cα, and Cβ sites in Aβ_1–40 fibril samples SU5, SU6, SU7, and CU6 are plotted in Fig. 2. Linewidths in the 1.5–2.5 ppm range in solid state ¹³C MAS NMR spectra are characteristic of well-structured peptides in rigid noncrystalline environments, whereas significantly larger linewidths are observed in disordered biopolymers (32, 33). Fig. 2 shows that the N-terminal segment of Aβ_1–40 is disordered in the fibrils, with full structural order beginning after Y10. The N-terminal residues in Aβ_1–40 and Aβ_1–42 fibrils are not required for fibril formation (34) and have been shown to be susceptible to proteolysis in brain tissue (35, 36) and in vitro (37).

Fig 2.

¹³C NMR linewidths for CO, Cα, and Cβ sites in Aβ_1–40 fibrils, determined from 2D solid state NMR spectra as in Fig. 1. Linewidths of 2.5 ppm or less indicate well-ordered conformations. Larger linewidths in the N-terminal segment indicate structural disorder.

Identification of β-Strand Segments.

NMR chemical shifts obtained from 2D ¹³C-¹³C correlation spectra as in Fig. 1 and from 2D ¹⁵N-¹³C correlation spectra (data not shown) are summarized in Table 1. As shown previously by NMR experiments (38, 39) and ab initio calculations (40), secondary shifts Δδ ≡ δ_fibril − δ_coil are strongly correlated with peptide or protein backbone conformation, where δ_fibril is the chemical shift in the folded or fibrillized state and δ_coil is the random coil shift (i.e., the shift for the same residue type in an unstructured peptide in aqueous solution). In particular, Δδ values for β-strand segments are characteristically negative for ¹³Cα and ¹³CO sites and positive for ¹³Cβ sites.

Table 1.

¹³C and ¹⁵N NMR chemical shift values (ppm) for ¹³C- and ¹⁵N-labeled sites in Aβ_1–40 fibrils, referenced to TMS (tetramethylsilane) or liquid NH₃

Residue	CO	Cα	Cβ	Cγ	Cδ	Cκ	Cζ, Nζ	N	Sample
A2	173.7	49.9	18.2					ND	SU6
	(176.1)	(50.8)	(17.4)
D7	∼173.0	51.5	40.4	177.9				120.6	SU6
	(174.6)	(52.5)	(39.4)	(178.3)				(120.4)
G9	169.3	42.9						107.2	SU6
	(173.2)	(43.4)						(108.8)
Y10	172.0	55.0	39.5	126.5	130.7	116.5	156.2	122.4	SU6
	(174.2)	(56.2)	(37.1)	(128.9)	(131.6)	(116.5)	(155.6)	(120.3)
V12	173.0	58.7	33.2	18.8, 18.8				127.0	SU6
	(174.6)	(60.5)	(31.2)	(19.4, 18.6)				(119.2)
K16	171.5	52.7	34.1	24.0	28.6	39.8	33.7	ND	CU6
			36.9	24.8
	(174.9)	(54.5)	(31.4)	(23.0)	(27.3)	(40.2)	(32.7)
L17	172.8	52.3	∼44.5	26.0	∼24.4, ∼23.3			ND	CU6
	173.0	51.6	∼40.8	∼27.0	∼24.8, ∼23.1
	(175.9)	(53.4)	(40.7)	(25.2)	(23.2, 21.6)
V18	170.3	58.9	33.6	19.2				121.7	CU6
	(174.6)	(60.5)	(31.2)	(19.4, 18.6)				(119.2)
F19	170.2	55.3	41.0	135.7	129.6	129.6	125.8	130.5	CU6, SU7
	(174.1)	(56.0)	(37.9)	(137.2)	(130.2)	(129.8)	(128.2)	(120.3)
F20	170.2	54.6	41.0	135.7	129.2	129.2	125.8	ND	CU6
	(174.1)	(56.0)	(37.9)	(137.2)	(130.2)	(129.8)	(128.2)
A21	172.7	48.2	21.0					130.9	CU6
	174.0	48.0	18.9					126.3
	(176.1)	(50.8)	(17.4)					(123.8)
D23	173.1	51.0	41.9	180.2				118.5	SU5
	174.1	52.4	39.4	178.0				123.3
	(174.6)	(52.5)	(39.4)	(178.3)				(120.4)
V24	173.8	58.6	31.3	19.9, 18.3				125.0	SU7
	173.6	59.0	32.8	19.9, 19.9				125.0
	(174.6)	(60.5)	(31.2)	(19.4, 18.6)				(119.2)
G25	174.2	44.4						113.9	SU7
	171.1	46.9						117.8
	171.1	∼44.2						113.9
	(173.2)	(43.4)						(108.8)
K28	174.3	52.8	35.6	24.7	27.8	42.0	33.0	119.5	SU5
	172.4	53.5	33.4	22.3	28.5	39.1	32.9	112.7
	(174.9)	(54.5)	(31.4)	(23.0)	(27.3)	(40.2)	(32.7)	(120.4)
G29	172.4	47.2						117.0	SU5
	168.6	42.4						104.1
	(173.2)	(43.4)						(108.8)
A30	173.2	48.4	20.5					122.1	SU7
								127.4
	171.3	49.5	20.5					119.2
	(176.1)	(50.8)	(17.4)					(123.8)
I31	172.5	58.4	38.0	25.7, 13.8	13.3			120.6	SU7
	(174.7)	(59.4)	(37.1)	(25.5, 15.7)	(11.2)			(119.9)
I32	173.8	56.7	40.2	25.2, 15.9	12.4			125.0	SU5
	172.2	57.0	38.7	24.6, 15.3	12.1			125.0
	(174.7)	(59.4)	(37.1)	(25.5, 15.7)	(11.2)			(119.9)
L34	171.0	52.1	44.8	27.0	∼24.0, 22.5			∼128.0	SU7
			44.1	26.3	24.0, 22.9			∼128.0
	(175.9)	(53.4)	(40.7)	(25.2)	(23.2, 21.6)			(121.8)
M35	171.2	52.1	34.6	30.8		16.7		125.4	SU7, SU6
	(174.6)	(53.7)	(31.2)	(30.3)		(15.2)		(119.6)
V36	171.8	58.8	31.9	18.9				126.6	SU5
	(174.6)	(60.5)	(31.2)	(19.4, 18.6)				(119.2)

Values preceded by ∼ have an uncertainty of 0.6 ppm. Otherwise, the uncertainty is 0.3 ppm. Values that could not be determined are indicated by ND. Values in parentheses are random-coil shifts, taken from Wishart et al. (51) and adjusted to the TMS reference.

Certain labeled residues exhibit more than one distinct set of chemical shifts, resulting in more than one set of 2D crosspeaks. The relative intensities of the crosspeaks in different sets vary with fibrillization conditions. We attribute the multiplicity of chemical shifts to differences in molecular structure associated with the differences in fibril morphology apparent in Fig. 1a and typically observed for Aβ fibrils (29) and other amyloid fibrils (30). Although the nature and degree of structural differences at the molecular level are not yet clear, all sets of ¹³C chemical shifts for residues 9–21 and 30–36 in Table 1 consistently indicate β-strand conformations. In contrast, at least some ¹³C chemical shifts for D23, V24, G25, and G29 are inconsistent with expectations for a β-strand. Thus, the chemical shift data qualitatively suggest a conformation for the structurally ordered part of Aβ_1–40 consisting of two β-strands that are separated by a bend or loop contained within residues 23–29. The conformation in the bend segment may vary with fibril morphology and fibrillization conditions.

¹³C chemical shifts for CO, Cα, and Cβ sites and ¹⁵N chemical shifts for backbone amide sites were analyzed with an algorithm that predicts the backbone torsion angles φ and ψ for each uniformly labeled residue (see Materials and Methods). Predictions for two different choices of chemical shift values are given in Table 2. Both choices lead to φ = −135° ± 25° and ψ = 140° ± 20°, consistent with a β-strand conformation, for all residues in the 9–21 and 30–36 segments. Non-β-strand φ and ψ values (and significant differences for different choices of chemical shift values) occur at D23, G25, and G29.

Determination of Backbone Torsion Angles at Non-β-Strand Sites.

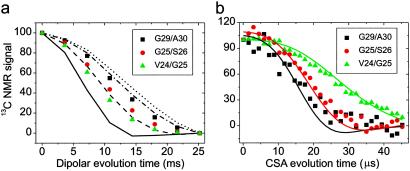
Measurements were carried out on the DLn samples to further constrain the backbone conformation in residues 23–30. Three solid state NMR techniques that place independent constraints on the φ and ψ torsion angles of the second labeled residue in each sample (i.e., V24 in DL1, G25 in DL2, S26 in DL3, G29 in DL4, and A30 in DL5) were used (20, 21, 23). Fig. 3 a and b shows fpRFDR-CT and DQCSA data for three samples and simulations that illustrate the sensitivity of these data to backbone conformation. In fpRFDR-CT measurements, the decay of ¹³C NMR signals from the labeled carbonyl sites reflects the strength of ¹³C-¹³C dipole-dipole couplings, which depends primarily on the intramolecular ¹³C-¹³C distance and hence the φ angle. In DQCSA measurements, the decay of ¹³C NMR signals from the labeled sites reflects the relative orientation of the labeled carbonyl groups, which depends on both φ and ψ. As is apparent in Fig. 3, fpRFDR-CT and DQCSA data for different samples are significantly different, indicating significant differences in φ and ψ. Qualitatively, this result indicates the presence of non-β-strand conformations. Data from 2D MAS exchange measurements (not shown) are also significantly different for different DLn samples.

Fig 3.

Solid state NMR data on DLn Aβ_1–40 fibril samples with ¹³C labels at the indicated backbone carbonyl sites. These data constrain the φ and ψ angles of the second labeled residue. (a) fpRFDR-CT data and simulations for φ = 40° (solid line), 80° (dashed line), 120° (dot-dashed line), and 160° (dotted line). Simulations are scaled and baseline-corrected to match the first and last experimental data points. (b) DQCSA data and simulations for φ, ψ = −70°, −40° (green); 70°, −65° (red); and −165°, 135° (black).

Values of φ and ψ were determined from the fpRFDR-CT, DQCSA, and 2D MAS exchange data by comparison with numerical simulations as follows: (i) a range of φ values that gave an acceptable fit to the fpRFDR-CT data was determined; (ii) the best-fit values of φ and ψ for DQCSA and 2D MAS exchange data contained within this range were determined; and (iii) the averages of the two best-fit φ and ψ values were taken as the final values, which are reported in Table 2. Note that these measurements are invariant to the substitution φ, ψ → −φ, −ψ because of symmetry considerations (23). Signs of φ and ψ values in Table 2 were chosen by molecular modeling to give an Aβ_1–40 conformation consistent with the required cross-β structural motif. Agreement between torsion angles determined from DLn samples and predicted from chemical shifts is reasonable for V24 and A30. Agreement for G25 and G29 is not quantitative, but predictions from chemical shifts for non-β-strand glycines are considered unreliable.

Intermolecular Distance Constraints.

Recent measurements of intermolecular ¹³C-¹³C dipole-dipole couplings in Aβ_1–40 fibrils (11, 12) indicate intermolecular distances of 4.8 ± 0.5 Å between backbone carbonyl carbons of V12, L17, F20, V24, L34, and V39, β-carbons of A21 and A30, and α-carbons of G9. These distances imply an in-register parallel alignment in the cross-β motif, extending from G9 through V39. For A2 and F4, intermolecular distances are greater than 6 Å, consistent with N-terminal disorder.

Discussion

Structural Model for Aβ_1–40 Fibrils.

Fig. 4 presents a structural model for Aβ_1–40 fibrils consistent with the conformational constraints and intermolecular distance constraints described above, and incorporating the cross-β structural motif established by x-ray diffraction data (3, 27, 28). This model results from a constrained energy minimization procedure (see Materials and Methods). Significant features of the model are as follows: (i) residues 1–8 are omitted because of the N-terminal structural disorder; (ii) the peptide conformation contains two β-strands, separated by a 180° bend formed by residues 25–29; (iii) the β-strands form two in-register parallel β-sheets, which interact through sidechain-sidechain contacts; (iv) except for D23 and K28, sidechains in the core of the resulting double-layered structure (Q15, L17, F19, A21, I31, M35, and V39) are neutral and primarily hydrophobic; (v) sidechains of D23 and K28 form a salt bridge across the bend; (vi) sidechains of A30, I32, L34, V36, and V40 form a hydrophobic face; and (vii) other charged and polar sidechains are distributed on the opposite face, on the convex side of the bend, and in the N-terminal segment.

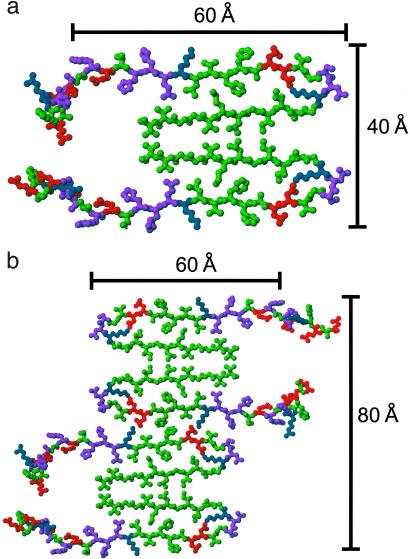
The double-layered β-sheet structure in Fig. 4 a and b constitutes a single molecular layer, or “cross-β unit.” The MPL of a cross-β unit, given by the molecular mass divided by the 4.8 Å spacing between hydrogen-bonded chains in a β-sheet, is 9.0 kDa/Å. Measurements by scanning transmission electron microscopy indicate a minimal MPL equal to twice this value for Aβ_1–40 fibrils (29), as well as for Aβ_1–42 and Aβ_10–35 fibrils (13). Given these MPL data and the single hydrophobic face described above, fibrils with minimal MPL may be formed by juxtaposing two cross-β units as in Fig. 5a. The structurally ordered part of the resulting fibril has cross-sectional dimensions of ≈40 Å × 60 Å, in good agreement with the dimensions of the narrowest fibrils in Fig. 1a. Note that residues 10–40 of Aβ_1–40 would have a length of ≈100 Å in a single β-strand. Thus, the experimental fibril dimensions require non-β-strand conformations and a large net bend angle between β-strands, consistent with the NMR data.

Fig 5.

(a) Cross section of an Aβ_1–40 fibril with the minimal MPL indicated by scanning transmission electron microscopy (13, 29), formed by juxtaposing the hydrophobic faces of two cross-β units from Fig. 4. Residues 1–8 are included with randomly assigned conformations. (b) Possible mode of lateral association to generate fibrils with greater MPL and greater cross-sectional dimensions.

Fibrils with minimal MPL, as in Fig. 5a, may be termed “protofilaments.” Fibrils with greater MPL and greater diameters may be laterally associated protofilaments (30). One possible mode of lateral association is depicted in Fig. 5b. The spacings between β-sheet layers in Fig. 5 are ≈9.5 Å, in good agreement with the equatorial spacing in experimental fiber diffraction data (3, 27, 28).

Significance of Hydrophobic and Electrostatic Interactions.

Amyloid fibrillization is generally considered to be driven by hydrophobic rather than electrostatic interactions (34, 41–43). Aβ_1–40 contains central (residues 17–21) and C-terminal (residues 30–40) hydrophobic segments. The in-register parallel alignment of Aβ_10–35, Aβ_1–40, and Aβ_1–42 chains within the β-sheets in the fibrils, determined experimentally by solid state NMR (11–16), maximizes the hydrophobic contacts of these segments. However, an in-register parallel alignment also results in short distances (≈5 Å) between like charges on neighboring peptide molecules. In the low dielectric environment that may exist in the interior of an amyloid fibril, electrostatic repulsions between like charges might destabilize the parallel β-sheet structure by ≈100 kcal/mol, overwhelming the favorable hydrophobic energy. The ionization states of sidechains in Aβ_1–40 fibrils may be determined experimentally from NMR chemical shifts. Cγ shifts for D7 and D23 in Table 1 indicate deprotonated sidechains (44), whereas Nζ shifts for K16 and K28 indicate protonated sidechains (45).

Figs. 4 and 5 show both how favorable hydrophobic interactions can be maximized and how electrostatic destabilization can be avoided. The only charged sidechains in the core of the structure in Fig. 4 are those of D23 and K28, which form a salt bridge that may stabilize the structure. All other charged or potentially charged sidechains are at positions where they could be solvated as the fibrils grow. If protofilaments associate laterally as in Fig. 5b, intermolecular salt bridges between K16 and E22 would also prevent electrostatic destabilization.

In support of D23-K28 salt bridges, we have detected a ¹⁵N-¹³C dipole-dipole coupling between Cγ of D23 and Nζ of K28 in SU5 Aβ_1–40 fibril samples, corresponding to an interatomic distance of ≈4 Å, using the heteronuclear recoupling technique of Jaroniec et al. (46).

Comparison with Other Aβ Fibril Models.

Models for full-length Aβ fibrils suggested previously were based on antiparallel β-sheet structures (6–10) and are at variance with experimental intermolecular distance constraints (11–13). Several models include a true β-hairpin centered in residues 24–29, with intramolecular hydrogen bonding between β-strands on either side of a β-turn (6, 7, 10, 34). Such intramolecular hydrogen bonding is incompatible with the in-register parallel intermolecular alignment determined experimentally (11–13). A model proposed by Tjernberg et al. (8) includes a bend in residues 23–26 but is otherwise quite different from Figs. 4 and 5.

Lynn, Meredith, Botto, and coworkers have proposed a model for Aβ_10–35 fibrils in which the peptide chain forms a single, continuous β-strand (15, 16). An alternative model for Aβ_10–35 fibrils similar to that in Fig. 4 has been proposed independently by Ma and Nussinov (47), based on the solid state NMR data for Aβ_10–35 fibrils (14–16), molecular modeling, and dynamics simulations. The simulations of Ma and Nussinov, which include solvent molecules, indicate the stability of structures similar to that in Fig. 4 in an aqueous environment.

Several groups (10, 48, 49) have suggested that certain amyloid fibrils have β-helical molecular structures, similar to the β-helices observed in proteins such as P.69 pertactin (50). The model in Fig. 4 resembles a β-helix in that C-terminal and N-terminal residues of separate β-strand segments are brought into proximity by bend segments with non-β-strand conformations (especially at glycine residues). In a β-helical version of this model, the C terminus of one Aβ_1–40 chain would contact a residue near the N terminus of the next chain in the cross-β unit. Such contacts have not been established or ruled out experimentally.

Finally, the models of the cross-β unit and the Aβ_1–40 protofilament in Figs. 4 and 5 are likely to be refined as new experimental data become available, such as additional constraints on backbone and sidechain torsion angles and additional constraints on intramolecular and intermolecular sidechain-sidechain contacts. We believe that these models represent substantial progress toward full elucidation of the molecular structure of amyloid fibrils.

Abbreviations

• EM, electron microscopy

• MAS, magic-angle spinning

• fpRFDR, finite-pulse radio-frequency-driven recoupling

• DQCSA, double quantum chemical shift anisotropy

• DLn, nth double labeled sample

• MPL, mass-per-length