A systematic approach to reconstructing transcription networks in Saccharomyces cerevisiae

Abstract

Decomposing regulatory networks into functional modules is a first step toward deciphering the logical structure of complex networks. We propose a systematic approach to reconstructing transcription modules (defined by a transcription factor and its target genes) and identifying conditions/perturbations under which a particular transcription module is activated/deactivated. Our approach integrates information from regulatory sequences, genome-wide mRNA expression data, and functional annotation. We systematically analyzed gene expression profiling experiments in which the yeast cell was subjected to various environmental or genetic perturbations. We were able to construct transcription modules with high specificity and sensitivity for many transcription factors, and predict the activation of these modules under anticipated as well as unexpected conditions. These findings generate testable hypotheses when combined with existing knowledge on signaling pathways and protein–protein interactions. Correlating the activation of a module to a specific perturbation predicts links in the cell's regulatory networks, and examining coactivated modules suggests specific instances of crosstalk between regulatory pathways.

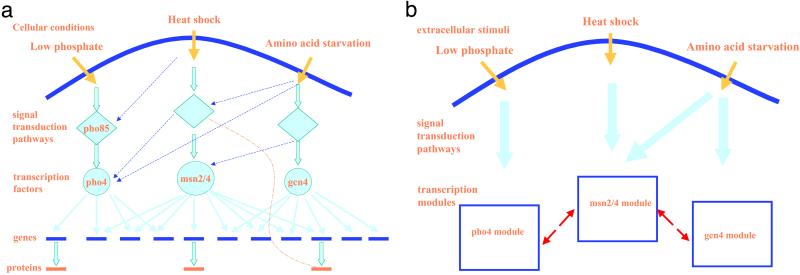
Inference of intracellular regulatory networks is rapidly evolving into one of the major research topics in computational biology (1–5), which is not surprising, because virtually every biological process is constrained by these networks. Many diverse changes in the cellular environment are detected, causing signals to be transduced, ultimately resulting in molecular responses (Fig. 1a). Often, particular transcription factors (TFs) are activated and they recognize, sometimes in a combinatorial fashion, specific DNA segments, called regulatory elements, that generally lie upstream of the coding sequence and regulate transcription of the corresponding genes. The protein products of these genes can interact with other proteins in the same or other signaling pathways, to further tune responses to the extracellular stimuli, producing a variety of potential feedback loops.

Fig 1.

(a) A schematic diagram of the intracellular networks. Solid orange arrows represent detection of different cellular conditions, blue dashed arrows represent possible activation of signaling pathways other than the default one, solid cyan arrows represent transcription factors' regulation of their target genes, and the orange dashed line represents possible protein–protein interactions. (b) Decomposition of the intracellular networks into transcription modules. Solid orange and cyan arrows represent detection and transduction of extracellular signals, respectively, and red dashed arrows represent interactions between transcription modules.

Decomposing the networks into functional modules and defining roles of each gene in a module are logical first steps toward a full understanding of the structure and dynamics of the intracellular networks (Fig. 1b). This study focuses on computationally identifying transcription modules (i.e., a factor and all its target genes), relating each module to the cellular conditions or perturbations that control it, and discovering interactions between such modules, by integrating the DNA sequence, gene function, and gene expression data. In other words, by computing on the basis of these input data, we want to answer the following: (i) Which genes are regulated by a particular TF? (ii) Which TFs are activated by which extracellular stimuli or perturbation to the cell? (iii) Which patterns of gene expression are the results of coactivation (or deactivation) of more than one module under a particular condition or perturbation?

Our approach consists of three steps:

• 1. Identification of transcription modules, which includes two substeps:…A.  Identification of the conserved core of the DNA regulatory motif(s) in the promoter region recognized by a particular TF. For this we use the REDUCER algorithm (6).

• B.  Identification of all of the genes likely to be directly regulated by this TF by using an expression-weighted profile method that we describe below.

• 2. Determination of which transcription modules are activated (or deactivated) under particular experimental conditions. To this end we define a statistic, the X value, that weights genes according to both the expression ratio and the frequency of occurrences of a specific motif. We then correlate X values under varying conditions to those in the absence (by mutation or deletion) or sometimes superabundance (by overexpression) of the transcription factor.

• 3. Inference of interactions between coactivated transcription modules by identifying genes shared by coactivated modules and other annotation information, such as protein–protein interaction and the hierarchy of known signaling pathways, obtained from suitable databases.

We first identify conserved core regulatory motifs in a wide range of microarray experiments by using the REDUCER algorithm recently proposed by Bussemaker et al. (6). REDUCER performs multivariate fitting of motif occurrence to mRNA expression level, to identify core (i.e., generally up to ≈7 bases) regulatory motifs in the promoter region. It does not depend on clustering of gene expression patterns; motifs are determined to be significant or not significant in a single microarray experiment. If the only perturbation in a microarray experiment is deletion or mutation or overexpression of a transcription factor, we call it a transcription factor perturbation experiment (TFPE). The most significant motif identified by REDUCER is usually the regulatory motif recognized by the perturbed TF.

We then enhance the output of REDUCER to more exactly identify both the target genes and the regulatory elements, which may well be longer than 7 bases. To this end, we build a profile for each DNA motif and its flanking regions; unlike the standard profile method, each gene's contribution to the profile is weighted by its mRNA expression in the corresponding experiment. This weighted profile should favor true target genes of the TF. In practice, this profile method seems to greatly reduce the number of apparent false positives found with motif-matching methods alone. In addition, the weighted profile method can also reduce false negatives by allowing identification of those target genes that do not contain an exact core motif.

To identify the conditions that activate a particular transcription module, we compare the gene expression profile of an experiment of interest to that of the TFPE in which the transcription module is indeed activated or deactivated. Instead of comparing the expression of the whole set of genes in the genome, we focus on a subset of genes that are likely targets of the TF. This approach is similar to a local similarity search in sequence alignment. For this purpose, we define our statistic, the X value, which is the product of gene expression ratio (log₂ transformed) and the total number of occurrences of a particular core regulatory motif (i.e., the REDUCER output) in the promoter region (600 bases upstream of the ORF) of a gene. X values for all of the genes form a vector. After we identify the regulatory motif recognized by a particular TF, we calculate the Pearson correlation coefficient between the X value vector for the TFPE and that for another experiment. A significant value for the Pearson correlation coefficient suggests activation/deactivation of the TF under the corresponding condition. The advantage of comparing X value vectors is that all genes regulated by a TF should have the particular regulatory motif and, thus, only these genes have nonzero, presumably large, X values. In this way we reduce the comparison space to a subset of the whole genome, thereby increasing signal-to-noise ratio. Identifying conditions under which a transcription module is active allows us to gain insight into the functions of the module and predict new links in the cell's regulatory networks based on existing knowledge of signaling pathways.

When two transcription modules are both activated under a particular condition, it is possible that they may interact. By examining genes shared by coactivated modules, we can obtain evidence of any combinatorial regulation on the genes' expression by different TFs. Combining this evidence with information on protein–protein interaction, one might be able to predict crosstalk between different signaling pathways.

Methods

The Expression-Weighted Profile Method.

Starting from the core motif identified by REDUCER (6), we extract the sequences matching the core motif and 7 base pairs flanking region at the each end. Thus, the length of the extracted sequence is ≈20 bases, enough to cover informative regions in most known yeast binding sites.

A profile is built for the extracted DNA sequences, while at each position each gene's contribution to the profile is weighted by the mRNA expression ratio of that gene. The probability of nucleic acid z (A or C or G or T) at the ith position of the motif, P_i(z), is calculated as:

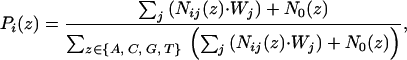where N_ij(z) = 1, if z appears of the jth sequence at the ith position and N_ij(z) = 0 otherwise. N₀(z) is the pseudocount for each type of nucleic acid. We use the background frequencies in the whole genome promoter regions as pseudocounts, i.e., N₀(A) = 0.314, N₀(T) = 0.311, N₀(C) = 0.189, N₀(G) = 0.185; W_j is the weight of the jth sequence and is calculated as:

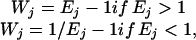where E_j is the expression ratio (not logarithm base 2). W_j represents how much change the jth sequence (gene) has. If one gene has m copies of a motif, the weight of each copy of the motif is W_j/m. This weighting scheme is used to diminish overrepresentation of any single gene.

The profile matrix obtained from Eq. 1 was used to score all subsequences of width of the matrix by using the standard scoring scheme (7), with background frequencies taken as those in the whole genome promoter regions. The best score of each sequence (gene) was taken as its profile score. The distribution of the profile score is approximated by the extreme value distribution, P(x ≥ x₀) = 1 − [1 − ∫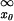 N(x, μ, σ)dx]^m, where P(x ≥ x₀) is the probability by chance the profile score is equal or larger than x₀, N(x, μ, σ) is the distribution of the score over all subsequences that can be approximated by a normal distribution, and m is the number of subsequences for each gene. The threshold x₀ determines the false positive rate, which was 0.01 for this study.

Definition of X Value and Calculation of P Value of Pearson Correlation Coefficient.

To include both expression and sequence information, we define an empirical parameter called X value by using an intuitive weighting scheme:

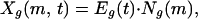where X_g(m, t) is the X value of gene g corresponding to motif m in the experiment t, E_g(t) is the logarithm base 2 of the expression level of gene g in the experiment t, and N_g(m) is the total number of occurrences of the motif m (identified by REDUCER) in the 600 bases upstream of translation start site of gene g.

P value of the Pearson correlation coefficient ρ is estimated by bootstrap. We randomly permutated gene expression in both experiments and number of motif occurrences in each gene. We calculated ρ for 1,000 permutated data and fit the distribution of ρ by a normal distribution. The P value of observed ρ for the real data are calculated based on the normal distribution.

Results and Discussion

Construction of Transcription Modules.

Identification of core regulatory motifs.

We first applied REDUCER to identify significant motifs in the upstream regulatory regions of ORFs in 513 microarrays: 300 were deletion/wild type comparisons (8), 174 derived from time courses under environmental stress (9), 9 were from a time course during sporulation (10), 8 were from experiments studying the metabolism of phosphate (11), and 22 derived from cell cycle synchronization/time course experiments (12). In REDUCER runs, we considered only all possible oligonucleotides up to 7 bases long. Overall, REDUCER identified 1,093 distinct oligonucleotides with lengths between 5 and 7 bases that are significant in one or more microarray measurements. On average, several motifs were identified per microarray measurement and, typically, the number of motifs we found is consistent with the range of the cellular response to the specific condition. For example, a large number of motifs were found under amino acid starvation where the activation of multiple TFs responsible for regulating the synthesis of amino acids is expected. In contrast, only a few motifs (including the Pho4p binding site) were found in the PHO4 mutation experiment. Many previously known regulatory elements were identified under the expected conditions, such as MCB and SCB sites during cell cycle, MSE site during sporulation, the Pho4p site in phosphate metabolism, the Gcn4p site in amino acid starvation and nitrogen depletion, and the STRE site in the general stress response experiments. Many of the 1,093 motifs were consistently identified across multiple time points of the same experiment (e.g., the Gcn4p site across different time points of nitrogen depletion) or across multiple experiments (e.g., the stress response element across all stress response experiments). A large number of these motifs were unknown before; thus, they may represent the binding sites of uncharacterized TFs (complete data available at http://genome-www.stanford.edu/networks).

Twenty-five TFs listed in the SCPD database (13) were studied in the deletion experiments (8) and three known TFs, PHO4, MSN2, and MSN4, were studied in experiments in which they were mutated (11) or overexpressed (9). The significant DNA motifs identified by REDUCER in each above experiment were examined manually. The DNA-binding sites of eight TFs, Gcn4p, Mbp1p, Msn2p, Msn4p, Pho4p, Rtg1p, Ste12p, and Yap1p, were already listed in the SWISS-PROT database (Table 2). All but one (Rtg1p) of these motifs was also identified as the most significant motif in the corresponding TFPE. In the RTG1 deletion experiment, REDUCER identified the binding site of Rtg1p as the second most significant, whereas the STRE element AGGGG was identified as the most significant, which suggests that the cells experienced stress when growing in the absence of Rtg1p. Therefore, for the TFs with known binding sites, REDUCER was able to identify the correct core motif with high specificity in the corresponding TFPE.

Table 2.

TFs and the most significant DNA motif identified by REDUCER in the corresponding TFPE

TF	Motif	P value	Known binding site	Biological process	Activation conditions
GCN4	TGACTCA	10−80	TGA(C/G)TCA	Transcriptional activator of amino	AA, END
	TGAGTCA	10−26		acid biosynthetic genes
MBP1	ACGCGT	10−27	MCB site  ACGCG(T/A)	DNA replication, cell cycle control	CC, DS, LND, mHSdo
MSN2	AGGGG	10−26	AGGGG	Stress response	ES, PHO
MSN4	AGGGG	10−33	AGGGG	Stress response	ES
PHO4	CACGTGG	10−30	CACGTG	Phosphate metabolism	PHO, HOO
RTG1	GGTCACG	10−5	GGTCAC	Interorganelle communication	AA, END
STE12	TGAAAC	10−14	PRE site  TGAAAC(G/A)	Invasive growth, pheromone  induction, pseudohyphal growth	LND
YAP1	TGACTCA	10−8	TGACTCA	Regulation of certain oxygen  detoxification enzymes	AA, END
MAC1	TGCACCC	10−80	Unknown	Cu/Fe utilization, stress resistance	CC, H2O2, SSC, SST
SIN3	CGCGCGC	10−24	Unknown	Transcription	None
TUP1	AGGCAC	10−25	Unknown	Glucose repression	LND, YPD

^*The known binding site of each transcription factor is based on the SWISS-PROT database.

^† Biological process for each transcription factor is taken from the Gene Ontology (GO) Consortium and SWISS-PROT.

^‡ Activation conditions: AA, amino acid starvation; CC, cell cycle; DS, diauxic shift; END, early nitrogen depletion (<8 h); ES, all environmental stresses; H₂O₂, constant 0.32 mM H₂O₂ exposure; HOO, hypoosmotic shock; LND, late nitrogen depletion (≥8 h); mHSdo, mild heat shock from 29 to 33°C at various osmolarities; PHO, phosphate metabolism; SSC, steady-state growth on alternative carbon sources; SST, steady-state growth at various temperatures; YPD, stationary phase in yeast extract/peptone/dextrose medium.

It should be noted that because of the complexity of the cell regulatory networks, the most significant motif identified in a TFPE might not necessarily be the motif directly bound by the factor. Instead, the identified motif might be the binding site of its cofactor or another factor that is activated under the perturbation.

For the remaining 20 transcription factors whose binding sites are unknown (some of the factors may not directly bind to DNA), we found significant motifs in each of the corresponding deletion experiments. Particularly strong motifs were found in the deletion of MAC1 (TGCACCC, P value ≈10⁻⁸⁰), SIN3 (CGCGCGC, P value 10⁻²⁴), and TUP1 (AGGCAC, P value ≈10⁻²⁵ and ACCCC, P value ≈10⁻²⁴). If a motif is the correct binding site of a transcription factor (or a multisubunit aggregate containing the factor), genes containing this motif in the promoter region should have functions (as judged from gene annotations) consistent with the regulatory function of the factor and have significant changes of expression in the corresponding TFPE. Mac1p is a metal-binding transcription activator and critical for regulating iron/copper uptake (14). Many genes involved in iron uptake, e.g., FIT1/2/3, FET3, FTR1, and FRE1/2/3/4/5, containing the motif TGCACCC are up-regulated in the MAC1 deletion experiment. Interestingly, the motif TGCACCC is also recognized by Aft1p, which regulates iron uptake (14). This finding may suggest that MAC1 and AFT1 function together. Sin3p is not a DNA-binding protein itself, but is part of a transcription complex responsible for silencing many genes (15, 16). The motif we found is likely to be the binding site of one of its partners. Tup1p is a general repressor and works together with its cofactors to repress gene expression (17). One of its cofactors, Mig1p, brings the Ssn6p-Tup1p repressor to DNA and represses glucose-repressible genes (17). Using the motif AGGCAC identified by REDUCER, which is not the same as the known Mig1p site, we found that many glucose transporter genes, such as HXT15/16/17, are induced in the TUP1 deletion experiment. We speculate that this motif is the binding site of a different factor or a variant of Mig1p site.

We also screened for DNA motifs in the 3′ region in the 513 microarray measurements. Such motifs are believed to play roles in regulation of mRNA stability (18, 19). REDUCER identified 946 distinct and significant oligonucleotides. Relating 3′ motif occurrence with particular gene deletion may provide insights into proteins involved in mRNA degradation (see http://genome-www.stanford.edu/networks for full data).

Identification of the targets of a TF with high specificity and sensitivity by using the expression-weighted profile method.

We constructed weighted profiles for each of the 28 TFs. We found that we could recover target genes from the TFPE with few apparent false positives. An example is given in Table 1. Genes whose expression ratio changes were >2-fold in the PHO4 mutation experiment were ranked by their weighted profile scores. By choosing relatively conservative cutoffs for both the weighted profile score (P = 0.01) and for minimum expression ratio difference (2-fold here), we ensure a low frequency of false positives.

Table 1.

Target genes of Pho4p identified by the weighted profile method

Rank	Gene	Motif	Expression ratio, log2	Ogawaet al.	Carrollet al.
1	PHO89	AATGCAGCACGTGGGAGACAA	5.262	√	√
2	SPL2	ATGTACGCACGTGGGCGAAAG	4.605	√
3	PHO84	TTTCCAGCACGTGGGGCGGAA	5.491	√	√
4	PHO11	GCGTTCACACGTGGGTTTAAA	4.287	√	√
5	PHO12	GCGTTCACACGTGGGTTTAAA	4.159	√	√
6	VTC4	TCATCCGCACGTGGCTGCACA	3.296	√	√
7	PHO5	GCACTCACACGTGGGACTAGC	2.816	√	√
8	PHM6	TCGCTGACACGTGGGAGGTGG	2.998	√	√
9	PHO8	ATCGCTGCACGTGGCCCGACG	1.546	√	√
10	KRE2	ATCGCTGCACGTGGCCCGACG	1.233
11	VTC3	GAGGGCCCACGTGGCTTAATA	4.297	√	√
12	CTF19	GAGGGCCCACGTGGCTTAATA	1.864	√	√
13	HOR2	TTTACGTCACGTGGGAGGCCC	1.021	√
14	VTC2	CAAGCAGCACGTGGGTTTTTT	1.599	√	√
15	YMR291W	AACCTAACACGTGGAGGTTTT	1.257
16	YLR402W	GAGTTTGCAGGTGGGACTAAT	2.223
17	YAR069C	GTTCACACTCGTGGGGCCCAC	1.438
18	VTC1	ATATTAGCACGTGTCTCGGAG	2.485	√	√
19	CDA1	ATACCAACAAGTGGGTTGATT	1.852
20	CTT1	GACGAGGCACATGGGGATAGA	1.251
21	PHO86	GCGCCCGCACGTGCTCTTTAT	1.356	√	√
22	YJL119C	GCGCCCGCACGTGCTCTTTAT	1.070
23	YJR039W	CCTGTTCCACATGGGCGGTTA	1.876
24	HIS1	GTGTACGCACGTAGCCAACGA	1.275	√

^*Genes experimentally identified as targets of Pho4p by Ogawa et al. (11) or Carroll et al. (20) are marked with checks.

In this example, the profile score cutoff fell between ORFs HIS1 and YAL053W. Therefore, we predicted the top 24 candidates as target genes of Pho4p. It turned out that all but 8 of these 24 genes (Table 1) were previously characterized as PHO-regulated genes (11, 20). Among the 8 remaining putative target genes, YJL119C and PHO86 are a pair of divergently transcribed genes, as are KRE2 and PHO8. Close examination of the data of Ogawa et al. (11) reveals that expressions of YJL119C and KRE2 have >2-fold changes in two and three phosphate metabolism experiments, respectively. YJL119C also has 1.78- and 1.85-fold changes in two low-phosphate vs. high-phosphate experiments. These observations suggest that YJL119C and KRE2 might be regulated by Pho4p as well.

PHO81, YPL110C, PHM5, PHM7, PHM8, and YER038C are also listed as PHO-regulated genes by Ogawa et al. (11) because their expression profiles are similar to other Pho4p target genes. The profile score of PHM5 is close to our cutoff, and thus can be counted as a false negative. The remaining five genes all have <2-fold expression changes in the PHO4 mutation experiment. The profile score of PHO81 is between YAR069C and VTC1, and YPL110C is between VTC2 and YMR291W. The high profile score and low expression change may suggest that these two genes are also regulated by other TFs in the PHO4 mutation experiment. The other three genes, PHM7, PHM8, and YER038C have low profile scores and low expression changes. Our hypothesis is that they are not real primary targets of Pho4p, although they nevertheless play roles in the phosphate-metabolism pathway. PHM7 is experimentally shown not to be a target of Pho4p, and PHM8 is an ambiguous target (D. Wykoff and E. O'Shea, personal communication). Thus for this example, our method appears to have provided additional specificity and identified additional targets of a quite well-studied TF.

The above PHO4 example illustrates the power of the weighted profile method for identifying target genes of a TF. The method identified the true targets of Pho4p with high sensitivity and specificity, given only one microarray measurement (PHO4 mutation). In contrast, clustering-based methods need multiple carefully designed microarray measurements to cluster Pho4p targets. The increased specificity of the weighted profile is because of the additional information in the flanking region. In the PHO4 example, we found several flanking positions with strong base preferences, contributing a total of 3.3 bits of information to the whole profile (equivalent to decreasing false positive matches by a factor of 2^3.3 = 9.8). Similar flanking region information contents were observed for some other profiles constructed from TFPEs. This additional information in the flanking region allows the identification of target genes such as VTC1 and HIS1, which do not have the exact core motif. For comparison, only 0.3 bit of information was obtained from the flanking regions in the PHO4 example if the extended profile was not weighted. It is worth emphasizing that, because target genes of a TF are selected based not only on sequence profile scores but also on their expression changes, transcription modules are context-dependent.

Inference of Activation of a Transcription Module.

To infer which transcription module is activated under what condition, we calculate the Pearson correlation coefficient between the X value vector of the TFPE and those of individual arrays under other conditions. The additional arrays were derived from studies of environmental stress responses (9), sporulation (10), phosphate metabolism (11), and cell cycle (12). Significant correlations were found (Table 2) from which we could make inferences about transcription module activation. We considered a TF activated only when P values of the X vector correlation were <10⁻⁵ in >70% of arrays in a particular experimental condition. Twenty-one conditions were considered and each involved at least four arrays. This stringent requirement was imposed to minimize false positives. We have yet to investigate how much this stringency could be lowered and still produce useful results. The 10 nitrogen depletion arrays were divided into early (<8 h) and late (≥8 h) stages because they appear to reflect substantial biological differences.

Twenty-eight TFs were studied by TFPE. Several TFs were known to be activated under particular conditions; for example, Pho4p under low phosphate, Msn2p and Msn4p under heat shock, Gcn4p under amino acid starvation, and Mbp1p during cell cycle. By using our stringent requirement, all of the above TFs are identified as activated by the corresponding conditions (Table 2), which can be taken as prima facie validation of our method.

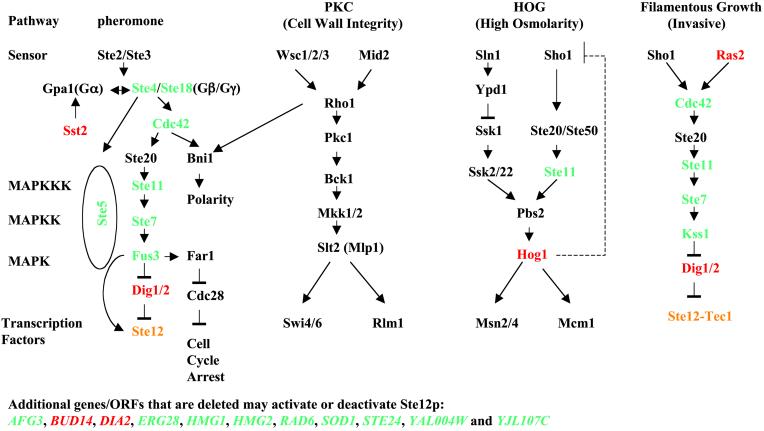
An additional application of our method can be seen in the results. Using X value to examine activation/deactivation of TFs in gene deletion experiments can suggest signaling pathways' new components. For instance, Ste12p is strongly (P < 10⁻²⁰) activated or deactivated by deleting many genes (highlighted in Fig. 2). It is not unexpected that deleting any “upstream” gene in the pheromone and filamentation–invasion pathways can activate or deactivate Ste12p (Fig. 2) (21–24). Although the mechanism is still not clear, the HOG pathway exerts negative regulation on the pheromone pathway (25, 26), which is consistent with our observation that HOG1 deletion activated Ste12p. Several genes, such as CDC42, STE11, STE7, and DIG1/DIG2, participate in more than one pathway. Pathway specificity is thought to be achieved, at least partially, by assembling component proteins with different scaffold proteins responding to different signals, such as assembling Ste11p and Ste7p with Ste5p in responding to a pheromone. Potential crosstalk between pathways might happen if any of these component proteins is deleted. YAL004W and YJL107C are ORFs whose functions are not known; Afg3p, Bud14p, Dia2p, Erg28p, Hmg1p, Hmg2p, Rad6p, Sod1p, and Ste24p were not previously known to be associated with the pheromone-response pathway, but their annotations suggest they may play roles in mating (see SGD, http://genome-www.stanford.edu). Deletion of all above genes except for BUD14 and DIA2 deactivates Ste12p. These observations may shed light on functions of the above genes/ORFs and identify new regulatory mechanisms to pheromone response. The above discussion of Ste12p activation shows that examining activation or deactivation of downstream transcription modules can help identify component proteins of a signaling pathway. Further, when combined with protein–protein interaction data, this strategy can help determine the pathway hierarchy and interactions between pathways.

Fig 2.

Mitogen-activated protein kinase (MAPK) pathways [modified from Roberts et al. (23)]. Genes, if deleted, to activate or deactivate Ste12p, as inferred from X vector comparison, are correspondingly red or green.

In Table 2, we also see unexpected activation of transcription factors. For example, Pho4p appears to be activated in the five hypoosmotic shock experiments, where the P values of the X vector correlation were 10⁻⁹, 10⁻⁹, 10⁻¹², 10⁻²⁴, and 10⁻¹⁴, respectively. Transcription of most (but clearly not all) Pho4p target genes was induced in these experiments. Among the five hypoosmotic shock experiments, the 45-min time point has the highest correlation coefficient, 0.8, and the smallest P value, 10⁻²⁴. In this experiment, among the total of 69 genes with >2-fold up-regulation changes, there are 8 known Pho4p target genes, SPL2, VTC3, PHO12, PHO84, PHO81, VTC1, PHO89, and PHO11. Thus, Pho4p targets are significantly enriched in the subset of 69 genes (expect 0.2, observe 8, chance probability <10⁻²⁰). It is worth mentioning that the activation of Pho4p module in hypoosmotic stress could not have been identified by global correlation. Determining the biological significance of Pho4p activation in hypoosmotic shock will require further experimentation.

In amino acid starvation and the early stage of nitrogen-depletion experiments, our algorithm indicates the activation of Gcn4p, Yap1p, and Rtg1p. It is interesting that these TFs appear not to be activated in the late stage of nitrogen depletion (≥8 h) experiments; instead our algorithm predicts the activation of Mbp1p, Ste12p, and Tup1p. This result suggests that the physiology of the cell after 8 h of nitrogen depletion has been changed significantly. Another interesting observation is the predicted activation of Msn2p, but not Msn4p, in phosphate metabolism studies. It is worth noting that in many gene deletion experiments, the most significant motif was the Gcn4p-binding site. One possibility is that GCN4 is a general regulator playing a wider role than amino acid regulation.

The algorithm also predicts other previously unreported instances of TF activation: Mac1p in H₂O₂ exposure, steady-state growth on various carbon sources, steady-state growth at different temperatures and cell cycle, Tup1p in stationary phase in yeast extract/peptone/dextrose medium, Mbp1p during the diauxic shift, and mild heat shock at various osmolarities. All these remain to be confirmed and studied by future experiments.

Interactions Between Transcription Modules.

There are a number of scenarios in which interactions between modules might occur. Some genes could be regulated by several different modules, leading to combinatorial control and possibly synergistic effects. This mode of interaction can be detected by examining genes shared by different modules. Alternatively, the transcriptional targets of different modules might interact physically through protein–protein interaction, or more interestingly, the targets of one module may interact with the proteins in the pathway upstream of another module (see a schematic sketch in Fig. 1a). To detect these modes of interaction, it may often be necessary to have fuller knowledge of pathways and protein–protein interactions.

As an example, consider the transcriptional response to amino acid starvation. There are four distinguishable modules regulated by Msn2p/4p, Gcn4p, Yap1p, and Rtg1p, respectively. We detected significant overlaps between modules, such as Rtg1 and Msn2/4 modules. This result suggests that genes important in amino acid starvation response are probably regulated by several factors in a combinatorial fashion.

In addition to coregulating genes, the Rtg1 module may also interact with Msn2/4 modules at the protein level. In Munich Information Center for Protein Sequences (MIPS) database (http://mips.gsf.de), a target gene of Rtg1p, SER33, interacts with SER3, which is putatively regulated by Msn2p and Msn4p.

In another example, we observed that a putative target gene of Mbp1p, SPA2, interacts with proteins in the signaling pathway upstream of other TFs. Among proteins that interact with Spa2p (MIPS database), Ste20p, Ste11p, and Ste7p function in the upstream of TF Ste12p in the pheromone and filamentous growth pathways, and Mkk1p, Mkk2p, and Slt2p are involved in the protein kinase C (PKC) pathway, which can activate TFs Swi4/6p complex and Rlm1p (22) (Fig. 2); therefore, activation of one module such as the Mbp1 module may further tune the activity of other transcription modules such as the Ste12 module.

We believe as information on pathways and protein–protein interactions becomes more complete, analyzing interactions between modules along these lines will allow discovery of more links among regulatory networks.

Conclusion

The great challenge in understanding biological complexity is to reconstruct the regulatory networks governing observed patterns of expression. Here we propose a systematic approach to tackle this problem from a new, to our knowledge, perspective, by constructing transcription modules and identifying the conditions under which they are activated. Combined with REDUCER, the expression-weighted profile method can be used to identify transcription modules in a single microarray measurement, which cannot be done by the conventional clustering approach. We were able to use the X value, which combines information from expression data and regulatory sequences, to reveal activation of the same transcription module under different conditions, even when the corresponding expression profiles are “globally” dissimilar. In addition, X value comparison can distinguish activation of different TFs that share the same core regulatory motif, such as Pho4p (CACGTG) and Cbf1p sites (CAYGTGA) (SWISS-PROT), because of the difference between the corresponding expression data. In this study, for simplicity, we constructed X values based on the number of occurrences of core motifs. A potential improvement is to replace the number of core motifs by 1 or 0, depending on whether the gene is in the constructed module or not.

Our results indicate that the binding site and the targets of a TF can be determined, based on a single TFPE using REDUCER and the weighted profile. This finding suggests that microarray profiling of TFPEs for all of the TFs in the genome, followed by our analysis, may be a comprehensive and efficient way to map transcription networks on a genomic scale. It also should be noted that microarray data are only one of many possible inputs. The approach can be extended to analyzing other genome-wide functional data such as protein array data, and of course it can be compared with empirical methods such as chromatin immunoprecipitation followed by DNA array hybridization.

Abbreviations

• TF, transcription factor

• TFPE, TF perturbation experiment