High-throughput screening for evidence of association by using mass spectrometry genotyping on DNA pools

Abstract

To facilitate positional cloning of complex trait susceptibility loci, we are investigating methods to reduce the effort required to identify trait-associated alleles. We examined primer extension analysis by matrix-assisted laser desorption/ionization time-of-flight mass spectrometry to screen single-nucleotide polymorphisms (SNPs) for association by using DNA pools. We tested whether this method can accurately estimate allele frequency differences between pools while maintaining the high-throughput nature of assay design, sample handling, and scoring. We follow up interesting allele frequency differences in pools by genotyping individuals. We tested DNA pools of 182, 228, and 499 individuals using 16 SNPs with minor allele frequencies 0.026–0.486 and allele frequency differences 0.001–0.108 that we had genotyped previously on individuals and 381 SNPs that we had not. Precision, as measured by the average standard deviation among 16 semidependent replicates, was 0.021 ± 0.011 for the 16 SNPs and 0.018 ± 0.008 for the 291/381 SNPs used in further analysis. For the 16 SNPs, the average absolute error in predicting allele frequency differences between pools was 0.009; the largest errors were 0.031, 0.028, and 0.027. We determined that compensating for unequal peak heights in heterozygotes improved precision of allele frequency estimates but had only a very minor effect on accuracy of allele frequency differences between pools. Based on these data and assuming pools of 500 individuals, we conclude that at significance level 0.05 we would have 95% (82%) power to detect population allele frequency differences of 0.07 for control allele frequencies of 0.10 (0.50).

Association studies provide a powerful approach to identify the DNA variants underlying complex traits (1). Currently, association studies can be especially useful for narrowing a complex trait candidate interval identified by linkage analysis (2, 3), although improved genotyping technology and a map of single-nucleotide polymorphisms (SNPs) identifying the common haplotypes in the human genome may enable association studies of loci spanning the entire genome. A rate-limiting step for association studies is to obtain the large number of genotypes needed. Currently, a linkage region expected to contain a complex trait locus typically spans 10–20 Mb, and even with a priori knowledge of the linkage disequilibrium between DNA variants, thousands of densely spaced SNPs with a range of allele frequencies may need to be screened (4). In addition, sample sizes of hundreds or even thousands of individuals may be required to have sufficient power to detect loci with modest effect.

A reliable screening method to identify SNPs associated with disease without genotyping all individuals would be efficient and economical. Screening SNPs by typing a limited number of DNA pools representing cases and controls in principle requires vastly fewer genotypes for each SNP, reducing labor and reagent costs. Genotyping cost becomes essentially independent of sample size, allowing larger, more powerful samples to be studied. In addition, the amount of DNA used from each person for each genotype can be dramatically reduced, an important consideration when DNA samples are limited.

An optimal technique to screen SNPs for association would accurately and precisely identify SNPs that show a difference between cases and controls. Because the major experimental question is not the absolute allele frequencies, but whether there are allele frequency differences between cases and controls, a consistent under- or overestimate of pooled allele frequencies, if modest or correctable, would not preclude a method from use. Several methods for typing SNPs in pooled DNA, including mass spectrometry, have been described (5–21). These methods currently have varying suitability to a high-throughput setting. For many of these methods, the precision and accuracy in estimating allele frequency differences between pools remain to be established, as does the variability associated with pool formation and each stage of the genotyping process.

Primer extension analysis by mass spectrometry is a potentially attractive method for allele frequency estimation based on pools because it can be easily automated. Design of assays based only on local sequence allows automated assay design with uniform assay conditions. This similarity of assay conditions permits extensive use of robotics, which limits human error. Mass spectrometry data collection is fast and automated, based on the size of extended products.

The precision of mass spectrometry has been evaluated in a limited number of studies (19–21). Ross and coworkers (19) tested the quantitative range and detection limits of the technique and were able to quantitate allele frequencies as low as 0.05. Buetow et al. (20) used 81 assays to evaluate precision; when each primer extension reaction was dispensed four times or when each PCR was repeated four times, they observed a median standard deviation (SD) of 0.016 or 0.017, respectively. Werner et al. (21) observed a median SD of 0.017 in artificial pools and 0.016–0.024 for estimates from pools of 94–280 individuals.

We have extended the work of previous studies by assessing the ability of mass spectrometry to reliably estimate allele frequencies in pools and allele frequency differences between pools and by estimating the sources of variability in these estimates. We performed primer extension assays and used spectrotyper software (Sequenom, San Diego) to quantitate allele frequency estimates from relative peak areas. We compared estimated allele frequencies and allele frequency differences to those obtained from typing individual DNA samples for 16 SNPs in three DNA pools of laboratory interest. We also assessed precision in allele frequency estimates for 381 additional SNPs assayed only in pools. We used the estimates of the variability from PCR and primer extension, and product dispensing and mass spectrometry to estimate the power of pooled genotyping and to compare its power with that for genotyping individual samples. The data demonstrate that this method has the necessary characteristics to be used successfully for pooled genotype analysis.

Methods

Study Samples.

The DNA samples used are from participants in the Finland-United States Investigation of Non-Insulin Dependent Diabetes Mellitus Genetics (FUSION) Study, in which we seek to identify genetic variants that predispose to type 2 diabetes or are responsible for variability in diabetes-related quantitative traits. Families were enrolled based on sibling pairs affected with type 2 diabetes (22); controls included 194 nondiabetic spouses of affected family members and 231 unrelated elderly controls. Informed consent was obtained from all participants.

Construction of Case and Control DNA Pools.

We selected samples to create one DNA pool representing cases with type 2 diabetes and two pools representing controls. We selected one affected individual from each of 525 families for a pool designated F1, 194 unaffected spouses for a pool designated SP, and 231 unrelated elderly nondiabetic controls for a pool designated EC. Based on an initial quantitation by spectrophotometer (Beckman DU-640), each sample was diluted to an expected concentration of ≈50 ng/μl and requantitated by using a PicoGreen assay (Molecular Probes) on a fluorometer (Molecular Devices SpectraMAXGeminiXS). Four independent measurements were performed by using the low range standard protocol and the concentrations were averaged. If the independent measurements varied from the mean by >10%, the measurement was repeated. Samples that were determined to have less than the required amount of DNA for each pool were omitted. Based on the concentrations of individual samples, we calculated the volumes needed to obtain equimolar amounts of each sample. We combined samples to create subpools of ≈100 individuals and adjusted the concentration of each subpool to 50 ng/μl by using the same criteria for quantitation as the individual samples. The appropriate subpools were combined and diluted to 10 ng/μl before use. The final pool sizes were 499 individuals for F1, 182 for SP and 228 for EC.

PCR, Primer Extension Reactions, and Mass Spectrometry.

Most PCR primers and primer extension assays were designed by using spectrodesign software (Sequenom) specifying an optimal PCR product of 100 nucleotides with a range of 60–400. SNP assays were designed to generate extension products of different masses, usually by incorporating one dideoxynucleotide or one deoxynucleotide and one dideoxynucleotide, depending on the SNP allele. Primer sequences for the 16 SNPs typed on pools and individuals are available in Table 3, which is published as supporting information on the PNAS web site, www.pnas.org. A set of 381 additional SNPs were typed in pools and on 7–11 individuals as part of a large-scale SNP screening project. Assay designs were uploaded with spectroimporter software (Sequenom). We used 20 ng of genomic DNA as template in 20-μl PCR, all of which was used for a magnetic-bead based isolation of template before performing primer extension reactions using standard conditions as described (23). We used a Spectrojet piezoelectric nanoliter dispensing system (Sequenom) to apply the extension products onto chips prespotted with a matrix of 3-hydroxypicolinic acid (24) and a modified Bruker Biflex III matrix-assisted laser desorption/ionization time-of-flight (MALDI-TOF) mass spectrometer (Sequenom) to determine genotypes by the appearance of peaks corresponding to the expected extension product masses. To minimize variability caused by depurination of extension product peaks, we scanned chips within 24 h after dispensing extension products, although we do not know whether depurination would be unequal between pools and introduce variability.

To genotype individuals for the 16 SNPs, we dispensed primer extension products one time each and set mass spectrometry spectroacquire software (Sequenom) to collect sets of 20 spectra until a genotype could be called unambiguously or five sets of 20 spectra were collected, whichever came first. The 16 SNPs were on average 97% successful (range 94–98%) on the 909 individuals comprising the pools. We routinely performed a limited manual review of spectra to detect and remove questionable individual genotype calls, usually calls with low signal intensity. We genotyped 4 of every 90 samples in duplicate. We have observed an error rate among duplicates of 0.03%.

To genotype pools, we performed four replicate PCRs for each SNP on each pool and dispensed primer extension products onto four spots of a 384-spot chip, yielding a total of 16 observations (four PCRs × four spots per PCR) for each pool for each SNP. We set the mass spectrometry spectroacquire software to collect five sets of 20 spectra and raster to all positions. We obtained peak areas from spectrotyper software by integration of the area under the spectral peak at the expected mass of the extension product.

Review of SNP Assays Tested for Association by Using DNA Pools.

When we tested the 381 novel SNPs on DNA pools, we applied the following criteria to remove poor quality data. We removed spectra with signal-to-noise ratios below 3.5 or with a peak height below 1.0 intensity unit. We removed SNPs for which less than 8 of 16 possible observations remained for any pool or for which the SD of any pool was greater than 0.05. At the same time that we determined SNP genotypes in DNA pools, we genotyped one negative control sample and 7–11 individual samples to help detect assay artifacts. For each individual, we performed a single PCR and dispensed the extension product onto four spots on a chip, yielding a total of four observations per individual. To mimic a high-throughput procedure, we did not select individuals by prior knowledge of genotypes. We discarded SNPs from further analysis if all individuals were heterozygotes, although we recognized that as many as one reliable SNP assay in 2ⁿ, where n is the number of individuals successfully tested, may show all heterozygotes by chance. We also discarded SNPs in which heterozygotes showed widely skewed peak ratios (peak area of one allele at least four times greater than peak area of the other allele), because our experience, as well as that of others (25, 26), suggests that these SNPs are difficult to score correctly. Finally, we discarded SNPs for which observed allele frequencies in heterozygotes differed dramatically from one another (SD > 0.10), because we have found such assays often fail tests of Hardy–Weinberg equilibrium.

Of the original 381 SNPs, 90 (23.6%) failed to meet one or more of the above criteria. A total of 58 (15.2%) had a pool with <8 successful observations, 11 (2.9%) had a pool with allele frequency SD >0.05, 17 (4.5%) had all heterozygous individuals, 11 (2.9%) had severely skewed average heterozygous peak ratios, and 22 (5.8%) had heterozygotes with dramatically different peak ratios.

Statistical Analysis.

Given four PCRs and four spots per PCR, up to 16 observations were available to estimate the allele frequency for each SNP in each pool. For each of these observations, we initially used the pool peak areas A and B of the lower- and higher-mass alleles, respectively, to obtain the pool-based allele frequency estimate p̂= A/(A + B). As an alternative, we adjusted the estimate to take into account the unequal peak area of the two alleles in heterozygotes. To do so, we calculated the sample mean k̂of the ratios a/b, where a and b represent peak areas of the lower- and higher-mass alleles for an individual; we calculated k̂over all measurements on the individuals heterozygous for the SNP. The resulting allele frequency estimate for each of the up to 16 pool-based observations was p̃= A/(A + k̂B) (7). For either of these estimation methods, we then calculated the overall allele frequency estimate as the average of the up to 16 observation-specific estimates. For the 25 (8.6%) of 291 SNPs without data on individual heterozygotes, we used p̂.

To test for allele frequency differences between cases and controls based on our pooled results, we estimated the difference in allele frequencies between case and control pools, and compared this difference to its standard error by using the statistic T = (p̃₁ − p̃₂)/[Var(p̃₁ − p̃₂)]^1/2. Here, p̃_i is the mean estimated allele frequency in group i (1 = case, 2 = control) and Var represents variance.

To estimate Var(p̃₁ − p̃₂), we note that this variance reflects the combined effects of population sampling and measurement error caused by carrying out allele frequency estimation on pools, or Var(p̃₁ − p̃₂) = σ_sampling² + σ_measurement². We estimated the sampling variance by s_sampling² = p̃₁₂(1 − p̃₁₂)/[1/(2n₁) + 1/(2n₂)], where p̃₁₂ = (n₁p̃₁ + n₂p̃₂)/(n₁ + n₂) is the weighted average of the case and control allele frequency estimates and n_i is the number of individuals in pool i.

We modeled the measurement error caused by allele frequency estimation based on pools as σ_measurement² = σ_pcr² + σ_spot². Here, σ_pcr² and σ_spot² are variances caused by PCR and primer extension, and sample dispensing and mass spectrometry analysis, respectively. We estimated σ_pcr² and σ_spot² for each SNP with a mixed effects analysis of variance by using the MIXED procedure in sas (SAS Institute, Cary, NC). In this analysis, allele frequency estimate was the response variable, indicators for each pool were included as fixed effects, and PCR was included as a random effect nested within pool. By specifying this model, we implicitly assume the absence of variability caused by pool construction. Because we did not construct multiple pools for each sample, we could not estimate this variability directly. Subsequent data analysis suggests this variability is modest and that assuming its absence has not significantly adversely affected our test (see Results).

Given n_pcr,i PCRs and n_spot,i spots for group i = 1, 2 (in the absence of missing data, n_pcr,i = 4 and n_spot,i = 16), replicate measurements result in an overall variance estimate of Vãr(p̃₁ − p̃₂) = s_sampling² + s_pcr² (1/n_pcr,1 + 1/n_pcr,2) + s_spot² (1/n_spot,1 + 1/n_spot,2).

We estimated the false positive rate and power to detect significant allele frequency differences between pools by computer simulation. Each simulated pool contained 200 or 500 individuals, had control allele frequencies of 0.10, 0.50, or 0.80, and had case-control allele frequency differences of 0.00, 0.05, 0.07, or 0.10. For each replicate, we simulated observations for case and control pools with four PCRs per pool and four spots per PCR and for a single heterozygote with one PCR and four spots per PCR. For each set of simulation replicates, the heterozygous individuals were assigned a mean k value of 1.00, 1.29, 1.50, 2.40, or 4.00, and a SD for k of 0.11, as we observed in our data. We assumed PCR and spot variability were absent (corresponding to individual genotyping) or were equal to their estimated values of 1.18 × 10⁻⁴ and 3.82 × 10⁻⁴, respectively, as observed in our data.

Results

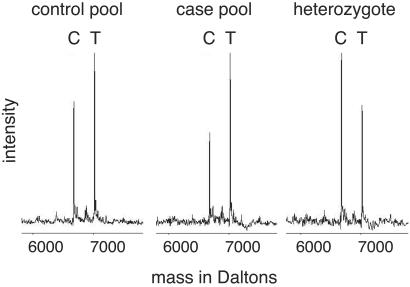
To assess whether the SNP genotyping method of primer extension–mass spectrometry was sufficiently accurate and precise to detect modest allele frequency differences between pools, we tested 16 SNPs with individual genotypes previously determined as part of our diabetes research project. These SNPs were selected to have a range of minor allele frequencies and frequency differences between cases of type 2 diabetes, unaffected spouse controls, and unaffected elderly controls. The frequency differences of 0.001–0.108 are modest but reflect our intention to use pooling to scan for association in complex diseases, where allele frequency differences are not expected to be dramatic. The 16 assays were not individually optimized, although they were chosen from a set of assays that had been successfully typed on >94% of individuals comprising the pools. We tested each DNA pool with quadruplicate PCR and extension reactions, each of which we dispensed and scanned four times for a total of up to 16 frequency estimates per SNP-pool combination. Over the course of our initial studies, we observed that increased peak intensity and signal-to-noise ratio decreased SDs between replicates (data not shown); for this analysis, we dispensed sample twice onto each spot before scanning. Example spectra are shown in Fig. 1. We observed unequal allele intensity in heterozygous individuals, a characteristic that has been described (25) and that we have observed for individual heterozygous samples with most of the hundreds of SNPs that we have typed on individual samples.

Fig 1.

Sample spectra and frequency estimates based on the peak area. Frequency estimates of the C allele are 0.424 and 0.355 in the control and case pools, respectively, showing a difference of 0.069. Given the C allele frequency is overestimated in the heterozygote as 0.570, allele frequencies in the pools can be adjusted to 0.357 and 0.293, respectively. True frequencies of the C allele based on genotyping of the individuals comprising the pools are 0.377 and 0.313 for the controls and cases, respectively, so the estimate of allele frequency difference from the pool analysis is very accurate. In practice, we estimate pooled allele frequencies and the heterozygote ratio from multiple replicate observations, rather than from the single observations used here for purposes of illustration.

We calculated allele frequency estimates both with (p̃) and without (p̂) adjustment for unequal peak heights in heterozygotes, and compared the accuracy with which these two pool-based methods estimated allele frequencies. The average heterozygote ratio k = a/b for the 16 SNPs was 1.19 ± 0.18, whereas the average SD of k was 0.12 ± 0.05. The absolute average difference between pool-based and individual-based allele frequency estimates was 0.033 ± 0.021 (range 0.001–0.083) for p̂ and 0.014 ± 0.010 (range 0.000–0.037) for p̃, suggesting that adjustment resulted in more accurate allele frequency estimates. We use the heterozygote-adjusted allele frequency data in what follows unless otherwise noted. Table 1 shows the minor allele frequency estimates for 16 SNPs in three pools as well as the corresponding estimates obtained from individual genotypes. The average allele frequency SD we observed for up to 16 replicate values from 48 SNP-pool combinations was 0.021 ± 0.011, and the maximum SDs were 0.073, 0.049, and 0.035.

Table 1.

Frequencies of SNPs as estimated by genotyping DNA pools and individual samples

SNP	Cases (F1)		Spouses (SP)		Elderly controls (EC)		Prediction error
	Indiv	Pool	Indiv	Pool	Indiv	Pool	F1–SP	F1–EC	SP–EC
GLUT10_14	0.035	0.028  ± 0.009	0.036	0.026  ± 0.009	0.026	0.015  ± 0.010	0.003	0.005	0.001
GLUT10_1	0.057	0.046  ± 0.011	0.063	0.043  ± 0.018	0.078	0.060  ± 0.012	0.009	0.007	0.001
SNP63	0.118	0.125  ± 0.013	0.120	0.125  ± 0.011	0.115	0.119  ± 0.010	0.002	0.004	0.002
PPARg2	0.145	0.182  ± 0.016	0.194	0.230  ± 0.017	0.224	0.252  ± 0.023	0.001	0.008	0.007
ss146316	0.146	0.128  ± 0.019	0.135	0.103  ± 0.022	0.095	0.067  ± 0.020	0.014	0.010	0.004
ss121557	0.156	0.140  ± 0.014	0.141	0.115  ± 0.009	0.115	0.089  ± 0.015	0.009	0.009	0.000
ss146317	0.176	0.165  ± 0.024	0.146	0.144  ± 0.012	0.130	0.118  ± 0.022	0.009	0.001	0.010
ss93115	0.236	0.251  ± 0.012	0.251	0.249  ± 0.021	0.312	0.317  ± 0.032	0.017	0.009	0.008
SNP43	0.257	0.286  ± 0.032	0.259	0.274  ± 0.049	0.246	0.246  ± 0.073	0.014	0.028	0.015
ss64248	0.309	0.298  ± 0.023	0.316	0.311  ± 0.024	0.312	0.317  ± 0.027	0.007	0.016	0.010
ss1304220	0.313	0.318  ± 0.021	0.379	0.399  ± 0.020	0.377	0.395  ± 0.021	0.015	0.013	0.002
ss121556	0.382	0.381  ± 0.026	0.409	0.405  ± 0.021	0.462	0.448  ± 0.021	0.003	0.013	0.010
ss148393	0.429	0.428  ± 0.010	0.392	0.389  ± 0.012	0.348	0.352  ± 0.013	0.002	0.005	0.007
ss86782	0.433	0.423  ± 0.034	0.442	0.459  ± 0.028	0.443	0.429  ± 0.027	0.027	0.004	0.031
SNP56	0.438	0.456  ± 0.016	0.428	0.446  ± 0.016	0.415	0.437  ± 0.021	0.000	0.004	0.004
ss86876	0.486	0.488  ± 0.035	0.428	0.404  ± 0.029	0.378	0.361  ± 0.028	0.026	0.019	0.007

F1, cases of type 2 diabetes; SP, unaffected spouses; EC, elderly nondiabetic controls; Indiv, individuals. Frequencies for pools are mean ± SD. Prediction error is the absolute difference of the frequency estimates based on pools compared to individual genotypes.

We compared the SD from the 16 SNPs to a larger number of SNPs that were not typed on the individuals comprising the pools. For the 291 additional SNPs that met our criteria for analysis (see Methods), we observed an average SD from the 873 SNP-pool combinations of 0.018 ± 0.008. The average heterozygote ratio k in the sample of 266 of 291 SNPs with at least one heterozygous individual was 1.29 ± 0.39, whereas the average SD of k was 0.11 ± 0.07.

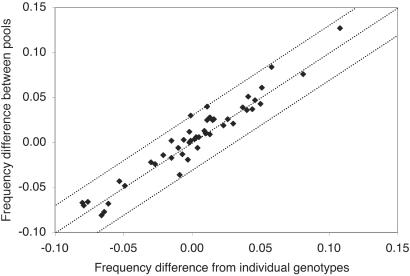
For the 16 SNPs, we compared the estimated allele frequency differences based on case and control pools to frequency differences estimated from genotyping individuals comprising the pools (Table 1, Fig. 2). The mean absolute error in estimating the allele frequency difference between pools calculated from 48 SNP-pool comparisons was 0.009 ± 0.008, and the maximum absolute errors were 0.031, 0.028, and 0.027. The mean absolute error was unchanged (0.009 ± 0.008) when the allele frequencies were not adjusted for the heterozygote ratio.

Fig 2.

Comparison of allele frequency difference estimated from pools to the frequency difference determined from individual genotypes. Each point represents one comparison between F1 and SP, F1 and EC, or SP and EC for 1 of the 16 SNPs. The lines represent the expected result ± 0.03.

We combined the data from the 16 SNPs to estimate the sources of experimental variability and to compare the experimental variability to the sampling variability associated with selecting individuals from the population. The estimated measurement variance caused by PCR or primer extension (s_pcr² = 1.18 × 10⁻⁴) is smaller than that caused by sample dispensing and mass spectrometry analysis (s_spot² = 3.82 × 10⁻⁴). For a pool with n = 500 and allele frequency of 0.50, the summed measurement variances of (1.18 + 3.82) × 10⁻⁴ = 5.00 × 10⁻⁴ are larger than the sampling variability of (0.50)(0.50)/[2 (500)] = 2.5 × 10⁻⁴, but replicate PCRs and spots allow us to reduce the measurement variability substantially. For example, when n_pcr = 4 and n_spot = 16 (4 PCRs × 4 spots per PCR), measurement variability is reduced to (1.18/4 + 3.82/16) × 10⁻⁴ = 0.53 × 10⁻⁴. Sampling variability of allele frequency estimates is an unavoidable consequence of a finite pool size.

Under the conservative assumption that the 291 additional SNPs would be expected to show no association with diabetes, they provide an opportunity to assess empirically the false positive rate associated with our pool-based test statistic T. Based on the 266 SNPs with at least one typed heterozygous individual, we have 2 × 266 = 532 case-control comparisons and so would expect 532 × 0.05 = 26.6 comparisons significant at the 0.05 level. When basing our test on p̃(adjusting for the heterozygote ratio k), we observed 24 (4.5%) comparisons significant at the 0.05 level. When we omitted adjustment for k and used p̂, we observed 26 (4.9%) significant comparisons, 22 of which were also observed in the significance test based on p̃.

We estimated by computer simulation the power to detect case-control allele frequency differences of 0.05, 0.07, and 0.10 by using samples of 200 and 500 cases and controls given either individual genotyping or genotyping of pools (Table 2). Our calculations for pools assume four PCRs per pool and four spots per PCR, and that σ_pcr² and σ_spot² are equal to their mean values estimated for the 16 SNPs. Our results suggest only modest decreases in power for pool-based analyses compared with individual-based analyses. For example, the power to detect a 0.07 allele frequency difference between cases and controls at a 0.50 control allele frequency was 82% given genotyping of two pools with 16 replicates each and 87% given genotyping of 500 × 2 = 1,000 individuals.

Table 2.

Power (%) of pools and individually typed samples to detect 0.05–0.10 allele frequency differences in cases and controls at significance level 0.05

n	Method	Case-control difference
		Control allele frequency = 0.10			Control allele frequency = 0.50
		0.05	0.07	0.10	0.05	0.07	0.10
200	Pool	48	75	94	28	48	78
	Individual	55	81	97	32	52	80
500	Pool	78	95	100	55	81	97
	Individual	92	99	100	61	87	98

Power was estimated by computer simulation assuming k = 1.29, σ_PCR² = 1.18 × 10⁻⁴ and σ_spot² = 3.82 × 10⁻⁴, and four PCRs and four spots per PCR for each pool replicate.

Discussion

Primer extension analysis by mass spectrometry successfully estimates allele frequency differences between DNA pools with sufficient accuracy and precision to be used as a screening step in large-scale association studies. To test a large number of SNPs on pools, automated assay design, standard assay conditions, and automated data collection are critical. We sought to develop standard methods and quality control criteria that would enable us to screen SNPs accurately and quickly.

Compared with an association study based on genotypes of individuals, a pooled DNA association study offers advantages and disadvantages. The primary advantages are the reduced reagent and labor costs and time required to generate fewer genotypes. In addition, less DNA per sample is used per genotype when the sample is included in a DNA pool. In our laboratory, DNA pooling offers an ≈32-fold savings in reagent cost and an ≈16-fold savings in labor compared with our higher-throughput method for typing individual samples. Because pooling must result in some loss of information, including loss of haplotype information, either a larger sample or a less significant detection threshold is required to achieve power comparable to that for genotyping individuals (Table 2).

Our current high-throughout pooling analysis follows a three-step design. First, we test SNP assays without replication on a crudely quantitated DNA pool to confirm that the assay design succeeds and that the SNP minor allele frequency is >0.05. This practice limits the use of our valuable carefully quantitated pools to successful SNP assays. Although some SNP assays fail under standard conditions, we prefer to develop quality control criteria to discard SNPs rather than spend time adjusting assay conditions, because our purpose is high-throughput screening. Second, we genotype each successful SNP on case and control pools and 7–11 individuals. For each pool, we carry out 16 replicate genotypes. We discard SNP assays if we detect any evidence of an artifact (see Methods) or if the SD of the 16 replicates is >0.05. Third, we follow up SNPs identified as interesting by this pooling technique by genotyping individual samples to verify allele frequency differences and to allow haplotype analysis and genotype-based phenotypic comparisons.

In comparison to other SNP genotyping methods for screening DNA pools for association, primer extension–mass spectrometry is reasonably precise. The average allele frequency SD of 0.018–0.021 we report is similar to the 0.021 reported for kinetic PCR (11), slightly greater than the 0.014 reported for primer extension-denaturing high-performance liquid chromatography (9), the 0.009–0.017 reported for fluorescent nucleotide primer extension-capillary electrophoresis (14, 18), and the 0.011 reported for pyrosequencing (17), and less than the 0.038 reported for bioluminometric-primer extension (13). Further, mass spectrometry offers advantages in the potential for automation over several of these other methods.

For the 266 SNPs with at least one genotyped heterozygote, we observed significant results from both adjusted (4.5%) and unadjusted (4.9%) pool allele frequencies that were consistent with the expected false positive rates under the null hypothesis of no association, 5%. These results, although limited, suggest that our test is not particularly anticonservative, despite our decision to ignore variability owing to pool construction. Our simulations suggested that adjusting for k, even based on just a single heterozygote, was adequate to preserve the expected false positive rates. In the absence of adjustment for k, our simulations showed that the tests were either conservative or anticonservative, depending on the underlying allele frequency. This finding, especially in light of the value of individuals in quality control assessment, suggests that typing of a limited number of individuals is a useful component for pooling studies.

To assess the potential of mass spectrometry to screen for allele frequency differences between pools efficiently, we assessed the sources of variability in our approach. Experimental variability originates during pool construction, PCR, primer extension, product dispensing onto a chip, and mass spectrometer data collection. During pool construction, variability can arise if DNA concentrations are incorrect or pipetting is inaccurate. During PCR, variability may arise from unequal allele amplification given additional SNP(s) under the primer(s), simultaneous amplification of two SNPs, inaccurate pipetting of template DNA or reagents between wells, unequal PCR conditions between wells, and sample contamination. During primer extension, variability may be caused by differential incorporation of nucleotides and allele pausing, in which the primer for the two-nucleotide extension incorporates only the deoxynucleotide without addition of the final dideoxynucleotide. During product dispensing and mass spectrometer data collection, variability can arise because of incorporated baseline noise, especially at low peak intensity, decay of detection sensitivity with increasing mass, and inconsistent desorption and ionization.

Based on our study of 16 SNPs, we estimated variances of 1.18 × 10⁻⁴ caused by PCR or primer extension and 3.82 × 10⁻⁴ caused by product dispensing and data collection. To reduce this measurement variability, we performed four replicate PCR and primer extension reactions and dispensed each product with four replicates for mass spectrometry analysis. Depending on the desired level of accuracy, more or fewer of either replicate type could be undertaken. The appropriate replicate number depends on numbers of individuals in each pool. Carrying out many replicates to reduce experimental variability will have little practical value if sampling variability is much greater than experimental variability.

Because we only constructed each DNA pool once, we could not directly estimate the variance caused by pool construction. The fact that ignoring this variability did not appear to result in a strongly anti-conservative test suggests that, at least for our pools, this variability probably is small. This assumption could be tested directly by the construction of multiple pool replicates, but at the expense of considerable time and effort.

Determining the optimum number of pools for a given case or control sample, whether replicates or smaller pools, should also take into account the theoretical limit on the maximum number of individual DNA templates that can be assayed from any one pool. Given samples of 20 ng of pooled DNA and ≈13.4 picograms per diploid genome, chromosomes from a maximum of ≈1,500 individuals (20,000/13.4) can be represented once as template for PCR. If <20 ng of DNA is used, even fewer samples could be measured in pools. Samples of >1,000 case and control individuals would be desirable for complex disease association studies because of the decreased variability caused by sampling from the population. To effectively test a very large sample, the individual DNAs could be combined into several pools with fewer individuals or additional PCRs could be performed.

In conclusion, we have determined that primer extension analysis by mass spectrometry, with appropriate replication, is sufficiently accurate and precise to allow comparison of allele frequency differences between DNA pools. For studies that aim to compare genotypes in hundreds or thousands of case and controls, this approach offers fast, reliable screening of a candidate region with savings of labor, DNA, and reagent costs compared with genotyping individuals. With the expected development of a haplotype map of the human genome (4), yielding a set of 200,000–300,000 “gold standard” SNPs that allow whole genome association studies to become a reality, the pooling approach may allow large-scale analysis of the genetics of common disease at acceptable genotyping costs.

Abbreviations

• SNP, single-nucleotide polymorphism