Mutational analysis of the structural organization of polyglutamine aggregates

Abstract

The formation of amyloid-like aggregates by expanded polyglutamine (polyGln) sequences is suspected to play a critical role in the neuropathology of Huntington's disease and other expanded CAG-repeat diseases. To probe the folding of the polyGln sequence in the aggregate, we replaced Gln–Gln pairs at different sequence intervals with Pro–Gly pairs, elements that are compatible with β-turn formation and incompatible with β-extended chain. We find that PGQ₉ and PGQ₁₀, peptides consisting of four Q₉ or Q₁₀ elements interspersed with PG elements, undergo spontaneous aggregation as efficiently as a Q₄₅ sequence, whereas the corresponding PGQ₇ and PGQ₈ peptides aggregate much less readily. Furthermore, a P_DGQ₉ sequence containing d-prolines aggregates more efficiently than the peptide with l-prolines, consistent with β-turn formation in aggregate structure. Introduction of one additional Pro residue in the center of a Q₉ element within PGQ₉ completely blocks the peptide's ability to aggregate. This strongly suggests that the Q₉ elements are required to be in extended chain for efficient aggregation to occur. We determined the critical nucleus for aggregation nucleation of the PGQ₉ peptide to be one, a result identical to that for unbroken polyGln sequences. The PGQ_N peptide aggregates are structurally quite similar to Q₄₅ aggregates, as judged by heterologous seeding aggregation kinetics, recognition by an anti-polyGln aggregate antibody, and electron microscopy. The results suggest that polyGln aggregate structure consists of alternating elements of extended chain and turn. In the future it should be possible to conduct detailed and interpretable mutational studies in the PGQ₉ background.

Polyglutamine (polyGln) sequences of unknown function are found in a variety of normal proteins (1). In humans, eight of these proteins containing particularly long polyGln repeats are responsible for a family of hereditary neurodegenerative diseases, including Huntington's disease (2). In all of these diseases the genetic defect is the expansion of the CAG repeat encoding the polyGln sequence, which leads to a corresponding increase in polyGln repeat length. The shortest polyGln repeat length associated with disease risk is in the 35–40 range for all but one of these diseases (3), suggesting that the fundamental pathological driving force is related to a critical change in some property of the polyGln sequence as length increases through this threshold range.

One possible molecular basis for the repeat-length dependence of disease risk is the relationship between polyGln sequence length and aggregation. Intraneuronal inclusions staining with antibodies against the disease protein (such as huntingtin), polyGln, and/or ubiquitin are observed in both cellular and animal models of the disease (4, 5) and in patient tissue (5, 6). In some models, but not all, the appearance of aggregates corresponds to the onset of pathology (2, 7). Cells die when in vitro-produced polyGln aggregates are delivered into their nuclei (8). The length dependence of the aggregation kinetics (9–11) closely mirrors the repeat-length dependence of disease risk.

Given the suspected relevance of aggregation to these diseases, it is important to better understand the assembly and structures of polyGln aggregates. As with other protein aggregates, however, high-resolution structure analysis of polyGln aggregates is complicated by their large and heterogeneous sizes and their low solubilities. Soluble polyGln sequences both above and below the pathological repeat length threshold exhibit statistical coil CD spectra (10, 12, 13). In contrast, aggregated polyGln peptides exhibit strong β-sheet CD spectra (10, 11, 14). In electron microscopy (EM), polyGln aggregates exhibit a variety of fibrillar morphologies, including structures resembling amyloid fibrils (9, 14). Consistent with an amyloid-like structure, polyGln aggregates bind and shift the fluorescence spectrum of thioflavin T (ThT) and also bind amyloid-specific monoclonal antibodies (14). PolyGln aggregation kinetics also feature lag phases that can be abbreviated by seeding (11, 14, 15), in analogy to amyloidogenic peptides such as Aβ (16). Except for the fact that polyGln aggregates are rich in β-sheet, little is known about the folded structure of a polyGln peptide in the aggregated state. Details of amyloid structure in fibrils of the Alzheimer's peptide Aβ have been obtained using techniques such as fragment studies (17), limited proteolysis (18), chemical modification (19), hydrogen-deuterium exchange (20), and mutagenesis coupled with kinetics or structural studies (21, 22). Unfortunately, because of its homopolymeric nature, similar studies on polyGln sequences are not straightforward.

To test the hypothesis that the basic fold within the polyGln aggregate is composed of elements of antiparallel β-sheet, we introduced Pro–Gly pairs at different intervals along the polyGln sequence. Pro-Gly sequences are expected to favor β-turns (23) while avoiding β-sheet extended chains. Proline residues are strongly disfavored in interior strands of β-sheet,‡ are only rarely found in amyloidogenic sequences (25), and very efficiently block amyloid formation when inserted into amyloidogenic sequences (25). These observations led to the suggestion that Pro residues might have been used in molecular evolution to suppress off-pathway aggregation (25, 26), and to the use of scanning proline mutagenesis to evaluate amyloidogenic sequences (25, 27, 28).

Results presented here help place constraints on structural models of the polyGln aggregate and provide a sequence context for conducting interpretable mutational studies in the future.

Materials and Methods

Materials.

Peptides, including Aβ(1–40), were custom-synthesized by solid phase chemistry at the Keck Biotechnology Center at Yale University. Flanking pairs of lysine residues were incorporated to enhance solubility of the polyGln peptides (14). PolyGln peptides were subjected to a protocol (29) that rigorously removes aggregates while leaving the peptides chemically intact and structurally indistinguishable from biosynthetic polyGln (12, 13). Collagen I was purchased from Sigma.

Table 1 lists the polyGln peptides used in this study. As described in Results, peptides were designed with periodic substitutions of a Pro–Gly couple for a Gln–Gln couple to disallow extended chain formation and encourage turn formation at these positions. Most of the peptides are derivatives of PGQ₉, which consists of four Q₉ stretches interspersed with PG pairs. If this formula had been precisely followed for each of the different Q_N lengths tested, the total length of the sequences would have increased in steps of four throughout the series, simultaneously introducing variations in Q_N length and total length that would complicate the interpretation of results. In an attempt to minimize total length variation in the series, we included for the PGQ₇ and PGQ₈ peptides additional Gln residues, after the fourth designated β-turn, so that the total peptide lengths were identical to PGQ₉. In contrast, PGQ₁₀ was designed with four equivalent Q_N elements, despite the concomitant increase in length, because to decrease one of the four Q_N strands by four residues might have unduly diminished its aggregation potential. We consider these to be imperfect solutions to the dilemma of not being able to vary Q_N length independent of total length.

Table 1.

Structures of Pro-Gly mutants of polyglutamine

Abbreviation	Sequence	Total sequence length (extended-chain length)
PGQ7	K2-Q7-PG-Q7-PG-Q7-PG-Q7-PG-Q6-K2	46 (5)
PGQ8	K2-Q8-PG-Q8-PG-Q8-PG-Q8-PG-Q2-K2	46 (6)
PGQ9	K2-Q9-PG-Q9-PG-Q9-PG-Q9-K2	46 (7)
PGQ10	K2-Q10-PG-Q10-PG-Q10-PG-Q10-K2	50 (8)
PDGQ9	K2-Q9-PDG-Q9-PDG-Q9-PDG-Q9-K2	46 (7)
PGQ9(P1)	K2-Q4PQ4-PG-Q9-PG-Q9-PG-Q9-K2	46 (7)
PGQ9(P2)	K2-Q9-PG-Q4PQ4-PG-Q9-PG-Q9-K2	46 (7)
PGQ9(P1,2)	K2-Q4PQ4-PG-Q4PQ4-PG-Q9-PG-Q9-K2	46 (7)
PGQ9(P2,4)	K2-Q9-PG-Q4PQ4-PG-Q9-PG-Q4PQ4-K2	46 (7)
PGQ9(P2,3)	K2-Q9-PG-Q4PQ4-PG-Q4PQ4-PG-Q9-K2	46 (7)
PGQ9(P3,4)	K2-Q9-PG-Q9-PG-Q4PQ4-PG-Q4PQ4-K2	46 (7)
Q15PQ26	K2-Q15-P-Q26-K2	46
Q45	K2-Q45-K2	49

^*Extended-chain length based on the assumption of β-turns containing -QPGQ- elements.

Aggregates for seeding and for antibody studies were prepared as follows. Peptide was disaggregated, suspended in PBS containing 0.05% sodium azide (PBSA), and incubated at 37°C until the aggregation had gone to completion, as judged by the ThT reaction. Aggregates were collected by centrifugation (14,000 rpm, 25 min, Eppendorf microfuge) and resuspended in a small volume of PBS. An aliquot of this suspension was dissolved (29) and an aliquot injected onto HPLC to determine the concentration of polyGln aggregate.

Aggregation Kinetics Measurements.

Kinetics were followed as previously described, by a combination of light scattering, ThT fluorescence, and peptide solubility in an HPLC assay (10, 11, 14). Light scattering measurements were performed on a Perkin–Elmer LS50B luminescence spectrophotometer (emission and excitation wavelength, 450 nm; slit width, 2 nm). The ThT binding assay was carried out by adding 10 μl of a 2.5-mM ThT solution to a cuvette containing 300 μl of the peptide suspension [excitation wavelength, 450 nm (slit width, 5 nm); emission wavelength, 489 nm (slit width, 10 nm)]. Soluble peptide was quantified by centrifuging aliquots from the aggregation reaction at 14,000 rpm for 25 min, subjecting an aliquot of the supernatant to analytical reverse-phase HPLC, and converting the peptide peak area (A₂₁₅) to micrograms of peptide by using a polyGln standard curve (14).

For spontaneous aggregation kinetics, freshly disaggregated peptide solutions in pH 3 water were adjusted to various concentrations in PBSA. Reaction mixtures were tested immediately for light scattering, ThT fluorescence, and soluble peptide concentration, and the peptide solutions were then incubated in a 37°C incubator oven. Time points were analyzed as described above. Seeded aggregation kinetics were determined similarly, except that aggregate stock suspensions were first sonicated with five successive pulses of 20 s each on ice with a probe sonicator, and aliquots of the sonicated stocks (enough to deliver 5% by weight of aggregate compared with total peptide) were delivered to peptide solutions at t = 0 to initiate seeded polymerization.

Antibody Binding.

Assays were conducted as described previously for binding of antiamyloid antibodies to amyloid fibrils (30). The antibody used here, PGA11, is a monoclonal IgM generated from a mouse immunized with a polyGln aggregate and screened for the ability to bind to aggregated, and not monomeric, polyGln. Aβ(1–40) amyloid fibrils were prepared as described (30). High-binding microtiter plates (Costar) were coated with 200 ng per well of aggregate and blocked with 1% BSA in PBSA. The amount of PGA11 bound was detected using a 1:5,000 dilution of biotinylated goat anti-mouse antibody (Sigma), and the biotin was quantified using a 1:1,000 dilution of europium–streptavidin complex, with europium quantified on a Victor² time-resolved fluorescence microtiter plate reader (both reagent and instrument from Perkin–Elmer Wallac).

EM.

Aggregates were adsorbed onto carbon and formavar-coated copper grids, then negatively stained with 0.5% uranyl acetate solution. Stained samples were examined and photographed on a H-600 electron microscope (Hitachi, Tokyo) at the microscopy center at the University of Tennessee Division of Biology.

Results

Aggregation Kinetics.

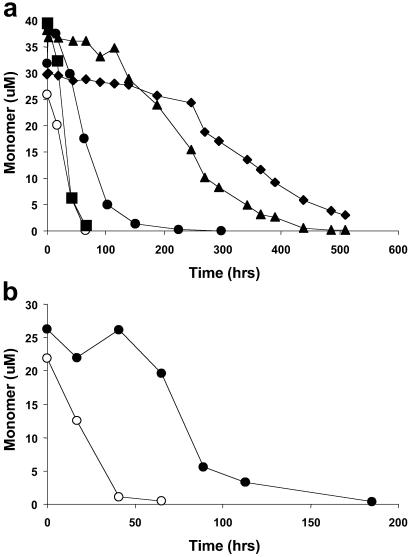
To test the hypothesis that the polyGln aggregation nucleus and repeat unit consists of some arrangement of a four-stranded antiparallel β-sheet, we designed the peptide PGQ₉, in which PG pairs alternate with Q₉ elements, yielding a total of four Q₉ elements in a mutated polyGln sequence spanning 42 residues [plus four flanking Lys residues for solubility (14)] (Table 1). Because single Q residues at each end of the Q₉ repeat would be expected to contribute to the β-turns (i.e., as QPGQ sequences), the length of the extended chain between turns in this design is predicted to be no more than 7 (Table 1). Despite the introduction of a total of three Pro residues into this sequence, PGQ₉ rapidly aggregates in PBS at 37°C with kinetics very similar to those of an unbroken Q₄₅ peptide (Fig. 1). This tolerance for appropriately placed Pro residues is in contrast to the elimination of amyloid formation when a Pro residue is placed in a presumed extended-chain region of an amyloidogenic polypeptide (25, 27, 28). The simplest explanation for the ability of PGQ₉ to form aggregates so readily is that the peptide folds in the aggregate in such as way as to place the PG elements into turn regions where they are tolerated (23). This hypothesis is further supported by the observation that replacing the PGs in PGQ₉ with P_DGs, which have a stronger preference for β-turns (23), enhances the aggregation efficiency of the peptide (Fig. 1b).

Fig 1.

Spontaneous aggregation kinetics of polyGln peptides in PBSA at 37°C monitored by the decrease in the concentration of soluble peptide. (a) Q₄₅ (○), PGQ₇ (⧫), PGQ₈ (▴), PGQ₉ (•), PGQ₁₀ (▪). (b) PGQ₉ (•), P_DGQ₉ (○).

To further test this hypothesis and to probe for the optimum length of extended chain between the turns, we designed the peptides PGQ₇, PGQ₈, and PGQ₁₀, corresponding to predicted extended-chain regions of 5, 6, and 8 residues, respectively, between QPGQ turns (Table 1). Fig. 1a shows that, although all four peptides in the PGQ_N series aggregate at significant rates, there is a clear trend of increasing aggregation rate with increasing extended-chain length. Both PGQ₇ and PGQ₈ aggregate very sluggishly compared with Q₄₅. The initial rate of PGQ₉ aggregation is ≈6- to 8-fold faster than that of PGQ₈ and is about as fast as the Q₄₅ control peptide. The aggregation rate of PGQ₁₀ is about two times faster than that of PGQ₉, but most of this difference is probably due to the additional four Gln residues in the former (Table 1, and see Materials and Methods); for unbroken polyGln peptides in this length range, repeat length increases of three to five Gln residues lead to rate increases of about a factor of two (10). Thus, the shortest polyGln extended-chain length giving maximal aggregation kinetics is 7, as found in the PGQ₉ peptide. This result is consistent with studies showing that the optimal length of an extended chain in antiparallel β-sheet is seven (31).

If the oligoGln sequences spanning PG elements in these peptides exist in extended-chain β-sheets in the aggregated state, then introduction of a single additional Pro residue at the midpoint of one of the extended-chain elements should significantly diminish aggregation (25, 27, 28). Fig. 2 shows that aggregation is completely abolished in PGQ₉P² (Table 1), a derivative of PGQ₉ in which a single additional Pro residue replaces the central Q in the second of the four Q₉ sequences. Thus, although the polyGln sequence can accommodate Pro replacements at certain sequence positions without affecting aggregation efficiency, it cannot tolerate a Pro residue inserted in a sequence element already constrained (by the preexisting prolines) to exist in a β-sheet extended chain in the aggregate. This result supports our hypothesis of how PGQ₉ folds and aggregates. Similar Pro replacements in other Q₉ elements of PGQ₉, singly or in combination, also very effectively inhibit aggregation (Fig. 2). The only exception is the mutant PGQ₉P¹, which aggregates moderately well, presumably because C-terminal to the inserted Pro there is a long run of oligoGln interspersed with PG, of sufficient length to support aggregation.

Fig 2.

Spontaneous aggregation kinetics of polyGln peptides in PBSA at 37°C monitored by the decrease in soluble peptide concentration (a) and by the increase in ThT fluorescence of the amyloid-like aggregation product (b). PGQ₉ (•), Q₁₅PQ₂₆ (○), PGQ₉(P¹) (⧫), PGQ₉(P²) (◊), PGQ₉(P^1,2) (▪), PGQ₉(P^2,3) (▴), PGQ₉(P^2,4) (▵), PGQ₉(P^3,4) (□).

The underlying premise of this paper is that data for mutants containing a single replacement within a long polyGln sequence will be difficult to interpret, because of the expected ability of such a sequence to adjust to the mutation when it folds into the aggregate. Fig. 2 shows this concern to have been justified. When a single Pro residue is inserted into a K₂Q₄₂K₂ sequence, at the position analogous to that occupied by the intrastrand Pro in the peptide PGQ₉P², this mutant, designated Q₁₅PQ₂₆ (Table 1), aggregates at a significant rate. Thus, the ability of a Pro substitution to effectively block aggregation is only experienced when it is constrained by other mutations to occupy an extended chain region.

Aggregate Structure.

The kinetics data described above can only be interpreted if it is clear that the PG peptides form aggregates with structures similar to those of unbroken polyGln sequences. We conducted several tests to compare aggregate structures.

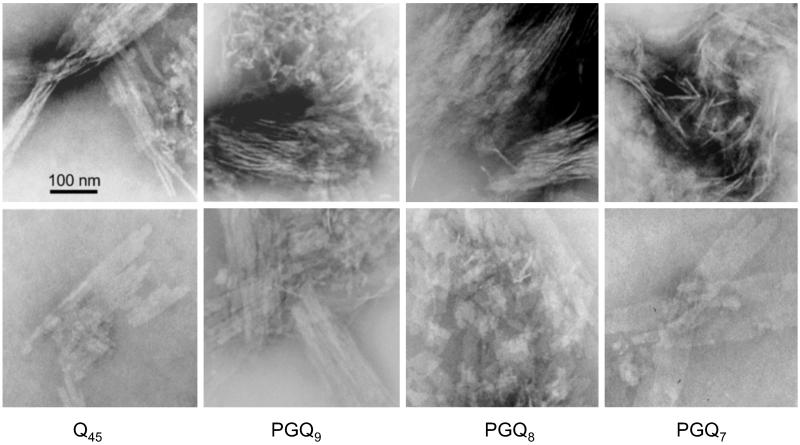
PolyGln aggregates exhibit a variety of morphologies, depending on growth conditions and repeat length (14). These range from curvilinear filamentous structures resembling the protofilaments described for Aβ aggregation intermediates (32, 33) to broad ribbons apparently composed of parallel-aligned filaments. EM (Fig. 3) shows that Q₄₅ aggregates grown at 37°C contain both fragmented ribbon structures and narrow, isolated filaments that appear to be the components of the ribbons. Aggregates formed from the peptides PGQ₇, PGQ₈, and PGQ₉ exhibit a very similar distribution of morphologies (Fig. 3). Surveying the entire EM grid, aggregates of Q₄₅ and other unbroken polyGln peptides grown at 37°C in PBSA tend to exhibit a lower percentage of isolated filaments than do aggregates of the PGQ_N series of peptides (not shown). This suggests that filaments of PGQ_N peptides may be impaired in the lateral associations necessary for forming plates and ribbons, which would be consistent with a role for Gln residues in β-turns in filament–filament contacts. Except for this minor difference, the EM analysis shows considerable ultrastructural similarity between Q₄₅ and PGQ_N aggregates.

Fig 3.

EM images of aggregates of various polyGln peptides grown in PBS at 37°C.

Another test of aggregate structures is their ability to bind aggregate-specific monoclonal antibodies (30). We have generated a family of mAbs recognizing polyGln aggregates (B. O'Nuallain, J. Ko, S. Ou, P. Patterson, and R.W., unpublished work). Table 2 lists the ability of one of these mAbs, PGA11, to bind to different aggregates. It can be seen that PGA11 is quite specific for polyGln aggregates, binding extremely well to Q₄₅ aggregates while not exhibiting significant binding either to Aβ(1–40) amyloid fibrils or to collagen. The high selectivity of PGA11 for polyGln aggregates is due to a structural epitope present only in the aggregated state, because this antibody does not bind to the soluble, low-molecular-weight form of Q₄₅ (B. O'Nuallain, S. Ou, J. Ko, P. Patterson, and R.W., unpublished work). The similarity of binding affinities (EC₅₀s) of PGA11 for the different polyGln aggregates suggests a strong structural similarity between the Q₄₅ and PGQ_N aggregates. The differences in binding amplitudes suggest that these aggregates contain varying numbers of antibody epitopes per unit weight.

Table 2.

Binding of the mAb PGA11 to various polyGln aggregates

Peptide aggregate	EC50, pM	Binding amplitude, fmol Eu+3
Q45	27  ± 1	29  ± 7
PGQ9	30  ± 3	41  ± 1.4
PGQ8	37  ± 3	105  ± 14
PGQ7	24  ± 2	61  ± 1.4
Aβ(1–40) fibrils	NO	1.7  ± 0.7
Collagen I	NO	0.43  ± 0.35

^*NO, none observable.

We also conducted a heterologous seeding analysis (“cross-seeding”) to evaluate structural similarities of the aggregates. Many amyloid fibrils seed the elongation of other amyloidogenic peptides, but generally only at much reduced efficiencies (1–5%) compared with a homologous seeding reaction (B. O'Nuallain and R.W., unpublished work). Generally, seeding efficiency depends on the number of growth sites in a given weight of the aggregate, as well as the molecular complementarity of the bulk phase monomer and the aggregate seed. We determined aggregation kinetics for the peptides Q₄₅, PGQ₇, PGQ₈, and PGQ₉ with and without seeding by each of the corresponding aggregates (Table 3). We then calculated the seeding efficiency of each aggregate by dividing the seeded growth rate by the unseeded growth rate for the solution-phase peptide. This calculation was only possible for solution-phase PGQ₉, because the unseeded kinetics of the other three peptides exhibit initial lag phases (Table 3 legend, Fig. 1); qualitatively, however, the four aggregates produce similar relative seeding efficiencies for the other three soluble peptides (Table 3). When added at 5% by weight of the solution-phase peptide, all four aggregates exhibit similar seeding efficiencies, in the range of 6- to 16-fold (Table 3). We take this to indicate significant structural similarity among the aggregates. The differences in efficiencies may be due to different numbers of growth sites per unit weight of aggregate, as discussed next.

Table 3.

Elongation rates for reactions seeded with different polyGln aggregates

Solution	Aggregates
	Q45	PGQ9	PGQ8	PGQ7
Q45	32	60	115	58
PGQ9	19	34	54	33
PGQ8	1.9	5.1	4.3	4.4
PGQ7	1.3	1.1	4.5	3.6
PGQ9, seeded/unseeded	5.6	10	15.9	9.7

Soluble peptides at ≈35 μM were seeded with 5% by weight with different aggregates, incubated as described in Materials and Methods, and additional aggregate formation was monitored by the ThT assay. Except for the last row (which shows a rate ratio), data are initial rates in arbitrary fluorescence units per h. Under these conditions, the unseeded soluble peptides alone behave as follows: Q₄₅, short lag phase; PGQ₉, initial rate 3.4; PGQ₈, long lag phase; PGQ₇, long lag phase.

Inspection of Tables 2 and 3 shows an unexpected correlation between the relative efficiencies of the four polyGln aggregates in seeding aggregate growth by the PGQ₉ peptide and the PGA11 binding amplitudes to these same four aggregates (R² of 0.90 for a linear, least squares fit; plot not shown). This correlation suggests that the PGA11 epitope may overlap with the growth face of these amyloid-like aggregates. Because the seeding efficiencies correlate with PGA11 binding amplitudes (number of epitopes) but not with apparent binding constants (detailed structure of the epitope), it is more likely that the differences in seeding efficiency observed for the four aggregates are due to variations in the number of growth ends per unit weight of fibril, rather than to any subtle differences in atomic-level structure. If this is true, then normalizing the seeding efficiencies for equal numbers of growth ends (PGA11 epitopes) would suggest that the component of seeding efficiency associated with atomic-level aggregate structure is essentially identical for all four aggregates, further suggesting a similar polyGln fold in all four aggregates.

Critical Nucleus.

One important aspect of fibril structure is the structure of the aggregation nucleus. Because the kinetic nucleus by definition exists only transiently and at very low concentrations, its structure cannot be determined directly and its very existence must be inferred from a nucleation kinetics analysis. In this analysis, kinetic parameters are obtained from the early portions of aggregation reactions at different peptide concentrations. The slope of a plot of the log of these kinetic parameters vs. log concentration yields a value equal to n* + 2, where n* is the critical nucleus or number of monomeric units in the nucleus (11, 34). In a recent analysis, calculated values for n* were obtained for different polyGln peptides ranging from 0.59 to 0.98. These values were rounded to the nearest nonzero integer (n* of 0 has no meaning in the nucleated growth polymerization pathway), yielding n* = 1 in each case, suggesting that nucleation corresponds to a highly unfavorable folding reaction within the polyGln monomer (11).

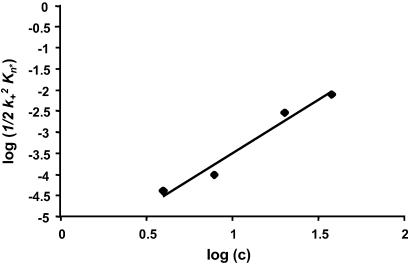
Here, we determined n* for PGQ₉ by the same methods. Fig. 4 shows the log–log plot used to determine the critical nucleus for the peptide PGQ₉. The slope of the line is 2.52, which yields a calculated value for n* of 0.52, or n* = 1 after rounding, the same result as our earlier studies on polyGln peptides with repeat lengths 28, 36, and 47 (11). If the Pro residues in PGQ₉ limited its ability to efficiently fold on itself to make a monomeric nucleus, we would expect the critical nucleus for PGQ₉ to be two or higher. However, because n* = 1 for PGQ₉, the nucleus must be able to efficiently form within the constraints of the regularly spaced PG elements. Thus, both the aggregation nucleus and the repeat unit in aggregate structure appear capable of efficiently forming despite the distribution of PG elements in the sequence.

Fig 4.

Nucleation kinetics analysis for the aggregation of PGQ₉ in PBSA at 37°C. Kinetics experiments were conducted at four peptide concentrations and monitored by the reduction in levels of soluble peptide over time, as described in Materials and Methods. The data for each concentration series were fit to the nucleation kinetics equation Δ = ½k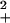K_n*c^(n*+2)t² by plotting log (soluble peptide) vs. t² (11). Fig. 4 shows a plot of the log of the slopes of these t² plots, ½kK_n*, vs. log (starting concentration).

Our nucleation analysis is based on a model in which the observed aggregation kinetics are determined by the interplay between the generation of the nucleus, through a preequilibrium with bulk phase monomer, and the elongation of the nucleus and aggregate, controlled by second-order rate constants (11, 34). In principle it should be possible to extract a term corresponding to the equilibrium constant for nucleus formation, but in practice this is made difficult by the inability to determine the elongation rate constants (34). Thus, although the collapse of Q₄₅ and PGQ₉ into their monomeric nuclei should be quantifiable in terms of free energies of folding, it is not possible to rigorously determine or compare these values. Nonetheless, the similarities in aggregation kinetics between Q₄₅, PGQ₉, and P_DGQ₉ suggest that the differences in the free energies of folding of their nucleation reactions are quite small (no more than a few kcal/mol). This suggests in turn that the role of the PG elements in these experiments is not so much to encourage turn formation (compared with the replaced QQ elements) as to discourage extended chain formation in PG-containing segments.

Discussion

The homogeneity of the polyGln sequence lends itself to a certain promiscuity in this molecule's folding and aggregation behavior. Interruption of a long polyGln sequence with a single point mutation is expected to have little effect, because the molecule might be capable of adjusting its folding so that any newly introduced, offensive residue could be placed in whatever environment generates the least overall destabilization. In the case of a Pro residue, for example, this would likely be in a turn or loop. Folded, evolved proteins tend to resist large folding changes on mutation through the cooperative action of a large ensemble of finely tuned, individually customized packing interactions. In contrast, an array of interlocking Gln residues might be easily capable of sliding into a new register without giving up stabilization energy, because all of the through-space interactions are of essentially equivalent energies. This feature poses a significant barrier to the design of interpretable point mutational experiments in pure polyGln peptides.

The results described here suggest that an antiparallel β-sheet folding motif is a reasonable model for the fundamental fold of the repeat unit in the polyGln aggregate. The fact that the aggregation behavior of PGQ₉ closely resembles that of a Q₄₅ peptide suggests that the inserted PG sequences provide for β-turns that are tolerated within this repeat unit. The fact that the P_DGQ₉ sequence aggregates more aggressively than PGQ₉ is also consistent with a β-turn localization for the PG sequences, because the d-Pro-Gly sequence is known to especially favor β-turns (23). Although aggregation rate differences of the PGQ_N peptides might be influenced by folding/stability differences in the solution-phase peptides, the CD spectra of the PGQ_N peptides are essentially identical to each other and to that of the Q₄₅ peptide (10). All of these peptides exhibit classic statistical coil CD spectra (data not shown).

Although the data supports a four-stranded antiparallel β-sheet structure for the fundamental repeat unit of aggregates of Q₄₅ and similar polyGln peptides, the details of the folding within this structure are not yet revealed. For example, the nucleus and aggregation repeat unit might consist of a single four-stranded sheet or, alternatively, a duplex of two two-stranded sheets (35). Our results may also be consistent with some formulations of the parallel β-helix folding motif, which has been discussed as a possible folding motif for the amyloid fibril (36, 37). Although our data argue against a model for the polyGln aggregate structure consisting of a “perfect” β-helix in which all backbone amide groups are involved in the H-bonded β-sheet (24), it is possible that our PGQ_N sequences might be accommodated into β-helical motifs more resembling those found in evolved β-helical proteins (36, 37).

We interpret the data in Fig. 1 to indicate that the fundamental fold accessed in aggregates of unbroken polyGln sequences like Q₄₅ is most closely replicated in the aggregates of PGQ₉ and PGQ₁₀. This implies that the ideal folding motif for polyGln aggregates consists of extended chains of seven residues alternating with chain reversal segments of four residues. In light of this, it is especially interesting that the length of polyGln required to make a four-stranded sheet composed of four seven-residue extended chains and three connecting four-residue reverse turns is 40, which is the shortest polyGln repeat length associated with 100% penetrance in Huntington's disease (3). Despite this interesting correspondence, because PGQ₇ and PGQ₈ also aggregate at significant rates and produce similarly structured aggregates, models of aggregate structure with shorter lengths of extended chain between turns cannot entirely be ruled out.

It is possible that through further mutagenesis experiments we can refine our emerging model for polyGln aggregation nuclei and aggregates. As we begin to build up structural features within the polyGln sequence capable of punctuating its secondary structure, we can probe the folding energetics of polyGln through further mutational analysis without undue concern about slippage due to promiscuous Gln–Gln interactions within the aggregate. The proline experiment embodied in peptide PGQ₉P² is an example of what is now possible. Once Q₇ extended chains have been fixed by the interspersed QPGQ elements, the additional inserted Pro in the center of a Q₇ stretch has to be accommodated comfortably within the β-sheet of the aggregate, or the aggregate cannot form. It should now be possible, for example, to use mutagenesis and spectroscopic analysis to map local environments (22), and other structural parameters to elucidate details of aggregate structure.

Abbreviations

• EM, electron microscopy

• PBSA, PBS containing 0.05% sodium azide

• polyGln, polyglutamine

• ThT, thioflavin T