Nonlinear Dependency of Intracellular Fluxes on Growth Rate in Miniaturized Continuous Cultures of Escherichia coli

Abstract

A novel mini-scale chemostat system was developed for the physiological characterization of 10-ml cultures. The parallel operation of eight such mini-scale chemostats was exploited for systematic ¹³C analysis of intracellular fluxes over a broad range of growth rates in glucose-limited Escherichia coli. As expected, physiological variables changed monotonously with the dilution rate, allowing for the assessment of maintenance metabolism. Despite the linear dependence of total cellular carbon influx on dilution rate, the distribution of almost all major fluxes varied nonlinearly with dilution rate. Most prominent were the distinct maximum of glyoxylate shunt activity and the concomitant minimum of tricarboxylic acid cycle activity at low to intermediate dilution rates of 0.05 to 0.2 h⁻¹. During growth on glucose, this glyoxylate shunt activity is best understood from a network perspective as the recently described phosphoenolpyruvate (PEP)-glyoxylate cycle that oxidizes PEP (or pyruvate) to CO₂. At higher or extremely low dilution rates, in vivo PEP-glyoxylate cycle activity was low or absent. The step increase in pentose phosphate pathway activity at around 0.2 h⁻¹ was not related to the cellular demand for the reduction equivalent NADPH, since NADPH formation was 20 to 50% in excess of the anabolic demand at all dilution rates. The results demonstrate that mini-scale continuous cultivation enables quantitative and parallel characterization of intra- and extracellular phenotypes in steady state, thereby greatly reducing workload and costs for stable-isotope experiments.

The flexible nature of metabolic networks is based on an extensive set of biochemical reactions whose activity is modulated by complex regulatory networks that operate at multiple levels. The core of this intricate network consists of about 100 central metabolic reactions that synthesize biosynthetic building blocks and regenerate cofactors from a wide variety of substrates. To understand the behavior and regulation of such networks, quantitative data on intracellular fluxes under different conditions and with defined mutants are required. A common problem with mutants, however, is their often dramatic differences in growth rates (2, 11, 50), such that detected flux differences may be nonspecific, growth rate-related phenomena (4, 29, 46).

To ensure highly comparable conditions, continuous cultures are the method of choice because, unlike with batch cultures, a defined steady-state growth rate that equals the externally controlled dilution rate is maintained (17, 31). The labor and cost associated with continuous cultures in controlled bioreactors, however, preclude systematic experiments on any larger scale. For bioprocess development in batch and fed-batch cultures, parallel reactor systems are becoming available (for a recent review, see reference 49), and microtiter plate-based cultivation devices were successfully used for quantitative batch experiments (2, 6, 11, 21, 51). Small-scale continuous-culture devices, in contrast, are used mostly in evolutionary biology with typical working volumes of 30 to 100 ml (7). A notable exception is the recently developed shake flask system for continuous operation on a 30- to 40-ml scale, which can be used for the determination of microbial growth kinetics and product formation (1).

Here, we develop a novel continuous-culture system for the quantitative analysis of microbial growth on 10-ml scale, with a focus on easy and robust handling, parallel operation, and a minimum of specialized technical equipment. This device is then used to elucidate the impact of growth rate on metabolic network operation systematically and quantitatively. The applicability of such mini-scale continuous-culture cultivation is demonstrated by determining intracellular carbon fluxes from ¹³C-labeling experiments (38) with glucose-limited Escherichia coli over a broad range of dilution rates.

MATERIALS AND METHODS

Bioreactors.

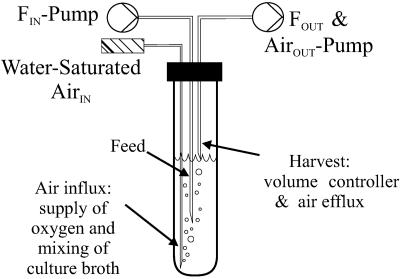
The cultivation vessel of the continuous-culture system was a 17-ml Hungate tube (Bellco Glass, Inc., Vineland, N.J.) with a working volume of 10 ml, a screw cap with a 9-mm-diameter opening, and a butyl rubber septum. The septum was pierced by three luer lock needles, one for substrate supply (0.8 by 120 mm; Sterican B. Braun, Roth AG, Reinach, Switzerland), one for air supply (0.8 by 150 mm; Huber & Co AG, Reinach, Switzerland), and one for withdrawal of culture broth and air efflux (0.8 by 120 mm; Sterican B. Braun, Roth AG, Reinach, Switzerland) (Fig. 1). A multichannel peristaltic pump was used to supply four parallel cultures with medium. To ensure proper mixing of the small feed volumes, the tip of the feed needle was positioned in the middle of the culture fluid. A constant volume of culture broth was maintained by positioning the tip of a needle at a predetermined height that corresponded to a 10-ml volume and connecting it to a separate multichannel peristaltic pump that removed excess fluid. Since the pump efflux rate was far in excess of the dilution rate, this needle was also used to induce aeration by generating negative pressure inside the Hungate tube. Water-saturated air at 37°C was then passively sucked in through a needle whose tip was placed at the bottom of the culture vessel. Unless specified otherwise, the volumetric aeration rate was 20 ml/min (corresponding to 2 volumes per volume per minute). Mixing was achieved through the rising air bubbles, and temperature was maintained at 37°C by placing the Hungate tubes in a water bath.

FIG. 1.

Schematic drawing of the developed chemostat system.

Strains and growth conditions.

E. coli MG1655 (λ⁻ F⁻ rph-1; Deutsche Sammlung von Mikroorganismen und Zellkulturen, Germany) was used for all experiments. Frozen glycerol stock cultures were used to inoculate 4-ml M9 precultures containing an additional 5% (vol/vol) Luria-Bertani complex medium. The precultures were grown overnight and used to inoculate (at a 1-to-10 ratio) the main culture in the Hungate tube, which was run 4 to 5 h in batch mode before continuous operation was initiated, for a minimum of seven volume changes.

The chemostat feed medium was M9 minimal medium with 1 g per liter glucose as the limiting substrate at a pH of 7.0. Please note that oxygen limitation might occur in this particular setup when glucose concentrations of 3 g liter⁻¹ and higher are used at dilution rates of 0.2 h⁻¹ and higher. M9 medium contained (per liter of deionized water) 0.8 g NH₄Cl, 0.5 g NaCl, 7.5 g Na₂HPO₄ · 2H₂O, and 3.0 g KH₂PO₄. The following components were sterilized separately and then added (per liter of final volume): 2 ml of 1 M MgSO₄, 1 ml of 0.1 M CaCl₂, 0.3 ml of 1 mM filter-sterilized thiamine HCl, and 10 ml of a trace element solution containing (per liter) 1 g of FeCl₃ · 6H₂O, 0.18 g ZnSO₄ · 7H₂O, 0.12 g CuCl₂ · 2H₂O, 0.12 g MnSO₄ · H₂O, and 0.18 g CoCl₂ · 6H₂O. Sterilized glucose was added to a final concentration of 1 g per liter. For ¹³C-labeling experiments, glucose was added either as a mixture of 50% (wt/wt) 1-¹³C-labeled isotope isomer (99%; Cambridge Isotope Laboratories, Andover, MA) and 50% (wt/wt) natural glucose or as a mixture of 20% (wt/wt) [U-¹³C]glucose (99%; Cambridge Isotope Laboratories, Andover, MA) and 80% (wt/wt) natural glucose, and the labeled medium was used for the whole experiment, including the batch phase.

Analytical procedures and physiological parameters.

Cell growth was monitored by determining optical density at 600 nm (OD₆₀₀). Glucose and acetate concentrations were determined enzymatically using commercial kits (Beckman-Coulter, Zurich, Switzerland, or Dispolab, Dielsdorf, Switzerland). The presence of other organic acids in the culture broth was determined in selected cases by high-pressure liquid chromatography, and the pH of the effluent medium was routinely monitored with a pH sensor. Dissolved-oxygen concentrations were measured in the steady state in separate experiments using an OM-4 oxygen meter (Microelectrodes, Inc., Bedford, NH). A hole in a Hungate butyl rubber septum was created for the oxygen sensor. To measure dissolved-oxygen concentrations, the whole Hungate screw cap was changed to introduce the oxygen sensor in the culture broth. The needles for substrate supply, air supply, and withdrawal of culture broth and air efflux were placed quickly through the new cap, and the dissolved oxygen concentration was monitored. The oxygen meter was calibrated, prior to measurement, by flushing an empty mini-reactor first with nitrogen and then with air.

All physiological parameters were determined during the steady-state phase after at least five volume changes of continuous operation. A predetermined correlation factor for cellular dry weight and OD₆₀₀ (0.41 g [dry weight] [gdw]/OD) was used to calculate specific biomass yields, consumption rates, or production rates. Measurement errors for all physiological parameters were considered, and Gaussian error propagation was used when necessary.

Metabolic-flux ratio analysis by GC-MS.

Samples for gas chromatography-mass spectrometry (GC-MS) analysis were prepared as described previously (12). Briefly, the ¹³C-labeled chemostat cultures were harvested after the OD₆₀₀ was stable for at least two volume changes (the minimum continuous operation was seven volume changes). Cell pellets were hydrolyzed in 6 M HCl at 105°C for 24 h in sealed microtubes. The hydrolysates were dried under a stream of air at around 60°C and then derivatized at 85°C in 30 μl dimethylformamide (Fluka, Switzerland) and 30 μl N-(tert-butyldimethylsilyl)-N-methyl-trifluoroacetamide with 1% (vol/vol) tert-butyldimethylchlorosilane (Fluka, Switzerland) for 60 min (14). Derivatized amino acids were analyzed on a series 8000 GC combined with an MD 800 mass spectrometer (Fisons Instruments, Beverly, MA). The GC-MS-derived mass isotope distributions of proteinogenic amino acids were then corrected for naturally occurring isotopes (12). The corrected mass distributions were related to the in vivo metabolic activities obtained with previously described algebraic equations and statistical-data treatment of metabolic-flux ratio analysis (12) using the software Fiat Flux (53).

Calculation of the OAA fraction from the PEP ratio when the glyoxylate shunt is active.

The equation to calculate the fraction of oxaloacetate (OAA) originating from phosphoenolpyruvate (PEP), as described previously (12), quantifies the contribution of OAA originating from PEP and CO₂ through PEP carboxylase relative to that of the fraction of OAA derived through the tricarboxylic acid (TCA) cycle. Since the fractional labeling of CO₂ is unknown and may be lower than the fractional enrichment of the input substrate, it must be considered an additional unknown. Normally, this unknown can be calculated from the available data, but the activity of the glyoxylate shunt introduces another unknown that must be considered for OAA biosynthesis, so that the original equation does not hold anymore. To estimate the fraction of OAA originating from PEP in [U-¹³C]glucose experiments under conditions with an active glyoxylate shunt, we derived a new equation that also takes the fraction of OAA derived through the glyoxylate shunt into account.

Generally, OAA molecules can be derived either through anaplerosis, the glyoxylate shunt, or the TCA cycle. If derived through anaplerosis, the OAA_1-4 (where _1-4 indicates that carbon atoms 1 to 4 of OAA are considered) molecule will have a mass distribution that is a combination of a PEP_1-3 molecule and a CO₂ molecule. If derived through the glyoxylate shunt, half of the molecules will be a combination of pyruvate_2-3 (Pyr_2-3) and OAA_1-2 and half a combination of OAA_3-4 and Pyr_2-3. If OAA molecules are derived through the TCA cycle, they will have the same mass distribution as a 2-oxoglutarate_2-5 (OGA_2-5) fragment. The labeling pattern of OAA_1-4 can therefore be expressed as follows:

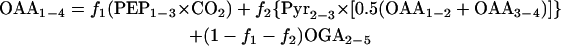(1)

where f₁, f₂, and (1 − f₁ − f₂) represent the fractions of OAA molecules derived through anaplerosis, the glyoxylate shunt, and the TCA cycle, respectively. This equation also takes the exchange flux between OAA and fumarate into account. The mass distribution vector for the sum of OAA_1-2 and OAA_3-4 cannot be determined directly from the measured mass distributions of the proteinogenic amino acids but can be calculated by listing all possibilities for the origins of OAA_1-2 and OAA_3-4. If OAA_1-2 and OAA_3-4 are derived through anaplerosis, they will be the sum of a PEP_2-3 molecule and the combination of CO₂ and a one-carbon atom (C₁) with the fractional labeling of the input substrate. If derived through the TCA cycle, they will be the sum of an OAA_2-3 molecule and a Pyr_2-3 molecule, and if derived through the glyoxylate shunt, they will be the sum of three-fourths of a Pyr_2-3 molecule and five-fourths of an OAA_1-2 molecule. Knowing in addition that the combination of a Pyr_2-3 molecule with an OAA_2-3 molecule is similar to an OGA_2-5 molecule, equation 1 becomes

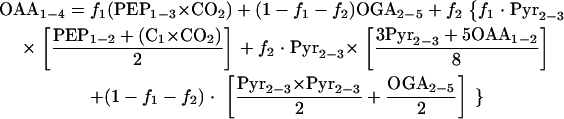(2)

To solve equation 2 for f₁, f₂, and the fraction of labeled CO₂, an iterative process that started with random initial values for f₁, f₂, and the fraction of labeled CO₂ was applied. Stable values for f₁, f₂, and the fraction of labeled CO₂ were obtained after approximately 20 iterations. The process was started several times from different random values and always arrived at the same solution.

Theoretically, the fraction of labeled CO₂ must be between 0% and the degree of fractional labeling in the input substrate (20% if using 20% [U-¹³C]glucose). If, by solving equation 2, the fraction of labeled CO₂ was not within these boundaries, it was estimated based on a linear correlation with dilution rate, which was determined from data sets with well-determined labeled CO₂ fractions (data not shown).

The standard errors for these two determined flux ratios as well as for the labeling fraction of CO₂ were evaluated numerically. Since all individual components in the mass distribution vectors have a standard deviation (12), normally distributed random values for these individual components were chosen using the MATLAB function normrnd (The Mathworks), with the constraint that the sum of the elements of a mass distribution is equal to one. These new mass distribution vectors were used to determine f₁, f₂, and the labeling fraction of CO₂ by repeating the process 1,000 times in a MATLAB-based program. The mean values and the standard deviations for the three parameters were determined from these 1,000 estimations. The mean values were within 3% of the calculated ratios, and the standard deviations were used as the errors for the parameters.

Since a potentially reversible isocitrate lyase flux would further complicate the situation, we assessed the unidirectionality of this flux. For this purpose, we assumed various degrees of reversibility for this reaction and assessed the quality of the fit for f₁, f₂, and the fraction of labeled CO₂ by comparing the measured and calculated mass distribution vectors for OAA_1-4. The best solution was always the absence of reversibility. Therefore, when active, the glyoxylate shunt operated in a unidirectional fashion as described before (13).

In the standard network for the metabolic-flux ratio calculations of Fiat Flux (53), the glyoxylate shunt is considered inactive, and the fraction of OAA originating from PEP can be determined as described previously (12). The activity of the glyoxylate shunt can be diagnosed from the calculated CO₂-labeling content from [U-¹³C]glucose experiments. If the calculated value falls outside its theoretical boundaries (0% and the degree of fractional labeling in the input glucose), the glyoxylate shunt is active and the flux ratio of OAA from PEP is determined with equation 2 as described above.

¹³C-constrained metabolic-flux analysis.

Intracellular net carbon fluxes were estimated with the previously described (14) stoichiometric model that contained all major pathways of central carbon metabolism, including the glyoxylate shunt and the Entner-Doudoroff (ED) pathway, using the software Fiat Flux (53). The reaction matrix consisted of 26 unknown fluxes and 21 metabolite balances (including the three experimentally determined rates of glucose uptake, acetate, and biomass production). To solve this underdetermined system of equations with 5 degrees of freedom, eight of the above calculated flux ratios were used as additional constraints as described before (14, 41): serine derived through the Embden-Meyerhoff-Parnas (EMP) pathway, pyruvate derived through the ED pathway, OAA originating from PEP, PEP originating from OAA, pyruvate originating from malate (upper and lower bounds), OAA derived through the glyoxylate shunt (upper bound), and PEP derived through the pentose phosphate (PP) pathway (upper bound). The first four ratios were used as equality constraints, while the latter four were used only as boundary constraints. Since equation 2 determines the fraction of OAA derived through the glyoxylate shunt and not only the fraction of OAA originating from glyoxylate (14), the constraint for this ratio was modified accordingly.

Fluxes into biomass were calculated from the known metabolite requirements for macromolecular compounds and the growth rate-dependent RNA and protein contents (8). The sum of the weighed square residuals of the constraints from both metabolite balances and flux ratios was minimized using the MATLAB function fmincon, and the residuals were weighed by dividing through the experimental error (14). The computation was repeated at least five times with randomly chosen initial flux distributions to ensure the identification of the global minimum, and the system always arrived at the same solution. For each metabolite that was used as a precursor for biomass synthesis, a proportional error of 4% was assigned (14). Only for the dilution rates of 0.044 h⁻¹ and 0.048 h⁻¹ was this error set to 0% to reinforce the constraint for a closed C balance.

RESULTS

Development and characterization of a mini-scale continuous-culture system.

To develop an easy-to-handle, small-scale chemostat system for robust and parallel operation without specialized equipment, the cultivation vessel was greatly simplified. Mixing was achieved through rising air bubbles. The simplification also involved the reduction of pumps, tubes, and needles for continuous operation, including the withdrawal of exhaust gas and culture broth through a single tube that induced a passive influx of air (Fig. 1). Dissolved oxygen concentrations and pH were not controlled online but were stably maintained in an optimal growth range through appropriate choice of operating conditions, i.e., sufficient aeration and a medium buffered with 64 mM phosphate. The pH of the outflowing culture broth was routinely measured and found to be within 0.1 pH unit of the set value of 7.0. Dissolved oxygen concentrations were determined in separate experiments with different glucose concentrations and an airflow rate of 20 ml per min. Under the conditions used here (i.e., 1 g per liter glucose), dissolved oxygen concentrations were above 70% at all dilution rates tested, up to 0.4 h⁻¹. With 3 g per liter glucose at a dilution rate of 0.4 h⁻¹, however, the dissolved oxygen concentration dropped significantly, and the medium acidified, strongly indicating oxygen limitation.

To elucidate technical accuracy and stable operation, several key parameters were tested. Rather than using an airflow controller for each vessel, passive aeration was implemented, under which conditions only the exhaust gas was actively removed through a peristaltic pump. The resulting low pressure inside the vessel caused a passive inflow of air at a rate that equaled the pumping rate of the exhaust gas. To minimize evaporation, the inflowing air was saturated with water by passage through a humidifier. This passive aeration achieved stable airflow rates of 1 to 40 ml per min for several days (data not shown). By weighing the amount of medium pumped into and out of the vessel, we also verified that the low pressure did not affect the steadiness of feed and harvest rates (data not shown). The overall error of a set dilution rate was determined by considering the errors for culture broth volumes and feed rates. The average error for 44 separate experiments was 4% of the dilution rate and hence very low.

Physiological validation.

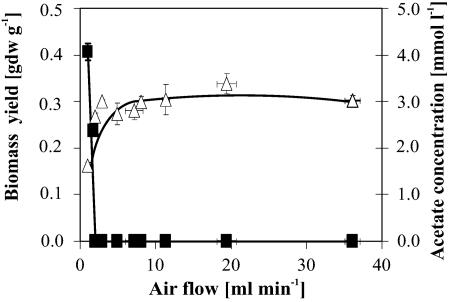
Sufficient oxygen supply is one of the key parameters of aerobic cultivations. To biologically validate sufficient oxygen supply, we used E. coli as a biological sensor, since acetate formation, at the low glucose uptake rates used here, is directly correlated with suboptimal oxygen supply (18, 28). The aerobic growth domain was determined from measurements of steady-state biomass yields and acetate concentrations at airflow rates ranging from 0 to 36 ml per min in cultures at a dilution rate of 0.1 h⁻¹ (Fig. 2). Only at airflow rates of 2 ml per min and below did the biomass yield drop and acetate formation occur. Hence, a flow rate of 20 ml per min, well above the threshold, was chosen to ensure fully aerobic growth and sufficient mixing. This airflow rate ensured dissolved oxygen concentrations above 70% at all tested dilution rates and with 1 g per liter glucose.

FIG. 2.

Influence of aeration rate on biomass yield (open triangles) and acetate concentration (black squares) at a dilution rate of 0.1 h⁻¹ in mini-scale E. coli chemostat cultures. Error bars represent the standard deviations from triplicate measurements. Trend lines were drawn by hand.

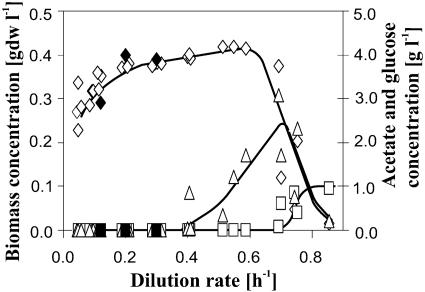
Biomass, glucose, and acetate concentrations were in excellent agreement with literature data on E. coli MG1655 from conventional stirred tanks (13, 19, 43) when plotted as a function of the growth rate in a multidimensional diagram (Fig. 3). Acetate formation did not occur at dilution rates below 0.4 h⁻¹, and biomass concentration gently rose with increasing dilution rates, indicating that a significant fraction of the consumed glucose was expended for cellular maintenance at low growth rates (18, 20). No further metabolic by-products were detected by high-pressure liquid chromatography. Above a dilution rate of 0.7 h⁻¹, washout occurred and glucose accumulated.

FIG. 3.

Multidimensional diagram for mini-scale chemostat cultures of E. coli. Concentrations of biomass (open diamonds), acetate (open triangles), and glucose (open squares) were normalized to a concentration of 1 g per liter glucose in the medium. Filled symbols represent published values for E. coli MG1655 grown at 37°C in stirred-tank reactors (13, 19, 43). Trend lines were drawn by hand.

Maintenance metabolism.

An important intrinsic property of each organism is its rate of maintenance metabolism, i.e., the energy required to maintain a viable and active state in the absence of growth. This so-called non-growth-associated maintenance energy coefficient can be quantified according to Pirt's chemostat model (30):

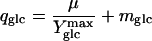(3)

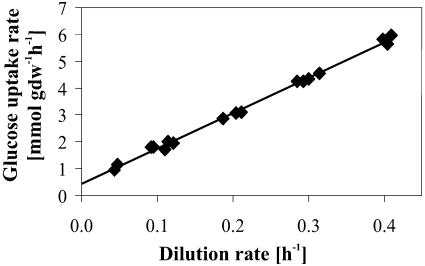
where q_glc is the specific rate of glucose consumption, m_glc the maintenance energy coefficient, and 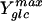the maximum molar growth yield, i.e., the biomass yield without maintenance-associated processes. At dilution rates below 0.4 h⁻¹, the specific glucose consumption rate increased linearly with dilution rate (Fig. 4) and hence was in agreement with Pirt's chemostat model. The maintenance coefficient, expressed as the glucose consumption rate required to fulfill the non-growth-associated demand, was determined by extrapolating the least-squares linear fit of the data to the zero growth rate (Table 1). Since maintenance energy and yield depend on temperature, medium composition, and strain (9, 22), these values compare favorably with published data that were typically obtained from analyses of stirred-tank systems with far fewer data points and without reported confidence intervals.

FIG. 4.

Effect of dilution rate on the rate of glucose consumption during aerobic glucose-limited growth of E. coli.

TABLE 1.

Comparison of maintenance coefficients and maximal molar growth yields obtained with glucose-limited cultures of different E. coli strains

Strain	Maintenance coefficient (mmol gdw−1 h−1)	Maximal molar growth yield (gdw mol−1)	Cultivation temp (°C)	Reference
MG1655	0.37 ± 0.09a	76 ± 3a	37	This study
B/r	0.26	82	Unknown	26
C(PC-1000)	0.30	79	Unknown	26
NTC9001	0.17	80	35	26
ML30	0.20		30	23
PS	0.31		30	23
TG1	0.11	103	28	20
W3110	0.38b		38	48
Unknown	0.31	94	30	44

^aThe 95% confidence interval is based on the data shown in Fig. 3.

^bCalculated from the reported maintenance coefficient of 7.6 mmol ATP gdw⁻¹ h⁻¹ by considering a P-to-O ratio of 1.33 (47).

Impact of growth rate on ratios of intracellular fluxes.

With the establishment of a novel mini-scale chemostat system with performance comparable to that of conventional stirred tanks under the chosen conditions, quantitative and systematic analyses of growth rate-dependent cellular processes are now feasible at costs and with workloads that are manageable. Here, we investigate whether the intracellular distribution of metabolic fluxes is directly related to the rate of growth and thus the overall rate of carbon flux into the cells. For this purpose, we performed 25 ¹³C experiments where cultures were grown during at least seven volume changes on labeled glucose. At least two to three of these volume changes were in the physiological steady state. Upon GC-MS detection of ¹³C-labeling patterns in proteinogenic amino acids, ratios of converging intracellular fluxes were determined with probabilistic equations (Table S1 in the supplemental material). These so-called metabolic-flux ratios (12, 45) are completely independent of the physiological measurements, and 9 of the 11 determined ratios are also independent of each other.

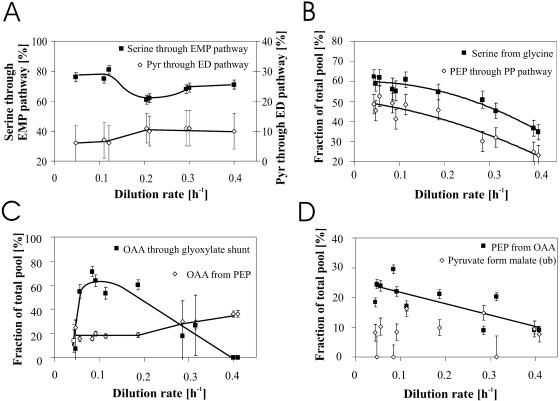
Initial glucose catabolism in E. coli may proceed via three alternative glycolytic routes: the EMP pathway, the PP pathway, and the ED pathway. While all three pathways were used to some extent (Fig. 5A and B), the fraction of pyruvate molecules derived through the ED pathway was expectedly low (12, 52) and did not change significantly with dilution rate. The fraction of serine derived through the EMP pathway was high at low dilution rates and somewhat lower at high dilution rates, with a pronounced dip at dilution rates of around 0.1 and 0.2 h⁻¹. The change is significant because this ratio is usually rather stable in E. coli (12, 29). The catabolic PP pathway flux is not directly accessible through a particular flux ratio but only in combination with the reversible exchange flux through the transketolase reaction as the fraction of PEP derived through the PP pathway (Fig. 5B). Since the majority of the carbon flux was catalyzed by the EMP pathway at all dilution rates, the pronounced negative correlation with PEP derived through the PP pathway is primarily a reflection of decreasing exchange fluxes through transketolase with an increasing growth rate. The higher influence of exchange fluxes on the ¹³C pattern at lower growth rates appears to be a general phenomenon, as is further illustrated by the negative correlation between the serine-from-glycine exchange and the dilution rate (Fig. 5B) that was also described elsewhere (8, 29).

FIG. 5.

Origins of key metabolic intermediates in E. coli during continuous glucose-limited growth at different growth rates as obtained from metabolic-flux ratio analysis by GC-MS. The fraction of serine derived through the EMP pathway and the fraction of pyruvate derived through the ED pathway were obtained from 50% [1-¹³C]glucose and 50% natural glucose. All other ratios were obtained from experiments with 20% [U-¹³C]glucose and 80% natural glucose. The experimental error was estimated from redundant mass distribution as described elsewhere (12). Error analyses for OAA from PEP and for OAA derived through the glyoxylate shunt are described in Materials and Methods. Trend lines were drawn by hand. ub, upper bound.

Large flux variations were observed around the OAA node, where two anaplerotic reactions converge (Fig. 5C). The fraction of OAA originating from PEP assesses flux through the first anaplerotic reaction catalyzed by PEP carboxylase, and this fraction was relatively stable at dilution rates below 0.2 h⁻¹ and increased steadily beyond. The upper bound for OAA molecules derived through the glyoxylate shunt, the second anaplerotic reaction, exhibited a pronounced maximum at a dilution rate of around 0.1 h⁻¹. Expectedly, glyoxylate shunt flux decreased at higher dilution rates (13, 33), but somewhat surprisingly it dropped also at very low dilution rates.

While catabolite repression (15, 37) generally causes absent or low gluconeogenic fluxes during batch growth on glucose (12, 29, 39, 45), fluxes through PEP carboxykinase were significant at low dilution rates and decreased with increasing dilution rate, as judged from the fraction of PEP originating from OAA (Fig. 5D). Similar PEP carboxykinase fluxes were reported for individual chemostat experiments at low dilution rates (8, 13, 43). No clear trend was discernible for the upper bound on the fraction of pyruvate originating from malate, which characterizes the flux through the gluconeogenic malic enzyme (Fig. 5D).

Metabolic net fluxes.

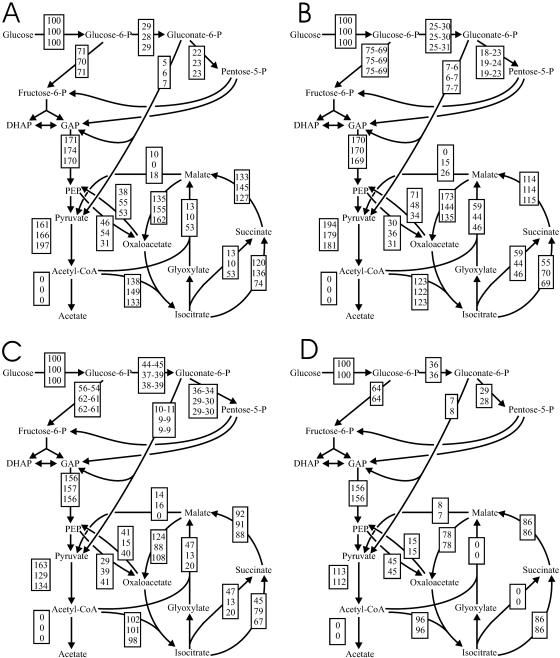
While local flux ratios are informative about the in vivo activity of individual pathways and reactions, they do not reveal the network-wide distribution of absolute fluxes. Hence, we identified the overall net flux distribution by integrating the determined extracellular fluxes in and out of the cell (Fig. 3; Table S2 in the supplemental material) and the intracellular-flux ratios (Table S1 in the supplemental material; Fig. 5) by ¹³C-constrained flux analysis (14). Since the specific glucose uptake rate increased linearly with dilution rate (Fig. 4), the overall flux throughout the network increased concomitantly. To facilitate comparison, the estimated absolute fluxes (mmol per g cells per h) (Table S2 in the supplemental material) were normalized to the glucose uptake rate, yielding a relative flux distribution (Fig. 6).

FIG. 6.

Metabolic-flux distribution at dilution rates of 0.05 h⁻¹ (A), 0.1 h⁻¹ (B), 0.2 to 0.3 h⁻¹ (C), and 0.4 h⁻¹ (D) in glucose-limited continuous cultures. The exact growth rates for the top, middle, and bottom values were as follows: (A) 0.044, 0.048, and 0.056 h⁻¹, respectively; (B) 0.09, 0.09, and 0.11 h⁻¹, respectively; (C) 0.19, 0.29, and 0.31 h⁻¹, respectively; and (D) 0.40 (bottom) and 0.41 h⁻¹ (top). Relative to the glucose uptake rate, assuming Gaussian error propagation, the confidence intervals were less than 40% for the TCA cycle, the glyoxylate shunt, and the lower part of the EMP pathway, while they were below 15% for all other fluxes. Arrowheads indicate the direction of a given flux. CoA, coenzyme A; DHAD, dihydroxyacetone-P; GAP, glyceraldehyde-3-P.

A particularly surprising finding was that the combined flux through the two anaplerotic reactions catalyzed by the PEP carboxylase and glyoxylate shunts largely exceeded the anabolic precursor requirements for OAA and 2-oxoglutarate at all dilution rates. Since only acetyl-coenzyme A, and not the C₄ compounds OAA and malate, can be catabolized to CO₂ in the TCA cycle, this excess anaplerotic flux was channeled back into catabolism through the gluconeogenic reactions catalyzed by PEP carboxykinase and malic enzyme (Fig. 6). This flux pattern is not easily explained by the traditional biochemical pathways, but two distinct metabolic activities contribute to various extents. First, the simultaneous operation of PEP carboxylase and PEP carboxykinase establishes an ATP-dissipating futile cycle between OAA and PEP that was particularly active up to a dilution rate of 0.3 h⁻¹ (Fig. 6A to C). Second, while the glyoxylate shunt is clearly the sole anaplerotic reaction during growth on acetate (5), its operation during glucose catabolism is more properly described as catabolic when gluconeogenic fluxes from C₄ compounds to PEP and pyruvate occur simultaneously. This has been described as the so-called PEP-glyoxylate cycle in slow-growing E. coli chemostat cultures (13), and a similar situation is seen here at dilution rates of 0.1 to 0.2 h⁻¹ (Fig. 6B and C), where the PEP carboxykinase flux exceeds by far the PEP carboxylase flux. Under most conditions, malic enzyme flux contributes additionally to this cycle by converting further C₄ units into catabolic substrates for the TCA cycle. While the overall PEP (pyruvate)-glyoxylate shunt pattern was highly reproducible, the particular contributions of the fluxes through PEP carboxykinase and malic enzyme appear to be subject to stochastic events or regulatory fine-tuning, as they vary somewhat at even identical dilution rates (Fig. 6B).

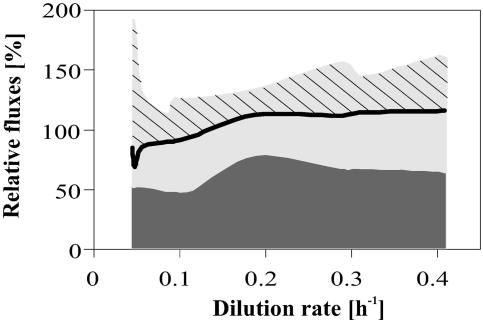
Another important quantity that can be assessed only from network-wide flux estimates is cofactor metabolism (39). Specifically, we wanted to know whether some of the flux changes in the NADPH-producing PP pathway and TCA cycle were driven by the anabolic demand for the reduction equivalent NADPH. For this purpose, we calculated the in vivo NADPH production rate from the sum of the carbon fluxes through the NADPH-producing oxidative PP pathway and isocitrate dehydrogenase. The in vivo consumption rate of NADPH is directly accessible from the known biochemical requirement of NADPH for growth rate-dependent macromolecule biosynthesis (8, 25, 32). In contrast to what occurred with batch cultures of E. coli where a significant portion of the NADPH must be synthesized via the PntAB transhydrogenase (39), glucose metabolism produced about 20 to 50% more NADPH than was required for biosynthesis at all dilution rates investigated, except for the extremely slow-growing cells (Fig. 7). Hence, in glucose-limited continuous cultures, the soluble UdhA transhydrogenase must operate to reoxidize this surplus NADPH at the expense of NAD⁺.

FIG. 7.

Relative NADPH formations in the PP pathway (dark-gray area) and isocitrate dehydrogenase (light-gray area) at different dilution rates. The black line represents the NADPH consumption rates for biosynthesis. Therefore, the hatched area represents the estimated NADPH overproduction. Since malic enzyme was considered here to be NADH dependent, the calculated NADPH production is a lower bound.

DISCUSSION

The mini-scale chemostat developed here enables quantitative and parallel characterizations of intra- and extracellular phenotypes under defined, steady-state environmental conditions. Taking advantage of these capabilities, we attempted a systematic physiological and intracellular-flux characterization of glucose-limited E. coli chemostat cultures over a large range of dilution rates. Generally, based on stoichiometric reasoning, monotonous changes in the relative distribution of intracellular flux are expected to result from the linear dependence of the specific glucose uptake rate on the dilution rate in chemostat cultures (18, 20, 42). The existence of such intracellular continuity, however, remained unproven, and our quantitative analysis clearly demonstrated discontinuous flux patterns in many pathways.

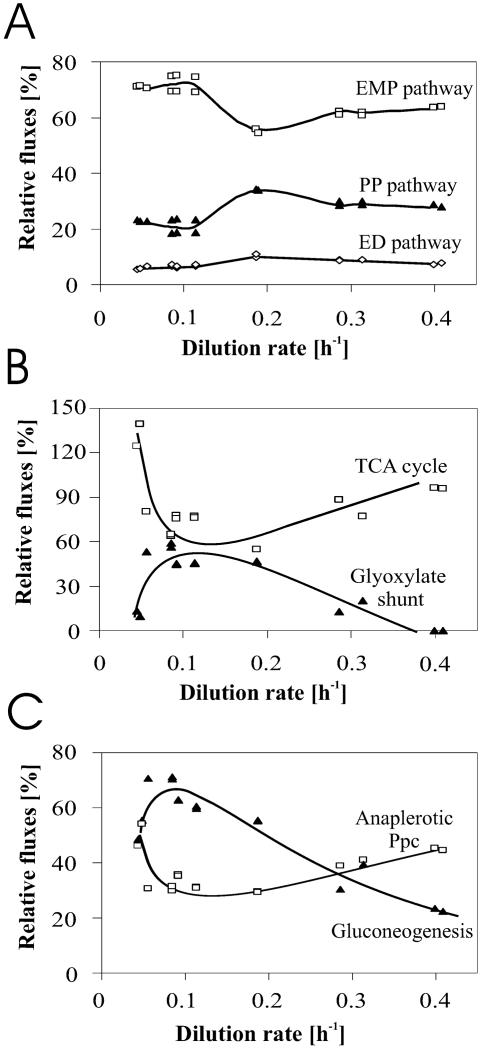
While the incoming flux of glucose increases monotonously with dilution rate (Fig. 4), the intracellular splitting of initial glucose catabolism between the EMP (70%) and PP (25%) pathways was constant up to a dilution rate of 0.1 h⁻¹ (Fig. 8A). After a small but significant dip in the EMP pathway flux at a dilution rate of around 0.2 h⁻¹, a relatively stable new metabolic state with a 60 to 35% splitting was assumed at dilution rates of 0.3 h⁻¹ and higher. Basically, all major fluxes at the PEP-pyruvate-OAA node—the main switch point of carbon metabolism (40)—varied discontinuously with dilution rate and exhibited distinct extremes between dilution rates of 0.05 h⁻¹ and 0.2 h⁻¹ (Fig. 8B and C). This discontinuity of fluxes demonstrates also the danger of deriving general conclusions from flux data (and possibly also related data such as metabolomics) that are obtained at a single dilution rate.

FIG. 8.

Growth rate dependence of relative fluxes through key metabolic pathways in glucose-limited chemostat culture. The gluconeogenic flux in panel C represents the sum of the PEP carboxykinase (Ppc) and malic enzyme fluxes. The trend lines were drawn by hand.

By investigating arbitrarily chosen dilution rates, in vivo glyoxylate shunt activity in slow-growing, glucose-limited chemostat cultures of E. coli was previously described (13, 33). Based on the observation that most of the (otherwise anabolic) glyoxylate shunt flux must eventually be rechanneled into catabolism, it has been argued that shunt flux under glucose conditions is best understood in a network context by its conjoint operation with the flux through the gluconeogenic PEP carboxykinase in the so-called PEP-glyoxylate cycle (13). While this cycle operates in parallel to the TCA cycle, its activity is discernible from two main observations: (i) anaplerotic fluxes far in excess of the anabolic requirements for TCA cycle intermediates and (ii) extensive gluconeogenic fluxes through PEP carboxykinase and/or malic enzyme. While our data are in qualitative agreement with this hypothesis, we additionally detected a small but significant contribution to this cycle by flux through the gluconeogenic malic enzyme. Why does this PEP (pyruvate)-glyoxylate cycle exhibit such pronounced discontinuous behavior with different dilution rates? Generally, all key reactions of the cycle are subject to the regulatory phenomenon known as catabolite repression (37), in which glucose represses the expression of several metabolic genes (15, 16, 34, 35). Since the residual glucose concentration is very low in glucose-limited cultures but increases with dilution rate, the stringency of catabolite repression increases likewise (3, 10, 24, 27, 36), and decreased PEP (pyruvate)-glyoxylate cycle activity at higher dilution rates is an expected consequence. At present, it remains unclear whether the highly reproducible decrease of PEP (pyruvate)-glyoxylate cycle flux at dilution rates below 0.05 h⁻¹—and the concomitant overproduction of NADPH (Fig. 7 and 8B)—is an adaptive behavior of the culture, results from a yet-unknown regulatory phenomenon, or results simply from discontinuous medium flow at these extremely low flow rates. The last possibility is the least likely because we observed a similar phenomenon also in a 1-liter chemostat with 100-fold-higher flow rates (E. Fischer and U. Sauer, unpublished). Moreover, it should be noted that the fine-tuning of regulatory processes, in particular, catabolite repression (33), often varies between different strains, and these differences will impact fluxes more directly under glucose limitation than in batch cultures with excess glucose.

The extraordinary low medium requirements of the novel mini-scale chemostat are particularly relevant for the stable-isotope experiments performed here that require expensive substrates. Comparing a standard 1-liter stirred-tank reactor with the mini-scale chemostats for a typical flux experiment with 20% [U-¹³C]glucose and eight mutants/conditions, costs are reduced by a factor of 100 and time by a factor of 8 (Table 2). Even if [¹³C]glucose is added for only one volume change, the costs are still 12-fold lower. Beyond ¹³C experiments, we believe that this mini-scale system may also be useful for other applications and can easily be set up in other labs because it is built from fairly standard equipment.

TABLE 2.

Comparison of the novel parallel mini-scale chemostat system and a conventional continuously stirred tank fermentor for metabolic-flux analysis^a

Method	Culture vol (liters)	No. of parallel bioreactors	Total duration of expt (days)	Total medium consumption (liters)	Costs in labeled glucose (U.S.$)
Parallel mini-scale chemostat	0.01	8	4	0.66	13.2
Conventional continuously stirred tank fermentor	1	1	32	66	1,320

^aAnalyses were performed on eight strains at a dilution rate of 0.1 h⁻¹ and with 1 g per liter of 20%[U-¹³C]glucose and 80% natural glucose in the medium.