Pure-Culture Growth of Fermentative Bacteria, Facilitated by H₂ Removal: Bioenergetics and H₂ Production

Abstract

We used an H₂-purging culture vessel to replace an H₂-consuming syntrophic partner, allowing the growth of pure cultures of Syntrophothermus lipocalidus on butyrate and Aminobacterium colombiense on alanine. By decoupling the syntrophic association, it was possible to manipulate and monitor the single organism's growth environment and determine the change in Gibbs free energy yield (ΔG) in response to changes in the concentrations of reactants and products, the purging rate, and the temperature. In each of these situations, H₂ production changed such that ΔG remained nearly constant for each organism (−11.1 ± 1.4 kJ mol butyrate⁻¹ for S. lipocalidus and −58.2 ± 1.0 kJ mol alanine⁻¹ for A. colombiense). The cellular maintenance energy, determined from the ΔG value and the hydrogen production rate at the point where the cell number was constant, was 4.6 × 10⁻¹³ kJ cell⁻¹ day⁻¹ for S. lipocalidus at 55°C and 6.2 × 10⁻¹³ kJ cell⁻¹ day⁻¹ for A. colombiense at 37°C. S. lipocalidus, in particular, seems adapted to thrive under conditions of low energy availability.

In anoxic environments, syntrophic organisms play an important role in the degradation of organic material (20). In syntrophic degradation, a single substrate is consumed by the concerted action of two or more microorganisms which are incapable of consuming the substrate individually. This process is mediated by interspecies electron transfer, and H₂ is a key intermediate. H₂ is both a product of fermentation reactions and a substrate for terminal electron-accepting processes such as methanogenesis and sulfate reduction. In the absence of an H₂-consuming organism, the H₂ partial pressure (P_H2) rapidly reaches a level that thermodynamically inhibits further fermentation. This has led to great difficulty in growing the H₂-producing organisms that perform these processes in pure cultures, although many of them are capable of pure culture growth on alternate substrates (7, 17, 25).

Valentine et al. (29) designed a culture vessel that purges H₂ as it is produced and then used this apparatus to grow an ethanol-oxidizing syntrophic organism in the absence of an H₂-consuming partner. By decoupling the syntrophic association, it is possible to manipulate the single organism's growth environment, to quantify the concentrations of catabolic substrates and products, and to calculate the Gibbs free energy (ΔG) available to the fermentative organisms under these conditions. The ΔG of a reaction is dependent on both the temperature and the concentrations of the reactants and products, such that, for the reactions shown in Table 1, ΔG is defined by the following equations:

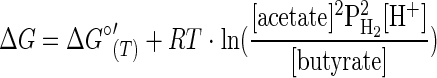(1)

(2)

where ΔG°′_(T) is the Gibbs free energy yield for the reaction under standard conditions, corrected for the entropy change caused by variation of the temperature (−TΔS); T is the temperature (kelvin); and R is the universal gas constant (0.008314 kJ K⁻¹ mol⁻¹). A more negative value indicates a more energetically favorable reaction.

TABLE 1.

Organisms and reactions studied, with their standard Gibbs free energy and entropy changes at pH 7 and a temperature of 298 K

Organism	Reaction	ΔG°′ (kJ mol−1)	ΔS° (kJ mol−1 K−1)	Reference
Syntrophothermus lipocalidus	CH3CH2CH2COO− + 2H2O → 2CH3COO− + 2H2 + H+	48.3	0.159	24
Aminobacterium colombiense	CH3CH(NH3+)COO− + 2H2O → CH3COO− + CO2 + NH4+ + 2H2	2.7	0.402	1

Previous studies (5, 10, 11, 12) have suggested that during syntrophic degradation, P_H2 is thermodynamically controlled in such a way that a constant ΔG is maintained over time, despite changes in environmental conditions. This critical ΔG value should correspond to the minimum energy quantum that can be harnessed to support microbial metabolism. This has generally been considered to be equal to the amount of energy required for the synthesis of one-fourth to one-third a mole of ATP (∼15 to 20 kJ mol⁻¹) (19), but a number of experimental (4, 6, 7, 10, 12, 21, 22) and theoretical (9, 14) studies point to microbial metabolism proceeding at ΔG values closer to thermodynamic equilibrium.

In order to address these issues for pure cultures of H₂-producing syntrophic organisms, we used the H₂-purging culture vessel to study the energetics of butyrate and alanine consumption by pure cultures of Syntrophothermus lipocalidus and Aminobacterium colombiense (Table 1). We measured H₂ production and calculated Gibbs free energy yields for various purging rates, concentrations of products and reactants, and temperatures. We also used cell counts to determine the cellular maintenance energy for each organism.

MATERIALS AND METHODS

Culture apparatus.

Cultures were grown in the H₂-purging culture vessel described by Valentine et al. (29). The reactor continuously purges a liquid culture with H₂- and O₂-free gas (80% N₂, 20% CO₂), replacing the H₂-consuming syntrophic partner. Downstream from the culture vessel, a gas chromatograph is used for automated measurements of the H₂ concentration.

Cultures and growth conditions.

A pure culture of Syntrophothermus lipocalidus (24) was obtained from Yoichi Kamagata (National Institute of Bioscience and Human Technology, Agency of Industrial Science and Technology, Japan) and was grown on a medium containing the following reagents (per liter): 0.15 g KH₂PO₄, 0.5 g NH₄Cl, 0.2 g MgCl₂ · 6H₂O, 0.15 g CaCl₂ · 2H₂O, 2.5 g NaOH, 0.3 g Na₂S · 9H₂O, 0.3 g cysteine HCl, 1 ml trace metal solution, and 1 ml vitamin solution. The trace metal solution contained the following reagents (per liter): 5.0 g sodium EDTA dihydrate, 1.5 g CoCl₂ · 6H₂O, 1.0 g MnCl₂ · 4H₂O, 1.0 g FeSO₄ · 9H₂O, 1.0 g ZnCl₂, 0.4 g AlCl₃ · 6H₂O, 0.3 g Na₂WO₄ · 2H₂O, 0.2 g CuCl₂, 0.2 g NiSO₄ · 6H₂O, 0.1 g H₂SeO₃, 0.1 g H₃BO₃, and 0.1 g Na₂MoO₄ · 2H₂O. The vitamin solution contained the following reagents (per liter): 2.0 mg biotin, 2.0 mg folic acid, 10.0 mg pyridoxine HCl, 5.0 mg thiamine HCl, 5.0 mg riboflavin, 5.0 mg calcium panthothenate, 0.1 mg vitamin B₁₂, 5.0 mg p-aminobenzoate, and 5.0 mg lipoic acid. The pH was adjusted to 6.2.

For initial growth, the medium was supplemented with crotonate to a concentration of 10 mM, and 10 ml was inoculated with 1 ml of the S. lipocalidus stock culture. After dense growth was observed, 5 ml of the resulting culture was used to inoculate 141 ml of the original medium, amended with butyrate to a concentration of 15.5 mM. The medium had been sparged in the H₂-purging culture vessel prior to inoculation. The culture was grown at 55°C, and the flow rate of the N₂-CO₂ gas mixture was 20 cm³ min⁻¹ (all flow rates were normalized to standard temperature and pressure). Butyrate was assumed to be the sole substrate supporting growth, as other organic amendments, namely, cysteine, do not support growth of this organism (24).

Aminobacterium colombiense (1) was obtained from the German Collection of Microorganisms and Cell Cultures (DSM 12261). The medium for A. colombiense contained the following reagents (per liter): 0.3 g KH₂PO₄, 0.3 g NH₄Cl, 0.4 g MgCl₂ · 6H₂O, 0.15 g CaCl₂ · 2H₂O, 0.5 g KCl, 1.00 g NaCl, 0.3 g Na₂S · 9H₂O, 0.3 g cysteine-HCl, 143 mg yeast extract, and 1 ml each of the trace element and vitamin solutions described above. The pH was adjusted to 7.3.

This medium was amended with 10 mM serine for the initial growth of A. colombiense. After dense growth was observed, 3 ml was used to inoculate 300 ml of the medium described above, amended with alanine to a concentration of 10 mM. The culture was grown at 37°C, and the gas flow rate was 20 cm³ min⁻¹. Alanine was assumed to be the primary substrate for growth of this organism, as amendments of additional organic compounds, namely, yeast extract and cysteine, were added at substantially lower concentrations than alanine. This assumption was supported by the observed fermentation balance, with 2.4 mmol alanine yielding 2.0 mmol acetate and 5.3 mmol H₂. Yeast extract does not support the growth of A. colombiense, but cysteine has been shown to serve as a growth substrate for this strain (1). The simultaneous oxidation of cysteine (present at a concentration of 1.9 mM) and alanine (10 mM) would cause a slight underestimation in the calculated cell-specific maintenance energy, although the calculated values of ΔG for alanine consumption would remain unchanged.

Experimental manipulations.

S. lipocalidus was used to determine the influence of the sparging gas flow rate on the production of H₂. The gas flow rate was set, and the response was monitored and recorded over 10-min intervals until a new steady-state P_H2 was reached. The flow rates used were 5, 10, 20, and 40 cm³ min⁻¹.

The effect of excess acetate (catabolic end product) on H₂ production was also investigated with S. lipocalidus. Small volumes of sterile, anoxic acetate (1.5 ml, 1.0 M) were added to the culture vessel, and the H₂ concentration was recorded at 10-min intervals. Once a steady state was reached, a 3-ml liquid sample was taken from the vessel for analysis of the pH as well as the acetate and butyrate concentrations.

Experiments were also performed to determine the effect of temperature on P_H2 in both S. lipocalidus and A. colombiense cultures. The incubation temperature was changed, and the concentration of H₂ flowing from the vessel was measured at 5-min intervals until a steady state was reached. The temperatures ranged between 45°C and 62.5°C for S. lipocalidus and between 20°C and 42°C for A. colombiense and were all within the known growth range for each organism (1, 24).

Sampling and analytical methods.

Throughout the course of the experiments, 8-ml liquid samples were removed from the culture vessels to measure the pH, substrate and product concentrations, and bacterial cell density. Five milliliters of each sample was used for organic acid analysis. These samples were filtered through 0.2-μm filters and stored frozen at −20°C. Samples were analyzed within 2 months of collection. Two-milliliter samples were used for bacterial cell counts.

Organic acid concentrations (acetate and butyrate) were analyzed by high-performance liquid chromatography (LC-600; Shimadzu Corp., Kyoto, Japan), using an organic acid column (IOA-1000; Alltech) and a UV/VIS detector (SPD-6AV; Shimadzu Corp., Kyoto, Japan) at 210 nm (0.5 mM H₂SO₄ mobile phase, 0.6 ml min⁻¹, 200-μl sample loop). Standards at known concentrations were analyzed in duplicate to calibrate the instrument. Alanine was quantified by an enzymatic assay using alanine aminotransferase and lactate dehydrogenase (32). The concentration of H₂ in the gas flowing out of the reaction vessel was measured using a gas chromatograph equipped with a reducing gas analyzer (Trace Analytical, Menlo Park, CA), as described by Valentine et al. (29). Bacterial cell counts were determined by DAPI (4′,6′-diamidino-2-phenylindole) staining (18).

Thermodynamic calculations.

The ΔG°′ value for each reaction was calculated by using the standard Gibbs free energies of formation for products and reactants shown in Table 2 and then corrected for temperature by using the following equation: ΔG°′_(T) = ΔG°′ − ΔS(T − 298). The ΔS value for each reaction was determined by using the standard entropy values shown in Table 2.

TABLE 2.

Standard Gibbs free energy and entropy values

Compound	ΔGa (kJ mol−1)	ΔSb (kJ mol−1 K−1)
CO2(g)	−394.36	0.2130
H2O(l)	−237.17	0.0699
H2(g)	0	0.1307
Alanine(aq)	−371.54	0.1321c
NH4+(aq)	−79.37	0.1134
Acetate(aq)	−369.41	0.0866
Butyrate(aq)	−352.63	0.1358d
H+	0	0

^aValues are from reference 27.

^bValues are from reference 16, except those for alanine and butyrate.

^cFrom reference 15.

^dCalculated from reference 5.

ΔG values over the course of the experiments were calculated using measured values for P_H2 and the concentrations of acetate, butyrate, and alanine (interpolated when necessary). Ammonium concentrations were calculated based on the initial concentration in the medium and were assumed to increase in stoichiometric proportion to hydrogen production in the case of A. colombiense. P_CO2 was assumed to remain constant at 0.2 atm. pH measurements were used to determine the proton concentration and to correct for the effect of nonstandard pH conditions on ΔG (−5.69 kJ mol⁻¹ per pH unit).

RESULTS

Growth and bioenergetic patterns.

By using an H₂-purging culture vessel, pure cultures of S. lipocalidus and A. colombiense were able to produce acetate from butyrate and alanine, respectively, coupled with growth (Fig. 1A and B; Table 3). For both organisms, this was accompanied by an initial increase in P_H2, reaching a maximum of 87 Pa at 173 h in the S. lipocalidus culture and of 52 Pa at 113 h in the A. colombiense culture (Fig. 1C and D). After this point, as the depletion of reactants and the accumulation of products made the reaction less energetically favorable, P_H2 decreased. This maintained ΔG at a nearly constant value for the remainder of each experiment (Fig. 1E and F). During that time, the mean ΔG (±standard deviation) was −10.3 ± 1.1 kJ mol butyrate⁻¹ (n = 8) for S. lipocalidus and −57.2 ± 1.1 kJ mol acetate⁻¹ (n = 4) for A. colombiense.

FIG. 1.

Catabolism and bioenergetics of S. lipocalidus and A. colombiense. (A) Consumption of butyrate (open circles) and production of acetate (filled circles) in S. lipocalidus. (B) Consumption of alanine (open triangles) and production of acetate (filled triangles) in A. colombiense. (C and D) Time course changes of hydrogen partial pressure. (E and F) ΔG values calculated for measured concentrations of products and reactants.

TABLE 3.

Cell-specific bioenergetics

Organism	Time (h)	Cell density (106 cells ml−1)	Cell-specific H2 production rate (10−14 mol cell−1 day−1)	Cell specific energy yield (10−12 kJ cell−1 day−1)	Mass specific energy yielda (kJ h−1 mol C−1)
S. lipocalidus	140	9.0	50.2	3.38	16.9
	175	7.3	73.1	3.84	19.2
	275	34.2	10.4	0.46	2.3
	355	19.7	9.6	0.49	2.5
	428	16.0	7.7	0.37	1.9
	475	4.4	2.3	1.25	6.3
	595	3.2	2.1	1.26	6.3
	640	3.0	2.6	1.50	7.5
A. colombiense	44	3.9	12.3	4.50	22.5
	162	77.7	2.4	0.68	3.4
	213	78.9	2.0	0.56	2.8
	287	69.2	1.7	0.48	2.4

^aAssuming one cell = 100 fg C.

It was also possible to calculate cell-specific energy yields using cell numbers from DAPI counts, hydrogen production rates, and the Gibbs free energy yields calculated for measured concentrations of products and reactants at each point (Table 3). During the exponential growth phase, the energy yields were 3 × 10⁻¹² to 4 × 10⁻¹² kJ cell⁻¹ day⁻¹ for both S. lipocalidus and A. colombiense, but later in the experiment, they dropped as low as 3.7 × 10⁻¹³ kJ cell⁻¹ day⁻¹ for S. lipocalidus and 4.8 × 10⁻¹³ kJ cell⁻¹ day⁻¹ for A. colombiense.

Purging rate.

Increasing the flow of the gas purging the culture vessel increases the removal rate of H₂. If the rate of hydrogen production does not change and if gas exchange is 100% efficient, doubling the purging rate would be expected to decrease the P_H2 by half, which would then change the ΔG of the reaction. In order to maintain a constant ΔG, the H₂ production rate would have to double as well, thereby keeping P_H2 constant. In S. lipocalidus cultures, the P_H2 changed in response to variations in the purging rate (Fig. 2A), but it changed less than would be predicted if the hydrogen production rate had remained constant at its initial value (predicted P_H2 values are shown by dotted lines in Fig. 2A). At a purging rate of 5 cm³ min⁻¹, the change was just 28% of what was predicted, and it was 34% of the predicted change at 10 cm³ min⁻¹ and 68% of the predicted change at 40 cm³ min⁻¹. This was possibly related to the efficiency of H₂ transfer from aqueous to gas phase.

FIG. 2.

Effect of purging gas flow rate on S. lipocalidus. (A) P_H2 over the course of the experiment. Vertical dashed lines indicate the times the purging rate was changed, with the rates given in cm³ min⁻¹. Horizontal dotted lines represent the P_H2 expected if the H₂ production rate remained constant at its initial value while the purging rate was changed from 20 cm³ min⁻¹. (B) H₂ production rate after stabilization at each purging rate. (C) Response of ΔG, calculated for steady-state P_H2 at each purging rate. The dashed line indicates the ΔG values expected if the H₂ production rate had remained constant at its initial value at the 20 cm³ min⁻¹ purging rate.

A difference between high and low purging rates was also observed in the hydrogen production rates (Fig. 2B), which increased as the purging rate increased but leveled off at high purging rates. Because of the changes in P_H2 over the course of the experiment, the calculated ΔG values varied between −9.1 and −14.6 kJ mol⁻¹, becoming more negative as the purging rate increased (Fig. 2C). This range is smaller than what would be predicted from the P_H2 values that would result if the hydrogen production rate had remained constant at its initial value (dashed line in Fig. 2C), with the greatest deviation at the lowest purging rate, 5 cm³ min⁻¹.

End product addition.

The accumulation of catabolic end products causes the ΔG of a reaction to become less energetically favorable. Therefore, in the absence of any other changes to the system, adding acetate, one of the end products of butyrate fermentation in S. lipocalidus, would be expected to cause an increase in ΔG. However, acetate additions caused the partial pressure of H₂, the other end product, to decrease (Fig. 3A). This decrease in P_H2 more than compensated for the change in ΔG attributed to increased acetate, causing ΔG to decrease slightly, from −10.1 to −12.9 kJ mol⁻¹ (Fig. 3B).

FIG. 3.

Effect of acetate concentration on S. lipocalidus. (A) Response of P_H2 to acetate. Dashed lines indicate times of acetate additions, and measured concentrations (mM) are noted. (B) Response of ΔG, calculated for the steady-state P_H2, at each acetate concentration. The dashed line indicates the ΔG values that would be expected if P_H2 had remained constant while acetate was added.

Temperature.

Temperature affects ΔG both through its effect on entropy (−TΔS) and through its effect on the RT(ln Q) term. For both reactions in Table 1, this leads to a more negative ΔG at higher temperatures in the absence of other changes. In both S. lipocalidus and A. colombiense cultures, the P_H2 increased in response to temperature increases and decreased in response to decreases (Fig. 4A and C). These changes in P_H2 were sufficient to balance the opposing effects of temperature variation, and ΔG remained constant throughout the course of the experiment (Fig. 4B and D). The mean ΔG value was −11.3 ± 0.6 kJ mol⁻¹ (n = 5) for S. lipocalidus and −58.6 ± 0.7 kJ mol⁻¹ (n = 11) for A. colombiense.

FIG. 4.

Effect of temperature on P_H2 of S. lipocalidus (A) and A. colombiense (C). Dashed lines indicate times of temperature changes, and the temperatures (°C) are noted. (B and D) Responses of ΔG, calculated for the steady-state P_H2 at each temperature, for S. lipocalidus (B) and A. colombiense (D). Dashed lines indicate the ΔG values that would be expected if the concentrations of products and reactants had remained at their initial values while the temperature changed.

DISCUSSION

Hydrogen production and Gibbs free energy yields.

As seen in the initial study using the H₂-purging culture vessel (29) and as also observed in other studies with true syntrophic organisms (21), these experiments showed that thermodynamics are an important control on hydrogen production in cultures of H₂-producing syntrophic organisms. When faced with changes in environmental conditions that would alter the Gibbs free energy yield, hydrogen production always shifted in such a way as to minimize the change in ΔG. In the case of the purging rate experiment, hydrogen production increased with increasing purging rates but apparently could not “keep up” with the increased removal rates. This may have been partially due to inefficient H₂ transport between the culture medium and the purging gas at higher flow rates or because the culture lacked a sufficient number of cells to sustain the higher rates of hydrogen production. The concentration of H₂ is measured in the purging gas exiting the culture vessel, but this will necessarily be lower than the concentration at the H₂-producing cell (2). This leads to a slight underestimation of P_H2, and consequently, the energy available is actually somewhat lower than that calculated (ΔG is less negative). With more rapidly flowing gas, bubbles become larger, possibly causing a kinetic limitation.

With the exception of the purging rate experiment, the critical ΔG value for each species remained fairly constant between experiments, but the values for S. lipocalidus and A. colombiense were distinct. For S. lipocalidus, the energy yields ranged between −8.8 and −12.8 kJ mol butyrate⁻¹, well below the −20 kJ mol⁻¹ that has generally been considered the theoretical minimum. This theoretical minimum was based on several assumptions considered by Schink (19) and Hoehler et al. (10), as follows. (i) The ATP/ADP ratio inside the cell is 10:1. The ΔG value required for phosphorylation of ADP would then be 49 kJ mol⁻¹. (ii) Cellular metabolism is not 100% efficient. Including energy lost as heat, ATP formation must require at least 60 kJ mol⁻¹. (iii) The translocation of three cations is required for the synthesis of one ATP molecule. The energy required for translocation of one ion is equal to the minimum quantum of biologically useful energy.

However, there are a number of reported observations of organisms capable of metabolism at ΔG values below this theoretical minimum (4, 6, 7, 10, 12, 21, 22; this study). Although some of these very low values may have been observed in cells not actually growing and synthesizing ATP, it is clear that one or more of these assumptions does not hold true for organisms adapted to a low-energy lifestyle. It has been suggested that organisms may vary the number of protons translocated to produce ATP (14), and recent results showed that in some organisms the translocation of four, or even five, ions may be coupled to produce one ATP (13, 26, 30). This would bring the minimum Gibbs free energy requirement down to −12 or −15 kJ mol⁻¹ (20), though this is still higher than the values reported in most of the studies referenced above.

Maintenance energy.

Maintenance energy can be considered the rate of energy consumption necessary to simply maintain cellular integrity (9). Tijhuis et al. (28) calculated maintenance energy requirements for microorganisms, both heterotrophic and autotrophic, under aerobic and anaerobic conditions over a large temperature range (5°C to 75°C). They determined that the maintenance energy (m_E), in kJ per hour per mole of biomass carbon, is primarily a function of temperature, related in anaerobic prokaryotes by the following equation:

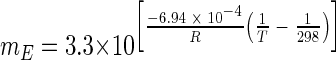(3)

where R is the universal gas constant in J K⁻¹ mol⁻¹ and T is the temperature (K). Using this equation, the predicted maintenance energy requirement for S. lipocalidus at 55°C is 42.7 kJ h⁻¹ mol C⁻¹, and the value is 9.7 kJ h⁻¹ mol C⁻¹ for A. colombiense at 37°C. However, in order to compare these theoretical values to those observed in this study, calculated using the cell-specific hydrogen production rate and the Gibbs free energy yield per mole of H₂, it was necessary to relate cell counts to biomass. We assumed that an average cell contained 100 fg carbon, which is toward the low end of the range observed in cultures but higher than what is observed in natural marine systems (3, 8, 23, 31). The converted energy yields are proportional to the conversion factor; therefore, they could be somewhat higher or lower than those shown in Table 3. The inclusion of inactive cells in cell counts could also cause our values to be slightly underestimated.

Early in the experiment, when the cell number was increasing, the energy yield reflected both the maintenance energy and the energy needed for growth. Near the end of the experiment, when the cell number was decreasing, the energy yield may have been less than the amount required for maintenance. Between these points, when cell numbers were fairly constant, the energy yield was taken as a reasonable approximation of the cellular maintenance energy. The limited amount of data made it difficult to determine exactly where the cell numbers peaked; the peak appeared to lag slightly behind hydrogen production. For S. lipocalidus, the best estimate of maintenance energy was at 270 h, with a value of 2.3 kJ h⁻¹ mol C⁻¹. For A. colombiense, cell numbers remained fairly constant between 162 h and 213 h, and the energy yields at these points were 3.4 and 2.8 kJ h⁻¹ mol C⁻¹.

For both organisms, the observed values were lower than the theoretical maintenance energies at these temperatures. For A. colombiense, some of this discrepancy may be due to the simultaneous consumption of cysteine. However, this discrepancy was greater for S. lipocalidus, which had a maintenance energy more than an order of magnitude below the value predicted by Tijhuis et al. (28) (2.3 versus 42.7 kJ h⁻¹ mol C⁻¹). Despite the uncertainties in our calculations, these results support the findings of Scholten and Conrad (21), who determined m_E values for the syntrophic consumption of propionate in a chemostat and also used data in the literature to calculate m_E values for the consumption of ethanol by both syntrophic organisms and pure cultures. In nearly every case, the value of m_E was lower than the value predicted by the equation of Tijhuis et al. (28), by up to an order of magnitude. It appears that maintenance energies for syntrophic organisms may be significantly lower than those for other bacteria, perhaps because they are adapted to conditions of perpetual energy stress.