The Influence of Prior Choices on Current Choice

Abstract

Three pigeons chose between random-interval (RI) and tandem, continuous-reinforcement, fixed-interval (crf-FI) reinforcement schedules by pecking either of two keys. As long as a pigeon pecked on the RI key, both keys remained available. If a pigeon pecked on the crf-FI key, then the RI key became unavailable and the crf-FI timer began to time out. With this procedure, once the RI key was initially pecked, the prospective value of both alternatives remained constant regardless of time spent pecking on the RI key without reinforcement (RI waiting time). Despite this constancy, the rate at which pigeons switched from the RI to the crf-FI decreased sharply as RI waiting time increased. That is, prior choices influenced current choice—an exercise effect. It is argued that such influence (independent of reinforcement contingencies) may serve as a sunk-cost commitment device in self-control situations. In a second experiment, extinction was programmed if RI waiting time exceeded a certain value. Rate of switching to the crf-FI first decreased and then increased as the extinction point approached, showing sensitivity to both prior choices and reinforcement contingencies. In a third experiment, crf-FI availability was limited to a brief window during the RI waiting time. When constrained in this way, switching occurred at a high rate regardless of when, during the RI waiting time, the crf-FI became available.

Thorndike (1911) originally proposed a “law of exercise” along with a positive and negative “law of effect.” According to the law of exercise:

Any response to a situation will, other things being equal, be more strongly connected with the situation in proportion to the number of times it has been connected to that situation and to the average vigor and duration of the connections. (p. 244)

We can translate Thorndike's language into choice-based terms:

Choice of any alternative from a given set of alternatives will, other things being equal, increase in probability in proportion to the number of times that alternative has been chosen in the past from that set of alternatives.

Thorndike later abandoned both the negative law of effect and the law of exercise. It is now generally agreed that he was wrong to have abandoned the negative law of effect (Rachlin & Herrnstein, 1969). Was he also wrong to have abandoned the law of exercise?

Although Guthrie (1935) based his theory of learning entirely on the principle of exercise, modern theories of choice have ignored it. The generalized matching law (Baum, 1974), for example, describes choice as a function of parameters of reinforcement (rate, amount, delay, and so forth) contingent on one or another choice. Theories derived from matching such as Fantino's delay reduction theory (Fantino & Abarca, 1985) also are phrased in terms of choice as a function of its consequences—not as a function of prior choices. Economic maximization theory (Rachlin, Battalio, Kagel, & Green, 1981) is explicit in disregarding prior choices. Organisms are said to choose so as to maximize utility; to do this, current choices must be focused entirely on the future. In any kind of maximization theory, whether momentary (Shimp, 1966) or long-term (Rachlin et al., 1981), the past is meaningful only to the extent that it predicts or determines future value. Otherwise it should be ignored. Your decision to buy or sell a stock, for instance, should not be influenced by the fact that you bought or sold it in the past but only by whether you believe it will go up or down in the future. Economists call those past choices “sunk costs.” If you did use such past choices to guide your present behavior (given that those choices themselves did not affect future value), you would have committed the “sunk-cost fallacy.”

The only conceivable biological advantage of past choices as such influencing present choice is if past choices had been based on more valid information about the future than are present choices; this (more valid) information might be obscured at the present time by current incentives. Such a reason for the sunk-cost effect would be psychological, not economic, and would apply in situations requiring self-control. We shall return to this issue in the General Discussion.

The present experiments attempted to test the law of exercise with pigeons by exposing them to a continuous choice between two concurrent schedules where reinforcer parameters—probability, delay, amount—of each alternative remained constant over time. In Experiment 1, as time passed between reinforcers, nothing changed except the pigeons' own prior choices. If, between reinforcers, a pigeon's current choice varied as a function of its prior choices, it could only have been because of the influence of those prior choices. The finding that current choice varied directly with prior choices would be evidence for a positive law of exercise; the finding that current choice varied inversely with prior choices would be evidence for a negative law of exercise.

At the beginning of each session and after a 3-s postreinforcement blackout that followed each reinforcer delivery in Experiment 1 (Condition 2), the pigeons were exposed to two lit keys. The purpose of the blackout was to increase the salience of the start of the random-interval (RI) waiting period. Pecks on one key were reinforced on an RI schedule; pecks on the other key were reinforced on a tandem continuous-reinforcement, fixed-interval (crf-FI) schedule. In the tandem schedule, the fixed interval did not start to time out until the crf-FI key was pecked. Moreover, that first peck on the crf-FI key turned off the RI keylight and made RI pecks ineffective. The values of the RI and crf-FI schedules were 60 s and 14 s. These intervals kept the average immediacy of the rewards constant as long as both alternatives were available.

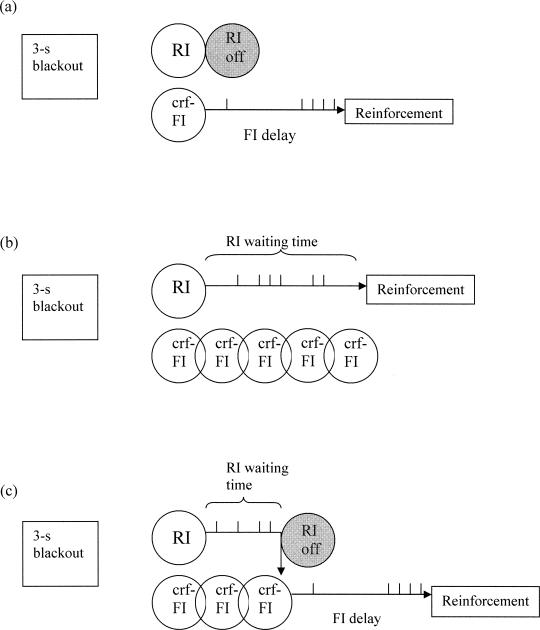
As long as the pigeon pecked exclusively on the RI key, both keys remained available. Therefore, at any point prior to RI reinforcement the pigeon could either (a) continue pecking the RI key until an RI peck eventually was reinforced, or (b) switch to the crf-FI key. If the pigeon switched, the RI key became unavailable until the crf-FI reinforcer had been obtained and a 3-s postreinforcement blackout had elapsed. Figure 1 illustrates the three possible postreinforcement sequences of responding. The first (a) shows the case where the pigeon's first peck is on the crf-FI; the RI key becomes unavailable and the FI delay begins. The second two cases (b and c) show the two possible sequences given that the first peck was on the RI key. In the middle sequence (b) the pigeon pecks the RI key and keeps pecking it exclusively (RI waiting time) until reinforcement is obtained. In the lower sequence (c) the pigeon pecks the RI key initially, pecks it for a while without reinforcement, then switches to the crf-FI key. At that point the RI key becomes unavailable and the FI schedule begins.

Fig 1. Schematic representation of the three possible response patterns during an interreinforcement interval (IRI), after a 3-s blackout or at the beginning of the session.

The upper diagram (a) illustrates the case in which the IRI starts with a peck on the crf-FI key, after which the RI key becomes unavailable and the FI delay begins to elapse. The next two diagrams (b and c) correspond to the two possible sequences given that the first peck was on the RI key. The middle diagram (b) illustrates an IRI in which the pigeon continues pecking on the RI key until reinforcement is delivered by that schedule. The lower diagram (c) illustrates an IRI in which the pigeon switches to the crf-FI prior to RI reinforcement. The RI waiting time is the time that elapses, during those IRIs initiated by a peck on the RI key, from that first peck until either (b) reinforcement is delivered in the RI or (c) the RI is abandoned by a switch to the FI. The overlapping representations of the crf-FI key indicate that even though the key is available during pecks to the RI, the FI interval does not start to elapse until the first peck on that key.

The random nature of the RI schedule ensured that the probability of RI reinforcement remained constant regardless of RI waiting time. Immediately after reinforcement, the expected time to reinforcement for pecks on the RI key was 60 s. After waiting any amount of time without RI reinforcement, the expected time to RI reinforcement was still 60 s and remained 60 s regardless of how long the pigeon waited (as long as the pigeon kept pecking the RI key at a normal rate). Correspondingly, the expected time to reinforcement for a switch to the crf-FI key remained constant at the FI value. Also, the amount of reinforcement delivered by either of the two schedules was the same (3 s of access to a hopper with mixed grain). These reinforcement-parameter constancies are the “other things” that both Thorndike's conception of the law of exercise and our relativistic conception of that law require be kept constant.

The choice contingencies of Experiment 1 differ crucially from those in concurrent variable-interval variable-interval (conc VI VI) schedules. In such schedules, the longer the time spent on either alternative without switching, the greater the probability that responding to the other alternative will be reinforced. Momentary maximization theories of choice such as Shimp's (1966) theory rely on this increased probability to explain switching. In Experiment 1, however, probability of reinforcement for switching from the RI to the crf-FI schedule remained constant (the pigeons could not switch from the crf-FI to the RI schedule).

Because the probability of reinforcement of both alternatives remained constant as long as the pigeon pecked the RI key, any choice theories based on reinforcement parameters would predict either: (a) exclusive choice of the more favorable alternative or (b) a constant probability of switching (from the RI to the crf-FI schedule) determined by some relative measure of the constant reinforcer values. If it is found that choice is neither exclusive nor constant but that it varies as a function of how long the pigeon has been pecking on the RI key (RI waiting time), then the variation must be explained in terms of either RI waiting time itself or the number of pecks on the RI key (the only parameters that systematically varied with RI waiting time). If local response rates had varied systematically during RI waiting time, then response rate could conceivably have been used to time the interval. But, as is typically the case with RI schedules, local rates did not vary in any systematic way for any pigeon and so could not have served this function.

Cognitive theories of choice—that is, theories relying on hypothetical internal mechanisms—also could not explain changes in the probability of switching from the RI schedule to the crf-FI schedule. As an example, consider Gibbon's scalar expectancy theory (SET; Gibbon, 1977; Gibbon, Fairhurst, Church, & Kacelnik, 1988). According to SET, the chooser repeatedly samples from a hypothetical internal distribution of prior interreinforcement times and current elapsed time to reinforcement (a pacemaker count). This yields a continuously varying estimate of time-left-to-reinforcement for each alternative. Actual choice is a function of the relative time-left estimates. But, in Experiment 1, as long as both alternatives were available (that is, prior to a switch from the RI to the crf-FI), time-left never changed for either alternative. During the RI waiting time, the time left on the RI 60-s schedule was always 60 s; the time left on the crf-FI schedule was always the FI value. Thus, because the time-left estimates would not change as a function of RI waiting time, SET must predict a constant rate of switching from the RI to the crf-FI, as must any theory that does not account in some way for effects of past choices per se on current choice.

One theory that does account for an influence of past events on current choice is Nevin's behavioral momentum theory (Nevin, Mandell, & Atak, 1983). But those events are past reinforcers, not past choices. In fact, behavioral momentum theory explicitly denies the relevance of past responding to current choice (Nevin & Grace, 2000).

Experiment 1 used the procedure illustrated in Figure 1 to determine whether the probability of a switch from the RI schedule would remain constant, increase, or decrease as a function of time spent pecking on the RI schedule without reinforcement. A constant switch probability over time would be evidence for the absence of an exercise effect in this experiment; a decrease in switch probability over time would be evidence of a positive exercise effect; an increase in switch probability over time would be evidence for a negative exercise effect.

Experiment 1

Method

Subjects

Three male White Carneau pigeons (Palmetto Pigeon Plant) maintained at approximately 80% of their free-feeding weight were housed individually in a colony room, with free access to grit and water, where they were exposed to a 12:12 hr light/dark cycle with controlled temperature. Their weight was monitored before and after each daily session; they received the postsession feeding necessary to maintain their target weights.

Apparatus

Sessions were conducted in four Extra Tall Modular Operant Test Chambers manufactured by MedAssociates, Inc. (30.5 cm wide, 24.1 cm deep, and 29.2 cm tall), each enclosed in a sound-attenuating box equipped with a ventilating fan that masked external noise. Mounted on the front panel of each chamber were three response keys (2.54 cm in diameter) arranged horizontally, 8 cm apart and 20 cm above the floor. The distance from the side walls to the center of each of the two side keys was 4 cm. The keys could be illuminated with green, red, or white light. Only the two side keys were used in this experiment, while the center key remained dark and inoperative. On the back panel of the chamber were three houselights (red, green, and white) that were not used during this experiment. Food reinforcement was access to mixed grain delivered by a food hopper located below the center key, 2 cm above the floor. During reinforcement the hopper was illuminated with white light. All events were controlled by a computer running Med-PC® for Windows.

Procedure

Because all pigeons had had previous experience with similar procedures, it was not necessary to shape their behavior; they were exposed directly to the first condition of the experiment. All sessions lasted 90 min or until 60 reinforcers had been collected, whichever happened first. Sessions started at approximately the same time every day and were run a minimum of 6 days per week.

Condition 1: RI60s Only

In this condition, subjects were exposed exclusively to the RI schedule, which was signaled with a green keylight for all pigeons. At the beginning of the session and 3 s after each reinforcer either the left or the right key was illuminated with green light (sides were assigned randomly after reinforcement). Pecks to the illuminated key were reinforced every 60 s, on average, according to an RI schedule of reinforcement (RI 60 s). In the RI schedule, there was a fixed per second probability (p  =  0.0167) of reinforcement being available. The first peck after reinforcement was set up turned off the keylight and activated the food hopper for 3 s. An interval of 3 s followed reinforcement, during which all lights in the chamber were turned off (blackout). Then either the left or the right key was illuminated again as at the beginning of the session. Pecks to nonilluminated keys had no scheduled consequences. This condition was maintained for 15 sessions.

Condition 2: Modified Concurrent Choice

In this condition (diagrammed in Figure 1), the pigeons chose between the RI 60 s of Condition 1 and a crf-FI 14-s schedule (for Pigeon 3, this was reduced to crf-FI 10 s, as explained below). At the beginning of the session and 3 s after each reinforcer, the left and right keys were illuminated with green and red light. Colors were randomly assigned to each side after reinforcement. Pecks on the RI (green) key had the same scheduled consequences as in the previous condition, and had no effect on availability of the crf-FI schedule. A peck on the crf-FI (red) key turned off the RI key (making it inoperative) and started the crf-FI timer; the first peck after 14 s extinguished the red keylight and activated the hopper for a 3-s reinforcement period. Again, a 3-s blackout followed each reinforcer. This condition was run for 20 sessions. Behavior was judged to be stable well before this point because the hazard functions for each pigeon (see below) showed no apparent change in height or shape after the first 10 sessions.

Condition 3: Exclusive Choice

In this condition, pigeons were again faced with a choice between the RI and the crf-FI (with crf-FI values set at 14 s for Pigeons 1 and 2 and at 10 s for Pigeon 3). The procedure was identical to that of the previous condition, except that the first peck to either key following the blackout eliminated the availability of the other key, and the reinforcer was available only after the corresponding delay. This condition was run for a minimum of 20 sessions after which the proportion of choices over the last five sessions was visually judged to be stable.

Results

Condition 1: RI60s Only

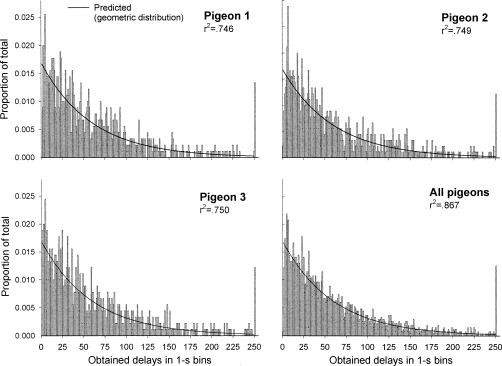
The purpose of this condition was to expose the subjects to the geometric distribution of reinforcement generated by the RI 60-s schedule. Distributions of obtained delays to reinforcement for the 20 sessions of this condition are shown in Figure 2. For each pigeon, the graphs show the proportion of obtained reinforcers at every second, as well as the theoretical geometric distribution of delays expected given the RI schedule value.

Fig 2. Proportion of obtained delays to reinforcement for each pigeon and collapsed across pigeons (bottom right) in the RI 60 s-only condition.

The graphs also present the curve corresponding to the programmed geometric distribution. The proportion of variance accounted for when fitting this function to the data (r-squared) is also shown.

The programmed distribution of delays (y  =  0.0167*(.9833)^(s-1)) was fitted to the data of the obtained delay distributions and the resulting proportion of variance accounted for by the fit for each pigeon is shown in the figure. The arithmetic average delays (scheduled and obtained), as well as their corresponding standard errors, are shown in Table 1. Together, these data show that the program was effective in generating a random distribution of reinforcement delays.

Table 1. Average delays to reinforcement and standard errors (in seconds) for data in the first condition of Experiment 1.

Delays	Pigeon 1		Pigeon 2		Pigeon 3		Overall
	M	SE	M	SE	M	SE	M	SE
Scheduled	58.05	1.94	58.81	1.93	59.82	1.97	58.89	1.12
Obtained	58.96	1.94	59.83	1.93	60.41	1.97	59.73	1.13

Condition 2. RI 60 s—crf-FI 14 s Modified Concurrent Choice

For this condition, the following information was recorded: number of RI and crf-FI initial choices (i.e., the first peck after the keys were lit), number of switches, and time at which each event (responses in RI or crf-FI, switches, and reinforcements) occurred. This information was used to compute the proportion of initial RI choices (number of times during an interreinforcer interval [IRI] in which the first peck occurred on the RI-key divided by total number of IRIs) and the proportion of switches to the crf-FI (number of times the pigeon switched to the crf-FI divided by total number of initial RI choices). The likelihood of a switch to the crf-FI as a function of time spent pecking on the RI key also was computed in order to determine the relation between switching behavior and RI waiting time.

Proportion of Choices and Switches

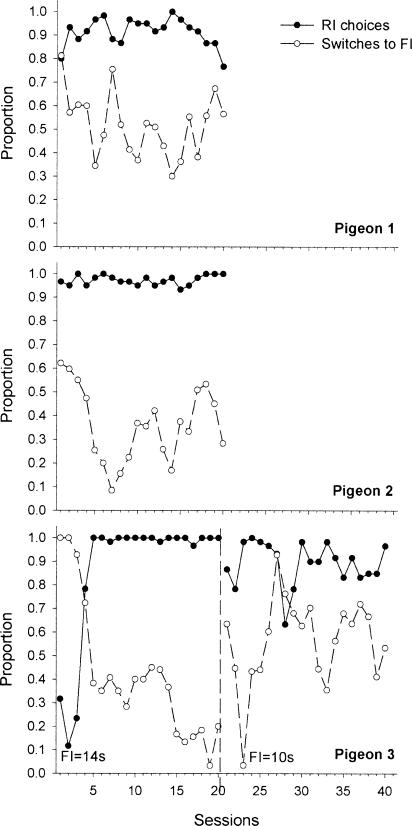
Figure 3 shows, for each pigeon, the proportion of IRIs with initial RI choices in each session, as well as the proportion of those IRIs that ended with a switch to the crf-FI schedule (i.e., the proportion of crf-FI choices conditional on initial RI choice). Note that by the 20th session, the proportion of switches made by Pigeon 3 had decreased and remained below 20%. Because our main interest was in the analysis of switches, the crf-FI value was decreased, for this pigeon only, from 14 s to 10 s. As a result, Pigeon 3's proportion of switches to the crf-FI increased, so that by the end of the second 20 sessions it fluctuated around 50%.

Fig 3. Proportion of RI choices (closed circles) and switches to crf-FI (open circles) for each session in the second condition of Experiment 1.

Note that the graph for Pigeon 3 includes two sections; one corresponding to the sessions run with crf-FI 14 s and the other to crf-FI 10 s.

The figure shows that all pigeons were predominantly starting IRIs by choosing the RI schedule. Table 2 shows the mean proportion of RI choices and switches across sessions and their corresponding standard deviations. For all pigeons, the mean proportion of RI choices was above 85%. That is, pigeons strongly preferred the RI schedule at the beginning of the IRI.

Table 2. Mean proportion of RI choices and switches and standard deviations per session for Condition 2 of Experiment 1.

Proportion	Pigeon 1		Pigeon 2		Pigeon 3
					Phase 1: crf-FI 14 s		Phase 2: crf-FI 10 s
	M	SD	M	SD	M	SD	M	SD
RI choices	0.91	0.06	0.97	0.02	0.87	0.28	0.89	0.09
Switches	0.52	0.14	0.36	0.16	0.42	0.28	0.56	0.19

Note. For Pigeon 3 there are two phases. Phase 1 corresponds to Sessions 1 through 20, with crf-FI 14 s; Phase 2 corresponds to Sessions 21 through 40, where the crf-FI value was decreased to 10 s.

Switching Behavior

Given the initial preferences, it is important to look at the times at which switches occurred between reinforcers in order to determine whether preferences changed as a function of time into the IRI.

For each pigeon, all IRIs during which the RI key was pecked first were taken for analysis. As sections b and c in Figure 1 illustrate, each RI waiting time could end with only one of two events: an RI reinforcer or a switch to the crf-FI. Each RI waiting time was divided into 5-s intervals. The frequencies of switches or RI reinforcements were obtained for each 5-s bin and collapsed across all RI waiting times. All intervals that did not include either of these terminating events were considered time spent “waiting.” A measure of the probability of switching in each interval was computed by dividing the number of switches in each interval by the number of times the pigeon was still waiting at the midpoint of the interval (this measure is known as the hazard rate).

Data were organized in thirty 5-s bins for which the frequency of RI reinforcements and switches were obtained; the 30th bin, starting at 150 s, included all the events from this point forward. This information was used to perform a survival analysis in which the degree of fit of the observed hazard rate to a model that assumes a constant hazard rate (i.e., exponential) was tested. The data were tested against an exponential model because, as explained in the introduction, current models of choice would predict a constant rate of switching to the crf-FI. The hazard rate is the probability of a switch to the crf-FI during an interval, given that the pigeon has stayed (not switched) prior to that point. For each pigeon, the tests showed that the best-fitting exponential model (i.e., the exponential function with the best-fitting parameters) was significantly worse at describing the data than a model that does not assume constant likelihood of switching. The statistical information on the degree of fit of the exponential model is shown in Table 3.

Table 3. Best-fit estimates (Lambda) of an exponential model that assumes a constant hazard rate to the observed rate, with the corresponding standard errors (SE), log-likelihood, chi-square, and significance values, indicating that the obtained distributions are significantly different from the exponential model that assumes a constant rate of switching as a function of waiting time.

Pigeon	Lambda	SE Lambda	Log-likelihood	Chi-square	df	p
1	.053	.004	−1,889.33	166.43	28	p < .001
2	.035	.003	−1,662.90	127.84	28	p < .001
3	.079	.007	−1,986.24	127.78	28	p < .001

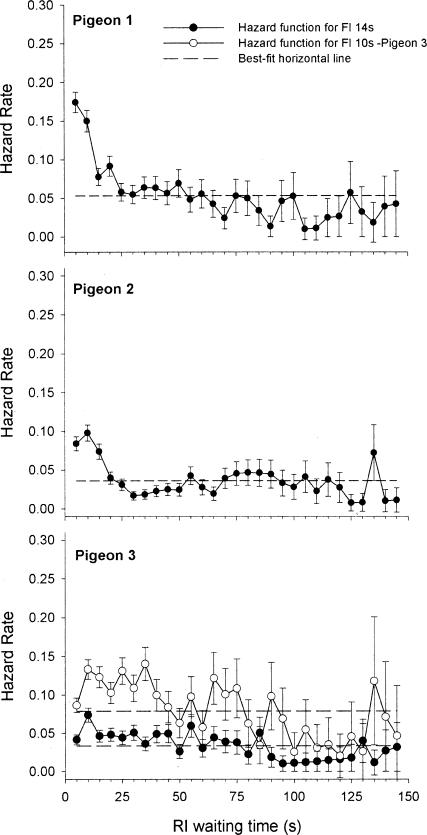
Figure 4 presents the obtained hazard rate functions for each pigeon, along with the best-fitting exponential model (for Pigeon 3, both the crf-FI 14-s and the crf-FI 10-s data are shown). Note that an exponential function is a horizontal line in Figure 4; this is because the likelihood of switching, according to the exponential model, is constant. In all cases, the lack of fit to the exponential model is due to the fact that the points at the beginning of the IRI are consistently above and the points at the end of the IRI are below the line corresponding to the exponential model. In the case of Pigeon 3, the hazard rate function for the crf-FI 14-s phase also follows this general pattern, although it is more horizontal than are those of the other pigeons. In general, the data of Pigeons 1 and 2 are closer to each other than to those of Pigeon 3, which are noisier for the crf-FI 10-s phase. However, although Pigeon 3's initial decrease is not as sharp as that of the other 2 pigeons, its rate of switching also decreases as a function of RI waiting time.

Fig 4. Hazard rate as a function of RI waiting time for all pigeons in the second condition of Experiment 1.

The tics on the x axis correspond to 5-s bins. For Pigeon 3, the two functions correspond to the crf-FI 14-s (closed circles) and the crf-FI 10-s (open circles) phases of the condition. The horizontal dashed lines are best-fit estimates for the exponential model that assumes a constant rate of switching.

Condition 3: Exclusive Choice

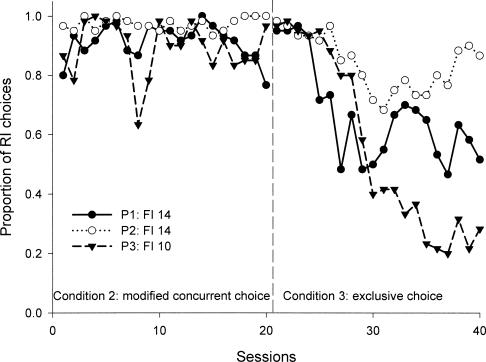
Figure 5 shows the proportion of initial pecks to the RI key for Condition 3. The corresponding data for Condition 2 are repeated here for comparison. Note that the proportion of times an IRI was initiated with a peck to the RI key decreased in Condition 3, when the availability of the crf-FI key was removed contingent on the first RI-peck. The mean proportion of RI choices in the last five sessions of the condition decreased from .91, .97, and .89 in Condition 2, to .60, .79, and .31 in Condition 3 for Pigeons 1, 2, and 3.

Fig 5. Proportion of RI initial choices for each session in Conditions 2 (modified concurrent choice) and 3 (exclusive choice) for each of the 3 pigeons.

Discussion

There were three main results. First, the pigeons did not show exclusive preference for the RI alternative throughout those IRIs where the RI key was pecked first. Although all pigeons initially chose the RI alternative on over 85% of the IRIs, they switched to the crf-FI on more than 35% of those IRIs. Second, preferences exhibited at the beginning changed as time into the IRI progressed. The poor fit to the exponential model (constant switching rate) is due to the fact that pigeons tend to switch more initially than later on during the IRI. Even though the hazard rate was low just after reinforcement, it decreased further as RI waiting time increased. That is, pigeons tended to choose the RI initially and, if not immediately rewarded, were more and more likely to switch to the crf-FI. Third, when the availability of the crf-FI key was removed by introducing a forced-choice procedure, initial preference for the RI decreased.

How would current models of choice explain these data? The pigeons did not maximize reinforcement rate over the session. In order to do that, they would have had to choose the crf-FI schedule exclusively; this would have yielded 3.53 reinforcers per minute. The rate of reinforcement actually obtained was 1.73, 1.36, and 1.95 reinforcers per minute for Pigeons 1, 2, and 3. This result is not surprising because a strong preference for a variable delay mixture over a fixed delay equal to the average delay of the mixture has been observed frequently (Bateson & Kacelnik, 1995, 1996, 1997; Cicerone, 1976; Davison, 1969; Herrnstein, 1964; Killeen, 1968; Mazur, 1984; Navarick & Fantino, 1976). The fixed-delay alternative was initially set at the harmonic average (average immediacy) of the random mixture (and then decreased for Pigeon 3). According to models that assume the maximization of immediacy (e.g., Bateson & Kacelnik, 1996; Mazur, 1984), Pigeons 1 and 2 should have been indifferent between the two alternatives. Yet a strong initial preference for the RI over the crf-FI was found. This preference may have been due to the fact that, in this procedure, subjects were not forced to commit to the random mixture once they chose it, but were allowed to sample it for as long as they chose and then switch. This freedom to leave the RI might have actually increased its initial value (Catania, 1980; Catania & Sagvolden, 1980; Cerutti & Catania, 1997). The results of the third condition seem to support this hypothesis. It seems probable that the RI in Condition 2 was more valuable initially than the crf-FI because of both the RI's potential for immediate reinforcement and the fact that pigeons could leave it any time.

None of these arguments implies that the hazard function should have varied as RI waiting time increased. Recall that, at every second, the prospective value of the alternatives faced by the pigeons was exactly the same; yet the probability of switching to the crf-FI decreased as a function of RI waiting time.

There is some similarity between this experiment and Gibbon and colleagues' time-left procedure (see, e.g., Gibbon & Church, 1981). However, in the time-left procedure, when variable delay mixtures (a truncated geometric distribution) were used, the fixed delay option was always the elapsing comparison and began to elapse at the beginning of the trial and not when subjects chose it (Brunner, Gibbon, & Fairhurst, 1994; Gibbon et al., 1988). Given the contingencies of the present experiment where, as long as the pigeon did not switch, the two options were always identical (i.e., the expected delay to reinforcement for each of them was always the same, regardless of how long the pigeon had been pecking on the RI key), whatever preference a model predicts at the beginning of the trial should apply as well further on into the RI waiting time. That is, according to Gibbon et al.'s SET, as well as other choice models (e.g., Grace, 1994; Killeen, 1982), the switching rate in this experiment should have remained constant.

In other words, investment of time in the RI schedule made future RI choices more likely. This positive exercise effect corresponds to the so-called sunk-cost “fallacy” cited in the human decision-making literature, whereby the likelihood of continuing a course of action increases as a function of previous investment in that alternative (e.g., Arkes & Blumer, 1985). The reason why this behavior is often considered fallacious, as stated in the introduction, is that current choices should be based on future benefits and costs (prospects) without regard to past choices (except to the extent that past choices may determine future values). That is, an exercise effect can disrupt utility maximization. However, as will be argued in more detail in the General Discussion, committing the sunk-cost fallacy may be useful in the context of self-control problems.

Of course, the fact that there was an exercise effect in this experiment does not mean that choice is only an effect of exercise or that the law of effect or any particular theory of choice is invalid. Compared to the effect of postchoice contingencies (the law of effect), the effect of prior choices on current choice (the law of exercise) would be expected to be weak. The purpose of Experiment 2 was to test this expectation. In Experiment 2, differential instrumental contingencies were imposed as waiting progressed. It was expected that when those postchoice contingencies opposed the effect of prior choices, the former would strongly dominate. At the same time, demonstration of typical postchoice contingency effects with the present procedure would show that the procedure itself does not somehow impose an exercise effect—in other words, that the exercise effect was not an artifact of the procedure of Experiment 1.

Experiment 2

In Experiment 1, the more time pigeons spent waiting for the RI reinforcement, the more likely they were to keep on waiting. This may have been at least partly due to the fact that, despite the uncertainty of the reward, reinforcement eventually always arrived. In Experiment 2, we introduced the possibility that the probabilistic reinforcement schedule would never deliver reinforcement. That is, if the pigeon waited on the RI for a specified time without switching to the crf-FI key, the probability of reinforcement dropped to zero. The specific point in time at which extinction was introduced for each pigeon was based on its behavior in Experiment 1.

Method

Subjects and Apparatus

Subjects and apparatus were the same as in Experiment 1.

Procedure

The general procedure was exactly the same as in the previous experiment, with the exception of the introduction of extinction after time T. If the pigeon started an IRI by pecking on the RI key, did not switch, and did not receive reinforcement by time T, then extinction was in place; that is, after T, pigeons had to switch to the crf-FI and satisfy the crf-FI requirement for a peck to be reinforced and the next IRI to begin. The value of T was established by obtaining the point at which the probability of waiting (number of waits divided by number of waits plus number of switches in 5 s-bins) reached 1.0 in the second condition of Experiment 1. This corresponded to 150, 185, and 125 seconds for Pigeons 1, 2, and 3, respectively. These values were used initially as the point at which the probability of reinforcement would drop to zero; pigeons were tested for 25 sessions under this condition. However, the frequency with which pigeons entered extinction was very low and the effect of the extinction constraint on behavior was hardly evident. For this reason, a second condition was run in which the extinction point was reduced to 75% of the original value (i.e., 113 s, 139 s and 94 s for Pigeons 1, 2, and 3). This condition was run for 30 sessions. As in Experiment 1, hazard functions for all pigeons did not change in apparent height or shape after 10 sessions.

Results

Proportion of RI Choices and Switches

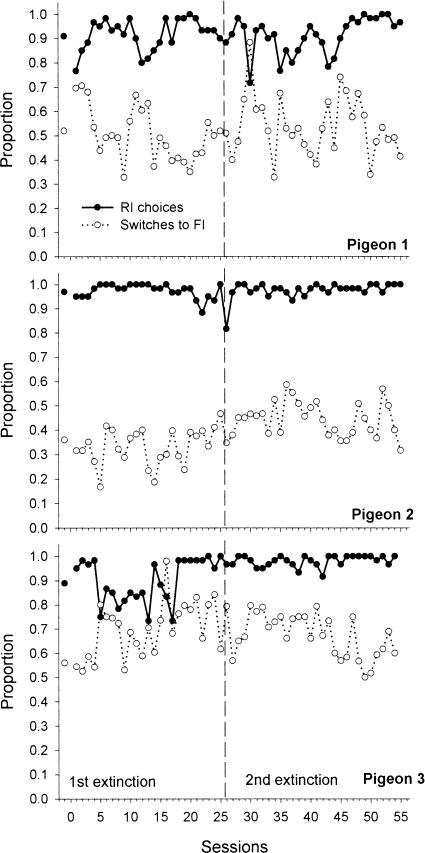
The proportion of RI choices and switches to the crf-FI for each session in each of the two extinction conditions are shown in Figure 6, with the corresponding means and standard errors shown in Table 4. In Figure 6, the leftmost points in each graph correspond to the average proportions of the second condition in the previous experiment.

Fig 6. Proportion of RI choices (closed circles) and switches to the crf-FI (open circles) for each session and for each condition of Experiment 2 for Pigeons 1, 2, and 3.

The vertical dashed line separates each of the two extinction conditions.

Table 4. Mean proportion of RI choices and switches to the crf-FI in the two conditions of Experiment 2 (labeled first extinction and second extinction, respectively). Standard deviations also are presented.

Proportion	Pigeon 1		Pigeon 2		Pigeon 3
	First extinction	Second extinction	First extinction	Second extinction	First extinction	Second extinction
RI choices
M	0.92	0.91	0.97	0.98	0.90	0.98
SD	0.06	0.07	0.03	0.03	0.09	0.02
Switches
M	0.50	0.53	0.33	0.44	0.69	0.67
SD	0.11	0.12	0.07	0.07	0.11	0.08

Switching Behavior

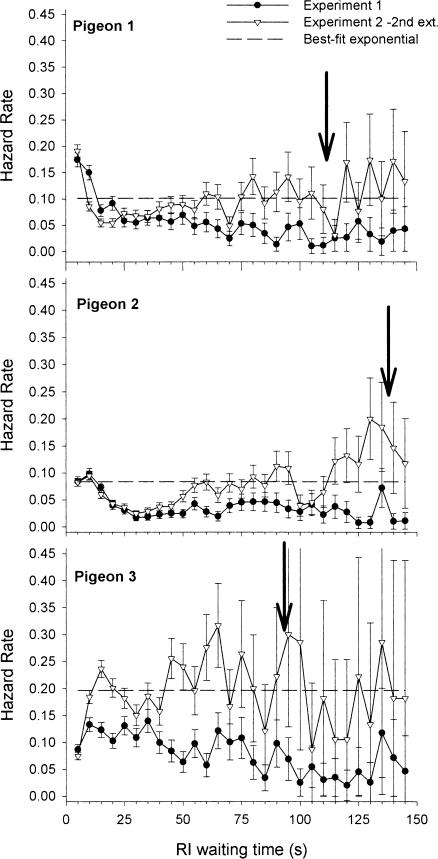
The hazard rate was computed using thirty 5-s bins (where the 30th includes every event after 150 s) and entered into a survival analysis. The hazard rate functions for this experiment again were significantly different from those of the best-fit exponential model (i.e., a constant rate of switching). Figure 7 presents the hazard rate functions for the second extinction condition, along with the baseline hazard rate from Experiment 1 and the best-fit exponential for the extinction function. For all 3 pigeons, the separation between the two curves increases as the extinction point approaches; again, the data for Pigeon 3 are noisier than those for the other 2. In the case of the first 2 pigeons, the separation between the two curves widens slowly after 25 seconds (fifth bin), whereas for Pigeon 3 the two curves diverge almost immediately. This difference may have been due to the fact that extinction for Pigeon 3 occurred sooner than for the other 2. The obtained reinforcement rates in the second extinction condition were 1.78, 1.46, and 2.25 reinforcers per minute for Pigeons 1, 2, and 3, respectively. Note that these values are not very different, for Pigeons 1 and 2, from those of the first experiment (1.73, 1.36, and 1.95). Pigeon 3 increased its obtained rate of reinforcement by increasing its proportion of switches out of the RI.

Fig 7. Hazard rate functions for each pigeon in the second extinction condition of Experiment 2 (triangles) and in Condition 2 of Experiment 1 with no extinction in place (closed circles).

For Pigeon 3, the no-extinction data correspond to the crf-FI 10-s condition. The arrows indicate the point at which extinction was entered. The horizontal dashed line corresponds to the best-fit exponential model for the second extinction condition.

In summary, the introduction of extinction increased switching as the extinction point approached. However, for Pigeons 1 and 2 the initial peak in the hazard rate function remained and was followed by virtually the same sharp decrease as in Experiment 1 before increasing. In the case of Pigeon 3, the divergence between the hazard rate functions of the two experiments occurs towards the beginning of the IRI; this pigeon had the shortest point of entrance to extinction. For all pigeons, the rise in switching probability occurred well before the point of extinction. Of course, any further rise is not meaningful, because the pigeons must eventually switch (or they would be in extinction for the remainder of the session). In fact, the pigeons stayed past the extinction point on less than 2% of the IRIs in which they initially chose the RI. The increases in error bar length with time into the IRI reflect the decreasing number of cases in which the pigeons waited that long before switching.

Discussion

The introduction of extinction towards the end of the IRI increased the probability of switching as time to extinction approached. The initial segment of the switching function remained virtually unchanged, at least for Pigeons 1 and 2. As in Experiment 1, switching rate decreased initially. However, further time into the IRI signaled the arrival of extinction, and the pigeons started switching again, presumably because the possibility of not receiving the reinforcement (law of effect) counteracted the effect of the time invested in the RI (law of exercise).

The increase in the rate of switching as extinction approached indicates that whatever mechanism is responsible for taking past time investments into account when making choices, the mechanism is not blind. That is, choice was sensitive to prospective as well as retrospective conditions.

Experiment 3

In Experiments 1 and 2, the pigeons were free to choose between the RI and crf-FI schedules at any point prior to RI reinforcement. That is, the pigeons could stay or they could switch. It may be the case, however, that the exercise effect did not depend on free choice per se (availability of the crf-FI alternative) but merely on exposure to the RI schedule. Experiment 3 tested this possibility by constraining pecks to the RI schedule (pigeons could not switch except during a single, brief time window). If the pigeons were to switch at the same rate during this window (after being constrained to the RI schedule alone) as they did during the equivalent postreinforcement period in Experiment 1 (where they freely chose to stay on the RI schedule), it would be evidence that the positive exercise effect (i.e., the sunk-cost effect) found in Experiment 1 was due to prior responding (exercise per se) as distinct from prior choice. One purpose of Experiment 3 was to test between these possibilities.

Timing theories of choice, whether behavioral (Killeen & Fetterman, 1988; Staddon & Higa, 1999) or not (Gibbon, 1977), attribute choice to timing. Such theories might explain the results of Experiment 1 in terms of a nonlinear relation between behavior and reinforcer probability over time. Although the actual probability of reinforcement was constant over time during the RI schedule, subjective (or behavioral) probability of RI reinforcement might have increased, yielding the decreasing hazard functions of Figure 4. For example, the RI schedule might have had the behavioral effect of a rectangularly distributed VI schedule where reinforcement probability increases as a function of time without reinforcement. In nonbehavioral terms, the pigeons could have misperceived time left to an RI reinforcer such that the more time they spent pecking on the RI key, the shorter the time-left appeared. Whatever timing mechanism caused the misperception should operate equivalently in Experiment 3 and Experiment 1. Perceived time left may be expected to depend on current waiting time and overall expected time to reinforcement (which was the same in this experiment as in Experiment 1) and not on the availability or unavailability of another alternative (which differed). The availability or nonavailability of a nonchosen alternative might conceivably affect timing to some small, quantitative extent but would not be expected to alter it in a drastic or qualitative manner. A second purpose of Experiment 3 was to test this time-perception account of the results of Experiment 1.

In the first condition, pigeons' access to choice between the RI and crf-FI schedules was restricted to a brief period, presented at a particular point into the IRI (the RI and crf-FI schedule values remained the same as in the previous two experiments). In the second condition, the pigeons were again exposed to the original choice procedure (Condition 2) of Experiment 1.

Method

Subjects and Apparatus

The 3 subjects used in Experiments 1 and 2 were used in this experiment. The apparatus was the same.

Procedure

Condition 1: Restricted Choice

In this condition, an IRI started with one of the two side keys illuminated green (sides assigned randomly on every IRI). That is, at the beginning of every IRI the only alternative available to the pigeon was the RI schedule. At a particular point into the IRI (based on data from Experiment 1, as described below), there was a brief period during which both alternatives were made available (choice window): the RI key flickered for 0.5 s, and both the houselight and the crf-FI (red) key were turned on. A peck on the crf-FI key at this point extinguished both the RI key and the houselight and started the FI timer; the FI alone was then in effect for the remainder of the IRI. A peck on the RI key extended the availability of the crf-FI key for 2 s further. If the pigeon did not switch to the crf-FI during those 2 s, both the crf-FI key and the houselight were extinguished and the RI schedule alone was in effect for the remainder of the IRI. The purpose of extending the time window 2 s beyond an RI peck was to ensure that the pigeon was facing the keys and responding, rather than engaging in interim behavior, during the period of crf-FI availability.

Only one choice window could become available during a postreinforcement period. However, not every postreinforcement period included a window, given that in some cases, RI reinforcement could be set up and delivered before the window was due to appear. The point into the IRI at which the choice window became available (X) was varied across phases of the experiment. In this way, we avoided IRIs with more than one choice window; with multiple windows, a pigeon's choice to stay on the RI during an earlier window could have influenced its choice during a later window.

There were five values of X for each pigeon, namely: 0.5 s, 1.5 s, 25%, 50%, and 75%. The percentages correspond to RI waiting time at which the pigeon had completed 25%, 50%, and 75% of its total switches in Condition 2 of Experiment 1; the data were obtained from the survival analysis. These values were 8.5 s, 36.5 s, and 116.5 s for Pigeon 1; 18.5 s, 84 s, and 248 s for Pigeon 2; and 12.5 s, 30 s, and 67 s for Pigeon 3. The number of times per session that the choice window was actually available decreased as a function of how far into the IRI it was scheduled to occur (see Table 5). For this reason, each pigeon was tested in each phase for as many sessions as necessary in order to obtain between 1,150 and 1,300 exposures to the choice period or a maximum of 100 sessions, whichever happened first. As in previous conditions, the stability of switching as a function of RI waiting time was obtained well before this point. The first phase for all pigeons corresponded to the shortest value of X (0.5 s), which then was increased and decreased from phase to phase. This procedure yielded two data points for each value of X, except for the 75% point, which was only run once.

Table 5. Number of sessions and total number of choice windows across all sessions for each phase in Experiment 3.

Time of choice	Pigeon 1		Pigeon 2		Pigeon 3
	Sessions	Windows	Sessions	Windows	Sessions	Windows
0.5 s	20	1,194	20	1,184	20	1,200
1.5 s	20	1,178	20	1,172	20	1,191
25%	25	1,305	28	1,197	26	1,282
50%	35	1,172	81	1,209	35	1,285
75%	100	852	100	86	65	1,262
50%	35	1,148	81	1,259	35	1,290
25%	25	1,262	28	1,217	26	1,257
1.5 s	20	1,176	20	1,180	20	1,194
0.5 s	20	1,191	20	1,196	20	1,197

Condition 2. Return to Baseline

In this condition, subjects were returned to the original choice procedure of Experiment 1 (Condition 2) for 20 sessions.

Results

Condition 1: Restricted Choice

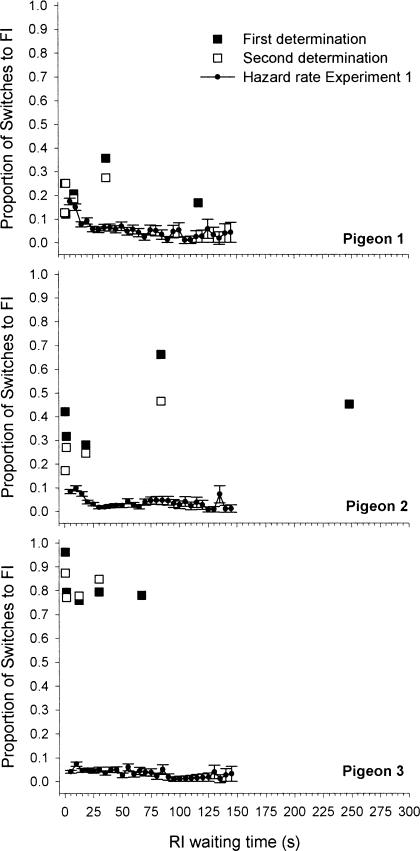
The number of sessions that each pigeon was tested in each phase is shown in Table 5, along with the total number of choice windows that occurred per phase. Figure 8 shows the proportion of times in which the choice window ended with a peck to the crf-FI (i.e., the total number of times the crf-FI schedule was chosen divided by the total of obtained choice windows in a phase). The figure also includes the hazard rate functions for the second condition of Experiment 1, when the choice was continuous. The closed squares correspond to the first determination of the proportions, when X was increasing from phase to phase. The second determination is presented with open squares. The squares are unconnected because only a single window of switching availability was presented in each phase of this experiment. That is, the postreinforcement position of the window varied from phase to phase, not within a session, so as to prevent earlier choices from influencing later choices.

Fig 8. Proportion of choices of the crf-FI for each condition in Experiment 3.

The graph shows the data for the first and second determinations (closed and open squares, respectively) for each pigeon. Also included for comparison are the hazard rate functions from Condition 2 of Experiment 1.

The proportion of switches to the crf-FI was much higher with the choice windows of the present experiment than it was with continuous choice availability in Experiment 1. Switching in the present experiment increased or remained relatively constant as a function of the time into the RI at which the choice was offered. There are two exceptions to this observation, namely the last point (at 75%) for both Pigeons 1 and 2. In all other cases it seems clear that the rate of switching is not a decreasing function of time spent pecking on the RI key. This result contrasts with the general decrease in likelihood of switching to the crf-FI alternative observed in the previous experiments.

Condition 2: Return to Baseline

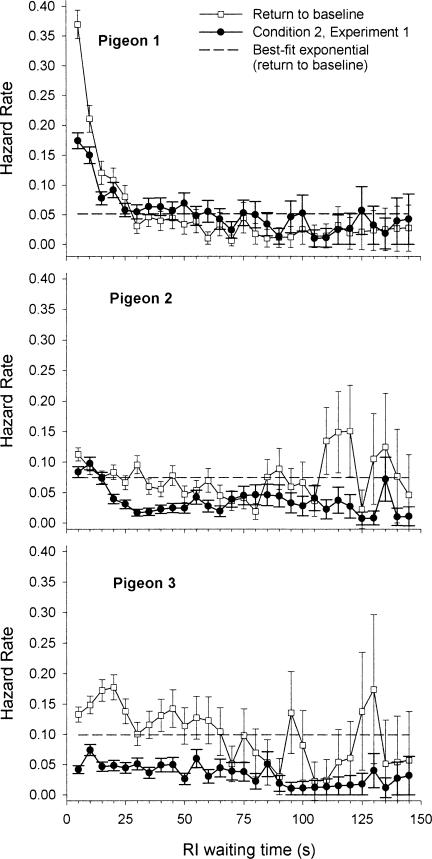
Figure 9 shows the hazard rate functions for all pigeons, along with the best-fit exponential model that assumes a constant rate of switching. Along with these functions, the figure also shows the data for the second condition of Experiment 1 (i.e., baseline). As in the previous two experiments, the hazard rate functions obtained in this condition were substantially different from the model that assumes a constant rate of switching.

Fig 9. Hazard rate functions for each pigeon in the return to baseline condition of Experiment 3 (open squares) and in the second condition of Experiment 1 (closed circles).

The horizontal dashed line corresponds to the best-fit exponential model for the data of the return to baseline.

Discussion

In the first condition of this experiment, where opportunity to switch from the RI to the crf-FI was constrained to a single, brief time window, the probability of switching typically was much higher than it was at corresponding periods in Experiment 1, where the pigeons were free to switch at any time during the wait. In the second condition, where pigeons were returned to the original baseline, the resulting switching rates decreased and switching returned to a generally decreasing function similar to that of Experiment 1 (original baseline). However, as Figure 9 shows, switching rates remained somewhat higher than they were in Experiment 1, perhaps due to residual effects of the first condition of this experiment.

There is a superficial similarity between the procedure of the first condition of this experiment and Gibbon and Church's (1981) time-left procedure. In both procedures, the schedule switched to was a fixed-interval schedule that began to time out only after the switch (a tandem crf-FI schedule). In both procedures, the schedule switched to became available only after a certain interval had passed on the schedule switched from. However, in the time-left procedure, the schedule switched from was also a fixed interval that elapsed with time. The longer the pigeon stayed on that schedule without switching, the closer it came to reinforcement. In the present case (first condition of Experiment 3), however, the schedule switched from was an RI schedule. This is a crucial difference because, in the time-left procedure, time-left steadily decreased; pigeons switched to the crf-FI early in the interval when time-left was long and did not switch late in the interval when time-left was short. The mean and variance of the switching point thus measured the mean and variance of pigeons' estimates of time-left. In the present procedure, in contrast, expected time-left never varied; elapsed time in the RI was not correlated with a reduction in time-left to RI reinforcement; there was no reason (except in terms of an exercise effect) for pigeons to switch at any point during the IRI.

Although there was considerable variability among pigeons in this experiment, the redeterminations (open squares) generally fell close to the original determinations; individual pigeons behaved consistently. Pigeon 3 switched to the crf-FI schedule at a relatively high rate whenever the choice window appeared. The near-zero slope of the squares in Figure 8 for Pigeon 3 indicates the absence of an exercise effect for this pigeon during this condition. Recall, however, that Pigeon 3 also showed the least exercise effect in Experiment 1. Usually, when Pigeon 3 chose the RI schedule freely it tended to stay with it; when its pecking was constrained to the RI schedule, Pigeon 3 tended to switch from the RI whenever it was free to do so.

Pigeons 1 and 2, however, showed a negative exercise effect, at least in the early stages (prior to the rightmost point) of the first condition of Experiment 3. In Experiment 1 and in the second condition of Experiment 3, the longer they were exposed to the RI schedule as a free choice, the greater was their tendency to stay on it while, in the first condition of Experiment 3, the longer they were constrained to the RI schedule only, the greater was their tendency to switch from it. For Pigeons 1 and 2, the rightmost point (the filled square) is lower than the others and gives an inverted-U shape to the functions for these pigeons in Figure 8.

However, even accounting for the variability among pigeons and the dip in the rightmost points in Figure 8 for Pigeons 1 and 2, Experiment 3 makes it clear that the positive exercise effect found in Experiment 1 depended on the pigeons' choices in that experiment, rather than on the mere fact that they had been pecking for a period on a key. That is, the exercise effect depends on exercise of choice rather than on exercise per se.

Experiment 3, moreover, provides some evidence against an account of the results of Experiment 1 in terms of a misperception of time. It seems unlikely that the existence or nonexistence of an alternative could have had such a strong qualitative and quantitative effect on timing as was shown in Experiment 3.

General Discussion

In Experiment 1, choice consequences remained constant as the interreinforcement interval progressed. We found that preferences changed despite the constancy of prospective value of these consequences; the likelihood of switching from the RI to the crf-FI schedule decreased as a function of prior choices of the RI schedule. This result is evidence for a positive effect of exercise on current choice independent of the effect of consequences on current choice. However, the exercise effect was not blind to changes in prospective value; pigeons' behavior adapted to the introduction of extinction, as shown in Experiment 2. Experiment 3 showed that the sharp decrease in switching during the interreinforcement interval in Experiment 1 depended on continuous availability of an alternative.

The positive exercise effect found in Experiment 1 (the decrease in switching during the interreinforcement interval) is equivalent to the sunk-cost effect commonly found in research with human subjects. Has it also been found with animals in nature? There is an ongoing discussion in the biological literature about whether animals commit the sunk-cost fallacy (known in that literature as the Concorde fallacy). Trivers' theory of parental investment (as cited in Dawkins & Brockmann, 1980), argues that, of the two parents of a brood, the most likely candidate to desert the brood and its partner is the one that has invested the least in the brood. This argument was later criticized by Dawkins and Carlisle (1976), who asserted that behavior must be driven by the ultimate final cause of fitness, which lies in the future, and which requires the evaluation of only prospective costs and benefits.

Since then, many attempts have been made with naturally occurring behaviors, mostly related to parental investment, to determine whether nonhumans commit the Concorde fallacy (for examples, see Dawkins & Brockmann, 1980; Lavery, 1995; and Weatherhead, 1979). According to some (Arkes & Ayton, 1999; Curio, 1987), all of the results claimed to support the existence of the Concorde fallacy could also be interpreted as driven by future benefits. Others argue that they have found the effect and attempt to explain it in terms of nonhuman cognitive limitations.

However, in nonhuman experimental situations, alternative explanations of sunk-cost effects are less plausible. Several studies with nonhumans have found reinforcer value to be enhanced by prior responding. Neuringer (1969), for example, found that pigeons preferred pecking a key followed by reinforcement to free reinforcers. Clement, Feltus, Kaiser, and Zentall (2000) found, also with pigeons, that colors associated with a higher work requirement were later preferred to those associated with a lower work requirement. Navarro & Fantino (2005) explicitly tested for a sunk-cost effect with pigeons. On a given trial, the pecks required to obtain reinforcement could suddenly increase. On these occasions, pigeons persisted in pecking the originally chosen key even when they could “escape” and begin a new trial with a shorter expected response requirement. Similarly, Kacelnik and Marsh (2002) showed that starlings preferred alternatives that had been paired previously with high work requirements over those that had been paired with low work requirements, despite the fact that both offered the same amount of food. Dawkins and Brockmann (1980) point out that committing the Concorde fallacy or paying attention to sunk-costs could in many cases result in maladaptive choices—choices that do not lead to maximization of fitness. That was certainly the case in the present experiments, where staying on the RI alternative sharply reduced overall reinforcement rate. However, as Dawkins and Brockmann also indicate, an overall strategy of paying attention to past investments when making a decision may be the result of adaptation if it solves an adaptive problem with the available resources. That is to say, the sunk-cost effect could be thought of as a “heuristic,” a rule of thumb of sorts (see, e.g., Gigerenzer & Todd, 1999). Following this line of reasoning, we would argue that positive weighting of previous investments can be useful in self-control situations.

The tendency to persist in previous choices may serve to bridge over the temptation of a small reward when it becomes imminent. This tendency may be seen as a primitive form of response-patterning—the organization of behavior into relatively rigid, temporally extended units (Rachlin, 1995). In an experiment by Siegel and Rachlin (1995), pigeons strongly preferred a smaller immediate reward to a large delayed reward. However, when they were required to make 31 pecks (FR 31) on either of two keys leading to the two rewards, preference for the smaller immediate reward was reduced by 44%. At the moment when the FR 31 requirement started, pigeons preferred the large delayed alternative. After the first peck on that alternative, the probability of switching to the smaller reward key dropped to around 0.01. It was argued that pigeons started a relatively rigid pattern of behavior; the cost of interruptions of this pattern committed them to their initial choice and allowed them to obtain the initially preferred alternative. They thus overcame the “temptation” of the small immediate reward. Siegel and Rachlin called this process “soft-commitment.” Given the results of the present experiment, the soft-commitment Siegel and Rachlin observed may be interpreted as a manifestation of the sunk-cost effect and vice versa.

Taken together, Experiments 1 and 3 show that Thorndike should not have withdrawn the law of exercise. Prior behavior may influence current choice and that influence depends on whether prior behavior is constrained to one alternative or freely allocated between two alternatives. But the results of Experiment 2 indicate that the law of exercise may be overwhelmed by the law of effect; at the point where the prospective value of one alternative was reduced, choice shifted away from that alternative regardless of prior choices.

One question left unanswered by the current experiments is whether the effect of past choices on current choice depends on active responding. In the present experiments, the responding was active in the sense that pigeons chose by repeatedly pecking the RI key or switching to a peck on the crf-FI key. We do not know whether the same effects would have been found if choices were made in a time-allocation procedure where, for example, a changeover key was used to switch from a random-time schedule (reinforcers delivered freely) to a fixed-time schedule (reinforcers delivered freely). This is a subject for future research.

Finally, these experiments say nothing about the mechanism underlying the law of exercise. An underlying tendency to persist in choice might conceivably have been constant during interreinforcement periods; that constant tendency might have been modulated by a countervailing tendency to switch that varied and caused the observed variation in choice. Or, an underlying tendency to stay and an underlying tendency to switch might both have varied; measured choice variation would then have been the resultant of those underlying opposing processes. These possibilities would be very difficult to separate, behaviorally, from simple persistence of choice but might be separable eventually by physiological investigation.