α/γ Transitions in the B-DNA backbone

Abstract

In the crystal structures of protein complexes with B-DNA, α and γ DNA backbone torsion angles often exhibit non-canonical values. It is not known if these alternative backbone conformations are easily accessible in solution and can contribute to the specific recognition of DNA by proteins. We have analysed the coupled transition of the α and γ torsion angles within the central GpC step of a B-DNA dodecamer by computer simulations. Five stable or metastable non-canonical α/γ sub-states are found. The most favourable pathway from the canonical α/γ structure to any unusual form involves a counter-rotation of α and γ, via the trans conformation. However, the corresponding free energy indicates that spontaneous flipping of the torsions is improbable in free B-DNA. This is supported by an analysis of the available high resolution crystallographic structures showing that unusual α/γ states are only encountered in B-DNA complexed to proteins. An analysis of the structural consequences of α/γ transitions shows that the non-canonical backbone geometry influences essentially the roll and twist values and reduces the equilibrium dispersion of structural parameters. Our results support the hypothesis that unusual α/γ backbones arise during protein–DNA complexation, assisting the fine structural adjustments between the two partners and playing a role in the overall complexation free energy.

INTRODUCTION

The canonical B-form of the DNA double helix undergoes various conformational changes during its interaction with proteins (1,2). Crystal and solution structures of protein–DNA complexes indicate that the DNA phosphodiester back bone can adopt different non-canonical conformations (3; D.Djuranovic and B.Hartmann, manuscript submitted), presumably stabilised by the direct or indirect effects of numerous contacts between the DNA backbone and amino acid side chains. The backbone has an important role in restricting the available conformational space for stacking bases (4) and in coupling the conformational properties of neighbouring dinucleotide steps in a sequence (5). Conformational changes involving ε (C_4′-C_3′-O_3′-P) and ζ (C_3′-O_3′-P-O_5′) torsion angles are commonly observed in DNA backbones on the nanosecond time scale (6,7). These structurally correlated torsions define two conformations: the lower energy BI is characterised by ε/ζ: t/g– with (ε–ζ) around –90° and BII is characterised normally by ε/ζ: g–/t with (ε–ζ) around +90° (8,9). The BI/BII conformations have been shown to result in altered phosphate positions and to influence groove parameters, stacking properties and helicoidal parameters (5,6,10–12). The fundamental role of sequence-dependent backbone flexibility in indirect readout has been shown in several studies (13–15), which point to the significant role of BI/BII sub-states in the early stage of protein–DNA recognition.

Much less is known about the structural and energetic consequences of other transitions in the backbone, such as those which involve α (O_3′-P-O_5′-C_5′) and γ (O_5′-C_5′-C_4′-C_3′) torsions. Analysis of the DNA backbone geometry in crystal structures shows almost exclusively the canonical α/γ: g–/g+ in B-DNA, but both the majority α/γ: g–/g+ and the alternative α/γ: t/t conformations were observed in A-DNA and RNA (10,16–19). The values of α and γ torsions can therefore exhibit a negative coupling, with γ increasing as α decreases (10,16–18). The canonical and alternative α/γ conformations show similar base stacking geometries, due to the intervening β torsion angle being in the trans conformation (10,20).

The spontaneous appearance of alternative α/γ conformations has been reported in early molecular dynamics (MD) simulations of B-DNA, with nuclear Overhauser effect distance restraints (21–24). A more recent NMR study of a DNA oligomer including a central AAA sequence found γ in a trans conformation and attributed this to an increased inter-phosphate distance and local unwinding of the duplex (25). In contrast, other recent MD simulations using accurate treatments of solvation and long range electrostatics do not show such α/γ transitions in free B-DNA.

Pearlman and Kim (26) systematically explored the conformational space of backbone torsions in dA₄ and rA₄ and found a strong correlation between α and γ using an energy contour map. Beyond the canonical α/γ: g–/g+, they noted the existence of other minima, such as α/γ: t/t, t/g+ and g+/t, on the potential energy surface (PES). The barrier to rotation for α between gauche– and trans and for γ between gauche+ and trans required 7 kcal/mol. It was remarked that the gauche+ state for α and gauche– state for γ are highly disfavoured (5 kcal/mol). It was also found that α/γ transitions were easier in RNA. Indeed, α/γ: t/t conformations have been observed in the RNA strand of a RNA/DNA hybrid (27). Recent ab initio calculations predict the interconversion barriers for γ in small model compounds to be 12 kcal/mol for a direct gauche+ to trans transition, 4 kcal/mol for gauche+ to gauche– and 6 kcal/mol for gauche+ to trans through the gauche– state (28,29). It is not well established if the alternative α/γ conformations in B-DNA are accessible in solution or what energetic and structural changes may occur along the lowest energy pathways between the canonical and unusual forms.

Our analysis (see below) of a crystallographic data set has shown that, in contrast to free B-DNA structures, protein-bound B-DNA oligomers regularly involve non-canonical α/γ conformations. These unusual α/γ arrangements represent up to 10% of the dinucleotides analysed and, on average, any oligomer includes at least two such steps. It is not clear if these deformations are readily accessible in solution at room temperature and can guide the specific recognition of a given DNA sequence or are induced during the protein binding process. In a continuing effort to understand the mechanics of DNA structures in solution, we have simulated the pathways for α/γ backbone transitions in the central GpC dinucleotide step (underlined) of a 5′-dGTCAGCGCATGG-3′ sequence. This sequence is the target for HhaI cytosine methyltransferase where the central cytosine flips out in the course of the enzymatic process. This flipping is associated with changes in α/γ values of the GpC step both in the protein–DNA complex (30) and during computer simulation of the flipping process without the enzyme (31,32). Moreover, our analysis of crystallographic protein–B-DNA complexes has revealed that GpC steps easily undergo α/γ transitions, as 37% of these steps are found to adopt unusual α/γ conformations.

The goal of the present study was to evaluate the free energy difference between the alternative α/γ conformations accessible to B-DNA and the effect of these transitions on the structure of DNA. We find that flipping of α and γ torsions requires >7 kcal/mol for the GpC step of our B-DNA oligomer. Thus it is unlikely that alternative α/γ conformations will be populated in a free DNA or can be exploited by the protein in the early stage of selective binding. Nevertheless, the structural perturbations associated with α/γ sub-states are significant. These results point to the active participation of the protein in inducing α/γ deformations and suggest that these conformations play a role in the structural adjustments linked to complex formation.

MATERIALS AND METHODS

Potential energy surface scan

The PES of the central GpC dinucleotide step in the 5′-dGTCAGCGCATGG-3′ sequence was scanned using JUMNA (junction minimisation of nucleic acids) (33,34). This approach models DNA using helical coordinates to position each nucleotide and internal coordinates (restricted to torsion angles and a limited number of valence angles) to treat changes in nucleotide conformation. Inter-nucleoside junctions and sugar rings are closed using harmonic distance restraints. Calculations were performed using the Parm99 force field (35) developed for AMBER for consistency with the MD simulations (see below). Solvent damping of electrostatic interactions was included using a sigmoidal distance-dependent dielectric function defined by a slope of 0.16 and a plateau value of 80 (36). Counterion effects were taken into account by reducing the net charge on each phosphate group to –0.5e.

The PES map was generated employing the procedure used earlier for studying BI/BII transitions (5,11,37). After energy minimisation of the DNA oligomer starting from a standard B conformation, the energy surface was obtained by varying the α and γ torsion angles in steps of 20° and using harmonic restraints. The full α/γ PES was built from separate calculations for each of its four quadrants using low energy starting structures. These quadrants were calculated with sufficient overlap and could be assembled into a continuous energy map, showing that the map was independent of the starting structures.

Free energy calculation

Model building and simulations were performed using a modified form of the AMBER 6 suite of programs (38) and the Parm99 parameter set (35). The standard B-DNA oligomer was neutralised with 22 Na⁺ ions and solvated with more than 5000 TIP3P water molecules in a truncated octahedral box. MD simulations were performed at constant temperature (300 K) and pressure (1 bar) using the Berendsen algorithm (39). An integration time step of 2 fs was used and all bond lengths involving hydrogens were constrained using SHAKE (40). Long-range electrostatic interactions were treated using the particle mesh Ewald approach (41,42) with a 9 Å direct space cut-off. The non-bonded pair list was updated heuristically and the centre of mass motion was removed every 10 ps during the simulation. Initially, the water molecules and ions were relaxed by energy minimisation and allowed to equilibrate at 300 K around the fixed DNA for 100 ps at constant volume; the entire system was then heated from 100 to 300 K during 10 ps and equilibrated during 40 ps with harmonic restraints of 5.0 kcal/mol/Ų on the solute atoms at constant volume. Subsequently, the simulation was continued at constant pressure; the restraints were gradually removed over a period of 250 ps and an unrestrained simulation followed for 1 ns.

A systematic search of the entire surface defined by the α and γ variables (with a reasonable convergence of the free energy) is beyond reach at present. Preliminary MD simulations using either the α or γ torsion angle as reaction coordinate showed that movement of these backbone torsions are inherently coupled; as the value of α was changed γ changed spontaneously and vice versa. Therefore, to preferentially sample the α/γ surface along the energy valleys, we have adopted a simple approach using a linear combination of the two torsion angles: α + γ to obtain movement of the torsions in the same direction and α – γ to obtain movement in opposing directions. This method, which was successfully used in earlier adiabatic mapping procedures (11,36), reduces the sampling problem to one dimension while obtaining the optimal α and γ values. The reaction coordinates were obtained using a harmonic restraining potential with a force constant of 0.02 kcal/mol/deg². The simulation of the transitions in backbone torsions consisted of consecutive windows of 100 ps MD at increasing or decreasing values of the reaction coordinate in steps of 10°. The final structure obtained in a given simulation window was used as the starting point in the subsequent one. To test the structural and energetic convergence of the results the simulations were extended to 200 ps in each window.

The restrained angle combinations were recorded at every step during the simulation. The free energy or the potential of mean force along the reaction coordinate was obtained by removing the bias introduced by the restraining potential and combining the angle values for all the windows using the constant temperature weighted histogram analysis method (43,44). To obtain uniform sampling along the reaction coordinate, selected regions were re-sampled at intermediate values. An analysis of the convergence of the free energy using separate 50 ps blocks of data showed that the free energy profile is converged to within 1 kcal/mol after the first 50 ps of simulation time in each window. MD simulations of regions corresponding to conformational sub-states were extended to 2 ns and the structural parameters obtained were compared with experimental results extracted from crystallographic data. In total, this study represents over 25 ns of simulation.

Crystallographic data set analysis

A total of 64 structures of B-DNA oligomers bound to proteins (1245 dinucleotide steps) were extracted from the Nucleic Acid Data Bank (September 2001) (45). All structures were resolved by X-ray crystallography to at least 2 Å. Beyond this resolution, it is well established that certain features of the structure become unclear, notably the sugar puckers and the backbone angles (46). The base content is almost equally distributed among the four bases and thus no sequence bias was introduced. End effects were tested, but were found to cause negligible differences and hence terminal base pairs were also considered in the present study. The NDB codes for structures used in this work are: pd0002, pd0006, pd0010, pd0011, pd0012, pd0020, pd0029, pd0037, pd0040, pd0068, pd0073, pd0088, pd0096, pd0101, pd0111, pd0114, pd0115, pd0129, pd0130, pd0131, pd0139, pd0143, pd0147, pd0151, pd0154, pd0155, pd0160, pd0163, pd0180, pd0187, pd0190, pd0225, pde006, pde0131, pde0132, pde0133, pde0139, pde0145, pde025, pde139, pdr009, pdr010, pdr021, pdr047, pdr048, pdt030, pdt031, pdt039, pdt043, pdt056, pdt057, pdt058, pdt059, pdt060, pdv001.

Backbone and helicoidal parameters

For a given dinucleotide we consider the inter-nucleoside linkage composed of torsion angles: ε, C_4′-C_3′-O_3′-P; ζ, C_3′-O_3′-P-O_5′; α, O_3′-P-O_5′-C_5′; β, P-O_5′-C_5′-C_4′; γ, O_5′-C_5′-C_4′-C_3′. The classical 3-fold staggered pattern of the torsions is used in this work: gauche+ (60 ± 40°), trans (180 ± 40°) and gauche– (300 ± 40°). To describe the sugar conformations, the pseudo-rotation phase angle of the sugars are divided into three conformational categories: ‘north’ (300–60°), ‘east’ (60–120°) and ‘south’ (120–220°) (28).

Analyses of DNA structures were carried out with the Curves 6.1 algorithm (47), which calculates an optimal helical axis and a complete set of helical parameters. Analyses were made both in terms of local and global parameters, however, the two analyses gave similar results, as expected for B-family structures, and only the global values are reported. All parameter definitions obey the Cambridge convention for DNA conformation (48).

RESULTS AND DISCUSSION

Canonical B-DNA has α and γ torsions in the g–/g+ conformational state. To explore the available phase space for these torsion angles four possible transition paths can be envisaged, where the torsions rotate in the same (A and B) or in opposite (C and D) directions:

Path A (α + γ increases) α: g– → [cis] → g+ → tγ: g+ → t → g–

Path B (α + γ decreases) α: g– → t → g+γ: g+ → [cis] → g– → t

Path C (α – γ increases) α: g– → [cis] → g+ → tγ: g+ → [cis] → g– → t

Path D (α – γ decreases) α: g– → t → g+γ: g+ → t → g–

Potential energy surface

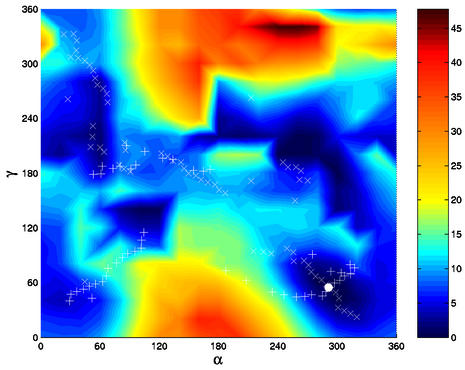
We have investigated the α/γ adiabatic transition pathways on the PES of a GpC step (Fig. 1). Three combinations of α/γ correspond to local energy minima on the surface; in order of decreasing stability, g–/g+ (canonical) > g–/t > g+/t. Three other arrangements, t/t > g+/g– > g+/g+, exhibit low energies (between 2 and 4 kcal/mol) with respect to the canonical conformation, however, they are separated from the other minima by negligible barriers of ∼0.2 kcal/mol. In contrast, the three remaining possible combinations, namely t/g–, t/g+ and g–/g–, are located in high energy zones of the PES. Changes of neighbouring angles away from canonical values are observed in three cases: α/γ: g–/t is associated with β in gauche+, α/γ: g+/g+ with β in gauche+ and (ε–ζ) 120–140°, and α/γ: g+/t is accompanied by (ε–ζ) ∼+30°.

Figure 1.

Energy map (kcal/mol) as a function of α and γ torsion angle values (in degrees) in the GpC dinucleotide calculated with JUMNA. The values of α and γ sampled in the MD simulations are plotted for the reaction coordinates α + γ (+) and α – γ (×). The white dot marks the global energy minimum α/γ: g–/g+.

Based on the two-dimensional energy map, it is possible to determine the energy barriers separating the various sub-states, starting from the canonical α/γ arrangement. The first energy barrier is found to be the highest one for all the four possible pathways: path B 30 kcal/mol, path C 9.8 kcal/mol and paths A and D 5.7 kcal/mol. Path B, which involves rotation of α via trans and γ via cis, as found earlier for ribonucleoside diphosphates (19), is energetically prohibitive. Similarly, path C, involving the counter-rotation of both the α and γ angles through the cis conformation, is clearly unfavourable. An energy decomposition shows that the barriers are essentially due to steric effects; the van der Waals component of the total energy correlates well with the increase in energy along the pathway although the stacking energy remains constant (data not shown). The energetically favoured paths A and D first go through the same maximum and both lead to the α/γ: g–/t conformation. To reach the g+/t minimum, a barrier of 5.2 kcal/mol must be overcome along path A, whereas path D involves a lower barrier of 2.5 kcal/mol. In conclusion, the lowest energy path (D) from the canonical conformation to the other α/γ sub-states involves a counter-rotation of α and γ via the trans form.

Free energy pathways

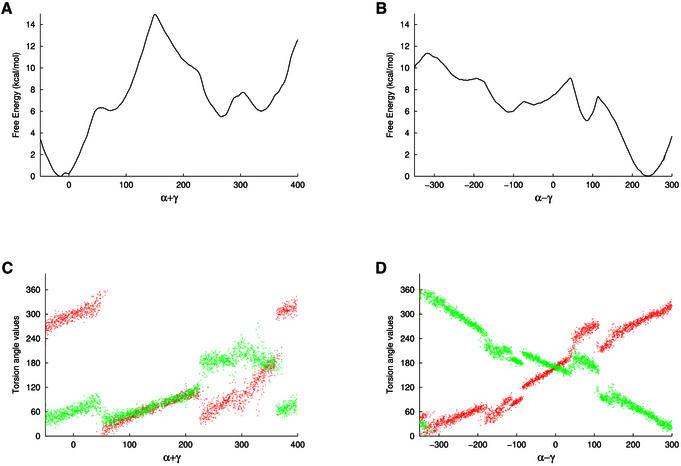
Four free energy pathways involving coupled α/γ transitions were studied, however, in line with the potential energy map described above, the direction in which γ makes a transition via the cis conformation is heavily penalised (paths B and C). Consequently, these simulations produced pathways in which only α undergoes conformational transitions and hence they were not analysed further. The alternative paths in which γ makes a transition via the trans conformation were, however, fully explored (paths A and D, Fig. 2).

Figure 2.

Profiles of the free energy (kcal/mol) associated with α/γ transitions as a function of (A) α + γ and (B) α – γ (in degrees); the free energy associated with the canonical conformation is set to 0. Variations of α (red) and γ (green) torsion angle values along the reaction coordinate α + γ and α – γ are shown in (C) and (D), respectively.

In path A, where the two torsions rotate in the same direction, α first flips to gauche+, resulting in a shoulder on the free energy profile at ∼6 kcal/mol, corresponding to a α/γ: g+/g+ sub-state. The remainder of this path is separated by a large barrier of 14 kcal/mol and gives sub-states α/γ: g+/t and then t/t at relative free energies of 5 and 6.5 kcal/mol, respectively. These conformations are separated by a small barrier of 2 kcal/mol along the reaction coordinate. In path D, where the torsions rotate in opposite directions, first γ flips to trans through a barrier of 7 kcal/mol to result in a stable α/γ: g–/t sub-state at 5 kcal/mol. It is interesting to note that this low energy conformation corresponds to the deformation observed in the HhaI methyltransferase–DNA complex (30). Passing a barrier of an additional 4 kcal/mol leads to the α/γ: t/t and then the g+/t conformations, observed previously in path A, now at energies of 6.5 and 6 kcal/mol, respectively. The barrier separating the two minima is <1 kcal/mol along this path. It is important to note that these minima were located by two independent paths and exhibit relative free energies within 1 kcal/mol, which indicates a good agreement between independent simulations. Since the barrier between the two minima is negligible, the two states can easily interconvert.

Further along the reaction coordinate, the α/γ: g+/g– conformation is located as a wide shoulder at 9 kcal/mol above the canonical state. Finally, the canonical conformation could be obtained via the cis/cis conformation at 11 kcal/mol. Thus, three minima were located, the canonical backbone conformation and two stable sub-states, α/γ: g–/t and g+/t. In addition, three meta-stable sub-states were found, α/γ: g+/g+, g+/g– and t/t. Although these states are not stable in an aqueous environment, they are expected to appear easily in protein–DNA complexes.

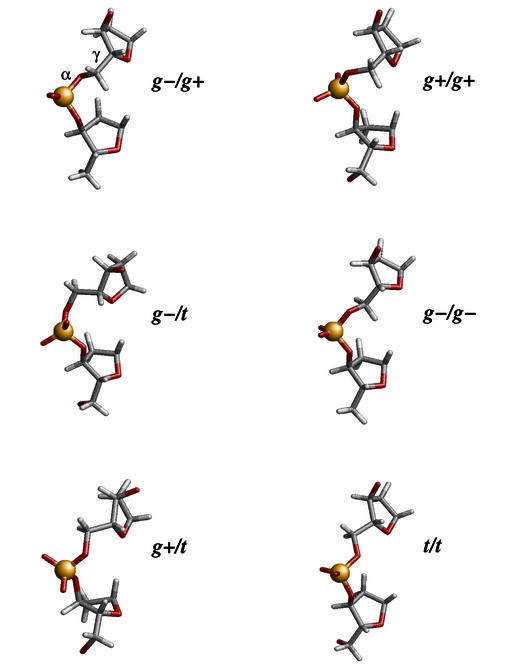
Figure 3 shows the average structures of the calculated α/γ states and the corresponding values of backbone angles and sugar puckers are given in Table 1. The β angle is mostly in the trans conformation, with the exception of the α/γ: g–/t and g+/g+ sub-states where it is in the rare gauche+ conformation. Further, beyond the usual BI conformation, we observe particular arrangements of ε/ζ in two cases. ε/ζ: g–/g+ is associated with α/γ: g+/t and ε/ζ: t/t with α/γ: g+/g+, giving rise to (ε–ζ) values that are very high (+169°) and very low (+46°), respectively. Thus, the BII conformation associated with the unusual α/γ backbone is different from that normally seen in the BII state of the free B-form DNA (ε/ζ: g–/t). Interestingly, stacking interactions are not perturbed even in the transition structures of the α/γ transition pathways.

Figure 3.

Average structures showing the various α/γ conformational sub-states of the central phosphate linkage of a GpC step. The canonical backbone is shown top left.

Table 1. Backbone angle sub-states and their associated torsion angle values and standard deviations (in parentheses) averaged over 2 ns of MD trajectory (all values in degrees).

	5′-Sugar	ε	ζ	(ε–ζ)	α	β	γ	3′-Sugar
BI/g–/t/g+	149 (34)	184 (9)	266 (13)	–82 (20)	295 (10)	176 (12)	54 (11)	142 (24)
BI/g–/g+/t	147 (14)	199 (8)	283 (8)	–85 (11)	262 (8)	62 (9)	182 (8)	160 (31)
BII/g+/t/t	140 (11)	288 (13)	119 (21)	169 (31)	79 (4)	219 (16)	189 (4)	163 (19)
BII/g+/g+/g+	145 (11)	209 (27)	162 (30)	46 (57)	32 (9)	72 (12)	45 (9)	97 (19)
BI/t/t/t	144 (32)	184 (9)	265 (13)	–82 (25)	142 (6)	183 (12)	183 (6)	131 (45)
BI/g+/t/g–	145 (13)	193 (9)	230 (9)	–37 (16)	63 (5)	183 (14)	273 (6)	188 (16)

It is worth noting that all the structural changes described above are in line with those obtained in the PES scan. Moreover, the regions sampled by the free energy pathways correspond well to the low energy regions of the PES map (Fig. 1). Thus, the energetics obtained for α/γ transitions using internal coordinate molecular mechanics and a simple continuum solvent representation show a good agreement with more refined free energy calculations.

Crystallographic data

It has been shown that the α and γ angles in B-DNA crystals are almost exclusively in the canonical g–/g+ conformation (49; D.Djuranovic and B.Hartmann, manuscript submitted). We find here that, in the crystal structures of protein–DNA complexes, while α/γ angles are again predominantly in the canonical state, they can also adopt several alternative conformations where the torsion angle α populates the gauche+ and trans conformations and γ populates the trans and gauche– conformations. Peaks in the α/γ angle distributions are clearly resolved with small standard deviations (<20°). Note that we have not extracted separate values for the GpC step from other dinucleotides in the analysis below.

In theory there are a large number of combinations available for α/γ and the other backbone torsions that compose the inter-nucleoside linkage, however, only a limited number of ε/ζ/α/β/γ combinations are actually observed. The crystallographic average values and the standard deviations of the (ε–ζ), α, β and γ backbone angles and of the sugar puckers for all the bound B-DNA combinations are given in Table 2. The canonical conformation in which ε/ζ is in BI and α/γ is in the g–/g+ conformation clearly prevails and β adopts the trans conformation centred on 175° in a large majority of cases. Alternative combinations involve variations in either ε/ζ or α/γ angles, except in one case which involves both sets of non-canonical conformations. The most populated non-canonical sub-state corresponds to the BII form of the phosphate groups, which is known to involve an easy transition (11,15,50). The (ε–ζ) values of the BII conformation are, however, centred around +35° and correspond to a ε/ζ: t/t conformation, whereas the BII state within free B-DNA mainly involves the ε/ζ: g–/t conformation. The other significant (>2%) arrangements are α/γ: g+/g–, t/t (with BI phosphates) and g+/t (with BII phosphates). In addition, we observe two combinations, α/γ: g–/t associated with β in gauche+ and α/γ: g+/t with the BI phosphate conformation, corresponding to 11 and 7 cases, respectively, which represent <1% of the total data set.

Table 2. Backbone angle sub-states and their associated torsion angle values and standard deviations (in parentheses) observed in crystal structures of protein–B-DNA complexes (all values in degrees).

(ε–ζ)/α/β/γ	%	5′-Sugar	(ε – ζ)	α	β	γ	3′-Sugar
BI/g–/t/g+	80.2	123 (55)	–73 (22)	299 (14)	174 (13)	48 (11)	124 (48)
BII/g–/t/g+	9.5	149 (20)	35 (13)	308 (10)	143 (7)	45 (8)	129 (56)
BI/g+/t/g–	4.0	158 (27)	–52 (15)	34 (17)	194 (20)	301 (20)	179 (29)
BI/t/t/t	2.4	71 (63)	–98 (27)	157 (21)	190 (16)	177 (14)	48 (52)
BII/g+/t/t	2.4	150 (8)	69 (22)	65 (17)	223 (7)	214 (13)	53 (56)
BI/g–/g+/t	0.9	144 (13)	–79 (11)	256 (7)	76 (15)	166 (10)	127 (53)
BI/g+/t/t	0.6	154 (11)	–23 (15)	91 (14)	223 (14)	214 (13)	73 (60)

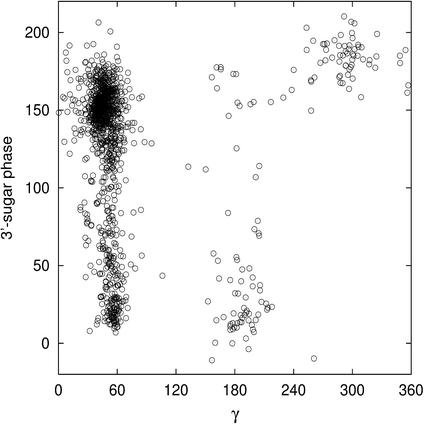
The most striking features of the unusual α/γ values are the associated sugars puckers. In protein-bound B-DNA the sugar conformation is variable, with 17% of north sugars, 10% of east sugars and 73% of south sugars. Outside the canonical α/γ range, which naturally accommodates any sugar pucker, a strong correlation between backbone angle and sugar conformations is observed. The α/γ: t/t conformation imposes both 5′- and 3′-sugars in north or east, whereas the α/γ: g+/g– arrangement is flanked by south sugars. More generally, a reciprocal effect between γ and its nearest sugar is observed (Fig. 4). The γ angle in trans tends to be associated with low phase angle values for the 3′-sugar, whereas γ in gauche– is linked to 3′-sugars in south. The influence of γ on its nearest sugar is supported by the fact that although the BII conformation with α/γ in its canonical state completely excludes both 3′- and 5′-sugars in north in free B-DNA (D.Djuranovic and B.Hartmann, manuscript submitted), the α/γ: g+/t conformation is associated with low phase angle values for the 3′-sugar in both the BI and BII conformations.

Figure 4.

3′-Sugar phase values versus γ torsion angle values (in degrees) in the protein–B-DNA crystallographic data set.

It is finally worth noting that ∼2% of the dinucleotide steps in free B-DNA are non-canonical and mainly involve the α/γ: g+/g– conformation. However, a careful analysis of the structures reveals that this α/γ conformation is always associated with particular regions in the system: (i) α/γ located on the first or last base pair junctions [BDJ051 (51) and BDJB50 (46)]; (ii) α/γ of a phosphate group in interac tion with a Mg²⁺ ion [BD0005 (52)]; or (iii) α/γ in A-tracts involving numerous inter-molecular contacts [BDJ081 (53)]. Consequently, the g+/g– conformation should not be considered as an alternative backbone conformation characteristic of free B-DNA except in exceptional circumstances.

Comparisons

Comparing the experimental and theoretical results, it is remarked that the majority of α/γ sub-states observed in the structural database were located in both the molecular mechanics and dynamics simulations. Theoretical structures did not result in the BI/g+/t/t sub-state, but indicated a possible α/γ: g+/g+ sub-state. The canonical form of α/γ is found to be the most stable in the theoretical study of B-DNA and is the most populated in the crystallographic structures of protein–DNA complexes. Unusual forms are destabilised by at least 5 kcal/mol according to our simulation of free DNA. These sub-states represent <10% of the dinucleotide steps in the crystallographic structures studied, where they can be assumed to be stabilised by the protein environment. The crystallographic percentages, however, do not strictly correlate with the calculated relative stabilities of the various arrangements. This may be due to the fact that proteins can stabilise alternative α/γ forms to different extents. Moreover, some sequence effects cannot be excluded, although the small variations in stacking energy along the pathway do not suggest major effects. This hypothesis cannot be tested at present, since the number of alternative α/γ forms for individual dinucleotide steps in protein–B-DNA complexes is not statistically significant. As an example, of the 46 GpC steps in our structural data set, only one BI/g–/g+/t, seven BII/g+/t/t and nine BI/g+/t/g– backbone conformations were found.

Concerning the coupling between backbone angle values, an almost perfect agreement is found between the crystallographic and calculated structures. In particular, one should note the change in the trans value of β associated with α/γ: g+/t and the low values of (ε–ζ) in the α/γ: g+/g– arrangement. However, (ε–ζ) in the BII/g+/t/t conformation is on average 69° in the crystallographic data, but 169° in the simulated structure. This very high (ε–ζ) value is found in only 14 dinucleotides of our crystallographic dataset, associated with either canonical or unusual α/γ forms, and exhibits the structural characteristics of a traditional BII state.

The sugar phase angles in the MD simulations for free DNA are mostly in the south conformation. This agrees well with the crystallographic data, except for the 3′-sugar for α/γ: g+/t and both 5′- and 3′-sugars for α/γ: t/t, where the experimental structures exhibit low phase angles. We tested the sugar conformations in the corresponding α/γ combinations by imposing north sugar phases in either the 5′ or the 3′ positions using JUMNA. However, the total energies of the minima increased by over 10 kcal/mol and the structures relaxed to the south minimum when the restraints were removed.

The α/γ structural effect on the helicoidal parameters essentially concerns roll and twist, two crucial parameters governing the overall curvature and winding of DNA. Table 3 shows these inter-base pair parameters for the simulated free DNA and the crystallographic structures of protein-bound DNA. For the unusual α/γ arrangements associated with BII phosphate conformations, the well-known influence of the BII state becomes apparent: large twist and negative roll (11,12,54). This indicates the predominant effect of the BII conformation over the α/γ changes. In contrast, it is clear that the twist values linked to the non-canonical α/γ conformations with BI phosphates are all reduced and, in addition, roll values become positive for α/γ: g+/g– and t/t.

Table 3. Average helicoidal parameters and standard deviations (in parentheses) calculated for the different backbone sub-states from MD simulations (MD) of free B-DNA and crystallographic data (Cr) of protein–B-DNA complexes (all values in degrees).

(ε–ζ)/α/β/γ	MD roll	Cr roll	MD twist	Cr twist
BI/g–/t/g+	–0.4 (6)	4.9 (17)	34.9 (5)	31.4 (9)
BI/g+/t/g–	4.4 (5)	4.4 (8)	31.6 (4)	30.2 (6)
BI/t/t/t	5.1 (5)	4.2 (7)	30.9 (4)	28.3 (6)
BI/g+/t/t	–	–1.7 (6)	–	30.4 (3)
BI/g–/g+/t	–1.4 (5)	–1.5 (7)	28.6 (5)	27.4 (5)
BII/g+/t/t	–9.2 (6)	–5.7 (7)	40.8 (3)	35.8 (4)
BII/g+/t/g+	–5.2 (6)	–	35.6 (3)	–

The average values from MD simulations and crystallographic data show a good correlation. However, the standard deviations of the structural parameters for the canonical conformation are clearly larger in the crystallographic data set than in the simulations. Indeed, while the experimental data cover 16 possible dinucleotide steps in different packing environments and flanked by various bases, our simulations are limited to a GpC step in a given sequence. Nevertheless, it is interesting to note that standard deviations in the crystal structures for non-canonical α/γ states are found to be about half of those seen for the canonical α/γ conformation, largely independently of the type of dinucleotide involved.

CONCLUSIONS

Molecular simulation techniques have been used to study the transitions of the α/γ backbone torsion angle in the central GpC step of a B-DNA dodecamer. Five α/γ sub-states were identified in addition to the canonical form. The free energy variations and the transition paths between these sub-states were determined. The lowest energy pathway from the canonical form to the unusual α/γ sub-states involves the α/γ: t/t combination and thus corresponds to a counter-rotation of α and γ. The lowest energy barrier is >7 kcal/mol and consequently none of these states seem to be accessible for B-DNA in solution. This result is in agreement with an analysis of crystallographic data which shows that unusual α/γ backbones are rarely encountered in free B-DNA, while they appear more frequently in B-DNA oligomers complexed to proteins.

Among the five non-canonical α/γ sub-states, two are well-defined minima and three are meta-stable, i.e. separated from the stable minima by negligible energy barriers. Four of these sub-states are found in the protein–B-DNA crystallographic structures and correlate with the calculated structures not only in terms of backbone torsions but also in terms of helicoidal perturbations. Unusual α/γ steps associated with (ε–ζ) > 0 are dominated by the characteristics of the BII state: negative roll and large twist values. In contrast, the unusual α/γ conformations in BI steps reduce the twist values below 31° and, in two cases, clearly favour positive rolls. Furthermore, unusual α/γ backbone states tend to fix the local parameters of the double helix more rigidly, reducing the dispersion of roll and twist values.

Finally, as unusual α/γ junctions do not seem to appear spontaneously in free B-DNA, they probably do not have a direct role in the early stage of protein–DNA recognition. The presence of a protein is required to change the energetics of these transitions and it is clear that further investigations are indispensable to clarify the precise role of the protein. Nevertheless, the non-negligible structural perturbations associated with unusual α/γ backbones support the hypothesis that they may intervene during the fine structural adaptation between the two partners.