Gas-Phase Reactions of Hydrated Alkaline Earth Metal Ions, M²⁺ (H₂O)_n (M = Mg, Ca, Sr, Ba and n = 4–7), With Benzene

Abstract

Gas-phase reactions of hydrated divalent alkaline earth metal ions and benzene were investigated by electrospray ionization Fourier-transform mass spectrometry. Rate constants for solvent-exchange reactions were determined as a function of hydration extent for Mg²⁺, Ca²⁺, Sr²⁺, and Ba²⁺ clusters containing four to seven water molecules each. All of the strontium and barium clusters react quickly with benzene. Barium reacts slightly faster than the corresponding strontium cluster with the same number of water molecules attached. For calcium, clusters with four and five water molecules react quickly, whereas those with six and seven water molecules do not. Magnesium with four water molecules reacts quickly, but not when five through seven water molecules are attached. The slow reactivity observed for some of these clusters indicates that the cation–π interaction between the metal ion and benzene is partially screened by the surrounding water molecules. The reactivity of magnesium with seven water molecules is intermediate that of the hexa- and pentahydrate and the tetrahydrate. This result is consistent with the seventh water molecule being in the outer shell and much more weakly bound. The unusual trend in reactivity observed for magnesium may be due to the presence of mixed shell structures observed previously. These results are the first to provide information about the relative importance of cation–π interactions in divalent metal ions as a function of metal hydration extent. Such studies should also provide a model and some insight into the relative binding affinities of divalent metal ions to aromatic residues on peptides and proteins.

Ion transport processes across cellular membranes are governed by the role of competitive intramolecular and intermolecular interactions between solvent molecules, proteins or peptides, and the ions of interest. The transfer of an ion through a hydrophobic environment can be effected by two mechanisms. The ion-carrier mechanism involves naturally occurring multidentate ligands known as ionophores. These ligands can arrange to form cavities with higher selectivity toward a specific ion in solution. Ionophores, such as valinomycin and nonactin, bind potassium ions preferentially over the other alkali metals [1]. Once the ion–ionophore complex is formed, the outer hydrophobic surface of the “carrier” facilitates the transport into or across the nonpolar environment. The second ion transport mechanism involves channel-forming ionophores, like the gramicidins [1], which form hydrophilic pathways extending across a hydrophobic membrane allowing the passage of ions. The selectivity observed in solution for complexes between ionophores and metal ions is a consequence of the small differences between the stability constants of the cations with water and those of the cations with the ionophores.

Both natural and synthetic ionophores have been studied extensively in an effort to gain a better understanding of the ion selectivity properties of these systems. Solution studies involving crown ethers and alkali metal ions indicate that the size of the ring cavity determines which metal ions bind more effectively. For example, the complex between 18-crown-6 and K⁺ has a higher stability constant than that between the crown and Na⁺ [2]. These complexes have been investigated using both molecular mechanic calculations [3] and gas-phase techniques [4–7]. Dearden and co-workers have investigated the gas-phase reactions of alkali metal ions with crown ethers and their acyclic analogs, the glymes [4, 5]. The stability of 1:1 complexes between the metals and both types of ligands follows an electrostatic trend; the small ions, Li⁺ and Na⁺, bind more strongly to the hosts than the larger K⁺ and Rb⁺ ions. However, size-selective behavior favoring the formation of 2:1 ligand:metal complexes of 12-crown-4 with Na⁺ and of 15-crown-5 with K⁺ was also observed. More recently, Dearden and co-workers investigated complexes of divalent alkaline earth metal ions with 12-crown-4 and triglyme and their solvent-exchange reactions with 18-crown-6 [8]. Brodbelt and co-workers have also reported binding selectivity from electrospray competition experiments involving Na⁺, K⁺, and 18-crown-6 [9]. Because the ions in solution must be at least partially desolvated in order for complexes to form, the balance between solvation energies and intrinsic complex stabilities is believed to account for the majority of the nonelectrostatic, but size-selective behavior observed in solution. Although selectivity has been observed in some gas-phase experiments, the role of solvent in the formation of these complexes has not been thoroughly investigated.

Another important interaction involved in ion transport processes is that between metal ions and the aromatic side chains of the hydrophobic amino acids tryptophan (Trp), phenylalanine (Phe), and tyrosine (Tyr). In studies of K⁺ gating channel proteins, the abundance of the Gly-Tyr-Gly sequence in the pore regions of the proteins has been reported [10]. The cation channels in these proteins are formed by tetrameric complexes in which the tyrosine side chains form rectangular passages that just fit the potassium ion. Dougherty and co-workers have extensively studied these “cation–π” interactions in aqueous solution by investigating the cation binding properties of synthetic hosts containing aromatic residues [11]. Experiments involving both metal and organic ions suggest that these noncovalent interactions which mimic hydrophobic binding sites in proteins can compete with those with water and can result in an ion being sequestered from solution [11a].

The interactions between cations and aromatic molecules have also been investigated in gas-phase experimental [12–16] and theoretical [17, 18] studies where benzene, phenol, and indole or pyrrole are used as models for the aromatic side chains of the amino acids phenylalanine, tyrosine, and tryptophan, respectively. Using high-pressure mass spectrometry, Kebarle and co-workers [12] determined that the binding energy of benzene to K⁺ is 18.3 kcal/mol. This value is slightly higher than the binding energy of the first water molecule to K⁺ (17.9 kcal/mol) [19], indicating a more favorable interaction between the metal and the benzene molecule. Studies by Meot-Ner and co-workers [13, 14] have also demonstrated the strong affinities between various alkyl ammonium ions and both benzene and benzene derivatives. Results from theoretical studies of Dougherty and co-workers [17] indicate that in the gas phase, the interactions between alkali metal ions and benzene follow a classical electrostatic trend in which the smaller Li⁺ and Na⁺ ions are more strongly bound to benzene than the larger K⁺ and Rb⁺ ions. In a simulated aqueous environment, however, the cation–π affinity follows the order K⁺ > Rb⁺ >> Na⁺, Li⁺ for formation of 2:1 benzene:metal complexes. This reordering in affinities has been attributed to the effect of the higher hydration energies of the smaller metal ions. More recently, Dunbar and co-workers have performed experimental [15, 16] and theoretical [18] studies involving aromatic π-bonding systems and singly charged metal ions. The role of π versus heteroatom bonding was investigated, and radiative association kinetics were used to determine the binding energies for the attachment of the first and second ligand to the metals.

Gas-phase studies between hydrated ions and ionophoric or aromatic compounds should provide a link between the size-selective behavior observed in solution and the intrinsic gas-phase reactivity. By varying the initial extent of ion hydration, the role of water can be investigated while the transition from a hydrophilic to a hydrophobic environment occurs. Lisy and coworkers recently investigated benzene/water clusters of K⁺ and Na⁺ using vibrational predissociation spectroscopy and collisionally activated dissociation experiments [20]. Hydrogen-bonding interactions and dissociation trends provided information about the structure of these mixed systems. For potassium, the intrinsic interaction between benzene and the potassium ion is favored over the metal–water interaction for molecules in the first solvation shell. In the second solvation shell, benzene and water molecules appear to have similar interaction energies. For sodium, water molecules in the first solvation shell are not displaced by benzene [20b]. These studies provide insight into the selectivity of ion channels for potassium and sodium.

It is evident from these previous studies that experiments on mixed-solvent metal clusters provide one way to investigate the competitive interactions between ions, solvent molecules, and aromatic residues. In the present work, an alternate method for studying these interactions is presented. Here, we investigate the reactions of hydrated divalent alkaline earth metals generated by electrospray ionization with benzene in a Fourier-transform mass spectrometer (FTMS). We have demonstrated that these hydrated metals can be easily generated and we have used blackbody infrared radiative dissociation (BIRD) experiments [21–23] and master equation modeling to determine binding energies of individual water molecules located in the first and second solvation shells around the metals. In the present work, the gas-phase solvent-exchange reactions between hydrated divalent alkaline earth metal clusters of Mg, Ca, Sr, and Ba, with four to seven water molecules and benzene are investigated. These studies should provide more information about the intrinsic interactions of ions with solvent and aromatic residues which are known to be relevant to biological recognition events like the binding of acetylcholine to its receptors [24] and the functioning of voltage-gated ion channels [25]. It is observed in our experiments that the smaller Mg and Ca ions show less reactivity toward solvent exchange when the initial cluster contains more than four and five water molecules, respectively, indicating a protective effect by the surrounding waters. As the number of water molecules around these metals decreases, the cation–π interaction is less effectively perturbed by the water molecules and dehydration occurs readily, resulting in solvent exchange. For the larger hydrated Sr and Ba ions, solvent-exchange reactions are fast and similar reactivity is observed for clusters containing four to seven water molecules. To our knowledge, this is the first experimental report of gas-phase ion–molecule reactions between hydrated divalent metals and an aromatic π-bonding system.

Experimental Methods

All experiments are performed using a home-built external electrospray ionization source FTMS that has been described previously [26]. Extensively hydrated ions are formed by nanoelectrospray ionization (solution flow rate ~10–100 nL/min) from aqueous solutions of the metal chloride salts [23]. The concentration of metal ions in solution is about 1 × 10⁻⁴ M. Hydrated ions are guided through five stages of differential pumping toward a rectangular cell located in the center of a superconducting magnet operating at a magnetic field strength of 2.7 tesla. Ions are loaded into the FTMS cell for 6–8 s. Nitrogen gas (~2 × 10⁻⁶ torr) is introduced during the ion accumulation event in order to collisionally trap and assist in the thermalization of the ions. The ion of interest is isolated using both single and broadband frequency excitation pulses and subsequently reacted with a constant pressure of benzene. Liquid benzene is degassed using several freeze–pump–thaw cycles, and its vapor is introduced to the cell through a sapphire leak valve (Varian Vacuum Products, Lexington, MA) to a pressure of ~1 × 10⁻⁸ torr. Reactions between the mass-selected hydrated ions and the benzene molecules are monitored by measuring the abundance of the precursor and all product ions as a function of time. Reaction times are varied between 0 and 60 s. Ions are excited for detection using a 3200 Hz/μs, 120 V_pk-pk frequency sweep (32K data points collected), and spectra are recorded using an Odyssey Data System (Finnigan, Madison, WI). The rate constants for ligand exchange reactions are obtained by fitting the data to pseudo first-order kinetics.

Results and Discussion

ESI Mass Spectra

Figure 1a shows the distribution of hydrated Mg²⁺ ions generated by nanoelectrospray ionization of an aqueous solution containing this metal. The spectrum shown in Figure 1b was obtained under similar experimental conditions, but with benzene vapor in the cell at a pressure of 1 × 10⁻⁸ torr. In addition to the original distribution of hydrated Mg²⁺ ions, peaks corresponding to mixed clusters containing water and one benzene molecule are also observed. The ion at m/z = 79 (~25% normalized abundance) is due to both the (A + 2) isotope of magnesium (~11%) and to protonated benzene, (B + H)⁺ (~14%). In the lower spectrum, the intensity of Mg²⁺(B)(H₂O)₃ is noticeably higher than that of any of the other corresponding mixed hydrates. This suggests that Mg²⁺(H₂O)₄ reacts more quickly with benzene than the more highly hydrated Mg²⁺ ions. After benzene introduction, a decrease in intensity is also observed for Mg²⁺(H₂O)₅ (m/z = 57). However, the corresponding solvent-exchange product, Mg²⁺(B)(H₂O)₄ (m/z = 87), is not abundant. This discrepancy could result from slightly different initial Mg²⁺(H₂O)₅ ion populations in the two spectra or it could be due to subsequent loss of water from Mg²⁺(B)(H₂O)₄ to produce Mg²⁺(B)(H₂O)₃.

Figure 1.

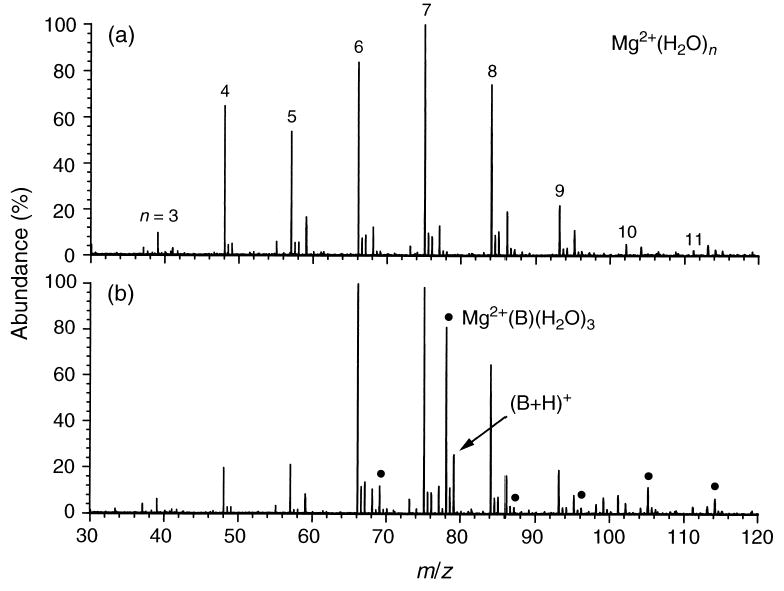
Nanoelectrospray ionization mass spectra of Mg²⁺(H₂O)_n ions obtained before (upper) and after (lower) introduction of benzene. Mixed clusters containing one benzene molecule and two to seven water molecules are indicated with filled circles. P(benzene) = 1 × 10⁻⁸ torr.

As observed with Mg²⁺(H₂O)_n, the distribution of Ca²⁺(H₂O)_n ions is also affected by the introduction of benzene, with hydrated ions that have fewer water molecules showing more reactivity. In contrast, the original relative distributions of hydrated clusters of Sr²⁺ and Ba²⁺ are not significantly affected by the introduction of benzene. Figure 2 shows the spectra obtained for Ba²⁺(H₂O)_n ions (a) before and (b) after introduction of benzene in the cell. A significant abundance of mixed clusters containing water and one, two, and three benzene molecules is observed. However, the original distribution of pure-water clusters is not significantly changed, indicating that these ions have similar rates of exchange.

Figure 2.

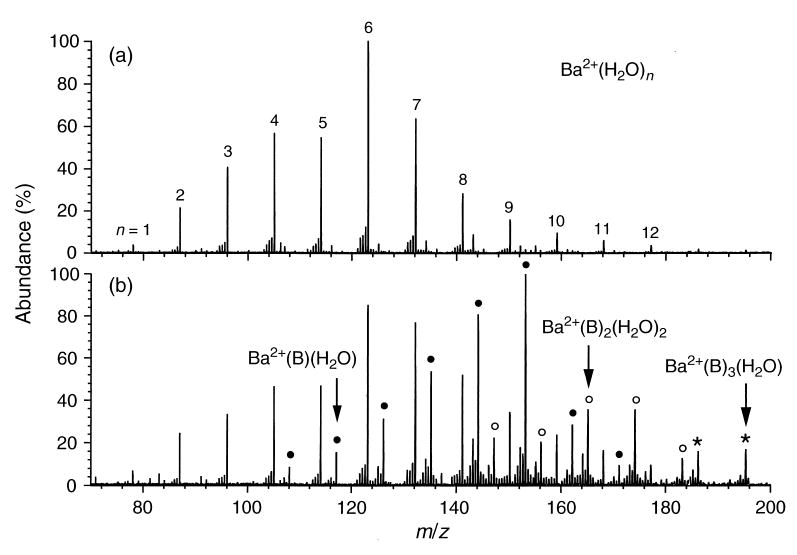
Nanoelectrospray ionization mass spectra of Ba²⁺(H₂O)_n ions obtained before (upper) and after (lower) introduction of benzene. Mixed clusters containing one, two, and three benzene molecules are indicated with filled circles, open circles, and asterisks, respectively.

Ion–Molecule Reactions

In general, reaction of the hydrated metal ions bound to four to six water molecules with benzene results in the sequential dehydration of the metal and the formation of mixed metal/water/benzene clusters. As an example, Figure 3 shows a plot of normalized ion abundance as a function of time for the reaction of Ca²⁺(H₂O)₅ with benzene at a pressure of 1 × 10⁻⁸ torr. Appearance/depletion curves are shown for the precursor and all product ions. At short times, the only product ion observed is Ca²⁺(B)(H₂O)₄ (B = benzene), corresponding to the exchange of one water molecule with one benzene molecule. At later times, additional solvent exchange leads to the formation of cluster ions containing two benzene molecules, Ca²⁺(B)₂(H₂O)₃. These ions subsequently undergo unimolecular dissociation, resulting in the loss of a water molecule and the formation of Ca²⁺(B)₂(H₂O)₂ clusters.

Figure 3.

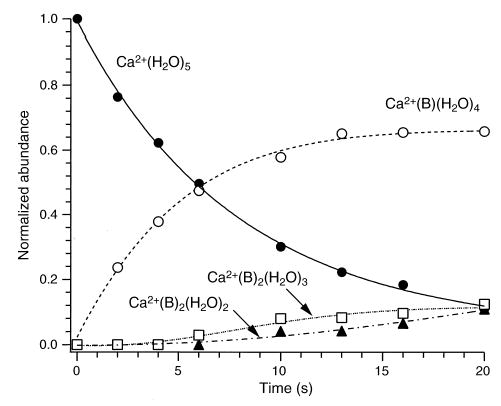
Appearance/depletion curves for the reaction of Ca²⁺(H₂O)₅ ions with benzene (B) at a pressure of 1 × 10⁻⁸ torr. Cell temperature is 25 °C.

Similar solvent-exchange reactions and unimolecular dissociation processes are observed for most of the metals investigated. The scheme shown in Figure 4 illustrates the possible reaction pathways observed with our experimental conditions. The extent of ligand exchange increases with the size of the metal. For example, reaction of tetrahydrated magnesium ions with benzene results in the exchange of only one water molecule by one benzene molecule. However, for tetra-hydrated barium ions under similar conditions, nearly all of the water molecules are exchanged by three or four benzene molecules.

Figure 4.

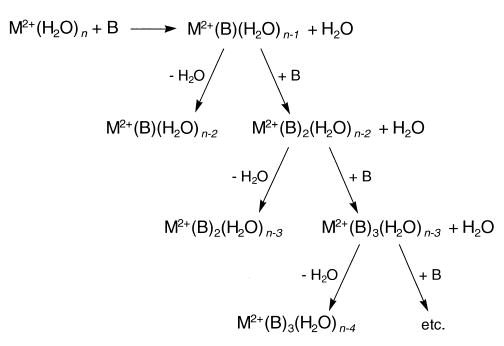
General scheme for solvent-exchange reactions between hydrated alkaline earth metal ions and benzene.

Most of the mass-selected hydrated metal precursor ions investigated only undergo solvent-exchange reactions. However, the heptahydrated metal ions also undergo unimolecular dissociation under the conditions of our experiments. That is, depletion of the precursor ion is the result of both solvent exchange and unimolecular dissociation for these ions. This is illustrated in Figure 5, which shows the appearance/depletion curves for the reaction of Mg²⁺(H₂O)₇ with benzene. For this ion, the principal reaction channel is unimolecular dissociation, resulting in the loss of a single water molecule and the formation of Mg²⁺(H₂O)₆ ions. The parallel solvent-exchange reaction producing Mg²⁺(B)(H₂O)₆ clusters represents less than 20% of the product ions after 30 s. The formation of Mg²⁺(B)(H₂O)₅ is also observed. This species is produced by the loss of water from Mg²⁺(B)(H₂O)₆.

Figure 5.

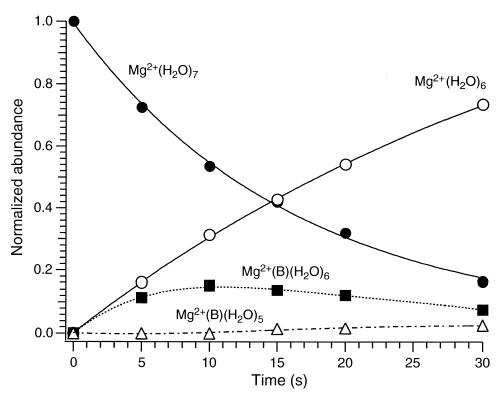
Appearance/depletion curves for the reaction of Mg²⁺(H₂O)₇ with benzene (B) at room temperature. The pressure of benzene is 1 × 10⁻⁸ torr.

Reaction Rate Constants

Rate constants for the first solvent-exchange reaction for the hexa-, penta-, and tetrahydrated metals are obtained by fitting the normalized abundance of the ratio of parent ion to fragment ion as a function of reaction time to pseudo first-order kinetics. As an illustration, Figure 6 shows plots of the kinetic data for the four hexahydrated ions investigated. These data are linear for all of the hydrated metal ions. From the slope of these data, rate constants for the solvent-exchange reactions are determined. These rate constants for each one of the hydrated alkaline earth metal ions are shown in Table 1. The reaction efficiency for each one of the solvent-exchange processes investigated was also determined by dividing the experimental rates by the corresponding Langevin collision rate constants [27]. Those values are also included in Table 1. For hexahydrated Mg²⁺, very little solvent exchange occurs for reaction times up to 60 s, as indicated by the low reaction efficiency of 0.2%. The Ca²⁺, Sr²⁺, and Ba²⁺ hexahydrated clusters undergo more facile solvent exchange, with the bigger strontium and barium ions exchanging at a faster rate (reaction efficiencies above 20%). Similar behavior is observed for the pentahydrated clusters. For these ions, Ca²⁺, Sr²⁺, and Ba²⁺ undergo fast reactions with benzene (reaction efficiency ~30%), whereas pentahydrated magnesium ions react ~70 times slower (0.4% efficiency). In contrast, all tetrahydrated ions react quickly, with Mg²⁺(H₂O)₄ having slightly higher reactivity than the other metal ions.

Figure 6.

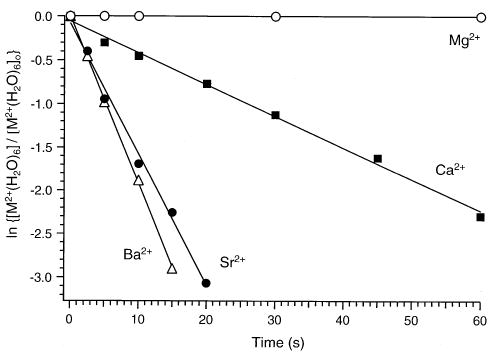
Kinetic data for the reactions of alkaline earth M²⁺(H₂O)₆ ions with benzene at room temperature. The pressure of benzene is 1 × 10⁻⁸ torr.

Table 1.

Reaction rate constants (and reaction efficiencies) for solvent exchange between alkaline earth metal ions and benzene. Rate constants are reported in × 10⁻¹⁰ cm³/molecule·s.^a Reaction efficiencies are reported in percentages (%) and were obtained using the calculated Langevin collision rate constants [27]

Metal	Hepta-	Hexa-	Penta-	Tetra-
Mg2+	0.5 ± 0.2 (5)	0.02 ± 0.01 (0.2)	0.04 ± 0.01 (0.4)	4.4 ± 0.2 (38)
Ca2+	0.4 ± 0.2 (4)	0.5 ± 0.2 (5)	3.3 ± 0.1 (31)	2.9 ± 0.1 (26)
Sr2+	1.8 ± 0.3 (18)	2.1 ± 0.1 (21)	2.8 ± 0.1 (28)	2.5 ± 0.1 (24)
Ba2+	3.8 ± 0.3 (39)	2.7 ± 0.1 (28)	3.2 ± 0.2 (32)	3.3 ± 0.1 (33)

^aThe reported errors correspond to the standard deviation of the rate constants determined from the kinetic data and do not include uncertainties in the measured pressure of benzene.

As discussed previously, the heptahydrated ions undergo both solvent exchange with benzene and unimolecular dissociation. The overall rate constant for depletion of the precursor ion is the sum of the individual rate constants for solvent exchange (k₁) and for loss of water (unimolecular dissociation, k₂), as illustrated below, where K₁ = k₁[B],

$${\text{M}}^{2+}{({\text{H}}_2\text{O})}_7+\text{B}\stackrel{k_1}{\to }{\text{M}}^{2+}(\text{B}){({\text{H}}_2\text{O})}_6+{\text{H}}_2\text{O}$$

$${\text{M}}^{2+}{({\text{H}}_2\text{O})}_7\stackrel{k_2}{\to }{\text{M}}^{2+}{({\text{H}}_2\text{O})}_6+{\text{H}}_2\text{O}$$

$$\text{ln}\left(\frac{{[{\text{M}}^{2+}{({\text{H}}_2\text{O})}_7]}_t}{{[{\text{M}}^{2+}{({\text{H}}_2\text{O})}_7]}_o}\right)=-(K_1+k_2)t$$

and [B] is the concentration of benzene. The rate constants for loss of water (k₂) from the heptahydrated alkaline earth metal ions at room temperature have been measured previously using BIRD [23]. Using these values, the rate constants for the solvent-exchange process are determined (Table 1). Solvent-exchange rate constants and reaction efficiencies for the Mg²⁺(H₂O)₇ and Ca²⁺(H₂O)₇ ions are intermediate, with 5% and 4% reaction efficiency, respectively. The rate constants for Sr²⁺(H₂O)₇ and Ba²⁺(H₂O)₇ are significantly higher (18% and 39% efficiency, respectively).

Factors Determining Reactivity

Several factors are expected to play a major role in the reactions of hydrated metal ions with benzene. First, the intrinsic electrostatic interaction (ion–dipole; ion–induced dipole) between the metal ions and the surrounding water molecules, and second, the intrinsic cation–π affinity, or ion–quadrupole moment interaction, between the metal ions and benzene, clearly must be important. Both of these interactions are expected to be large for small ions and to steadily decrease as the size of the metal increases. Reactions between singly charged alkali metal ions and a variety of solvent molecules have been extensively investigated [28]. For interactions with both water and benzene, binding energies follow the trend Li > Na > K > Rb. For the larger hydrate clusters, the relative solvent-shell affinities for benzene versus water should be important.

There are no previous experimental determinations of the binding energy between divalent alkaline earth metal ions and benzene. However, the intrinsic cation–π interaction is expected to follow a similar electrostatic trend as that observed for the singly charged alkali metals. That is, binding energies between divalent alkaline earth metals and benzene are expected to follow the order Mg > Ca > Sr > Ba. For the hydrated alkaline earth metal ions investigated here, the reactivity toward solvent exchange with benzene is expected to be determined by a delicate balance between the metal–water and the metal–benzene interactions.

Strontium and barium.

All of the hydrated Sr²⁺ and Ba²⁺ clusters investigated show fast solvent-exchange reactions with benzene, with rate constants on the order of ~2–4 × 10⁻¹⁰ cm³/molecule·s and reaction efficiencies between 18% and 39%. In addition, each one of the hydrated barium ions investigated shows slightly higher reactivity toward solvent exchange with benzene than the corresponding strontium clusters. This trend in reactivity is consistent with the trend in water-binding energies obtained from BIRD [22, 23] and high pressure mass spectrometry [29] experiments which indicate that individual water molecules are more weakly attached to barium than to strontium ions.

The reactivity observed for the larger strontium and barium ions can also be explained by the screening provided by the surrounding waters. Four to seven water molecules may not be enough to complete the first hydration shell around these large ions. Experiments by Kebarle and co-workers [29] suggest that Sr²⁺ clusters contain seven waters and Ba²⁺ clusters contain eight or more water molecules in the first solvation shell. An ineffective solvation by water would lead to a significant cation–π interaction between each one of the metals and benzene. The larger metal, barium, would be less effectively screened, and this would be consistent with the faster rate constants and higher reaction efficiencies observed.

Lisy and co-workers [20] have previously reported on the size selectivity observed for the solvation of K⁺ and Na⁺ by benzene and water. These results indicate that waters in the first hydration shell around K⁺ can be replaced by benzene molecules. However, first-shell dehydration is not observed for Na⁺, in which case the benzene molecules form a second solvation shell. Considering the ionic radii (R_i) of the alkali and alkaline earth metal ions, it is noted that K⁺ and Ba²⁺ have similar radii under similar coordination conditions (138 and 135 pm, respectively, for hexacoordination) [30]. Sr²⁺, on the other hand, is 15% smaller than K⁺ (R_i = 118 pm). It is possible that the higher reactivity observed during our experiments on Ba²⁺ clusters is the result of a size-selective interaction between the metal and benzene, similar to that previously reported for K⁺.

Calcium.

For divalent calcium ions, the reaction rate constants are more strongly dependent on the initial extent of ion hydration. For tetra- and pentahydrated ions, reaction rate constants are significantly higher than those for hexa- and heptahydrated calcium, a trend reflected in the reaction efficiencies of these ions. For Ca²⁺ ions initially solvated by seven and six water molecules, the reaction efficiencies are 4% and 5%, respectively. For penta- and tetrahydrated Ca²⁺, the efficiency of solvent-exchange reactions increases to 31% and 26%, respectively. The slow reaction rates observed when calcium is solvated by six or seven waters indicate that the calcium ion is effectively solvated by six water molecules but not by four or five. With four or five water molecules, benzene can interact more strongly with the metal, resulting in loss of water from the ion cluster.

It is also noted that the trend in reactivity observed for the hydrated calcium ions does not follow the trend in binding energies of the individual water molecules. Previous dissociation studies in our laboratory [21–23] as well as those of Kebarle and co-workers [29], indicate that individual water-binding energies to alkaline earth metal ions increase as the number of water molecules decreases. That is, the seventh water is more weakly bound than the sixth, which in turn is more weakly bound than the fifth, and so forth. If solvent-exchange reactions with benzene were determined only by individual water-binding energies, then the reaction rate constants and efficiencies would decrease for those clusters containing fewer water molecules. However, this is not the case.

Magnesium.

The reactions between hydrated magnesium ions and benzene show an unusual trend in behavior. The tetrahydrate is the most reactive of all of the hydrates studied, with a 38% reaction efficiency. This is nearly as high as that observed for heptahydrated Ba²⁺. The reactions of the hexa- and pentahydrates are less efficient (0.2% and 0.4%, respectively), whereas the reactivity of heptahydrated Mg²⁺ is intermediate (4.8%). This trend in reactivity is clearly different from that of the other metal ions. The low reaction efficiency of the hexa- and pentahydrates of magnesium is surprising. This result is consistent with a structure in which five or six water molecules are able to effectively screen the ion from benzene. The high reactivity of the tetrahydrate suggests that four water molecules are insufficient for effective screening. The intermediate reactivity observed for heptahydrated Mg²⁺ suggests that the seventh water molecule does not play a significant role in ion screening and can be more readily displaced by benzene. This observation, along with previous binding energy measurements [22, 23, 29], are consistent with this water molecule being located on the second solvation shell around the ion.

Previous BIRD experiments and molecular modeling studies suggested the presence of two isomeric structures for Mg²⁺(H₂O)₆ [22, 23]; a structure in which all six water molecules are in the inner shell at low temperature, and a structure in which two water molecules are in the outer shell at higher temperature [23]. Results for Mg²⁺(H₂O)₅ indicated a structure in which one water molecule is in the outer shell. For these two shell structures of penta- and hexahydrated Mg²⁺, the fifth and sixth second-shell water molecules are each hydrogen bonded to two first-shell water molecules. These double hydrogen-bonding interactions are probably stronger than the interaction between benzene and first-shell waters which would involve only one O–H—π type of interaction per benzene molecule (see work on Na⁺ by Lisy and co-workers [20b]). These structures for five and six water molecules are unique to magnesium and may account for the unusual solvent-exchange reactivity of these clusters. For the isomeric penta- and hexahydrated M²⁺ structures in which all water molecules are in the first solvation shell, the benzene metal ion interaction may be sufficiently screened, consistent with the low reaction efficiency observed for these species. A four-water first shell, as noted previously, is probably insufficient for effective screening.

Conclusions

The effects of hydration extent on the reactivity of divalent alkaline earth metal ions with benzene were investigated. Barium and strontium with four to seven water molecules undergo rapid solvent exchange with benzene (addition of benzene and loss of one water molecule), whereas the rate of solvent exchange for hydrated calcium and magnesium ions depends more strongly on solvation extent. The rates of solvent exchange for calcium with six or seven water molecules are much less than those of calcium bound to four or five water molecules. This result is consistent with six water molecules providing an adequate shielding effect that prevents benzene from closely interacting with calcium. For magnesium, the tetrahydrate is much more reactive than the penta-, hexa- or heptahydrate, indicating that five water molecules provide adequate shielding for this ion.

Studies of the competitive binding between divalent alkaline earth metal cations with water and benzene provide information about both the structure of the hydrated cations as well as the relative importance of hydration and aromatic π interactions. This information is important for understanding size-selective behavior in solution. Extending these studies to amino acid analogs should provide information about the selective binding of divalent metal ions to peptides and proteins.