Abstract
From equilibrium molecular dynamics simulations we have determined single-channel water permeabilities for Escherichia coli aquaporin Z (AqpZ) and aquaglyceroporin GlpF with the channels embedded in lipid bilayers. GlpF's osmotic water permeability constant pf exceeds by 2–3 times that of AqpZ and the diffusive permeability constant (pd) of GlpF is found to exceed that of AqpZ 2–9-fold. Achieving complete water selectivity in AqpZ consequently implies lower transport rates overall relative to the less selective, wider channel of GlpF. For AqpZ, the ratio pf/pd ≅ 12 is close to the average number of water molecules in the channel lumen, whereas for GlpF, pf/pd ≅ 4. This implies that single-file structure of the luminal water is more pronounced for AqpZ, the narrower channel of the two. Electrostatics profiles across the pore lumens reveal that AqpZ significantly reinforces water-channel interactions, and weaker water-water interactions in turn suppress water-water correlations relative to GlpF. Consequently, suppressed water-water correlations across the narrow selectivity filter become a key structural determinant for water permeation causing luminal water to permeate slower across AqpZ.
INTRODUCTION
Homotetrameric water channels, aquaporins (Aqps) facilitate in all life forms water permeation across biological membranes at high rates (1–5). Osmotically driven fluxes through Aqps are measured by reconstituting these channels into liposomes and monitoring their volume changes in response to media of different solute concentrations to which the liposome is impermeable (1,3,5–8). A major experimental challenge is that the precise protein-to-lipid composition of the liposome (7) or similar reconstituted systems (9,10), i.e., the density of water channels, must be determined to derive single-channel transport rates from membrane permeability measurements (11). This is in most cases not possible. The same applies to determination of the single-channel diffusive water permeability, which may be derived from isotopic labeling experiments (6).
Molecular dynamics (MD) simulations do not face this challenge since only a single Aqp tetrameric (or monomeric) channel embedded in a lipid bilayer patch, micelle, or water is considered (11–20). Given that the fast kinetics of an Aqp water channel can be well captured by MD simulations (21), such simulations offer a good alternative method for studying single-channel water transport in Aqps (14,15). Water structure and dynamics have also frequently been studied by means of MD simulations in model-channels such as gramicidin A (22–24), carbon-nanotubes (25–29), and related pore models (30).
In particular, diffusive permeabilities are easily measured in MD simulations (14–16). To measure the osmotic permeability a driving force—osmotic or hydrostatic— is typically imposed (11,17,28,29,31). Provided that the pressure or concentration gradients are sufficiently small, the resulting water flux will be linear in the driving force (11–17). However, to obtain significant transmembrane net fluxes of water in the simulations, one would have to impose quite large driving forces. This introduces a range of undesired problems with respect to conservation of channel architecture and the position of the channel relative to the bilayer, which together render computational recordings of flux-driving force relationships nontrivial (11,17,27). To circumvent this problem, a method allowing for accurate estimation of single-channel, osmotic (or hydraulic) permeability constants from equilibrium MD simulations has been proposed (29). This method relies on calculation of a collective coordinate accumulating simply the individual displacements of the luminal water molecules, and no biasing transmembrane gradient being imposed (29,31).
Medium-resolution models of human Aqp1 (hAqp1) (32,33) and high-resolution structures of bovine Aqp1 (bAqp1) (34) as well as of bovine and sheep Aqp0 (35–37) and of spinach SoPIP2;1 (38) have together with high-resolution x-ray structures of the Escherichia coli Aqps GlpF and AqpZ (15,39,40) provided detailed structural insight into Aqp function and selectivity. However, it is still unclear how channel radius, radius fluctuations, pore-polarity, and composition of the so-called Aqp selectivity filter (SF) and the lipid matrix determine and influence permeability across Aqps. The presence of atomic-level structures of two different Aqp water channels from the same organism, namely GlpF (2.2 Å resolution) and AqpZ (2.5 Å resolution) of E. coli (15,39,40) offers an excellent opportunity for investigating, in a comparative fashion, how channel architecture couples to channel selectivity and transport rates (41,42).
One important aspect of such a comparison is whether an orthodox, strictly water selective water channel, e.g., AqpZ, permeates water faster than a less selective aquaglyceroporin, e.g., GlpF. Pioneering MD simulations by de Groot and Grubmüller somewhat surprisingly suggested that the orthodox water channel hAqp1 permeates water diffusively at lower rates than aquaglyceroporin GlpF (14), which contrasted and still contrasts experimental data (7,9,10,43). Their diffusive permeation rates for GlpF were later confirmed in related studies (15,16,18). Moreover, computational measurements of the osmotic water permeability also found GlpF to permeate water at significantly higher rates than bAqp1 (11,17). Therefore, a discrepancy between simulation and experiment has prevailed since the very first MD simulations of orthodox Aqps and aquaglyceroporins.
In this article, we address this prevailing conflict. Specifically, we report single-channel osmotic and diffusive water permeabilities for E. coli GlpF and AqpZ. Relative to AqpZ, we find that GlpF permeates water osmotically at rates 2–3 times faster and diffusively 2–9 times faster. With respect to water permeation, a narrow, polar and completely water-selective channel as AqpZ is, according to MD simulations, seemingly not superior to a wider and less selective water channel of pronounced hydrophobicity as GlpF (44).
THEORY AND METHODS
In this section, we outline computation of water permeability constants from our simulations and describe modeling and simulation procedures.
Water permeabilities
Detailed treatments of theory and kinetics of water permeation in Aqps are given elsewhere (11,17,29,31). In brief, the key quantities characterizing transport properties of a water channel are the single-channel permeability constants pf (the osmotic permeability constant) and pd (the diffusive permeability constant), both measured in cm3s−1 and, in dilute solutions, related to the fluxes js and jtr due to solute (s) and tracer (tr) concentration differences (ΔC) (11,17), respectively
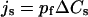 |
(1) |
 |
(2) |
Given that ΔP = RTΔCs, hydraulic (lp) and osmotic permeability constants are related as lp = pfvw/RT, with vw being the volume of a single water molecule (11,17,29,31). Experimentally, estimation of the single-channel quantities requires an exact determination of the water channel density (11). This does not apply to the ratio (45)
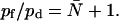 |
(3) |
The value  is predicted by the continuous-time random-walk (CTRW) model for idealized single-file water transport (44), stating that a water molecule must undergo
is predicted by the continuous-time random-walk (CTRW) model for idealized single-file water transport (44), stating that a water molecule must undergo 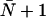 hops within the channel to completely traverse a channel of average occupancy
hops within the channel to completely traverse a channel of average occupancy  and constant length L (27,46). From the total number of complete permeation events, i.e., the number of water molecules that traverse the channel lumen per unit time (k0) during an MD simulation, we can obtain the single-channel diffusive permeability constant pd (17,31)
and constant length L (27,46). From the total number of complete permeation events, i.e., the number of water molecules that traverse the channel lumen per unit time (k0) during an MD simulation, we can obtain the single-channel diffusive permeability constant pd (17,31)
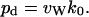 |
(4) |
In equilibrium and in the absence of a driving force, water molecules traverse the channel equally in either direction, i.e., k0 = k+ = k–.
By cumulating at time t each individual displacement relative to t – δt of all water molecules residing within the channel lumen, i.e., the constriction region (CR) of instantaneous length L(t), one may define the collective coordinate (29)
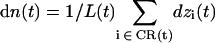 |
(5) |
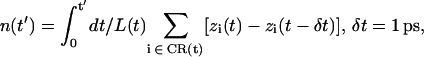 |
(6) |
leading to the collective diffusion constant (29)
 |
(7) |
in units of t−1, which in turn leads to the single-channel osmotic permeability constant pf (29)
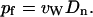 |
(8) |
From the relation lp = pfvw/RT, pf can again be converted into a single-channel hydraulic permeability constant lp (29). For nonrigid channels conserving on average their length, L(t) in Eqs. 5–6 can be substituted by the time-average  .
.
Modeling and simulation
We performed simulations of AqpZ and GlpF embedded in 16:0/18:1c9-palmitoyloleyl phosphatidylethanolamine (POPE) as well as in 16:0/18:1c9-palmitoyloleyl phosphatidylcholine (POPC) lipid bilayers. Modeling of GlpF/POPE with GlpF as a water channel is outlined (15,16). For setting up the GlpF/POPC system, we mutated the amine hydrogen atoms in the ethanolamine headgroup of the POPE bilayer into methyl groups, leaving lattice and hydration parameters unchanged and removed four glycerol molecules constrained to reside in the bulk water region in GlpF/POPE (15,16). With 317 lipid molecules, the GlpF/POPE and GlpF/POPC systems counted N = 106.245 atoms and N = 109.042 atoms, respectively (15,16,18).
The AqpZ/POPE (Fig. 1) and AqpZ/POPC systems were generated by replacing the GlpF tetramer, including crystal and all luminal water molecules, with an AqpZ tetramer, including crystal water molecules. The AqpZ tetramer, including crystal water molecules, was constructed as the GlpF tetramer (15,16). For GlpF, initial luminal hydration was ensured by removing glycerol from the structure (Protein Data Bank entry 1FX8) and subsequently inserting additional water molecules using DOWSER (15,16), whereas for AqpZ, no additional luminal water molecules were included besides the five per monomer as present in the x-ray structure of AqpZ (Protein Data Bank entry 1RC2) (40). GlpF/POPE and GlpF/POPC both hold four chloride counterions to neutralize these systems (15,16). No counterions were needed to overall neutralize AqpZ/POPE and AqpZ/POPC.
FIGURE 1.
Simulation snapshot of AqpZ/POPE at t = 26.5 ns. Lipid molecules are displayed without hydrogen atoms. Selected water molecules permeating two of the four monomers are displayed in red and white.
The protonation state of the histidine residue (H-174) located in the SF of AqpZ was chosen neutral with the proton positioned on Nδ. For the sake of completeness, we performed a 20 ns control simulation with the proton residing on Nε. We denote the two tautomeric states with H-174 being neutral as AqpZ(His-174:NHδ) and AqpZ(His-174:NHε), respectively. Water permeation across AqpZ does not exhibit pH-sensitivity in the pH-range 4.5 ≤ pH ≤ 7.5 (7,8,47) albeit the pKa of (free) histidine is 6.0. However, we did for completeness also simulate AqpZ with H-174 being protonated and denote the protonated state AqpZ(His-174:NHδ,ε). Four chloride ions were here added to obtain an overall neutral system. The system sizes were, respectively, 103.729 (AqpZ(His-174:NHδ)/POPE and AqpZ(His-174:NHε)/POPE), 106.582 (AqpZ(His-174:NHδ)/POPC), and 103.737 atoms (AqpZ(His-174:NHδ,ε)/POPE).
MD simulations were performed with NAMD (48) using the CHARMM 27 parameter set (49,50). The protein/lipid systems were initially minimized and equilibrated at constant temperature (T = 310 K) and pressure (P = 1 atm) for 100–250 ps with the protein being fixed. After releasing the protein, the systems were energy-minimized and NPT (T = 310 K, P = 1 atm) simulations were conducted subsequently. Periodic boundary conditions were imposed, and the particle-mesh Ewald method (51) was used for computation of electrostatic forces. For additional simulation details, see (15,16,18,52). Simulation times were as follows: GlpF/POPE, 26 ns; GlpF/POPC, 20 ns; AqpZ(His-174:NHδ)/POPE, 26.5 ns, AqpZ(His-174:NHε)/POPE, 20 ns; AqpZ/POPC, 20 ns; and AqpZ (His-174:NHδ,ε)/POPE, 18.5 ns. To assess whether the lipid headgroup polarity influenced water permeation, we performed two additional simulations on GlpF/POPE and GlpF/POPC each for 5 ns, where all charges of the lipid headgroup were suppressed. Lipid P and N atoms were in these simulations harmonically constrained with a force constant of 5 kcal/mol/Å2 to their position at t = 20 ns, where from these simulations started. Trajectories were analyzed using Visual Molecular Dynamics (53).
RESULTS AND DISCUSSION
In this section, we first report our results on osmotic and diffusive water permeabilities. Subsequently, we analyze and explain differences in water permeabilities in terms of channel structure, in particular of the SF region, channel polarity, and water dynamics. Finally, we discuss possible effects of the type of lipid headgroup on permeation.
Single-channel osmotic water permeabilities
To better understand the influence from the protein architecture on transport rates across a water channel, one wants to determine the single-channel osmotic and diffusive permeability constants pf and pd for different Aqps. Experimentally, one most often measures total membrane permeabilities Pf and Pd (measured in cm s−1). Dividing these quantities by the density of channels, i.e., the number of channels per unit area, in turn provides the single-channel permeability constants pf and pd (11).
Equilibrium MD simulations can provide pd and pf directly, which might help in interpreting experimental data (29,31). First we focus on pf. In Fig. 2 a, we display the dimensionless collective coordinate n(t) (Eqs. 5–6) for a representative simulation of GlpF. The corresponding mean-square displacements 〈n2(t)〉 (Eq. 7) are shown in Fig. 2 b. In Fig. 2 c, we display 〈n2(t)〉 for a representative simulation of AqpZ for comparison. 〈n2(t)〉 was computed by averaging over at least 200 100-ps time windows, requiring n(t = t′) = 0 for each time window starting at t′ (see Eq. 7). For computing n(t), we used an average channel length 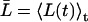 , which is reasonable for flexible but fairly rigid channels as GlpF and AqpZ.
, which is reasonable for flexible but fairly rigid channels as GlpF and AqpZ. 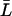 was taken as the average distance between R-189:Hη–G-60:O and R-206:Hη–G-65:O for AqpZ and GlpF, respectively, yielding values of 18.4 Å and 19.6 Å. All relevant details, e.g., values for the collective diffusion constant Dn, the average lengths
was taken as the average distance between R-189:Hη–G-60:O and R-206:Hη–G-65:O for AqpZ and GlpF, respectively, yielding values of 18.4 Å and 19.6 Å. All relevant details, e.g., values for the collective diffusion constant Dn, the average lengths 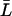 , etc., are given in Supplementary Material.
, etc., are given in Supplementary Material.
FIGURE 2.
Representative illustration of the collective coordinate n (Eqs. 5–6) as a function of simulation time for GlpF/POPC (a). Mean-square displacement of n, 〈n2〉 (Eq. 7) for GlpF/POPC (b) and for AqpZ/POPE (c).
From 〈n2(t)〉, we obtain via Dn, the osmotic permeability constant pf (Eqs. 7–8). The results are collected in Table 1. We find for GlpF (8.6 ± 1.1) × 10−14cm3s−1 ≤ pf ≤ (13.1 ± 3.4) × 10−14cm3s−1. For AqpZ we find (3.2 ± 0.7) × 10−14cm3s−1 ≤ pf ≤ (4.4 ± 0.7) × 10−14cm3s−1. Relative large uncertainties are found for pf. This relies is part on the long correlation time of n(t) (29). This is most severe for AqpZ, which exhibits the slowest kinetics (Fig. 2 c). We find that pf for AqpZ is independent of the tautomeric state of H-174. For AqpZ(His-174:NHδ) we obtained pf = (4.2 ± 1.8) × 10−14cm3s−1, whereas for AqpZ(His-174:NHε) we obtained pf = (3.2 ± 0.7) × 10−14cm3s−1. Moreover, protonation of H-174 (AqpZ(His-174:NHδ,ε)) led to a very similar permeability of pf = (4.4 ± 0.7) × 10−14cm3s−1 (Table 1) in accordance with pf for AqpZ exhibiting experimentally very little or no pH sensitivity for 4.5 ≤ pH ≤ 7.4 (7,8,47).
TABLE 1.
Single-channel osmotic and diffusive water permeability constants (pf, pd in units of 10−14cm3s−1) for AqpZ and GlpF calculated from simulations of duration as given in the first column (cf. Eqs. 4–8)
| Model | Mean ± SD | M1 | M2 | M3 | M4 | |
|---|---|---|---|---|---|---|
| GlpF/ | pd | 3.2 ± 0.8 | 2.8 | 3.7 | 4.0 | 2.2 |
| POPC | pf | 8.6 ± 1.1 | 9.4 | 9.5 | 7.4 | 8.0 |
| (20 ns) |  |
8.6 ± 0.3 | 8.7 | 8.1 | 8.7 | 8.8 |
| pf/pd | 2.9 ± 0.8 | 3.3 | 2.6 | 1.8 | 3.7 | |
| GlpF/ | pd | 2.7 ± 0.7 | 2.1 | 3.7 | 3.1 | 2.2 |
| POPE | pf | 13.1 ± 3.4 | 9.7 | 17.0 | 14.7 | 10.9 |
| (26 ns) |  |
8.1 ± 0.1 | 8.6 | 8.4 | 7.6 | 7.9 |
| pf/pd | 4.8 ± 0.2 | 4.6 | 4.6 | 4.8 | 5.0 | |
| AqpZ(HSD)/ | pd | 0.4 ± 0.2 | 0.5 | 0.4 | 0.2 | 0.5 |
| POPC | pf | 4.2 ± 1.8 | 6.7 | 2.7 | 3.1 | 4.4 |
| (20 ns) | 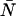 |
7.2 ± 0.5 | 6.6 | 7.6 | 7.1 | 7.4 |
| pf/pd | 13.0 ± 6.0 | 14.8 | 7.3 | 20.9 | 8.9 | |
| AqpZ(HSD)/ | pd | 0.5 ± 0.2 | 0.2 | 0.5 | 0.8 | 0.5 |
| POPE | pf | 4.2 ± 1.8 | 2.5 | 3.4 | 6.6 | 4.3 |
| (26.5 ns) |  |
8.0 ± 0.3 | 8.6 | 8.1 | 7.1 | 8.2 |
| pf/pd | 9.5 ± 2.9 | 13.7 | 7.3 | 8.6 | 8.3 | |
| AqpZ(HSE)/ | pd | 0.4 ± 0.1 | 0.5 | 0.5 | 0.3 | 0.5 |
| POPE | pf | 3.2 ± 0.7 | 2.2 | 3.8 | 3.7 | 3.2 |
| (20.0 ns) | 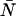 |
7.1 ± 0.8 | 6.5 | 8.2 | 7.0 | 6.8 |
| pf/pd | 7.7 ± 3.4 | 4.4 | 7.5 | 12.5 | 6.3 | |
| AqpZ(HSP)/ | pd | 1.3 ± 0.2 | 1.4 | 1.6 | 1.1 | 1.3 |
| POPE | pf | 4.4 ± 0.7 | 4.9 | 3.9 | 5.0 | 3.9 |
| (18.5 ns) | 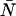 |
10.0 ± 0.5 | 10.3 | 9.4 | 9.9 | 10.4 |
| pf/pd | 3.5 ± 1.0 | 3.6 | 2.5 | 4.8 | 3.1 |
The average number water molecules occupying the channel lumen is given by 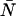 . Standard deviations of the mean are obtained from the variance among the four monomers (M1–M4).
. Standard deviations of the mean are obtained from the variance among the four monomers (M1–M4).
From nonequilibrium MD simulations of bAqp1 subjected to a transmembrane hydrostatic pressure gradient, pf was found to be pf = (7.1 ± 0.9) × 10−14cm3s−1 (17), whereas for GlpF, simulations led to pf = (14.0 ± 0.4) × 10−14cm3s−1 using a different protocol (11). Assuming that the performance of AqpZ is similar to that of bAqp1 ((7,8); see also below), our results for AqpZ are in very good agreement with those for bAqp1 (17), and the previously reported result for GlpF (11) is in very good agreement with the upper limit for pf obtained for GlpF in our work, i.e., pf = (13.1 ± 3.4) × 10−14cm3s−1 (Table 1). Taken together, these results indicate consistency among simulations. Moreover, a derivation of pf from equilibrium MD simulations as recently proposed (29) seems feasible.
Experimental osmotic water permeabilities for AqpZ and GlpF
By reconstituting AqpZ and GlpF into planar lipid bilayers, pf has been estimated experimentally to pf = 2.0 × 10−14cm3s−1 and pf = 0.7 × 10−14cm3 s−1 for AqpZ and GlpF, respectively (9,10). Another estimate for AqpZ of pf ≥ 10.0 × 10−14cm3s−1 has been proposed after reconstituting AqpZ into liposomes (7). This number could be recognized as a lower experimental estimate of pf for AqpZ, given that 100% efficiency of protein incorporation was assumed (7). With respect to AqpZ, we find a factor of 2–3 of discrepancy between experiment and simulation, which is satisfactory. The disagreement between our and experimental results for GlpF is more severe: approximately one order of magnitude, where the experimental value is the lowest. For a channel as GlpF, where the constriction region, i.e., the SF, is rather hydrophobic, one expects that permeation could be quite sensitive to van der Waals parameters (25–27,30). In addition, there might be several other reasons for this discrepancy as discussed below. However, given that the water model deployed here (TIP3) exhibits a bulk diffusion constant exceeding the experimental value by a factor of 2 (54), comparison of experimental and theoretical permeabilities on an absolute scale might be unwise. In particular, it is not obvious how one should correct for the too fast kinetics of TIP3 water within a protein confinement albeit possible (55). In line with comparative simulation results for the diffusive permeability of hAqp1 and GlpF (14), our values for pf suggest, on a relative scale, that GlpF permeates water at rates 2–3 times higher than AqpZ, whereas experimental data suggest the opposite in terms of pf (9,10). However, is could be that MD simulations may possess an intrinsic, yet undecided problem for GlpF (42).
Relative performance of GlpF and AqpZ as water channels incorporated into liposomes has been addressed from comparative membrane permeability measurements leading to osmotic membrane permeabilities Pf = 5.1 × 10−4cm s−1 and Pf = 4.9 × 10−3cm s−1 for GlpF and AqpZ, respectively (41). Assuming identical incorporation efficiencies for AqpZ and GlpF and that all incorporated channels are conducting, the experimental values for Pf are again at variance with our values for pf. In the planar lipid bilayer experiments quoted above, pf was derived from the membrane permeability Pf by calculating a density of channels using an assumed 50% efficiency of protein incorporation (9,10).
Besides other possible shortcomings of our simulations as discussed below, one possible explanation for the discrepancy between theoretical and experimental results might be that a significant fraction of the GlpF channels in the experiment become incorporated in the bilayers/liposomes in nontetrameric, nonconducting form whereas AqpZ in contrast is more stable as tetramer and hence is conducting (7,43). Presumably, a nontetrameric form of GlpF is not inserted in a transmembrane fashion into the bilayer since the hydrophobic thickness of a monomer is too short at the intermonomeric interface to completely span the bilayer (18,52,56). Consequently, only the tetrameric form, favored by Mg ions (7,37), of GlpF is likely to span the bilayer and to conduct water (52,56).
Single-channel diffusive water permeabilities
For determination of pd, we monitored the total number of water molecules completely traversing the channel in either direction, i.e., N+, N–, and N±, respectively. These quantities are displayed in cumulated form for two representative simulations of AqpZ and GlpF in Fig. 3, a and b. As expected, the cumulated number of permeation events grows approximately linearly with time, particularly for GlpF (Fig. 3 b), whereas the kinetics of AqpZ are significantly slower (Fig. 3 a). The number of permeation events occurring in either direction through the channel is approximately equal, as also expected from an equilibrium MD simulation (31). By dividing the number of cumulated bidirectional permeation events N± in Fig. 3, a and b, by two times the simulation time (tsim, discarding the first ns) and by the number of monomers (nm = 4), we obtain the unidirectional rate constant k0 = N±/2nmtsim, which further leads to the single-channel diffusive permeability constant pd (Eq. 4).
FIGURE 3.
Number of permeation events along +z and –z and their sum, i.e., N+, N–, and N± displayed as a function of time for two representative systems, AqpZ/POPE (a) and GlpF/POPC (b). For GlpF/POPC (b), the vertical gray line delineates onset for elimination of headgroup charges; only the first 20 ns were included in the calculation of pd (see text and Eq. 4). Panel c displays trajectories of selected permeation events for GlpF/POPC where the large number of permeation events (>150) allows for accurate estimation of the mean permeation (passage) time 〈τ〉 required to traverse the channel from one channel boundary to the other. The mean passage time through this constriction region 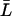 is related to the number of unidirectional permeation events as 〈τ〉 = k0−1. The mean positions of the channel boundaries defining
is related to the number of unidirectional permeation events as 〈τ〉 = k0−1. The mean positions of the channel boundaries defining  are delineated with dashed lines and taken as the average z-positions of R-206:Hη and G-65:O; z = −1.4 Å and z = 18.3 Å, respectively.
are delineated with dashed lines and taken as the average z-positions of R-206:Hη and G-65:O; z = −1.4 Å and z = 18.3 Å, respectively.
From pd we find that GlpF also diffusively permeates water at a higher rate than AqpZ (Table 1). The diffusive permeability is consistently ∼6–9 times higher in GlpF than in AqpZ (with neutral H-174) whereas the osmotic permeability was ∼2–3 times higher. From a 5 ns simulation of GlpF, 18 complete conduction events were observed over the last 4 ns (15,16), resulting in pd = 1.7 × 10−14cm3s−1, which is about half of the pd value obtained here for GlpF. Together with Fig. 3, a and b, this illustrates that a significant simulation time is required to accurately determine pd despite that individual permeation events occur within approximately one ns.
Relative to AqpZ, a large number of complete permeation events is observed for GlpF. This permits us to estimate the mean passage time 〈τ〉 required for a water molecule to permeate the channel in either of the two directions. Since τ is related to the number of unidirectional permeation events per unit time as 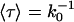 , this in turn provides an alternative route to determination of pd (Eq. 4). For a large number of permeation events and in absence of a biasing transmembrane gradient, the distribution of passage times will be Gaussian. In Fig. 3 c, we display representative trajectories of selected permeation events occurring in GlpF. One can discern that the passage times vary substantially for individual water molecules, which in part reflects that GlpF is a water channel where water-water exchange occasionally occurs (16). From the distribution of passage times, we find for GlpF a mean passage time 〈τ〉 ≅ (1.2 ± 0.2) ns. This is consistent with values computed from k0 ≅ 0.9 ns−1 via N± . Consequently, the pd values are consistent (Supplementary Material).
, this in turn provides an alternative route to determination of pd (Eq. 4). For a large number of permeation events and in absence of a biasing transmembrane gradient, the distribution of passage times will be Gaussian. In Fig. 3 c, we display representative trajectories of selected permeation events occurring in GlpF. One can discern that the passage times vary substantially for individual water molecules, which in part reflects that GlpF is a water channel where water-water exchange occasionally occurs (16). From the distribution of passage times, we find for GlpF a mean passage time 〈τ〉 ≅ (1.2 ± 0.2) ns. This is consistent with values computed from k0 ≅ 0.9 ns−1 via N± . Consequently, the pd values are consistent (Supplementary Material).
The pf/pd ratio
The ratio pf/pd is important in characterizing the conduction properties of a water channel. It can be measured experimentally for a channel of constant length without knowing the density of channels in contrast to pf and pd individually (17,31,45). The CTRW model developed for single-file transport predicts 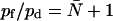 (27,46), i.e., it is related to the average occupancy number
(27,46), i.e., it is related to the average occupancy number  of the channel and hence to the effective number of steps (
of the channel and hence to the effective number of steps (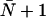 ) that a water molecule takes upon complete permeation across the channel. For GlpF, we find 2.9 ≤ pf/pd ≤ 4.8 and
) that a water molecule takes upon complete permeation across the channel. For GlpF, we find 2.9 ≤ pf/pd ≤ 4.8 and 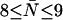 , whereas for AqpZ (His-174 neutral), 7.7 ≤ pf/pd ≤ 13.0 and
, whereas for AqpZ (His-174 neutral), 7.7 ≤ pf/pd ≤ 13.0 and  (Table 1). Hence,
(Table 1). Hence, 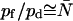 for AqpZ but not for GlpF. For a channel with luminal water perfectly aligned in single file,
for AqpZ but not for GlpF. For a channel with luminal water perfectly aligned in single file,  (27,46). Our results therefore illustrate that AqpZ, the narrower channel of the two (40), has more pronounced single-file structure of its luminal water than GlpF, where water occasionally interchanges position. Moreover, water-water interchange might in itself be an artifact of the simulations owing to unphysical breathing motions of the channel lumen. These motions are rather local and translate together with the wider lumen of GlpF into a higher water compressibility in GlpF than in AqpZ (42). However, water-water interchange will only cause pd to increase, i.e., more water molecules can pass the same point in the channel at the same time, whereas interchange leaves pf essentially invariant (31). For pf, only displacements of individual water molecules along the channel axis contribute to the collective diffusion coefficient (Dn, see Eqs. 5–7). Such displacements are independent of the presence of more water molecules at the same position. Hence, relative to GlpF, AqpZ can be expected to exhibit smaller pd and larger pf/pd ratio due to its smaller channel radius as found here. Despite somewhat large uncertainties (Table 1), the computed ratio 7.7 ≤ pf/pd ≤ 13.0 is for AqpZ in good agreement with the ratio pf/pd = 13.2 obtained experimentally for Aqp1 (45). Aqp1's water conduction performance has been assumed to be similar to that of AqpZ (7,8). Moreover, the channel radius of AqpZ should resemble more closely that of Aqp1 than that of GlpF, i.e., both are orthodox water channels and accordingly more narrow than the less selective GlpF (40). Along these lines, pf/pd = 11.9, as proposed by combining pf values from pressure-induced MD simulations of bAqp1 (17) with pd values from equilibrium MD simulations of an hAqp1 model (14), conforms well to our value pf/pd = 13.2 for AqpZ.
(27,46). Our results therefore illustrate that AqpZ, the narrower channel of the two (40), has more pronounced single-file structure of its luminal water than GlpF, where water occasionally interchanges position. Moreover, water-water interchange might in itself be an artifact of the simulations owing to unphysical breathing motions of the channel lumen. These motions are rather local and translate together with the wider lumen of GlpF into a higher water compressibility in GlpF than in AqpZ (42). However, water-water interchange will only cause pd to increase, i.e., more water molecules can pass the same point in the channel at the same time, whereas interchange leaves pf essentially invariant (31). For pf, only displacements of individual water molecules along the channel axis contribute to the collective diffusion coefficient (Dn, see Eqs. 5–7). Such displacements are independent of the presence of more water molecules at the same position. Hence, relative to GlpF, AqpZ can be expected to exhibit smaller pd and larger pf/pd ratio due to its smaller channel radius as found here. Despite somewhat large uncertainties (Table 1), the computed ratio 7.7 ≤ pf/pd ≤ 13.0 is for AqpZ in good agreement with the ratio pf/pd = 13.2 obtained experimentally for Aqp1 (45). Aqp1's water conduction performance has been assumed to be similar to that of AqpZ (7,8). Moreover, the channel radius of AqpZ should resemble more closely that of Aqp1 than that of GlpF, i.e., both are orthodox water channels and accordingly more narrow than the less selective GlpF (40). Along these lines, pf/pd = 11.9, as proposed by combining pf values from pressure-induced MD simulations of bAqp1 (17) with pd values from equilibrium MD simulations of an hAqp1 model (14), conforms well to our value pf/pd = 13.2 for AqpZ.
Gating and dynamics of the AqpZ selectivity filter
As suggested by two protomers in the x-ray structure (40) and observed in recent MD simulations of AqpZ (41), the side chain of the conserved arginine (R-189) of the SF exists in at least two different configurations denoted “up” and “down” (41). These are characterized by the dihedral angle  . The up configuration seemingly implies that the channel is in an open conducting state, whereas the SF is occluded in the down configuration (41). It was suggested that the channel lumen below the SF was emptied in the down configuration (41). In contrast the SF of GlpF exhibits a remarkable rigidity; it accommodates glycerol instead of water with only marginal conformational changes as found both experimentally and computationally (15).
. The up configuration seemingly implies that the channel is in an open conducting state, whereas the SF is occluded in the down configuration (41). It was suggested that the channel lumen below the SF was emptied in the down configuration (41). In contrast the SF of GlpF exhibits a remarkable rigidity; it accommodates glycerol instead of water with only marginal conformational changes as found both experimentally and computationally (15).
Indeed the R-189 side chain exhibits a highly dynamic behavior in all our simulations (Fig. 4). Besides previously observed up and down states of the R-189 side chain (41) and of the R-197 side chain in MD simulations of bAqp1 (11), we also observe an intermediate state denoted “mid” in our simulations. This is illustrated in Fig. 4 a by means of three representative snapshots from our simulation of AqpZ(His-174:NHδ). Instantaneous values for the dihedral angle  are given as insets. The mid and down states arise because the guanidinium group of R-189 is electrostatically attracted toward either the backbone oxygen atom of T-183 (mid state) or by the imidazole nitrogen (deprotonated) of H-174 (down state). In contrast, the R-189 guanidinium group interacts directly with none of these two groups in the up configuration. Transitions of the dihedral angle between up (∼−170°), mid (∼−60°), and down (∼−80°) configurations are depicted for the four monomers in Fig. 4 b. One recognizes that all three states are transiently stable. Transitions between these occur on a nanosecond timescale implying that our simulations might suffer from insufficient sampling. The left panel of Fig. 4 a also illustrates that conduction might at times be obstructed in the down configuration (Fig. 4 a, left panel), where the region across the SF is devoid of water in accordance with previous suggestions (41). In contrast, mid and up states (Fig. 4 a, mid and right panels) are conducting. Albeit we do observe the down configuration of R-189 for all possible configurations of H-174, the channel lumen does consistently remain occupied with water below the SF in all our simulations with
are given as insets. The mid and down states arise because the guanidinium group of R-189 is electrostatically attracted toward either the backbone oxygen atom of T-183 (mid state) or by the imidazole nitrogen (deprotonated) of H-174 (down state). In contrast, the R-189 guanidinium group interacts directly with none of these two groups in the up configuration. Transitions of the dihedral angle between up (∼−170°), mid (∼−60°), and down (∼−80°) configurations are depicted for the four monomers in Fig. 4 b. One recognizes that all three states are transiently stable. Transitions between these occur on a nanosecond timescale implying that our simulations might suffer from insufficient sampling. The left panel of Fig. 4 a also illustrates that conduction might at times be obstructed in the down configuration (Fig. 4 a, left panel), where the region across the SF is devoid of water in accordance with previous suggestions (41). In contrast, mid and up states (Fig. 4 a, mid and right panels) are conducting. Albeit we do observe the down configuration of R-189 for all possible configurations of H-174, the channel lumen does consistently remain occupied with water below the SF in all our simulations with 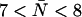 (H-174 neutral) and significantly higher N = 10 ± 0.5 with H-174 protonated; see Table 1. As observed from simulations of hAqp1 (14), the intermolecular hydrogen bonded network of the luminal water in AqpZ might also be disrupted across the SF. This kind of disruption, rare in GlpF (15,16), presumably influences permeation. Disruption is illustrated for AqpZ(His-174:NHε) in Fig. 5 a with the side chain of R-189 in the up configuration. Intermolecular hydrogen bonding along the water wire is intact and disrupted across the SF in left and right panels, respectively. Similar disruption occurred for AqpZ(His-174:NHδ). Protonation of H-174 led in AqpZ(His-174:NHδ,ε) to a widening of the SF (Fig. 6 a), increased water occupancy, and no disruption. Widening of the SF was also found in MD simulations of bAqp1 with H-182 (equivalent to H-174 of AqpZ) being protonated (19).
(H-174 neutral) and significantly higher N = 10 ± 0.5 with H-174 protonated; see Table 1. As observed from simulations of hAqp1 (14), the intermolecular hydrogen bonded network of the luminal water in AqpZ might also be disrupted across the SF. This kind of disruption, rare in GlpF (15,16), presumably influences permeation. Disruption is illustrated for AqpZ(His-174:NHε) in Fig. 5 a with the side chain of R-189 in the up configuration. Intermolecular hydrogen bonding along the water wire is intact and disrupted across the SF in left and right panels, respectively. Similar disruption occurred for AqpZ(His-174:NHδ). Protonation of H-174 led in AqpZ(His-174:NHδ,ε) to a widening of the SF (Fig. 6 a), increased water occupancy, and no disruption. Widening of the SF was also found in MD simulations of bAqp1 with H-182 (equivalent to H-174 of AqpZ) being protonated (19).
FIGURE 4.
Dynamics of the SF in AqpZ(H-174:NHδ). (a) Simulation snapshots of luminal water molecules, SF residues R-189, T-183, H-174, and of N-63 and N-186 of the NPA motifs. Some atoms have been omitted for clarity. The side chain of R-189 is seen to exist in three configurational states: “down”, “mid”, and “up”, according to the value of the dihedral angle  . These states are depicted in left, central, and right panels, respectively. Instantaneous values of
. These states are depicted in left, central, and right panels, respectively. Instantaneous values of  are given as insets. The side chain of H-174 is in a down configuration classified by means of
are given as insets. The side chain of H-174 is in a down configuration classified by means of 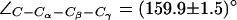 (see also Fig. 5). (b) Dynamic behavior of
(see also Fig. 5). (b) Dynamic behavior of 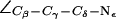 of R-189 for the four monomers M1–M4 in the simulation of AqpZ(His-174:NHδ).
of R-189 for the four monomers M1–M4 in the simulation of AqpZ(His-174:NHδ).
FIGURE 5.
Water disruption and configuration of the SF in AqpZ(His-174:NHε). (a) Simulation snapshots of the SF residues as in Fig. 4 a. The water file is hydrogen bonded across the SF region in the left panel whereas the hydrogen bonded network is disrupted in the right panel, despite an up configuration of the R-189 side chain (cf. Fig. 4 a). The side chain of H-174 is in an up configuration with  (cf. Fig. 4 a). (b) Distributions of the dihedral angles of R-189 (
(cf. Fig. 4 a). (b) Distributions of the dihedral angles of R-189 (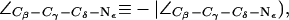 H-174 (
H-174 (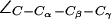 ), and F-43 (
), and F-43 (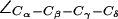 ) for all simulations of AqpZ. Distributions are annotated with u, m, d, c, and o for “up”, “mid”, “down”, “open”, and “closed”, respectively (see also Fig. 6).
) for all simulations of AqpZ. Distributions are annotated with u, m, d, c, and o for “up”, “mid”, “down”, “open”, and “closed”, respectively (see also Fig. 6).
FIGURE 6.
Gating in the SF in AqpZ(His-174:NH 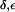 ). (a) Simulation snapshots of the SF residues as in Fig. 4 a. The F-43 side chain is shown instead of T-183. Some atoms have been omitted for clarity. For a protonated state of H-174, the R-189 side chain seemingly exists in only two states, mid and up (cf. Fig. 4 a). The mid configuration is depicted here. Instantaneous values of
). (a) Simulation snapshots of the SF residues as in Fig. 4 a. The F-43 side chain is shown instead of T-183. Some atoms have been omitted for clarity. For a protonated state of H-174, the R-189 side chain seemingly exists in only two states, mid and up (cf. Fig. 4 a). The mid configuration is depicted here. Instantaneous values of 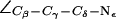 are given as insets. The H-174 side chain is consistently the up configuration with
are given as insets. The H-174 side chain is consistently the up configuration with 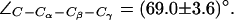 The F-43 side chain, classified by means of
The F-43 side chain, classified by means of 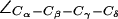 exists in two states: parallel (“open”; left panel) and perpendicular (“closed”; right panel) to the channel axis. The latter blocks the periplasmic half-channel between the SF and the NPA region. (b) Dynamic behavior of
exists in two states: parallel (“open”; left panel) and perpendicular (“closed”; right panel) to the channel axis. The latter blocks the periplasmic half-channel between the SF and the NPA region. (b) Dynamic behavior of 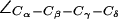 of F-43 for the four monomers M1–M4 in AqpZ(His-174:NHδ,ε). The open (parallel) orientation is seen to dominate (cf. Fig. 5 b).
of F-43 for the four monomers M1–M4 in AqpZ(His-174:NHδ,ε). The open (parallel) orientation is seen to dominate (cf. Fig. 5 b).  for R-189 is shown for reference.
for R-189 is shown for reference.
Interestingly, depending on tautomeric and protonation state, the side chain of H-174 also exists in up and down configurations according to the value of the dihedral angle 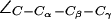 . The down configuration is present in the x-ray structure (40). Consequently, this is the initial configuration of the H-174 side chain in all our AqpZ simulations. For AqpZ(His-174:NHδ), the configuration remains down (Fig. 4 a), e.g.,
. The down configuration is present in the x-ray structure (40). Consequently, this is the initial configuration of the H-174 side chain in all our AqpZ simulations. For AqpZ(His-174:NHδ), the configuration remains down (Fig. 4 a), e.g.,  (in POPC). For AqpZ(His-174:NHε), electrostatic repulsion between the NHε proton and the R-189 guanidinium group causes a transition to the up configuration within the first few nanoseconds of simulations in all four monomers. This configuration remains stable for the remainder of the simulation;
(in POPC). For AqpZ(His-174:NHε), electrostatic repulsion between the NHε proton and the R-189 guanidinium group causes a transition to the up configuration within the first few nanoseconds of simulations in all four monomers. This configuration remains stable for the remainder of the simulation; 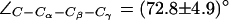 . In AqpZ(His-174:NHδ,ε) protonation of H-174 implies even stronger repulsion between the R-189 guanidinium group and the protonated imidazole ring. Again, this causes a rapid dihedral transition in all monomers to the up configuration. This configuration remains stable for the remainder of the simulation;
. In AqpZ(His-174:NHδ,ε) protonation of H-174 implies even stronger repulsion between the R-189 guanidinium group and the protonated imidazole ring. Again, this causes a rapid dihedral transition in all monomers to the up configuration. This configuration remains stable for the remainder of the simulation;  .
.
For completeness, we present in Fig. 5 b distributions of all dihedral angles R-189 ( ), H-174 (
), H-174 (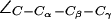 ), and F-43 (
), and F-43 (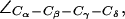 for AqpZ(His-174:NHδ,ε) only). The histograms clearly demonstrate that an interplay between the configuration of R-189 side chain and the tautomeric state of H-174 exists. Unfortunately, we cannot model this coupling in complete detail, i.e., the configuration of R-189 is coupled to the tautomeric (or protonation) state and side chain configuration of H-174 whereas the resulting overall SF configuration is a determinant for permeation (cf. Figs. 4 a and 5 a). Moreover, insufficient sampling of the side-chain dynamics of R-189 in AqpZ is a potential source of error in our simulations that also could influence pf and pd, i.e., the more dynamic behavior of R-189 relative to R-206 of GlpF might influence their relative permeation rates. Along these lines, we cannot rule out that other subtle shortcomings of the applied force-field, such as lack of polarization and charge transfer terms, are more severe for the more polar SF of AqpZ than for GlpF, whereas GlpF in turn should be more sensitive to van der Waals parameters owing to its more hydrophobic SF.
for AqpZ(His-174:NHδ,ε) only). The histograms clearly demonstrate that an interplay between the configuration of R-189 side chain and the tautomeric state of H-174 exists. Unfortunately, we cannot model this coupling in complete detail, i.e., the configuration of R-189 is coupled to the tautomeric (or protonation) state and side chain configuration of H-174 whereas the resulting overall SF configuration is a determinant for permeation (cf. Figs. 4 a and 5 a). Moreover, insufficient sampling of the side-chain dynamics of R-189 in AqpZ is a potential source of error in our simulations that also could influence pf and pd, i.e., the more dynamic behavior of R-189 relative to R-206 of GlpF might influence their relative permeation rates. Along these lines, we cannot rule out that other subtle shortcomings of the applied force-field, such as lack of polarization and charge transfer terms, are more severe for the more polar SF of AqpZ than for GlpF, whereas GlpF in turn should be more sensitive to van der Waals parameters owing to its more hydrophobic SF.
Protonation of the selectivity filer
An intriguing finding is a possible gating in the SF of AqpZ(His-174:NHδ,ε) by means of a rotation of the F-43 side chain 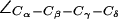 presented in Fig. 6 a. Two different F-43 side-chain configurations exist, parallel and perpendicular to the channel axis. This corresponds to an open (left panel) and closed (right panel) channel, respectively. From Fig. 6 b, one finds that the open (parallel) orientation is dominant (see also Fig. 5 b). According to Fig. 6 a, a rotation from parallel to perpendicular orientation completely blocks the channel. This transition was observed in all four monomers (Fig. 6 b) and occurred for both mid and up configurations of the R-189 side chain. The former is depicted in Fig. 6 a with instantaneous values of
presented in Fig. 6 a. Two different F-43 side-chain configurations exist, parallel and perpendicular to the channel axis. This corresponds to an open (left panel) and closed (right panel) channel, respectively. From Fig. 6 b, one finds that the open (parallel) orientation is dominant (see also Fig. 5 b). According to Fig. 6 a, a rotation from parallel to perpendicular orientation completely blocks the channel. This transition was observed in all four monomers (Fig. 6 b) and occurred for both mid and up configurations of the R-189 side chain. The former is depicted in Fig. 6 a with instantaneous values of  given with the inset. The H-174 side -chain remains in an up configuration with
given with the inset. The H-174 side -chain remains in an up configuration with 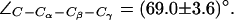 Complete sampling of this possible gating mechanism is probably not achieved in our simulations despite that transitions of the F-43 side chain frequently occur (Fig. 6 b).
Complete sampling of this possible gating mechanism is probably not achieved in our simulations despite that transitions of the F-43 side chain frequently occur (Fig. 6 b).
Whether a gating mechanism involving rotation of the F-43 side chain exists remains questionable. The concurrent widening of the SF in AqpZ(His-174:NHδ,ε) was also observed from MD simulations of bAqp1 with equivalent protonation of H-182 in the SF where the effect was considered unphysical (19). Owing to this widening, a significant increase in the water occupancy of the SF region relative to AqpZ(His-174:NHδ) and AqpZ(His-174:NHε) occurs (Fig. 6 a; see also Figs. 4 a and 5 a). The increased water population in the SF leads to a higher occupancy of the lumen overall (Table 1) and pd in AqpZ(His-174:NH 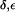 ) is increased 2–3-fold relative to AqpZ with H-174 neutral; from pd ≅ 0.5 × 10−14cm3s−1 to pd = (1.3 ± 0.3) × 10−14cm3s−1. The osmotic permeability pf = (4.4 ± 0.7) × 10−14cm3s−1 varies almost insignificantly from pf obtained for AqpZ with H-174 neutral (Table 1). This finding is in accordance with the lack of pH sensitivity of AqpZ observed for 4.5 ≤ pH ≤ 7.5 (7,8,47). The pf/pd ratio in turn decreases to pf/pd = 3.5 ± 1.0, reflecting less single-file structure of the luminal water owing to the widening and increased (nonsingle file) population of the SF region in AqpZ(His-174:NHδ,ε) (Fig. 6 b).
) is increased 2–3-fold relative to AqpZ with H-174 neutral; from pd ≅ 0.5 × 10−14cm3s−1 to pd = (1.3 ± 0.3) × 10−14cm3s−1. The osmotic permeability pf = (4.4 ± 0.7) × 10−14cm3s−1 varies almost insignificantly from pf obtained for AqpZ with H-174 neutral (Table 1). This finding is in accordance with the lack of pH sensitivity of AqpZ observed for 4.5 ≤ pH ≤ 7.5 (7,8,47). The pf/pd ratio in turn decreases to pf/pd = 3.5 ± 1.0, reflecting less single-file structure of the luminal water owing to the widening and increased (nonsingle file) population of the SF region in AqpZ(His-174:NHδ,ε) (Fig. 6 b).
Channel radii
Channel radii were computed from our simulations using HOLE (57). Averaging was carried out over ∼7000 configurations separated by 2 ps and taken from the last part of the simulations. The pore center was taken as the midpoint between the Nδ atoms of the asparagine residues of the NPA (asparagine-proline-alanine) motifs. Results are shown in Fig. 7 b for AqpZ (His-174 neutral) and GlpF. Average CR radii and root mean-square (RMS) fluctuations are given as insets in Fig. 7, a and c. As found from similar calculations on the crystal structures (40) and in previous simulations studies (41), we find that AqpZ (Fig. 7 a) along the entire channel lumen is the most narrow channel of the two, also when taking into account thermal radii fluctuations. Both channels exhibit minimal radii in the SF region located within the periplasmic half channel (z < 0 Å). RMS fluctuations are similar for the two channels: 0.5–0.7 Å. A profound stiffness of the channel lumen accordingly persists, ensuring conservation of small radii, which in turn provides the size-exclusion part of Aqp selectivity, important with respect to permitting, e.g., glycerol transport (21,39,41,52,56).
FIGURE 7.
Simulation snapshots of the water conducting part of AqpZ(His-174:NHδ) (a) and GlpF (c) with the luminal water molecules lined up in the respective constriction regions as single files displayed along with channel radius profiles (b) computed using HOLE (55). The radius profiles are averages over 7000 configurations taken from the last part of the simulations and separated by 2 ps. Origin of the z axis was taken as the center between the asparagine Nδ atoms of the NPA motifs. Mean radii and root mean-square deviations from the mean computed within the constriction region (CR), 〈r〉CR, are given for AqpZ and GlpF as insets in a and c, respectively. The bipolar configuration of the water molecules in a and c results from the electrostatic environment inside the channel and it ensures that protons cannot be conducted across aquaglyceroporins (10,15,16,27,58–61).
Electrostatics
Electrostatic profiles were evaluated as the (untruncated) sum
 |
(9) |
where w and s refer to atoms of water located within the CR and the surroundings, i.e., the protein in case of channel-water electrostatic interactions or other luminal water molecules in case of water-water electrostatic interactions, respectively. Included for GlpF and AqpZ(His-174 neutral) in the average profiles were 5000 configurations separated by 5 ps resolved along z with a resolution of 1 Å and shown in Fig. 8 a. For channel-water electrostatic interactions, the profiles were obtained by taking into account only the interactions between the luminal water molecules and the monomer, since this result is invariant to whether one includes the other three monomers of the tetramer (16). One recognizes from Fig. 8 a that water-water electrostatic interactions are of lower energy, thus stronger in GlpF compared to AqpZ. AqpZ, being more polar and more narrow along the entire lumen than GlpF, features, in contrast, stronger channel-water interactions peaking across the SF region; i.e., channel-water electrostatic interaction energy is manifestly lower in the AqpZ lumen than in lumen of GlpF. The weaker water-water electrostatics combined with stronger channel-water electrostatics across the entire lumen of AqpZ relative to GlpF explain the lower water permeation rates (Table 1) since these interactions serve to retain water more strongly in AqpZ relative to GlpF.
FIGURE 8.
Water-channel and water-water electrostatics profiles within the lumen of AqpZ(His-174:NHδ) and GlpF (a) (for both embedded in POPE bilayers; results for the channels embedded in POPC bilayers are quantitatively similar and therefore not shown). The profiles were obtained from Eq. 9 by considering all water molecules residing within the lumen of the channel at time t and computing the sum of (untruncated) Coulombic interactions with the surrounding monomer (i.e., channel-luminal water interactions) as well as with other water molecules residing within the lumen of the channel (i.e., luminal water-luminal water interactions). The electrostatic energy (E(z)) was assigned to a position z along the channel axis by using the O atom position of that water whose electrostatic interaction was in question. Averaging was over 5000 configurations separated by 5 ps. Averaging over monomers provides the mean electrostatic energy E(z) with variance  . Standard errors (SE) in E(z) are given as
. Standard errors (SE) in E(z) are given as 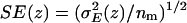 , with nm = 4 being the number of monomers. Origin of z axis was taken as in Fig. 7 b. (b) Water-water correlation for AqpZ(His-174:NHδ) and GlpF. Representative root mean-square deviations from the mean in the correlation profiles are shown for GlpF/POPC and AqpZ/POPC and obtained from the variances among 30, 500-ps-wide time windows. Origin of z axis was taken as in Fig. 7 b. Correlations were only computed within the constriction region according to Eq. 10.
, with nm = 4 being the number of monomers. Origin of z axis was taken as in Fig. 7 b. (b) Water-water correlation for AqpZ(His-174:NHδ) and GlpF. Representative root mean-square deviations from the mean in the correlation profiles are shown for GlpF/POPC and AqpZ/POPC and obtained from the variances among 30, 500-ps-wide time windows. Origin of z axis was taken as in Fig. 7 b. Correlations were only computed within the constriction region according to Eq. 10.
Interestingly, at the periplasmic entrance of the channel, water-channel electrostatic energy is lower in GlpF than in AqpZ. Given that water-water electrostatic energy at this position is identical in the two channels, this suggests that GlpF is more capable of recruiting (rehydrating) a water molecule entering the lumen from the periplasmic vestibule. It is also noteworthy that water-water electrostatic interactions in AqpZ are considerably weakened relative to GlpF across the remainder of the SF region, and reduced water-water correlation across this key constriction occurs. In AqpZ, water-water electrostatic interaction energy is close to zero at −8 Å ≤ z ≤ −4 Å owing to the presence of H-174 and T-183 (in GlpF F-200) in the SF. In addition to the conserved, positively charged arginine R-189 (in GlpF R-206) and F-43 (in GlpF W-48), H-174 and T-183 together result in a more polar SF in AqpZ than in GlpF (40). As discussed above, e.g., R-189:Hη and T-183:O form a hydrogen bond that may orient the charged side chain of R-189 in AqpZ away from the periplasmic vestibule, whereas in GlpF, both R-206:Hηs are always available as hydrogen bond donors to permeating water molecules, i.e., an up configuration prevails. This might explain why GlpF is more capable of recruiting a water molecule entering the lumen from the periplasmic vestibule. The more polar SF in AqpZ implies a more dynamical interaction pattern in this region, e.g., the R-189:Hη–T-183:O hydrogen bond is occasionally broken during the simulations, implying that both R-189:Hηs at times hydrogen bond to permeating water as discussed above (cf. Figs. 4–6). This gives rise to part of the errors (fluctuations) in the water permeation quantities for AqpZ (Table 1). Standard errors in water-water and channel-water electrostatics profiles are also largest for AqpZ within the SF region. Standard errors for GlpF are in general small.
Correlations
To gauge overall concertedness of the water movement through the channels, we deployed an integrated water-water correlation coefficient defined as
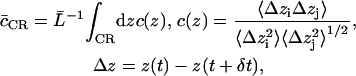 |
(10) |
where  is the average length of the CR. Water-water correlations resolved along the channel axis, i.e., c(z), the nonintegrated form of Eq. 10, are presented in Fig. 8 b for GlpF and AqpZ(His-174:NHδ) along with representative RMS fluctuations. The correlations were assigned a z value following Jensen et al. (16). Interestingly, the average correlation coefficient computed from Eq. 10 is
is the average length of the CR. Water-water correlations resolved along the channel axis, i.e., c(z), the nonintegrated form of Eq. 10, are presented in Fig. 8 b for GlpF and AqpZ(His-174:NHδ) along with representative RMS fluctuations. The correlations were assigned a z value following Jensen et al. (16). Interestingly, the average correlation coefficient computed from Eq. 10 is 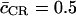 for both channels. Although AqpZ was found to exhibit more pronounced single-file characteristics in terms of the pf/pd ratio, this channel does not overall feature more concerted water motion than GlpF. This can be further explained in terms of c(z), which differs characteristically between the two channels. Although both profiles exhibit a minimum at the NPA motifs (z ≅ 0 Å), maximal correlation is featured oppositely in the two channels. For GlpF, maximal correlation occurs in the periplasmic half-channel across the SF region where the channel is most narrow (Fig. 7 b), whereas maximal correlation is featured in the cytoplasmic half-channel for AqpZ. For the wider GlpF channel (Fig. 7, b and c), the narrowest point is the SF region in the periplasmic half-channel, which leads to maximal correlation (Fig. 8 b). Water molecules at this position are more confined along z and less mobile laterally than in the cytoplasmic half-channel. This holds despite that maximal channel-water electrostatic interactions occur for GlpF within the SF region (Fig. 8 a). Strong confinement across the SF region of AqpZ also exists. However, the double mutation relative to GlpF discussed above renders the SF of AqpZ more polar and more narrow. Consequently, the AqpZ SF is stronger interacting with the permeating water molecules than the GlpF SF (Fig. 8 a). This reduces water-water correlation in the periplasmic half-channel of AqpZ (Fig. 8 b). As originally observed for hAqp1, disruption of intermolecular water-water hydrogen bonds occurs frequently across the SF region (14). Such disruption is complementary to water-water correlation (15,16). The results in Fig. 8 b depicting reduced correlation across the SF region of AqpZ are therefore in line with the results obtained from MD simulations of the hAqp1 model (14), noting that the SF polarity in hAqp1 is similar to that in AqpZ (32,33,38). In the cytoplasmic half-channel of AqpZ, water is still more confined than in GlpF, since AqpZ is the more narrow of the two channels (cf. Fig. 7). Relative to GlpF, this implies stronger correlation in AqpZ within this half-channel, noting that the cytoplasmic half-channels of AqpZ and GlpF are similar in terms of polarity. However, since channel-water electrostatic interactions here are weaker than in the periplasmic half-channel (Fig. 8 a), water-water correlation across this region has much less impact on water permeation compared to correlations across the SF region. Surprisingly, the degree of water correlation across the SF region observed for AqpZ, bAqp1, Aqp0, and GlpF in a recent, comparative MD study was almost identical (42). This might be the reason that these authors observed a pf value for AqpZ significantly exceeding our corresponding values in Table 1. The reduced correlation across the SF region as observed for AqpZ in our current work conforms, however, with a related analysis of water correlation across hAqp1(14).
for both channels. Although AqpZ was found to exhibit more pronounced single-file characteristics in terms of the pf/pd ratio, this channel does not overall feature more concerted water motion than GlpF. This can be further explained in terms of c(z), which differs characteristically between the two channels. Although both profiles exhibit a minimum at the NPA motifs (z ≅ 0 Å), maximal correlation is featured oppositely in the two channels. For GlpF, maximal correlation occurs in the periplasmic half-channel across the SF region where the channel is most narrow (Fig. 7 b), whereas maximal correlation is featured in the cytoplasmic half-channel for AqpZ. For the wider GlpF channel (Fig. 7, b and c), the narrowest point is the SF region in the periplasmic half-channel, which leads to maximal correlation (Fig. 8 b). Water molecules at this position are more confined along z and less mobile laterally than in the cytoplasmic half-channel. This holds despite that maximal channel-water electrostatic interactions occur for GlpF within the SF region (Fig. 8 a). Strong confinement across the SF region of AqpZ also exists. However, the double mutation relative to GlpF discussed above renders the SF of AqpZ more polar and more narrow. Consequently, the AqpZ SF is stronger interacting with the permeating water molecules than the GlpF SF (Fig. 8 a). This reduces water-water correlation in the periplasmic half-channel of AqpZ (Fig. 8 b). As originally observed for hAqp1, disruption of intermolecular water-water hydrogen bonds occurs frequently across the SF region (14). Such disruption is complementary to water-water correlation (15,16). The results in Fig. 8 b depicting reduced correlation across the SF region of AqpZ are therefore in line with the results obtained from MD simulations of the hAqp1 model (14), noting that the SF polarity in hAqp1 is similar to that in AqpZ (32,33,38). In the cytoplasmic half-channel of AqpZ, water is still more confined than in GlpF, since AqpZ is the more narrow of the two channels (cf. Fig. 7). Relative to GlpF, this implies stronger correlation in AqpZ within this half-channel, noting that the cytoplasmic half-channels of AqpZ and GlpF are similar in terms of polarity. However, since channel-water electrostatic interactions here are weaker than in the periplasmic half-channel (Fig. 8 a), water-water correlation across this region has much less impact on water permeation compared to correlations across the SF region. Surprisingly, the degree of water correlation across the SF region observed for AqpZ, bAqp1, Aqp0, and GlpF in a recent, comparative MD study was almost identical (42). This might be the reason that these authors observed a pf value for AqpZ significantly exceeding our corresponding values in Table 1. The reduced correlation across the SF region as observed for AqpZ in our current work conforms, however, with a related analysis of water correlation across hAqp1(14).
Bilayer influence on permeation
By eliminating lipid headgroup charges and constraining harmonically P and N headgroup atoms, we investigated whether k0 and hence the diffusive permeability pd (Eq.(4)) was influenced by the lipid headgroup, either directly by or indirectly via the headgroup-induced polarity of the interfacial water. Despite charge elimination and a huge (60%) concurrent reduction in headgroup hydration (data not shown), this, however, appeared not to be the case as discernible from Fig. 3 where the number of permeation events continues to grow linearly with time. Hence, the diffusive permeability exhibits no significant sensitivity to bilayer type. Correspondingly, for the osmotic permeability, we find for GlpF pf = (8.6 ± 1.1) × 10−14cm3s−1 and pf = (13.1 ± 3.4) × 10−14cm3s−1 in POPC and POPE bilayers, respectively (Supplementary Material). Within the statistical error, pf is seemingly a little larger in the POPE lipid bilayer. However, the corresponding results for AqpZ (Table 1), the statistics of the present simulations, and the total number of simulations are together insufficient to justify a statement claiming that pf is characteristically dependent on the lipid headgroup.
From the mean radii (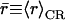 ), we find that the central part of the channels, positioned within hydrophobic core of the membrane, is marginally wider when embedded in POPC relative in POPE;
), we find that the central part of the channels, positioned within hydrophobic core of the membrane, is marginally wider when embedded in POPC relative in POPE; 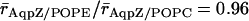 and
and 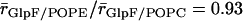 . Seemingly, the more bulky POPC headgroup redistributes lateral stress from the hydrophobic core of the membrane toward the headgroup region. This widening might be the reason for the slightly higher value for pd found for GlpF in POPC relative to POPE, which is at variance with earlier results derived from the CTRW model (18). In contrast, this does not apply to AqpZ (Table 1). Possibly, widening of the narrower AqpZ channel is still insufficient to significantly reduce channel-water electrostatic interactions and/or to permit water-water interchange that both eventually could lead to an increased pd. Overall, only channel architecture determines water permeation across aquaporins. The lipid matrix has, at most, only marginal influence on the permeation.
. Seemingly, the more bulky POPC headgroup redistributes lateral stress from the hydrophobic core of the membrane toward the headgroup region. This widening might be the reason for the slightly higher value for pd found for GlpF in POPC relative to POPE, which is at variance with earlier results derived from the CTRW model (18). In contrast, this does not apply to AqpZ (Table 1). Possibly, widening of the narrower AqpZ channel is still insufficient to significantly reduce channel-water electrostatic interactions and/or to permit water-water interchange that both eventually could lead to an increased pd. Overall, only channel architecture determines water permeation across aquaporins. The lipid matrix has, at most, only marginal influence on the permeation.
CONCLUSION
Pioneering MD simulations of de Groot and Grubmüller suggested the orthodox water hAqp1 channel to permeate water diffusively at lower rates than aquaglyceroporin GlpF (14), i.e., their observed permeation events translate into diffusive permeabilities of pd = 0.6 × 10−14cm3s−1 for hAqp1 and 1.5 × 10−14cm3s−1 ≤ pd ≤ 3.7 × 10−14cm3s−1 for GlpF (cf. Eq. 4). Our results obtained from significantly longer simulations are in line with their result; we find a 2–9-fold reduction of diffusive permeation across AqpZ relative to GlpF. For GlpF, our pd results also agree with results obtained from shorter (5 ns) simulations (15,16). Our results for the osmotic permeability constant (pf), obtained using a newly developed method (29), are in accordance with similar results obtained from pressure-induced MD simulations (11), whereas our results for AqpZ are compatible with results from pressure-induced MD simulations of bAqp1 (17). The pf result for AqpZ is independent of the tautomeric and protonation state of H-174 in agreement with the fact that water permeation across AqpZ does not exhibit pH-sensitivity in the pH range 4.5 ≤ pH ≤ 7.5 (7,8,47). In contrast, pd increases 2–3-fold due to a widening of the AqpZ SF caused by a repulsion between the positively charged guanidinium group of the conserved R-189 and the protonated imidazole ring of H-174. Together, this lowers the pf/pd ratio. Albeit questionable, this type of pH sensitivity can be tested experimentally through measurement of the pf/pd ratio, which is possible without knowing the density of channels (45). Presupposing that H-174 is protonated at strong acidic pH, complete blocking of the channel via this mechanism could be another efficient means of preventing proton conduction. GlpF exhibits less pronounced single-file characteristics and a pf/pd ratio of 3–4, which differs significantly from the water occupancy of the channel (8,9) since water molecules occasionally interchange position within the GlpF lumen (16). The pf/pd ratio for AqpZ(His-174 neutral) is larger (9–13) and significantly closer to the water occupancy of the channel (7,8). This is indicative of a more pronounced single-file structure of the luminal water in AqpZ but not of stronger water-water correlation.
Our pf results for GlpF are also in accordance with a recent related study comparing permeation rates across AqpZ, bAqp1, Aqp0, and GlpF, whereas, relative to our present work, a 2–3 times higher value for pf of pf = (10 ± 4) × 10−14cm3s−1 was found for AqpZ (40). No assignment of the protonation state of H-174 was given for AqpZ and no diffusive permeability was reported in Hashido et al. (42). Combination of our pd values for AqpZ with the pf results of Hashido et al. (40) leads to an unrealistically large pf/pd ratio: pf/pd ≅ 35, using pd values for AqpZ(His-174:NHδ) according to Table 1. Discrepancies between these simulation results and ours may rely on force-field, simulation protocol and time; e.g., 5 ns simulations were reported by Hashido et al. (42). Simulation times in our work are significantly longer. Sensitivity of Aqp-permeation rates to simulation time was originally observed for GlpF (14).
Therefore, with one exception (40), MD simulations consistently suggest regardless of method and force field, that the orthodox water channels, bovine and human Aqp1 and E. coli AqpZ, permeate osmotically water at 2–3-fold lower rates than the less selective aquaglyceroporin GlpF. This finding contrasts experimental reports (7–10,43), suggesting further computational and experimental studies. We cannot rule out that long time conformational changes or protein-protein interactions do influence permeation. These issues are not addressed in the present work. We do find that the interplay between the side chains of R-189 and H-174 of the AqpZ selectivity filter influences permeation. Short to intermediate timescale conformational changes involving transitions of side-chain dihedral angles of these key residues are possibly also insufficiently sampled in our simulations. Moreover, such transitions are very sensitive to the potential energy function. Only one tautomeric form of the (neutral) H-174 is treated in the same simulation. A dynamic equilibrium between the two tautomeric states could be present in reality. Even an equilibrium with the protonated histidine might be present at physiological conditions. Other shortcomings such as lack of explicit polarizability and charge transfer terms in the employed force field may also contribute to uncertainty of our computed permeabilities for both channels. It has been demonstrated from ab initio MD simulations of GlpF that such effects are likely to be important (58).
Our results and conclusions are, however, based on the to-date most extensive MD simulations of available high-resolution x-ray structures of GlpF and AqpZ (39,40). These suggest that the determinant of water permeation of aquaporins is a balance between channel radius and channel polarity and that water-water correlations are important as previously suggested (14–16). Achieving complete water selectivity in AqpZ lowers transport rates relative to the less selective GlpF, which has a wider lumen. Considering that aquaporins are rather stiff channels and not responding significantly to changes in lateral stress, it is not surprising that lipid-protein interactions only marginally influence water permeation across AqpZ and GlpF.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Supplementary Material
Acknowledgments
We thank Fangqiang Zhu and Emad Tajkhorshid for useful discussions.
This work was supported by the Danish National Research Foundation and the Danish Center for Scientific Computing. All molecular images in this article were made with Visual Molecular Dynamics (53).
References
- 1.Preston, G. M., P. Piazza-Carroll, W. B. Guggino, and P. Agre. 1992. Appearance of water channels in Xenopus oocytes expressing red cell CHIP28 water channel. Science. 256:385–387. [DOI] [PubMed] [Google Scholar]
- 2.Agre, P. 1998. The aquaporins, blueprints for cellular plumbing systems. J. Biol. Chem. 273:14659–14662. [DOI] [PubMed] [Google Scholar]
- 3.Borgnia, M., S. Nielsen, A. Engel, and P. Agre. 1999. a. Cellular and molecular biology of the aquaporin water channels. Annu. Rev. Biochem. 68:425–458. [DOI] [PubMed] [Google Scholar]
- 4.Yasui, M., T. H. Kwon, M. A. Knepper, S. Nielsen, and P. Agre. 1999. Aquaporin-6: an intracellular vesicle water channel protein in renal epithelia. Proc. Natl. Acad. Sci. USA. 96:5808–5813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kozono, D., M. Yasui, L. S. King, and P. Agre. 2002. Aquaporin water channels: atomic structure and molecular dynamics meet clinical medicine. J. Clin. Invest. 109:1395–1399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Finkelstein, A. 1987. Water Movement through Lipid Bilayers, Pores, and Plasma Membranes. John Wiley & Sons, New York.
- 7.Borgnia, M. J., D. Kozono, G. Calamita, P. C. Maloney, and P. Agre. 1999. b. Functional reconstitution and characterization of AqpZ, the E. coli water channel protein. J. Mol. Biol. 291:1169–1179. [DOI] [PubMed] [Google Scholar]
- 8.Calamita, G. 2000. The Escherichia coli aquaporin-z water channel. Mol. Microbiol. 37:254–262. [DOI] [PubMed] [Google Scholar]
- 9.Pohl, P., M. S. Saparov, M. J. Borgnia, and P. Agre. 2001. Highly selective water channel activity measured by voltage clamp: analysis of planar lipid bilayers reconstituted with purified AqpZ. Proc. Natl. Acad. Sci. USA. 98:9624–9629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Saparov, S. M., S. P. Tsunoda, and P. Pohl. 2005. Proton exclusion by an aquaglyceroprotein: a voltage clamp study. Biol. Cell. 97:545–550. [DOI] [PubMed] [Google Scholar]
- 11.Zhu, F., E. Tajkhorshid, and K. Schulten. 2002. Pressure induced water transport in membrane channels studied by molecular dynamics. Biophys. J. 83:154–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kong, Y., and J. Ma. 2001. Dynamic mechanisms of the membrane water channel Aquaporin-1 (AQP1). Proc. Natl. Acad. Sci. USA. 98:14345–14349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhu, F., E. Tajkhorshid, and K. Schulten. 2001. Molecular dynamics study of Aquaporin-1 water channel in a lipid bilayer. FEBS Lett. 504:212–218. [DOI] [PubMed] [Google Scholar]
- 14.de Groot, B. L., A. Engel, and H. Grubmüller. 2001. A refined structure of human aquaporin-1. FEBS Lett. 504:206–211. [DOI] [PubMed] [Google Scholar]
- 15.Tajkhorshid, E., P. Nollert, M. Ø. Jensen, L. J. W. Miercke, J. O'Connel, R. M. Stroud, and K. Schulten. 2002. Global orientational tuning controls the selectivity of the AQP water channel family. Science. 296:525–529. [DOI] [PubMed] [Google Scholar]
- 16.Jensen, M. Ø., E. Tajkhorshid, and K. Schulten. 2003. Electrostatic control of permeation and selectivity in aquaporin water channels. Biophys. J. 85:2884–2899. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu, F., E. Tajkhorshid, and K. Schulten. 2004. Theory and simulation of water simulation in Aquaporin-1. Biophys. J. 86:50–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Jensen, M. Ø., and O. G. Mouritsen. 2004. Lipids do influence protein function—the hydrophobic matching hypothesis revisited. Biochim. Biophys. Acta. 1666:205–226. [DOI] [PubMed] [Google Scholar]
- 19.Vidossich, P., M. Cascella, and P. Carloni. 2004. Dynamics and energetics of water permeation through the aquaporin channel. Proteins. 55:924–931. [DOI] [PubMed] [Google Scholar]
- 20.Patargias, G., P. J. Bond, S. S. Deol, and M. S. P. Sansom. 2005. Molecular dynamics simulations of GlpF in a micelle vs. in a bilayer: conformational dynamics of a membrane protein as a function of environment. J. Phys. Chem. B. 109:575–582. [DOI] [PubMed] [Google Scholar]
- 21.de Groot, B. L., and H. Grubmuller. 2005. The dynamics and energetics of water permeation and proton exclusion in aquaporins. Curr. Opin. Struc. Biol. 15:176–183. [DOI] [PubMed] [Google Scholar]
- 22.Pomes, R., and B. Roux. 1996. Structure and dynamics of a proton wire: a theoretical study of H+ translocation along the single-file water chain in the gramicidin A channel. Biophys. J. 71:19–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chiu, S.-W., S. Subramaniam, and E. Jakobsson. 1999. Simulation study of a gramicidin/lipid bilayer system in excess water and lipid. II. Rates and mechanisms of water transport. Biophys. J. 76:1939–1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.de Groot, B. L., D. P. Tieleman, P. Pohl, and H. Grubmuller. 2002. Water permeation through gramicidin A: Desformylation and the double helix: a molecular dynamics study. Biophys. J. 82:2934–2942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- 26.Beckstein, O., and M. S. P. Sansom. 2003. Liquid-vapor oscillations in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Zhu, F., and K. Schulten. 2003. Water and proton conduction through carbon nanotubes as models for biological channels. Biophys. J. 85:236–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kalra, A., G. Hummer, and S. Garde. 2003. Osmotic water transport through carbon nanotube membranes. Proc. Natl. Acad. Sci. USA. 100:10175–10180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Zhu, F., E. Tajkhorshid, and K. Schulten. 2004. Collective diffusion model for water permeation through microscopic channels. Phys. Rev. Lett. 93:224501. [DOI] [PubMed] [Google Scholar]
- 30.Beckstein, O., and M. S. P. Sansom. 2004. The influence of geometry, surface character, and flexibility on the permeation of ions and water through biological pores. Phys. Biol. 1:42–52. [DOI] [PubMed] [Google Scholar]
- 31.Tajkhorshid, E., F. Zhu, and K. Schulten. 2005. Kinetic theory and simulation of single-channel water transport. In Handbook of Material Modeling, Vol. 1: Methods and Models. S. Yip, editor. Springer, The Netherlands. 1797–1822.
- 32.Murata, K., K. Mitsuoka, T. Hirai, T. Walz, P. Agre, J. B. Heymann, A. Engel, and Y. Fujiyoshi. 2000. Structural determinants of water permeation through Aquaporin-1. Nature. 407:599–605. [DOI] [PubMed] [Google Scholar]
- 33.Ren, G., V. S. Reddy, A. Cheng, and A. K. Mitra. 2001. Visualization of a water-selective pore by electron crystallography in vitreous ice. Proc. Natl. Acad. Sci. USA. 98:1398–1403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Sui, H., B.-G. Han, J. K. Lee, P. Wallan, and B. K. Jap. 2001. Structural basis of water specific transport through the AQP1 water channel. Nature. 414:872–877. [DOI] [PubMed] [Google Scholar]
- 35.Harries, W. E. C., D. Akhavan, S. Miercke, L. J. W. Khademi, and R. M. Stroud. 2004. The channel architecture of aquaporin 0 at a 2.2-Å resolution. Proc. Natl. Acad. Sci. USA. 101:14045–14050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gonen, T., P. Sliz, J. Kistler, Y. Cheng, and T. Walz. 2004. Aquaporin-0 membrane junctions reveal the structure of a closed water pore. Nature. 429:193–196. [DOI] [PubMed] [Google Scholar]
- 37.Gonen, T., Y. Cheng, P. Sliz, Y. Hiroaki, Y. Fujiyoshi, S. C. Harrison, and T. Walz. 2005. Lipid-protein interactions in double-layered two-dimensional AQPO crystals. Nature. 438:633–638. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Törnroth-Horsefield, S., Y. Wang, K. Hedfalk, U. Johanson, M. Karlsson, E. Tajkhorshid, and P. Kjellbom. 2006. Structural mechanism of plant aquaporin gating. Nature. 439:688–694. [DOI] [PubMed] [Google Scholar]
- 39.Fu, D., A. Libson, L. J. W. Miercke, C. Weitzman, P. Nollert, J. Krucinski, and R. M. Stroud. 2000. Structure of a glycerol conducting channel and the basis for its selectivity. Science. 290:481–486. [DOI] [PubMed] [Google Scholar]
- 40.Savage, D. F., P. F. Egea, Y. Robles-Colmenares, J. D. O'Connell, and R. M. Stroud. 2003. Architecture and selectivity in Aquaporins: 2.5 Å resolution x-ray structure of Aquaporin Z. PLoS Biol. 1:334–340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang, Y., K. Schulten, and E. Tajkhorshid. 2005. What makes an aquaporin a glycerol channel: a comparative study of AqpZ and GlpF. Structure. 13:1107–1118. [DOI] [PubMed] [Google Scholar]
- 42.Hashido, M., M. Ikeguchi, and A. Kidera. 2005. Comparative simulations of aquaporin family: AQP1, AQPZ, AQP0 and GlpF. FEBS Lett. 579:5549–5552. [DOI] [PubMed] [Google Scholar]
- 43.Borgnia, M. J., and P. Agre. 2001. Reconstitution and functional comparison of purified GlpF and AqpZ, the glycerol and water channels from Escherichia coli. Proc. Natl. Acad. Sci. USA. 98:2888–2893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Heller, K. B., E. C. Lin, and T. H. Wilson. 1980. Substrate specificity and transport properties of the glycerol facilitator of Escherichia coli. J. Bacteriol. 144:274–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mathai, J. C., S. Mori, B. L. Smith, G. M. Preston, N. Mohandas, M. Collins, P. C. van Zijl, M. L. Zeidel, and P. Agre. 1996. Functional analysis of aquaporin-1 deficient red cells. J. Biol. Chem. 271:1309–1313. [DOI] [PubMed] [Google Scholar]
- 46.Berezhkovskii, A., and G. Hummer. 2002. Single-file transport of water molecules through a carbon nanotube. Phys. Rev. Lett. 89:064503. [DOI] [PubMed] [Google Scholar]
- 47.Pohl, P. 2004. Combined transport of water and ions through membrane channels. Biol. Chem. 385:921–926. [DOI] [PubMed] [Google Scholar]
- 48.Kalé, L., R. Skeel, M. Bhandarkar, R. Brunner, A. Gursoy, N. Krawetz, J. Phillips, A. Shinozaki, K. Varadarajan, and K. Schulten. 1999. NAMD2: greater scalability for parallel molecular dynamics. J. Comput. Phys. 151:283–312. [Google Scholar]
- 49.Schlenkrich, M., J. Brickmann, A. MacKerell Jr., and M. Karplus. 1996. Empirical potential energy function for phospholipids: criteria for parameter optimization and applications. In Biological Membranes: A Molecular Perspective from Computation and Experiment. K. M. Merz, and B. Roux, editors. Birkhauser, Boston. 31–81.
- 50.Feller, S. E., and A. MacKerell. 2000. An improved empirical potential energy function for molecular simulations of phospholipids. J. Phys. Chem. B. 104:7510–7515. [Google Scholar]
- 51.Darden, T., D. York, and L. Pedersen. 1993. Particle Mesh Ewald: An N log(N) method for Ewald sums in large systems. J. Chem. Phys. 98:10089–10092. [Google Scholar]
- 52.Jensen, M. Ø., E. Tajkhorshid, and K. Schulten. 2001. The mechanism of glycerol conduction in aquaglyceroporins. Structure. 9:1083–1093. [DOI] [PubMed] [Google Scholar]
- 53.Humphrey, W., A. Dalke, and K. Schulten. 1996. VMD—Visual Molecular Dynamics. J. Mol. Graph. 14:33–38. [DOI] [PubMed] [Google Scholar]
- 54.Jorgensen, W. L., J. Chandrasekhar, J. D. Medura, R. W. Impey, and M. L. Klein. 1983. Comparison of simple potential models for simulating liquid water. J. Chem. Phys. 79:926–935. [Google Scholar]
- 55.Aksimentiev, A., and K. Schulten. 2005. Imaging α-hemolysin with molecular dynamics: ionic conductance, osmotic permeability and the electrostatic potential map. Biophys. J. 88:3745–3761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jensen, M. Ø., S. Park, E. Tajkhorshid, and K. Schulten. 2002. Energetics of conduction through aquaglyceroporin GlpF. Proc. Natl. Acad. Sci. USA. 99:6731–6736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Smart, O., J. Goodfellow, and B. Wallace. 1993. The pore dimensions of gramicidin A. Biophys. J. 65:2455–2460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Jensen, M. Ø., U. Röthlisberger, and C. Rovira. 2005. Hydroxide and proton migration in aquaporins. Biophys. J. 89:1744–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ilan, B., E. Tajkhorshid, K. Schulten, and G. A. Voth. 2004. The mechanism of proton exclusion in aquaporin channels. Proteins. 55:223–228. [DOI] [PubMed] [Google Scholar]
- 60.Chakrabarti, N., B. Roux, and R. Pomes. 2004. Molecular basis of proton blockage in aquaporins. Structure. 12:65–74. [DOI] [PubMed] [Google Scholar]
- 61.Chakrabarti, N., B. Roux, and R. Pomes. 2004. Structural determinants of proton blockage in aquaporins. J. Mol. Biol. 343:493–510. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.










