Probing Surface Structures of Shewanella spp. by Microelectrophoresis

Abstract

Long-range electrostatic forces substantially influence bacterial interactions and bacterial adhesion during the preliminary steps of biofilm formation. The strength of these forces depends strongly on the structure of the bacterium surfaces investigated. The latter may be addressed from appropriate analysis of electrophoretic mobility measurements. Due to the permeable character of the bacterium wall and/or surrounding polymer layer, bacteria may be regarded as paradigms of soft bioparticles. The electrophoretic motion of such particles in a direct-current electric field differs considerably from that of their rigid counterparts in the sense that electroosmotic flow takes place around and within the soft surface layer. Recent developments of electrokinetic theories for soft particles now render possible the evaluation of the softness degree (or equivalently the hydrodynamic permeability) from the raw electrokinetic data. In this article, the electrophoretic mobilities of three Shewanella strains (MR-4, CN32, and BrY) presenting various and well-characterized phenotypes of polymer fringe are reported over a wide range of pH and ionic strength conditions. The data are quantitatively analyzed on the basis of a rigorous numerical evaluation of the governing electrostatic and hydrodynamic equations for soft particles. It is clearly shown how the peculiar surface structures of the bacteria investigated are reflected in their electrohydrodynamic properties.

INTRODUCTION

Bacterial cell surface properties are central to understand the intricacies of interfacial phenomena in aqueous media such as bacterial adhesion, biomineralization, or biofilm formation. The assessment of bacterial properties at the molecular, microscopic, and macroscopic levels is far from being an easy task because of the plethora of polymer cell envelope structures that possibly exist and because of the intrinsic dynamic nature of these structures. In the past decade, a large set of data has been compiled using macroscopic methods so as to quantify the overall properties of bacterial suspensions. Such macroscopic approaches are based mostly on the quantitative estimation of i), the bacterial charge, as obtained from the characteristic isoelectric point (1,2) and ii), the hydrophobic character of bacterial strains from contact angle measurements or from the analysis of data related to the bacterial adhesion onto various substrates (3). Although such approaches have played their roles in the progress of our understanding of bacterial reactivity, several questions regarding the impacts of the structural, chemical, and biological heterogeneities on these overall (or, equivalently, averaged) characteristics remain open. The analysis of the physico-chemical properties of the various polymeric-type structures beyond the outer membrane of gram-negative bacteria is a prospective and promising way to gain further insight into the processes underlying the bacterial reactivity.

The cell wall of a gram-negative bacterium exhibits an asymmetric outer membrane located above the periplasmic space containing a thin peptidoglycan layer and a gel-like matrix. Underneath the periplasmic space, the plasma membrane constitutes the last part of the gram-negative envelope that withstands the turgor pressure of the protoplast. Thus, the outer membrane is usually considered to be the outermost layer of the gram-negative cell wall. This asymmetric membrane consists of inner leaflet mostly composed of close-packed phospholipid chains whereas the outer leaflet contains the lipopolysaccharide (LPS) molecules. Other surface layer organizations above the bacterial cell wall (such as capsules, S-layers, or sheets) are frequently encountered (4). The three dimensionality of such specific structures may vary following the bacterial strain, as a result of the growth conditions or changes of the surrounding environment. Whereas the effects of those structures on the bacterial reactivity are now recognized, they still remain poorly understood and therefore require further attention.

Given the context sketched above, a breakthrough has recently been reached by assessing at a molecular scale the specific and nonspecific interactions of bacterial surfaces as a function of the chemical characteristics of the lipopolysaccharide layer (5,6). The data suggest that there is no correlation between the thickness of the LPS layer and the macroscopic adhesion propensity of the bacteria. This important result has been further confirmed and reported by other researchers (7,8). One of the major difficulties for analyzing the bacterial adhesion phenomena is to address and decouple the roles played by the microscopic and macroscopic physicochemical properties of the bacterial surface. Such apparent intricacy motivates further investigation on the structure and the dynamics of the bacterial interfaces in aqueous media.

Following the above considerations, the primary goal of this article is the analysis of the dependence of the electrophoretic mobility of various Shewanella strains (MR-4, CN32, BrY) on the characteristics of their respective polymer surface layers. The latter were described previously in the study of Korenevsky et al. (9) by freeze-substitution preparation for preserving the most delicate surface ultrastructure. Table 1 summarizes the results obtained by Korenevsky et al., which pertain to the external polymer features of the Shewanella bacteria used in our study. Basically, the cell surfaces of MR-4 revealed an extensive polymer fringe (from 70 to 130 nm) whereas those of CN32 were devoid of any fibrous or capsular materials. Unlike MR-4 and CN32 bacteria, cell population of the BrY strain exhibited an unequal expression of polymeric surface structures yielding very heterogeneous bacterial populations that presented characteristics of both the MR-4 and CN32 strains. Furthermore, Shewanella organisms are frequently encountered in aquatic habits, soils, and in the agri-food industry (10–12). In these different environments, Shewanella bacteria can form biofilms (12,13). There are classically depicted as one of the most efficient and versatile dissimilatory metal-reducing type of microogranism (14). Finally, they are also relevant within the fields of veterinary and medical bacteriology especially the Shewanella putrefaciens and Shewanella algae (15,16). However, few studies have so far been carried out on the analysis of the surface properties of Shewanella cells. Quantitative description of those properties at a microscopic level is the mandatory requirement for understanding the mechanisms at the bacterium/aqueous solution interface.

TABLE 1.

Nature and type of external polymeric surface structure for the Shewanella strains according to the study of Korenevsky et al. (9)^*

Designation	Bacterial strain	Characteristics of cell surface structures
CN32	S. putrefaciens	Devoid of any fibrous material and not capsulated†
BrYFC	S. algae	Heterogeneous populations of bacteria with and without capsular polysaccharides structures (from 60 to 90 nm)†
MR-4	S. oneidensis	Capsular polysaccharides structures (from 70 to 130 nm)†

^*In addition, they demonstrated on the basis of proteinase K/sodium dodecyl sulphate-polyacrylamide gel electrophoresis that all these strains presented rough LPS (with core oligosaccharide and no O-side chain).

^†From freeze-substitution electronic images (9).

Having in mind the assessment of the physico-chemical properties of the Shewanella bacteria as a function of their respective and aforementioned surface structures, we report in this article their electrophoretic mobilities measured at various pH and ionic strength values. The data were interpreted on the basis of a theory for the electrokinetics of soft particles (1,17–20) so as to derive the bacterial softness and the volumic charge density of the permeable layer. Knowledge of these parameters is crucial in the understanding of the role played by the various gram-negative Shewanella strains in many environmental processes such as bioreduction of minerals in soils or in iron corroded surfaces, food industries, clinical specimens, and oil drilling (14,21–23).

MATERIALS AND METHODS

Bacterial cultures

S. algae BrY^FC (ATCC 51181), S. oneidensis MR-4, and S. putrefaciens CN32 (ATCC BAA-453) were kindly provided by Professor T. J. Beveridge (University of Guelph, Ontario, Canada). Bacterial strains were revived from a stock suspension at −80°C on a TSA medium (bioMérieux, Marcy l'Etoile, France) twice successively for 48 h at 30°C. Precultures were then prepared in 250 mL Erlenmeyer flasks containing 20 mL bacterial suspension (NaCl 0.7%; optical density: OD_600nm = 0.5) and 200 mL TSB (bioMérieux, 30 g/L) that were incubated for 14 h while shaking (300 rpm, 30°C). Cells were then harvested by centrifugation (10 min at 10,000 × g) and suspended in aqueous media (NaCl 0.7%, OD_{600 nm} = 2.0). Cell suspensions (10 ml) were subsequently used to inoculate 750 mL TSB in a 1.5 L batch reactor (300 rpm, 30°C, 25 L/h air flux). Cells of the midexponential (5 h) and pseudostationary growth (24 h) phases were harvested by centrifugation (10 min at 10,000 × g), washed twice with appropriate potassium nitrate solutions, suspended in different ionic strength solutions (0.001, 0.01, and 0.1 mol/L of KNO₃) of bacterial concentration ranging from 5.10⁶ to 1.10⁷ cells/mL, and immediately used for microelectrophoresis experiments.

Electrophoretic mobility measurements

Electrophoretic mobility (EM) measurements were performed (Zetaphoremeter IV, CAD Instrumentations, Les Essarts le Roi, France) in a quartz suprasil cell at 24°C from the reflection of a laser beam by bacteria tracked with a charge-coupled device camera. By means of an image analysis software, recorded images were processed in real time to calculate the electrophoretic mobilities from the displacement (migration motion) of the bacteria subjected to a constant direct-current electric field (800 V/m). Different cycles were recorded to perform 100 measurements of the bacterial mobility at every pH and ionic strength values investigated. For each ionic strength, fresh cell suspensions prepared as described above were analyzed by adjusting the pH of the suspension with acid (HNO₃) or base solution (KOH).

Modeling the EM of a diffuse soft particle

The electrophoretic mobilities, measured as a function of the ionic strength, were quantitatively interpreted on the basis of the recent theory developed by Duval et al. (18–20) that accounts for the electrokinetic response of a soft particle without any restriction of size, charge, and Debye thickness. The theoretical approach is based on the rigorous numerical evaluations of the fundamental transport and electrostatic equations of a soft particle. This particle consists of an impermeable hard-core component of radius a, and a permeable polyelectrolyte layer of thickness δ (Fig. 1). In their interfacial modeling, Duval et al. introduced the possibility of inhomogeneous distribution for the polymer segments within the polymeric shell (Fig. 1). This was done by considering a diffuse interface where the properties of the soft (“fuzzy”) layer gradually change from bulk polyelectrolyte to bulk electrolyte solution. The theoretical calculation of the electrophoretic mobility μ is done based on a consistent numerical evaluation of i), the electroosmotic velocity profile inside and outside the polymer fringe as governed by the Navier-Stokes equation, ii), the distribution of the local equilibrium electrostatic potential, as defined by the Poisson-Boltzmann equation (electrostatics) and, iii), the local variation of the electrochemical potential of the ionic species distributed in/around the particle due to polarization of the double layer by the externally applied field. Full details of the theory are available elsewhere (18–20). This theoretical approach for the electrokinetics of the so-called diffuse soft particles extends that originally developed by Ohshima (1), who derived various approximate analytical expressions for the mobility of a particle within restricted ranges of size, charge, and double layer thickness.

FIGURE 1.

Schematic representation of a soft particle, composed of a hard core of radius a and a permeable charged polyelectrolyte layer of thickness δ, moving with a velocity in an electrolyte subjected to direct-current electric field 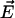. The polar coordinates 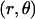are indicated. The electrophoretic mobility μ is defined as the ratio 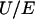. For the sake of illustration, a scheme of a soft diffuse interface is given. Within the scope of such interfacial modeling, the volumic density of polymer segments, noted φ, decreases from the value φ₀ in the bulk polymer layer to zero in the bulk electrolyte medium. The mathematical function chosen for describing the interface is , where α denotes the typical decay length of the polymer density across the interface (18). For α = 0, the model corresponds to that of a step function representation for the interface.

The bacteria investigated in our study may be assimilated to infinitely long cylinders with core radius a close to 500 nm whereas the thickness δ of the polymeric surface layer was estimated by electronic imagery (Table 1). For all bacterial strains examined within this article, the ratio surface layer thickness to core size indicates that the electrophoretic behavior of the various Shewanella strains is, at least for sufficiently large electrolyte concentrations (i.e., within the concentration range where the mobility hardly deviates from the high ionic strength plateau value), identical to that of a spherical particle with the dimensions and δ for the bare and permeable components (24). Given these considerations, we derived the relevant electrostatic and hydrodynamic parameters of the various Shewanella strains on the basis of the numerical theory recently developed by Duval et al (20) for the electrophoresis of spherical, charged soft particles. Within the ionic strength range where plateau mobility is approximately reached (i.e., for electrolyte concentration higher than, let's say, 50 mM), all bacteria investigated satisfy the conditions derived by Ohshima (24) that underlie the assimilation of the electrophoretic mobility of a cylinder to that of an equivalent spherical particle.

From the numerical theory aforementioned, the experimental mobilities were fitted using two unknown parameters determined by least-square method: i), the permeability parameter, denoted as λ₀, the quantity 1/λ₀ characterizing the typical flow penetration length within the soft polymeric layer, and ii), the volumic charge density ρ₀ of that layer. The computed results from the exact numerical theory reported in Duval et al. (18–20) were systematically compared with those obtained from the approximate analytical expression of Ohshima (1), written

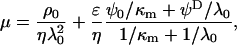(1)

where 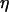and 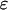represent the dynamic viscosity and dielectric permittivity of water, respectively, and 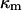the reciprocal Debye thickness of the soft layer surrounding the bacterium. is the surface potential, i.e., the potential at the position corresponding to the location of the outer boundary of the surface layer, and 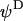the Donnan potential. 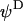is obtained from the balance in the bulk surface layer between charges stemming from the mobile ions and fixed ionogenic sites. 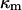, , 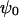and 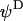may be obtained from the following expressions (1):

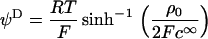(2)

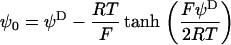(3)

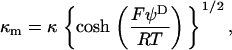(4)

with κ the classical reciprocal screening Debye length and 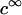the bulk concentration (ionic strength) of the 1:1 electrolyte considered. Equations 1–4 are valid within the limits 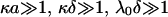, and low Donnan potentials for which the polarization of the double layer by the applied electric field is negligible. For the cases where 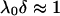or 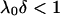, Eq. 1 becomes (18,20):

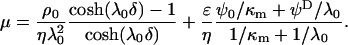(5)

RESULTS

EM distributions of single-strain bacterial population

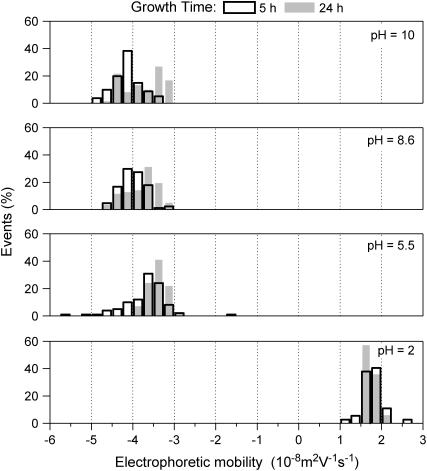
The electrophoretic mobilities of single-strain bacterial population were measured in solutions of different ionic strength and pH values. The experimental setup used for that purpose allowed the recording of the mobilities of the individual cells to quantify the mobility distribution on a statistical basis. The goal was to differentiate presumably heterogeneous subpopulations in the microbial cultures, as done in a previous work (25). In a first set of experiments, the effect of the bacterial growth time for the bacterial population (midexponential versus pseudostationary) on the EM distribution was examined for the different Shewanella strains. Fig. 2 illustrates the results of bacterial mobility for CN32 cells harvested after 5 and 24 h of growth in the midexponential and stationary phases, respectively. The typical pattern obtained for the mobility distribution indicates relatively monodisperse populations over the whole pH range investigated. No significant differences were observed for the EM during the growth phase (from midexponential to stationary phase). Standard deviations calculated from the electrophoregrams of Fig. 2 were in the ±0.3.10⁻⁸ m²V⁻¹s⁻¹ range, which is very acceptable for biological systems. Similar Dirac-like EM distributions were obtained for the S. oneidensis MR-4 when varying the total ionic strength of the suspension in the range 1–300 mM (not shown). In contrast, S. algae BrY clearly exhibited different subpopulations, as illustrated in Fig. 3. The larger the charge carried by the bacteria, i.e., the larger the deviation of the pH as compared to the isoelectric point (∼2), the easier the identification of the two subpopulations. From these distributions, mean values and standard deviations for the EM of the two respective subpopulations at different pH were calculated. In the following, those two subpopulations will be referred as BrY1 and BrY2.

FIGURE 2.

Distributions of the electrophoretic mobility measured for S. putrefaciens CN32 suspended in a 1 mM sodium nitrate solution at different pH values and two growth conditions before experimentation: extraction sampling 5 h for the midexponential phase and 24 h for the stationary phase.

FIGURE 3.

Distributions of the electrophoretic mobility measured for S. algae BrY suspended in a 1 mM sodium nitrate solution at different pH values.

EM of Shewanella spp.

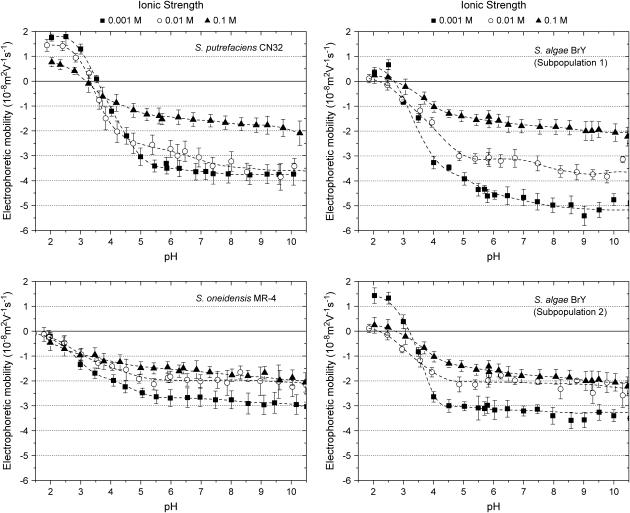
The electrophoretic mobilities of the various Shewanella strains investigated are reported in Fig. 4 as a function of pH and ionic strength of the electrolyte solution. For all strains, the EM values are negative over a wide range of pH values, as found for most bacterial cells. Regardless of the ionic strength value and the bacterial strain, the EM significantly decreases (in absolute value) when decreasing the pH solution, whereas in the pH range 5–10, the EM levels off. This feature indicates that the ionogenic sites of the Shewanella species are either partly or entirely (see Discussion below) responsible for the overall electrokinetic charge carried by the bacteria via sorption/desorption of protons, or and that they are fully deprotonated for pH above 5. For all bacterial strains examined, the isoelectric point (iep), defined as the pH of zero mobility, is found to be located below 3.5 (Table 2). Slight deviations of the iep values were observed when varying the ionic strength, possibly as the result of any specific structuration of the bacterial surface (26) or specific adsorption of ions onto the pristine charged sites. S. putrefaciens CN32 shows the highest iep value (close to 3.2) whereas S. oneidensis MR4 the lowest one (<2). The iep of the other Shewanella species ranged between these two limits. The same trend was observed for the point of zero salt effect (pzse) that corresponds to the crossover between the mobility curves measured for different ionic strengths (Table 2). These two characteristic points are very close, which indicates that specific ion adsorption is probably not predominant. However, intrinsic experimental error prevents from drawing a firm conclusion.

FIGURE 4.

Electrophoretic mobility of the various Shewanella strains investigated in this study as a function of pH and ionic strength of the electrolytic solution.

TABLE 2.

Summary of the relevant electrokinetic characteristics of the Shewanella strains studied

	Iep
Strain	0.001 M	0.01 M	0.1 M	Pzse
BrY	3.1	2.0	2.7	3.2–3.5
MR-4	<2	<2	<2	2.3–2.9
CN32	3.3	3.4	3.1	3.0–4.0

For all bacterial strains studied, the EM showed a dependence on ionic strength that is in agreement with the predictions expected from electrostatic double layer theory. When increasing the ionic strength, the EM decreases as the result of the screening of bacterial charge distributed throughout the wall and/or the polymer fringe. This feature is particularly marked in the pH range 5–10.

As intuitively expectedly, the nature of the bacteria investigated has also an influence on the magnitude of the EM. This is particularly clear from the mobility measurements carried out for sufficiently high ionic strength and pH values. In Fig. 5, comparison is made between the EM plateaus for the different bacterial strains as reached in the pH range 6–10 at a given electrolyte concentration (0.01 M). It appears that CN32 and BrY1 present higher EMs compared to those of BrY2 and MR-4. In the next section, the electrokinetic properties of the various bacterial strains, as reported in Figs. 2–5, are quantitatively analyzed to derive their electrohydrodynamic characteristics, which will be further discussed in relation with their surface structures.

FIGURE 5.

Comparison of the mobility plateaus reached at pH values from 5 to 10 for the various Shewanella strains and their respective populations. KNO₃ solution, ionic strength = 0.01 M.

Diffuse soft particle analysis of the EM

As a general rule, the EM of a soft particle differs from that of a hard (rigid) colloid in the sense that the EM reaches asymptotically a nonzero value for sufficiently high ionic strengths. This plateau is the specific signature of the presence of a soft, hydrodynamically permeable layer that surrounds the particle. From Eq. 5, one easily shows that in the high electrolyte concentration regime, the following relation

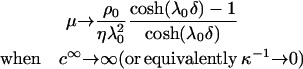(6)

applies. Reported in Figs. 6 and 7 are the experimentally determined EMs of the different investigated strains for different ionic strength levels and for a neutral pH value. The value pH 7 was considered because at that particular pH, EMs reach a constant value with respect to the pH variation, as shown in Fig. 4. For a given electrolyte concentration, the mobilities are higher (in magnitude) within that range of pH values (between 5 and 10) so that the corresponding analysis of the electrohydrodynamic properties are more accurate and are influenced to a lesser extent by the inherent experimental error. For all bacterial strains, the EMs reach a nonzero constant value upon increase of the ionic strength, in line with expectation from electrokinetic theory for soft particles. The data were subjected to the analytical (and approximate) theory by Ohshima (Eqs. 1–4) and to the numerical approach (no approximations regarding the size and the charge of the particle) developed by Duval et al. (18–20). The results are given in Figs. 6 and 7 together with the experimental data. As suggested by the comparison of the mobility plateaus reported in Fig. 5, two different behaviors were observed regarding the Shewanella species.

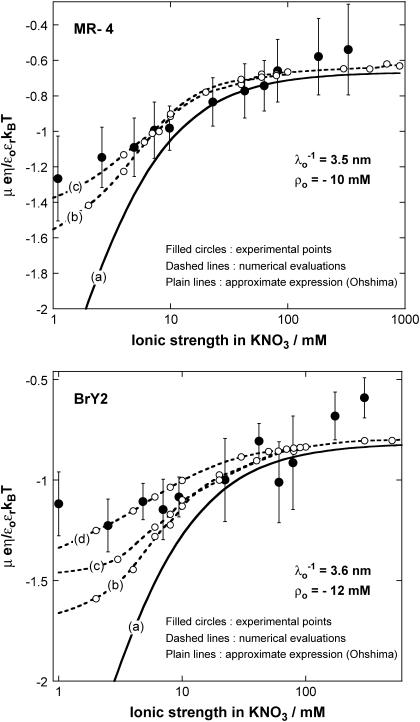
FIGURE 6.

Electrophoretic mobilities (expressed in dimensionless form) as a function of ionic strength (•) of S. oneidensis strain MR-4 (top panel) and of the subpopulation BrY2 of S. algae (bottom panel). The plain lines (curves a) correspond to the best fit calculated from the approximate expressions derived by Ohshima (Eqs. 1–4) (1) whereas the dashed lines (curves b to d) represent the rigorous numerical evaluations on the basis of the theory developed by Duval et al. (18,19). Those different approaches were computed with 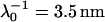, ρ₀ = −10 mM for MR-4, and 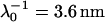, ρ₀ = −12 mM for BrY-2. Two different polymer shell thicknesses were considered in the numerical evaluations: δ = 60 nm for curves b, and δ = 90 nm for curves c. For BrY2, a diffuse interface representation of thickness α = 5 nm (see Fig. 1) is considered (curve d) to reproduce the possibility of inhomogeneous distribution of charges in the polymeric shell. The dashed lines are guide to the eye for the points (○) theoretically calculated.

FIGURE 7.

Electrophoretic mobilities as a function of ionic strength (•) of S. putrefaciens strain CN32 (top panel) and of the subpopulation BrY1 of S. algae (bottom panel). The plain lines correspond to the best fit calculated from the approximate expressions derived by Ohshima (Eqs. 1–5) (1) computed with 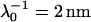, ρ₀ = −40 mM for CN32, and 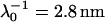, ρ₀ = −40 mM for BrY1. The curves (a) do not consider the size of the polymeric shell (Eq. 1) whereas curves b takes into account the shell thickness δ = 5 nm (Eq. 5). The dashed lines represent the rigorous numerical evaluations on the basis of the theory developed by Duval et al. (18,19) calculated with 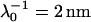, δ = 5 nm for CN32, and 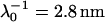, δ = 5 nm for BrY1. The curves (c) consider a fixed volumic charge density ρ₀ = −40 mM for CN32 and BrY1 whereas curves (d) were calculated after adjustment of the ρ₀ parameter with the electrolyte concentration (see text for further detail). The dashed lines are guide to the eye for the points (○) theoretically calculated.

For MR-4 and BrY2 (Fig. 6), the discrepancy between the experimental data (solid circle) and the results computed on the basis of the approximate expressions (curves a) increases significantly upon decrease of the ionic strength. This is due to the inaccuracy of Eqs. 1–4 to predict the EM at low ionic strength where i), the condition κδ ≫ 1 is not respected (the thickness of the polymer fringe is δ ∼ 100 nm and the reciprocal Debye length is κ⁻¹= 1–10 nm in the concentration range 100–1 mM), and ii), the polarization of the electric double layer (not taken into account in Eqs. 1–4), which acts as a breaking (retarding) force for the migration of the particle, starts to play a significant role. In contrast, the mobilities calculated from the rigorous numerical evaluations of the key electrokinetic equations (curves b, c, and d) better reproduce the data over the whole range of electrolyte concentration. It is important to note that iterative adjustment (by least-square methodology) of the softness parameter λ₀ and the volumic charge density ρ₀ yielded the same results for those two parameters in all theoretical cases considered. This is so because the analytical theory by Ohshima (1) constitutes the high electrolyte concentration-limit of the rigorous theory and because the EM plateau value is depending on λ₀ and ρ₀ only (see the first term in the right-hand side of Eq. 1).

The aforementioned numerical theory (Fig. 6, dashed lines) allows for considering different thicknesses of the permeable polyelectrolyte layer (fringe) with or without a diffuse interface. In the case of MR-4 strain, the increase of shell thickness from 60 nm (Fig. 6, top panel, curve b) to 90 nm (curve c) improves the description of the experimental data. For the BrY2 strain (Fig. 6, bottom), such adjustment failed slightly to reproduce satisfactorily the data especially at low ionic strengths (curves b and c). To improve this description, a diffuse interface was considered to introduce the possibility of inhomogeneous distribution for the polymer segments within the polymeric shell, and interfacial step function modeling (see Fig. 1) was abandoned. A typical decay length α of 5 nm was used to reasonably fit the experimental data (Fig. 6, bottom panel, curve d). Because of the significant inaccuracy of the experimental data as compared to the differences in computed EM when considering or not a diffuse interface, no hard conclusion regarding the respective inhomogeneity of the polymer fringes of the MR-4 and BrY2 can be done. However, the values obtained for the softness parameter and the volumic charge density unambiguously indicate that MR-4 and BrY2 cells present a fairly similar and large hydrodynamic permeability (3.5 and 3.6 nm) and are weakly charged (−10 and −12 mM).

For CN32 and BrY1 (Fig. 7), the analytical expressions given by Eq. 1 (curve a) and Eq. 5 (curve b) are clearly inadequate to account for the data mainly because the high volumic charge density carried by the bacteria is responsible for large local electrostatic potentials where analytical treatment of the electrokinetic equations is no longer acceptable. In passing, it is noted that the EM plateaus reached at high electrolyte concentrations are better reproduced by Eq. 5, which takes into account the finite thickness δ of the polymer fringe (the approximation 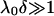clearly does not hold for CN32 and BrY1 bacteria). The value of δ = 5 nm was chosen for the calculation on the basis of the known and reported dimension of the wall thickness of gram-negative stain bacteria (9,27). As already mentioned, the expression by Ohshima (1) is strictly valid within a given range of charge (or potential), polyelectrolyte shell thickness, and Debye length. The description of the experimental data on the basis of the electrokinetic theory for soft spherical particles (numerical evaluation) remains poor, especially at low ionic strength levels (curve c). Besides the assumption that consists in assimilating the mobility of an infinitely long cylinder to that of a spherical particle, which is certainly questionable at low ionic strength levels, another pitfall in the analysis is that the volumic charge density is taken constant over the whole range of electrolyte concentrations. However, it is well established that ionic strength may strongly modify the volumic charge density and that this modification is intrinsically related to the magnitude of this charge. In other words, not only the chemistry (number and nature of ionogenic sites distributed throughout the bacterium wall) but also the electrostatics (magnitude of the charge and local electrostatic potential) mediate the intrinsic charge carried by the bacterium (28). Whereas for the weakly charged MR-4 and BrY2 bacterial strains the assumption of a constant ρ₀ when varying the electrolyte concentration seems reasonable, it clearly needs to be revisited for the highly charged CN32 and BrY1 strains. Consequently, the experimental EM for CN32 and BrY1 were fitted by considering adjustable ρ₀ at each ionic strength level (Fig. 7, curves d). The corresponding ρ₀ are given in Fig. 8 for the two types of cells. When lowering the ionic strength, the magnitude (in absolute value) of ρ₀ decreases in agreement with expectations from theory (28). In both cases, the softness parameters are significantly lower (2 and 2.8 nm) than that determined for the bacteria surrounded by a polymer fringe but is still characteristic of the presence of a permeable, soft layer, i.e., the bacterial wall itself.

FIGURE 8.

Plot of the volumic charge density ρ₀ used to fit the electrophoretic data pertaining to the BrY1 and CN32 cells (curves d of Fig. 7).

DISCUSSION

Microelectrophoresis has been long used to evaluate the surface charge of colloidal particles from electrophoretic mobility measurements. Clearly, the theoretical concepts developed for the electrophoresis of rigid particles (Smoluchowski-Henry equations, e.g., (29)) are not valid for deriving the electrostatic and hydrodynamic properties of biological systems (1). As a major difference, the notion of ζ-potential is, for such soft systems, unambiguously physically irrelevant because it is impossible to locate a priori the position of the slip plane within the hydrodynamically permeable soft corona surrounding the particle.

Fortunately, electrokinetic equations for soft particles have been derived and their recent numerical resolution allows the analysis of the electrophoretic migration of biological cells (30–35). However, the application of these models for bacterial cells is still sparse and difficult due, for example, to i), the possible heterogeneous character of microbial suspensions, and ii), the intricacy and diversity of surface ultrastructures of bacteria. In this study, the strains investigated have been chosen for their complementarities in terms of the presence or not of polymer fringe beyond the outer membrane (Table 1). Whereas the cell surfaces of CN32 are devoid of such surface appendage, those of MR-4 are covered by a polymeric shell. As far as the BrY strain is concerned, both phenotypes are present. These different and well-characterized bacterial phenotypes are very suitable for testing the interrelationship that exists between electrokinetic (i.e., electrophoretic) properties and bacterial surface structures.

As demonstrated in this article, the electrophoretic mobility distribution for a given microbial culture provides useful and key information related to its heterogeneous character. An illustrative example given here is the identification of two distinct subpopulations for the BrY strain, which is in line with previous observations of electronic micrographs (9) (Table 1). The two other strains investigated (CN32 and MR-4) depict a monodisperse pattern also consistent with electronic observations. Comparison of the electrophoretic mobility for the various Shewanella strains analyzed (particularly in the pH range 5–10, Fig. 5) indicates that the electrohydrodynamics of the bacteria is significantly influenced by the presence or not of a polymer fringe at the surface, the CN32 and BrY1 cells exhibiting larger mobility values than MR-4 and BrY2 cells. Since the presence of a polymer layer around the cell is intuitively expected to retard its migrative motion because of increasing electroosmotic drag (that is increasing friction forces), Fig. 5 suggests a priori that the first subpopulation of BrY strain (called BrY-1) is devoid of any polymeric appendage whereas the second one (BrY2) behaves as bacterial cells with polymer fringe. The presence or not of a fuzzy polymer layer around the bacterium has, apparently, also an impact on the iep values. Whereas the strain with polymer fringe (MR-4) exhibited values <2.5, the CN32 cells present an iep >3.1. Because of their heterogeneous character and since it is impossible to distinguish the BrY1 and BrY2 strains at low pH values, the effective iep for BrY lies in between the two aforementioned limits. As stated, the electrophoretic migration of a given bacterium is governed by a subtle balance between electrostatic processes, as the result of the presence of chemical groups within the cell wall or around the bacterium (9,26,36) and hydrodynamic processes.

To quantitatively identify the balance between these two contributions, approximate analytical and rigorous theoretical expressions were employed to analyze the electrophoretic mobility changes in response to ionic strength variation. Regardless of the equations used, the permeability parameter (λ₀) and the volumic charge density (ρ₀) obtained from the fitting procedure are the same for all different theoretical approaches considered. Whereas Eqs. 1–4 are inadequate to account for the data at low ionic strengths, rigorous theory seems to provide a better description at such ionic strength level even if it should be kept in mind that the assimilation of the bacteria to spheres at low ionic strength levels may become questionable. Since there is so far no available numerical and rigorous theory for the electrophoresis of soft cylinders, we discuss the results within the framework of the spherical geometry theory, which provides the accurate electrohydrodynamic parameters λ₀ and ρ₀ (basically computed from the analysis of the mobility data measured at high ionic strengths).

The values for λ₀ and ρ₀ obtained for the various bacterial strains are collected in Table 3. As a general comment, cells without a polymer fringe (i.e., CN32 and BrY1) exhibit a rather large volumic charge density and a relatively low hydrodynamic permeability as compared to cells that present such a fringe (i.e., MR-4, BrY2). In other words, the bacterium wall is more rigid (i.e., less permeable) and more charged than the bacterial material constituting the soft polymeric structure around the cell wall. It is thereby added that although the electrophoretic migration of CN32 and BrY1 is obviously determined by the electrohydrodynamic properties of the cell wall, that of MR-4 or BrY2 is solely caused by the outer soft layer (∼90 nm thickness) of the bacteria, the “slipping plane” (or the spatial zone of zero electroosmotic flow) being located well beyond the bacterial wall (we have λ₀δ ≫ 1). In other words, it is definitely correct to assign the λ₀ and ρ₀ values to the bacterial wall when referring to the analysis of the CN32 and BrY1 strains, and to the outer polymer fringe when dealing with the MR-4 and BrY2. Qualitatively, the respective electrostatic and hydrodynamic properties of the wall and polymer fringe of the—here studied—gram negative bacteria is in very good agreement with those obtained on bald and fibrillated oral streptococcal strains (28).

TABLE 3.

Summary of the volumic charge density (ρ₀) and the softness parameter (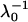) obtained from the best fitting procedure for the different strains investigated (Figs. 6 and 7)

Strain	Subpopulation	ρ0 (mM)	λ0−1 (nm)
CN32	–	−40	2
BrY	BrY1	−40	2.8
	BrY2	−12	3.6
MR-4	–	−10	3.5

Going further in the analysis, it is interesting to compare the volumic charge density obtained in the case of CN32 strain with that derived from the potentiometric titration performed by Sokolov et al. (37) on the same strain. Whereas the comparison is rendered difficult by the necessity to know accurately the number of bacteria present in the titration cell for estimating an apparent volumic charge density ρ₀, the exercise unambiguously reveals the following finding: the volumic charge density obtained from the titration data at 0.1 M ionic strength is estimated from ∼−0.2 to −15 M, which is about 1–2 orders of magnitude larger than the value obtained from the analysis of the electrophoretic mobility versus ionic strength curves. The significant discrepancy between the electrokinetic charge (as evaluated from electrophoresis) and the pristine charge (as measured by titration) has been for long observed for rigid colloids and very recently for soft bacteria (28). It principally originates from the accumulation of counterions in the bacterial cell wall as the result of electrostatic and specific adsorption processes. This leads to an effective charge, the electrokinetic charge, which is significantly lower than the pristine titrable charge. Results obtained in Duval et al. (28) for bald oral-streptococcal bacterial strain indicate that, depending on the pH and ionic strength conditions, the electrokinetic charge may represent only a few percent of the total charge measured by protolytic titration. This is well in qualitative agreement with the conclusions led out for the Shewanella CN32 bacteria of this study. Other reasons that possibly account for the difference between electrokinetic and titrable charges may be found by evoking the presence of metabolic processes of the bacteria that lead to a consumption of proton/hydroxide ions during the potentiometric titration without any protonation or deprotonation of the functional groups (proton pumping, exudation of organic acids. etc.). The occurrence of such processes has recently been emphasized by Claessens et al. (38).

Summarizing the preceding sections, the principal results of this study show the relationship that exists between the nature of the bacterium surface structure and its electrophoretic behavior. The presence of a polymer fringe confers the bacterium a relatively low electrokinetic charge density and a rather important hydrodynamic permeability. In the other situation, i.e., in the absence of any polymeric shell, the electrokinetic bacterial charge is largely increased due to ionization of functional groups located within the outer membrane and the permeable character significantly decreased.