Calcium Instabilities in Mammalian Cardiomyocyte Networks

Abstract

The degeneration of a regular heart rhythm into fibrillation (a chaotic or chaos-like sequence) can proceed via several classical routes described by nonlinear dynamics: period-doubling, quasiperiodicity, or intermittency. In this study, we experimentally examine one aspect of cardiac excitation dynamics, the long-term evolution of intracellular calcium signals in cultured cardiomyocyte networks subjected to increasingly faster pacing rates via field stimulation. In this spatially extended system, we observed alternans and higher-order periodicities, extra beats, and skipped beats or blocks. Calcium instabilities evolved nonmonotonically with the prevalence of phase-locking or Wenckebach rhythm, low-frequency magnitude modulations (signature of quasiperiodicity), and switches between patterns with occasional bursts (signature of intermittency), but period-doubling bifurcations were rare. Six ventricular-fibrillation-resembling episodes were pace-induced, for which significantly higher complexity was confirmed by approximate entropy calculations. The progressive destabilization of the heart rhythm by coexistent frequencies, seen in this study, can be related to theoretically predicted competition of control variables (voltage and calcium) at the single-cell level, or to competition of excitation and recovery at the cell network level. Optical maps of the response revealed multiple local spatiotemporal patterns, and the emergence of longer-period global rhythms as a result of wavebreak-induced reentries.

INTRODUCTION

Instabilities in cardiac repolarization, known as T-wave alternans (TWA) in the electrocardiogram, are observed in a variety of pathological conditions, and can be used as predictors of arrhythmic events (1,2). Previous findings that action potential duration (APD) can alternate in single cardiac cells confirmed TWA's cellular-level origin (3). Recently, compelling experimental and modeling evidence demonstrated that APD and TWA not only may reflect abnormalities in repolarizing ionic currents, but may directly stem from alternations in intracellular calcium cycling, or be closely linked to calcium-related processes. Supporting evidence includes: inhibition of APD alternans by decreasing L-type calcium-current magnitude or calcium-induced inactivation in a computer model (4) and elevation of the threshold for APD alternans by calcium chelation (5). Additionally, small-scale oscillations in the sarcoplasmic reticulum load were proposed as a possible mechanism in the generation of cell-level alternans (6); moreover, calcium alternans were shown to persist in action potential clamp conditions both in computer models and experiments (7,8). Overall, the important role of intracellular calcium ([Ca²⁺]_i) dynamics in the onset and evolution of cardiac instabilities makes calcium signals a natural choice for mechanistic studies of cardiac rhythm destabilization.

Experimentally, instabilities in calcium handling, known as alternans, usually refer to beat-to-beat alternations (large-small) in the magnitude of the calcium transients. They have been examined at the tissue level (9–12) and at the subcellular level (6,13) using fluorescent indicators. Constant-magnitude alternans by themselves can persist for a long time without necessarily deteriorating into highly complex arrhythmias, thereby presenting an indirect indicator of possible arrhythmogenesis. An interesting question is how exactly further destabilization of the alternans occurs, and which route toward chaotic or chaos-like signals, as observed, for example, in ventricular fibrillation, is followed. At least three classical routes to chaos have been outlined previously in nonlinear dynamics theory: period-doubling, intermittency, and quasiperiodicity (14). Each of these local bifurcation paths can reveal information about the system and the mechanisms leading to its destabilization.

There is a dearth of experimental evidence for the evolution of calcium dynamics into higher-order rhythms (beside constant-magnitude alternans) despite predictions of theoretical models for such rich dynamic behavior. Due to technical difficulties with fluorescent measurements using calcium-sensitive probes (e.g., photobleaching and mechanical movement), long-term calcium dynamics is an under-studied and not well understood process. This study explores the temporal evolution of instabilities in intracellular calcium at the cellular level while cells are in their natural (cell-network) environment. In contrast to previous reports, the measurements are done in 1), an externally stimulated (nonoscillating) and 2), a spatially extended (nonclamped) system, with measurement sites at least several space constants away from the electrodes. The experimental model, anisotropic cultured cardiomyocyte networks on elastic microgrooved surfaces (15), was previously reported to operate in a wider dynamic range of calcium handling (16), i.e., exhibiting larger systolic calcium levels, a faster rise in diastolic calcium with rapid pacing, etc. This wider dynamic range is expected to facilitate the observation of richer calcium dynamics. In this study, we use long-term calcium recordings and nonlinear dynamics analysis to address the following questions: 1), What routes does temporal evolution of calcium instabilities follow? 2), Can a multicellular monolayer model system exhibit complex fibrillation-like behavior with no discernable temporal patterns? and 3), How does the evolution of local dynamics relate to the global response and the propagation patterns in spatially extended tissue?

MATERIALS AND METHODS

Experimental model and stimulation conditions

The protocol of primary cardiomyocyte culture has been documented previously (15). Briefly, the ventricles of the hearts of 3-day-old Sprague-Dawley rats were digested enzymatically using trypsin and collagenase, cardiomyocytes were collected after centrifugation and preplating, and the cardiomyocytes were seeded on fibronectin-coated, microgrooved polydimethylsiloxane scaffolds (0.8 × 1 cm in size) at a high density of 0.4 × 10⁶ cells/cm². Cell constructs were kept in Medium 199 at 37°C. Polydimethylsiloxane was molded out of metal templates designed using acoustic micromachining (17) to enforce anisotropy. Spatial optical mapping confirmed connectedness and wave propagation across the samples (15).

Calcium measurements were performed at days 4–6 after culturing. Rectangular samples (1.2 × 0.8 cm) were perfused with Tyrode's solution at 30 ± 2°C. Electrical field stimulation was applied with 5-ms bipolar pulses delivered through embedded platinum electrodes in the sides of the chamber, parallel to the longer scaffold sides and to the direction of anisotropy. The strength of the field was 5–10 V/cm, guaranteeing field strengths at least two times the threshold for stimulation, which was 2–3 V/cm at 1-Hz pacing. The frequency of pacing was varied in the range 0.5–9 Hz.

Local intracellular calcium measurements in cardiomyocyte networks

Intracellular calcium levels were determined locally using a Fura-2 ratiometric fluorescence measurement technique, as described previously (15,16). The imaged area was restricted by a mechanical aperture to ∼200 × 100-μm area in the central portion of the scaffold. Reduced-excitation light and high-sensitivity detector (photomultiplier tube (PMT), Electron Tubes Ltd., Middlesex, UK) allowed for continuous exposure and recordings without apparent signs of photobleaching and toxicity. In a subset of samples, cells were colabeled with di-8-ANEPPS and Fura-2. Colocalized, sequential-in-time measurements of voltage and calcium were then performed only for patterns stable over time. Temporal markers (stimulus timing) were used to relate voltage and calcium response.

Spatial optical maps of propagation

In a subset of samples (n = 4), spatial optical mapping was performed to uncover 1), the patterns of direct polarization during electrical field stimulation at various field strengths; and 2), the spatiotemporal patterns at the induction and evolution of instabilities. We applied ultra-high-resolution imaging with an intensified camera system (CMOS, 1280 × 1024 pixels, Cooke, Romulus, MI), using temporal resolution of 200 frames/s and spatial resolution of 20 μm/pixel. Data processing of the raw unbinned data included subtraction of baseline fluorescence, temporal Savitzky-Golay filter (width 7, order 2) and a spatial Gaussian filter with 5-pixel kernel. Color maps of propagation were generated from the original images by converting intensity into phase values using the Hilbert transform (18); wavefront was tracked by a black line. Activation maps were generated by calculating times of activation (maximum slope) for each pixel and displaying contour maps of isochrones. Sequences of frames were combined in movies with playback at four-times-slower speed. Movies are made available as supplemental on-line information.

Data processing and analysis of temporal patterns

All data processing and analysis was automated using a custom-developed program written in MatLab 7 (The MathWorks, Natick, MA). The raw experimental data from the PMT recordings were filtered using Savitzky-Golay filter (width 31, order 2). Calcium systolic levels were determined using peak height of calcium transients with respect to the preceding diastolic levels (at the foot of the transient). The latter was automatically detected by analyzing time-shifted versions of the original signal. In the case of fibrillation-like data, peak detection was manually confirmed due to the high irregularity in the signals. In this study, >20,000 PMT recordings of calcium transients were analyzed.

Classification of instability patterns

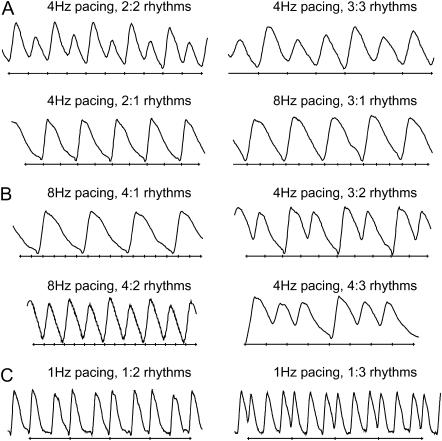
The patterns of intracellular calcium dynamics were defined as N:M rhythms, where M calcium transients are recorded in response to N external stimuli. The data were classified into three categories (Fig. 1, A–C):

• a. N = M > 1 alternans or higher-order periodicities, e.g., 2:2 and 3:3 rhythms.

• b. N > M skipped beats or blocks, e.g., 2:1, 3:1, 3:2, 4:1, 4:2, and 4:3 rhythms (including Wenckebach (N + 1):N patterns).

• c. N < M extra beats, e.g., 1:2 and 1:3 rhythms.

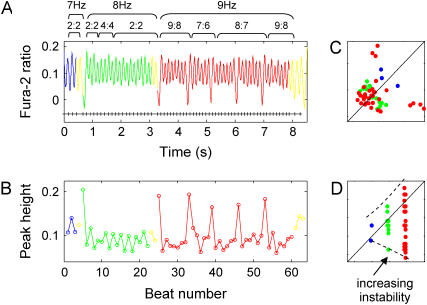
FIGURE 1.

Calcium instability patterns. (A) Alternans and higher-order periodicity (N = M > 1): 2:2 and 3:3 rhythms are shown. (B) Skipped beats and blocks (N > M): 2:1, 3:1, 4:1, 4:2, 3:2, and 4:3 rhythms are shown. (C) Extra beats (N < M): 1:2 and 1:3 responses are shown. External stimuli marks are plotted below the calcium transients.

Only patterns that appeared at least twice contiguously were classified as a pattern. In the text, we treat longer-period rhythms (higher N and M) or rhythms with a larger difference between N and M as more “complex”. Furthermore, we use the terms “monotonic” or “nonmonotonic” switch of patterns to define progressively increasing (or decreasing) complexity in time (monotonic) or a combination of decrease and increase in complexity with time (nonmonotonic).

Poincaré and frequency maps

Poincaré maps are a classical tool in nonlinear dynamics for determining whether a system is deterministic or random by plotting current value of a state variable against its previous value (14). A discernable pattern in the Poincaré plot is formed for a deterministic system in contrast to a formless space-filling structure in a random system. One-to-one response and purely periodic signals appear as tight clusters. Poincaré maps were constructed by plotting peak height value of a calcium transient, p(n), against the peak value of the previous transient, p(n − 1).

Frequency maps are an alternative representation, displaying how well cells respond to external pacing, by relating stimulation frequency (x axis) and response rate (y axis). In general, points on the diagonal of the frequency map refer to normal 1:1 response or alternans (N = M), whereas points falling in the region to the left of the diagonal are associated with extra beats (N < M), and points to the right represent skipped beats/block (N > M) (Fig. 2). A greater distance from the diagonal reflects higher instabilities or failure to externally control the system. In some cases, different frequencies were color-coded for better tracking of the calcium response in the phase and frequency plane.

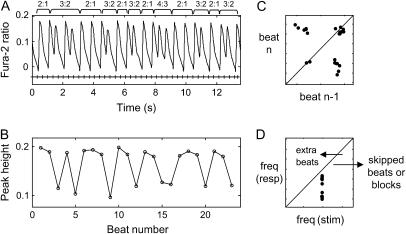
FIGURE 2.

Wenckebach calcium rhythms. (A) Contiguous episode of mixed 3:2, 4:3, and 2:1 rhythms. (B) Calcium peak-height variations from beat to beat. (C) Poincaré map. (D) Frequency map. All points fell in the region to the right of the diagonal, indicating the existence of skipped beats/blocks.

Short-time Fourier transform

Short-time Fourier transform (STFT) is a signal processing technique for time-variant spectral analysis (19). In contrast to traditional fast Fourier transform (FFT), STFT takes into consideration the time variations in the signal and partitions it into a series of time segments by applying a window function for the application of FFT. A Hamming window was chosen here. STFT can be mathematically expressed as follows:

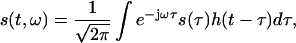(1)

where 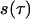is a signal in the time domain, 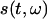is the FFT time-dependent spectrum, and 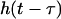is the window function.

In this study, STFT was performed on data from both original calcium transients and peak systolic levels (one value per period) for pattern detection. In the former case, the dynamics of the instability patterns was examined in the frequency domain. For example, two frequency bands in the STFT plot usually imply the occurrence of 2:2 alternans in the original signal. The second application of STFT was targeting the detection of patterns and slow modulation embedded in ventricular-fibrillation (VF)-like calcium signals. Systolic calcium levels (one point per transient) were used in this case instead of the original signals. Since calcium peak height values are not equally sampled in the time domain due to changing oscillation rate, the output of the STFT was expressed as normalized periodicity (beats⁻¹) with beat number instead of frequency with time. This analysis approach was found to be superior in pattern detection.

Approximate entropy as a complexity measure

The approximate entropy (ApEn) has been used as a measure of system complexity (20). A low value of ApEn usually reflects predictability and regularity in a system, whereas a high value indicates disorder and randomness in a system. We found this complexity measure to be more practically applicable (than traditionally used Lyapunov exponents, for example) considering the typical length of the recorded calcium signals. The parameters in the ApEn calculations were adopted from previous heart-rate variability studies: filter factor r was set to 20% of the standard deviation (SD) of the original data, with an embedded dimension m of 2 and a time lag τ of 1 applied. Paired t-test was used for statistical analysis.

RESULTS AND DISCUSSION

Temporal dynamics of calcium instabilities in response to external pacing

To investigate the time evolution of calcium instability patterns in anisotropic samples, a total of 42 long episodes (>1 min) under external pacing were examined. No artifacts from photobleaching in the signals of interest (transient magnitude) were registered for the durations used here. Two modes of external stimulation were employed. First, to examine whether the induced patterns are stable over time or undergo further changes, the pacing frequency was increased to the point at which instabilities were registered and maintained for the duration of recording. Second, the frequency was increased progressively to examine the dynamics beyond the threshold for induction of alternans. For a subset of samples, fast pacing was found to induce nondriven activity. We used stimulation at higher voltages to attempt effective cardioversion (recovery of controlled regular rhythm) in these cases. Spontaneously beating cultures were generally not included, unless overdrive pacing was successful at relatively low frequencies. This resulted in N:M patterns with N < M at an average frequency less than or around 1 Hz, with one exception (Table 1).

TABLE 1.

Diversity and incidence of calcium instability patterns

N:M	1	2	3	4	5	6	7	8
1		27	7	1
		0.8 ± 0.1 Hz	0.9 ± 0.1 Hz	0.5 Hz
2	47	35	7		3
	3.4 ± 0.2 Hz	3.9 ± 0.3 Hz	1.1 ± 0.2 Hz		0.8 ± 0.2 Hz
3	8	18	6	1
	6 ± 1 Hz	2.8 ± 0.2 Hz	2.3 ± 0.4 Hz	3 Hz
4	4	1	7
	6 ± 1.7 Hz	8 Hz	3 ± 0.4 Hz
5				6
				3.5 ± 0.2 Hz
6		1			2	1
		3 Hz			3 Hz	4 Hz
7						3	1
						5 ± 2 Hz	4 Hz
8							1
							9 Hz
9				1				1
				3 Hz				9 Hz

Diagonal terms, represented in regular roman type, indicate N = M > 1 patterns of alternans and higher-order periodicities; terms represented in italic type indicate extra beats (N < M); terms represented in bold print indicate skipped beats and blocks (N > M). Numbers in the corresponding cells indicate the number of observations and the average stimulation frequency at which the patterns were observed.

It was expected that higher rhythm complexity in calcium dynamics would follow one or more of the following classical paths of local bifurcation: period-doubling, intermittency, and quasiperiodicity. They can be distinguished by “local” (Poincaré map) analysis of the structure of state space. In contrast, global bifurcations (such as crises) require tracking the behavior of the system over a considerable portion of the state space, analyzing the evolution and interaction between local structures. In crises, an attractor suddenly disappears or changes size, and this is thought to result from collision between the attractor and an unstable fixed point or unstable limit cycle (14). In experimental systems, crises can be precipitated by the presence of noise (21,22), and in our system they are likely to occur due to coarse frequency stepping. Our analysis did not include tracking the size of attractors over long periods of time; thus, the crisis-based route to chaos remains beyond the scope of this study.

Typical period-doubling, where the pattern changes from 1:1 to 2:2, 4:4, 8:8, etc., has been the focus of multiple studies dealing with repolarization APD alternans (23–25). Intermittency transition to chaos is seen when the system's behavior switches between two qualitatively different states at constant control parameters of the system, as, for example, shown in simulations with the Lorenz model (14). This route has been demonstrated previously in a computer model of calcium oscillations (26). In contrast, skipped beats and blocks including Wenckebach-like rhythms (Figs. 1 and 2) are believed to be the outcomes of phase-locking (27), where two independent frequencies lock into a rational ratio, e.g., 1:2, 3:2, 3:4, etc. (14). When the ratio between the two underlying frequencies becomes irrational, quasiperiodicity emerges (14). In an experimental setting, with a finite precision in the computer-acquired signals, it is impossible to differentiate between rational and irrational ratios; therefore, we used a surrogate measure for quasiperiodicity, such as the presence of distinct structures in the Poincaré maps (28). The interaction between extrinsic and intrinsic pacing, or the competition between two control processes at incommensurate frequencies can induce oscillation at one frequency that is amplitude-modulated at another frequency, as demonstrated below in examples of quasiperiodicity.

To examine the stability of alternans over time, we maintained the same pacing frequency at the threshold at which alternans were observed in 29 cultures. In 21 episodes (72%), dynamically changing N:M instability patterns were registered, whereas in eight episodes (28%) the N:M patterns persisted but the magnitude varied (effective low-frequency modulation). From the eight persisting stable N:M patterns under constant pacing frequency, a majority (six cases) showed nonmonotonic low-frequency oscillations in magnitude, whereas two cases had a monotonic decrease (“damping”) in instability magnitude and transition to blocks. As shown in Fig. 3, A–C, the amplitude of 2:2 alternans decreased monotonically with time at 4-Hz pacing, confirmed also in the frequency domain (3D STFT plot), where the energy of the 2-Hz component increased while the energy of the dominant 4-Hz component was decreasing, indicating gradual disappearance of 2:2 alternans and the emergence of a 2:1 block. In contrast, in Fig. 3, D–F, a more readily observed case of quasiperiodicity is shown, where nonmonotonic variation in peak height of 2:2 alternans at 3-Hz pacing resulted in a shift of energy peaks between 3- and 1.5-Hz components in the STFT plot. It was also noticed that a burst of 3:3 alternans (intermittency episode) occurred in the interval dominated by 2:2 alternans. Low-frequency modulations and bursts of patterns were often observed in our experiments. Episodes having nonmonotonic change in patterns at a constant pacing rate also support the possible existence of intermittency (Fig. 4) in calcium dynamics.

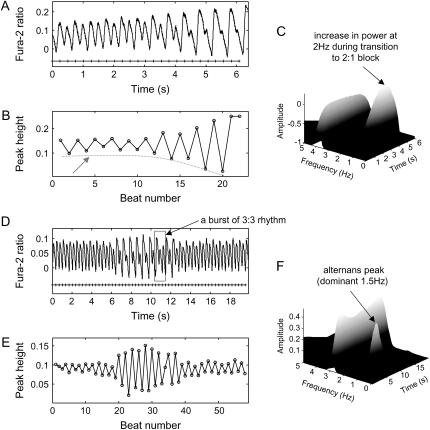
FIGURE 3.

Modulation of alternans magnitude under constant pacing frequency. (A) During 4-Hz pacing, 2:2 alternans gradually disappeared with the emergence of a 2:1 block; (B) A plot of peak-height values against beat number (dashed red line follows alternans magnitude). (C) STFT plot showing the energy of the 2-Hz component increasing as the energy of the 4-Hz component is decreasing. (D) During 3-Hz pacing in another sample, the magnitude of 2:2 alternans changed nonmonotonically, and a burst of 3:3 alternans was also observed. (E) A plot of peak-height values against beat number, indicating the existence of a slow modulation. (F) STFT plot: the energy magnitudes of 3 and 1.5 Hz alternated.

FIGURE 4.

Pattern transitions under constant pacing frequency. (A) During 4-Hz pacing, Wenckebach 4:3 and 3:2 rhythms alternated and eventually switched completely to a 2:1 block. (B) A plot of calcium peak-height values against beat number. (C) Poincaré map. (D) Frequency map. (E) During 3-Hz pacing in another sample, a switch between 2:2, 1:1, 3:3, and 4:4 rhythms occurred. (F) A plot of calcium peak-height values against beat number. (G) Poincaré map. (H) Frequency map.

Of the dynamically changing N:M patterns, 13 cases (62%) exhibited a nonmonotonic switch between patterns of different complexity, seven cases (33%) transitioned from alternans or skipped beats to blocks, and only one case transitioned from blocks to skipped beats or alternans. For example, as shown in Fig. 4, A–D, when paced at 4 Hz, 4:3 rhythms alternated with 3:2 rhythms but eventually switched completely to 2:1 blocks, whereas in Fig. 4, E–H, instability patterns varied spontaneously between 1:1 response, 2:2, 3:3, and 4:4 alternans while pacing was maintained at 3 Hz.

In a second set of experiments, we examined the effect of further increase in external pacing rate beyond the threshold for alternans. When progressively increasing the pacing frequency in 13 samples, nine episodes (70%) exhibited transitions from alternans or Wenckebach-like rhythms to blocks, and four episodes (30%) had a monotonic increase in the order of complexity. This latter case is illustrated in Fig. 5, where increasing the pacing frequency from 7 to 8 Hz maintained 2:2 alternans with a transient 4:4 rhythm; when further increasing the pacing rate to 9 Hz, complex Wenckebach patterns (9:8, 7:6, and 8:7 rhythms) completely replaced the 2:2 alternans. Accordingly, the frequency map shows a funnel-like pattern of the increasing complexity as frequency of stimulation increases. Overall, nonmonotonic behavior or divergence of the instabilities was prevalent.

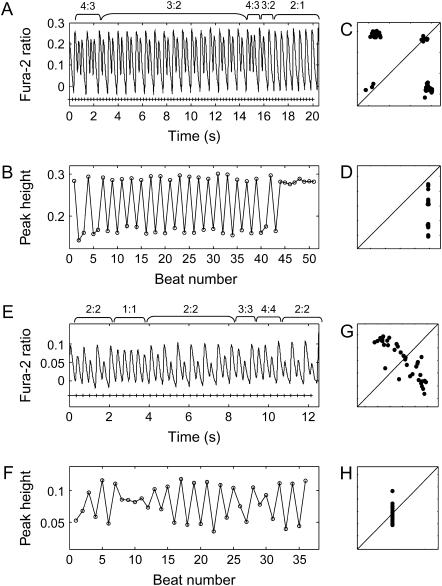
FIGURE 5.

Increase in complexity when gradually increasing external pacing frequency. (A) A transient 4:4 alternans appeared in between the 2:2 alternans when increasing the pacing rate from 7 Hz to 8 Hz. More complex patterns including 9:8, 7:6, and 8:7 rhythms completely replaced 2:2 alternans at 9-Hz pacing. (B) A plot of calcium peak-height values against beat number. (C) Poincaré map demonstrating wide scatter. (D) Frequency responses forming a funnel-like pattern as the pacing rate increases.

Classical period-doubling cascade in our experimental recordings was rare. This might indicate a subtle difference in the dynamics of calcium versus voltage and a certain degree of uncoupling between the two, or could be a result of our approach to analyzing the traces. More specifically, our summary of calcium patterns was a relatively conservative estimate, where only those rhythms present at least twice in a row were taken into account as a pattern. For example, as shown in Fig. 4, a 4:4 pattern did exist as a transient event, but was not included in the summary (Table 1). Therefore, the incidence and category of calcium patterns could be underestimated due to the stringent criterion. In addition, the increments in external stimulation rate were rather coarse, which might obscure possible bifurcations. Further reasons for not seeing period-doubling cascades are discussed below in conjunction with the stimulation conditions. Quasiperiodicity and intermittency periods in calcium dynamics were much more prevalent, both while maintaining external frequency at the alternans threshold level and when the system was further perturbed into more complex patterns.

Calcium instabilities and VF-like episodes

We asked the question whether pacing-triggered instabilities in calcium dynamics in our cardiomyocyte networks ever reach the level of fibrillation-like sequence without a discernable pattern. A total of six sustained (>20 s) VF-like episodes were registered, typically triggered by rapid external pacing. In two of these episodes a very slow frequency modulation was observed, one episode demonstrated bursts of irregular behavior in between 1:1 responses, two episodes exhibited abrupt acceleration of rate and decrease in peak height, and the remaining one case exhibited no distinct pattern.

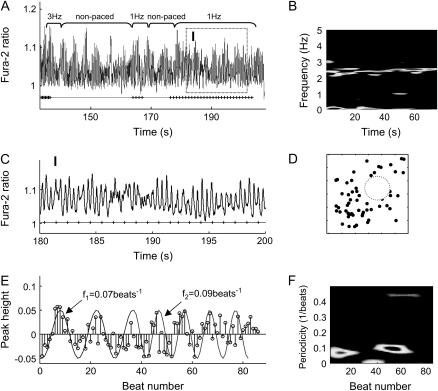
As shown in Fig. 6, after a short period of 3-Hz pacing, cells exhibited a very irregular rhythm around 2.5 Hz (see STFT performed on the original calcium transients over a 70-s interval (Fig. 6 B)) in the absence of external stimulation as well as during attempted low-magnitude (5 V/cm) 1-Hz pacing (magnified in zone I (Fig. 6 C)). A stem plot of zero-baseline peak-height signals from zone I revealed the existence of slow modulations (Fig. 6 E), which were confirmed by STFT performed on peak-height signals (one value per period) (Fig. 6 F). The low-frequency modulation switched from 0.07 beats⁻¹ to 0.09 beats⁻¹ during the recording period, whereas the Poincaré map exhibited space-filling properties with a possible central hole, enhanced with a dotted-line circle in Fig. 6 D. We tested whether these low-frequency modulations might be due to inherent noise in the measurements rather than being the result of competing processes with incommensurate frequencies. A 1:1 response signal at a comparable pacing rate (3 Hz) and level of noise was recorded and analyzed. The root mean-square (RMS) of noise was found to be an order of magnitude lower (0.0059 in this case versus 0.05 peak deviations in Fig. 6 D). The negligible contribution of noise to low-frequency modulations seen in the 1:1 signal corroborated the existence of true frequency modulations in this VF-like episode. Additionally, high-frequency pacing sometimes triggered spontaneous VF-like activity (Fig. 7 A). This episode was represented with a hollow-core Poincaré map again revealing quasiperiodicity-consistent behavior for nonpaced activity (Fig. 7 F). In this recording, a successful termination of the disorganized activity (effective cardioversion) was achieved by a 13-V/cm electric field stimulation (zone II).

FIGURE 6.

VF-like signals with low-frequency modulation. (A) Cells exhibited irregular oscillation at ∼2.5 Hz as shown in (B) STFT on original recording. (C) Magnified version of zone I. (D) A central hollow structure was seen in the Poincaré map. (E) Stem plot of calcium peak-height values from zone I, with superimposed two simulated envelope curves at 0.07 beat⁻¹ and 0.09 beat⁻¹, indicating the existence of low-frequency modulations. (F) STFT on peak-height values confirms the time low-frequency modulations.

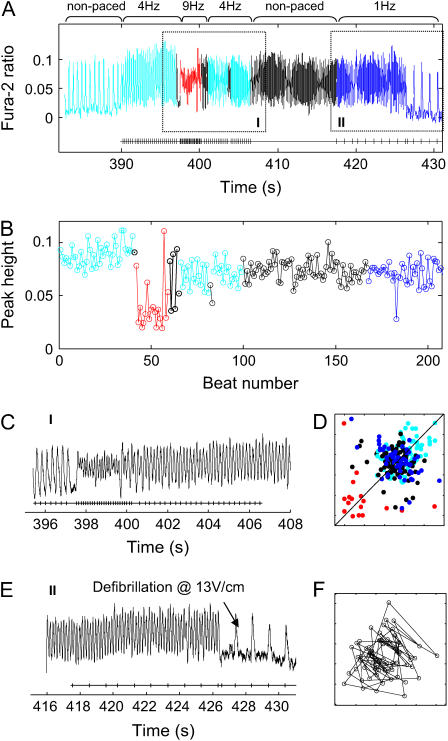
FIGURE 7.

VF-like signals showing quasiperiodicity followed by defibrillation. (A) Entire recording shown with two zones magnified for better illustration. Acceleration of the signal is shown in zone I, which persists during the stop of external stimulation. In zone II, a cardioversion is shown using 13 V/cm electric field pulses at 1 Hz. (B) A plot of peak-height values against beat number for the entire period in A. (C) Zone I magnified. (D) Poincaré map of peak-height values from the entire episode. (E) Zone II magnified. (F) Poincaré map of peak-height values from the nonpaced region, demonstrating the presence of a central hole, typical for quasiperiodic signals.

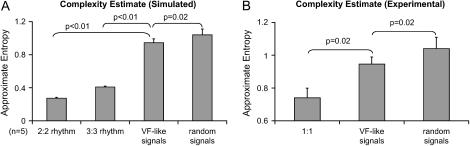
An interesting question is whether the complexity of these VF-like calcium recordings is quantifiably higher than the complexity in our other results with complex yet distinctive patterns. To address this question, approximate entropy values were computed to quantify the system's complexity. As shown in Fig. 8, the VF-like recordings had higher complexity (p < 0.001) than a simulated periodic signal with noise (simulated 2:2, 3:3 alternans with 20% additive Gaussian noise), but were also different from a purely random system (p < 0.02). Comparison of ApEn values in experimental signals confirmed a difference between pattern-exhibiting and VF-like recordings in the presence of similar levels of noise (p < 0.02). We attempted calculation of Lyapunov exponents (positive value of maximum exponents would have confirmed chaotic behavior), but failed due to lack of sufficient data length. Qualitative Poincaré maps demonstrating distinct structures (central holes) and quantitatively lower ApEn value compared to a random system (Fig. 8) supported the idea that the VF-like calcium traces most likely exhibit higher dimension deterministic chaos, in agreement with previous theoretical and experimental studies of electrical cardiac signals (28–31). The data presented here constitute one of the first examples of quantifiable VF-like behavior in a thin (<100-μm), “healthy” (nonischemic or treated), and nonoscillating mammalian cardiac preparation, but ultimately a spatially resolved mapping is needed to further ponder the underlying mechanisms. Previous experimental studies in a similar cultured cell model system have demonstrated wavebreaks and highly irregular rhythms (32–36). This behavior was not externally stimulated but evolved spontaneously in self-oscillatory cell networks. It was quantified and linked to cell density and cell coupling (36) or attributed to local structural heterogeneities (35).

FIGURE 8.

Approximate entropy of VF-like signals. (A) ApEn computed for the six episodes of VF-like signals was significantly higher than the ApEn values of simulated 2:2 and 3:3 alternans with 20% Gaussian noise and same length (p < 0.01), but differed from purely random signals (p < 0.02). (B) The ApEn value of experimental signals at a similar noise level and 1:1 response was significantly lower than the value of VF-like signals (p < 0.02), confirming the obvious difference between signals with discernable pattern and our VF-like signals.

Although several lines of evidence confirmed the existence of different routes to chaos in our system, most of the instability patterns did not directly result in fibrillation. Of the episodes, 70% had a general transition from other patterns to blocks when pacing frequency was changed. Previously, it was found that APD alternans evolved into 2:1 blocks instead of turning into more complex rhythms when structural obstacles were present (37). The particular topography (microgrooves) used to grow highly anisotropic cell networks might have presented periodic change of connectivity (across the grooves), thus providing the equivalent of structural obstacles to stabilize the propagating waves.

Links of quasiperiodicity to internal V_m-[Ca²⁺]_i coupling

Can the observed calcium dynamics be instructive of the properties of the system? Recent theoretical models have examined the interaction between transmembrane voltage (V_m) and [Ca²⁺]_i as competing control variables within a single cell. Shiferaw et al. (38) predict that the mode of V_m-[Ca²⁺]_i interaction/coupling can dictate the instability dynamics of the system. The regime of coupling, outlined in this model, depends on inherent ionic mechanisms, linking calcium processes to voltage changes, including the calcium-induced inactivation of the L-type calcium current, and the degree of contribution of the sodium-calcium exchanger. For example, if V_m and [Ca²⁺]_i are linked by negative coupling, a single cell is capable of exhibiting four different dynamics modes, namely: 1:1 response, concordant (in-phase) V_m-[Ca²⁺]_i alternans, discordant (out-of-phase) V_m-[Ca²⁺]_i alternans, and even quasiperiodicity as a single-cell phenomenon (38). In conditions of positive V_m-[Ca²⁺]_i coupling, the expected cardiac excitation dynamics is simpler: only 1:1 response and concordant V_m-[Ca²⁺]_i alternans are predicted by the theoretical model.

Our experimental results showed low-frequency modulations in alternans magnitude in six episodes of paced activity, such as in Fig. 3, as well as in two episodes of high complexity (VF-like episodes) (Figs. 6 and 7) with hollow cores in the Poincaré maps. This behavior is indicative of the presence of incommensurate frequencies in the system, or quasiperiodicity. To directly test whether negative V_m-[Ca²⁺]_i coupling might be the driving force behind prevalent quasiperiodic dynamics in our experimental model, we double-labeled a subset of samples (n = 9) to record transmembrane voltage and calcium in the same cells during pacing-driven stable alternans patterns. Depending on applied frequency, this experiment yielded regions of stable 1:1 response, concordant (in-phase) V_m-[Ca²⁺]_i alternans, and quasiperiodicity; discordant V_m-[Ca²⁺]_i alternans was observed only once (the same sample exhibited both concordant and discordant alternans within a different pacing context). Hence, we concluded that our data are highly suggestive of, but not proving, cellular origin of quasiperiodicity via negative V_m-[Ca²⁺]_i coupling.

Alternative explanations for the quasiperiodicity include at least four multicellular mechanisms. One example is modulated parasystole (39), that is, the coexistence of ectopic ventricular rhythm with the sinus rhythm, or, in the context of our experiments, ectopic site(s) along with the external pacing. Another multicellular mechanism includes meandering spiral waves (28,40–42), which can also appear as magnitude-modulated signals. Both of these (ectopic sites or meandering waves) had to be induced by fast pacing and had to persist through further external pacing. Additional possibilities for quasiperiodic behavior include processes driven by conduction velocity restitution, when a circular path (ring of tissue) permits wavefront-wavetail interactions of a self-sustained wave (43,44) or when regions of spatially discordant alternans form and their borders drift with respect to the pacing site (45).

Our data were obtained from a single location within a well coupled cell network (lacking macroscopic obstacles) externally paced via electric field stimulation, where modulated parasystole and quasiperiodicity in a ring are less likely. An unperturbed meandering spiral and discordant alternans caused by conduction velocity restitution will be hard to sustain due to a spatially restricted region between the directly polarized borders by the electrodes. However, to definitively confirm the mechanism leading to coexistence of incommensurate frequencies in our cardiac model, spatial mapping is needed. Preliminary spatial data provided below illustrate the development of long-period patterns and suggest likely quasiperiodicity scenarios in our model.

This experimental model contrasted to previous studies of instability patterns

Most of the previous systematic studies on instability patterns in cardiac preparations have dealt with zero-dimensional or space-clamped systems, where the overall size of the tissue (cell cluster) was small and/or the observation point was in close proximity to the pacing site; electrical stimulation was applied in the form of direct current injection (23,46–50). In such conditions, the spatial extent of the stimulated tissue plays a minimal role in determining the observed response. Regardless of the type of the stimulated tissue—oscillatory (47) or nonoscillatory (i.e., Purkinje (48,49)) and ventricular (50)—in the above conditions, the instability patterns are believed to arise from inherent nonlinear recovery processes. For simple cases of monotonic recovery of excitability, a framework of pattern formation and evolution was proposed by Guevara et al. in the form of a Farey tree (47)—a frequency-independent representation of common N:M response paths. Analysis (46) showed that in zero-dimensional systems low stimulation strengths are likely to produce Wenckebach patterns, such as those seen in this study. At medium and high strengths, Wenckebach patterns practically disappear and simple 2:1 blocks and alternans (2:2) are seen, along with hysteresis and bistability (multiple patterns at the same pacing frequency depending on the approaching path).

The experiments reported here were done in a spatially extended system (>1 cm²) at suprathreshold values: stimulus strengths were 2.5–5 times the threshold for stimulation. Instead of current injection, electric field stimulation was used (Fig. 9). In these conditions, a gradient of stimulus strengths will be seen over space, with the largest polarization expected at the tissue borders facing the electrodes and decreasing fast toward the center. The polarization (transmembrane potentials, V_m) induced by this extracellular field stimulation can be expressed in simplified form for a one-dimensional case (51) along the width of the scaffolds, L, under assumptions for 1), constant electric field (constant E); and 2), uniform tissue properties (constant conductivity):

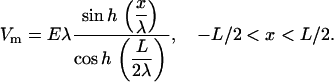(2)

FIGURE 9.

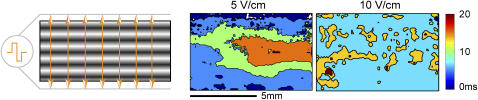
Polarization patterns in response to low-frequency electric field stimulation. Activation maps (isochronal contours of excitation times) are shown for stimulations 2.5 times the threshold (5 V/cm) and five times the threshold (10 V/cm) at 1 Hz, invoking a 1:1 response. Minimal propagation is noted at 5 V/cm, whereas whole-sample activation occurs at 10 V/cm. Movies of the activation are available as Supplementary Materials.

The strength of the applied field is E (V/cm), and the space constant for the tissue is λ (cm). For our experimental preparation the estimated space constant is 0.036–0.05 cm (52). Using the above values, and considering the threshold for activation of 30 mV (deviation from resting potential), one can show that the tissue within 0.5–1.8 mm at each border will get directly depolarized/hyperpolarized by the applied stimulation (5–10 V/cm). For homogeneous tissue, this leaves a central nonexcited region of ≥3 mm width. Thus, limited propagation is theoretically possible in the transverse direction from the borders toward the center. The anisotropic structure of our samples features periodic high resistance regions, spaced ∼120 μm apart across the width of the scaffolds. Gradient in tissue conductivity is known to serve as effective “activation function” and to bring about polarization away from the borders (53). Experimental test of these considerations was done by multisite imaging of the response to 2, 5, 10, 15, and 20 V/cm. Spatial optical mapping of polarization and propagation patterns at low pacing rates (1 Hz) revealed that for E = 10 V/cm (typical stimulating conditions) or higher, almost instantaneous excitation occurred across the scaffold, whereas at 5 V/cm there was some propagation of border-initiated waves colliding in the middle of the scaffold (Fig. 9, and corresponding movies available as Supplementary Materials). However, at higher pacing rates, the pattern of propagation changed, and space-allowed propagation started playing a more prominent role, as shown below in conjunction with Figs. 10 and 11.

FIGURE 10.

Spatiotemporal instability patterns at breakpoint frequency. (A) Shown is the global (space-integrated) signal over an entire scaffold at 10-V/cm stimulation at breakpoint frequency. The image to the left explains how phase-related color encodes the relative temporal position along a transient with the color scale bar underneath a schematic transient. (B) Pseudo-PMT signal (mean intensity over PMT-equivalent area) taken from the region indicated with a white square. Gray boxes are used to illustrate the period of the arrhythmia: here a period 8 (8:8 rhythm) is observed on the macroscopic level. (C) Phase portraits during the time highlighted in red above demonstrate a period 3 spatiotemporal pattern. Each column represents an individual successive beat and each row shows the evolution during a beat (selected frames are 40 ms apart). (D) Selected beats and spatiotemporal patterns that have spontaneously evolved while maintaining the 5-Hz pacing. After ∼6 s, a period 8 pattern emerges (8:8 alternans in the global, and 8:5 block in the local signal), and after another three cycles the period 8 pattern shifts abruptly into a different period 8 pattern shown here in light and dark blue rectangles. Again, each column represents a successive beat and each row shows a frame 40 ms later than the previous row. The last four rows represent the next eight beats of the pattern in the same format as above. Sites of wavebreak-induced transient reentries are indicated by an arrow. See text for further details; movies are available as Supplementary Materials.

FIGURE 11.

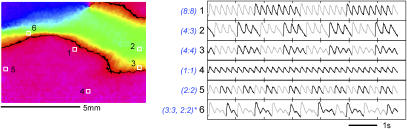
Multitude of local instability patterns. On the left is a phase portrait corresponding to the beginning of the traces on the right, with white boxes indicating simulated PMT regions (200 × 200 μm) for the respective traces. The lower half of the scaffold, regions 4 and 5, exhibits a simple 1:1 response or 2:2 alternans. As one approaches the wave collision border (regions 1, 3, and 6) more complex patterns are seen without any skipped beats. Region 6, in particular, has a combination of 3:3 and 2:2 alternans with varying multiples of each pattern. Beyond the collision border, in region 2 and at other points in the green area ahead of regions 6 and 1 (data not shown), skipped beats are seen. To aid in visualization of the patterns, alternate periods are shaded in light gray in the traces.

All local measurements were done in the larger central region of the scaffold, away from the directly stimulated borders. In contrast to previous studies in zero-dimensional systems, a range of stimulus strengths over space led to propagated waves rather than direct polarization in some regions (e.g., the center of the scaffolds). This might be viewed as a more “natural” rhythm perturbation. Consistent with this view, we observed a combination of patterns, previously predicted for a wide range of stimulation strengths (46)—Wenckebach, alternans, and hysteresis. This may also explain the lack of period-doubling cascades, which are expected at higher stimulus strengths. The spatial extent of our samples might have contributed to the complexity of responses, especially at higher frequencies, where conduction velocity restitution can result in slower propagation and larger effective space.

Spatiotemporal view of dynamic instabilities

To track the genesis and evolution of instability patterns in time and space under electric field stimulation, we optically mapped calcium signals in response to pacing in a small subset of samples. At low frequencies, the polarization patterns (1:1) were weakly dependent on field strength and were consistent with theoretical predictions (Fig. 9). As frequency increased, the polarization spread slower from the borders toward the center leaving a larger effective space for propagation-influenced response.

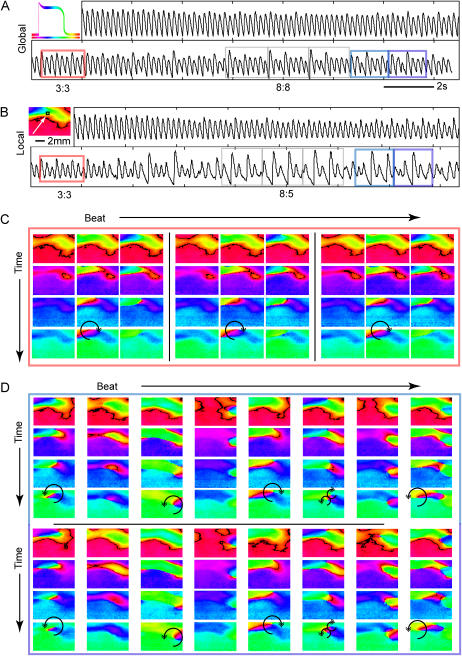
Alternans and higher-order rhythms were seen not only over time, but also in space. Fig. 10 is a representative example of the evolution of instabilities in response to 10-V/cm pacing at the breakpoint frequency (frequency at which the 1:1 response failed), which was 5 Hz in this case. The temporal global signal over the entire scaffold is shown in Fig. 10 A, whereas Fig. 10 B presents a local (PMT-equivalent) signal (200 μm²). The same sample shown in Fig. 9 is used, previously demonstrated to have minimal propagation at 10 V/cm (almost instantaneous polarization). Colored boxes indicate periods of time from which the phase portraits are computed (Fig. 10, C and D). Gray boxes are used only to illustrate the period of the arrhythmia: here, a period 8 signal (8:8 rhythm) is observed on the macroscopic level. A different pattern emerges in the later portion of the recording: specifically, skipped or blocked beats are present in the local recording but not in the global (macroscopic) view.

Fig. 10, C and D, represents higher-order rhythms in space-time as phase portraits. The phase encodes the relative temporal position along a transient as illustrated in the inset with the color scale bar underneath a schematic transient. Phase portraits during the time highlighted in red above demonstrate a period 3 spatiotemporal pattern (Fig. 10 C). Each column represents an individual successive beat and each row shows the evolution during a beat (selected frames are 40 ms apart). The first beat occurs normally but delayed repolarization in the region near the simulated PMT recording permits the formation of a short-lived wavebreak (arrow) in the very next beat (beat 2 of three beats). This delayed activation (wavebreak leading to a reentrant wave) then presents a conduction block on the last beat. By the time the next stimulus occurs, enough time has elapsed for normal propagation to recur (first beat of the next period). Thus, the coexistence of a wavebreak with the regular stimulus-induced pattern leads to the development of a period 3 rhythm. Movies of longer recordings including these patterns are available as Supplementary Materials.

The evolution of longer-period rhythms was caused by multiple wavebreak-triggered transient reentrant waves, occurring at different spatial locations. Fig. 10 D shows selected beats and spatiotemporal patterns that have spontaneously evolved while maintaining the 5-Hz pacing. After ∼6 s a period 8 pattern emerges (8:8 rhythm in the global, and 8:5 block in the local signal), and after another three cycles the period 8 pattern shifts abruptly into a different period 8 pattern shown here in light and dark blue rectangles. Again, each column represents a successive beat and each row shows a frame 40 ms later than the previous row. The last four rows represent the next eight cycles of the pattern in the same format as above. A second phase singularity is now observed in the lower right corner, and the interaction of the two wavebreaks and the electrode-triggered polarization results in a higher-order, longer-period arrhythmia. From the movie of this pattern development, it is seen that the wavebreaks at the different locations in the still images are not stationary but drift or meander over space, and this can potentially lead to longer-period rhythms and quasiperiodicity, observed in the local records. The particular wavebreak location seems to coincide with curved regions of the wavefronts revealed at lower field strengths even during 1:1 low-frequency response. Local wavebreak-induced reentries interacting with the paced wavefronts were confirmed to give rise to longer-period rhythms and complex patterns in three more spatially mapped samples.

Electric field stimulation allowed for spatial distribution and interactions of different instability patterns. Fig. 11 illustrates a multitude of local patterns of calcium instabilities that can coexist in a spatially extended system (same sample used in Fig. 9). Several locations are shown. The lower half of the scaffold, regions 4 and 5, exhibits simple 1:1 response (close to the electrode) or 2:2 alternans. As one approaches the natural wave collision border, far from the electrodes (see Fig. 9 and corresponding supplemental movie)—regions 1, 3, and 6—more complex patterns are seen without any skipped beats. Region 6, in particular, has a combination of 3:3 and 2:2 alternans with varying multiples of each pattern. Beyond the collision border, in region 2 and other points in the green area ahead of regions 6 and 1 (data not shown), skipped beats are seen, including Wenckebach (4:3). To aid in visualization of the patterns, alternate periods are shaded in light gray in the traces. Consistent with spatially varying polarization brought about by electric field stimulation, a wide range of patterns can be seen in the spatial domains adjacent to the electrodes and the central regions where propagated waves collide. Interactions between these connected spatial domains and movement of their borders over time may partially explain the variety of local (PMT) responses in the central region and their complex temporal evolution. Overall, these observations underscore the important role of space in shaping the response of the tissue to high-frequency pacing and the higher likelihood of Wenckebach patterns and blocks to be seen in local but not necessarily global signals. Seemingly analogous dynamic changes in the Wenckebach type of patterns have been experimentally reported for atrioventricular node-conduction blocks and mathematically modeled by considering repolarization, “facilitation” (APD restitution), and “fatigue” (conduction velocity restitution) as essential tissue properties (54). However, the variations observed here in the local patterns, only possible in spatially distributed systems (in contrast to the spatially restricted atrioventricular node) draw attention to the potential importance of heterogeneous response, and can provide a starting point for future theoretical work incorporating space.

CONCLUSIONS

In this study, instabilities in intracellular calcium, including classical 2:2 alternans, were induced by rapid pacing via field stimulation in a spatially-extended cardiac system. They were found to dynamically evolve over time, changing magnitude and/or pattern. Quasiperiodic and intermittent behaviors were prevalent in calcium dynamics, whereas period-doubling was rare. Spatial optical maps revealed longer-period patterns in both time and space during electric field stimulation at high frequency; multiple spatial domains (local patterns) coexisted and interacted within the context of a simpler global rhythm. This highlights the importance of space in shaping the progression of cardiac dynamic instabilities. Pacing-induced VF-like episodes (with significantly higher approximate entropy values) were observed in our experimental 2D cell networks, making this cultured system a potential model for development of new control strategies. This study demonstrates the wider boundaries of calcium dynamics in a spatially extended cardiac system compared to previous space-clamped results, paving the way toward better understanding and potential control of arrhythmias.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.