Abstract
In this report, we present a study of carotenoid-bacteriochlorophyll energy transfer processes in two peripheral light-harvesting complexes (known as LH2) from purple bacteria. We use transient absorption spectroscopy with ≈10 fs temporal resolution, which is necessary to observe the very fast energy relaxation processes. By comparing excited-state dynamics of the carotenoids in organic solvents and inside the LH2 complexes, it has been possible to directly evaluate their energy transfer efficiency to the bacteriochlorophylls. In the case of okenone in the LH2 complex from Chromatium purpuratum, we obtained an energy transfer efficiency of ηET2 = 63 ± 2.5% from the optically active excited state (S2) and ηET1 = 61 ± 2% from the optically dark state (S1); for rhodopin glucoside contained in the LH2 complex from Rhodopseudomonas acidophila these values become ηET2 = 49.5 ± 3.5% and ηET1 = 5.1 ± 1%. The measurements also enabled us to observe vibrational energy relaxation in the carotenoids' S1 state and real-time collective vibrational coherence initiated by the ultrashort pump pulses. Our results are important for understanding the dynamics of early events of photosynthesis and relating it to the structural arrangement of the chromophores.
INTRODUCTION
Carotenoids are among the most investigated organic molecules. They are ubiquitous pigments in photosynthetic systems, performing several vital functions (1). They photoprotect the photosynthetic apparatus by dissipating the excess solar energy and quenching both triplet excited (bacterio)chlorophyll (BChl) and singlet oxygen due to their low-lying triplet state (1–4). This is their essential role and there would be no photosynthesis in the presence of oxygen without them. They also serve as accessory light-harvesting pigments: light absorbed by donor carotenoids in the blue-green region of the spectrum is transferred to acceptor (B)Chls via singlet-singlet energy transfer (ET) with very high efficiency (up to ≈100%), thereby making it available to drive photosynthesis. Carotenoids also have distinct structural functions (as structure stabilization) (5) and are involved in plants in nonphotochemical quenching via the xanthophyll cycle (6).
Carotenoids have a characteristic strong absorption in the visible region, due to the optically allowed electronic transition from their ground state S0 (of 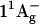 symmetry, according to the C2h point group, in analogy to all-trans-polyenes), to their second excited singlet state
symmetry, according to the C2h point group, in analogy to all-trans-polyenes), to their second excited singlet state 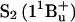 (7,8). The first excited state
(7,8). The first excited state 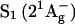 has the same symmetry as the ground state and is therefore optically forbidden (dark state): it is, however, reached in a few hundreds of femtoseconds after photoexcitation, via an ultrafast internal conversion (IC) from S2, denoted IC21 in the following (9–12). Nonradiative decay from S1 to S0 (indicated as IC10) then occurs on a 10-ps timescale (13,14). Intersystem crossing to the triplet manifold is rather inefficient but does occur in some purple bacterial antenna complexes (15,16). Carotenoid photophysics has been recently excellently reviewed by Polívka and Sundström (17).
has the same symmetry as the ground state and is therefore optically forbidden (dark state): it is, however, reached in a few hundreds of femtoseconds after photoexcitation, via an ultrafast internal conversion (IC) from S2, denoted IC21 in the following (9–12). Nonradiative decay from S1 to S0 (indicated as IC10) then occurs on a 10-ps timescale (13,14). Intersystem crossing to the triplet manifold is rather inefficient but does occur in some purple bacterial antenna complexes (15,16). Carotenoid photophysics has been recently excellently reviewed by Polívka and Sundström (17).
Most studies on excited state dynamics of carotenoids have used the three-state model described above to interpret their results. However, previous theoretical work by Tavan and Schulten had indicated the possible existence of additional excited singlet states (e.g., 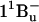 and
and 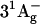 ) between S2 and S1 for carotenoids with more than approximately nine conjugated double bonds (18,19). Recently, experimental results based on resonance Raman profiles (20–22), fluorescence spectroscopy (23), and time-resolved absorption spectroscopy (24–28) have suggested the involvement of these intermediate states in the internal conversion of carotenoids from S2 to S1. In particular, transient absorption spectra with 10-fs time resolution showed a photoinduced absorption (PA) band in the near-IR rising instantaneously and decaying with a 10−20-fs time constant (depending on the carotenoid chain length) (25,27,28). This initial step in excited state dynamics was interpreted as a signature of conversion from S2 to an intermediate state. Experiments suggesting the presence of intermediate states are, however, at odds with fluorescence up-conversion data showing for the emissive state a 150-fs lifetime which corresponds to the time constant for formation of the S1 state (10,11). Therefore, the existence of intermediate excited states in carotenoids and their involvement in the IC21 process is still a matter of controversy.
) between S2 and S1 for carotenoids with more than approximately nine conjugated double bonds (18,19). Recently, experimental results based on resonance Raman profiles (20–22), fluorescence spectroscopy (23), and time-resolved absorption spectroscopy (24–28) have suggested the involvement of these intermediate states in the internal conversion of carotenoids from S2 to S1. In particular, transient absorption spectra with 10-fs time resolution showed a photoinduced absorption (PA) band in the near-IR rising instantaneously and decaying with a 10−20-fs time constant (depending on the carotenoid chain length) (25,27,28). This initial step in excited state dynamics was interpreted as a signature of conversion from S2 to an intermediate state. Experiments suggesting the presence of intermediate states are, however, at odds with fluorescence up-conversion data showing for the emissive state a 150-fs lifetime which corresponds to the time constant for formation of the S1 state (10,11). Therefore, the existence of intermediate excited states in carotenoids and their involvement in the IC21 process is still a matter of controversy.
Purple photosynthetic bacteria are anaerobic prokaryotes that use carotenoids and BChls as their main photosynthetic pigments (29). Peripheral light-harvesting (LH2) complexes from purple bacteria are excellent model pigment-protein complexes for investigating the basic mechanisms of photosynthetic light harvesting, because their structure is known with high resolution (30,31) and because, unlike in plants and algae, the spectral features of the different pigments are well separated (29). In particular, they enable us to study the ET processes from the carotenoids to the BChls.
A prototypical purple bacterium is Rhodopseudomonas acidophila (R. acidophila); its LH2 complexes have a ring structure, consisting of nine monomeric units, each formed by a pair of αβ-apoproteins which bind, noncovalently, three molecules of BChla and one or two molecules of the carotenoid rhodopin glucoside (30,32). BChls molecules are organized into two groups, commonly denoted BChl 800 and BChl 850, referring to the position of their low-lying absorption bands. There are nine BChl 800 groups forming a ring on the cytoplasmic side of the complex, and 18 BChl 850 groups forming a tightly coupled ring near the periplasmic side of the complex. The well-resolved carotenoids have an extended S-shape, all-trans (33) conformation and span the entire depth of the complex, coming into van der Waals contact with both groups of BChls. The LH2 complex from Chromatium purpuratum (C. purpuratum) has an unusual absorption spectrum in the near-infrared (with a single major absorption peak at ≈830 nm) and contains the carotenoid okenone (34). There is no structural information available for this LH2 complex.
The BChls have two absorption bands relevant to the ET process: the Qy transition at ∼800–850 nm and the Qx transition at ∼590 nm (in the following, we will refer to Qx/Qy as the states reached by the Qx/Qy transitions, respectively). The S2 state of carotenoids can transfer excitation energy to the Qx state (denoted ET2 channel in the following). On the other hand, ET to Qy (denoted ET1 in the following) can occur from the carotenoid S1 state when the energy of this S1 state is higher than that of Qy, which happens for carotenoids with shorter conjugation lengths (typically less than 11 conjugated double bonds) (35). Given the 1–2 orders-of-magnitude shorter lifetime of the S2 carotenoid state as compared to the S1, one would expect ET1 to be the dominant channel; however, it has been demonstrated, by fluorescence up-conversion measurements (36–38) and transient absorption measurements (16,38), that ET2 is active in all photosynthetic bacteria studied so far and even predominant in some of them. The ET2 process, being a transition between two allowed optical states, can be described to the first order by the Förster-type mechanism, i.e., coupling between transition dipole moments of the molecules; a more accurate theoretical description is obtained using full Coulombic interaction including higher-order multipoles (39). Although the forbidden nature of the S0–S1 transition initially suggested that the Dexter mechanism, i.e., transfer through electron exchange, was responsible for the ET1 process (40), more detailed calculations (39,41) later showed that it is dominated by higher-order Coulombic and polarization interactions.
Given the very fast timescale of both IC21 and ET2 processes, their full characterization challenges the ≈100-fs temporal resolution of standard pump-probe or fluorescence up-conversion systems; in particular the need of deconvolving the instrumental response from the measured dynamics can lead to ambiguities in the assignment of the underlying processes. The recent availability of pulses with 10−20-fs duration tunable throughout the visible spectrum (42) makes it possible to probe the early events of energy relaxation in carotenoids with unprecedented temporal resolution. In this work we use 10-fs light pulses to study the early steps of excited state dynamics of two carotenoids, okenone and rhodopin glucoside, in organic solvents and in the LH2 complexes from two purple bacteria, C. purpuratum and R. acidophila, respectively. Exploiting the improved temporal resolution, we can follow the details of the IC21 process; by comparing the dynamics of the carotenoids alone and in the LH2 complexes, we are able to measure directly the efficiency of the ET2 process. By subsequently studying the IC10 process, we can also determine the role of ET1.
In our experiments on okenone and rhodopin glucoside, we did not detect any short-lived PA signal which could provide evidence of intermediate states. Such short-lived PA is best observed in the near-IR, where the PA bands from S2 and (possibly) the intermediate states are located. In the LH2 complexes, however, these bands overlap with the photobleaching (PB) and PA bands of BChl. This spectral congestion of signals coming from different species makes it very hard to detect the presence of intermediate states in the antenna complexes. For these reasons, we analyzed our data using the classical three-level picture.
MATERIALS AND METHODS
Sample preparation
Okenone, rhodopin glucoside, and the LH2 complexes (C. purpuratum and R. acidophila) were isolated and purified as previously described (34,38,43). The purity of the carotenoids was determined by thin layer chromatography on silica gel plates while the purity and integrity of the antenna complexes was checked by spectrophotometric measurements. The LH2 complex from C. purpuratum was found to be rather unstable. We therefore used chromatophore membranes rather than the isolated LH2 complex. Previous studies (34) showed that the LH2 complex represents >90% of the pigment-protein complexes in C. purpuratum membranes under the cell growth conditions used for our samples. In this case, no sample degradation was detected.
Ultrafast spectroscopy
The setup used for the experiments starts with a mode-locked Ti:sapphire system with chirped pulse amplification, producing 500-μJ, 150 fs pulses at 790 nm, and 1 kHz repetition rate. These pulses are used to pump two non-collinear optical parametric amplifiers (NOPAs), which have the capability of generating broadband visible pulses (44–46). The first NOPA produces 15-fs transform-limited pulses with tunable center frequency; the second NOPA generates ultrabroadband visible pulses with bandwidth spanning the 500−700 nm wavelength range and sub-10-fs duration. For both NOPAs, the pulses are compressed by multiple reflections onto chirped dielectric mirrors, which are particularly insensitive to alignment and allow obtaining consistently short pulses. The temporal structure of the compressed pulses has been characterized by measuring their spectral amplitude and phase using the SPIDER technique (46). The pulses derived from the NOPAs are synchronized by a delay line and focused on the sample using only reflective optics, in a standard non-collinear pump-probe configuration: an intense pulse from the first NOPA serves as the pump, while a weaker, delayed pulse from the second NOPA probes the differential transmission changes (ΔT/T). To minimize vibronic relaxation effects, our pump pulses were tuned in such a way as to excite predominantly the first vibrational level of the S2 excited state of the carotenoids. After the sample, the probe beam was spatially selected by means of an iris. By inserting a mirror before the sample, it was possible to perform a cross-correlation between pump and probe pulses, so as to exactly determine the zero time delay and the instrumental response function. Day-by-day verification of the setup performance was made by standard non-collinear cross-correlation, which had a width of 15−20 fs.
Time-resolved measurements at specific probe wavelengths were obtained by spectrally filtering, with 10-nm bandwidth interference filters, the probe beam after it passed through the sample, and combining differential detection with lock-in amplification. Transmission difference spectra over the entire bandwidth of the probe pulse at specific delays are then reconstructed from the time traces, after low-pass filtering to suppress the coherent oscillations superimposed on the dynamics. In all measurements, the maximum ΔT/T signal was <10%, thereby ensuring that saturation did not occur. Linearity of the excitation regime was confirmed by varying the intensity of the pump pulses and checking that the measured dynamics were independent of the intensity of the excitation pulse.
The solutions were kept at room temperature in a homemade cuvette, employing 200-μm-thick fused silica windows and with an optical path of ≈200 μm. Since the average power is quite low, in the μW range, no sample degradation is observed during the experiments. Nevertheless, the solution was replaced at the beginning of each experimental run.
Data analysis
The pump-probe time traces have been analyzed using a fitting procedure based on a rate equations model describing population balance. We chose the simplest model able to reproduce the main observed phenomena, namely:
Internal conversion processes within the excited states in the carotenoids.
Vibrational relaxation within the excited states.
Energy transfer from carotenoids to the BChls in the LH2 complexes.
With respect to global fitting analyses, using singular-value decomposition and extracting species-associated difference spectra, this approach has the advantages of simplicity and of providing direct physical insight in the ongoing processes.
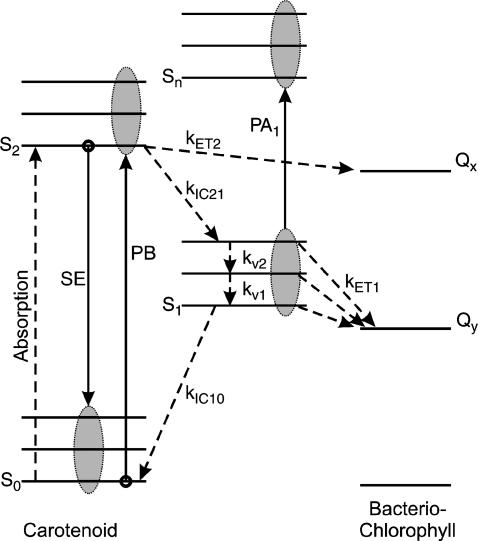
A scheme of the electronic and vibrational levels of carotenoids and bacterio-chlorophylls used in the model is shown in Fig. 1. For the carotenoids in solution, we consider three electronic states: the S2 state, populated by the pump pulse on its lowest vibrational level; this exponentially decays with rate constant kIC21 to the S1 state; and this in turn relaxes to the S0 ground state, with rate constant kIC10. Vibrational relaxation within the S1 state is modeled by considering three associated vibrational levels, with kV2 and kV1 deactivation rate constants. The rate equations model is
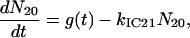 |
(1a) |
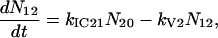 |
(1b) |
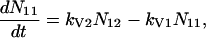 |
(1c) |
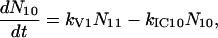 |
(1d) |
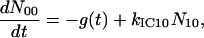 |
(1e) |
where Nij (i,j = 0,1,2) is the population of the Si electronic state in its jth vibrational level and g(t) is the pump beam temporal profile, assumed to be an hyperbolic secant square function with 15-fs, full-width half-maximum, duration.
FIGURE 1.
Scheme of the electronic and vibrational levels of carotenoids and bacterio-chlorophylls used in the model. Population dynamics are indicated with dashed arrows, ΔT/T signals with solid arrows. After photoexcitation from the carotenoid S0 ground state to the S2 state, internal conversion occurs to the S1 state (with kIC21 rate constant), where vibrational relaxation is modeled as energy cascade within three consecutive vibrational levels (with kV2 and kV1 rate constants). Relaxation back to the ground state then takes place with kIC10 rate constant. When the carotenoid is in the LH2 complex, energy transfer can occur from the S2 state to the bacterio-chlorophyll Qx with kET2 rate constant or from the carotenoid S1 state to the bacterio-chlorophyll Qy with kET1 rate constant.
For the carotenoids in the LH2 complexes, two additional relaxation pathways are added: ET from S2 to Qx (with rate kET2) and ET from S1 to Qy (with rate kET1). We consider the ET1 process to be active with equal efficiency from all vibrational levels of the S1 state. The corresponding rate equations are
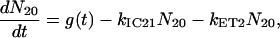 |
(2a) |
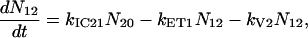 |
(2b) |
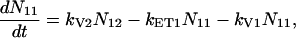 |
(2c) |
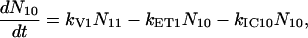 |
(2d) |
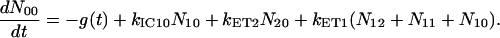 |
(2e) |
Equations 1a–e and 2a–e are solved numerically. The ΔT/T differential transmission signal at a certain probe wavelength λ and pump-probe delay τ is then calculated as
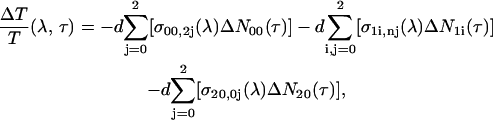 |
(3) |
where d is the sample thickness and σpi,qj(λ) is the cross section (in cm2) for the vibronic transition between the ith vibrational level of Sp and the jth vibrational level of Sq. The first term of Eq. 3 represents PB of the S0–S2 transition (in which i = 0 because only the first vibrational level of the ground state is occupied at room temperature), the second term describes PA from S1 to a higher-lying Sn state (both represented by three vibrational levels), and the third corresponds to stimulated emission (SE) from S2 (in which i = 0 because the pump pulse is only resonant with the 0–0 transition) to S0. Each of these contributions consists of the sum of the vibronic transitions between the different vibrational levels associated to the electronic states. The cross-section is (47,48)
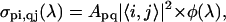 |
(4) |
where Apq is a coefficient including the square of the dipole moment for the Sp–Sq electronic transition, |〈i,j〉|2 are the Franck-Condon factors, and φ(λ) is a Gaussian line-shape. Finally, to take into account the finite probe pulse duration, the differential transmission signal is convoluted with the probe pulse temporal profile, having a 7-fs duration.
The fitting procedure was iterated until the best set of parameters was found to minimize the root-mean-square error between the measured and calculated ΔT/T(λ,τ). A nonlinear minimization procedure based on the simplex method was used. To evaluate the uncertainties of the extracted parameters, we have deliberately changed each parameter from the best fit until we obtained an increase in the root-mean-square error of 10%, which we chose as a reasonable estimation of the goodness of the fit.
RESULTS
Ultrafast dynamics of okenone in solution
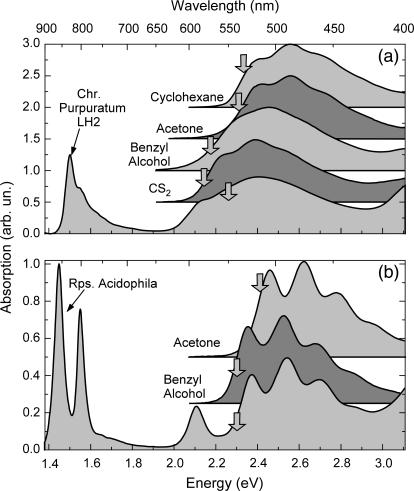
The main aim of this study was to determine the efficiency of the carotenoid-to-BChl ET by directly comparing the IC dynamics of carotenoids in organic solvents and in the LH2 complexes. To obtain a meaningful comparison, it is essential to choose the correct solvent for the carotenoid that best mimics the protein environment in the LH2 complex. We therefore performed an extensive study of the dynamics of okenone's excited states in various organic solvents. It is well known that the energy of the S0−S2 transition in carotenoids depends on the refractive index n of the solvent and it shifts almost linearly with its polarizability R = (n2−1)/(n2+2) (11,49), both for polar and nonpolar solvents. On the other hand, the position of the dark S1 state does not strongly depend on the solvent. Fig. 2 a shows steady-state absorption of LH2 complex from C. purpuratum and its carotenoid (okenone) in various solvents: acetone (R = 0.219), cyclohexane (R = 0.256), benzyl alcohol (R = 0.314), and carbon disulfide (CS2, R = 0.354). Carotenoid absorption extends in the visible region from ≈400 nm to ≈600 nm; BChl Qy absorption has two peaks in the near-infrared region at 800 nm and 830 nm, and BChl Qx band is partially visible at ∼590 nm. As expected, a clear trend in the position of the S2 state energy of the carotenoid was seen upon changing solvent: the absorption peak moved from ≈486 nm to ≈520 nm going from low to high polarizability. The closest superposition with okenone's absorption in the LH2 complex was found for CS2.
FIGURE 2.
(a) Steady-state absorption spectra of okenone in cyclohexane, acetone, benzyl alcohol, CS2 solution, and of the LH2 complex of C. purpuratum. (b) Steady-state absorption spectra of rhodopin glucoside in acetone and benzyl alcohol solution and of LH2 complex of R. acidophila. Pump central wavelengths are indicated by an arrow.
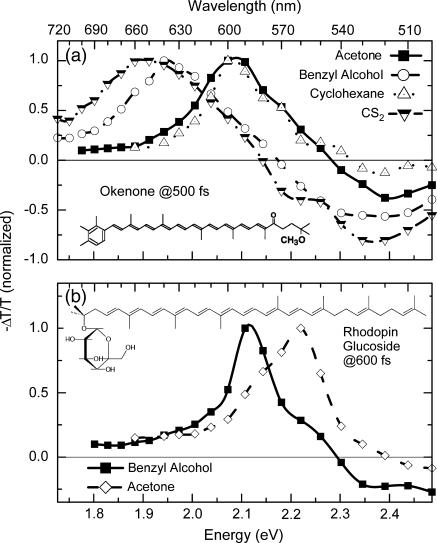
Fig. 3 a shows −ΔT/T spectra of okenone in various solvents for 500 fs pump-probe delay. Pump central wavelengths (indicated with an arrow in Fig. 2 a) correspond to 530 nm (cyclohexane), 535 nm (acetone), 570 nm (benzyl alcohol), and 580 nm (CS2). A broad PA band in the visible region is observed (PA1 band), peaking at 590−650 nm, depending on the solvent. The PA1 band is a well known feature of carotenoids corresponding to the S1→Sn absorption and is the signature of the dark S1 state. The transmission increase on the short wavelength side of these spectra is due to PB of the ground state. In general, PA1 is formed with a time constant of ≈100 fs and decays with time constant of ≈4.5 ps. This signal reveals the sequential steps of the IC21 and IC10 processes. The measured dynamics are observed to be solvent-dependent. Table 1 reports the time constants obtained fitting with exponential rise and decay the ΔT/T signals at the peak of the PA1 band. It can be observed that the time constant for S1 formation decreases from 130 fs in cyclohexane to 95 fs in CS2, in agreement with the reduction of the S2−S1 energy difference and the energy gap law (50,51). Due to the insensitivity of the S1 state energy to the solvent, the time constant for the S1 decay only varies from 4.2 ps to 4.65 ps.
FIGURE 3.
(a) Chemical structure and transient absorption spectra of okenone in different solvents at ≈500 fs probe delay. (b) Chemical structure and transient absorption spectra of rhodopin glucoside in acetone and benzyl alcohol solution at ≈600 fs probe delay.
TABLE 1.
PA1 band formation and decay time constants for okenone and rhodopin glucoside in various solvents, measured at the indicated wavelength corresponding to the peak of the S1–Sn photoinduced absorption band
| Sample | Solvent | PA1 band peak wavelength | PA1 formation time constant | PA1 decay time constant |
|---|---|---|---|---|
| Okenone | Cyclohexane | 600 nm | 130 fs | 4.2 ps |
| Acetone | 600 nm | 110 fs | 4.3 ps | |
| Benzyl alcohol | 640 nm | 100 fs | 4.65 ps | |
| CS2 | 650 nm | 95 fs | 4.2 ps | |
| Rhodopin | Acetone | 560 nm | 145 fs | 4.02 ps |
| glucoside | Benzyl alcohol | 590 nm | 180 fs | 4.45 ps |
Carbon disulfide has been chosen as the best solvent to reproduce the in vivo environment for okenone since this solvent gives the closest match to the absorption of okenone in the LH2 complex. This solvent was also used in a previous study on the carotenoid-to-BChl ET in the LH2 complex from C. purpuratum (52).
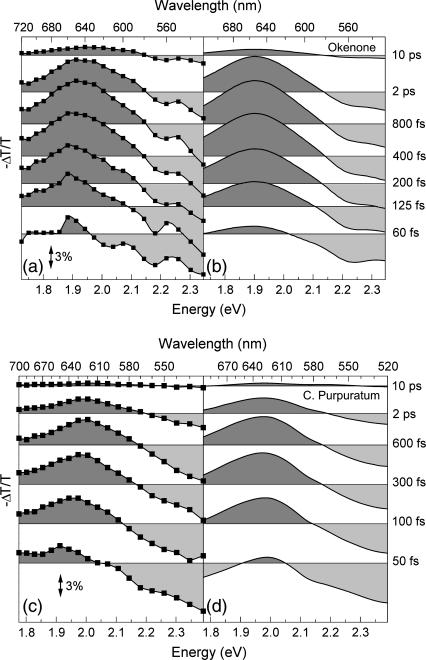
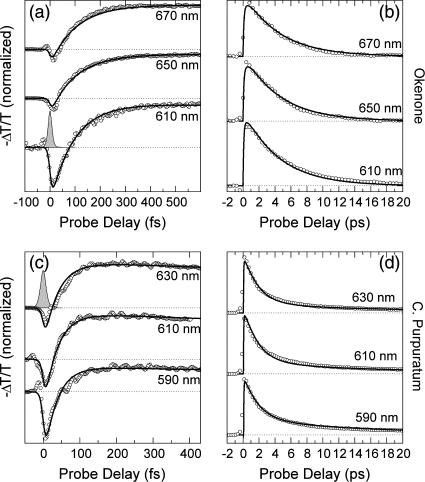
The ΔT/T spectra of okenone in CS2 at different pump-probe delays are shown in Fig. 4 a. The rapid formation and subsequent decay of the PA1 band peaking at 650 nm can be observed in detail. The increased transmission present on the short wavelength side of the spectra is due to a superposition of PB of the ground state (530−580 nm) and, for early delays, stimulated emission (SE) from the S2 state (580−630 nm). Note the strong blue-shift of the isosbestic point for increasing delays. The ΔT/T dynamics at selected probe wavelengths for short and long timescales are shown in Fig. 5, a and b, as circles, respectively. There is a significant wavelength dependence of the dynamics of the buildup and decay of PA1: faster at the red edge and slower at the blue edge. The same behavior is seen in the PA1 spectra (Fig. 4 a), which change in position during the IC processes. The oscillatory patterns superimposed on some of the population dynamics, observed in this and other figures, are due to coherent vibrational motions initiated by the short pump pulse and will be addressed in Discussion, below.
FIGURE 4.
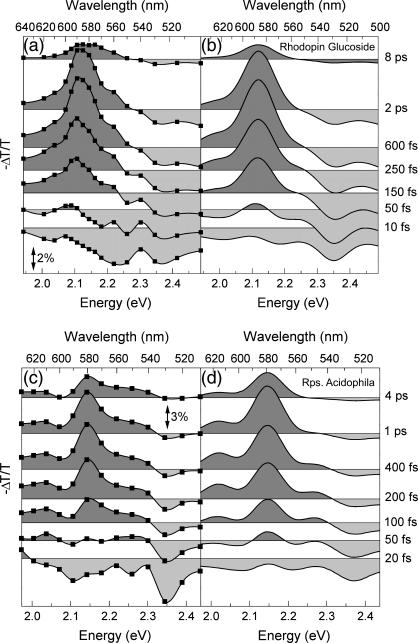
(a) Experimental ΔT/T spectra of okenone in CS2 solution at selected pump-probe delays; (b) simulated ΔT/T spectra of okenone according to the model described in the text; (c) experimental ΔT/T spectra of LH2 complex from C. purpuratum; and (d) simulated ΔT/T spectra of the LH2 complex.
FIGURE 5.
(Circles) ΔT/T dynamics at different probe wavelengths of okenone in CS2 (a and b) and the LH2 complex from C. purpuratum (c and d). Thick solid lines are fits obtained using the model described in the text. Pump-probe cross-correlation is shown as shaded area.
The ΔT/T spectra and dynamics were fitted globally with the model described above and the results are shown in Fig. 4 b and in Fig. 5, a and b, as solid lines. The obtained parameters for the best fit are listed in Table 2. The rate constants for the IC21 and IC10 processes are kIC21 = (95 fs)−1 and kIC10 = (4.46 ps)−1, respectively. Note that our value of kIC10 differs by a factor of 2 from the result reported by Andersson et al. (52).
TABLE 2.
List of the parameters used in the global fitting procedure for the four samples studied
| Okenone/C. purpuratum | Rhodopin glucoside/R. acidophila | |
|---|---|---|
| S1–Sn energy gap | 1.91 eV (Okenone) | 2.12 eV (Rhodopin glucoside) |
| 2 eV (C. purpuratum) | 2.145 eV (R. acidophila) | |
| S1–Sn vibrational energy | 110 ± 10 meV | 125 ± 10 meV |
Gaussian linewidth 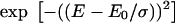
|
σ = 200 ± 12 meV | σ = 63 ± 7 meV |
| S1–Sn Huang-Rhys factor γ | 0.105 ± 0.005 | 0.124 ± 0.005 |
| (kIC21)−1 | 95 (−5 +8) fs | 137 (−11 +10) fs |
| (kIC10)−1 | 4460 (−160 +180) fs | 4280 (−190 +160) fs |
| (kET2)−1 | 55.7 (−6 +2) fs | 140 (−15 + 10) fs |
| (kET1)−1 | 2780 (−110 +270) fs | 80,000 ± 10,000 fs |
Ultrafast dynamics of okenone inside the LH2 complex of C. purpuratum
Fig. 4 c shows the ΔT/T spectra of the LH2 complex in membranes of the bacterium C. purpuratum, upon resonant photoexcitation of the okenone chromophore. The visible pump pulses are tuned to ≈550 nm central wavelength (as indicated by the arrow in Fig. 2 a) to minimize the excitation of the Qx transition of the BChls. This leads, however, to partial excitation of the second vibrational level of S2. Again, the formation of the PA1 band and its subsequent decay are clearly observed. The increased transmission seen at the blue side (580−500 nm) is due to a combination of PB and SE. Within the protein environment, the PA1 band of okenone peaks at 620 nm, i.e., ≈20 nm red-shifted with respect to its position in CS2. The rise time of the PA1 band is faster in LH2 and is essentially completed within 200 fs. Relaxation of S1 back to the ground state is also considerably faster in LH2 as compared to okenone in CS2. The faster buildup and decay of PA1 are seen more clearly by following the detailed kinetics at selected probe wavelengths (see Fig. 5, c and d).
The ΔT/T spectra and dynamics were fitted using the model described previously, keeping the same parameters used for okenone in solution and adding the energy transfer channels. The results are shown in Fig. 4 d and in Fig. 5, c and d, as solid lines; the obtained ET rates are kET2 = (55.7 fs)−1 and kET1 = (2.78 ps)−1. A blue-shift of the PA1 band peak and isosbestic point on the picosecond timescale is also observed in okenone within the LH2 complex. Note that our measurements differ from the previously reported ones (13) because the fast decay component of S1 (400–500 fs) is not present.
The S1 decay does not follow a single exponential law: most of the PA1 signal decreases on a few-picoseconds timescale, whereas a small residual signal lasts a few tens of picoseconds. This slow component can be assigned to photoinduced absorption either from the Qy BChl electronic level (which is long-lived) or from an additional carotenoid excited state, named S*, which is a precursor on an ultrafast fission reaction pathway to the carotenoid triplet state. A similar energy level has been already observed in LH1 complexes from Rhodospirillum rubrum (15) and in LH2 complexes from Rhodobacter sphaeroides (16). Both interpretations give rise to a long-lived plateau in the PA signals, which was introduced in the fittings.
Ultrafast dynamics of rhodopin glucoside in solution
Ultrafast dynamics of the LH2 system of R. acidophila, together with its carotenoid rhodopin glucoside, has already been studied, with lower temporal resolution, by several groups (38,53,54). Our results partially confirm those findings, but also provide some new insights into the early events during carotenoid-to-BChl energy transfer.
Fig. 2 b shows steady-state absorption spectra of rhodopin glucoside and the LH2 complex from R. acidophila. Pump central wavelengths are indicated with an arrow and correspond to 540 nm (R. acidophila and rhodopin glucoside in benzyl alcohol) and 515 nm (rhodopin glucoside in acetone). BChl has the Qx absorption band at ≈590 nm and the two Qy peaks at 800 nm and 850 nm. The carotenoid absorbs in the green-blue region and has a marked vibronic structure, with the 0–0 transition peaking at ≈524 nm in the LH2 complex. Absorption of rhodopin glucoside in benzyl alcohol and acetone solution is also presented in Fig. 2 b, showing the 0–0 line at 510 and 530 nm, respectively. It can be seen that benzyl alcohol mimics well the protein environment both for the absorption peak and its vibronic structure.
The −ΔT/T spectra of rhodopin glucoside in two different solvents at the probe delay corresponding to the maximum signal from S1 (≈600 fs) are shown in Fig. 3 b. PB of the ground state matches steady-state absorption of the carotenoid: it extends up to 520 nm when dissolved in acetone and 540 nm in benzyl alcohol. The broad PA1 band in the visible peaks at 560 nm in acetone and 590 nm in benzyl alcohol. Also in rhodopin glucoside the dynamics are solvent-dependent, as shown in Table 1, reporting PA1 formation and decay time constants at the peak of the band. The S1 buildup and decay are faster in acetone than in benzyl alcohol. The S1 decay in acetone is even faster than for LH2 (see later).
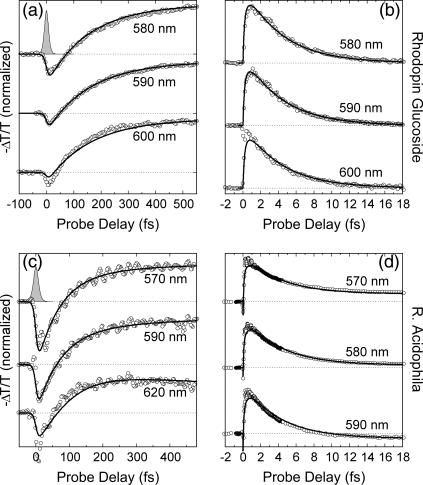
The −ΔT/T spectra of rhodopin glucoside in benzyl alcohol, for different pump-probe delays, are shown in Fig. 6 a. At early times, SE from S2 (640–540 nm) and PB bands (500–540 nm) appear throughout the visible. The corresponding ΔT/T dynamics are shown in Fig. 7, a and b, as circles. Blue-shift in time of the PA1 band and of the isosbestic point, previously observed in okenone, is also present in rhodopin glucoside, and is clearly seen in both the time evolution of the spectra (Fig. 6 a) and the wavelength dependence of the dynamics, which are faster at the red edge than at the blue edge (Fig. 7, a and b).
FIGURE 6.
(a) Experimental ΔT/T spectra of rhodopin glucoside in benzyl alcohol solution at selected pump-probe delays; (b) simulated ΔT/T spectra of rhodopin glucoside according to the model described in the text; (c) experimental ΔT/T spectra of LH2 complex from R. acidophila; and (d) simulated ΔT/T spectra of the LH2 complex.
FIGURE 7.
(Circles) ΔT/T dynamics at different probe wavelengths of rhodopin glucoside in benzyl alcohol (a and b) and the LH2 complex from R. acidophila (c and d). Thick solid lines are fits obtained using the model described in the text. Pump-probe cross-correlation is shown as shaded area.
Global fittings of the ΔT/T spectra and dynamics (shown in Figs. 6 b and 7, a and b, as solid lines) yields, for the IC21 and IC10 processes, the following rate constants: kIC21 = (137 fs)−1 and kIC10 = (4.28 ps)−1. These results are in good agreement with those reported by Macpherson et al. (38), who found a lifetime of the S2 state of rhodopin glucoside in benzyl alcohol, determined by fluorescence up-conversion, of 124 ± 8 fs, and a lifetime of the S1 state of 4.8 ± 0.2 ps.
Ultrafast dynamics of rhodopin glucoside inside the LH2 complex of R. acidophila
Fig. 6 c shows a sequence of −ΔT/T spectra of the LH2 complex of bacterium R. acidophila, upon resonant photoexcitation of the rhodopin glucoside chromophore. At early pump-probe delays a broad SE band from S2 is seen, which rapidly gives way to the buildup of the PA1 band, while PB is left over below ≈540 nm. Within the protein environment, the peak position of the PA1 band is blue-shifted by <10 nm with respect to that of rhodopin glucoside in benzyl alcohol, indicating that this solvent is indeed a good approximation of the protein matrix. PB of the BChl Qx transition burns a weak hole in the PA1 band that is observable at ∼590 nm. In the LH2 complex, the rise time of the PA1 band is faster than in benzyl alcohol and is essentially complete within 250 fs. The subsequent relaxation of S1 back to the ground state is only very slightly faster than for rhodopin glucoside in benzyl alcohol. The faster PA1 buildup and decay were investigated in greater detail by measuring the kinetics at selected probe wavelengths (Fig. 7, c and d). Analogously to C. purpuratum, a small residual PA signal was still present after 40 ps, in addition to the Qx PB. This PA probably reflects the formation of the S* state of the carotenoid within the LH2 complex (53,54). The usual wavelength dependence of the S1 rise and decay (slower in the blue than in the red) is also seen in this LH2 complex.
Also in this case, the ΔT/T spectra and dynamics were fitted using the model described previously, keeping the same parameters used for rhodopin glucoside in solution and adding the energy transfer channels. The resulting ET rates are kET2 = (140 fs)−1 and kET1 = (80 ps)−1. The present data are in good agreement with the results of Macpherson et al. (38), who reported an S2 lifetime of the carotenoid in the LH2 complex, measured by fluorescence up-conversion, of 57 ± 2 fs. On the other hand, Rondonuwu et al. (54), using pump-probe spectroscopy with 160 fs instrumental response width, proposed a quite different relaxation pathway for the LH2 complex of R. acidophila. This involves initial energy relaxation to the  state with a time constant of ≈80 fs and subsequent delayed formation of the S1 state, with a time constant of ≈400 fs. Our measurements do not find any evidence of a delayed formation of the S1 state.
state with a time constant of ≈80 fs and subsequent delayed formation of the S1 state, with a time constant of ≈400 fs. Our measurements do not find any evidence of a delayed formation of the S1 state.
DISCUSSION
Vibrational relaxation
In all the ΔT/T spectra and dynamics presented in this article, both in solution and within the LH2 complexes, we observe common features in the evolution of the PA1 band:
Faster buildup in the red than in the blue side.
Slower decay in the blue than in the red side.
Blue-shift of the isosbestic point and of the PA1 peak.
Spectral narrowing of the band within the first ≈500 fs (best observed in rhodopin glucoside because of its narrower spectral features).
These effects are attributed to intraband vibrational relaxation associated to dissipation of the excess energy (≈5000 cm−1) initially deposited in S1. Previous studies (53,55–57) have observed a wavelength-dependent dynamics in S1, typically occurring on the 500-fs timescale, and attributed it to vibrational relaxation. Our enhanced temporal resolution shows that an additional faster relaxation process is taking place on the 50-fs timescale, giving rise to the wavelength-dependent buildup time of the PA1 band and its spectral narrowing. Therefore, in our model we introduced two excited vibrational levels in S1 and assumed that relaxation from the v = 2 to the v = 1 level proceeds with a kv2 = 50 fs time constant, while relaxation from the v = 1 to the v = 0 level occurs with a slower kv1 = 500 fs time constant. Using these parameters, the model gives satisfactory fits for both carotenoids in the different environments (solution and LH2 complex), indicating that vibrational relaxation in S1 is a general feature in carotenoids. Although the values of the kv2 and kv1 relaxation constants cannot be determined to a great accuracy, nevertheless our simple model appears to give an accurate description of the ongoing photophysics.
We note that an alternative explanation of the wavelength-dependent PA1 dynamics has been given (58). It has been proposed that conformational relaxation of the carotenoid from a twisted configuration—created by the photoexcitation—to the all-trans form takes place with a time constant of 300−400 fs during the IC21, resulting in a blue-shift of the PA1 band.
Carotenoid-to-BChl energy transfer
The shortening of the S2 and S1 lifetimes of okenone and rhodopin glucoside in their corresponding LH2 complexes is due to the opening of new relaxation channels. In the LH2 complexes, in addition to internal conversion of S2 to S1 and S1 to S0, energy transfer from both S2 and S1 to the BChls is possible. To determine the ET rates and efficiencies in the LH2 complexes, the lifetimes of both S2 and S1 must be determined for both carotenoids in organic solvents and in the LH2 complexes. Ideally, this comparison requires the environment of the carotenoids to be the same in both situations, so that the kIC21 and kIC10 rates remain virtually unchanged; in practice this is not perfectly achievable. By comparing the ground state absorption and excited-state dynamics of both carotenoids in a range of organic solvents, it has been possible to select a solvent in which the carotenoid's environment is the best approximation to that in the protein. Calculation of the efficiency of ET from the carotenoids to the BChls from analysis of the rate constants for the decay of the S2 and S1 states depends critically on the values for these decays in the absence of ET. As we showed above, both of these decays depend on the solvent in which the carotenoids are dissolved. All of the subsequent calculations and discussions assume that our choice of the optimal solvent has been reasonable. It is important, however, to realize this limitation.
For okenone, the results of our fitting procedure are as follows:
Internal conversion in CS2 solution from S2 to S1 states occurs with rate kIC21 = (95 fs)−1, and from S1 back to S0 with rate kIC10 = (4.46 ps)−1.
Energy transfer from okenone S2 state to Qx state in LH2 complex of C. purpuratum membranes has a rate constant kET2 = (55.7 fs)−1.
Similarly, the energy transfer from okenone S1 state to Qy state in LH2 has a rate constant kET1 = (2.78 ps)−1.
It then follows that the energy transfer efficiencies are 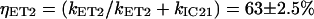 from S2 and
from S2 and 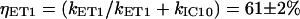 from S1. The overall ET efficiency is then calculated by adding to the ηET2 the ηET1 properly weighted by the fraction of photoexcited molecules that enter the S1 state: ηokenone = ηET2 + (1−ηET2) × ηET1 = 85.6 ± 1.5%. In a previous study, Andersson et al. (52) determined a value of 95 ± 5% for the ET efficiency of the LH2 complex from C. purpuratum from the fluorescence excitation spectrum. However, that measurement appears to be not very well corrected, since in some spectral regions (400−500 nm) the efficiency exceeds 100%. This overestimate can explain the discrepancy with our result.
from S1. The overall ET efficiency is then calculated by adding to the ηET2 the ηET1 properly weighted by the fraction of photoexcited molecules that enter the S1 state: ηokenone = ηET2 + (1−ηET2) × ηET1 = 85.6 ± 1.5%. In a previous study, Andersson et al. (52) determined a value of 95 ± 5% for the ET efficiency of the LH2 complex from C. purpuratum from the fluorescence excitation spectrum. However, that measurement appears to be not very well corrected, since in some spectral regions (400−500 nm) the efficiency exceeds 100%. This overestimate can explain the discrepancy with our result.
Using rhodopin glucoside (and using the same notation and methodology described above for okenone) the following rate constants were determined: kIC21 = (137 fs)−1, kET2 = (140 fs)−1, kIC10 = (4.28 ps)−1, and kET1 = (80 ps)−1. This translates into the following ET efficiencies: ηET2 = 49.5 ± 3.5%, and ηET1 = 5.1 ± 1%, which produces an overall ηRG = 52.1 ± 3%. These results are in excellent agreement with those obtained using fluorescence up-conversion where the time resolution was much longer (140–200 fs) (ηET2 = 51–56%, ηET1 = 5 ± 2%, 38). Other values for this overall ET efficiency in LH2 complexes from R. acidophila also obtained from transient absorption studies have yielded values of 53% (53) and 54% (54).
Coherent oscillations analysis
The dynamics in Figs. 5, a and c, and 7, a and c, have a superimposed oscillatory pattern, which is due to collective vibrational coherence initiated in the ensemble of photoexcited molecules by the ultrashort pump pulse (59,60). The oscillations are slowly damped and persist on a timescale longer than 1 ps. Fourier analysis of the signals, after subtraction of the slowly varying component, is shown in Fig. 8 a for okenone in CS2 and in the LH2 complex from C. purpuratum, and in Fig. 8 b for rhodopin glucoside in benzyl alcohol and in LH2 complex from R. acidophila. To test the accuracy of this mathematical analysis, the inset of Fig. 8 a shows a plot (solid line) of the fit obtained by simply adding two sinusoidal functions at the extracted frequencies (with appropriate amplitudes and phases) corresponding to those obtained in the Fourier analysis. An excellent agreement was found with the experimental data (dashed line).
FIGURE 8.
Fourier-transform of oscillatory component of ΔT/T signal in (a) okenone, with LH2 of C. purpuratum, and (b) rhodopin glucoside, with LH2 of R. acidophila. Inset shows the oscillatory component superimposed on the temporal trace of okenone at 580 nm, together with a fit based on the frequencies extracted from the Fourier analysis.
Several coupled modes are present, the strongest being at ≈1155 cm−1 and ≈1510 cm−1 for both carotenoids in the organic solvents. By comparing these to the vibrational frequencies obtained for a variety of carotenoids with resonance-Raman spectra (61,62), it is possible to assign them to ag-type C−C and C=C symmetric stretching modes of the conjugated backbone, respectively. At ∼1000 cm−1 another smaller feature is visible in some of the pump-probe traces, corresponding to the overlap of methyl in-plane rocking and C–H out-of-plane wagging Raman lines (62). The vibrational frequencies for rhodopin glucoside in benzyl alcohol and in the LH2 complex are very similar. In the case of the LH2 complex from C. purpuratum the main vibrational frequencies are shifted to somewhat lower values.
It now remains for us to discuss upon which electronic state(s) the observed vibrational wavepacket(s) is/are moving. Excitation by an ultrashort pulse can create a vibrational wavepacket in the excited electronic state (S2 in our case) as well as in the ground state (S0), due to a mechanism known as resonant impulsive stimulated Raman scattering (63). In addition, in principle, the internal conversion process to S1 could take place coherently, i.e., preserving the phase of the collective nuclear motion in the final state (64). In our case, due to the short lifetime of the S2 state, the long-lasting oscillations must be assigned to either S0 or S1, or both. Since our measured frequencies match very well those obtained from ground state resonant Raman scattering (62) and the frequencies coupled to S1 are known to be different from those coupled to S0 (65), we can assign at least the major observed vibrational wavepackets to the ground state.
CONCLUSIONS
In conclusion, we have presented pump-probe measurements, with 10-fs temporal resolution, on carotenoids both in solution and inside the LH2 complex of two different light-harvesting purple bacteria. Our data provide a real-time picture of the IC, ET, and vibrational relaxation processes and enable us to calculate the energy transfer efficiencies. This study has been restricted to the dynamics that can be measured in the visible region of the spectrum. It will be interesting to see, when these measurements are extended with equal or better time resolution into the near-IR, whether involvement of any excited singlet states, which are located between S2 and S1, can be seen to contribute to ET to the BChls.
Acknowledgments
The authors are indebted to Cristian Manzoni for help with the experimental setup.
R.J.C. acknowledges support from the Biotechnology and Biological Sciences Research Council and from the European Community-Access to Research Infrastructure action of the improving Human Potential Program, contract No. RII3-CT-2003-506350 (Center for Ultrafast Science and Biomedical Optics).
References
- 1.Frank, H. A., and R. J. Cogdell. 1996. Carotenoids in photosynthesis. Photochem. Photobiol. 63:257–264. [DOI] [PubMed] [Google Scholar]
- 2.Siefermann-Harms, D. 1987. The light harvesting protective functions of carotenoids in photosynthetic membranes. Physiol. Plant. 69:561–568. [Google Scholar]
- 3.Mimuro, M., and T. Katoh. 1991. Carotenoids in photosynthesis-absorption, transfer and dissipation of light energy. Pure Appl. Chem. 63:123–130. [Google Scholar]
- 4.Koyama, Y. 1991. Structures and function of carotenoids in photosynthetic systems. J. Photochem. Photobiol. B. 9:265–280. [Google Scholar]
- 5.Lang, H. P., and C. N. Hunter. 1994. The relationship between carotenoids biosynthesis and the assembly of the light-harvesting LH2 complex in Rhodobacter sphaeroides. Biochem. J. 298:197–205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yamamoto, H. Y., R. C. Bugos, and A. D. Hieber. 1999. The Photochemistry of Carotenoids. H. A. Frank, A. J. Young, G. Britton, and R. J. Cogdell, editors. Kluwer Academic Press, The Netherlands. 295–325.
- 7.Hudson, B. S., and B. E. Kohler. 1972. A low-lying weak transition in the polyene α,ω-diphenyloctatetraene. Chem. Phys. Lett. 14:299–304. [Google Scholar]
- 8.Schulten, K., and M. Karplus. 1972. On the origin of a low-lying forbidden transition in polyenes and related molecules. Chem. Phys. Lett. 14:305–309. [Google Scholar]
- 9.Shreve, A. P., J. K. Trautman, T. G. Owens, and A. C. Albrecht. 1991. Determination of the S2 lifetime of β-carotene. Chem. Phys. Lett. 178:89–96. [Google Scholar]
- 10.Kandori, H., H. Sasabe, and M. J. Mimuro. 1994. Direct determination of a lifetime of the S2 state of β-carotene by femtosecond time-resolved fluorescence spectroscopy. J. Am. Chem. Soc. 116:2671–2672. [Google Scholar]
- 11.Macpherson, A. N., and T. Gillbro. 1998. Solvent dependence of the ultrafast S2–S1 internal conversion rate of β-carotene. J. Phys. Chem. A. 102:5049–5058. [Google Scholar]
- 12.Polli, D., G. Cerullo, G. Lanzani, S. De Silvestri, H. Hashimoto, and R. J. Cogdell. 2003. Excited-state dynamics of carotenoids with different conjugation length. Synth. Met. 139:893–896. [Google Scholar]
- 13.Andersson, P. O., S. M. Bachilo, R.-L. Chen, and T. Gillbro. 1995. Solvent and temperature effects on dual fluorescence in a series of carotenes. Energy gap dependence of the internal conversion rate. J. Phys. Chem. 99:16199–16209. [Google Scholar]
- 14.Frank, H. A., R. Z. B. Desamero, V. Chynwat, R. Gebhard, I. van der Hoef, F. J. Jansen, J. Lugtenburg, D. Gosztola, and M. R. Wasielewski. 1997. Spectroscopic properties of spheroidene analogs having different extents of π-electron conjugation. J. Phys. Chem. A. 101:149–157. [Google Scholar]
- 15.Gradinaru, C. C., J. T. M. Kennis, E. Papagiannakis, I. H. M. van Stokkum, R. J. Cogdell, G. R. Fleming, R. A. Niederman, and R. van Grondelle. 2001. An unusual pathway of excitation energy deactivation in carotenoids: singlet-to-triplet conversion on an ultrafast timescale in a photosynthetic antenna. Proc. Natl. Acad. Sci. USA. 98:2364–2369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Papagiannakis, E., J. T. M. Kennis, I. H. M. van Stokkum, R. J. Cogdell, and R. van Grondelle. 2002. An alternative carotenoid-to-bacteriochlorophyll energy transfer pathway in photosynthetic light harvesting. Proc. Natl. Acad. Sci. USA. 99:6017–6022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Polívka, T., and V. Sundström. 2004. Ultrafast dynamics of carotenoid excited states—from solution to natural and artificial systems. Chem. Rev. 104:2021–2071. [DOI] [PubMed] [Google Scholar]
- 18.Tavan, P., and K. Schulten. 1986. The low-lying electronic excitations in long polyenes: a PPP-MRD-CI study. J. Chem. Phys. 85:6602–6609. [Google Scholar]
- 19.Tavan, P., and K. Schulten. 1987. Electronic excitations in finite and infinite polyenes. Phys. Rev. B. 36:4337–4358. [DOI] [PubMed] [Google Scholar]
- 20.Sashima, T., H. Nagae, M. Kuki, and Y. Koyama. 1999. A new singlet-excited state of all-trans-spheroidene as detected by resonance-Raman excitation profiles. Chem. Phys. Lett. 299:187–194. [Google Scholar]
-
21.Sashima, T., Y. Koyama, T. Yamada, and H. Hashimoto. 2000. The
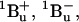 and
and 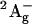 energies of crystalline lycopene, β-carotene, and mini-9-β-carotene as determined by resonance-Raman excitation profiles: dependence of the
energies of crystalline lycopene, β-carotene, and mini-9-β-carotene as determined by resonance-Raman excitation profiles: dependence of the 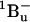 state energy on the conjugation length. J. Phys. Chem. B. 104:5011–5019. [Google Scholar]
state energy on the conjugation length. J. Phys. Chem. B. 104:5011–5019. [Google Scholar] -
22.Furuichi, K., T. Sashima, and Y. Koyama. 2002. The first detection of the
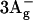 state in carotenoids using resonance-Raman excitation proðles. Chem. Phys. Lett. 356:547–555. [Google Scholar]
state in carotenoids using resonance-Raman excitation proðles. Chem. Phys. Lett. 356:547–555. [Google Scholar] -
23.Fujii, R., T. Ishikawa, Y. Koyama, M. Taguchi, Y. Isobe, H. Nagae, and Y. Watanabe. 2001. Fluorescence spectroscopy of all-trans-anhydrorhodovibrin and spirilloxanthin: detection of the
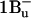 fluorescence. J. Phys. Chem. A. 105:5348–5355. [Google Scholar]
fluorescence. J. Phys. Chem. A. 105:5348–5355. [Google Scholar] -
24.Zhang, J.-P., T. Inaba, Y. Watanabe, and Y. Koyama. 2000. a. Excited-state dynamics among the
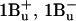 and
and 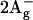 states of all-trans-neurosporene as revealed by near-infrared time-resolved absorption spectroscopy. Chem. Phys. Lett. 332:351–358. [Google Scholar]
states of all-trans-neurosporene as revealed by near-infrared time-resolved absorption spectroscopy. Chem. Phys. Lett. 332:351–358. [Google Scholar] - 25.Cerullo, G., D. Polli, G. Lanzani, S. De Silvestri, H. Hashimoto, and R. J. Cogdell. 2002. Photosynthetic light harvesting by carotenoids: detection of an intermediate excited state. Science. 298:2395–2398. [DOI] [PubMed] [Google Scholar]
- 26.Fujii, R., T. Inaba, Y. Watanabe, Y. Koyama, and J.-P. Zhang. 2003. Two different pathways of internal conversion in carotenoids depending on the length of the conjugated chain. Chem. Phys. Lett. 369:165–172. [Google Scholar]
-
27.Nishimura, K., F. S. Rondonuwu, R. Fujii, J. Akahane, Y. Koyama, and T. Kobayashi. 2004. Sequential singlet internal conversion of
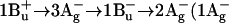 ground) in all-trans-spirilloxanthin revealed by two-dimensional sub-5-fs spectroscopy. Chem. Phys. Lett. 392:68–73. [Google Scholar]
ground) in all-trans-spirilloxanthin revealed by two-dimensional sub-5-fs spectroscopy. Chem. Phys. Lett. 392:68–73. [Google Scholar] - 28.Polli, D., G. Cerullo, G. Lanzani, S. De Silvestri, K. Yanagi, H. Hashimoto, and R. J. Cogdell. 2004. Conjugation length dependence of internal conversion in carotenoids: role of the intermediate state. Phys. Rev. Lett. 93:163002. [DOI] [PubMed] [Google Scholar]
- 29.Cogdell, R. J., N. W. Isaacs, T. D. Howard, K. McLuskey, N. J. Freser, and S. M. Prince. 1999. How photosynthetic bacteria harvest solar energy. J. Bacteriol. 181:3869–3879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.McDermott, G., S. M. Prince, A. A. Freer, A. M. Hawthornethwaite-Lawless, M. Z. Papiz, R. J. Cogdell, and N. W. Isaacs. 1995. Crystal structure of an integral membrane light harvesting complex from photosynthetic bacteria. Nature. 374:517–521. [Google Scholar]
- 31.Koepke, J., X. Hu, C. Muenke, K. Schulten, and H. Michel. 1996. The crystal structure of the light-harvesting complex II (B800–850) from Rhodospirillum molischianum. Structure. 4:581–597. [DOI] [PubMed] [Google Scholar]
- 32.Papiz, M. Z., S. M. Prince, T. Howard, R. J. Cogdell, and N. W. Isaacs. 2003. The structure and thermal motion of the B800–850 LH2 complex from Rps. acidophila at 2.0 Å resolution and 100 K: new structural features and functionally relevant motions. J. Mol. Biol. 326:1523–1538. [DOI] [PubMed] [Google Scholar]
- 33.Robert, B., and M. Lutz. 1985. Structure of antenna complexes of several Rhodospirillaceae from their resonance Raman spectra. Biochim. Biophys. Acta. 807:10–23. [Google Scholar]
- 34.Cogdell, R. J., A. M. Hawthornthwaite, M. B. Evans, L. A. Ferguson, C. Kerfeld, J. P. Thornber, F. van Mourik, and R. van Grondelle. 1990. Isolation and characterisation of an unusual antenna complex from the marine purple sulphur photosynthetic bacterium Chromatium purpuratum BW5500. Biochim. Biophys. Acta. 1019:239–244. [Google Scholar]
- 35.Zhang, J.-P., R. Fujii, P. Qian, T. Inaba, T. Mizoguchi, Y. Koyama, K. Onaka, and Y. Watanabe. 2000. b. Mechanism of the carotenoid-to-bacteriochlorophyll energy transfer via the S1 state in the LH2 complexes from purple bacteria. J. Phys. Chem. B. 104:3683–3691. [Google Scholar]
- 36.Ricci, M., S. E. Bradforth, R. Jimenez, and G. R. Fleming. 1996. Internal conversion and energy transfer dynamics of spheroidene in solution and in the LH-1 and LH-2 light-harvesting complexes. Chem. Phys. Lett. 259:381–390. [Google Scholar]
- 37.Krueger, B. P., G. D. Scholes, R. Jimenez, and G. R. Fleming. 1998. a. Electronic excitation transfer from carotenoid to bacteriochlorophyll in the purple bacterium Rhodopseudomonas acidophila. J. Phys. Chem. B. 102:2284–2292. [Google Scholar]
- 38.Macpherson, A. N., J. B. Arellano, N. J. Fraser, R. J. Cogdell, and T. Gillbro. 2001. Efficient energy transfer from the carotenoid S2 state in a photosynthetic light-harvesting complex. Biophys. J. 80:923–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Damjanović, A., T. Ritz, and K. Schulten. 1999. Energy transfer between carotenoids and bacteriochlorophylls in light-harvesting complex II of purple bacteria. Phys. Rev. E. 59:3293–3311. [Google Scholar]
- 40.Cogdell, R. J., and H. A. Frank. 1987. How carotenoids function in photosynthetic bacteria. Biochim. Biophys. Acta. 895:63–79. [DOI] [PubMed] [Google Scholar]
- 41.Krueger, B. P., G. D. Scholes, and G. R. Fleming. 1998. b. Calculation of couplings and energy-transfer pathways between the pigments of LH2 by the ab initio transition density cube method. J. Phys. Chem. B. 102:5378–5386. [Google Scholar]
- 42.Cerullo, G., and S. De Silvestri. 2003. Ultrafast optical parametric amplifiers. Rev. Sci. Instrum. 74:1–18. [Google Scholar]
- 43.Cogdell, R. J., and A. M. Hawthornthwaite. 1991. Bacteriochlorophyll-binding protein. In CRC Handbook on “The Chlorophylls”. H. Scheer, editor. CBC Press, Boca Raton, FL. 493–528.
- 44.Cerullo, G., M. Nisoli, S. Stagira, and S. De Silvestri. 1998. Sub-8-fs pulses from an ultra-broad-band optical parametric amplifier in the visible. Opt. Lett. 16:1283–1285. [DOI] [PubMed] [Google Scholar]
- 45.Zavelani-Rossi, M., G. Cerullo, S. De Silvestri, L. Gallmann, N. Matuschek, G. Steinmeyer, and U. Keller. 2001. Pulse compression over a 170-THz bandwidth in the visible by use of only chirped mirrors. Opt. Lett. 26:1155–1157. [DOI] [PubMed] [Google Scholar]
- 46.Zavelani-Rossi, M., D. Polli, G. Cerullo, S. De Silvestri, L. Gallmann, G. Steinmeyer, and U. Keller. 2002. Few-optical-cycle laser pulses by OPA: broadband chirped mirror compression and SPIDER characterization. Appl. Phys. B. 74:S245–S251. [Google Scholar]
- 47.Henry, B. R., and W. Siebrand. 1975. Radiationless transitions. In Organic Molecular Photophysics, Vol. 1. J. B. Birks, editor. J. Wiley, London. 153–237.
- 48.Manneback, C. 1951. Computation of the intensities of vibrational spectra of electronic bands in diatomic molecules. Phys. 17:1001–1010. [Google Scholar]
- 49.Andersson, P. O., T. Gillbro, L. Ferguson, and R. J. Cogdell. 1991. Absorption spectral shifts of carotenoids related to medium polarizability. J. Photochem. Photobiol. 54:353–360. [Google Scholar]
- 50.Englman, R., and J. Jortner. 1970. The energy gap law for radiationless transitions in large molecules. Mol. Phys. 18:145–164. [Google Scholar]
- 51.Chynwat, V., and H. A. Frank. 1995. The application of the energy gap law to the S1 energies and dynamics of carotenoids. Chem. Phys. 194:237–244. [Google Scholar]
- 52.Andersson, P. O., R. J. Cogdell, and T. Gillbro. 1996. Femtosecond dynamics of carotenoid-to-bacteriochlorophyll a energy transfer in light-harvesting antenna complexes from the purple bacterium Chromatium Purpuratum. Chem. Phys. 210:195–217. [Google Scholar]
- 53.Wohlleben, W., T. Buckup, J. L. Herek, R. J. Cogdell, and M. Motzkus. 2003. Multichannel carotenoid deactivation in photosynthetic light harvesting as identified by an evolutionary target analysis. Biophys. J. 85:442–450. [DOI] [PMC free article] [PubMed] [Google Scholar]
-
54.Rondonuwu, F. S., K. Yokoyama, R. Fujii, Y. Koyama, R. J. Cogdell, and Y. Watanabe. 2004. The role of the
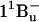 state in carotenoid-to-bacteriochlorophyll singlet-energy transfer in the LH2 antenna complexes from Rhodobacter sphaeroides G1C, Rhodobacter sphaeroides 2.4.1, Rhodospirillum molischianum and Rhodopseudomonas acidophila. Chem. Phys. Lett. 390:314–322. [Google Scholar]
state in carotenoid-to-bacteriochlorophyll singlet-energy transfer in the LH2 antenna complexes from Rhodobacter sphaeroides G1C, Rhodobacter sphaeroides 2.4.1, Rhodospirillum molischianum and Rhodopseudomonas acidophila. Chem. Phys. Lett. 390:314–322. [Google Scholar] - 55.Cerullo, G., G. Lanzani, M. Zavelani-Rossi, and S. De Silvestri. 2001. Early events of energy relaxation in all-trans-β-carotene following sub-10 fs optical-pulse excitation. Phys. Rev. B. 63:R241104(1–4). [Google Scholar]
- 56.Billsten, H. H., D. Zigmantas, V. Sundström, and T. Polívka. 2002. Dynamics of vibrational relaxation in the S1 state of carotenoids having 11 conjugated C = C bonds. Chem. Phys. Lett. 355:465–470. [Google Scholar]
- 57.Lanzani, G., G. Cerullo, D. Polli, A. Gambetta, M. Zavelani-Rossi, and C. Gadermaier. 2004. Photophysics of conjugated polymers: the contribution of ultrafast spectroscopy. Phys. Stat. Sol. (a) 201:1116–1131. [Google Scholar]
- 58.de Weerd, F. L., I. H. M. van Stokkum, and R. van Grondelle. 2002. Subpicosecond dynamics in the excited state absorption of all-trans-β-carotene. Chem. Phys. Lett. 354:38–43. [Google Scholar]
- 59.Cerullo, G., G. Lanzani, M. Muccini, C. Taliani, and S. De Silvestri. 1999. Real-time vibronic coupling dynamics in a prototypical conjugated oligomer. Phys. Rev. Lett. 83:000231 (1–4). [Google Scholar]
- 60.Lanzani, G., G. Cerullo, C. Brabec, and N. S. Sariciftci. 2003. Time domain investigation of the intrachain vibrational dynamics of a prototypical light-emitting conjugated polymer. Phys. Rev. Lett. 90:047402 (1–4). [DOI] [PubMed] [Google Scholar]
- 61.Fujii, R., C.-H. Chen, T. Mizoguchi, and Y. Koyama. 1998. 1H NMR, electronic-absorption and resonance-Raman spectra of isomeric okenone as compared with those of isomeric β-carotene, canthaxanthin, β-apo-8′-carotenal and spheroidene. Spectrochim. Acta [A]. 54:727–743. [Google Scholar]
- 62.Robert, B. 1999. The electronic structure, stereochemistry and resonance Raman spectroscopy of carotenoids. In Photochemistry of Carotenoids. H. A. Frank, A. J. Young, G. Britton, and R. J. Cogdell, editors. Kluwer Academic Publishers, Dordrecht, The Netherlands. 189–222.
- 63.Pollard, W. T., H. L. Fragnito, J.-Y. Bigot, C. V. Shank, and R. A. Mathies. 1990. Quantum-mechanical theory for 6 fs dynamic absorption spectroscopy and its application to Nile blue. Chem. Phys. Lett. 168:239–245. [Google Scholar]
- 64.Wang, Q., L. Peteanu, R. W. Schoenlein, C. V. Shank, and R. Mathies. 1994. Vibrationally coherent photochemistry in the femtosecond primary event of vision. Science. 266:422–424. [DOI] [PubMed] [Google Scholar]
- 65.Hashimoto, H., Y. Koyama, Y. Hirata, and N. Mataga. 1991. S1 and T1 species of β-carotene generated by direct photoexcitation from the all-trans, 9-cis, 13-cis, and 15-cis isomers as revealed by picosecond transient absorption and transient Raman spectroscopies. J. Phys. Chem. 95:3072–3076. [Google Scholar]