Prediction of Growth Factor Effects on Engineered Cartilage Composition Using Deterministic and Stochastic Modeling

Abstract

In the design of engineered tissues, guided balance of biomaterial degeneration with tissue synthesis offers refined control of construct development. The objective of this study was to develop a mathematical model that describes the steady state metabolism of extracellular matrix molecules (ECM: glycosaminoglycan and collagen) in an engineered cartilage construct taking into account localized environmental changes that may arise because of the application of growth factors. The variable effects of growth factors were incorporated in the form of random noise rather than the difference in rates of synthesis and catabolism. Thus, the frequency of ECM accumulation for each matrix molecule in the steady state under the random influence of growth factor was produced relative to the matrix carrying capacity. Published synthesis-rate time constants and steady state ECM conditions from chondrocyte-polymer scaffold composites provided both input and validation for the model. Although the presence of growth factors in the presented system dynamics were considered randomized, the results described a positive feedback or promotional ECM synthesis at low levels of growth factors. While a negative feedback or inhibition of ECM synthesis was characterized at higher levels of growth factors. This transition phenomenon is based on a comparison with the results of a steady state condition in the form of a deterministic model and supports previous reports of guided accumulation in musculoskeletal, connective, and neuronal tissues.

INTRODUCTION

In the design of engineered tissues, balancing the processes of biomaterial degeneration with tissue synthesis is critical during construct development. The combination of these two processes represents the efflux and influx of materials that maintain the biological and mechanical health of the dynamic composite. Cell–polymer constructs as used in engineered cartilage, for example, consist of cells seeded on scaffolds of biodegradable polymers. The scaffolds typically take the form of meshes, foams, or fleeces, and once seeded with cells can be cultured in vitro in a bioreactor or static culture,^7,9,27 or in vivo in an animal model.³ Synthetic scaffolds degrade passively in culture, as the cells proliferate and assemble an extracellular matrix (ECM), which in turn replace the scaffold. The major biomolecules within the neotissue are: structural proteins, specialized proteins, and proteoglycans. Structural proteins consist of collagen and elastin, specialized proteins consist of fibrillin, fibronectin, and laminin, and proteoglycans are a core protein to which is attached to the long chains of repeating disaccharide units termed as glycosaminoglycans (GAG).

In addition to structural support, ECM also acts as a reservoir of growth factors and cytokines, such as IGF-1 (insulin like growth factor), TGF-β (transforming growth factor), and IL-1 (interleukin), respectively.¹ Meaney Murray et al.²⁰ observed that a number of selective growth factors could remarkably increase the collagen production in ECM. Both in vivo and in vitro experiments show that some growth factors enhance the production of biomolecules and some inhibit it.^6,28,32,33

The degeneration and synthesis processes are spatially complementary. Over time the cells deposit and remodel proteins to assume the space of the degrading polymer scaffold. Much of the tissue engineering literature is focused on the processes of scaffold degradation and ECM synthesis through empirical characterizations. There are a few published relationships, however, that quantify the mechanistic factors behind the transient composition of these constructs.²⁴ A basis for biosynthesis kinetics can also be drawn from native tissue research^5,10 and the application of quantitative concepts to cartilage metabolism.^13,14 Balancing the timing of the degradative and synthetic processes through a cellular feedback perspective is critical to understanding the composite construct viability.

Buschmann et al.⁴ have reported on the study of engineering cartilage that there exists a strong negative correlation between GAG molecules deposition and its synthesis rate. A similar type of result has been obtained by Handley and Lowther¹¹ in chondrocyte culture. A mathematical model for native proteoglycan synthesis was described by Hascall et al.^13,14 and restated by Wilson et al.³⁶ for application to engineered cartilage in which:

$$\frac{d(\text{ECM})}{dt}=k_0\{{(\text{ECM})}_{\text{SS}}-(\text{ECM})\}$$ (1)

where, k₀ is a rate constant and the subscript SS denotes the steady state condition (long-term, “mature” engineered tissue at t → ∞ and d(ECM)/dt = 0). Equation (1) then implies:

$${(\text{ECM})}_t={(\text{ECM})}_{\text{SS}}[1-e^{-k_{0}t}]$$ (2)

In this model, specific interactions between the chondrocytes and ECM molecules are addressed as rate constants. The steady state condition is assumed to be a ratio of matrix synthesis and catabolism rates which are indeed influenced by metabolic mediators such as growth factors.¹³ However, the variation in growth factor influence is not stated as a mathematical function, only as a defined rate comparison.

The present article deals with the deposition of ECM molecules in Cell–polymer constructs. The main objective of this paper is to describe deterministic and stochastic models which characterize the steady state accumulation of different ECM molecules in a theoretical engineered cartilage construct. The stochastic model development incorporates localized environment changes that may arise due to the application of growth factors relative to the baseline steady state condition and ECM carrying capacity. Here, the effects of growth factors were incorporated in the form of random noise within the model system. This mathematical model explores a potential mechanism behind the functional characteristics of growth factors within the Cell–polymer construct.

MATERIALS AND METHODS

Model I: Deterministic Model without Growth Factor Variability

Initially, a deterministic model is developed that describes the accumulation of ECM molecules of either primary component (GAG or collagen) in a Cell–polymer construct. In this theoretical arrangement, it is assumed that accumulation of GAG and collagen are independent. This assumption is based on a presumed scaffold cell seeding scenario such that a combination of responses to growth factors, from isolated chondrocytes and chondrocytes in their ECM, would lead to overall independent collagen and GAG metabolism.²¹ In addition, a steady state condition can be achieved in the long-term similar to Eq (2) because of metabolic mediators such as “growth factors.¹³ The formulation of this ECM dynamics model, on the basis of a logistic scheme, is:

$$\frac{d(\text{ECM})}{dt}={{\lambda }^{\prime }}_0(\text{ECM})\left[1-\frac{(\text{ECM})}{K_0}\right]$$ (3)

where λ′₀ in a Cell–polymer construct. K₀ is the carrying capacity for the specific ECM molecule and is drawn from population dynamics as an analogue to the maximized steady state condition.²² The dimensionless form of the modeled system (3) is:

$$\frac{d\omega }{d\tau }={\lambda }_0\omega (1-\omega )$$ (4)

where,

$$\begin{array}{l}\text{ECM}=K_0\omega \\ t=K_0\tau ,\\ {\lambda }_0={{\lambda }^{\prime }}_0{K}_0\end{array}$$ (5)

The general solution to Eq (4) is:

$$\omega =\frac{c{e}^{{\lambda }_0\tau }}{1+c{e}^{{\lambda }_0\tau }}$$ (6)

where, the arbitrary constant, c, can be obtained from the initial condition (τ = 0; ω = ω₀), such that:

$$c=\frac{{\omega }_0}{1-{\omega }_0}\approx {\omega }_0,\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\mathrm{\hspace{0.17em} }\text{as\hspace{0.28em}}{\omega }_0\ll 1$$ (7)

At the steady state condition, τ → ∞ and then ω → 1. Therefore, the solution for GAG molecule accumulation within the ECM is then characterized as:

$$GA{G}_{\tau }=K_1\left(\frac{c_1{e}^{{\lambda }_1\tau }}{1+c_1{e}^{{\lambda }_1\tau }}\right)$$ (8)

Concomitantly, the solution for collagen molecule accumulation is:

$${\text{Collagen}}_{\tau }=K_2\left(\frac{c_2{e}^{{\lambda }_2\tau }}{1+c_2{e}^{{\lambda }_2\tau }}\right)$$ (9)

where, K₁, K₂ are the carrying capacities within the construct, λ₁, λ₂ are the growth rates, and c₁, c₂ are the ar- bitrary constants of GAG and collagen molecules, respectively. These parameters can be evaluated by using the initial condition in Eq (7) and applied to long-term, “maturing” engineered cartilage at τ = 0 → ∞, or inferred from published literature.

Thus, the steady state values for GAG and collagen molecules (when ω → 1) are the carrying capacities, K₁ and K₂, respectively. This steady state analogue is assumed similar to that presented by Hascall et al. as a constant ECM quantity defined by the rate of matrix synthesis per a catabolism proportionality constant.¹³ Actual carrying capacity values are assumed fixed and dependent upon a specific level of growth factor such that d(ECM)/dt = 0. Finally, the total construct mass during steady state metabolism, M_∞ which would include the cellular-mass, M_Cell, and remaining scaffold components, is then:

$$M_{\infty }=M_{\text{Cell}}+K_1+K_2+{\text{Lim}}_{\tau \to \infty }{(\text{Scaffold})}_{\text{initial}}{e}^{-k_2\tau }$$ (10)

where the scaffold degradation dynamics are assumed to follow first order decay kinetics described by Rodriguez³¹ and applied to engineered tissue in Wilson et al.³⁶

Model II: Stochastic Model with Growth Factor Variability

In the metabolism of ECM, the anabolic effects of IGF-1 and TGF-β are in contrast with catabolism because of IL-1. We now extend the anabolic/catabolic interplay into the dynamics of ECM molecule deposition as random fluctuations in the form of Gaussian white noise. This approach enhances the dynamics described in Model I (Eq (3)) to include growth factor variability. The initial model then becomes:

$$\frac{d(\text{ECM})}{dt}=\{{{\lambda }^{\prime }}_0+{\rho }_0{}^{\prime }\eta (t)\}(\text{ECM})\left[1-\frac{(\text{ECM})}{K_0}\right]$$ (11)

or in dimensionless form, from Eq (5):

$$\frac{d\omega }{d\tau }=\{{\lambda }_0+{\rho }_0\eta (\tau )\}\omega (1-\omega )$$ (12)

Where, η (τ) is the Gaussian white noise and ρ₀ = ρ′₀K₀ > 0 is the concentration of growth factor as an additional influence on the dynamics of matrix synthesis. This formulation does not account for the fractional content of the active versus inactive forms of the growth factors. Using a replacement term, which follows directly from the interpretation of the integral of η(τ):⁸

$$dW(\tau )=W(\tau +d\tau )-W(\tau )=\eta (\tau )d\tau$$ (13)

where,

$$dW(\tau )~N(0,d\tau )$$ (14)

such that, N (μ; σ ) is a Normal distribution with mean, μ, and standard deviation, σ . Equation (12) can then be rewritten as:

$$d\omega ={\lambda }_0\omega (1-\omega )d\tau +{\rho }_0\omega (1-\omega )dW$$ (15)

The corresponding probabilistic distribution of the matrix molecules can be described via the Fokker–Planck (FP) equation as:^8,25

$$\begin{array}{l}\frac{\partial P(\omega ,\tau )}{\partial \tau }=-\frac{\partial }{\partial \omega }[{\lambda }_0\omega (1-\omega )P(\omega ,\tau )]\\ +\frac{1}{2}\frac{{\partial }^2}{\partial {\omega }^2}[{\{{\rho }_0\omega (1-\omega )\}}^{2}P(\omega ,\tau )]\end{array}$$ (16)

where, P(ω τ) is the probability density function (PDF) of ECM deposition at time τ.

The growth factor concentration coefficient, ρ₀ is assumed to be increasing as the matrix molecules within the construct are increasing. Therefore, we assume,

$${\rho }_0=\frac{{\Re }_0}{1-\omega }$$ (17)

where, ℜ₀ is the level of growth factor randomly influencing an ECM component.

At the steady state, the PDF of ECM deposition P_∞(ω) is proportional to:³⁰

$${\omega }^{2\left(\frac{{\lambda }_0}{{\Re }_0^2}-1\right)}\text{exp}\left\{-\frac{2{\lambda }_0}{{\Re }_0^2}\omega \right\}$$ (18)

where,

$${\int }_0^1{P}_{\infty }(\omega )d\omega =1$$ (19)

Therefore, the frequency of GAG accumulation in engineered cartilage, which is known to be dependent upon the competing rates of synthesis and catabolism at the steady state condition because of a baseline growth factor level, are now extended to include the random influence of growth factors:

$$\begin{array}{l}{P}_{\infty }(\text{GAG})=C_1{\left(\frac{{\text{GAG}}_{\text{SS}}}{K_1}\right)}^{2\left(\frac{{\lambda }_1}{{\Re }_1^2}-1\right)}\\ \times \text{exp}\left\{-\frac{2{\lambda }_1}{{\Re }_1^2}\left(\frac{{\text{GAG}}_{\text{SS}}}{K_1}\right)\right\}\end{array}$$ (20)

The probabilistic density function for collagen is similar:

$$\begin{array}{l}{P}_{\infty }(\text{Collagen})=C_2{\left(\frac{{\text{Collagen}}_{\text{SS}}}{K_2}\right)}^{2\left(\frac{{\lambda }_2}{{\Re }_2^2}-1\right)}\\ \times \text{exp}\left\{-\frac{2{\lambda }_2}{{\Re }_2^2}\left(\frac{{\text{Collagen}}_{\text{SS}}}{K_2}\right)\right\}\end{array}$$ (21)

where, ℜ₁, ℜ₂ are the levels of growth factor with respect to GAG and collagen molecule synthesis, respectively, and C₁, C₂ are the constants of the proportionalities obtained by applying Eq (19).

Now, let us consider dimensionless forms on the basis of the carrying capacities, $X=\frac{\text{GAG}}{K_1}$, and $Y=\frac{\text{Collagen}}{K_2}$, where the total matrix molecules (Z) within the construct can be represented by a linear relationship:

$$Z=X+Y$$ (22)

The probability density function for the total matrix molecules can then be represented by

$$P\{z<Z<z+\Delta z\}={\int }_{x=0}^{z+\Delta z}{f}_x(x){\int }_{y=z-x}^{z+\Delta z-x}{f}_y(y)dydx$$ (23)

where,

$$f_x(x)=C_1{x}^{2\left(\frac{{\lambda }_1}{{\Re }_1^2}-1\right)}\text{exp}\left\{-\frac{2{\lambda }_1}{{\Re }_1^2}x\right\}\mathrm{\hspace{0.17em} }\text{and}$$ (24)

$$f_y(y)=C_2{y}^{2\left(\frac{{\lambda }_2}{{\Re }_2^2}-1\right)}\text{exp}\left\{-\frac{2{\lambda }_2}{{\Re }_2^2}y\right\}$$ (25)

are the density functions of X and Y , respectively. Hence, the probability density function of Z is:

$$f_z(z)={\int }_0^z{f}_x(x)f_y(z-x)dx$$ (26)

that implies,

$$\begin{array}{l}{f}_z(z)=C_1{C}_2\times B\left(\frac{2{\lambda }_2}{{\Re }_2^2}-1,\frac{2{\lambda }_1}{{\Re }_1^2}-1\right)\\ {\times }_2{F}_2\left\{\begin{array}{l}1,\frac{2{\lambda }_1}{{\Re }_1^2}-1;2\left(\frac{{\lambda }_1}{{\Re }_1^2}-\frac{{\lambda }_2}{{\Re }_2^2}\right)z\\ 1,2\left(\frac{{\lambda }_1}{{\Re }_1^2}+\frac{{\lambda }_2}{{\Re }_2^2}\right)\end{array}\right\}\\ \times z^{\left(\frac{2{\lambda }_1}{{\Re }_1^2}+\frac{2{\lambda }_2}{{\Re }_2^2}-3\right)}\times \text{exp}\left(-2\frac{2{\lambda }_2}{{\Re }_2^2}z\right)\end{array}$$ (27)

where,

$$B(\alpha ,\beta )=\frac{\Gamma (\alpha )\Gamma (\beta )}{\Gamma (\alpha +\beta )}\mathrm{\hspace{0.17em} }\text{and}$$ (28)

$$\Gamma (z)={\int }_0^{\infty }{t}^{z-1}{e}^{-t}dt\mathrm{\hspace{0.17em} }\text{or},$$

$$\Gamma (z)-{{\int }_0^1\left[\text{in}\left(\frac{1}{t}\right)\right]}^{z-1}dt,\mathrm{\hspace{0.17em} }\text{for\hspace{0.28em}}real(z)>0$$

are the Beta function and the Gamma function, respectively, and

$$\begin{array}{l}{}_p{F}_q\left\{\begin{array}{l}{a}_1,\dots \dots \dots ,a_p;u\\ b1,\dots \dots \dots ,b_q\end{array}\right\}\\ =\sum _{k=0}^{\infty }\frac{{(a_1)}_k\dots \dots \dots {(a_p)}_k}{{(b_1)}_k\dots \dots \dots {(b_q)}_k}\left(\frac{u^k}{k!}\right)\end{array}$$ (29)

is the generalized Hypergeometric function.

For simplicity, we assume that the influence of growth factors do not affect the scaffold dynamics. As such, we will use first order decay kinetics for scaffold degradation:^31,36

$$\frac{d(\text{Scaffold})}{dt}=-\gamma [\text{Scaffold}]$$ (30)

Finally, by assuming that cell–mass is constant (although this is not the case in reality as described by Meaney Murray et al.²⁰), then the mean total engineered cartilage construct mass during steady state metabolism can be described by:

$$\begin{array}{l}{M}_{\infty }=M_{\text{Cell}}+(K_1+K_2){\int }_0^{2}z{f}_z(z)dz\\ +{\text{Lim}}_{\tau \to \infty }{(\text{Scaffold})}_{\text{initial}}{e}^{-k_2\tau }\end{array}$$ (31)

In addition to the ECM carrying capacities, important parameters of the two probability models within Model II (Eqs 20 and 21) are the growth rates of ECM molecules, λ₁ and λ₂, and the levels the growth factor with respect to matrix molecule synthesis, ℜ₁ and ℜ₂. Wilson et al. substituted λ_i , (where i = 1, 2 for GAG and collagen) with one over a characteristic time constant, χ_i (where i = 1, 2 for GAG and collagen), and defined its value via a model fitting technique.³⁶ Similarly, the growth fctor levels, ℜ_i (where i = 1, 2 for GAG and collagen) are input parameters which can be experimentally observed to achieve steady state metabolism,¹³ or adjusted within the mathematical model to guide construct design, as will be done here. Experimental results of matrix molecule accumulation have been reported by others and are shown in Table 1. These data were used as input for the presented mathematical model simulation.

TABLE 1.

A subset of published matrix accumulation, modeling parameters,³⁶ applied to the deterministic and stochastic models.

Scaffold	Cell type	Reference	GAGss	Collagenss	χ (days)
Agarose	BAC	Buschmann et al. (1992)	17.2 mg/ml		17.1
Alginate	BAC	Ragan et al. (2000)		15.7 μg/μg DNA	22.4
PGA/PLA	BAC	Wilson et al. (2002)	6.1% dw		187
PGA/PLA	BAC	Wilson et al. (2002)		6.5% dw	18.9

Note. BAC = Bovine articular cartilage; PGA = Polyglycolic acid; PLA = Polylactic acid.

COMPUTER SIMULATION RESULTS

For the numerical analysis based on the mathematical model where growth factor effects are not directly manipulated (Model I), the GAG molecule growth rate, λ₁, was approximated by 1/χ₁ (Table 1). The numerical solution of GAG accumulation (dimensionless form) with respect to time (dimensionless form) was determined (Fig. 1). Accumulation curves over time were obtained by estimating the parameter λ₁ from experimental data reported by Buschmann et al.⁴ and Wilson et al.³⁶ Qualitatively, the numerical solutions of GAG accumulation were similar to that of the experimental data points from which the model was based.^4,36

FIGURE 1.

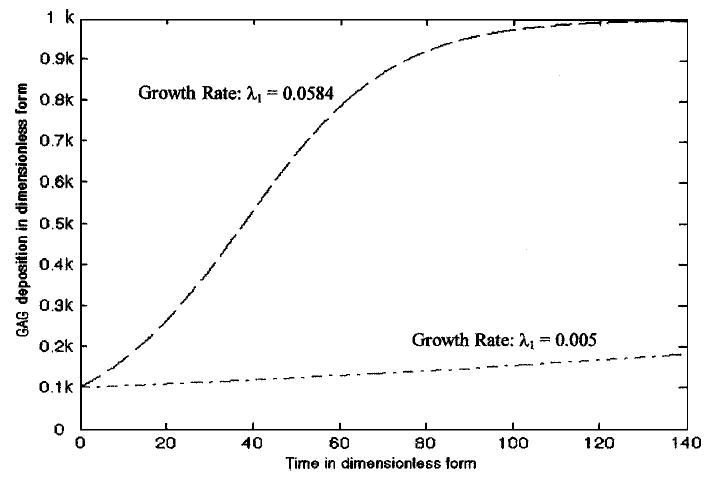
Numerical solution of GAG accumulation in an engineered cartilage construct without growth factor variability (Model I Eq 8). The top curve (dash line) was obtained by approximating the growth rate as λ₁ = 0.0584 (estimated from the data reported by Buschmann et al.⁴) and the bottom curve (dash–dot line) has been obtained by approximating λ₁ = 0.005 (estimated from the data reported by Wilson et al.³⁶). Here k is the carrying capacity of the GAG molecules in engineered cartilage constructs (noted as K₁ in the text).

The numerical solution of collagen accumulation (dimensionless form) with respect to time (dimensionless form) without direct growth factor manipulation was determined (Fig. 2). The accumulation curves were obtained by estimating the collagen growth rate parameter λ₂ from experimental data reported by Wilson et al.³⁶ and Ragan et al.²⁹ The numerical solution of collagen accumulation was qualitatively similar to the experimental results from Wilson et al.³⁶ but does not match with the Ragan et al.²⁹ data.

FIGURE 2.

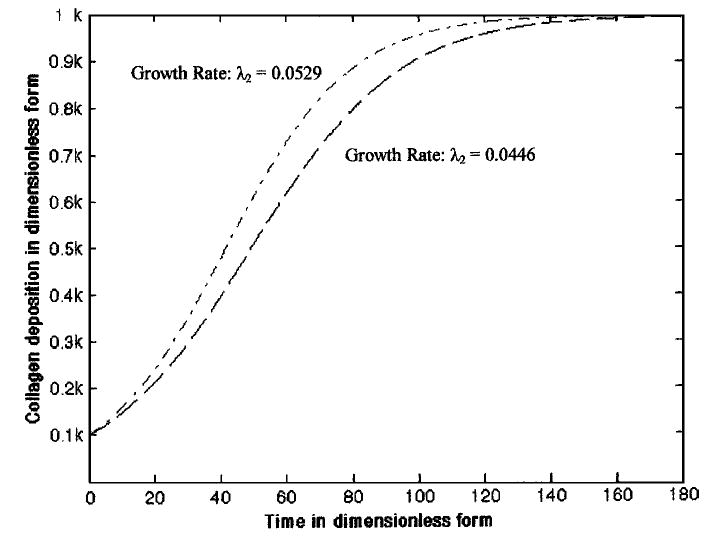
Numerical solution of collagen deposition in an engineered cartilage construct (Model I Eq. 9). The bottom curve (dash line) has been obtained by approximating the growth rate λ₂ = 0.0446 (estimated from the data reported by Ragan et al.²⁹) and the top curve (dash–dot line) has been obtained by approximating λ₂ = 0.0529 (estimated from the data reported by Wilson et al.³⁶). Again, k is the carrying capacity of the collagen molecules in engineered cartilage constructs (noted as K₂ in the text).

For Model II, which modified Model I to include growth factor variability, the steady state probability density functions of GAG and collagen molecules incorporated in equations (20) and (21) were determined (Figs. 3 and 4). These results indicate how the potential stochastic environment would affect ECM synthesis on a local level. Additionally, the computational results indicated the following features in engineered cartilage constructs dynamics: First, the effect of growth factor was not necessarily the same on both the matrix molecules. Utilizing experimental data on engineered cartilage accumulation,³⁶ the simulated level of growth factor for GAG synthesis varied within the interval 0.004 < ℜ₁ < 0.099, whereas for collagen molecules, the level term varied, 0.02 < ℜ₂ < 0.316. The regulatory effects due to different types of mediator molecules, such as decorin and biglycan with dermatan sulfate chains, and fibromodulin with keratan sulfate chains may be primarily responsible for this but were not modeled.

FIGURE 3.

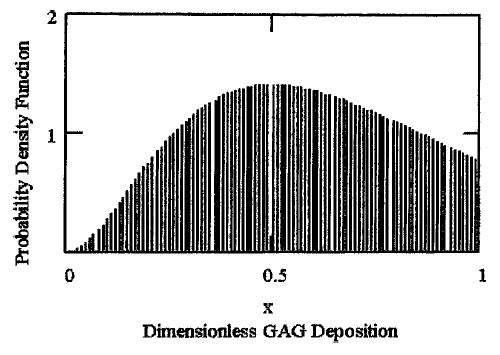
The steady state probability density function for GAG accumulation as a fraction of construct carrying capacity under the simulated variability of growth factor (described by equation 20), where λ₁ = 1/187,³⁶ and ℜ₁ = 0.05.

FIGURE 4.

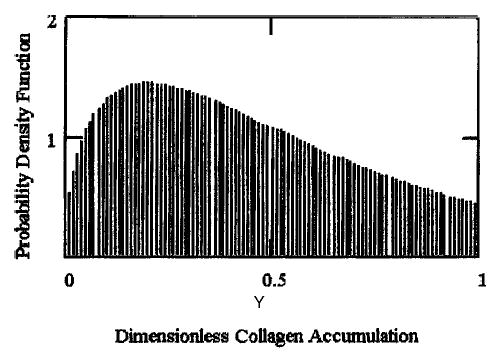
The steady state probability density function for collagen deposition as a fraction of construct carrying capacity under the simulated variability of growth factor (described by equation 21), where λ₂ = 1/18.9,³⁶ and ℜ₂ = 0.2.

Second, both inhibition and stimulation of total matrix deposition within the construct were entirely dependent upon the level of growth factor within the simulated construct. The numerical outcome of the total matrix molecule deposition (GAG + Collagen) in the steady state was determined (Fig. 5) on the basis of the parametric values given in Table 1. From the simulation, when the combined effects of the growth factor (ℜ₁ + ℜ₂) were less than a threshold value of ~0.2, then the overall matrix molecule deposition in the steady state was higher than its deterministic counterpart (i.e., Model I). In that case, the combined effects of growth factor stimulate the overall deposition of matrix molecules within the construct. Alternatively, when the growth factor state (ℜ₁ + ℜ₂) was less than the thresh-old value, additional growth factors appeared to inhibit the deposition of matrix molecules.

FIGURE 5.

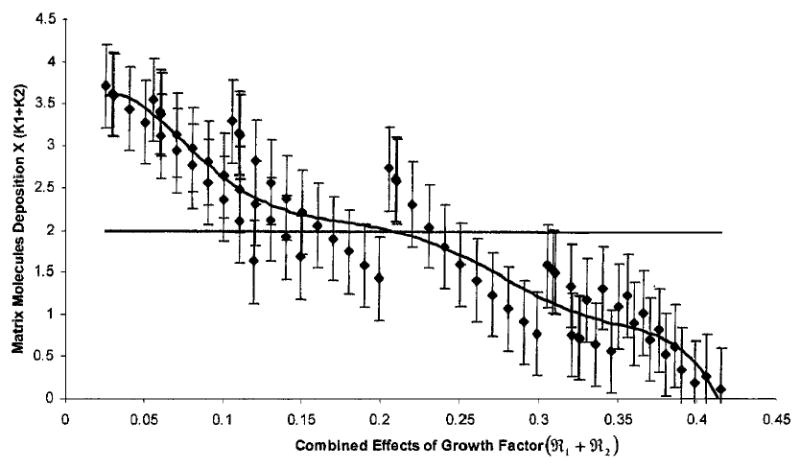
A plot demonstrating the simulated deposition of GAG plus collagen molecules in the steady state condition (τ → ∞) due to a perturbation in growth factors. The abscissa indicates the leve of growth factors (ℜ₁ + ℜ₂) and the ordinate represents the deposition of matrix molecules as a coefficient of the carrying capacities (K₁ + K₂). The solid horizontal line in the middle of the plot represents the total ECM accumulation where the variability of growth factor was not extended beyond that achieving a fixed, steady state condition (outcome of Model I). Data points are mean ECM accumulation (±5% of the combined probable distributions) for possible steady state conditions when made dependent upon different levels of additional growth factor (outcome of Model II). The curve represents the line of best fit. The model parameters were chosen from the experimental data of Table 1.³⁶

DISCUSSION

It is well-known from experimental reports that growth factors have some effect on the dynamics of Cell–polymer constructs. Investigators have made great strides in deciphering the sophisticated signal transduction processes triggered by application of a growth factor to a cell, or engagement of a receptor by a growth factor. These discoveries have not all been reduced to definitive mechanistic models for tissue engineering. Experimentalists are still exploring growth mechanisms in native and engineering tissues via controlled methods, resulting in a few definitive conclusions. As potential insight to this complex issue, this study incorporates the effects of growth factor dynamics as a stochastic fluctuation into the system’s environment and examines the effects on the overall composition.

Although the numerical analysis simulating ECM synthesis in Model I was driven toward a deterministic state based on experimental steady state conditions, the dynamic influence of growth factors was only explored in Model II. Nonaggregating proteoglycans such as decorin, biglycan and fibromodulin are common in all cartilage tissue. These small molecules interact with collagen fibrils and regulate transforming growth factor β’s (TGF-β) activities by sequestering it within the ECM.¹⁶ It has been reported by several other researchers that these small proteoglycan molecules are responsible for regulating the activities of TGF-β within the ECM.^15,19,23,34 Although, the exact mechanisms of how the growth factors release its effects on the matrix molecules are not clear, there is evidence that the functional activity of the growth factor increases as matrix molecule concentration increases. On the basis of this hypothesis, a monotonic increasing function of matrix molecules (Model I) was modified with a function involving randomized effects of additional growth factor (Model II).

Working principles of ECM metabolism within the cartilage Cell–polymer constructs are not fully known. Researchers understand that growth factors and cytokines have strong anabolic and catabolic influences, respectively, on the dynamics of matrix molecules. However, deterministic physiological laws have not yet been identified. From a mathematical point of view, the effects of growth factors in the presented system dynamics were considered randomised (via Gaussian white noise) and the ECM components independent in the cellular environment. It has been reported that synthesis of collagen and proteoglycans by chondrocytes are dependent upon the state of the surrounding matrix and respond uniquely if that matrix is absent.^12,26 Our results indicate that an inhibition or stimulation of matrix molecules deposition may be modeled as dependent upon the initial application of growth factor within the system. In a recent growth model of native cartilage explants,¹⁸ residual stresses were considered which describe a compressive state within the proteoglycans because of the increased fixed charge density while being balanced against a tensile stress supported by the collagen network. This result offers insight for in vivo developmental cartilage growth (chondrocytes surrounded by their own matrix), however, cell-seeded constructs may not have the same mechanical boundary constraints or functional cultured time frame because of varying seeding densities, cell adhesions, scaffold porosities, transport phenomena, and culture states.

Relevant comparisons between the mathematical outcomes shown here and published experimental findings examining growth factor influences are available. Pei et al. reported from their experimental work on in vitro generation of cartilaginous constructs, that the combination of growth factors TGF-β₁ and FGF-2, applied sequentially from day 3 to day 10, inhibits the collagen and GAG accumulation in ECM deposition remarkably.²⁸ Additional evidence of this inhibition was reported by Horton et al.¹⁷ Meaney Murray et al. reported from their experimental work on human anterior cruciate ligament cells that the growth factors TGF-β₁ and PDFG-AB (platelet derived growth factor) have a significant role in enhancing the production rate of collagen.²⁰ Finally, it has been reported by Weiser et al. that the production of proteoglycan was significantly hampered under the influence of PDGF-BB.³⁵ In non-connective tissue, low doses of brain-derived neurotrophic factor, BDNF (0.5 to 2 μg/day for 28 days), which includes nerve growth factor, NGF, and neurotrophin, NT, promoted axonal regeneration after axotomy.² While high doses of BDNF (12 to 20 μg/day for 28 days) significantly inhibited motor axonal regeneration after immediate nerve repair. Thus the presented model may offer a predictive tool for the reported transition phenomenon from promotion to inhibition during guided ECM synthesis.

A question that arises from this work is whether growth factors alter the overall construct mass in the steady state. By design, the mathematical approach described in Model I (Eq 10) drives the construct to a final, deterministic state because of a presumed growth factor precondition that has established steady state metabolism. This phenomenon was described experimentally when 20 ng/ml of insulin-like growth factor maintained a steady state condition in proteoglycan concentration.¹³ However, Model II (Eq 31) alters the dynamics in the final state of Model I by providing a mathematical means for probabilistic steady state end points in the construct design. Actual steady state mass of the total composite may be static if growth factors act as an inhibitor of a particular type of matrix molecule while activating or enhancing the production of other ECM molecules in addition to promoting or enhancing chondrocyte proliferation. As such, a long-term balance may be maintained and overall construct mass may be regulated through a suggested product inhibition machanism.^13,36 Of course, neotissue synthesis and scaffold degradation would require guided dynamics during the early stages of development through time points leading to steady state. This time dependency is incorporated in both developing constructs: Model I (with deterministic endpoints in equations 8 and 9) and Model II (with probabilistic endpoints in equations 20 and 21). An additional level of mathematical complexity would incorporate growth factor dependencies into the ECM_ss and carrying capacity endpoints as empirically reported by Hascall et al.¹³

The computer simulations show that the effects of growth factors as a probabilistic ECM distribution, controlled the steady state total GAG and collagen accumulations whether through stimulation or inhibition. For lower amounts of growth factor, an increase in collagen and GAG accumulation was noted in comparison with the steady state value derived without accounting for additional growth factor influence. In addition, excessive amounts of growth factor may inhibit the steady state deposition of collagen and GAG molecules. Finally, only steady state analysis was described in this paper. Long-term, transient analysis of the above system is under construction.