Extension of the SIMLA Package for Generating Pedigrees with Complex Inheritance Patterns: Environmental Covariates, Gene-Gene and Gene-Environment Interaction

Abstract

We have previously distributed a software package, SIMLA (SIMulation of Linkage and Association), which can be used to generate disease phenotype and marker genotype data in three-generational pedigrees of user-specified structure. To our knowledge, SIMLA is the only publicly available program that can simulate variable levels of both linkage (recombination) and linkage disequilibrium (LD) between marker and disease loci in general pedigrees. While the previous SIMLA version provided flexibility in choosing many parameters relevant for linkage and association mapping of complex human diseases, it did not allow for the segregation of more than one disease locus in a given pedigree and did not incorporate environmental covariates possibly interacting with disease susceptibility genes.

Here, we present an extension of the simulation algorithm characterized by a much more general penetrance function, which allows for the joint action of up to two genes and up to two environmental covariates in the simulated pedigrees, with all possible multiplicative interaction effects between them. This makes the program even more useful for comparing the performance of different linkage and association analysis methods applied to complex human phenotypes. SIMLA can assist investigators in planning and designing a variety of linkage and association studies, and can help interpret results of real data analyses by comparing them to results obtained under a user-controlled data generation mechanism.

A free download of the SIMLA package is available at http://wwwchg.duhs.duke.edu/software.

Introduction

Many software packages for linkage and association analysis of complex human diseases are currently available. Methodological advances continue to be implemented in new versions of existing software, or entirely new analysis packages, as evidenced by the frequent updates of online software listings (e.g., http://linkage.rockefeller.edu). However, only a few generally available programs exist that can simulate pedigree data based on user-specified generating models and allow the investigator to evaluate and compare the performance of several competing linkage or association analysis methods prior to applying them to a real data set. These packages include SLINK (Ott 1989; Weeks et al. 1990), SIMLINK (Boehnke 1986; Ploughman and Boehnke 1989), and SIMULATE for linkage applications, and POWERFBAT (Laird et al. 2000) for family-based association simulations. In addition, several statistical genetic analysis packages, such as MERLIN (Abecasis et al. 2002) and SOLAR (Almasy and Blangero 1998), provide simulation-based empirical p-values. However, in most cases, the null and alternative hypotheses are constrained to answer very specific questions. Our goal in creating the simulation package SIMLA (SIMulation of Linkage and Association) (Bass et al. 2004) was to develop a simulation package that can be used to answer a variety of questions of interest to those developing statistical methods for genetic analysis. SIMLA is also a valuable tool for investigators conducting studies of complex disorders, who may wish to evaluate the performance of competing linkage or association analysis methods prior to applying them to a real data set.

We have previously developed and distributed an earlier version (2.3) of SIMLA, which was instrumental for the development and evaluation of several novel analysis methods and corresponding software packages for linkage and association analysis (Martin et al. 2000; Martin et al. 2003; Hauser and Boehnke 1998; Hauser et al. 2004; Boyles AL et al. 2005). The previous SIMLA version implemented the simulation of three-generational pedigrees with binary (affected/unaffected) disease phenotypes under various user-specified ascertainment criteria (e.g., affected proband, affected sibling pair, discordant sibling pair etc.). It was able to simulate up to 10 unlinked biallelic disease genes with user-specified mode of inheritance, penetrance values and allele frequencies, but only one of them could segregate within a single pedigree. Up to 350 markers with up to 7 alleles each could be generated, and these markers could be linked to any single disease locus according to a user-specified map of recombination frequencies between loci. Data sets with genetic heterogeneity were simulated by specifying the proportion of families linked to a particular disease locus. Random genotype error and selection of individuals with available genotypes for analysis was also possible. A unique feature of the program was the ability to generate various levels of linkage disequilibrium (LD) between marker haplotypes and disease loci by specifying conditional marker allele or haplotype frequencies for chromosomes with and without a disease allele.

Limitations of the previous SIMLA version included the inability to simulate segregation of more than one disease gene per pedigree and failure to account for the contribution of environmental factors to the risk for a complex disease phenotype. Consequently, gene-gene (G×G) and gene-environment (G×E) interactions could not be simulated. Here, we present an extension of the SIMLA package (version 3.0) that incorporates these important features and is therefore able to generate pedigree data under more complex models, which are likely to better approximate the reality of human disease phenotypes. Our particular motivation for implementing these extensions was an ongoing genetic study of age-related macular degeneration (AMD), which is a complex, relatively common ophthalmologic disorder with substantial evidence of both genetic and environmental contributions to disease risk (Gorin et al. 1999). Previous genome screen analyses of our data suggested that known risk factors for AMD, such as body mass index, systolic blood pressure, and pack-years of cigarette smoking, may define subgroups of genetically more homogeneous families with increased evidence of linkage to certain genomic regions (Schmidt et al. 2004). Candidate gene analyses raised the possibility that the disease risk conferred by genotypes at the apolipoprotein E (APOE) locus on chromosome 19q13 may vary by an individual’s smoking history (Scott et al. 2004). To better interpret these interesting findings in our real data set, it is important to evaluate the performance of genetic analysis approaches when data are generated under a controlled simulation mechanism using models that reflect the inherent complexity in this and other disorders.

Methods

The simulation of pedigree data with SIMLA is performed according to a user-specified control file, which is the only required input for the program. Compared to SIMLA version (2.3), setting up this control file has been simplified with a text-based user interface that provides default parameter values and performs various plausibility checks, as detailed in the user manual. Software, a user manual and an example control file are available for download at http://wwwchg.duhs.duke.edu/software. The code was written to compile on Microsoft Visual C++ 6.0 and GNU C++ 3.0.2. It runs on most Unix and Windows-based operating systems. SIMLA has been tested on Windows 2000, Windows XP and on Solaris 8. Since SIMLA uses the same programming code to compile on Windows and Solaris, it should only require minor modifications to successfully compile and run on Mac OSX and Linux. To accommodate other operating systems, we will make source code available to interested users. Registration is required for future notification regarding program upgrades, and contact information is not used for any other purpose.

The following sections describe several parameters specified in the SIMLA control file, with an emphasis on the newly implemented penetrance function. Disease risk may simultaneously be influenced by up to two (linked or unlinked) disease loci, a binary and/or a continuous environmental covariate, and interactions between these risk factors.

The chromosome and loci structure

For each pedigree member, up to three chromosomes with up to 1000 marker loci each can be generated under Hardy-Weinberg equilibrium. Chromosome-specific genetic maps with intermarker distances are specified in Morgan (M) and converted to recombination fractions according to the Haldane or Kosambi mapping functions. Up to two biallelic disease loci may be distributed on these chromosomes, with the third chromosome providing the option to analyze markers completely unlinked to any disease locus. We use the term normal allele or “d_i” to describe the non-susceptibility allele and “D_i” to describe the disease susceptibility allele. The susceptibility allele at each disease locus, D₁ for disease locus G₁ and D₂ for disease locus G₂, may be in linkage disequilibrium (LD) with a particular single marker allele, or a haplotype of several marker alleles. LD is generated via user-specified haplotype frequencies for chromosomes with and without the D₁ or D₂ allele.

The pedigree structure

Each pedigree has the same general structure consisting of three generations of family members: Two grandparents, the parental sibship with two assumed matings, which generate the proband sibship and one cousin sibship. The total maximum pedigree size is specified via the sibship size, which may range from 2 to 5 and applies to each of the three sibships. Figure 1 illustrates a pedigree with sibship size equal to three. All pedigrees generated by SIMLA 3.0 conform to this general structure (Figure 1). Variability in family structure may be introduced by concatenating output files obtained by running SIMLA with different parameter files. To generate only nuclear families, for example, the user may specify the deletion of individuals in the non-proband generations. Each generated pedigree has exactly four founders, the two grandparents and the two married-in spouses, and thus there are eight possibly distinct founder alleles at each locus. For computational convenience, each individual’s alleles are stored as numbered founder alleles that are converted into observed alleles via a lookup table, taking into account user-specified allele (or haplotype) frequencies, Mendelian inheritance rules, and recombination frequencies. If a genotype error rate of 1 ≥ P(err) > 0 is entered, the true allele will be misread with probability P(err) and substituted with a random allele with probability P(1/n) for an n-allelic marker.

Figure 1.

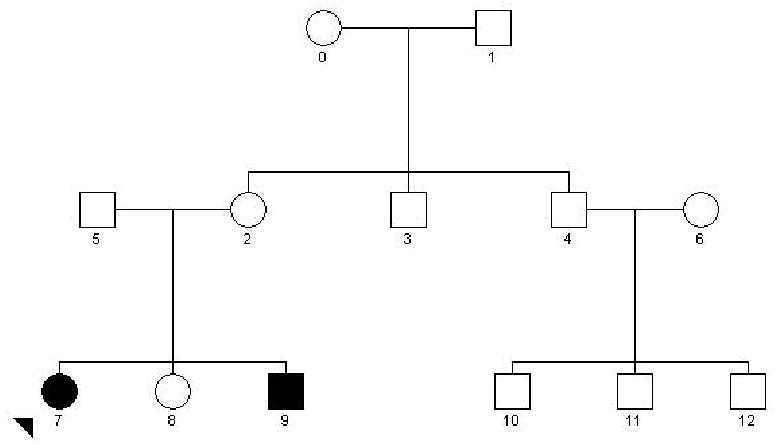
A standard pedigree created by the SIMLA program. All generated pedigrees have the same structure and size, determined by the user-specified sibship size (here 3) for the three sibships.

Simulation of meiosis

SIMLA initially generates eight founder chromosomes for the four founders of each pedigree. Chromosomes are passed down from parents to children in Mendelian fashion. Crossovers occur randomly based on the mapping distance specified in the control file. Meiosis takes part in two stages. During stage 1, the parental chromosome that will be passed to the offspring is determined and up to two disease loci segregate through the pedigree. During the second stage, all markers are taken into consideration working from the disease loci out towards the ends of the marker map. After stage 1, the pedigree has all the data needed to determine the disease status of all its members. The motivation for this algorithm is the fact that most pedigrees will not meet the ascertainment criteria, especially when simulating rare diseases. These pedigrees will be rejected before they reach stage 2, where most of the computational effort is expended. An interesting problem arises when both disease loci are located on the same chromosome and have several markers separating them. In this case all recombination events between them are recorded during the first stage, starting at G₁ and proceeding all the way to the G₂ locus. Only if the pedigree meets ascertainment criteria are these recombination events translated into actual alleles that were passed to the next generation. The simulation algorithm is illustrated in Figure 2.

Figure 2.

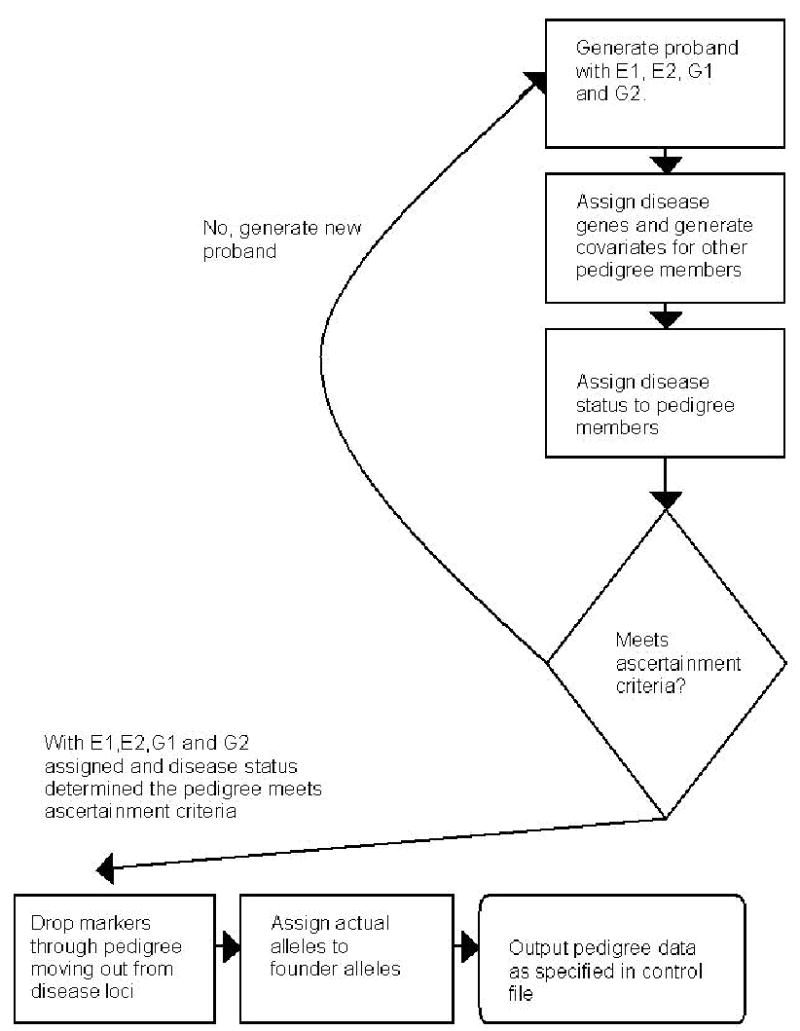
Flowchart describing proband and pedigree generation. E1: binary environmental covariate 1, E2: continuous environmental covariate 2, G1:biallelic disease gene 1, G2: biallelic disease gene 2.

Simulation of environmental covariates

SIMLA can generate up to two environmental covariates, one binary, denoted by E₁, and one continuous, denoted by E₂. To account for familial correlations of environmental risk factors, each covariate can be positively correlated within a sibship or within the entire pedigree. While the binary covariate can only take on the values 0 or 1 by definition, the distribution of the continuous covariate is more complex and can be thought of as a “double-truncated” normal distribution. Since the penetrance function is specified in terms of relative risk (RR) parameters for a unit increase in covariate values (see below), it is desirable to scale the continuous covariate to the interval [0,1] to be directly comparable to the binary covariate. For some covariates, a value of 0 may have a particular meaning. For example, if E₂ represents the variable “pack-years of cigarette smoking”, which is a known risk factor for AMD, the value 0 corresponds to non-smokers (i.e., absence of exposure). The user may choose to assign this value to a fixed proportion of individuals, which may be based on available real data sets for the disorder under study. The left tail of the distribution of E₂ is thus truncated so that a user-specified proportion of individuals are assigned the lowest possible E₂ value of 0. The right tail of the distribution is truncated at 99% of the probability mass, and simulated E₂ values exceeding this upper limit are assigned the highest possible value of 1. After double-truncation and scaling to the interval [0,1], the actual distribution from which E₂ values are sampled resembles Figure 3 if 25% of the population are assumed to be unexposed (E₂ = 0).

Figure 3.

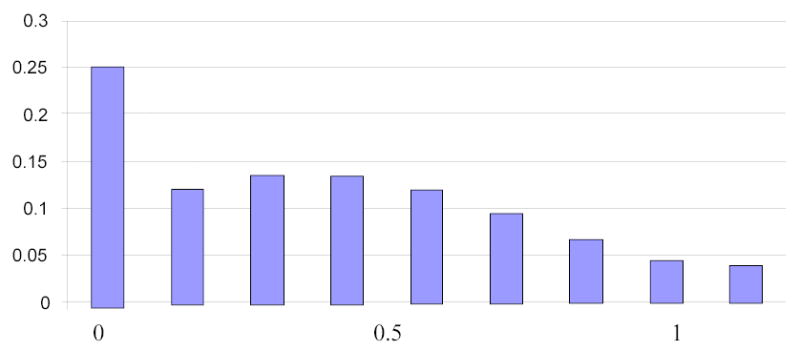
“Double-truncated” standard normal distribution from which E2 covariate values are sampled, with 25% of individuals in the general population assumed to be unexposed (E2=0).

The penetrance function is specified by the 17 user-defined parameters shown in Table 1. Penetrance values are calculated from a prospective logistic regression model, in which the logit (log-odds) of being affected is defined as a linear function of the covariates of interest (equation 1):

Table 1.

Parameter vector for user-specified penetrance function (see text for details).

	Parameter name	Description
1	P(D1)	Allele frequency of disease allele D1 at locus G1
2	W(G1)	Code for mode of inheritance at disease locus G1
3	P(D2)	Allele frequency of disease allele D2 at locus G2
4	W(G2)	Code for mode of inheritance at disease locus G2
5	P(E1 = 1)	Frequency of exposure to binary covariate E1
6	P(E2 = 0)	Frequency of non-exposure to continuous covariate E2
7	RR(D1/D1)	Relative risk of homozygous disease genotype at G1
8	RR(D2/D2)	Relative risk of homozygous disease genotype at G2
9	RR(E1)	Relative risk for unit increase in binary covariate E1
10	RR(E2)	Relative risk for unit increase in continuous covariate E2
11	RR(G1, E1)	Relative risk for G1×E1 interaction
12	RR(G1, E2)	Relative risk for G1×E2 interaction
13	RR(G2, E1)	Relative risk for G2×E1 interaction
14	RR(G2, E2)	Relative risk for G2×E2 interaction
15	RR(G1, G2)	Relative risk for G1×G2 interaction
16	RR(E1, E2)	Relative risk for E1×E2 interaction
17	k	Disease prevalence in general population

$$\text{ln}\left(\frac{P(affected|\overrightarrow{x})}{1-P(affected|\overrightarrow{x})}\right)={\beta }_0+\sum _{i=1}^{10}{\beta }_i{x}_i$$ (1)

Equation (1) is equivalent to

$$P(affected|\overrightarrow{x})=\frac{\text{exp}({\beta }_0+\sum _{i=1}^{10}{\beta }_i{x}_i)}{1+\text{exp}({\beta }_0+\sum _{i=1}^{10}{\beta }_i{x}_i)}$$

The β_i parameters of the model correspond to the natural logarithm (ln(x)) of the desired relative risks (RRs) of disease due to a one-unit increase in the respective covariate value x_i (see table 1 and table 2 for details). The 17 parameters include allele frequencies at the two disease loci (G₁ and G₂), exposure frequency for E₁, proportion of unexposed individuals for E₂, RR parameters for the effect of G₁ and G₂ in the absence of exposure to E₁ and E₂ (“main genetic effects”), RR parameters for the effect of E₁ and E₂ in carriers of the “normal” (non-susceptible) genotypes at G₁ and G₂ (“main environmental effects”), and RR parameters for the 6 possible interaction effects on the multiplicative scale, which are coded as product terms in the logistic regression model (table 2).

Table 2.

Definition of covariates for penetrance function (equation 1). E1: binary environmental covariate 1, E2: continuous environmental covariate 2, G1:biallelic disease gene 1, G2: biallelic disease gene 2.

Variable in logistic regression model	Definition
x1	0 for genotype d1/d1 at disease locus G1; W(G1) for genotype D1/d1 at locus G1; 1 for genotype D1/D1 at locus G1
x2	As above for disease locus G2
x3	Environmental covariate E1 ∈ {0,1}
x4	Environmental covariate E2 ∈ [0,1]
x5	= x1x3, G1×E1 interaction
x6	= x1x4, G1×E2 interaction
x7	= x2x3, G2×E1 interaction
x8	= x2x4, G2×E2 interaction
x9	= x1x2, G1×G2 interaction
x10	= x3x4, E1×E2 interaction

The coding of susceptible and non-susceptible genotypes in the model is determined by the user-specified mode of inheritance (dominant, recessive, multiplicative (i.e., additive on the log-scale) or intermediate), as described below. Once all exposure frequencies and RR parameters are specified, the desired population prevalence of the disease, denoted by k, is used to compute the intercept β₀ of the logistic regression model, which is the logarithm of the baseline disease risk in the absence of any exposure. An iterative algorithm calculates this unique value of β₀. Our implementation uses a slight modification of Newton’s method. Once β₀ is determined, the penetrance function is fully specified.

Mode of inheritance

The mode of inheritance can be specified by a weight factor, W ∈ [0,1], that is assigned to the heterozygous genotype Dd. By definition; RR(dd) 1. Let a = RR(DD) and b = RR(Dd), with a ≥ b ≥ 1 and ln(b) W *ln(a). Then, W = 0 specifies a recessive model (b = 1), W = 1 specifies a dominant model (a = b) and W = 0.5 specifies a multiplicative model (b² = a ). If desired, various intermediate “additive” models can be specified by choosing $W=\frac{\text{ln}(a+1)-\text{ln }2}{\text{ln }a}\in (\frac{1}{2},1)$. This intermediate coding corresponds to a more general group of inheritance models where the risk for the heterozygous genotype 1 is midway between the two homozygous genotypes $(b=\frac{a+1}{2})$. The covariate coding used in the logistic regression model for each of these options is shown in table 2. The user is responsible for supplying the value of W corresponding to the desired inheritance model.

Generation of covariate values for the proband

Covariate values for the proband have to be generated conditional on the fact that the proband is known to be affected. Since E₂ is a continuous covariate, a rejection algorithm would have to be implemented to allow any of the infinitely many possible values of the E₂ covariate to be assigned to probands (Gauderman 1995). However, to make the simulation algorithm computationally more efficient, we chose to sample E₂ values from a finite number of discrete categories derived from the assumed “double-truncated” normal distribution described above. Specifically, two categories correspond to the truncated probability mass in the left and right tail of the E₂ distribution. The remaining probability mass is distributed equally across 28 categories, for a total of 30 distinct intervals of E₂ values. The midpoint of each interval is used as the actual value that may be assigned to a proband. We thus have 3 possible values for genotypes at each of the two disease loci G₁ and G₂, 2 possible values for the binary E₁ covariate, and 30 possible values for the “categorized continuous” E₂ covariate. Assuming population independence of G₁, G₂, E₁ and E₂, this leads to 3×3×2×30=540 possible values for covariate combinations. Let X_i denote random variables corresponding to the 10 model covariates in table 2, and let x_i denote the particular values they may take on. Let $f(\overrightarrow{X})$ be our penetrance function with $c_i=f(\overrightarrow{x_i})$ and $p_i=P(\overrightarrow{x_i})$ for i = 1,…,540. The disease prevalence is $k={\sum }_{i=1}^{540}{c}_i{p}_i$ with ${\sum }_{i=1}^{540}{p}_i=1$. For any fixed 1 ≤ j ≤ 540, the probability of that particular covariate combination for the proband is then derived by Bayes’ formula:

$$\begin{array}{l}P\{(X_1,\dots ,X_{10})=(x_1,\dots ,x_{10})|affected\}\\ =\frac{P(affected|(X_1,\dots ,X_{10})=(x_1,\dots ,x_{10}))\times P((X_1,\dots ,X_{10})=(x_1,\dots ,x_{10}))}{P(affected)}\\ =\frac{c_j{p}_j}{k}\end{array}$$ (2)

All 540 partial sums $S_n=\sum _{i=1}^n{c}_i{p}_i,n\in \{1,\dots ,540\}$, with S_n+1 ≥ S_n are listed in a lookup table. Then a random number r ∈ [0, k] is generated, and its index in the lookup table is determined to efficiently generate a proband’s realized covariate combination. After the proband’s disease genotype has been determined, the corresponding founder alleles are assigned to that genotype based on an allele lookup table.

Generation of covariate values for relatives

The program has three options for assigning environmental covariates to non-proband pedigree members. The proband’s covariate values are determined given that this individual is affected, as described above. The first option assumes independence of covariates within families. With the second option, the covariate values of the four founders are assigned randomly, but covariate realizations within sibships are correlated. The user assigns a positive correlation coefficient for each of the three sibships in a pedigree and the program determines correlated standard normal values accordingly. A positive correlation coefficient is necessary in order to obtain a positive definite correlation matrix. The third option is to choose the same positive correlation coefficient for the entire pedigree, including married-in spouses.

To generate correlated values within the parent and cousin sibship, we use the fact that X_nx1 = AZ + μ_nx1 is a vector of n correlated standard normal variables with mean μ, where A_nxn is the desired correlation matrix, Z_nx1 is a vector of randomly generated independent standard normal variables, and μ is a vector of means. In our calculations we chose μ = 0 since all values are normalized to be within the interval [0,1]. Calculations are more involved when one of the n variables is predetermined, as is the case when the proband is one of the individuals involved. In this case, let $A_{nxn}=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)$ where the submatrix A₁₁ is of size (n−1)x(n−1), which determines the dimension of all other submatrices. In particular, we note that A₂₂ = a_nn is a non-zero scalar. The new covariance matrix is defined as $B=A_{11}-A_{22}^{-1}{A}_{12}{A}_{21}$ and the new mean vector is defined as $\tilde{\mu }={\mu }_{(n-1)x1}+(X_n-{\mu }_n)A_{12}{A}_{22}^{-1}$. Then, the vector of correlated standard normal variables, given that one element in that vector is already determined, is generated as ${\tilde{X}}_{(n-1)x1}=\sqrt{B_{(n-1)x(n-1)}}{Z}_{(n-1)x1}+{\tilde{\mu }}_{(n-1)x1}$.

Simulation of linkage disequilibrium (LD)

As mentioned previously, a unique feature of SIMLA is the ability to implement LD between a disease allele and one or more marker alleles by specifying conditional haplotype probabilities for chromosomes carrying the D_i (susceptibility) or d_i (normal) allele. One particular haplotype can be associated with each of the D_i alleles at disease loci G₁ or G_2. These haplotypes may be composed of up to six not necessarily contiguous marker loci with up to five alleles each. Given an already assigned D_i or d_i allele at the disease locus, a marker haplotype (set of alleles) for all individual founder chromosomes is randomly generated based on the conditional haplotype probabilities. Remaining markers are assigned independently based on specified allele frequencies. Once founder haplotypes have been assigned, they are dropped through the pedigree according to Mendelian inheritance rules and may be broken up by recombination, consistent with the user-specified intermarker distances. Examples for the relationship of conditional haplotype frequencies and standard measures of LD, such as Lewontin’s D’ (Lewontin 1988), can be found in the original SIMLA publication (Bass et al. 2004). Blocks of LD may be simulated by selecting a subset of markers to be in LD with a disease locus, while other markers are in linkage equilibrium with the disease locus.

Implementation

Program input

The only input required by the SIMLA program is a control file specifying the various simulation parameters. They include number of replicates, number of families per replicate, sibship size, ascertainment criterion, number of chromosomes, number of disease and marker loci, number of alleles at each locus, marker maps and allele frequencies, optional familial correlation of environmental covariates, optional conditional haplotype frequencies, and optional genotype error rate. Disease allele and environmental exposure frequencies, the weight parameter W that codes mode of inheritance at each disease locus, population prevalence k of the disease and up to 10 distinct RR values for the various model covariates make up the parameter vector that completely specifies the penetrance function, according to equation (1). A text-based user interface for assisting in the creation of control files is provided and includes default parameter values and various plausibility checks. The order in which parameters appear in the file does not matter since the program finds all required input values by searching for a keyword rather than a particular line number. The user may choose to use one of two provided random number generators. If a seed value of zero is given in the control file, the random number generator is based on real numbers (doubles) instead of integers. In this case, the seed for random number generation is derived from the current time and process ID number, and two consecutive runs with the same control file will produce different output files due to random variation. The second option is to provide a non-zero integer seed in the control file. In this case an integer-based random number generator is used and two consecutive runs with identical control files will produce identical output files. Detailed documentation for creating the SIMLA control file as well as an example file is included with the download of the package from http://wwwchg.duhs.duke.edu/software.

Program output

SIMLA creates post-makeped LINKAGE-format pedigree (*.ped) and marker (*.dat) files, as well as MEGA2-format map files (Mukhopadhyay et al. 2005). Additional flags are available for creating pedigree files in SIBLINK format (Hauser and Boehnke 1998) and OSA covariate files with per-family averages of either or both environmental covariates (Hauser et al. 2004). SIMLA can also print MERLIN-formatted (Abecasis et al. 2002) input files (*.dat, *.ped, *.map, *.freq) for the entire pedigree or for just the proband’s nuclear family.

Version 3.0 of SIMLA provides the option to print several statistics about the simulated pedigrees, which are useful for error checking and for evaluating data characteristics prior to analyzing the simulated data with a particular software package of interest. For example, the married-in cousin parent (individual 6 in figure 1) is the only person not genetically related to the proband, and thus represents an individual randomly sampled from the general population, unless environmental covariates are correlated within the entire pedigree. A comparison of the genotype and environmental exposure data generated for all such cousin parents across replicates to the target parameters specified in the control file serves as a verification of correct data simulation. Detailed options for obtaining a variety of summary statistics for the generated pedigrees are described in the online user manual, available at http://wwwchg.duhs.duke.edu/software.

Program performance

Tables 3a and 3b summarize performance statistics for running SIMLA on a Unix workstation while table 3c contains the performance data for a PC with MS Windows operating system. For fixed sibship size (2), number of families (1000) and ascertainment criterion (affected sibling pair), the number of markers, disease allele frequencies and population disease prevalence are the major determinants of program run time. Despite a faster processor, the I/O operations under Windows have a substantial impact on program performance (not shown in table 3c). A Sun workstation is greatly superior in terms of printing a large number of pedigree files. Profiling results show that about half the processing time is expended on meiosis prior to ascertainment if both disease loci are on the same chromosome with at least half the markers separating them. This represents the worst-case scenario in terms of computational efficiency.

Table 3a.

SIMLA performance on Solaris 8 workstation with 1.28 Ghz processor, with two disease loci on distinct chromosomes. Constants: Sibship size 2, ascertainment criterion: affected sibling pair, 1 replicate of 1000 families, 7 alleles per marker, markers distributed equally over three chromosomes, no effect of environmental covariates, all printing turned off. Table entries are run times in seconds.

	P(D1)=0.15, P(D2)=0.05 G1 and G2 on distinct chromosomes			P(D1)=0.015, P(D2)=0.005 G1 and G2 on distinct chromosomes
	No. of markers			No. of markers
Prevalence	9	90	900	9	90	900
0.1	2.0	5.6	59.6	2.1	5.8	59.0
0.01	6.4	12.8	90.7	7.4	14.1	98.4
0.001	47.9	77.2	396.3	61.2	99.8	517.1

Table 3b.

SIMLA performance on Solaris 8 workstation with 1.28 Ghz processor, with two disease loci on the same chromosome. Constants: Sibship size 2, ascertainment criterion: affected sibling pair, 1 replicate of 1000 families, 7 alleles per marker, markers distributed equally over three chromosomes, no effect of environmental covariates, all printing turned off. Table entries are run times in seconds.

	P(D1)=0.15, P(D2)=0.05 G1 and G2 on same chromosome			P(D1)=0.015, P(D2)=0.005 G1 and G2 on same chromosome
	Total no. of markers (no. of markers between G1 and G2)			Total no. of markers (no. of markers between G1 and G2)
Prevalence	9 (1)	90 (10)	900 (100)	9 (1)	90 (10)	900 (100)
0.1	1.9	5.7	60.0	2.2	6.0	60.6
0.01	6.9	14.0	131.7	7.9	16.1	143.0
0.001	52.3	97.6	550.0	63.9	115.0	715.1

Table 3c.

SIMLA performance on PC with Pentium 4 2.8 Ghz processor, with two disease loci on distinct chromosomes. Constants: Sibship size 2, ascertainment criterion: affected sibling pair, 1 replicate of 1000 families, 7 alleles per marker, markers distributed equally over three chromosomes, no effect of environmental covariates, all printing turned off. Table entries are run times in seconds.

	P(D1)=0.15, P(D2)=0.05 G1 and G2 on distinct chromosomes			P(D1)=0.015, P(D2)=0.005 G1 and G2 on distinct chromosomes
	No. of markers			No. of markers
Prevalence	9	90	900	9	90	900
0.1	2.7	5.4	34.0	2.1	5.6	32.9
0.01	6.3	11.2	57.7	8.1	12.1	61.8
0.001	47.0	63.2	260.9	61.3	80.5	356.8

The algorithm is optimized to spend a minimum amount of computational effort on a pedigree prior to checking whether or not it meets the ascertainment criteria. User-specified disease prevalence has an effect on performance because a drop in disease prevalence makes it less likely for a pedigree to meet the ascertainment criterion of having two affected siblings. An increase in sibship size has the opposite effect. The increased burden of having to manage a larger pedigree is offset by the increased likelihood of finding one additional affected sibling among the larger number of siblings. The placement of the disease loci is another factor that influences performance. If the two disease loci are placed on distinct chromosomes (tables 3a and 3c) the algorithm only has to account for inheritance of two loci before making the ascertainment decision. If both disease loci are placed on the same chromosome, a larger number of markers between the loci will increase the computational effort since possible recombination events between the two loci have to be taken into account before any ascertainment decision is made (table 3b).

Discussion

Our new version (3.0) of SIMLA greatly increases the complexity of simulated phenotypes by allowing for more than one disease gene per pedigree, modeling the contributions of two environmental covariates with or without familial correlations, and incorporating gene-gene and gene-environment interactions. The key to implementing these extensions is the use of a logistic regression model as the penetrance function. Logistic regression is a standard modeling tool for genetic epidemiologists, who are familiar with specifying effect sizes in terms of relative risk parameters. With this extension, the new version of SIMLA is even more useful for assessing the performance of various pedigree analysis methods, especially linkage and association methods that incorporate environmental covariates or search for more than one disease gene at a time. SIMLA can be used to estimate power and sample size requirements for real data sets ascertained with various study designs, whose common goal is the detection, localization and characterization of genes underlying complex human traits. Just as importantly, SIMLA can assist researchers in interpreting results from real studies of human diseases by examining the relationship of different assumed generating models and observed results when the same analysis approaches are applied to real and simulated data.

Planned extensions of SIMLA include simulation of quantitative and age-at-onset traits, simulation of X-linked disease and marker loci, parent-of-origin effects and effects mediated by maternal genotypes, as well as genetic effects on disease progression (modifier genes) in addition to the currently implemented effects on disease risk (susceptibility genes).