RNA canonical and non-canonical base pairing types: a recognition method and complete repertoire

Abstract

The problem of systematic and objective identification of canonical and non-canonical base pairs in RNA three-dimensional (3D) structures was studied. A probabilistic approach was applied, and an algorithm and its implementation in a computer program that detects and analyzes all the base pairs contained in RNA 3D structures were developed. The algorithm objectively distinguishes among canonical and non-canonical base pairing types formed by three, two and one hydrogen bonds (H-bonds), as well as those containing bifurcated and C-H...X H-bonds. The nodes of a bipartite graph are used to encode the donor and acceptor atoms of a 3D structure. The capacities of the edges correspond to probabilities computed from the geometry of the donor and acceptor groups to form H-bonds. The maximum flow from donors to acceptors irectly identifies base pairs and their types. A complete repertoire of base pairing types was built from the detected H-bonds of all X-ray crystal structures of a resolution of 3.0 Å or better, including the large and small ribosomal subunits. The base pairing types are labeled using an extension of the nomenclature recently introduced by Leontis and Westhof. The probabilistic method was implemented in MC-Annotate, an RNA structure analysis computer program used to determine the base pairing parameters of the 3D modeling system MC-Sym.

INTRODUCTION

During the past year, two important RNA structures have been determined at high resolution by X-ray crystallography: the large and small ribosomal subunits [PDB nos 1FFK and 1FJG (1,2)]. The addition of these two structures not only confirms important progress that has been accomplished in the field of RNA crystallography, but also marks an important leap in the complexity of the available RNA three-dimensional (3D) structures and in the difficulty of RNA structure analysis. Until recently, there were no tools available to extract the useful RNA structure information automatically, which hindered efforts to fully exploit them. An important paradigm switch in RNA structural analysis is needed, as the observation and discovery processes need to be automated so as to provide the speed and objectivity that are necessary to fulfill our hopes towards these structures. A method that automatically identifies hydrogen-bonding (H-bonding) patterns among nitrogen bases using the nomenclature proposed in Leontis and Westhof (3) is presented in this paper.

H-bonding patterns that form between nitrogen bases are particularly important interactions in RNAs. Efforts have been made to establish a repository of base pairs from published literature to show the diversity of nitrogen base pairing types with a particular emphasis on non-canonical ones (4), and a systematic nomenclature has been proposed (3). From a modeler’s perspective, the spatial relations defined by such H-bonding interactions can be used to define the conformational search space of RNA. For instance, in the RNA 3D modeling software MC-Sym (www-lbit.iro.umontreal.ca/mcsym), these spatial relations are learnt from known examples and applied to the construction of new RNA structures (5). In earlier versions of MC-Sym (6), the database was built from base pairs that were identified and annotated using interactive visualization. However, the number of newly determined RNA 3D structures is such that it has become difficult to ensure the MC-Sym database remains up-to-date simply by continuing to apply such a slow and subjective method. During the development of an automated RNA 3D structure annotation program, we realized that no objective method existed for identifying base pairing types in RNA 3D structures. All currently available ones are limited to the detection of single H-bonds and, therefore, base pairing types must be identified in a further step by visual examination or by using heuristics (7). All existing methods detect H-bonds from the distance between either the hydrogen or donor atom and acceptor atom, as in Manip (8), and the angle between the hydrogen, donor and acceptor atoms, as in the molecular graphics software insightII (Biosym/MSI) and Hbexplore (7). The use of such strict parameters is subject to false positives and negatives when applied to RNA 3D structures that contain distorted base pairs, either due to experimental conditions, density map resolutions or variations in the application of computer optimization protocols.

We present here a new method that resulted from the search for an automated and objective method for finding and identifying base pairing types in RNA 3D structures. The probabilistic method provides a degree of certainty for the presence of each H-bond in the structure by considering the formation of H-bonds from competing donors and acceptors. This dependency between H-bonds that share a donor or an acceptor is implemented as a maximum flow problem in a bipartite graph. The decisions are thus taken to maximize the total number of expected H-bonds in a structure without involving a donor or acceptor more than once. The maximum flow problem formulation was adapted to search for an equilibrium solution that better suits the chemical nature of the problem. Base pairs are identified if the total flow, representing the mathematical expectation of the number of H-bonds forming, is higher than a predefined cutoff (typically 0.5). This cutoff can be varied depending on the application and on the desired sensibility of the detection process.

The only a priori knowledge used in selecting the parameters of the probabilistic approach is the near aligned geometry of H-bonds. The approach consists of collecting all local geometries of donor/acceptor pairs, and building a model of this distribution. Using the assumption of near aligned geometries, the model is decomposed in two components: one for the instances that represent the H-bond geometry, and one for those that do not. Consequently, a mixture of Gaussians (with full co-variance matrices) was selected as the form of density function for the model, and the parameters of this mixture were optimized using the EM algorithm (9) from a data set extracted from physically determined RNA 3D structures. The method is robust, reliable and immune to local distortions due to experimental conditions and computer optimization protocols. The method was implemented in a newly developed RNA 3D structure analysis computer program that is available on the Internet (http://www-lbit.iro.umontreal.ca/). This method was also used to define the base pairing and base stacking parameters of MC-Sym, as well as for matching larger RNA 3D patterns and motifs.

In order to identify a base pairing type, the naming scheme proposed by Leontis and Westhof (10) was used and extended. An algorithm that automatically names a base pairing using the information from the maximum flow optimization is presented. This algorithm was applied to 165 high resolution (≤3 Å) X-ray structures in the PDB (11) HR-RNA-SET (see Table 1 for a list). The collected base pairs were classified, resulting in a complete repertoire of the base pairing types in RNA structures (available at http://www-lbit.iro.umontreal.ca/).

Table 1. HR-RNA-SET.

The PDB identifiers of the X-ray RNA structures with a resolution of 3.0 Å or better. This list was compiled on February 1, 2001. Two structures were removed from the list: 1QCU and 406D. These two structures contain multiple models with different chain identifiers and have improper MODEL/ENDMDL tags. These structures can be downloaded from the Internet at http://www.rcsb.org/pdb/.

Our analysis of RNA 3D structures led us to three main results. First, we developed a method to automatically identify base pairing types in RNA 3D structure. Second, we refined an existing nomenclature and implemented its definitions in a computer program. Third, we built the repertoire of base pairing types found in high-resolution RNA X-ray structures.

MATERIALS AND METHODS

Data set

The subset of PDB structures used in this work, HR-RNA-SET, is composed of those that contain at least one RNA nucleotide, and that were determined by X-ray crystallography with a resolution of 3 Å or less, as of February 1, 2001. Table 1 shows the list of 3D structures that are included in HR-RNA-SET. Two files in the initial list were rejected: 1QCU and 406D. Both structures contain multiple models with different chain identifiers, and do not have proper MODEL/ENDMDL tags. This non-conformity to the PDB syntax precludes us from applying our automated procedure to these two structures. To ensure complete uniformity of hydrogen atom names, they were removed, if present, and then added using bond lengths and angles from the Cornell et al. force field (12). When appropriate, lone pair pseudo-atoms (LP) were placed 1 Å from their atom in the direction of the lone electron pair, as determined by the sp2 geometry of the base atoms. Names for the LP were assigned by following the standard nomenclature of hydrogen atoms in the PDB, replacing the H by LP.

Base pair identification

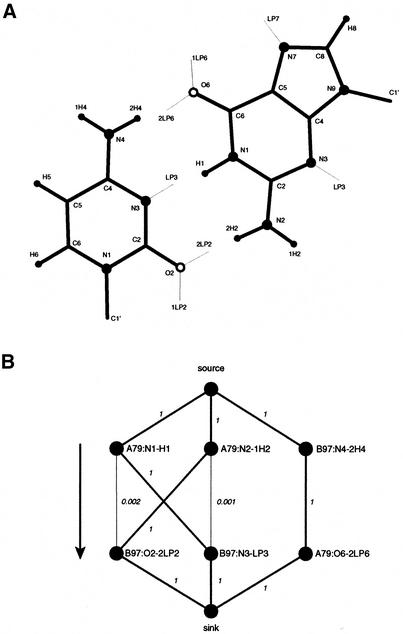
In order to guide the reader through the steps of this method, we exemplified each computation by using a canonical G·C Watson–Crick base pair extracted from positions A79 and B97 of the loop E motif from Escherichia coli 5S rRNA [PDB no. 354D (13)] (Fig. 1A). The method is divided into three steps: (i) compute the probabilities of H-bonds between each pair of donor and acceptor groups and build a graph representing these interactions; (ii) compute the maximum flow in this graph to account for competing donors and acceptors; (iii) assign the types of base pairs according to the probabilities of H-bonds forming.

Figure 1.

A base pairing and associated graph. (A) A canonical G·C Watson–Crick base pair extracted from positions A79 and B97 of the loop E motif from E.coli 5S rRNA (PDB no. 354D). The thin lines indicate the direction of LP, named using the same convention as for the hydrogen atoms. (B) Corresponding graph showing the probabilities associated with this base pair (see Table 2 for the actual measurements and probabilities). The donor groups are located in the upper row of nodes, and the acceptor groups in the bottom row. The arrow shows the direction of the flow from the source to the sink. The capacities are indicated beside each edge (only edges with capacity >10^–4 are shown). The thin lines show the edges with no flow after the optimization of the maximum flow. The thick lines between acceptor and donor groups correspond to the selected H-bonds.

For each base in the structure, the hydrogens are added according to geometries defined in Cornell et al. (12). LP are added and placed 1 Å from the oxygen or nitrogen atoms in the direction of the orbital. We use the term donor group to refer to a pair of associated donor and hydrogen atoms and the term acceptor group to define a pair of associated acceptor and LP.

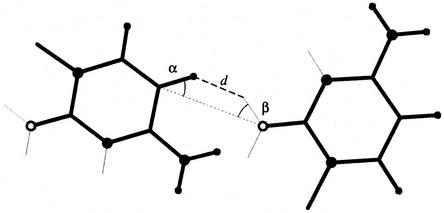
Given the list of potential donor and acceptor groups for a 3D structure, we compute the probability of forming a H-bond from the values of three measurements: the distance between the hydrogen and the LP; the angle between the hydrogen, the donor and the acceptor atoms (referred to as the hydrogen angle); and the angle between the donor and acceptor, and the LP (referred to as the LP angle). Figure 2 shows a H-bond with these three measurements identified.

Figure 2.

H-bond parameters. The putative H-bond shown is a weak C-H…O. The hydrogen and LP angles are identified by α and β, respectively, and the distance between the hydrogen and LP is indicated by d. Nitrogen and hydrogen atoms are shown by large and small filled circles, respectively. Oxygen atoms are shown by open circles. Thin lines are used to indicate the direction of the LP.

Our data set is built by extracting these values from all pairs of donor and acceptor groups in HR-RNA-SET (see Table 1 for the list of 3D structures), resulting in a data set χ = {x¹,…, xⁿ}, where xⁱ = (xⁱ₁, xⁱ₂, xⁱ₃) is a vector defining the distance, the hydrogen angle and the lone pair angle. To reduce the amount of data, we extracted only the values from pairs of residues that contain a pair of atoms at 3 Å of distance or less.

To obtain both flexibility and efficiency, we applied a semi-empirical approach that models the distribution of data points by a sum of Gaussians. Because the geometrical nature of the measurements introduces a bias in the distribution of data points, the raw distributions of the extracted values cannot be directly modeled by a sum of Gaussians. To obtain a proper distribution, a transformation x′ = F(x) was applied to each data point. This process is similar to histogram equalization in computer graphics (14), and allows us to transform any arbitrary distribution into another. Here, we wished to derive a transformation so that the data points measured from randomly scattered points in space resulted in a uniform distribution and, thus, to remove the geometrical bias. Such transformation was obtained by computing the cumulative probability density given the random model for each dimension of the data points. In the case of the distance, the cumulative probability density is proportional to the volume of a sphere of radius x₁. For the angles, the cumulative probability density is proportional to the volume of a spherical cone of angle x₂ (or x₃). The transformation we obtained is given by F(x) = [x³₁,cos(x₂),cos(x₃)].

However, this transformation is inappropriate to model the distribution as a sum of Gaussians since only a specific range is accessible in each of the three dimensions of the data points (x₁ ≥ 0, 0 ≤ x_2,3 ≤ 1). To solve this problem, a further transformation was applied to the data points so that each dimension was distributed in [–∞,∞]. The complete transformation is then F(x) = {ln(x³₁), arctanh[cos(x₂)],arctanh [cos(x₃)]}.

The distribution of transformed data points is modeled as a sum of Gaussians without any constraint on the mean vector and the co-variance matrix. This model has the advantage of modeling the dependencies between the dimensions of the distribution. A possible drawback is the increase in the number of parameters, which increases the risk of overfitting the data (15). However, our data points represent a large sample of the distribution, and in practice this is not the case. The parameters of the model (mean vector, co-variance matrix and weight for each Gaussian) are optimized using the EM algorithm (9,15). To avoid local minima, a variant of the algorithm was used where only 25 000 randomly chosen data points were considered at each iteration. The EM algorithm is known to minimize the negative log-likelihood and, thus, to return the parameters that maximize the likelihood of generating the data set. Once the parameters of the model are optimized, a visual inspection of the characteristics of each Gaussian was sufficient to determine which one(s) is responsible for the data points forming H-bonds.

The probability that a local geometry, x, forms a H-bond is equivalent to the probability that x is drawn from the Gaussian describing H-bond geometries, H = h, and not from the others. P(H = h | x) can be computed using Bayes theorem:

P(H = h | x) = [p(x | H = h) P(H = h)]/[p(x)] = [p(x | H = h)P(h)]/[Σ⁷_j=1p(x | H = j)P(H = j)]1

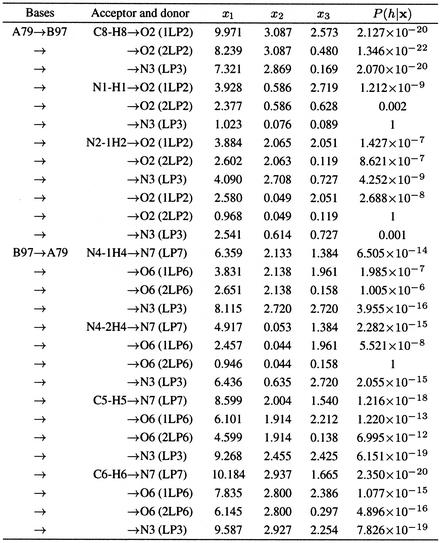
where p(x | H = h) is the probability of generating x from Gaussian h, P(H = h) is the prior probability of forming a H-bond and p(x) is the probability of observing geometry x. Table 2 shows the measurements and modeled probability according to equation 1 for each pair of donor and acceptor groups for the G·C Watson–Crick base pair extracted from positions A79 and B97 of the loop E motif from E.coli 5S rRNA [PDB no. 354D (13)]. (The nucleotides in the PDB format are labeled by a chain identifier and a residue number. We refer to a base pair by a reference to the two residue PDB labels seperated by a colon. Quotes are used to distinguish between a numerical chain identifier and the residue numbers. The quotes are not necessary when a letter is used for the chain identifier.)

Table 2. Base pair G:A79·C:B97 of the loop E motif from E.coli 5S rRNA (354D).

The three transformed measurements and the modeled probabilities are shown for each pair of donor and acceptor groups. The values were rounded to the third decimal. The names used to identify LP are built using the same rules as the standard PDB hydrogen atoms names.

Consider a specific donor or acceptor group. We define as stable a set of one or more H-bonds that involve this donor or acceptor group if the sum of their associated probabilities is ≤1. Consequently, one can interpret the probabilities as the proportion of time a group is occupied in the formation of each H-bond in a stable set (Fig. 3). The stable set of a given group is chosen in order to maximize the total number of H-bonds in the structure. This is computed efficiently by defining a maximum flow problem on a directed bipartite graph connecting donors to acceptors. The graph, G = (N,A), where N is the node set and A the arc set, is a bipartite graph that contain the set, I, of nodes for the donor groups and the set, J, of nodes for all acceptor groups. If the probability of forming a H-bond between donor i ∈ I and acceptor j ∈ J is >10^–4, an arc (i,j) is added to the graph with capacity, u_ij, equal to the probability of forming this H-bond. Two special nodes are then added to the graph, s and t, called the source and the sink, respectively. Arcs that link the source to all donor, (s,i) ∈ A ∀i ∈ I, and all acceptors to the sink, (j,t) ∈ A ∀j ∈ J, are added with a capacity of 1. The maximum number of H-bonds that can form in the molecule is obtained by solving the maximum flow problem of this graph from node s to t, resulting in values x_ij for i ∈ I and j ∈ J, which indicate the resulting flow.

Figure 3.

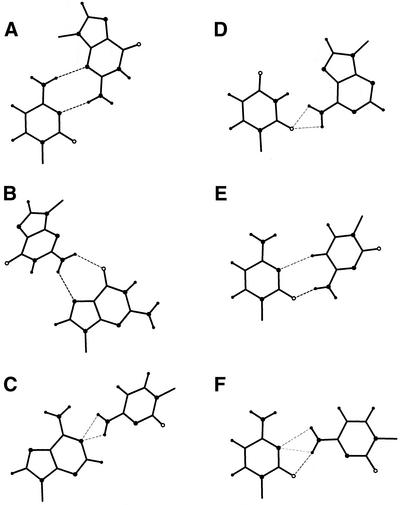
Base pairing type examples. These were found in only one structure of HR-RNA-SET. (A) The C·G Ww/Ss trans base pair found at positions ‘9’26:‘9’22 and ‘9’46:‘9’43 in 1FFK. (B) The G·G Hh/Bs trans base pair found at position A260:A265 in 1FJG. (C) The A·C Ww/Bh cis base pair found at position 38:32 in 1YFG. (D) The U·A Ws/Bh trans base pair found at positions ‘0’1116:‘0’1246, ‘0’1244:‘0’1118 and ‘0’2661:‘0’2812 in 1FFK. (E) The C·C Ww/Hh trans base pair found at position ‘0’1834:‘0’1841 in 1FFK. (F) The C·C Ww/Bh cis base pair found at position ‘0’937:‘0’1033 in 1FFK. The H-bonds are indicated by dotted lines. Empty, small filled and large filled circles are used for oxygen, hydrogen and nitrogen atoms, respectively

Algorithms that solve the maximum flow problem return an extremal solution (16). In the context of H-bond probabilities, an extremal solution means that the algorithm, when faced with a situation where two equivalent H-bonds can form exclusively of one another, will favor the complete formation of one of the H-bonds and leave the rest of the flow (typically 0) to the other. Since here we are more interested in the equilibrium state of the system, a criterion needs to be added, when allowed [notation used as in Ahuja et al. (16)]:

x_ij ≥ x_ik or x_ij = u_ij for i ∈ I and j,k ∈ J2

x_ij ≥ x_kj or x_ij = u_ij for i,k ∈ I and j ∈ J3

This criterion is satisfied by modifying the preflow-push algorithm (17). As the FIFO variant of the preflow-push algorithm [see Ahuja et al. (16) for a complete description of the algorithm, and Ahuja et al. (18) for theoretical and empirical performance comparisons] was selected for its simplicity of implementation, the push/relabel() operation was modified in the following way:

procedure push/relabel(i);

begin

 let O be the set of admissible output arcs for node i;

 let n be the size of O;

 sort arcs (i,j) ∈ O by their r_ij;

 for (i,j) ∈ O do:

  δ ← min[r_ij,e(i)/n];

  x_ij ← x_ij + δ;

  e(i) ← e(i) – δ;

  n ← n – 1;

 if e(i) > 0 then

  let I be the set of admissible input arcs for node i;

  let n be the size of I;

  sort arcs (i,j) ∈ I by their r_ij;

  for (i,j) ∈ I do:

   δ ← min[r_ij,e(i)/n];

   x_ij ← x_ij – δ;

   e(i) ← e(i) – δ;

   n ← n – 1;

 if e(i) > 0 then

  d(i) ← min[d(j) + 1: (i,j) ∈ A(i) and r_ij > 0];

end;

Nomenclature

Several schemes were proposed to name RNA base pairing types (10,19–21). The proposition from Leontis and Westhof (3), LW, was retained, where a base pair is described by a pair of names that are associated with the faces of the bases involved. This nomenclature has several advantages. First, the names are easy to remember and there is no need to reference any documentation. Second, the name alone gives a good idea of the base pair geometry. Third, isosteric pairs have the same name.

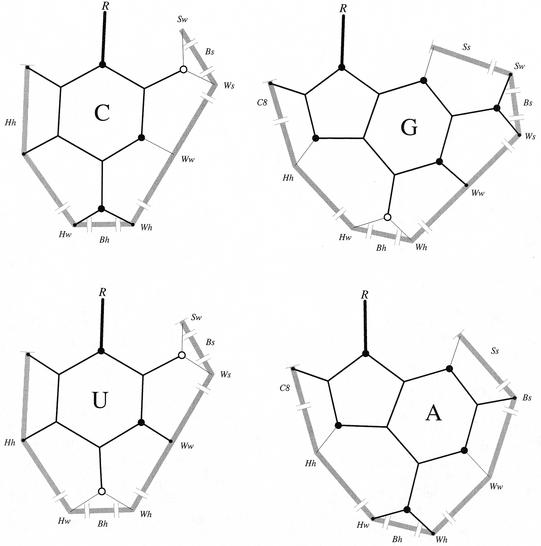
Despite these advantages, LW cannot differentiate base pairing types that differ by a sliding of the bases along the interacting faces, especially in the context of single H-bond base pairs. Thus, to increase the precision of LW, we defined LW+ by decomposing the faces in sub-faces. Then, we defined and implemented an algorithm to reduce possible identification ambiguities to anecdotal occurrences. However, the current implementation does not support the detection of water-mediated, protonated, ribose- or phosphate-moiety involved base pairs. Figure 4 shows the four RNA bases and associated faces. For convenience, the Watson–Crick edge was abbreviated to W, the sugar edge to S and the Hoogsteen/C-H edge to H. The sub-face names are indicated by combining face abbreviations, for instance Ww corresponds to the central section of the W face, and Hw to the section of the H face that is adjacent to the W face. Bifurcated base pairs of LW were renamed by creating small faces at the center of amino and keto groups. These faces are named Bh and Bs for the bifurcated base pairs involving the Hoogsteen side amino/keto group and the sugar side amino/keto group, respectively. The C2-H2 group of the adenosine was named Bs to facilitate the identification of isosteric base pairing types (see Fig. 4). We also introduced a special face, C8, for the C8-H8 donor group of the purines. The order of the faces is the same as the order of the bases. The cis and trans semantic for the relative orientation of the glycosidic bond with respect to the base pair axis are the same as in LW. Note that the local strand orientation and base–sugar conformation are not specified in the base pair notation since they belong rather to nucleotide conformations.

Figure 4.

RNA base faces. Nitrogen atoms are shown by large black circles, hydrogen by small filled circles and oxygen atoms by open circles. The LP are shown with thin lines. The ribose moiety is shown by the letter R.

The face involved in a base pairing type is obtained by computing the contact point, defined by the weighted mean of the hydrogen and LP of each base. The weights correspond to the calculated probabilities of each H-bond as returned by the maximum flow algorithm. The face containing the contact point is returned.

To compute the glycosidic bond orientation the visual contact point is defined, a variant of the contact point, obtained by replacing the LP by the acceptor atoms. The vector between the two visual contact points, the contact vector, is used as the axis of the base pair, and the glycosidic bonds are attached to its extremities. A cis orientation is defined by a torsion around the contact vector <90°, and the trans orientation otherwise.

Availability

The software was developed using the MC-Sym development library under the Linux operating system, which is publicly available at mccore.sourceforge.net. The code is written in C++ and, therefore, is easily portable to other Unix platforms, such as IRIX and SunOS. The probabilistic method has been integrated to the MC-Annotate system (22), and is accessible on the Web. RNA 3D structures can be submitted for the identification of base pairing types and complete analysis at www-lbit.iro.umontreal.ca/mcannotate.

RESULTS

Base pair identification

The data set collected from HR-RNA-SET contained 1 607 756 data points. The distributions of the transformed data points are shown in Figure 5 as shades of gray.

Figure 5.

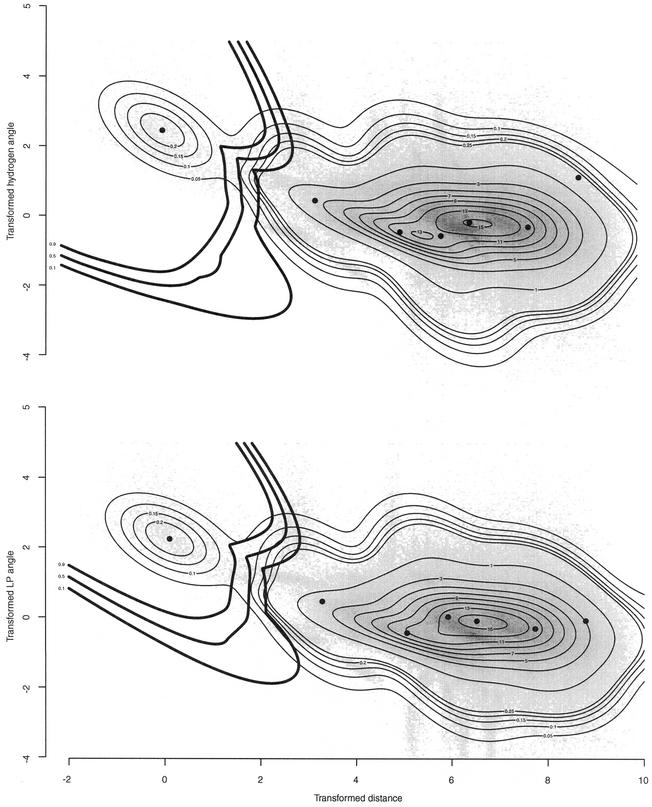
Superimposed two-dimensional projections of the data set histogram, modeled probability density and surface of decision. The histogram of the data set is shown in shades of grey. The modeled probability density is shown by thin isocontours. Between 0 and 0.25 they were plotted at each 0.05 interval, whereas between 1 and 15 they were plotted at each interval of 1. An integration was carried out on the axis of projection corresponding to the effect observed by the histogram. The surface of decision is shown with thick lines isocontoured at probabilities 0.1, 0.5 and 0.9. The maximum probability is returned on the axis of projection. The circles represent the optimized mean of the seven Gaussians.

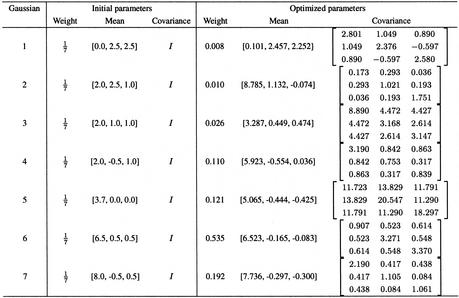
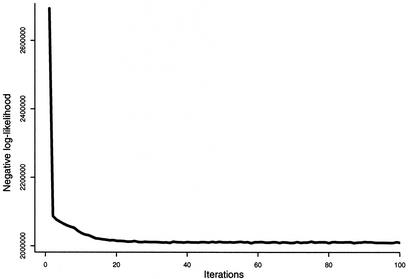
Initial values for the parameters were determined by visual inspection of the data set, and seven Gaussians provided an accurate model of the data set. The EM algorithm was initialized with seven Gaussians, the initial parameters are shown in Table 3. Figure 6 shows the negative log-likelihood of generating the data set with the current parameters as the algorithm progresses. One hour of CPU time was necessary on a PIII/600 Mhz to complete the learning process. As a result, only one Gaussian (the one centered on the smallest distance and angles) is sufficient to represent H-bonds, the six other Gaussians provide an accurate model of the distribution of non-bonded donor–acceptor pairs. Table 3 shows the initial and final parameters of the seven Gaussians before and after optimization. Figure 5 shows the optimized model (thin black lines) superposed with the extracted data (gray shades).

Table 3. Initial and optimized parameters.

The initial parameters of the seven Gaussians are determined manually after examining the distributions of transformed measurements, equal weight and identity co-variance are used. The optimized parameters are obtained after 100 steps of the EM algorithm. The values were rounded at the third decimal.

Figure 6.

Minimization of the negative log-likelihood for the mixture of seven unconstrained Gaussians on the transformed data set by the EM algorithm. The procedure was stopped after 100 steps, corresponding to 1 h of CPU time on a PIII-600.

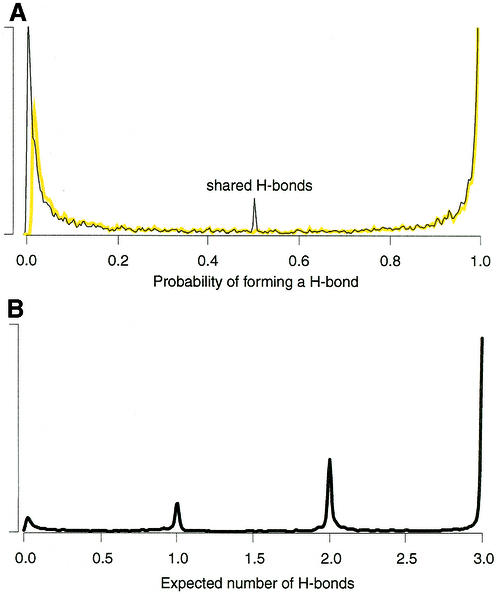
Figure 7 shows the flows resulting from the computation of the stable H-bond set in HR-RNA-SET. In Figure 7A, both distributions of capacities and flows are shown. The distribution of Figure 7B shows the total flow obtained for every base pair. The discrete character of this distribution suggests that a cutoff can be applied in the identification of base pairs with at least one H-bond, thus assuming that a base pair forms only if the total flow between two bases is ≥0.5. This parameter can be adjusted to reflect stringency of the identification process.

Figure 7.

Probability densities for x_ij, u_ij and the total flow of the base pairs. The probabilities were computed for all base pairs in HR-RNA-SET. Only those with a probability >10^–4 are plotted. (A) The probability density for x_ij and u_ij are shown with a thin black line and yellow line, respectively. The center peak for x_ij (the optimized flow) is the result of bifurcated H-bonds. (B) The distribution of total flows obtained between every base pair in HR-RNA-SET. The total flow can be seen as the mathematical expectation of the number of H-bonds forming between two bases. The distribution clearly shows the discrete nature of this value. The area of each peak shows the relative proportion of one, two and three H-bond base pairs.

Repertoire of base pairing types in RNA

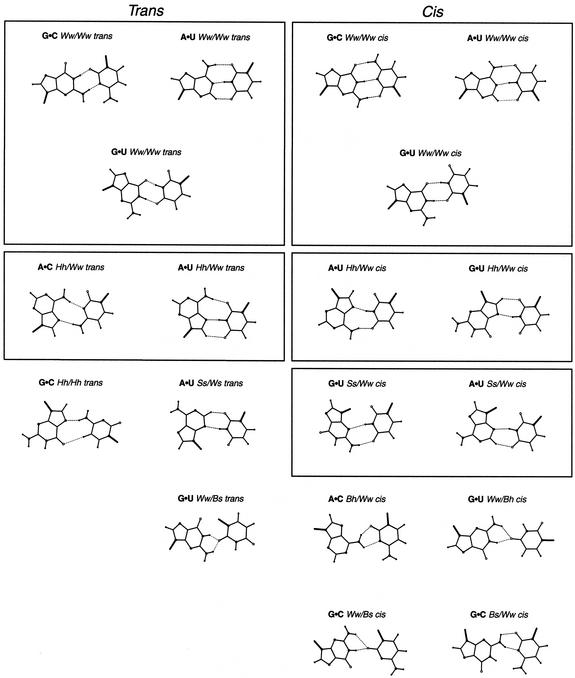
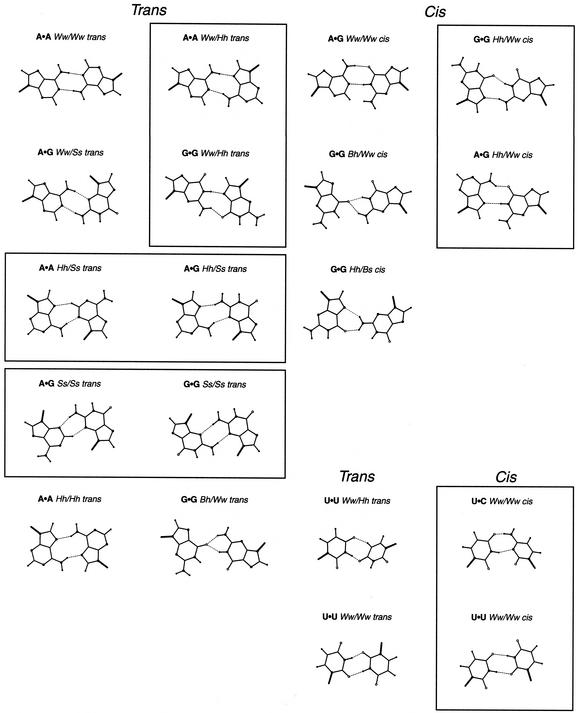
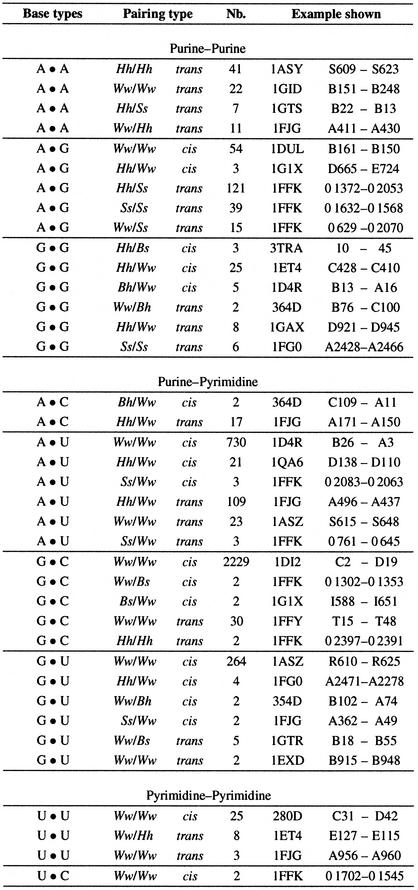
The algorithm presented here allowed us to perform a systematic survey of all of the base pairs in high resolution X-ray RNA structures, and to study their geometrical diversity. For HR-RNA-SET, the complete repertoire was built in <4 min on a PIII-600. Figure 8 presents 38 base pairing types that occur at least twice in HR-RNA-SET. Because of space constraints, base pairing types that form only one H-bond were not included in this survey. The structure that minimizes the sum of RMSD (23,24) with all other base pairs of the same type is shown. Structure and position information about these specific base pairs is shown in Table 4. In order to optimize the identification of representative base pairs, the RMSD calculations were limited to the first 200 examples for each base pair type. These results are also available in PDF documents that include the superimposition of all the base pairs of the same type (see various documents about base pair types at our web site www-lbit.iro.umontreal.ca).

Figure 8.

(Previous page and above) Two H-bond base pairing types found in HR-RNA-SET. Base pairing types that occur at least twice are shown. The 19 purine·pyrimidines base pairing types are on the opposite page. The 15 purine·purine base pairing types are on this page. The four pyrimidine·pyrimidine base pairing types are located at the bottom right corner of this page. Base pairing types were classified as either trans (left columns) or cis (right columns). Boxes are used to group isosteric base pairing types together.

Table 4. The 38 base pairing types in HR-RNA-SET.

Each base pairing type was found at least twice in HR-RNA-SET. The example selected for each type for Figure 8 is identified in the last column. The four letter code refers to the PDB identifier. The nucleotides are labeled according to the PDB chain identifier and residue number.

The base pair types that appear in only one structure in HR-RNA-SET were examined. Figure 3 shows 6, among 86, such examples that we found of particular interest. Figure 3A shows a C·G Ww/Ss trans that was found in positions ‘9’26:‘9’22 and ‘9’46:‘9’43 of the 5S rRNA (1FFK). This base pair type was also found in a recent structure of the group I intron (25), and was conserved in a refined version of the large ribosomal subunit (26). In the latter case, base pair ‘9’26:‘9’22 was slightly tilted to the Ww/Sw trans type. The two examples of the 5S rRNA of H.marismortui are located 23 Å apart, and were found in very different 3D contexts. The ‘9’46:‘9’43 base pair is a member of a base triplet (‘9’46:‘9’43:‘9’37) that stabilizes a local phosphodiester chain reversal of an unusual 13 nt loop between positions ‘9’33 and ‘9’47. The other base pair of this type, at positions ‘9’26:‘9’22, stabilizes a disordered internal loop. It is worth noting here that a theoretically generated example of this base pair type has been included in the MC-Sym modeling system (6) since its very first version, as the 119 base pair.

Figure 3B shows a base pair of type G·G Hh/Bs trans found at positions A260:A265 in the structure of T.thermophilus 30S ribosomal subunit (1FJG). Again, here, an example of this base pair type was theoretically generated and included in the first version of the MC-Sym database, and was referred to as base pair 34. This base pair is flanking a 7 nt loop that interacts with protein S20.

Figure 3C shows a base pair of type A·C Ww/Bh cis found at positions 38:32 of the yeast initiator tRNA (1YFG). Here, we use the term bifurcated to qualify a base pair in which two H-bonds either share the same hydrogen or LP. The equilibrated maximum flow settles the probability of each H-bond to values close to 0.5, expressing the shared nature of the interaction and, hence, the pairing of Figure 3C is a perfect example of a bifurcated base pair. The base pair of type U·A Ws/Bh trans presented in Figure 3D is another example of a bifurcated base pair, as found at positions ‘0’1116:‘0’1246, ‘0’1244,‘0’1118 and ‘0’2661:‘0’2812 of 1FFK.

Figure 3E presents a base pair of type C·C Ww/Hh trans found at positions ‘0’1834:‘0’1841 of structure 1FFK. This non-canonical base pair closes a short helix, and stabilizes a bulged out adenosine and a 6 nt loop. The interaction is maintained by a H-bond between the extra cyclic amino of one C to the oxygen of the other base, and by the formation of a weaker C-H…N H-bond. Note that these H-bonds were included in the H-bond data set used to optimize the parameters of the mixture of Gaussians and, although they usually exhibit geometrical parameters slightly different to the other types of H-bonds, they are properly identified by the probabilistic model.

Figure 3F shows a convoluted network of three partial H-bonds obtained after the resolution of the equilibrated maximum flow problem. The base pair was observed at positions ‘0’937:‘0’1033 in 1FFK, the first non-canonical base pair of a 10 nt internal loop that is adjacent to a G·A sheared tandem. The H-bond network describes a double bifurcated base pair, as the LP of N3 is shared between both hydrogens of the extra cyclic amino group, and one of these hydrogens is in turn shared with one of the LP of the O2 atom. The probability for each H-bond is such that their sum is maximized, and respect the stable set constraint. The base pair is recognized by the probabilistic system despite its peculiar geometry.

DISCUSSION

Distance versus probabilistic models

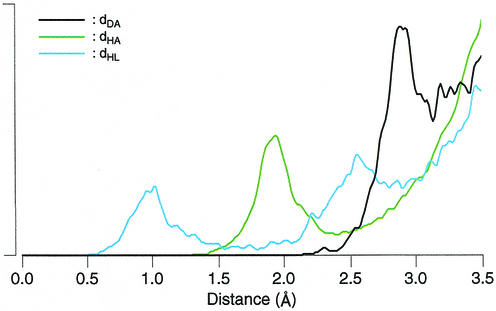
The most employed distance for recognizing H-bonds is the one between the donor and acceptor atoms, d_D–A, which is easy to compute and to observe interactively, and it does not require either the hydrogen or LP. Figure 9 presents the distributions of three distances as measured from HR-RNA-SET. The distribution of d_D–A (black line) does not contain a clear separation between H-bonds (first peak) and non H-bonds and, thus, does not provide a good classification criterion. The distance used in Massire and Westhof (8), between the hydrogen and the acceptor atoms, d_H–A, is a better one, as shown by the green line. Massire and Westhof suggested a cutoff at 2.1 Å, but from the distribution in Figure 9, a cutoff at 2.4 Å would be a better solution. The 2.1 Å cutoff was retained to reduce the number of false negatives in the context of molecular modeling (E. Westhof, personal communication). Finally, the distance between the hydrogen and LP, d_D–LP, among the three distances is the best, if only one distance must be used. As indicated from the blue line distribution, a cutoff between 1.5 and 1.8 Å would be effective for d_H–LP.

Figure 9.

Distance-based parameters. The distributions are computed for all base pairs in HR-RNA-SET. The black line shows the distribution of distances between the donor and acceptor atoms, d_DA. The yellow line shows the distribution of distances between the hydrogen and acceptor atoms, d_HA. The blue line shows the distribution of distances between the hydrogen and LP, d_HL.

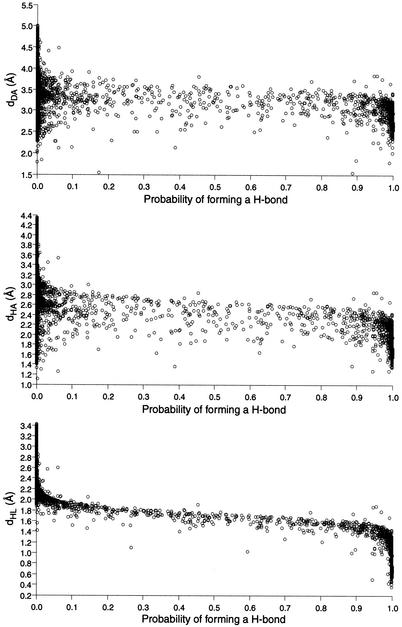
In order to quantify the power of using a probabilistic over the strict distance approach, a scattered plot where each dot represents one putative H-bond was created. Figure 10 shows that a significant number of H-bonds were assigned a probability 0 by using the probabilistic method, whereas they would have been identified as forming H-bonds using d_H–A with a cutoff at 2.1 Å, and as proposed by Massire and Westhof (8). Moreover, most of the H-bonds that were assigned a probability of 1 using the probabilistic model would have been rejected by the distance method.

Figure 10.

Distance criteria versus probabilities of forming H-bonds. Each scatter plot shows the correlation between a distance criterion and the probabilities of forming H-bonds. Each dot represents the evaluation of a pair of donor and acceptor groups. The pairs separated by >5 Å were not considered.

Strictness parameter

Our probabilistic method returns the mathematical expectation of the number of forming H-bonds between two nitrogen bases. As a default value, two bases are identified as making an ‘interaction’ if the expected number of H-bonds is ≥0.5. This value can be redefined by the user to reflect the type of interactions that need to be identified. In a context where a structure has been determined imprecisely, the cutoff can be lowered to a value as low as 10^–4. However, if only the strong two H-bond base pairs are desired in the output, the value of the cutoff could be raised to as much as 1.8. As an example, during the determination of the 3D structure of the catalytic core of the hairpin ribozyme, a weak cutoff of 10^–4 was used to examine the first generation of thousands of structures that were obtained from secondary structure and low-resolution experimental data. This is a typical first step in RNA 3D modeling. In several generated structures, the probabilistic method detected a H-bonding pattern that formed a base triplet involving two bases in the ribozyme and one base in the substrate. The geometry of the base pairs in the first generation of structures was far from satisfying the strong H-bonding parameters. Nevertheless, this observation was reported to the experimentalists who decided to check for the presence of the triplet in the hairpin. The predicted triplet was later experimentally determined to form in at least one of the catalytic reaction steps (27). In the further modeling iterations, a more stringent cutoff, typically 0.5, was used to identify generated 3D structures that contained ‘nicer’ base pairs.

MC-Sym base pairs

The probabilistic method was applied to the annotation of all available RNA 3D structures. The identified base pairs were collected and corresponding transformation matrices inserted in the MC-Sym RNA 3D modeling computer program database. The previous MC-Sym databases were built from visual examination of all RNA 3D structures, a long and subjective process. With the determination of the ribosome structure, a visual annotation would have been a daunting task. The probabilistic method, on the other hand, is automatic, fast and objective. It completed the base pair recognition process with a throughput of 7042 bp/s on a PIII-600. Now, every time a new RNA 3D structure is made available to us, the MC-Sym database and parameters are completely updated to address the most recent knowledge brought by the new structure in <4 min. The most recent MC-Sym database contains 10 times more nitrogen base spatial relations than the original version of 1991.

Distortion in RNA structure databases

During the computation of the probabilities of all H-bonds in all available RNA structures, the base pairs that were assigned an expected number of H-bonds near 0.5 were visualized and analyzed. Some of these base pairs pointed us to interesting features of the RNA 3D structures that are currently in public databases. First, several structures that contain stable Watson–Crick G·C base pairs are distorted, which could be the result of the refinement process where H-bonds are represented by simple harmonic restraints on the distance between the donor and acceptor atoms. The mean distance for H-bonds changes from one structure to another, and can even sometimes reach a value of 3.9 Å, for the H-bond between C:N4 and G:O6 (see for instance 1AOI). We believe this kind of variation can be explained by the use of different force fields and refinement parameters and procedures. Given the observed variations, it becomes evident that methods based on strict distance and angle values are prone to identification errors and, hence, the use of a more flexible approach, such as the one presented here, is strongly recommended for an objective analysis of RNA 3D structures.

Ribosome contribution

When structures of the large and small ribosomal subunits were introduced into the database, it was believed that they would substantially contribute to RNA structural knowledge. During the building of the repertoire of two H-bond base pairs, we determined that these two structures alone account for 1522 bp among a total of 3852 that were indexed and, thus, represent 40% of the base pairs in HR-RNA-SET. Despite the fact that the term non-canonical suggests rare occurrences, our analysis revealed that G·C and A·U Ww/Ww cis (canonical Watson–Crick base pairs) account for 77% of all examples, where the G·C base pair accounts for 58% alone. This leaves a large, 23%, fraction of ‘non-canonical’ base pairs. If we remove the G·U Ww/Ww cis base pair (wobble base pair), then the non-canonical base pairs still represent over 16% of the indexed base pairs in the repertoire. The results of this analysis cover 629 bp, excluding those that require a water-mediated H-bond or a protonated nitrogen base. The repertoire in Figure 8 contains 38 base pairing types that contain at least two H-bonds. Seven base pairing types are formed by one typical H-bond and a weaker C-H….{O,N}.

Nomenclature

Leontis and Westhof (3) have emphasized that their proposed nomenclature has the interesting property of naming all isosteric base pairing types with the same name. This feature is of utmost importance since it allows one to easily describe RNA motifs without having to specify different base pairing types that correspond to sequence variations. This important feature is also a characteristic of LW+, and goes beyond by discriminating base pairing types that differ only by a sliding along the pairing faces.

An important exception to this is the G·U W/W trans, which occur in two different forms that involve two H-bonds of the W faces. The first form involves two H-bonds on the h side of the W face, and the second form involves two H-bonds on the s side of the W face. Because the contact points represent an average when two H-bonds are present, it is impossible with this approach to modify the face definitions so that these two base pairing types can be differentiated, and without introducing undesired new names for each variation of the classic A·U Hh/Ww trans and A·U Ww/Ww cis. This is the only ambiguity left in the proposed LW+ nomenclature. The situation could be resolved by introducing an exception, by naming both base pairing types G·U Wh/Wh trans and Ws/Ws trans. We decided to postpone the implementation of such an exception until proper feedback is obtained from the RNA community.

In LW, the presence of bifurcated H-bonds has to be notified explicitly in the name. This is due to the fact that such base pairs often involve hydrogens or LP from two different faces on one of the bases. The introduction of the contact points alleviates this ambiguity, and the addition of the Bh and Bs faces results in precise names.

The current probabilistic system does not identify water-mediated H-bonds because most of the currently published RNA structures do not contain water molecules, and when they do most of them do not specify the actual positions of the water hydrogen atoms. Identification of water-mediated H-bond in an automated manner requires the correct placement of water molecules around the nitrogen bases, which is known to be a difficult problem.

Another limitation of the probabilistic system is that H-bonds involving the O_2′ group in the ribose moiety are not considered. Again, this is due to the fact that an automated method requires the exact position of the hydrogen atom. The H is free to rotate around the O_2′ group and, thus, the task of computing its optimal position is not trivial, although currently under investigation.

The probabilistic method introduced here describes the first available algorithm and computer implementation of an automated base pairing type recognition procedure, which also objectively classifies and presents the base pairs of an RNA 3D structure. The probabilistic method successfully recognized all base pairing types that are present in available RNA 3D structures, and allowed us to automate their classification. In particular, a complete and well-organized repertoire of observed RNA base pairing types has been made available on the Internet.

The systematic annotation of all RNA 3D structures, as determined by high-resolution crystallography, provided us with a convincing confirmation that a slightly revised version of the nomenclature proposed by Leontis and Westhof (3) is perfectly suitable to a high-throughput RNA structure analysis context.

ACKNOWLEGEMENTS

We thank Patrick Gendron, Sergei Chteinberg and Fabrice Leclerc for providing RNA structure expertise, and Yoshua Bengio for suggesting the use of a mixture of Gaussians. This work was supported by a grant to F.M. from the Canadian Institutes of Health Research (CIHR) (MT-14604). S.L. holds a PhD scholarship from CIHR.