Automatic classification of protein structure by using Gauss integrals

Abstract

We introduce a method of looking at, analyzing, and comparing protein structures. The topology of a protein is captured by 30 numbers inspired by Vassiliev knot invariants. To illustrate the simplicity and power of this topological approach, we construct a measure (scaled Gauss metric, SGM) of similarity of protein shapes. Under this metric, protein chains naturally separate into fold clusters. We use SGM to construct an automatic classification procedure for the CATH2.4 database. The method is very fast because it requires neither alignment of the chains nor any chain–chain comparison. It also has only one adjustable parameter. We assign 95.51% of the chains into the proper C (class), A (architecture), T (topology), and H (homologous superfamily) fold, find all new folds, and detect no false geometric positives. Using the SGM, we display a “map” of the space of folds projected onto two dimensions, show the relative locations of the major structural classes, and “zoom into” the space of proteins to show architecture, topology, and fold clusters. The existence of a simple measure of a protein fold computed from the chain path will have a major impact on automatic fold classification.

Importance of Structural Comparison

One of the main tasks of biology is to describe and compare biological structures. The forefathers of evolutionary biology (1, 2) inferred ancestral links and constructed classifications by studying structural similarities among species. Today we investigate biological molecules, which are many orders of magnitude smaller. The size decrease of subjects has made some tasks easier: for example, we can trace the evolutionary relationships by examining the DNA sequence directly. On the other hand, we can no longer discover function by direct observation, and must instead infer it through indirect evidence. Structure of biological molecules is a very important clue to understanding and manipulating biological function. Consequently, we need robust tools for describing, comparing, and classifying the universe of protein shapes.

In the postgenomic era scientists have mounted a major cooperative effort called structural genomics. It will expand our knowledge of protein structure by coordinating research worldwide. The success of the effort is linked to our ability to organize and understand the wealth of information it will produce. With the number of known proteins currently >16,000 and growing by >400 per month, the need for reliable and automatic structural comparison has never been greater.

In this paper we introduce a set of tools for describing the shape of proteins. These tools are fundamentally different from the current distance-based coordinate and distance rms deviation (RMSD_c and RMSD_d, respectively; ref. 3) methods. We show that, even in a basic form, our topological measures successfully sort and display the diversity of protein structures. We hope that researchers will accept these measures and use them to construct new structural comparisons and structural databases.

Motivation for a New Approach to Structural Comparison

Koehl (4) has written an excellent review of the various methods used to detect structural relationships. He concluded that “though significant progress has been made over the past decade, a fast, reliable and convergent method for protein structural alignment is not yet available.” The deficiencies of current methods arise from their reliance on distance-based [RMSD; see Kabsch (3)] measures of similarity, and also from their consequent requirement for sequence alignment.

RMSD is an excellent measure of similarity for nearly identical structures (5), but once the shape of two proteins begins to diverge, RMSD looses its effectiveness. Two completely unrelated proteins may have a large RMSD, but so may two related chains which consist of identical subunits oriented differently with respect to each other. RMSD cannot distinguish the first case from the second.

This drawback is usually addressed by using various sophisticated sequence alignment techniques that find related subunits (6–11). While this corrects to some extent the “large RMSD” problem by finding shorter subunits with smaller RMSDs, it also introduces a host of complications. First, such alignment methods are computationally intensive. Second, they introduce many undetermined parameters: gap and insertion penalties, similarity weights, etc. Third, and most important, procedures that use sequence alignment are fundamentally flawed for anything but close relationships because they must violate the triangle inequality.

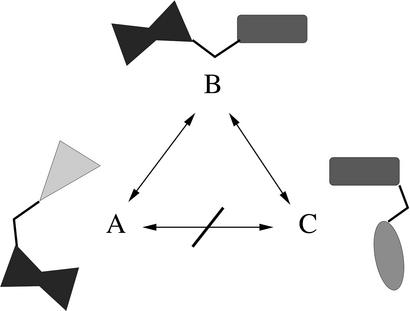
To illustrate the last point, let us consider three proteins made of subunits in the following manner: protein 1 = ABC-LMN, protein 2 = DEF-LMN, protein 3 = DEF-OPQ. There is similarity between protein 1 and protein 2 in the LMN subregion, and between protein 2 and protein 3 in the DEF region; however, these two similarities cannot be used to infer any similarity between proteins 1 and 3. (The example is diagrammed in Fig. 1.) In mathematical terms, the structural measures used today do not satisfy the triangle inequality: d(x, y) + d(y, z) ≥ d(x, z). When a method violates the triangle inequality, it is fundamentally unable to judge dissimilarity, and this problem worsens with increasing distance.

Figure 1.

Failure of current subset-matching structural measures to satisfy the metric conditions, in particular, the triangle inequality 4. This violation prohibits transitive inference of relationship (A ∼ B and B ∼ C does not imply A ∼ C), and it makes intermediate and distant similarity meaningless. In this figure conformation A is similar (by subset matching) to conformation B, which is in turn similar to conformation C. However, there is no relationship between conformations A and C.

Two methods that stand somewhat separate from the rest are pride (12) and minarea (13). pride does not focus on distances, but on statistical distributions of local distances. Published results indicate that pride is very effective in detecting close relationships in the CATH classification (C, class; A, architecture; T, topology; H, homologous superfamily), is fast, and contains few adjustable parameters. pride may not be effective in evaluating dissimilarity because of its reliance on local C^α–C^α distances. Carugo and Pongor (12) do suggest that pride can be used as a classifier, and we are looking forward to seeing the details. minarea, like pride, does not require alignment. The classification possibilities of minarea are also unknown.

Knot Theory in Biology

The challenges outlined in the preceding section motivated us to step away from distance-based methods, and to instead compare and classify proteins on the basis of their topological properties. The protein backbone is a space curve, and mathematicians have been analyzing and comparing curves for a long time. One well-known measure of how two curves interact with one another is the Gauss integral, which is related to Ampere's law of electrostatics. The first biological applications of this measure are found in studies of DNA structure. In 1969 White (14) derived an elegant expression stating that the sum of the writhe and the twist of a closed DNA strand is equal to its linking number (the writhe may be seen as the self-inductance of a wire):

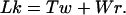1

One of us (15, 16) has used this result in analyzing properties of supercoiled DNA. Knot theory has been applied to proteins by Chen and Dill (17), who investigated symmetries in secondary structure motifs. Two of the simplest structural measures we consider, the writhe and the average crossing number, have previously been applied to analyze protein structures. Levitt (18) used the writhe to distinguish different chain threadings. Arteca and Tapia (19) used the average crossing number and the most probable overcrossing number as protein shape descriptors.

New developments in knot theory (20) have placed Gauss' original integral as the first of a series of mathematical descriptors of curves and knots. Recently Røgen and Bohr (21) developed a method to use a family of generalized Gauss integrals as global measures of protein structure. The generalized Gauss integrals originate in integral formulas of Vassiliev knot invariants (a good technical introduction to Vassiliev invariants is ref. 22) and give absolute measures of protein geometry. The integrals may be understood as crossing numbers and correlations (along the backbone) of crossing numbers.

In this paper we use the topological invariants developed by Røgen (21) to construct a geometric measure, scaled Gauss metric (SGM), of the conformation of a protein. We then use the measure to provide a distance between protein shapes. Unlike the methods mentioned in the previous section, SGM satisfies the triangle inequality, as well as the other two pseudometric conditions 4 on the chains of CATH2.4.§

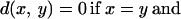2

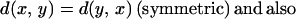3

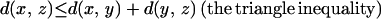4

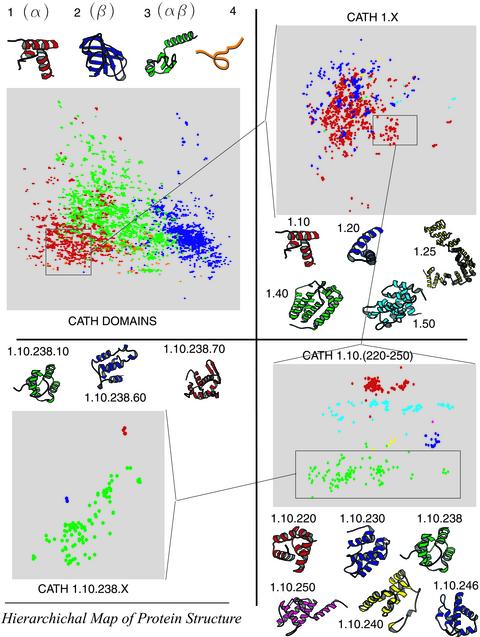
The triangle inequality (4) implies that the Gauss metric is able to identify meaningful intermediate and marginal similarities, and to distinguish between various degrees of dissimilarity. Consequently, we can examine more distant structural relationships, to construct a meaningful clustering of protein shapes, and, remarkably, to visualize the whole space of protein structures (Fig. 2).

Figure 2.

The map of the CATH hierarchy. For visual clarity we have omitted the CATH chains with “0” name (about half the chains). The full map is similar, but more cluttered. The figure is a projection from ℝ³⁰ to ℝ² along the directions of largest variation. The structures shown are representatives of their respective classes. The rectangle in the Upper Left contains all the chains in CATH, colored according to their class membership: α, β, αβ, and little secondary structure. Note that the αβ members are located between α and β islands, a consequence of the triangle inequality. Next, in the Upper Right, we enlarge CATH class 1, the helical proteins, and its five constituent architectures. In the Lower Right we display in larger details topologies 1.10.(220–250). Finally, in the Lower Left we show the H categories of topology 1.10.238. Although it is difficult to reproduce the cluster separation adequately in two dimensions, when one descends to lower levels of the hierarchy and the topological diversity, the clusters corresponding to different folds become more distinct.

The Gauss metric has another desirable property: it requires neither sequence nor structural alignment between chains, which makes pairwise comparison almost instantaneous. A brief mathematical description of the method is in Appendix A. More details can be found in Røgen and Bohr (21).

Results

Representing Proteins in ℝ³⁰.

For our study we selected 20,937 connected domains from CATH2.4. We chose domains that have no more than three α-carbon atoms missing and that are at most 1,000 residues long. For each of these, we computed the topological invariants of the polygonal curve connecting the α carbon (C^α) atoms. Each domain is assigned a 30-dimensional vector containing its length and the 29 measures, in a manner described in Appendix A.

The invariants described in Appendix A are simply sums over the length of the chain and are, consequently, straightforward to compute. The computation is also fast: a 1-GHz Pentium processor extracts the 29 measures for all 20,937 CATH2.4 domains in <2 hr. This is equivalent to >400 million (438,357,969) pairwise alignments which, using current methods, would occupy a single workstation for several hundred years. Because the speed of SGM is perfectly satisfactory, we have not, at this point, explored optimization of the algorithm. Once each polypeptide is mapped onto a point in ℝ³⁰, we use the usual Euclidean metric to compare chains:

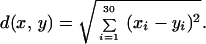5

We call this metric SGM, the scaled Gauss metric.

The Structural Protein Universe.

SGM is a proper pseudometric on CATH2.4, which implies that we can visualize the entire space of protein structures. Because the complete structural universe lives in ℝ³⁰ and is therefore difficult to represent on a journal page, we have projected the 30-dimensional object onto the plane along the first two principal difference components. (In other words, we select the projection that best preserves the distances between the chains.) Fig. 2 is a map of the protein structure universe. As the observer “zooms” into the cloud of points, and the structural diversity of the subsets decreases, the separation between the different CATH classes becomes clearer. (Please refer to the legend of Fig. 2 for a more detailed explanation.)

Automated Classification of CATH2.4 Domains.

Extending existing databases.

There are several established projects that maintain web-accessible hierarchical classifications of Protein Data Bank entries. Of these the most commonly used are FSSP, CATH, and SCOP (23–25). These hierarchies are constructed by different methods: FSSP uses a fully automatic comparison algorithm, DALI, whereas CATH and to a larger extent SCOP use some human expert judgment.

We wanted to reproduce these databases with an automatic classification procedure. Automatic classification is desirable because it will save considerable time and effort. It will also provide insight into structural comparison by replacing complex human judgment with a simple set of rules. These rules can serve as a component of any algorithm that needs structural classification for a subunit, for example, a program for automatic fold recognition.

We decided against using SGM to cluster chains ab initio because the most natural SGM clustering might not correspond to biologically interesting classification, and also because the lines between functionally different proteins may be blurred because of insufficient representation. We felt it would have been unwise to discard the effort and expert judgment that makes the existing databases biologically useful. Therefore we chose to take an existing database (CATH), to examine it, and to duplicate and extend it with an automatic algorithm that uses SGM. We have not replaced expert human judgment; rather, we have incorporated it by using the existing classifications as a training set.

We discovered that if we use the length of the proteins and the Gauss invariants of order 1, 2, and 3 (see Appendix A for details), then we can capture the geometry of the CATH database with only one adjustable parameter (see Fig. 3 and legend). The adjustable parameter is simply the ratio of inter- to intracluster distance, and is common to all folds. When CATH is examined with SGM it naturally coagulates into clusters that correspond to individual C, A, T, and H subcategories.

Figure 3.

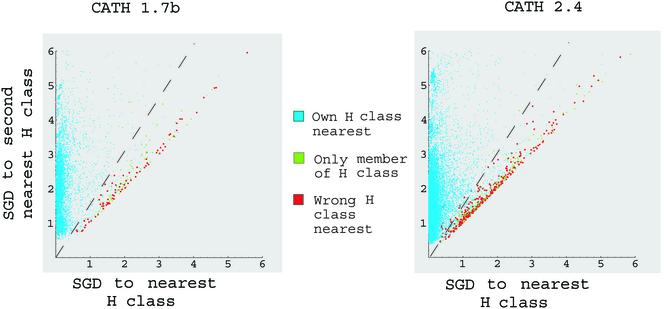
Classification into the first four CATH categories (C, A, T, and H). The plots display D₁ vs. D₂ (defined in step 2 in the text) for all chains in CATH1.7b (Left) and CATH2.4 (Right). The light blue chains are ones for which D₁ points to the correct CATH classification; the red points are ones for which D₁ points to the incorrect one. The green points are single representatives of their respective CAT and H clusters. The decision boundary described in the text is shown as a broken line. The subregion with the red and green points is the “unknown” region in the classification.

The algorithm.

A good classification procedure must (i) classify a majority of members correctly and (ii) make very few mistakes. Instead of making misclassifications, the procedure should flag cases as “unsure” and refer them for further expert examination.

The distribution of proteins embedded in ℝ³⁰ shows a strong clustering consistent with the CATH classification. Closest-neighbor pairs belong to the same CAT and H designation 97.8% of the time. Furthermore, the gaps between clusters are larger than the distances between chains within each cluster. We used these observations to design an automatic classification procedure. This is how it works: Given a chain C, we

1.

Calculate the point corresponding to C by computing the 30 invariants described in Appendix A.

2.

Locate C's nearest and second-nearest clusters, 𝒞₁ and 𝒞₂, at corresponding distances D₁ and D₂.

3.

The decision stage. The CATH assignment is made using the ratio of D₁ to D₂.

if D₂ ≥ 1.75 D₁. This means that C lies in a populated region of 𝒞₁. C joins 𝒞₁

else (D₂ < 1.75 D₁). In this situation C is either equally close to two different clusters or is far away from both. We declare C's classification to be unknown, with a suggestion to examine 𝒞₁ and 𝒞₂ as possible candidates.

Our single “adjustable parameter,” 1.75, is actually an observation about the nature of CATH. Chains that are equidistant to several clusters are hard to classify. Chains that are far away from any known clusters are probably new folds. The definition of “far” for CATH is 1.75. Fig. 3 illustrates this point and the procedure. The distribution of D₁ vs. D₂ shows two very nice features. First, the chains that might be misclassified as well as the chains that are only representatives of their H class cluster separately from chains with correct classifications. This clustering allows us to flag a portion of the chains as “unknown” rather than making a classification error. Second, a large majority (95.53%) of the chains reside in the “known” region and can therefore be classified with certainty. The figure shows that chains which are equidistant to different clusters are hard to classify; and also chains which are far away from other clusters are probably new folds.

Performance.

We picked the decision boundary based on classification performance on CATH1.7b (Fig. 3 Left). We then tested the performance on the latest release of CATH, CATH2.4. Using the automatic classification algorithm described above, we assign 95.51% (19,996/20,937) of CATH2.4 domains their appropriate C, A, T, and H designation. Furthermore, we correctly identify as “unknown and/or possibly new” 171 domains that are solitary members of their H cluster (i.e., all new folds are found). The total success rate is 96.32%. A total of 3.65% (765/20,937) of the chains cannot be assigned an H designation. Finally, there are five mistakes: 1piqA0, 1czqA0, 1pfiA0, and 1xtcC0 are assigned the correct C, A, and T, but not H; 1favA0 receives the correct C and A but not T and H.

In all five cases the misclassified chain is a single long α-helix. The first four are members of T 1.20.5, which contains “single α-helices involved in coiled-coils or other helix-helix interfaces” (www.biochem.ucl.ac.uk/bsm/cath_new/), which implies that the H designation was made by considering the chains' environments and cannot be reproduced by geometrical considerations alone. 1fav is a member of the T family “helix hairpins”; SGM, however, considers it to be closer to a straight α-helix.

When we wish to assign only the first three CATH descriptors, C, A, and T, we use the algorithm described above but without considering the H level. In the decision stage we use the decision boundary given by D₁ = 1.7D₂ in the case of C, A, and T classification. This modified algorithm assigns 96.34% (20,171/20,937) of CATH2.4 domains their appropriate C, A, and T designation. Ninety-two chains are solitary members of their T topology and are classified correctly as “new and/or possibly unknown.” The total success rate is 96.78%. A total of 3.20% (671/20,937) of the chains cannot be assigned a T designation. Finally, there are three mistakes that we place closer to the 1.20.5 topology than to their own topology. The case of 1favA0 is as before. 1a2xB0 consists of one α-helix only but is classified 4.10.310 by CATH2.4. Similarly 1tbgE0 consists mainly of α-helix pieces, making it impossible for our algorithm to place it in the FSS (few secondary structures) class of CATH2.4.

We assign CATH descriptions C and A in the same way once again, this time using the decision boundary given by D₁ = 1.7D₂. The success rate drops slightly to 96.64%, primarily because there is only one member of an A class. Last, when assigning the C class alone, the success rate is 97.35%. In both of these cases there are two mistakes; namely the previously encountered 1tbgE0 and 1a2xB0.

For comparison we note that during the construction of CATH2.4, the C-class assignments are automatic for >90% of the domains, and the A-architecture and beyond assignments are largely manual.

We considered nudging the performance of the algorithm even higher by constructing more complicated decision boundaries. We also contemplated reducing the number of “unknown” chains by making the decisions cluster-dependent. We decided, in view of the excellent performance stated above, to present the simplest possible scheme. The simplicity of the algorithm shows that our measures are a natural and powerful way to look at protein structure. We shall examine more elaborate algorithms in a future work.

Discussion

Future Directions.

This work opens up many future directions. One possible venue is to investigate the topological measures themselves. While we have a geometric interpretations of the writhe (I₁₂) and the average crossing number (I_|12|), we would like to understand the meaning of the other generalized Gauss integrals used in this work.

It will also be fruitful to investigate the various ways the generalized Gauss integrals can be combined. Perhaps some measures are not as important as others; or there may be better ways to combine them.

By choosing to classify CATH chains we glossed over the problem of finding domains. A new structure coming to SGM for classification will not be broken down into basic biologically and structurally significant pieces. We would like to establish collaborations to combine SGM with existing domain analysis methods. We also would like to develop an algorithm that uses SGM to locate matching (to CATH domains) subsets within a given protein.

Another subject for further work is making the classification algorithms more elaborate by incorporating cluster-specific information. We think that this will be necessary in automatic classification of the SCOP (23) hierarchy. One of the most enticing directions of future work is investigating the correlation and inference from sequence to structure. The Gauss integrals are a powerful and elegant way of looking at protein structure. Using them will make the interplay between sequence and structure more well defined and applicable across more distant relationships.

Conclusion.

We have shown that the diversity of protein structures is captured by 30 structural measures. The protein space has been visualized through two-dimensional projections, which showed a clear separation of protein fold classes. We used the intracluster separation of protein structures to design a simple, robust and highly reliable algorithm that classifies >96% of the considered protein domains without making mistakes. The algorithm itself is a useful tool that will speed up the process of classification and save expert human judgment for the more interesting cases. The simplicity of the classification rule suggests that (armed with topological insight) one is looking at a 30-dimensional periodic table of protein folds. Remarkably, the Gauss integrals are an absolute measure of structure, devoid of pairwise comparisons. In the future we hope to see the development of many very fast and comprehensive algorithms using the generalized Gauss integrals.

Abbreviations

RMSD_c

coordinate rms deviation

RMSD_d

distance rms deviation

SGM

scaled Gauss metric

Gauss Invariants

The first structural measure considered here is the writhe of a space curve, known from the famous Cǎlugǎreanu–White self-linking formula. The writhe, Wr, of a closed space curve, γ, may be calculated by using the Gauss integral

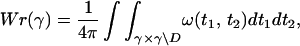A1

where ω(t₁, t₂) = [γ′(t₁), γ(t₁) − γ(t₂), γ′(t₂)]/|γ(t₁) − γ(t₂)|³, D is the diagonal of γ × γ, and [γ′(t₁), γ(t₁) − γ(t₂), γ′(t₂)] is the triple scalar product. As ω(t₁, t₂) = ω(t₂, t₁), the writhe may be calculated as an integral over a 2-simplex, namely

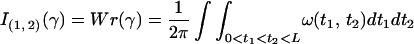A2

For a polygonal curve μ the natural definition of writhe is

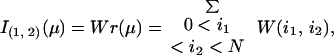A3

with

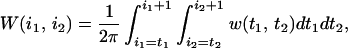A4

where W(i₁, i₂) is the contribution to writhe coming from the i₁th and the i₂th line segments, which equals the probability from an arbitrary direction to see the i₁th and the i₂th line segment cross, multiplied by the sign of this crossing. Therefore, geometrically writhe is still the signed average number of crossings averaged over the observer's position located in all space directions. The unsigned average number of crossings seen from all directions, known as the average crossing number, is

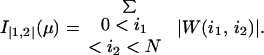A5

A whole family of structural measures containing, e.g.,

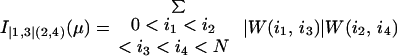A6

and

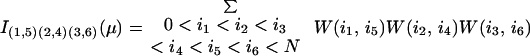A7

may be constructed by using writhe and average crossing number as the basic building blocks. These measures are inspired by integral formulas for the Vassiliev knot invariants (26).

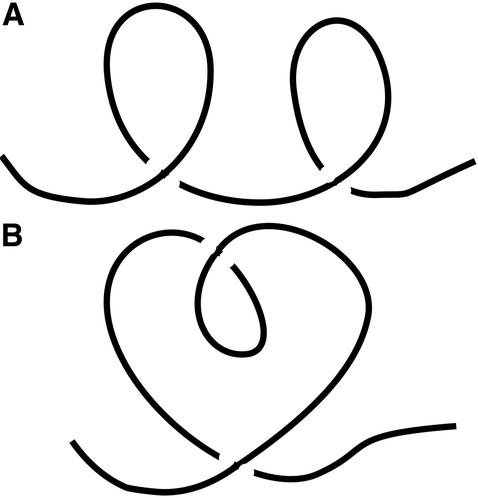
The invariants from Eq. A6 form a natural progression of descriptors of curves, much as moments of inertia and their correlations describe solids. We illustrate the usefulness of the higher order invariants in Fig. 4, which shows plane curves that have the same writhe and average crossing number, but can, nonetheless, be distinguished by the higher-order integrals.

Figure 4.

Plane curves A and B possess the same writhe and average crossing number. The higher-order invariants, A6, however, distinguish the two curves.

Røgen and Bohr (21) give an explicit formula for the writhe contribution, W(i₁, i₂), from two line segments. They also show that the six double sums defining I_{(1,5)(2,4)(3,6)}(μ) may be reduced to give a calculation time proportional to the third power of the number of line segments.

The first premeasure of protein structures used in this paper is the number of α carbon atoms, N. The other premeasures of protein structures are naturally grouped into three groups. The first group consists of I_(1,2)/N and I_|1,2|/N. We use crossings per length rather than just crossings to make the two premeasures less sensitive to the size of the protein, which is already recorded by N. The next group contains the premeasures I_(1,2)(3,4)/N², I_(1,3)(2,4)/N², and I_(1,4)(2,3)/N² together with the nine premeasures obtained by taking absolute value once or twice. Finally, there are the 15 premeasures given by I_{(1,2)(3,4)(5,6)}, I_{(1,2)(3,5)(4,6)}, I_{(1,2)(3,6)(4,5)}, I_{(1,3)(2,4)(5,6)}, I_{(1,3)(2,5)(4,6)}, I_{(1,3)(2,6)(4,5)}, I_{(1,4)(2,3)(5,6)}, I_{(1,4)(2,5)(3,6)}, I_{(1,4)(2,6)(3,5)}, I_{(1,5)(2,3)(4,6)}, I_{(1,5)(2,4)(3,6)}, I_{(1,5)(2,6)(3,4)}, I_{(1,6)(2,3)(4,5)}, I_{(1,6)(2,4)(3,5)}, resp. I_{(1,6)(2,5)(3,4)} divided by N³. In the last group of premeasures the introduction of one, two, or three absolute values would give 105 new premeasures, which is the same as the number of premeasures given by four index pairs. To have a reasonable number of premeasures we have chosen to stop with the 1 + 2 + 12 + 15 = 30 above.

We then normalize the premeasures to have the same standard variance of one on a set H-class representatives of CATH2.4. This was done to treat the information contents of the 30 premeasures equally, and to make the measures dimensionless.¶

Verification with structal

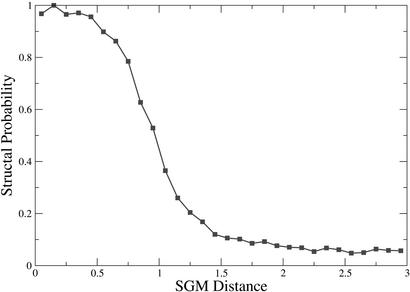
We took an opportunity to test our method under “battle conditions,” in the CASP V experiment (http://predictioncenter.llnl.gov). The Levitt team needed to sort out and align domains that were too new to be included in the latest SCOP 1.59 (ref. 23). They produced a nonredundant (fasta E value ≥ 10⁻⁴) set of new domains, 1,625 in total (M. Levitt, personal communication). They also selected, with the same sequence requirement, a set of 3,411 SCOP fold representatives. The total number of comparisons (5,542,875) was far too great to perform with current structural alignment methods in the short time available during CASP. We performed the alignments with SGM (in <10² seconds) and the team then used structal (27) to produce structural alignments on the pairs that we found to be similar. The two methods display remarkable agreement. In Fig. 5 we plot the structal hits and misses produced in the verification vs. SGM distance. Despite the fact that the current method was not designed to bind to fold representatives, virtually every small SGM distance results in a bona-fide structal structural alignment.

Figure 5.

Probability of getting a structal hit vs. SGM distance: CASP coverage test. At small SGM almost every relationship produces a bona-fide structal alignment.