Genetic interactions between polymorphisms that affect gene expression in yeast

Abstract

Interactions between polymorphisms at different quantitative trait loci (QTLs) are thought to contribute to the genetics of many traits, and can dramatically impact the power of genetic studies to detect QTLs¹. Interacting loci have been identified in many organisms^1–5. However, the prevalence of interactions^6–8, and the nucleotide changes underlying them^9,10, are largely unknown. Here we search for naturally occurring genetic interactions in a large set of quantitative phenotypes—the levels of all transcripts in a cross between two strains of S. cerevisiae⁷. For each transcript, we searched for secondary loci that interact with primary QTLs detected by their individual effects. Such locus pairs were estimated to play a role in the inheritance of 57% of transcripts; statistically significant pairs were identified for 225 transcripts. Among these, 67% of secondary loci had individual effects too small to be significant in a genome-wide scan. Engineered polymorphisms in isogenic strains confirmed an interaction between the mating-type locus MAT and the pheromone response gene GPA1. Our results suggest that genetic interactions are widespread in the genetics of transcript levels, and that many QTLs will be missed by single-locus tests but can be detected by two-stage tests that allow for interactions.

Most heritable traits are affected by inheritance of alleles at multiple loci, and the identification of these loci is a key challenge of modern genetic research. We recently showed that gene expression levels in yeast typically show multigenic inheritance and provide a good model for investigating the genetic basis of complex traits^7,11,12. Here we use this system to examine the prevalence of genetic interactions in a large set of phenotypes. A genetic interaction between a pair of loci (sometimes termed epistasis) occurs when the effect of an allele at one locus changes as a function of the allele at the other. Previous biometric analyses have provided evidence for many interactions underlying transcript levels^6,7. We sought to identify the loci involved in such interactions in a cross between a lab strain of yeast, BY, and a wild strain, RM. For this analysis, we used previously described genotype and gene expression data from 112 segregants⁷. We first tested all possible pairs of loci for evidence of interaction underlying each transcript level. This strategy had little statistical power to map interactions due to its requirement for a very large number of tests and the corresponding stringent correction of significance thresholds for multiple testing¹³.

To improve power, we used a two-stage search strategy. For each transcript, we first identified the “primary” QTL with the strongest individual linkage. We then partitioned segregants based on inheritance (either BY or RM) at the primary locus and tested each subgroup for further “secondary” loci. We computed the joint significance of the strongest such secondary QTL with the primary locus using a newly developed statistical method based on estimation of the false discovery rate¹³ (see Methods). This method provides an estimate of the overall fraction of transcripts for which both loci are involved in the genetics, as well as a probability for each transcript that both loci are true positives. This analysis indicated that the locus pairs identified for 57% of all transcripts were true positives, and it identified locus pairs for 225 transcripts at a false discovery rate of 5% (i.e. fewer than 12 of these are expected to have either locus as a false positive).

Because the two-stage search takes account of inheritance at the primary locus in assessing the effect of the secondary locus, it can identify locus pairs with interactions, as well as locus pairs that act additively. We tested each of the 225 locus pairs for interacting effects by fitting a regression model relating inheritance at the linking loci to the transcript level. The model included an additive effect for each locus and a term representing the interaction between loci; the latter term was significant at p < 0.05 for 65% of transcripts. For comparison, we considered 547 transcripts for which two loci were identified as significant by their individual effects. Of these, only 13% had an interaction term significant at p < 0.05. A false discovery rate analysis¹⁴ indicated that the interaction term represented a true positive for 91% of locus pairs mapped by the two-stage search, compared to 13% of pairs mapped independently.

We next sought to determine whether the secondary loci mapped by the two-stage search could have been detected by a single-locus linkage test. Under some interaction scenarios, the individual effects of the loci are undetectable, while under others the loci retain an individual effect. We tested the individual effect of each secondary locus on the corresponding transcript, and found that 87% of these were significant at p < 0.05, indicating that most secondary loci do have a residual individual effect. However, this significance threshold does not take into account the multiple tests carried out in a genome scan. When we asked how many of the secondary loci were detectable at a false discovery rate of 5% in the context of a genome scan⁷, we found that only 74 (33%) of the 225 were, indicating that 67% of secondary loci would have been missed without the two-stage search.

To identify pairs of interacting QTLs with effects on many transcripts, we constructed a histogram of the genetic positions of linking locus pairs, analogous to previous analyses with single loci^11,15. Most of the pairs affected single transcripts, but a few affected multiple transcripts (Figure 1). The largest number of transcripts linking to a single locus pair was 14, with four additional transcripts linking nearby (Figure 1); as this group contained both YCR040W/MATα1 and its silenced copy YCL066W/HMLα1, we eliminated the latter from further analysis, leaving 17 transcripts that linked to this locus pair. The primary QTL of the pair lay near MAT, which confers α or a mating type on a haploid yeast cell depending on integration of genes at the locus. The secondary locus contained the gene encoding the G-protein subunit Gpa1, in which a single polymorphism in the BY parent strain, S469I, has previously been shown to affect expression of pheromone response genes¹². Of the 17 transcripts whose linkage to the MAT and GPA1 loci was detected by the two-stage search, 11 were previously shown to be regulated by mating type, of which seven are also regulated by the pheromone response pathway; two have known function that does not involve mating, and four have no known function¹⁶. For 14 of the transcripts, the MAT and GPA1 loci showed direct evidence for interaction in the regression model at p < 0.05; the independent effect of the GPA1 locus exceeded the genome-wide significance threshold for single-locus linkage for only one of these 17 transcripts.

Figure 1.

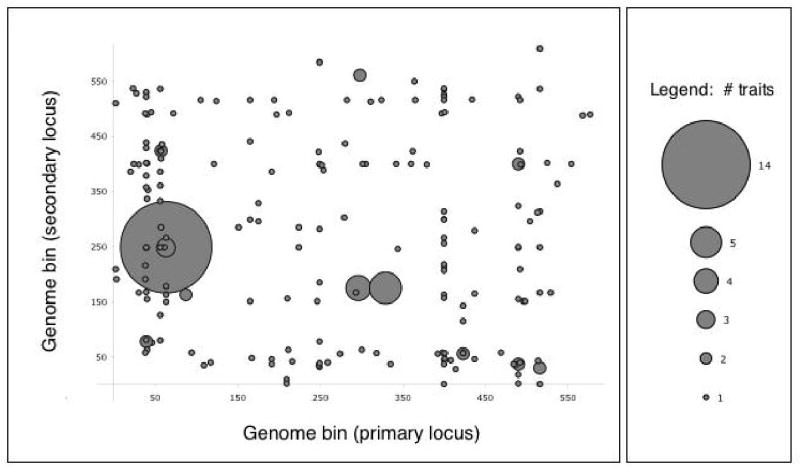
Genome distribution of QTL pairs detected by the two-stage linkage search. On each axis the genome is divided into 611 bins of 20 kb each, shown in chromosomal order. The set of transcripts mapping to QTLs in each pair of bins in the two-stage analysis is represented as a circle, with the width proportional to the number of such co-linking transcripts; circles are centered on the corresponding bins. The largest circle represents the MAT-GPA1 locus pair.

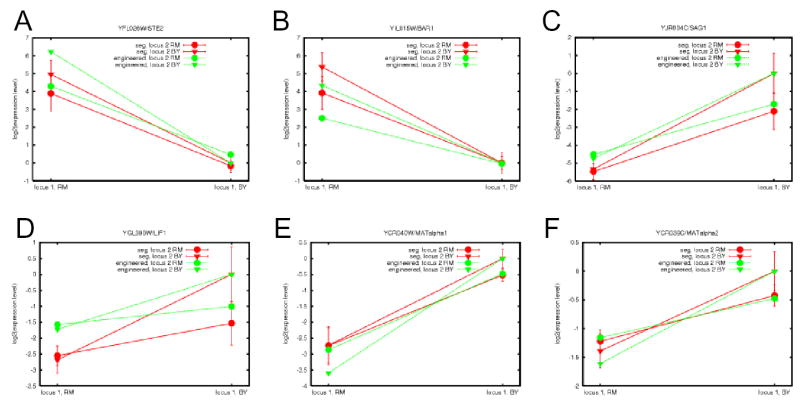
To test the hypothesis that variation at MAT and the S469I mutation in GPA1p interact genetically, we engineered isogenic yeast strains carrying each of the four possible combinations of alleles at the two loci. For each such combination, we compared expression in the engineered strains to expression in segregants with the same allele combination (but with varying inheritance for the rest of the genome). For 7 of 11 transcripts previously known to be regulated by mating type, and 3 of 4 transcripts of unknown function, the pattern of effect of MAT-GPA1 genotype on expression was the same in engineered strains as in segregants (Figure 2 and Supplementary Information), indicating that variation at MAT and GPA1 is sufficient to explain transcript level differences across segregants. YOR090C/PTC1 and YOR162C/YRR1, which have known functions unrelated to mating, did not show agreement between engineered strains and segregants (Supplementary Information), suggesting that these effects represent either false positives or QTLs linked, but unrelated, to MAT or GPA1.

Figure 2.

Example transcripts showing genetic interaction between MAT and GPA1. Each panel represents one transcript. “Locus 1” denotes MAT and “locus 2” denotes GPA1; RM is MATa and BY is MATα. Each red point represents the mean expression level over segregants with the indicated genotype, normalized by the mean over segregants inheriting the BY allele at both loci; red error bars represent standard deviations among segregants with the indicated genotype. Each green point represents the expression level in the indicated engineered strain, normalized by the level in the engineered strain with the BY allele at both loci.

In a wild-type haploid cell exposed to pheromone, GPA1 activates the pheromone response pathway to prepare for mating^17,18. We showed previously that, in the absence of endogenous pheromone, the S469I variant is associated with upregulation of genes involved in mating-type-independent mating functions (e.g., cytoskeletal rearrangement and cell fusion)¹². By contrast, most genes affected by the genetic interaction between MAT and GPA1 perform mating-type-specific mating functions (e.g., pheromone detection and cell conjugation). Levels of α–specific transcripts in the a background have been measured at < 1 copies/cell¹⁹. This suggests a molecular model for the interaction between MAT and GPA1: due to tight repression by MAT, other regulators have no impact on a-specific transcripts in the α background, and vice versa (Figure 2A-D and Supplementary Information). This scenario is analogous to a polymorphism with effects on sex-limited traits in each of the two sexes.

Surprisingly, GPA1 polymorphism affected expression of MATα1 and MATα2 (Figure 2E,F). This is in contrast to results from genome-wide studies^18,20 and a classic molecular biology report²¹ showing no significant regulation of MAT genes by the pheromone response pathway. The discrepancy could indicate that the S469I variant of Gpa1p impacts regulation directly at MAT via a different pathway from that of exogenous pheromone. Alternatively, GPA1 may act indirectly through other regulators of MAT²². We speculate that expression changes due to polymorphism at GPA1 may affect the regulatory activity of MAT-encoded proteins on their downstream targets. Interestingly, for a number of transcripts, polymorphism in GPA1 appeared to show opposing effects in the two mating types (Figure 2E,F and Supplementary Information); whether this represents a true result or an artifact is unclear.

Mapping of genetic factors that underlie polygenic physiological, medical and agricultural traits in outbred populations has met with limited success. It has been suggested that modest individual locus effect sizes due to genetic interactions between loci may be a main cause¹, but the prevalence of interactions has not been well characterized. Our results suggest that genetic interactions underlie the inheritance of roughly half of all transcript levels in yeast, and that at least one member of an interacting locus pair typically has too small an individual effect to be identified on its own. We have shown that a two-stage search provides a useful strategy for the identification of such secondary loci. Because this strategy relies on identification of primary loci by their individual effects, detection of interacting locus pairs in which both individual effects are small remains a challenge, and thus the overall prevalence of interactions may be even higher than estimated here. The discovery here of previously uncharacterized genetic effects in the well-studied yeast pheromone response network underscores the importance of interaction mapping in genetic analyses.

Methods

Strains and expression measurements

Segregants, genotypes, expression measurements, and single-locus linkage results were those of ref. 7. To find multiple independent linkages, for each transcript we identified the marker with the strongest linkage score on each chromosome; if two or more such chromosome peaks exceeded the genome-wide single-locus cutoff in ref. 7, we classified these as multiple independent QTLs. For the direct test of MAT-GPA1 interaction, the I469 and S469 alleles of GPA1 were each engineered into the S288c derivatives BY4709 (MATα URA3Δ0) and BY4724 (MATa LYS2Δ0 URA3Δ0) as in ref. 12; expression arrays were performed as in ref. 7, except that the reference sample was a 1:1 mixture of RNA from the BY and RM strains. For two-stage mapping and interaction tests on the resulting loci, spatial loess normalization was performed on expression data using the genes in ref. 12. Missing genotype data were imputed using a standard hidden Markov model algorithm implemented in R/qtl²³. Missing expression data were imputed using a K = 15 nearest neighbors method²⁴.

Two-locus mapping

A two-stage procedure was employed in order to identify pairs of linked loci for each expression trait. For each transcript and marker, a Wilcoxon rank-sum statistic was formed to quantify expression differences between the segregants grouped by inheritance at the locus. We identified the “primary” QTL for each transcript as the locus with the most significant Wilcoxon rank-sum statistic. We then partitioned segregants based on inheritance (either BY or RM) at the primary locus and similarly tested each subgroup for further “secondary” loci. The locus with the highest statistic among either partition was chosen as the secondary locus. At both stages, the expression traits were randomly permuted (5 times) and analogous maximal statistics were recalculated from this null distribution. These null statistics were pooled across transcripts, for a total of ~30,000 at each stage.

We considered a transcript to be a “false discovery” if either the primary or the secondary locus was a false positive. Under this definition of a false discovery, it is not straightforward to calculate a p-value for each transcript because the null distribution must account for an unknown mixture of three scenarios: both loci are false positives, the primary locus only is a false positive, or the secondary locus only is a false positive. Therefore, we employed a new statistical method to rank the expression traits for significance and calculate the false discovery rate for each significance cut-off¹³. Briefly, we formed nonparametric empirical Bayes estimates of the posterior probability that the primary QTL is a true positive, and then the posterior probability that the secondary QTL is a true positive given that the primary locus is a true positive. The joint probability that both loci are true positives is equal to the product of these two probabilities. The observed and permutation-based null statistics for each stage were used to form conservative estimates of these probabilities (cf. ref. 13). In the Bayesian setting, the false discovery rate is exactly equal to the probability that a transcript is a false positive given that it is called significant²⁷. Equivalently, it can be written as one minus the probability the transcript is a true positive, given that it is called significant. The estimated joint linkage probabilities can be used to directly estimate this latter quantity, yielding an estimate of the false discovery rate for any chosen joint linkage probability cut-off. With a cut-off corresponding to a 5% false discovery rate, 225 expression traits were called significant for two-locus linkage using this method.

Interaction test

For each locus pair mapped in the two-stage model or mapped independently, we fit the model

$$t=ax+by+cxy+d$$

over all segregants. Here t is log₂ of the ratio of expression between the strain of interest and a reference sample, a, b, c, and d are parameters that are specific to the given transcript, x is inheritance at the first locus, and y is inheritance at the second locus. A standard F-test was used to test the null hypothesis that c = 0 by comparing the goodness of fit of the above full model to the purely additive model t = ax + by + d. Because these tests were performed on transcripts and locus pairs previously mapped by the two-stage or independent linkage calculations, there is a potential that the significance could be artificially inflated. However, because the model used in each linkage search is a restricted version of the purely additive model, the interaction term can in fact be tested on previously mapped locus pairs without incurring a bias. The program QVALUE (faculty.washington.edu/~storey/qvalue) was applied to these p-values to estimate the total proportion of transcripts showing evidence for interaction.