Unimolecular Reactions of Dihydrated Alkaline Earth Metal Dications M²⁺(H₂O)₂, M = Be, Mg, Ca, Sr, and Ba: Salt-Bridge Mechanism in the Proton-Transfer Reaction M²⁺(H₂O)₂ → MOH⁺ + H₃O⁺

Abstract

The unimolecular reactivity of M²⁺(H₂O)₂, M = Be, Mg, Ca, Sr, and Ba, is investigated by density functional theory. Dissociation of the complex occurs either by proton transfer to form singly charged metal hydroxide, MOH⁺, and protonated water, H₃O⁺, or by loss of water to form M²⁺(H₂O) and H₂O. Charge transfer from water to the metal forming H₂O⁺ and M⁺(H₂O) is not favorable for any of the metal complexes. The relative energetics of these processes are dominated by the metal dication size. Formation of MOH⁺ proceeds first by one water ligand moving to the second solvation shell followed by proton transfer to this second-shell water molecule and subsequent Coulomb explosion. These hydroxide formation reactions are exothermic with activation energies that are comparable to the water binding energy for the larger metals. This results in a competition between proton transfer and loss of a water molecule. The arrangement with one water ligand in the second solvation shell is a local minimum on the potential energy surface for all metals except Be. The two transition states separating this intermediate from the reactant and the products are identified. The second transition state determines the height of the activation barrier and corresponds to a M²⁺–OH⁻–H₃O⁺ “salt-bridge” structure. The computed B3LYP energy of this structure can be quantitatively reproduced by a simple ionic model in which Lewis charges are localized on individual atoms. This salt-bridge arrangement lowers the activation energy of the proton-transfer reaction by providing a loophole on the potential energy surface for the escape of H₃O⁺. Similar salt-bridge mechanisms may be involved in a number of proton-transfer reactions in small solvated metal ion complexes, as well as in other ionic reactions.

1. Introduction

The gas-phase reactivity and structure of hydrated singly charged metal ions have been extensively studied by both experiment and theory.¹ Valuable information can be gained from these gas-phase clusters about the interaction of metal ions in solution, e.g., sequential hydration enthalpies.² Especially intracluster reactions of hydrogen-bonded systems containing a single metal ion have received considerable attention.³ By comparison, much less is known about the gas-phase chemistry of hydrated divalent metal ions. These ions have been investigated with theoretical methods by a number of researchers.⁴ Fewer experimental studies have been reported primarily because hydrated divalent ions are less readily formed by conventional methods.^5,6 Gas-phase reactivity studies of bare doubly charged transition metal cations with alkanes have shown that, in addition to partial charge transfer from the metal dication to the neutral, charge reduction may also occur by hydride transfer, yielding MH⁺, where M is Ti or Nb.⁷ Charge-transfer and association reactions of the alkaline earth metal dications Mg²⁺, Ca²⁺, and Ba²⁺ with various neutrals have been studied by Spears et al.⁸ The metals underwent different reactions with water. Charge transfer occurs for Mg²⁺. One H₂O molecule was observed to attach to Ca²⁺. Addition of a second water molecule resulted in spontaneous charge separation by a proton-transfer reaction to form the metal hydroxide CaOH⁺ and H₃O⁺. For Ba²⁺, several water molecules were attached without hydroxide formation.

Electrospray ionization has been widely used to form multiply charged ions of molecules, such as proteins and DNA, directly from solution. In a series of pioneering experiments, Kebarle and co-workers⁵ demonstrated that gas-phase hydrated metal dications can be readily produced by electrospray ionization, extending the earlier thermospray work by Schmelzeisen-Redeker et al.⁹ Ions of the composition M²⁺(H₂O)_n, (n = 0–15) were observed for the group II metals Mg, Ca, Sr, and Ba as well as for most first-row transition metals. However, only singly charged hydrated metal hydroxide species, MOH⁺(H₂O)_n, were observed with both Be and Cu. Collisional activation of M²⁺(H₂O)_n using argon with a 5 eV center of mass collision energy resulted in dissociation by two pathways: loss of water molecules (reaction 1) and proton transfer to form singly charged metal hydroxide and protonated water (reaction 2).

$${\text{M}}^{2+}{({\text{H}}_2\text{O})}_n\to {\text{M}}^{2+}{({\text{H}}_2\text{O})}_{n-m}+m{\text{H}}_2\text{O}$$ (1)

$${\text{M}}^{2+}{({\text{H}}_2\text{O})}_n\to {\text{MOH}}^{+}{({\text{H}}_2\text{O})}_{n-m}+{\text{H}}_3{\text{O}}^{+}+(m-2){\text{H}}_2\text{O}$$ (2)

Kebarle found that the maximum number of water molecules in the hydrated dication for which proton transfer (reaction 2) was observed decreases with the second ionization potential (IP) of the metal. From these experimental results, the first solvation shell hydration energies were estimated using a thermochemical cycle for the activation energy of the proton-transfer reaction 2, H(2):

$$\begin{array}{l}H(2)=H_{r,0}({\text{M}}^{2+})-\text{IE}({\text{M}}^{+})-D({\text{M}}^{+}-\text{OH})-\\ H_{r-2,0}({\text{MOH}}^{+})+H(4)+E_{\text{cou}}\end{array}$$ (3)

Here, H_x,0(Y) is the binding energy of x water molecules to Y, IE(M⁺) is the second IP of the metal, D is the bond dissociation energy, H(4) is defined in eq 4, and E_cou is the energy released

$$2{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+\text{OH}+{\text{e}}^{-}$$ (4)

by the Coulomb explosion of the products. Kebarle and coworkers discussed the contribution of the various factors and concluded that the two terms IE(M⁺) and D(M⁺–OH) are dominant.

This analysis of the experimental results is entirely correct, though it has apparently resulted in some confusion in the literature. Subsequent publications^4c,f,6 focus exclusively on the charge-transfer aspect implied by the ionization potential while neglecting the equally important metal–hydroxide bond dissociation energy. In a theoretical work,^4f the charge-transfer reaction 5 was given as an example of a competitive reaction to water loss, though this reaction was not observed in Kebarle’s experiment.

$${\text{M}}^{2+}{({\text{H}}_2\text{O})}_n\to {\text{M}}^{+}{({\text{H}}_2\text{O})}_{n-1}+{\text{H}}_2{\text{O}}^{+}$$ (5)

Although eq 3 is correct, it does not provide a chemically intuitive model of the proton-transfer reaction 2. The explicit inclusion of the second ionization potential suggests that a charge transfer to the metal resulting in a singly charged M⁺ and a neutral OH occurs. Especially for alkaline earth metals, however, MOH⁺ is more correctly considered to be an ionic complex consisting of closed-shell M²⁺ and OH⁻ species, rather than a neutral OH covalently bound to M⁺. Equation 3 was formulated in a way to allow the use of tabulated data, such as IE(M⁺) and D(M⁺–OH), which does not necessarily mean that each term corresponds to a step of the actual chemical reaction. Indeed, it is straightforward to reformulate eq 3 in a chemically more pleasing way by introducing the bond dissociation energy D(M²⁺–OH⁻), which is derived from IE(M⁺), D(M⁺–OH), and the electron affinity of OH, EA(OH):

$$D({\text{M}}^{2+}-{\text{OH}}^{-})=\text{IE}({\text{M}}^{+})+D({\text{M}}^{+}-\text{OH})-\text{EA}(\text{OH})$$ (6)

The new eq 3′ reads, with a modified term H(4′)

$$\begin{array}{l}H(2)=H_{r,0}({\text{M}}^{2+})-D({\text{M}}^{2+}-{\text{OH}}^{-})-H_{r-2,0}({\text{MOH}}^{+})+\\ H(4^{\prime })+E_{\text{cou}}\end{array}$$ (3′)

Thus, the two dominant terms from eq 3 have merged into one that reflects the concept of an ionic bond. In addition, the free electron suggestive of a charge transfer in reaction 4 becomes attached to OH, resulting in the proton-transfer reaction 4′.

$$2{\text{H}}_2\text{O}\to {\text{H}}_3{\text{O}}^{+}+{\text{OH}}^{-}$$ (4′)

Previous theoretical work focused on the charge-transfer problem,^4a–c the geometries and hydration enthalpies of doubly charged metal ions,^4d–i and the activation barrier of the water exchange reaction between the first and second solvation shells.4j,k The experimentally observed proton-transfer reaction 2, however, has, to the best of our knowledge, not been computationally treated before. The goal of the present study is to fill this gap and to come to a qualitative and quantitative understanding of the dissociation reactivity of hydrated metal dications and derive a chemically intuitive model of these reactions. As a model system, the smallest clusters were chosen that can undergo all reactions in question, M²⁺(H₂O)₂, with M being the alkaline earth metals studied by Kebarle, i.e., M = Be, Mg, Ca, Sr, and Ba. Thermochemical values are obtained for reactions 1, 2, and 5, and the transition states and intermediates of the proton-transfer reaction 2 are located on the potential energy surface. The charge-transfer aspect is discussed on the basis of a natural population analysis,¹⁰ and the energetics modeled by assigning formal Lewis charges.

2. Computational Details

The calculations were performed using the B3LYP¹¹ hybrid density functional method implemented in the Gaussian94¹² program package. For geometry optimizations, frequency calculations, and potential energy surface scans on beryllium and magnesium species, the large 6-311G(3df,2pd) basis set in Gaussian94 was used on all atoms. Calcium, strontium, and barium species were treated with the quasi-relativistic effective core potential basis set from the Stuttgart/Dresden group¹³ on the metal, denoted SECP in this work, which is a 6s6p5d/4s4p2d basis set on a 10-valence-electron pseudopotential, and the 6-311G(d,p) basis set in Gaussian94 on oxygen and hydrogen. Zero-point corrections were taken from this level of theory. Single-point energy calculations were performed including diffuse functions, employing the Gaussian94 6-311+(3df,2pd) basis set on hydrogen, oxygen, beryllium, and magnesium, and again the SECP on calcium, strontium, and barium. All calculations were done on either an SGI Power Challenge or a DEC AlphaStation 500.

Starting geometries for the transition state search,¹⁴ implemented as QST3 (quasi-Newton, synchronous transit-guided) in Gaussian94, were obtained by relaxed potential energy surface scans. The lowest energy structures of M²⁺(H₂O)₂ can have either D_2d (M = Be and Mg) or C_s (M = Ca, Sr, and Ba) symmetry.^4d,e Figure 1 shows the more general C_s structure of M²⁺(H₂O)₂. Starting from these structures, we progressively shortened the O2–H2 distance in 20 steps to a typical H₃O⁺ bond length of 0.98 Å. Keeping this distance fixed, geometry optimization was performed at each step.

Figure 1.

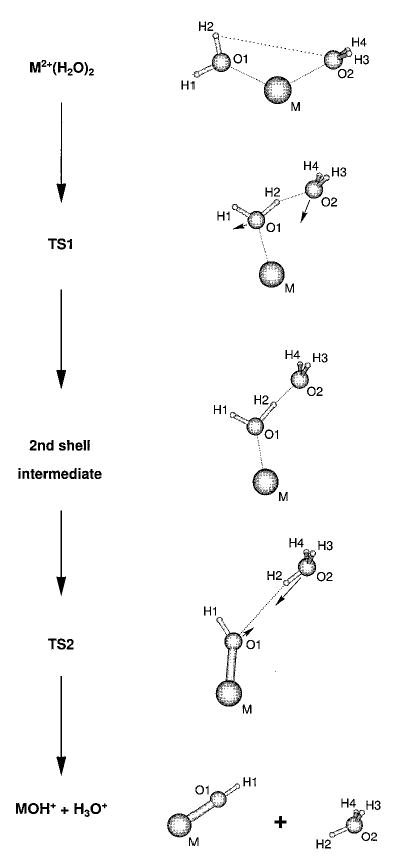
The general proton-transfer reaction pathway for dissociation of M²⁺(H₂O)₂ to produce MOH⁺ and H₃O⁺ for magnesium, calcium, strontium, and barium. First, one water molecule is promoted from the first to the second solvation shell via transition state 1 (TS1) to form a second-shell intermediate structure. Second, proton transfer occurs via a salt-bridge structure in TS2. The two charged products separate due to Coulomb repulsion after TS2. The second-shell intermediate and TS2 do not exist for beryllium. The arrows in TS1 and TS2 indicate the reaction modes.

For beryllium, the energies went through a single maximum corresponding to a transition state denoted TS1, followed by a smooth “Coulombic explosion”. For all the heavier metal ions, a second local minimum was observed. This corresponds to one molecule bound in the second solvation shell, labeled as “2nd shell intermediate” in Figure 1. In each case, the highest energy structure on this path is taken as a starting geometry for the transition state search. In the case of Ba²⁺(H₂O)₂, the first transition state could not be located with the QST3 method, as it lies too close to the second-shell local minimum. Instead, the transition state region was scanned in 0.01 Å steps along the O2–H2 coordinate, and the highest energy structure was identified as the transition state. The local minimum was found using an unconstrained geometry optimization, and gave the initial geometry for an additional relaxed potential energy surface scan. This time, the O1–H2 bond was lengthened in steps of 0.1 Å, thus enforcing the formation of an H₃O⁺ ion. Again, the highest energy structure of the scan formed the starting geometry for the transition state search.

All minima and transition states were verified by frequency calculations. Vibrational frequencies were scaled by a factor of 0.90 as used by Pavlov et al.¹⁵ and were applied to calculate zero-point energy corrections.

3. Results

3.1. Comparison with Experimental Values.

Hydration enthalpies of doubly charged beryllium, magnesium, calcium, and zinc have been recently calculated using B3LYP.⁴ⁱ For Ca(H₂O)_n²⁺, n = 5, 6, and 7, these values are in excellent agreement with values measured using blackbody infrared radiative dissociation in a Fourier transform mass spectrometer.¹⁶ Although no other experimental values for inner shell water molecules are currently available, the good agreement between experiment and theory for calcium suggests that accurate energetics can be obtained with B3LYP for these hydrated cations, as was previously shown for singly charged hydrated transition metal ions.¹⁷ To further test the reliability of the B3LYP functional and the basis sets, especially the effective core potentials, on systems with different charge states and spin multiplicities, various thermochemical values were calculated and compared to the available experimental data. Table 1 gives the first and second ionization potentials of the metals, the ionization potential of water, the electron affinity of OH, and D°₀(M⁺–OH) values. All calculations are in reasonable agreement with the experimentally measured values. This indicates that the chosen level of theory is adequate for calculating the potential energy surfaces in question.

Table 1.

Zero Point Corrected Thermochemical Values (kJ/mol) Obtained at the B3LYP/6-311+G(3df,2pd)/SECP Level, Compared with Experiment

quantity	calculation	experimenta	% relative error
IP(Be)	879.5	899.4	2.2
IP(Be+)	1794.3	1757.1	2.1
IP(Mg)	745.6	737.7	1.1
IP(Mg+)	1492.0	1450.7	2.8
IP(Ca)	597.1	589.7	1.3
IP(Ca+)	1161.4	1145	1.4
IP(Sr)	555.6	549.5	1.1
IP(Sr+)	1079.8	1064.2	1.5
IP(Ba)	504.9	502.8	0.4
IP(Ba+)	974.1	965.1	0.9
IP(H2O)	1218.6	1216.8	0.1
EA(OH)	169.7	176.5	3.9
D°0(Mg+–OH)	299.9	318.4 ± 28.9b	6.0
D°0(Ca+–OH)	454.7	435.1 ± 14.5c	4.4
D°0(Sr+–OH)	431.1	440.9 ± 9.6c	2.3
D°0(Ba+–OH)	464.8	530.6 ± 19.3b	12.5

^aUnless otherwise noted, thermochemical data are taken from S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin, and W. G. Mallard, J. Phys. Chem. Ref. Data 1988, 17, Suppl. 1.

^bE. Murad, J. Chem. Phys. 1981, 75, 4080–4085.

^cE. Murad, J. Chem. Phys. 1983, 78, 6611–6613.

3.2. Geometries.

To evaluate the energetics for the loss of water (reaction 1) and charge-transfer (reaction 5) reactions, calculations of M⁺(H₂O) and M²⁺(H₂O) are necessary. Both have C_2v symmetry for all metals studied. The geometry parameters are summarized in Tables 2 and 3. These tables also include for comparison the calculated parameters of free H₂O. The M–O distances in M²⁺(H₂O) deviate slightly from those reported by Pavlov et al.⁴ⁱ and Glendening and Feller,^4f presumably due to the different basis set and method used in the present study. The charged metal center produces an elongation of the O–H bond, which is more pronounced at higher charge and shorter M–O distance.

Table 2.

Geometry Parameters of M⁺(H₂O), C_2v Symmetry^a

M	M–O (Å)	O–H (Å)	∠HOH (deg)
Be	1.55	0.97	109.8
Mg	2.04	0.97	106.6
Ca	2.30	0.97	106.3
Sr	2.48	0.97	105.8
Ba	2.65	0.97	105.7
H2O		0.96	105.1

^aThe values for the free H₂O molecule are included for comparison.

Table 3.

Geometry Parameters of M²⁺(H₂O), C_2v Symmetry

M	M–O (Å)	O–H (Å)	∠HOH (deg)
Be	1.48	0.99	107.7
Mg	1.91	0.98	105.7
Ca	2.23	0.98	104.2
Sr	2.41	0.97	103.8
Ba	2.60	0.97	103.7

As was calculated previously,^4d,e the lowest energy structures of M²⁺(H₂O)₂ reactant ions were found to have D_2d symmetry for M = Be and Mg, and C_s symmetry for Ca, Sr, and Ba. The bent structure for the larger metal ions was attributed to core polarization. Glendening and Feller^4f reported a C₂ structure for Ca, Sr, and Ba, using a somewhat smaller basis set. Kaupp and Schleyer^4e studied several different isomers and found that the linear D_2d, the bent C_s, and the bent C_2v structures differ by no more than 4 kJ/mol. The effects are very delicate, but overall, larger basis sets seem to favor the C_s symmetry.

The structures corresponding to stationary points on the potential energy surface of the proton-transfer reaction 2 for the dihydrated dications are shown in Figure 1. The first step in the reaction involves promoting one water molecule from the first to the second solvation shell via TS1. This results in a second-shell intermediate that is a local minimum for all metals except beryllium. Similar stable second-shell structures have been found by Feller et al.^1c for dihydrated alkali metal cations M⁺(H₂O)₂, M = Li, Na, and K. For beryllium, the second-shell structure is unstable and the MOH⁺ + H₃O⁺ products are on a repulsive surface with no further activation barriers after TS1. The instability of the second-shell intermediate for Be was verified by replacing Mg by Be in the second-shell Mg²⁺(H₂O) structure, and performing a geometry optimization. The geometry readily converged to the separated reaction products, BeOH⁺ + H₃O⁺.

For magnesium, proton transfer occurs prior to the second-shell intermediate. In contrast, the intermediate structures for calcium, strontium, and barium consist of a slightly distorted water dimer attached to the metal ion. The hydrogen atoms of the hydrogen bond acceptor molecule are tilted away from the metal. For these larger metals, proton transfer to form H₃O⁺ occurs after the intermediate but prior to TS2. This second transition state separates the attractive from the repulsive part of the multipole potential created by the distorted MOH⁺. MOH⁺ is linear in the final products for all metals except magnesium, for which the hydroxide is bent at an angle of 137.1°.

The most significant geometric parameters of these structures and their changes during the reaction are given in Table 4 for each of the metals.¹⁸ Both the M–O1 and M–O2 distances (Table 4A,B) increase with the ionic radius of the metal. For the larger metals, the bond distance M–O1 is considerably reduced in going from the reactant ions to the second-shell intermediate, as the coordination number of the metal changes from two to one. Magnesium exhibits the most significant change in going from TS1 to the second-shell intermediate, as this step already involves the proton transfer and formation of MgOH⁺. For the heavier metals, this hydroxide formation only occurs upon going from the second-shell intermediate to TS2, causing a concurrent pronounced decrease in the M–O1 bond by up to 0.24 Å. Removal of the polarizing H₃O⁺ results in relaxation to the even shorter M–O1 distance in free MOH⁺. M–O2 increases rapidly as the water molecule is promoted from the first to the second solvation shell and then finally as separation of H₃O⁺ occurs via Coulomb repulsion.

Table 4.

Significant Geometry Parameters for the Stationary Points of the Reaction M²⁺(H₂O)₂ → MOH⁺ + H₃O^+a

A. M–O1 Distance (Å)
M	M2+(H2O)2	TS1	second shell	TS2	MOH+ + H3O+
Be	1.51	1.43			1.32
Mg	1.93	1.86	1.83	1.79	1.74
Ca	2.27	2.14	2.13	1.97	1.90
Sr	2.44	2.31	2.31	2.11	2.04
Ba	2.63	2.49	2.49	2.25	2.17
B. M–O2 Distance (Å)
M	M2+(H2O)2	TS1	second shell	TS2	MOH+ + H3O+
Be	1.51	2.45			∞
Mg	1.93	3.15	3.98	5.36	∞
Ca	2.27	3.59	4.06	5.61	∞
Sr	2.44	4.07	4.19	5.99	∞
Ba	2.63	4.25	4.35	6.25	∞
C. O1 –H2 Distance (Å)
M	M2+(H2O)2	TS1	second shell	TS2	MOH+ + H3O+
Be	0.98	1.15			∞
Mg	0.97	1.04	1.37	2.79	∞
Ca	0.97	1.04	1.09	2.99	∞
Sr	0.97	1.04	1.05	3.18	∞
Ba	0.97	1.03	1.03	3.31	∞
(H2O)2			0.97
D. O2 –H2 Distance (Å)
M	M2+(H2O)2	TS1	second shell	TS2	MOH+ + H3O+
Be	3.69	1.32			0.98
Mg	4.52	1.49	1.09	0.98	0.98
Ca	4.32	1.51	1.37	0.98	0.98
Sr	4.28	1.50	1.47	0.98	0.98
Ba	4.21	1.53	1.51	0.98	0.98
(H2O)2			1.95
E. ∠O1H2O (deg)
M		TS1	second shell	TS2
Be		140.4
Mg		150.8	176.9	168.4
Ca		158.3	174.9	169.7
Sr		167.6	172.9	171.0
Ba		169.1	172.2	170.1
(H2O)2			170.9

^aCorresponding values in free (H₂O)₂ are included for comparison.

Parts C and D of Table 4 list the O1–H2–O2 distances that reflect the formation of the hydrogen bond between the two water molecules and the subsequent proton transfer. The corresponding values for the free water dimer are included for comparison. As the two water molecules align, the O1–H2 distance increases due to polarization, and the smaller the metal, the more pronounced this effect is. For beryllium, O1–H2 is elongated by 0.17 Å in TS1, indicating that proton transfer has already started in this transition state. For all the other metals, however, there is only a slight (0.07 Å) elongation of this bond in TS1, consistent with the formation of a hydrogen bond. This bond is present in the second-shell intermediate. Compared to free (H₂O)₂, the O1–H2 distance in TS1 and the second-shell intermediate is elongated due to polarization, and the H2–O2 distance is shortened as the negative end of the water dipole is drawn toward the metal center. For beryllium, the polarization is so strong that the intermediate is unstable. For magnesium, the polarization is sufficiently strong that proton transfer is initiated, whereas with the larger metal cations, the elongation of the O1–H2 bond is significantly less pronounced. Formation of H₃O⁺ is complete in TS2 as indicated by the O2–H2 distance of 0.98 Å. The O1–H2–O2 hydrogen bond angle in TS1 (Table 4E) changes from bent for beryllium to almost linear for barium. In the second-shell intermediate and TS2, O1–H2–O2 is almost linear for each of the metals.

3.3. Energies.

The potential energy surfaces for loss of water (reaction 1), proton transfer (reaction 2), and charge transfer (reaction 5) are shown in Figure 2 in which the M–O2 distance is the reaction coordinate. The energies of the various structures are given in Table 5, which in addition includes energies for the monohydrated species. The binding energies of water are within 5 kJ/mol in agreement with those calculated previously with density functional theory,⁴ⁱ and within 10 kJ/mol with those calculated by post-Hartree–Fock methods.^4d,f

Figure 2.

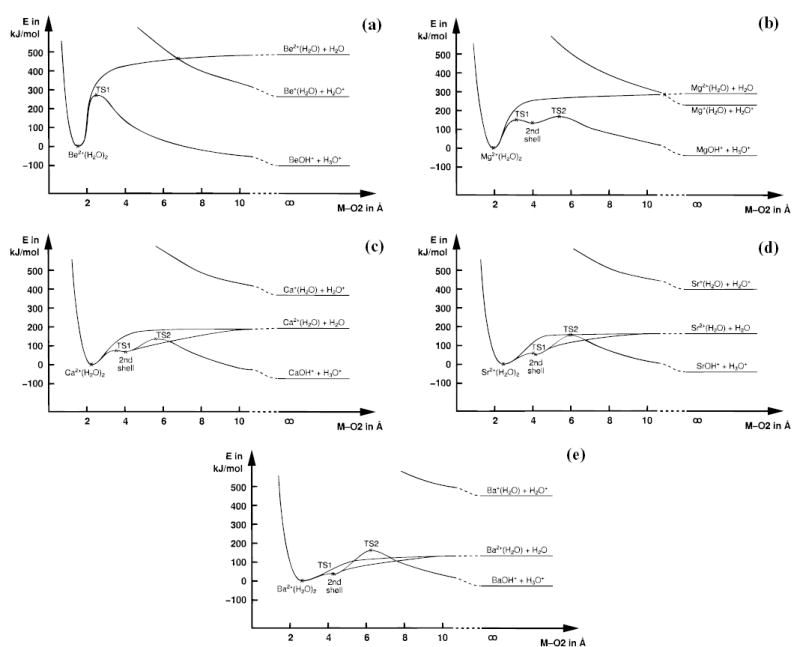
Potential energy surface profiles along the M–O2 distance for three unimolecular reaction pathways of M²⁺(H₂O)₂ for (a) beryllium, (b) magnesium, (c) calcium, (d) strontium, and (e) barium. The only real curve crossings are the charge transfer vs water loss crossings in (a) and (b); all others result from the projection of a multidimensional potential energy surface on two dimensions. In each case, the proton transfer reaction to form MOH⁺ + H₃O⁺ is exothermic and yields the lowest product energies. It was experimentally observed for Mg, Ca, and Sr (b, c, d), ref 5. For Ba (e), TS2 forms a barrier that is higher than the abstraction energy of a water molecule, and accordingly, water loss instead of proton transfer was observed.

Table 5.

Relative Energies (kJ/mol) on the M²⁺(H₂O)₂ Surface

	Be	Mg	Ca	Sr	Ba
M+ + H2O+ + H2O	+531.3	+366.3	+489.5	+498.6	+546.3
est curve crossing	+988.8	+606.3
M2+ + 2H2O	+1107.1	+639.7	+432.4	+359.8	+301.8
M+(H2O) + H2O+	+269.1	+236.0	+374.2	+404.1	+458.1
est curve crossing	+468.0	+294.6
M2+(H2O) + H2O	+491.7	+297.1	+199.3	+167.7	+141.4
M2+(H2O)2	+0.0	+0.0	+0.0	+0.0	+0.0
TS1	+275.9	+152.9	+78.0	+57.9	+40.5
second shell		+131.9	+71.4	+56.6	+39.9
TS2		+165.0	+139.4	+157.3	+161.9
MOH+ + H3O+	−104.8	−33.6	−65.3	−32.6	−18.6

The location of the crossing between the water loss and the charge-transfer curve on the Be²⁺(H₂O)₂ and Mg²⁺(H₂O)₂ potential energy surfaces is estimated from the leading terms in the electrostatic interaction. At larger distances, the M²⁺(H₂O) – H₂O energy consists of essentially an attractive charge–dipole interaction, and the M⁺(H₂O) – H₂O⁺ energy is the repulsive Coulomb energy of two charges. At the curve crossing, these two contributions sum up to the energy difference ΔE of the two reaction channels at infinite separation, eq 7. From this

$$\mathrm{\Delta }E=2\mu e/4\pi {\varepsilon }_{0}r{(\text{M}-\text{O}2)}^2+e^2/4\pi {\varepsilon }_{0}r(\text{M}-\text{O}2)$$ (7)

relation, the energy and the M–O2 distance at which curve crossing occurs are calculated. Energy estimates are included in Table 5; the corresponding M–O2 distances are 3.03 and 6.86 Å for the mono- and dihydrated beryllium species, and 5.75 and 23.3 Å for the corresponding magnesium species, respectively. The relatively large distances for the curve crossings of the dihydrated systems indicate that the approximation is justified, as higher order electrostatic as well as covalent contributions decrease rapidly with distance.

For calcium, strontium, and barium, the second IP of the metal is lower than the first IP of water so that curve crossing to the charge-transfer exit channel cannot occur. In the case of magnesium, the charge-transfer products are 70 kJ/mol higher in energy than TS2, which defines the activation energy for the proton-transfer reaction. For beryllium, the charge-transfer products are lower in energy than TS1, but the curve crossing occurs at more than 1 eV higher energy due to the large reverse activation barrier for this reaction. In every case, observation of the charge-transfer products by collisional activation of M²⁺(H₂O)₂ is highly improbable.

A true competition evolves for the loss of water (reaction 1) versus the proton-transfer (reaction 2) for the larger metals. In Be²⁺(H₂O)₂, the transition state for reaction 2 is 210 kJ/mol lower in energy than water loss. Thus, hydroxide formation is highly energetically favored. The difference in energy between the two channels narrows to 130, 60, and 10 kJ/mol for magnesium, calcium, and strontium, respectively. For barium, the relative energies are reversed; loss of water is favored by 20 kJ/mol over the proton-transfer reaction.

An interesting aspect of these calculations is the stability of the second-shell intermediate for the larger metals. The well depth of the second-shell minimum is 20 kJ/mol for magnesium. Thus, this species should be experimentally observable. For the larger metals, the geometry of TS1 approaches that of the second-shell intermediate, resulting in a corresponding decrease in the well depth for this species, which is only 7 kJ/mol for calcium and roughly 1 kJ/mol for strontium and barium.

The lack of a second-shell minimum and TS2 for beryllium seems somewhat surprising, since a second-shell structure was found for Li⁺(H₂O)₂.^1c However, the double charge leads to a significantly reduced M–O1 bond length in the lowest energy structure, 1.51 Å for Be²⁺ vs 1.90 Å for Li⁺. As polarization effects are nonlinear, the reduced distance and higher charge can lead to a significantly different chemistry. The distance argument also applies for the other alkaline earth metals, where the ionic radii correlate with the trend in the energy difference between TS1 and TS2 for the different metals. These differences decrease with decreasing metal size: 120, 100, 60, and 12 kJ/mol for barium to magnesium, respectively. Thus, TS2 and TS1 converge with decreasing metal ion size and meet for beryllium, which makes the second-shell intermediate disappear. The results of the present study do not support the idea of a covalent Be–O bond in hydrated Be²⁺ as put forward by Hashimoto et al.^4l–n It was based on the calculation of the interaction energy of two water molecules in the optimized geometry of Be²⁺(H₂O)₂, with the Be²⁺ ion removed.^4l This approach is problematic since the dipole moments of the water molecules are significantly different with and without the strongly polarizing Be²⁺ ion in between.

3.4. Natural Charges.

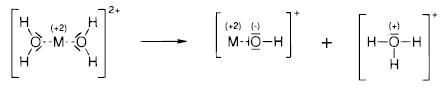
The values of natural charges computed in a natural population analysis¹⁰ are included in Table 6 for calcium. Values for the other metals are similar and are therefore not reported. The charge on the metal changes by only −0.1 e during the proton-transfer reaction. This indicates that charge transfer to the metal is not the primary driving force of this reaction. By adding the charge corresponding to the atoms in the products, CaOH⁺ (Ca + O1 + H1) and H₃O⁺ (H2 + H3 + H4 + O2), the total charge rearranged during the reaction can be obtained; this value is 0.4 e. Most of this charge is transferred between the two oxygen atoms. The charges on the hydrogen atoms do not change significantly. This is consistent with only the oxygen atoms undergoing a change in formal charge within the Lewis formalism, as illustrated in Scheme 1. The major change in natural charges occurs from the second-shell intermediate to TS2, i.e., during the proton transfer, which also corresponds to the change in Lewis charges.

Table 6.

Natural Partial Charges for the Stationary Points of the Ca²⁺(H₂O)₂ → CaOH⁺ + H₃O⁺ Reaction

unit	Ca2+(H2O)2	TS1	second shell	TS2	CaOH+ + H3O+
Ca	+1.94	+1.94	+1.94	+1.87	+1.84
O1	−1.07	−1.13	−1.16	−1.36	−1.35
H1	+0.55	+0.55	+0.54	+0.49	+0.51
H2	+0.55	+0.54	+0.53	+0.58	+0.58
O2	−1.07	−0.96	−0.92	−0.76	−0.74
H3, H4	+0.55	+0.53	+0.54	+0.59	+0.58
sum
CaOH+	+1.42	+1.36	+1.32	+1.00	+1.00
H3O+	+0.58	+0.64	+0.69	+1.00	+1.00

Scheme 1.

4. Discussion

The results of this computational study reflect perfectly well the experiments by Spears et al.,⁸ which started from the bare M²⁺ dication, M = Mg, Ca, and Ba. Charge transfer to water is energetically accessible only for Mg²⁺, as IP(Mg⁺) = 15.0 eV and IP(H₂O) = 12.6 eV.^5c This process was the only one observed with this metal. Monohydrated calcium, Ca²⁺(H₂O), undergoes the equivalent of the proton transfer (reaction 2) in the collision with another water molecule. The activation energy for this process (reaction 2) is supplied by the binding energy of the second water molecule (Figure 2c). In the case of monohydrated barium, Ba²⁺(H₂O), association of multiple H₂O to Ba²⁺ occurs; no proton transfer is observed. This is consistent with the barrier for proton transfer being higher than the binding energy of a second water molecule (Figure 2e).

Similarly, our results are consistent with the experimental observations made by Kebarle and co-workers.⁵ For barium, no proton transfer was observed, consistent with our calculations that indicate that TS2 is 20 kJ/mol higher in energy than the water loss channel. For strontium and calcium, proton transfer and water loss are competitive. For strontium, the activation energies for proton transfer and water loss are nearly equal (ΔE_a = 10 kJ/mol) whereas for calcium, the barrier is 60 kJ/mol lower for proton transfer. The observation of water loss for calcium may indicate that the difference in energy is actually lower or that the process for loss of water has a larger transition-state entropy. For magnesium, proton transfer and H₃O⁺ formation are observed with two and three water molecules in the experiment. This indicates that magnesium shows a higher propensity for the proton-transfer reaction, due to the large energy gap between TS2 and the water loss. The proton-transferred second-shell structure illustrates that magnesium polarizes the O–H bond more strongly than the larger ions.

The comparison for beryllium is less clear since Be²⁺(H₂O)_n was not observed experimentally, although stable structures for n ≤ 12 were calculated by Pavlov et al.⁴ⁱ Be²⁺(H₂O)₂ is the most stable of the ions investigated by us. Observing this ion experimentally starting with doubly charged ions may be difficult. Condensing water onto bare Be²⁺ will almost certainly result in charge transfer, as IP(Be⁺) = 18.2 eV and IP(H₂O) = 12.6 eV. It is also unlikely that this ion can be formed by evaporation of water from more extensively hydrated clusters. The difference in activation barriers for water loss vs proton transfer is by far the greatest for beryllium. Thus, formation of monohydrated Be²⁺(H₂O) from Be²⁺(H₂O)₂ should not occur because the proton-transfer reaction is highly energetically favored. This is more pronounced for beryllium than for any other alkaline earth metal. It is likely that this trend also holds for more highly hydrated clusters. This would indicate that if the hydrated metal ions formed by electrospray are formed by solvent evaporation from even larger clusters, then proton transfer, driven by the polarization of first solvation shell water molecules by the very small beryllium, is preferred over water loss in the size regime accessible in Kebarle’s experiment. A similar observation was made when using aqueous solutions of M(III) salts in electrospray,¹⁹ where only MOH²⁺(H₂O)_n−1 and no M³⁺(H₂O)_n clusters were observed. The higher charge seems to have the same effect as the small ionic radius of beryllium.

In Kebarle’s experiment, the chemistry of copper is similar to that of beryllium even though its ionic radius is almost the same as that of magnesium. The electron configuration of Cu²⁺ is [Ar]3d⁹. Due to the hole in the d shell, the ligand is more strongly attracted along the direction of reduced electron density. This leads to a significantly reduced bond length. A similar rationalization has been reported for NbAr₄⁺ which has a [Kr]d⁴ configuration.²⁰ In addition, the positive charge is not spherically symmetrically shielded by the d electrons, which leads to stronger electrostatic forces along the metal–ligand bond. These two effects may compensate for the larger size of copper compared to beryllium, and lead to a comparable polarization of the water ligands which induces proton transfer and Coulomb explosion. It is known that Cu²⁺ complexes exhibit very large Jahn–Teller distortions due to these same effects.²¹

The natural population analysis as well as the Lewis charge formalism both indicate that the charge state of the metal does not change during the proton-transfer reaction. To test how well the concepts of formal charge represent the actual charge distribution, we calculated two energies that should be dominated by Coulomb forces. First, the D°₀(M²⁺–OH⁻) bond dissociation energy representing a purely ionic bond is compared to the second ionization potential and the tabulated D°₀(M⁺–OH) binding energy (Table 7 and Figure 3). D°₀(M²⁺–OH⁻) smoothly decreases with increasing metal ion radius. In contrast, D°₀(M⁺–OH) has no obvious trend. The Coulomb energy, E_cou(M²⁺–OH⁻), defined as the energy of a double positive and a single negative charge at the metal–oxygen distance in Figure 4a, accurately reproduces the B3LYP energies for D°₀(M²⁺–OH⁻) (Figure 3). In other words, the bonding in MOH⁺ can be quantitatively described by a simple Coulomb potential with a double charge centered on the metal and a single charge centered on the oxygen. Thus, eqs 3’ and 4’ provide a more intuitive description of these reactions than do eqs 3 and 4 although both sets of equations are correct.

Table 7.

Comparison of the Ionic Radius r(M²⁺), the Second Ionization Potential IP(M⁺), D°₀(M⁺–OH), D°₀(M²⁺–OH⁻), and E_cou(M²⁺–OH⁻)^a

M	r(M2+)b	IP(M+)c	D°0(M+–OH)c	D°0(M2+–OH−)c	Ecou(M2+–OH−)d
Be	0.41	1794.3	536.0	2160.7	2106.1
Mg	0.86	1492.0	299.9	1622.2	1597.7
Ca	1.14	1161.4	454.7	1446.5	1463.2
Sr	1.32	1079.8	431.1	1341.2	1362.7
Ba	1.49	974.1	464.8	1269.2	1281.1

^aRadius in angstroms and energies in kilojoules per mole.

^bIonic radii are taken from J. E. Huheey, Anorganische Chemie, Walter de Gruyter, Berlin, 1988, p 78f. Values are taken for coordination number four for beryllium and six for the other metals.

^cZero-point corrected B3LYP/SECP/6-311+G(3df,2pd) values.

^dCoulomb energy of a double positive and a single negative charge at distance M–O1, Figure 4a.

Figure 3.

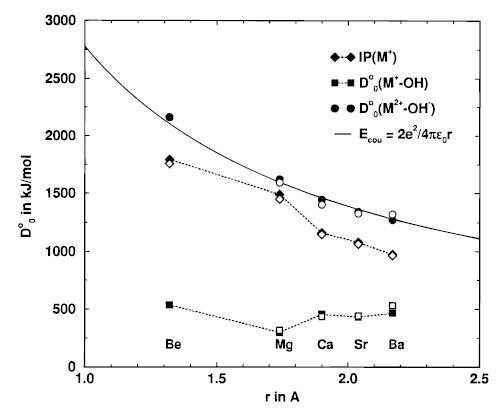
Experimental (open symbols) and calculated (filled symbols) values of IP(M⁺), D°₀(M⁺–OH), and D°₀(M²⁺–OH⁻) that are used in the thermochemical cycles (eqs 3 and 3’), as a function of the M–O1 distance in MOH⁺. The value of D°₀(M²⁺–OH⁻) smoothly follows the Coulomb energy of a double and a single charge at distance r (solid line).

Figure 4.

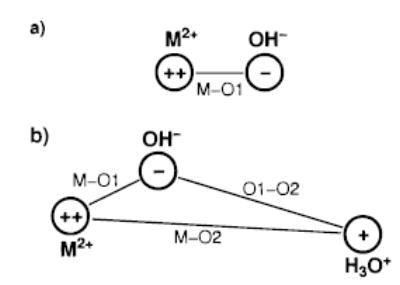
(a) MOH⁺ as an electrostatic complex of M²⁺ and OH⁻, with the charges located on M and O1. (b) TS2 as a M²⁺–OH⁻–H₃O⁺ salt-bridge structure with the charges located on M, O1, and O2.

The TS2 structure can be analyzed in a similar way. Figure 4b shows TS2 viewed as a salt-bridge arrangement with a double positive charge on the metal, a single negative charge on O1 representing OH⁻, and a single positive charge on O2 representing H₃O⁺. The reverse activation barrier of reaction 2 is the energy required to overcome the repulsion between MOH⁺ and H₃O⁺ before entering the attractive region of the salt-bridge structure. It is calculated from the B3LYP results as the energy difference between the products and TS2 (Table 8). E_cou is the Coulomb term in Kebarle’s work, here calculated as the Coulomb energy of two positive single charges at the M–O2 distance. The value for E_sb is calculated using a simple Coulomb potential for the charges shown in Figure 4b. The values of E_sb consist of the repulsion between a double charge at M and a single charge at O2, the attraction between the two single charges at O1 and O2, and the diminished attraction between M and O1 caused by the elongation of the M–O1 bond in TS2 as compared to that in free MOH⁺.

Table 8.

Reverse Activation Barrier of the Proton-Transfer Reaction M²⁺(H₂O)₂ → MOH⁺ + H₃O⁺, Calculated in Three Different Ways^a

M	B3LYP	Ecou	Esb
Be	380.7	567.3	700.1
Mg	198.6	259.3	193.6
Ca	204.7	247.8	196.5
Sr	189.9	232.1	175.2
Ba	180.5	222.4	165.5

^aB3LYP denotes the difference between TS2 and the products, E_cou is the Coulomb energy of two positive charges at the M–O2 distance, and E_sb is the Coulomb energy of H₃O⁺ estimated in a multipole environment according to Figure 4b and eq 8.

$$\begin{array}{l}{E}_{\text{sb}}=\frac{e^2}{4\pi {\varepsilon }_0}(\frac{2}{r(\text{M}-\text{O}2)}-\frac{1}{r(\text{O}1-\text{O}2)}-\frac{2}{r(\text{M}-\text{O}1)}+\\ \frac{2}{r{(\text{M}-\text{O}1)}_{{\text{MOH}}^{+}}})\end{array}$$ (8)

For beryllium, this approach applied to TS1 does not work since the proton transfer is not yet accomplished and the interaction between O2 and M is attractive rather than repulsive. For the other metals, E_cou is higher than the ab initio value by 40–50 kJ/mol, while E_sb is lower by less than 15 kJ/mol. This demonstrates that the Lewis formalism of integer charges localized on individual atoms can produce reasonably accurate results. The salt bridge lowers the reverse activation barrier due to the attraction between H₃O⁺ and OH⁻, and thereby reduces the activation barrier for the proton-transfer reaction 2. Therefore, we suggest the term “salt-bridge mechanism” for the reaction path depicted in Figure 1. Salt-bridges have been proposed to play a role in gas-phase H/D exchange²² and in producing specific cleavages after acidic residues in peptides and proteins.²³ Evidence for stable salt bridges in gas-phase peptides²⁴ and in protonated dimers of small molecules²⁵ has also been reported.

Proton-transfer reactions between a first- and a second-shell solvent molecule in small solvated metal ions with one charge have been observed previously.^{3c,g, 26} The salt-bridge mechanism may be common in these reactions as well. The charge on the metal remains unchanged, and a deprotonated solvent anion in the first and a protonated solvent cation in the second solvation shell are formed in a quasi-linear arrangement. Similar to ionic salts, this arrangement of charges may be energetically favored.

The results indicate that the second ionization potential of the metal is not the driving force for proton transfer in doubly charged metal–water clusters. The potential energy surface of the reaction is a function of distances between charged species determined primarily by the ionic radii of the metal. This is similar to the chemistry of metal ions in solids and in solution. These gas-phase proton-transfer reactions (reaction 2) may have counterparts in aqueous solution. In a simplified picture of diluted solutions of aluminum salts, hexacoordinated aluminum(III) goes from Al³⁺(H₂O)₆ in strongly acidic environment to Al(OH)₆³⁻ in strongly basic environment via AlOH²⁺(H₂O)₅, Al(OH)₂⁺(H₂O)₄, Al(OH)₃(H₂O)₃, Al(OH)₄⁻₍H₂O)₂, and Al(OH)₅²⁻(H₂O) at intermediate pH.27 Although the corresponding solution chemistry is much more complicated than the chemistry of these gas-phase clusters, and competing reactions involving several aluminum atoms are possible, the underlying chemical principles may be the same for certain reaction steps. The salt-bridge mechanism proposed for these gas-phase ions may be equally applicable in solution.

Charge transfer from the multiply charged ion to the neutral water molecule is not observed experimentally for any of the hydrated metals studied in this work.^5,19 Although the second or higher IP of a metal is always larger than the first, a charge transfer to a neutral is not necessarily more favored than for singly charged ions. In the latter case, there is typically no significant reverse activation barrier and the difference between the IPs of the ion and neutral is available to drive the reaction. For a charge transfer between a neutral and a multiply charged cation, the reverse activation barrier is significant.²⁸ A multiple charge has a stabilizing effect on a nearby ligand with respect to charge transfer. This is analogous to the kinetic stability of multiply protonated ions with respect to proton transfer.²⁹ If lower energy channels, such as in the present case, the proton-transfer reaction 2, are present, the charge-transfer reaction 5 is not significant. The experimental observation of Mg²⁺(H₂O)Ar_n by Velegrakis et al.³⁰ suggests that even Mg²⁺(H₂O) could be accessible in the experiment.

5. Conclusion

The reaction of dihydrated alkaline earth metal dications to form MOH⁺ and H₃O⁺ does not result in a significant change in the charge state of the metal. The correlation between IP(M⁺) and the occurrence of this reaction is only indirect. The reactivity of these hydrated ions is more directly correlated to the radius of the metal ion. The potential energy surface is predominantly determined by the Coulomb interactions, i.e., charge and distance, and these proton-transfer reactions can be quantitatively interpreted on the basis of simple ionic interactions. A key feature of these proton-transfer reactions is a salt-bridge structure of the form M²⁺–OH⁻–H₃O⁺ in the transition state. This salt-bridge structure lowers the activation energy for the proton-transfer process. Similar salt-bridge mechanisms may play an important role in proton-transfer reactions observed for other hydrated metal ions, as well as in completely different ionic reactions. The concept of ionic bonding, known from solutions and solids, in which integer charges are localized on individual atoms, seems to quantitatively model these gas-phase solvated ion reactions. The validity of these statements for more highly hydrated systems approaching solution chemistry has to be tested in the future.