Self-consistent determination of the transition state for protein folding: Application to a fibronectin type III domain

Abstract

We present a general approach in which theory and experiments are combined in an iterative manner to provide a detailed description of the transition state ensemble (TSE) for folding. The method is illustrated by applying it to TNfn3, a fibronectin type III domain protein. In the first iteration, a coarse-grained determination of the TSE is carried out by using a limited set of experimental φ values as constraints in a molecular dynamics sampling simulation. The resulting model of the TSE is used to determine the additional residues whose φ value measurement would provide the most information for refining the TSE. Successive iterations with an increasing number of φ value measurements are carried out until no further changes in the properties of the TSE are detected or there are no additional residues whose φ values can be measured. In the study of TNfn3 three iterations were necessary to achieve self-consistency. A retrospective application of the method can be used to determine the accuracy of the TSE results and to find “key residues” for folding, i.e., those that are most important for the formation of the TSE. The approach reported here is an efficient method for finding the structures that make up the TSEs for protein folding. Its use will improve future efforts for their experimental determination and refinement.

The protein engineering method (1) provides experimental information concerning the interactions of residues in the ensemble of conformations that make up the transition state for folding. The essential element of the method is the measurement of the ratio φ_i between the change in stability of the transition state, ΔΔG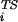, and that of the native state, ΔΔG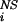, caused by the mutation of residue i. The experimental results have generally been interpreted by assuming that φ values near unity correspond to a locally native-like transition state ensemble (TSE) structure and φ values near zero to denatured regions. We show here how a much more detailed description of the TSE can be obtained from measured φ values and how an iterative approach can be used to assess the reliability of the resulting TSE. To determine the structures making up the TSE, we have developed an approach based on Monte Carlo or molecular dynamics sampling with a pseudoenergy function that restrains the ensemble to satisfy the experimental φ values (2, 3). The TSE is obtained by performing simulations in which the relative weight of the φ values and the molecular mechanics force field in the pseudoenergy function is varied so as to sample a broad range of structures compatible with the experimental data. A model for the TSE is made up of the subset of structures whose calculated average φ value is close to the measured one.

Unlike the native state, which is well represented by a set of very similar structures, such as those obtained by optimization procedures based on NMR data, the TSE is structurally heterogeneous. The method described in ref. 3 provides a description at near-atomic resolution of the conformations corresponding to the TSE, that is, the equilibrium distribution of conformations corresponding to the pseudoenergy function that includes the φ value restraints. By use of the method it has also been shown that the fold or architecture of the transition state can be obtained if the φ values of only a few residues are known (2–4). The contacts of these so-called “key residues” determine the network of interactions that define the TSE and its overall architecture. This observation prompted the present study in which an iterative procedure is introduced for optimizing the choice of φ values to be measured and for testing the convergence of the simulation results for the TSE. Because protein engineering is a rather demanding experimental technique, a reduction in the required number of measured φ values is a significant advance. One possible implementation of this approach would begin with φ value measurements for a set of residues that are key in the sense that they occupy a central position in the network of interactions that stabilize the native structure, e.g., as measured by the betweenness (4). Alternatively, φ values for a subset of residues based on their hydrophobic nature and/or their presence in the hydrophobic core can be used to start the iterative procedure. Once the TSE has been determined with the initial (limited) data, residues whose calculated φ values vary most within the ensemble of structures can be singled out as the best candidates for additional φ value measurements. In this way the convergence of the TSE can be evaluated in a self-consistent manner and the required number of φ value measurements can be reduced.

Application of the approach to the fibronectin type III domain of tenascin (TNfn3) is particularly revealing because the experimental φ values are generally low, suggesting a broad ensemble of structures that contribute to the transition state. Moreover a comparison can be made between the results that were inferred from the φ values per se and the conclusions from the present approach. The iterative procedure shows that the TSE has well-defined features that can be determined by using a set of 30 experimental φ values. This set of 30 φ values, which corresponds to one-third of the total number of residues, is complete in the sense that additional φ values would not change the essential features of the TSE. We also show that four carefully chosen φ values are sufficient for a coarse-grained description of the structure of the TSE. The specific example of TNfn3 illustrates how the iterative method can be used to determine and evaluate the TSEs for protein folding.

Methods

System and Model.

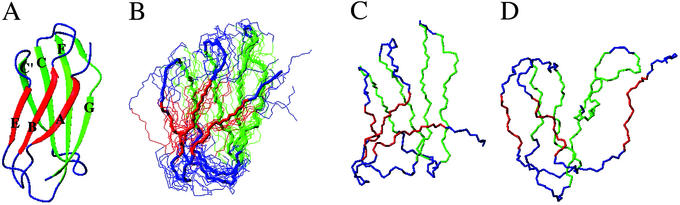
The third fibronectin type III domain of human tenascin, TNfn3, is a single-domain, β-sandwich protein with two β-sheets enclosing a hydrophobic core composed of residues from both β-sheets. The N-terminal β-sheet is composed of strands A-B-E, and the C-terminal β-sheet is composed of strands C′-C-F-G. The crystal structure of TNfn3 (5) (entry 1TEN in the Protein Data Bank) has been used as the starting and reference structure** in all of the simulations and calculations; it is shown in Fig. 1A.

Figure 1.

(A) NMR structure of TNfn3. The secondary structure is represented as ribbon and computed with dssp (21). The figure was drawn with the program molmol (22). The TNfn3 secondary structure elements are β-strand A (residues 5–10), B (residues 17–22), C (residues 30–37), C′ (residues 45–50), E (residues 55–58), F (residues 66–75), and G (residues 78–88); residues between these regions are parts of loops. See figure 4 of ref. 6 for the identity and position of mutated residues. (B) Eight most representative structures (thin line) of the TSE and their average structure (thick line). (C and D) A native-like structure (C) and a highly non-native structure (D), both compatible with the experimental restraints. In all cases the fold is native-like and the residues of the nucleus are in contact.

TNfn3 folds and unfolds in a two-state fashion over a wide range of external conditions (8). A large set of φ values of TNfn3 has been determined and published (6); it includes 48 mutations at 32 sites in the core and loop regions of TNfn3. All mutations were selected as nondisruptive deletions that did not introduce new interactions. If more than one mutation was made at a single site we used the φ values corresponding to the largest deletion (e.g., I→A instead of I→V, T→A instead of T→S, etc.), which is expected to yield the most meaningful result. Because in the calculations all side-chain interactions were considered, the correct change in the number of contacts is included. We disregarded the information provided by negative φ values because they cannot be interpreted simply in terms of the fraction of native contacts used in the model. The total number of previously published φ values that remains is 26.

From the analysis of these φ values, a model in which a “ring” involving four residues in different strands in both sheets forms early in folding was proposed (6). This ring appears to be a common feature of Ig-like proteins (9, 11).

Microscopic Definition of φ Values.

For a configuration at time t the calculated φ value of residue i was defined as

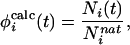1

where N_i is the number of native side-chain contacts made by residue i. A contact is defined as pair of atoms <5.5 Å apart and at least two residues apart (i, i+2) along the sequence. A definition based on side-chain contacts is appropriate because experimental φ values are primarily a measure of the loss of side-chain contacts at the transition state, relative to the native state. Although the microscopic definition of φ values used here is based on the fractional number of native contacts and not the measured free energy ratios, we have shown that there is a good correlation between these two quantities for native states and for transition states that are relatively close to the native state (10). Moreover, a good correlation has been demonstrated for mutations in this protein between loss of stability and loss of hydrophobic side-chain contacts within ≈6 Å (11). In any case, only nonpolar φ values are considered in the present study (6). Longer-range interactions might result from polar side chains, but even for such residues it has been shown that the interaction cutoff is ≈6 Å (12).

An approximation made in the model is that there are no significant native contacts in the denatured state. No data on this question are available for TNfn3. In a number of other proteins, recent measurement by NMR suggests that some residual structure, possibly with native contacts, is present. This would require some change in the interpretation of the φ values, so that the true TSE would be somewhat more native-like in the regions around the specific residues involved.

Sampling of TSE with the φ Value Restraints.

Molecular dynamics simulations were performed by using an all-atom model of the protein (13, 14) and an implicit model for the solvent (EEF1) (15) that provides a potential-of-mean-force description of the solvent. The TSE is sampled by introducing a small energy perturbation ρ(t) that forces the system to follow trajectories that, starting from the native state, lead to decreasing deviations between the experimental and calculated φ values. The perturbation is defined as

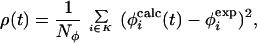2

where K is the list of the N_φ available experimental φ values, φ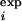. In brief, ρ is the mean square deviation between φ^exp and φ^calc. The TSE is reached by introducing a bias in the dynamics that gradually decreases the quantity ρ to near zero over a period of 2 ns. Starting from this transition state-like conformation, the TSE is sampled by performing 1-ns simulations at 300 K and at higher temperatures in the presence of the EEF1 potential and a term proportional to ρ(t) that restrains φ^calc to remain in the neighborhood of φ^exp.

An artificial sampling “temperature” is introduced as a parameter to weigh the contribution of the EEF1 potential relative to the restraining potential; the weight of the latter is such that ρ(t) remains small (≤0.03) at all temperatures. The temperature is varied between 300 and 780 K to sample states that range from being quite native-like to being rather denatured. To select those corresponding to the TSE, we assume that the average φ^exp value, 〈φ^exp〉, for the residues that were mutated is a measure of the overall degree of nativeness of the transition state. Specifically, we select structures for the TSE that have 〈φ^calc〉 (computed over all residues, measured or not) such that 0.7〈φ^exp〉 ≤ 〈φ^calc〉 ≤ 〈φ^exp〉. This criterion for the TSE leads to an ensemble that is considerably narrower than that obtained by using all of the structures that satisfy the φ value restraints. Thus, we are able to obtain a good coverage of the conformation space without including unrealistic structures in the TSE. We allow for 〈φ^calc〉 to be somewhat smaller than 〈φ^exp〉 to account for the usual bias in the choice of the mutations, which are selected to probe regions that are expected to be most structured in the TSE.

Protein Engineering and Kinetic Experiments.

The mutations were introduced and the protein was expressed as described (6). The effect of mutation on stability, the refolding rate constants, and the φ values were extrapolated at 0 M denaturant as described (6). All experiments were performed at pH 5 and 25°C.

Results

Because a large number of φ values had been determined experimentally when this study was initiated, we begin with this set and iterate to completion. However, we also investigate whether a significantly smaller number of φ values give sufficient information that could have been used as a starting point for the iterative procedure.

Determination of the TSE: The Iterative Procedure.

First iteration.

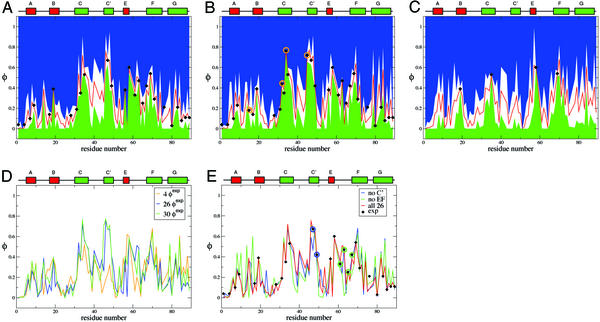
The first determination of the TSE was carried out with the 26 published φ^exp (6) (see Methods). In Fig. 2A the calculated φ values for the TSE of TNfn3 are plotted; the ranges of the calculated values are also indicated. The calculated values are very close to the experimental ones. The absolute value of the maximum deviation is 0.04 and ρ = 0.018, which is lower than the typical experimental errors of the φ values reported by Hamill et al. (6). For residues that have not been mutated, the calculated φ values provide a prediction, and the standard deviation of the predicted values measures the variability of the fractions of native contacts in the TSE. The latter indicates how precisely the TSE is determined by the φ value restraints. If the variability is small (i.e., if the width of the white region bound by the blue and the green region in Fig. 2A is small), the available set of φ^exp determines precisely the fraction of native contacts that a residue has in the TSE. By contrast, the residues that have a large uncertainty in their calculated φ values are good candidates for additional φ value measurements.

Figure 2.

Experimental and calculated φ values for the TSE of TNfn3. (A) For the initial set of 26 φ^exp (first iteration). (B) For the set of 30 φ^exp (third and last iterations); the additional φ^exp are indicated by a circle. (C) φ values calculated by using only key residues. (D) Comparison of φ^calc obtained in the various iterations indicated. (E) φ values calculated by using structurally related subsets of the available φ^exp. The diamonds show the experimental φ values. The red curve is the average calculated φ value, and the blue and green curves represent the average ±1 SD.

A set of seven additional residues were selected in this way, i.e., from those with large variability; they are T15, E32, T34, I37, V40, R44, and T45. From Fig. 2A, there are other residues (e.g., in the region R75-G76) that could have also been chosen. All of these residues were mutated to alanine and for those (T15, E32, T34, and T45, see Table 1) having a large enough ΔΔG_D−N, experiments were undertaken to measure the φ values.

Table 1.

Additional mutations and experimental φ values

Mutant	ΔΔGD–N	ΔΔGD–‡	φexp
T15A	1.39 ± 0.18	0.25 ± 0.01	0.2 ± 0.1
E32A	1.08 ± 0.15	0.48 ± 0.08	0.4 ± 0.1
T34A	0.85 ± 0.24	0.65 ± 0.12	0.8 ± 0.3
I37A	0.17 ± 0.20	—	—
V40A	0.11 ± 0.16	—	—
R44A	0.35 ± 0.16	—	—
T45A	1.04 ± 0.16	0.75 ± 0.25	0.8 ± 0.3

Free energy differences in kcal⋅mol⁻¹. 

For three of these residues (T15, E32, and T34), the measured φ^exp (φ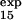 = 0.2 ± 0.1, φ 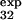= 0.4 ± 0.1, and φ 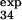= 0.8 ± 0.3) is within the standard deviation of the prediction (φ 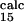= 0.2 ± 0.2, φ 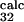= 0.5 ± 0.2, and φ 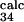= 0.7 ± 0.2). Interestingly, E32 and T34, both pointing outward, have a large φ^exp and φ^calc, although the mutation L33A in strand C, which deletes interactions in the core of the protein, gave φ^exp = 0.35 ± 0.01 (6). Analysis of the TSE shows that the large φ value of both residues E32 and T34 is caused mainly by the persistence of the interactions with the outward pointing side chains of residues T46 and D48 in strand C′. For the other residue, T45, for which additional experimental data were obtained, the agreement between experiment and simulation is less good, with large errors in both experimental and the theoretical estimations (φ 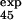= 0.8 ± 0.3 and φ 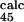= 0.3 ± 0.2). As we shall see, the agreement improves significantly in the following iterations.

Second iteration.

In the second iteration, the TSE of TNfn3 was determined by the same procedure as in the first iteration, but included a larger set of φ^exp values, i.e., the initial 26 plus three new ones (T15, E32, and T34). The restraints caused by the three additional residues decrease the size of the region of conformation space corresponding to the TSE, i.e., there is a significantly smaller number of conformations where all of the experimental φ values are simultaneously satisfied. The two profiles are similar but not identical (see Fig. 2D). The correlation between the two sets of calculated φ values is 0.85. It is interesting that for residue T45 we now predict a φ value of 0.71 ± 0.06, in excellent agreement with experiment (φ^exp = 0.72). The reason is that 70% of the contacts with T35 are now preserved, an indirect effect caused by the restraints on residues E32 and T34.

Third iteration.

A third iteration was done by using one additional result, φ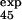, as a restraint, i.e., with a set of 30 experimental φ values. The coefficient of correlation between the set of φ^calc computed in the second and third iterations is 0.99. The estimated φ values and uncertainties in the third iteration are shown in Fig. 2B. The standard deviations are generally small (0.13 on average), although some regions (e.g., residues 40–45) have larger uncertainties, which would require additional φ value measurements that appear to be difficult experimentally; i.e., because they tend to be solvent exposed residues, it was anticipated that the ΔΔG_D−N would be too low for a reliable φ value to be obtained.

Also, as shown in Table 2, the macroscopic properties of the TSE at successive iterations are very similar, supporting the idea that the procedure has converged approximately.

Table 2.

Properties of the TS for TNfn3

N (φexp)	RMSD, Å	Rg, Å	S, Å	〈φcalc〉	〈φexp〉
26	7.1 (1.3)	14.09 (0.40)	6,800 (400)	0.234	0.28
29 (26 + 3 new)	6.9 (1.7)	14.18 (0.57)	6,900 (600)	0.245	0.30
30 (26 + 4 new)	6.4 (1.4)	14.07 (0.49)	6,800 (500)	0.260	0.31

The average 〈φ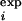〉 is computed from the residues for which there is a φ^exp, while the average 〈φ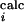〉 is computed from all the residues that have a non-zero number of side-chain native contacts. RMSD is the rms distance from the native conformation, R_g is the radius of gyration, and S is the solvent accessible surface area. For comparison, in the native state R_g is 13 Å and S is 5,250 Ų. The number reported in parentheses corresponds to 1 SD. 

The Inverse Procedure: Determination of the Key Residues.

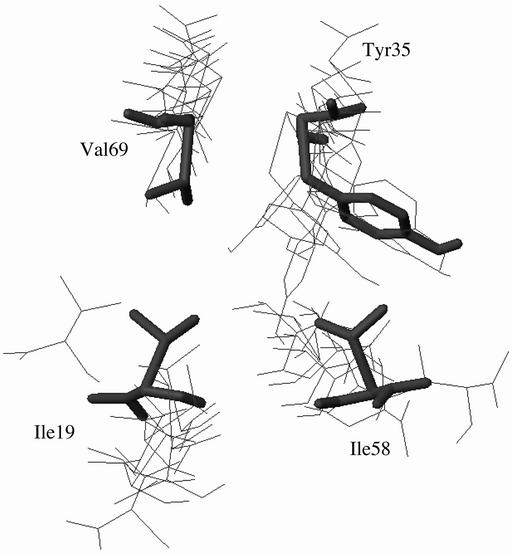
The iterative procedure described above can be reversed, in that one progressively reduces the number of φ values used as restraints in the determination of the TSE by molecular dynamics simulations. We have used such an “inverse procedure” to verify whether the residues identified by Hamill et al. (6) as forming the folding nucleus (I19, Y35, I58, and V69) are key residues in the sense proposed by Vendruscolo et al. (2). As in ref. 2, we determine whether use of the φ values for the key residues alone specifies the overall fold of the TSE and gives information about the additional φ values to be measured.

We calculated the TSE by using only the φ^exp values of the four residues identified by Hamill et al. (6) as those making up the folding nucleus (I19, Y35, I58, and V69). The results are shown in Table 3. The overall properties of the TSE are very similar to those determined by using the entire set of 30 experimental φ values, as is the architecture of the TSE, even if the coefficient of correlation between the full set of φ^exp and the φ^calc is only 0.5.

Table 3.

Properties of the TS for TNfn3 obtained by using subsets of the experimental φ^exp available

N (φexp)	RMSD	Rg, Å	S, Å	〈φcalc〉
4 (key)	6.9 (1.0)	14.03 (0.42)	6,680 (380)	0.230
24 no-C′	6.6 (0.9)	13.98 (0.28)	6,840 (310)	0.244
22 no-E-F	7.0 (1.3)	14.03 (0.42)	6,990 (440)	0.238

See legend to Table 2. 

The rms distance (RMSD) between the mean structures in the two cases is ≈3 Å. This is of particular interest because the φ values of the key residues are not large, 0.4–0.6, much lower than the ones of AcP, in the range of 0.76–0.98 (16), so the restraints are not very strong. Nevertheless, when the restraints are considered together with the chain connectivity and degree of compactness of the protein, the overall architecture and significant details of the structure are defined. Specifically, the φ values of these four residues are sufficient to specify the strand register and the central packing of the core, essential elements of the Ig-like fold.

Fig. 2C shows the profile of φ values obtained with four key residues. The uncertainties in the φ values are much larger than in Fig. 2A so that additional φ^exp are needed to obtain a precisely defined TSE. It is interesting to note that a simulation without φ^exp of residue I58 leads to a significantly more diffuse TSE (RMSD ≃10 Å).

Properties of the TSE: General Aspects.

The conformations making up the self-consistent TSE, including all 30 experimental φ values as restraints, were clustered by using a 3-Å cutoff (3). Only cluster centers with at least six structures are considered in the analysis; there are 59 such clusters with the largest one including 81 structures. Some of these structures are very native-like and others are rather unfolded, even though they are all consistent with the experimental φ values, i.e., ρ is <0.003. These structures are quite heterogeneous in terms of RMSD from the native structure (between 4.5 and 12 Å), radius of gyration, and solvent-exposed surface area (see Table 2).

Despite the heterogeneity of the TSE the contributing conformations generally have a well-defined native-like fold (see Fig. 1A). The average structures of the eight most populated cluster centers (each with at least 20 members) were analyzed (Fig. 1B). The eight cluster centers have a backbone RMSD from the native structure in the range of 5–10 Å and a mean increase in solvent-accessible surface area of ≈30%. This finding agrees with the increase in solvent-accessible surface determined from measured m values (17). Because the mutations did not change the equilibrium m value (6), it appears that the TSE was not globally displaced in this study, in contrast to what happens in some other proteins (18). Representative structures of the most native-like and most unfolded cluster centers have properties that vary considerably. In Fig. 1 C and D the two structures with the lowest and the largest RMSDs from the native structure are shown. Fig. 1C is ≈4.5 Å RMSD from the native structure, and its accessible surface is only ≈10% larger than the native value, whereas the radius of gyration is very close to the native one. By contrast, the structure in Fig. 1D is >12 Å RMSD from native, and its accessible surface is ≈70% larger and the radius of gyration is 33% larger. Nevertheless, both structures have a native-like fold.

The nucleus residues (I19 in the B strand, Y35 in the C strand, I58 in the E strand, and V69 in the F strand) are in contact at the center of all of the structures. The A-B-E sheet is largely disordered, with the A strand being almost completely disconnected in most structures, and in most of the structures few, if any, hydrogen bonds are present between the B and E strands. The C′-C-F-G sheet is significantly more structured, and more hydrogen bonds are formed. The central strands are more ordered than the edge stands. The C-C′ and F-G loops are disordered in all cases. Where there are hydrogen bonds between the strands, they are centered around the nucleus residues: hydrogen bonding is found close to the nucleus and lost as the strands approach the turns. From an analysis of each of the eight most representative structures it appears that the interactions of the nucleus residues establish both the register of the strands within a sheet (i.e., whatever hydrogen bonds are formed are native) and the packing of one β-sheet on the other.

Comparison with Experimental Analysis.

In most experimental studies, the φ values are mapped onto the native structure and, based on that, structural features of the TSE are suggested. For a protein like TNfn3 where there are no high φ values (I19, a proposed nucleus residue, has a φ value of only 0.39) this procedure is less meaningful than for proteins where the φ values are closer to unity. The calculated structures for the TSE described here allow some of the suggestions from the experimental study (6) to be tested directly. Although the main conclusions are supported, the simulations provide significant information concerning the structural ensemble making up the transition state.

The Folding Nucleus.

In the original study (6) the residues forming the folding nucleus were selected as those with the highest φ values in the B, C, E, and F strands and on the basis that they were in contact with each other. Using the inverse approach, we showed above that residues I19, Y35, I58, and V69 do indeed constitute a possible folding nucleus, in the sense that the experimental φ values of these residues are sufficient to determine a TSE, which is a good approximation to that obtained from the full set of φ values. It was proposed (6) that the nucleus residues form a closed ring of contacts in the transition state, the inference being that they were all equally important in the formation of the transition state. Although the nucleus residues remain in close contact in all structures, they are more correctly described as forming an open ring or a “horseshoe-shaped” arrangement. The nucleus residues are shown in Fig. 3 for the eight structures in Fig. 1B. In six of the eight clusters the contacts between the nucleus residues in the B and F strands are essentially lost in the TSE, and the distance between these residues is significantly larger than in the native state, e.g., the side-chain atoms of I19 and V69, which are in contact in the native state, can be as far apart as 13 Å in the TSE. In another cluster, the B-F contacts are retained and the interactions between the B and E strands are lost. In most of the structures there are contacts across the open ring, between the C and F strands or between the B and C strands that keep the open ring compact. The strongest contacts in the open ring structure are those involving the largest residue (Y35) in the nucleus, which maintains a large number of interactions with I58 and I69. It was also suggested (6) that W21, which could not be mutated because it was used as fluorescent probe, would not have a higher φ value than I19 and the simulations bear this out; a φ value of ≈0.1 is found for W21.

Figure 3.

Four-residue ring in the TSE of TNfn3. Thick line, native. Thin line, the structures shown in Fig. 1B.

Robustness of the Method.

To demonstrate that the approach presented here is robust against experimental errors and limited rearrangements of the structure on mutation, we have made some test calculations. A random change of ±0.1 of the φ^exp values did not affect the results presented in Tables 2 and 3, within the error bars. Drastic perturbations do change the results significantly. For example, use of a randomly assigned set of φ values between 0 and 0.6 (the experimental range) yielded a very different TSE. The resulting TSE corresponds to a diffuse, compact structure with no clear folding nucleus, indicating that crucial information about the folding process has been lost.

The peripheral A and G strands.

On the basis of the analysis of the φ values (0.13 on average for six residues), it was proposed that the A and G strands were unstructured in the TSE (36). In the present study, we found that the A strand is detached almost completely from the B strand in all but the most native-like of the clusters. However, the G strand, also characterized by low (0.1–0.2) φ values, remains attached to the F strand in most of the structures, fraying toward the C terminus. The simulations thus illustrate how, even when the φ values are very low, a significant ordering may persist in the TSE.

The C′ strand.

It was proposed that, despite having large experimental φ values, I47 and L49 should not be considered as part of the nucleus, but rather that the C′ strand is “obliged” to fold by formation of the nucleus (6). The calculated TSE shows that the C′ strand is the least structured in the C′-C-F-G β-sheet and that it forms contacts and H bonds with the C strand only close to the nucleus. To test the “obligatory packing” hypothesis, a series of simulations, called no-C′, were performed. In these simulations the φ values of the C′ strands were not used as restraints. The results of the no-C′ simulations are shown in Fig. 2E, and the macroscopic properties of the TSE are shown in Table 3. Thus, it is possible to correctly predict its φ^exp, confirming the suggestion in ref. 6.

The B-C and E-F loops.

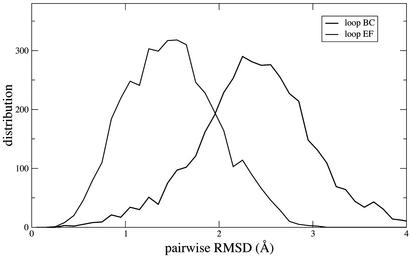
The experimental φ values in the E-F loop are significantly higher than those in the B-C loop. Because these loops constitute the inter-sheet connections it had been proposed (19) that they might be important for the nucleation of folding. In the experimental φ value study (6) it was suggested, by contrast, that the E-F loop was more structured than the B-C loop and that it was constrained to be so by the closeness of the folding nucleus. The first suggestion is confirmed by an analysis of the structural variability in the loops E-F and B-C in the TSE. We isolated these loops from the rest of the protein, compared every pair of structures, and clustered similar ones together (with a cutoff of 1 Å). In Fig. 4 the distribution of the pairwise RMSD between all pairs of structures is shown. The B-C loop of TNfn3 have the largest RMSD, whereas the others are similar, although that of the E-F loop in TNfn3 is the narrowest.

Figure 4.

Distribution of the pairwise RMSD between loop structures. Results for loops B-C and E-F are shown.

To follow up the second suggestion we performed an additional set of simulations, called no-E-F, where the φ^exp of the mutations L61A, P63A, T65A, and Y67F (in loop E-F and strand F) were disregarded. In this case, whereas low φ values of L61 and T65 (φ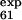 = 0.33 and φ 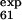= 0.25) are correctly predicted, the larger ones (φ 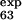= 0.47 and φ 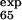= 0.42) are predicted to be small (φ 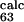= 0.02 and φ 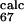= 0.23). This means that without the information provided by the φ^exp for residues L61, P63, T65, and Y67 the loop E-F is predicted to be disordered in the TSE. Thus, these residues are more important than was suggested in ref. 6.

The no-C′ and the no-E-F simulations show that the disregarded residues are not key residues because the overall φ^calc profile is little altered by their neglect; the coefficient of correlation between the full set of φ^exp and φ^calc is 0.93 and 0.81 for no-C and no-E-F, respectively.

Transition state energetics.

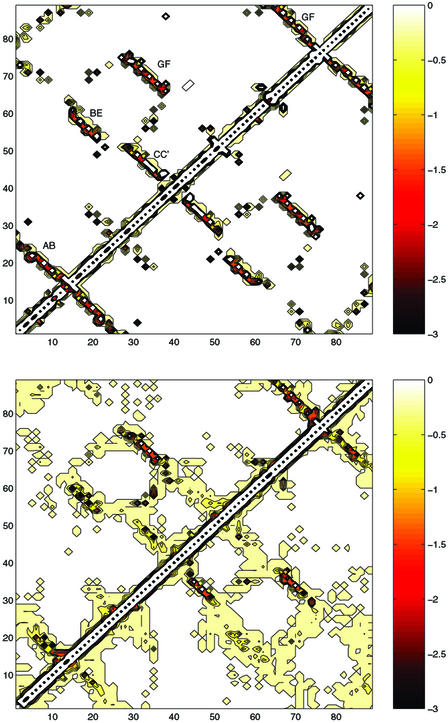
An energy map (Fig. 5) is a useful representation of the network of pairwise interactions (3). It illustrates in a clear way that certain native interactions are preserved in the transition state while others are lost. Non-native interactions do occur in the energy maps of TNfn3. However, in most cases, the non-native interactions appear as a consequence of the fact that native interactions are smeared out over a broader region in the TSE than in the native state. In other words, most of the non-native interactions are small and between residues that are not far apart in the native structure. This finding confirms that the overall native architecture is to a large extent preserved in the TSE and that non-native interactions contribute, although to a small extent. In the TSE of TNfn3, the largest non-native interactions are made by residues K23 (with several residues), Y35 (with I19 and Y56), and R75 (with S80 and N81).

Figure 5.

Energy maps in the native state (Upper) and the TSE (Lower), both calculated with largest number of φ^exp available (upper part of the matrix) and with only the four key residues (lower part of the matrix). This is a graphical representation of interaction matrices where the element I, J, is the EEF1 interaction between residues I and J. The scale of the energies is indicated; all values are in kcal/mol.

It is instructive to observe the similarity of the energy maps obtained with all 30 φ^exp available (upper part of the matrix in Fig. 5) and with only the four key residues (lower part of the matrix in Fig. 5), which supports the similarity of the two TSEs.

Conclusions

We have presented a self-consistent iterative procedure based on simulations and experiments for determining the structure of the transition state for protein folding. In the first iteration, a set of φ values is used to determine a coarse-grained TSE. To select the mutations, one possible choice is the graph theoretical betweenness criterion for the native state (4), supplemented by visual inspection to select core residues. Use of the analysis of conservation in multiple sequence alignment (20) would also be of interest. Having determined the TSE with the initial set of measured φ values, analysis of the variation of the calculated φ values throughout the structure can then be used to suggest the additional φ values that are likely to be most effective in improving the TSE. This procedure is then iterated until convergence (when no further change in the properties of the TSE is detected) or when no additional residues can be mutated. Test applications to TNfn3 demonstrates the efficacy and the robustness of the approach. Further, a detailed analysis of the converged TSE for TNfn3 shows where uncertainties still exist and provides a criterion for the precision of the TSE determination. Because TNfn3 had been studied experimentally before the simulations, a comparison between the conclusions from the simulations and those based on the native structure and the φ value measurements, per se, clearly demonstrates that additional information is obtained from the simulations.

Abbreviations

TSE

transition state ensemble

RMSD

rms distance